The paper addresses the problem of providing a framework and an algorithm to evaluate super and sub replicating prices, for European options, having interesting risk-reward characteristics. A general operational framework is put forward and illustrated by an algorithmic construction of one-dimensional models for option pricing. Asset models are defined based on a class of investors characterized by how they operate on financial data leading to potential portfolio rebalances. Once observable variables are selected for modeling, necessary conditions constraining these variables and resulting from the operational setup are derived. Future uncertainty is then reflected in the construction of combinatorial trajectory spaces satisfying such constraints. As the risky asset unfolds, it can be tested dynamically for the validity of observable sufficient conditions that rigorously imply the validity of the models. The paper describes the resulting algorithmic construction of such trajectory spaces and, in the absence of probability assumptions, a minmax algorithm that is available to evaluate the super and sub replicating prices.
1.
Introduction
It is well known (see Eberlein and Jacod (1997) and Carassus et al. (2006)) that a large class of stochastic models put forward in the literature, and in order to obtain financial options' prices, provide non informative super and sub replicating bounds. More specifically, these bounds degenerate into absolute bounds. The latter refers to bounds that hold for all possible no arbitrage models and hence, are non informative (Merton (1973)).
Here, we address the following problem: can we justify simple models for asset evolution where we can evaluate sub and super replication prices and, in such a way that these quantities have useful risk-rewards characteristics?
An algorithmic construction, and its mathematical justification, that evaluates such bounds has already been provided in Degano et al. (2018). The said algorithm operates in a general probability-free context. To motivate such a setting, we point out that the support of an stochastic process is an offshoot of its assumed probability distribution and implicitly incorporates several analytical constraints. As such, it can include paths which can never appear as a rebalancing stock value (e.g. Brownian Motion has infinite speed). One speculates, from our perspective, that this latter feature is the cause for worst case bounds to degenerate into absolute bounds.
The issue at stake is the meaning of a price provided by a stochastic model (e.g. the Black and Scholes model): can you superhedge pathwise (in particular perfectly hedge) with such a price? The answer is no and this is so for several reasons: the price assumes continuous time rebalancing, market conditions for the applicability of the model are not spelled out, it is not clear how and when unfolding chart paths will correspond to a process's path, etc. The same issues are also present when superhedging is replaced by risk-taking investment, the above list of reasons will make the meaning of the model's profit and loss profile unclear. In this paper, we propose models that are robust, the superhedging property is then expected to be uphold for future unfolding trajectories. Superhedging is what you aim for as the cheaper alternative of exact hedging is not available given that real markets are incomplete (we are not allowing to use options for hedging). So it boils to a question on how robust and realistic the proposed models are and how tight the computed prices are. The whole paper is an attempt to address these issues.
The above reasoning suggests to place emphasis in, well justified, scenario construction as a prior step to imposing a probability distribution. Proceeding with this motivation, we show, by example, models with realistic bounds and useful risk-reward characteristics. The paper Carassus and Vargiolu (2018), using a completely different approach but emphasizing properties of the support of the process, does provide examples of useful price bounds. On the other hand, Kahalé (2017) employs convex programming for the estimation of bounds in a context of trading with a larger pool of assets.
We provide an implementation of the general algorithm from Degano et al. (2018). Most importantly, we put forward a general methodology, based on financial operations, observations and worst case estimation, to algorithmically construct a non-probabilistic asset model evolution. We show, via simple examples, how an operational approach based on observable variables can be put to work to price an option written on a single risky asset. The paper could be considered to provide a proof of concept by introducing an alternative approach to asset model construction and it is here illustrated in specific models. The methodology is general as it is based on constructing scenarios (trajectories), from a worst case perspective, and superhedging a future obligation. The mathematical framework is presented in Ferrando et al. (2019) and Degano et al. (2018). The financial setting is the most basic one, namely a riskless bank account paying zero interest rates and a risky asset with no transaction costs (in particular there is no bid-ask spread). The goal is to define models based on observable quantities that relate directly to a class of investors interested in objectively gauging the market price of a European option Z written on the asset. For simplicity we restrict ourselves to path independent European options. No analytical or probabilistic assumptions are required; the basic modeling object, to be constructed, is a set of trajectories S. The algorithmic construction and justification for the trajectory sets is the main thrust of the paper. It is known (Degano et al. (2018)) that, under some general conditions, knowledge of S allows the evaluation of lower and upper bounds for the option's price. In the absence of a probabilistic structure, these bounds are defined via a minmax optimization giving sublinear/superlinear operators acting on general functions. The upper bound represents the minimal investment required for the existence of a portfolio that superhedges the option for each trajectory S∈S (with a dual meaning for the lower bound). Section 2 summarizes the notions and results that we use from Degano et al. (2018). We recall that worst option bounds in a stochastic setting can be obtained by considering all equivalent martingale measures ((Föllmer and Schied (2013)).
The paper constructs trajectory sets S via combinatorial definitions, this is in contrast to the modeling with random paths from a stochastic process. The trajectory sets are obtained by imposing constraints that in turn correspond to how a class of investors sample a financial chart and how they rebalance their portfolios as a response to changes of their data summaries. We allow for all possible trajectories satisfying the said constraints. The constructions naturally rely on operational constraints and observable quantities, the latter are estimated via a worst case methodology; on this topic we refer to Sniedovich (2016) for a general discussion (we do not rely on any specifics of that paper).
Expressed in other words: we describe an operational setup that provides a model for chart values x(ti) and times ti at which investors rebalance their portfolios. Such setting is based on observable variables that result from sampling a given chart and the ensuing portfolio rebalances. Trajectory sets model the times ti and the values x(ti) plus any other relevant variables that restrict the future manifold of trajectories (in this paper we concentrate on the variation but other possibilities could be incorporated as well). The trajectory construction is described by an algorithm.
There could be at least two quick criticisms to the setting outlined above; we deal with them briefly now and offer the rest of the paper as additional arguments. i) the models are subjective as they are investor dependent and so, in this way, are quite idiosyncratic. The proposed models are not subjective as they depend on objective actions, namely: specific sampling of charts, accumulation of quantities and portfolio rebalances as a response to values of observed variables. These actions define, implicitly, a nonempty class of investors. Our assumptions only involve results from measurements and operations, both allow for a precise discussion on how and when an unfolding chart x(t) may fail to be associated to some S∈S. In particular, the models do not intend to reproduce option's market prices (which may require considering multiple classes of investors and their bets on the risky asset) but to provide a particular investor class with an objective tool to assess risk-reward alternatives. ii) the combinatorial definition (i.e. considering all possible cases), used to construct trajectory sets based on worst case estimation, will produce unrealistic option prices. Clearly, the obtained option bounds could be too wide but, we argue, this feature will depend on the relevance of the proposed trajectory set. We show, by example, that the bounds we obtain for some models are realistic when compared to market prices. In fact, in the proposed type Ⅱ models, we isolate a specific feature, based on a general property that can naturally be incorporated in any model construction, that restricts the effect of a worst case estimated parameter propagating into the price bounds' spread (see Section 11). Moreover, the fundamental risk-reward alternative, in the proposed setting, can be analyzed objectively given that we only rely on observable quantities. That is, one can know the empirical implications on risk and reward due to specific observable conditions not being satisfied by the unfolding chart. This is not the case in the usual modeling with stochastic processes in finance. As an example, we indicate the difficulty in the analysis of parameter estimation and the unknown logical repercussions of calibrating to market values (e.g. the use of implied volatility, see Section 9.3.5 in J.Y. Campbell and MacKinlay (1997) as well as Schoutens et al. (2006)).
A third criticism relates to robustness of worst case estimation; this is an empirical concern that crucially depends on the relevance of the chosen model variables. We make specific comments on this issue at appropriate times along the paper, see for example Sections 6.3 and 9.2.
The approach does not preclude adding probabilities to the models; the methodology introduces possible future events prior to probabilities. Once a trajectory space is in place, if deemed appropriate, probabilities can be added a posteriori. In the case of a continuous time stochastic process model {Xt}, one could set x(t)=Xt(w) and consider that the samples x(ti) are given by a sequence of, investor dependent, stopping times {τi}; that is, x(ti)=Xτi(w)(w). Our approach dispenses with any modeling of x(t), in particular, it avoids unnecessary implicit assumptions related to the stochastic process {Xt}.
Chart paths are observable but are not uniquely defined, e.g. their values will depend on the sampling frequency. In our models, a sampled trajectory uniquely emerges as a result of restricting ourselves to a class of investors whose operations act as preconditions resulting on the observed samples. This is analogous to a measurement setup in physics. The basic modeling ingredients are trajectory coordinates values Si and times Ti associated to portfolio rebalances. The paper shows by example that there are interesting ways to construct trajectory sets with relevant financial features that produce models supporting a rigorous risk-reward analysis.
Noise driven stochastic models provide access to a powerful stochastic calculus and are put to good use to model an array of important financial situations (e.g. Brigo and Mercurio (2006)). From our point of view, a deficiency in the foundations of that modeling approach is that the sources of uncertainty (noise) appearing in the modeling equations are not, in the majority of cases, empirically linked to an actual phenomena. Therefore, repercussions on the stochastic model due to changing market conditions (e.g. non stationary effects) are difficult to detect. This foundational deficiency undermines the meaning of financial implications dependent on the underlying model. One speculates that the proliferation of asset models in finance indicates the lack of general, external, criteria to asses their suitability. Justification of some of the proposed models is then sought in statistics but, without external criteria of validity, a moderately large number of modeling assumptions provides unreliable conclusions. We refer to Pfleiderer (2014) for a general (critical) discussion of models in finance and economics. We are aware of Feng et al. (2012), and related literature, were attempts are made to link investment behaviors in agent based models with stochastic emerging phenomena. We also remark on the economic literature on rule-based decisions (see Gilboa (2009)).
In contrast to the above described situation, we use the proposed methodology to establish rigorous results (see Section 6) showing when the models will succeed. The results allow to detect dynamically, i.e. as the chart unfolds, when hypothesis, required for validity of the said results, could fail. In this way we establish objective conditions implying falsifiable models.
The paper uses some overlapping of explanations across different, but related, sections. In this way the formal definitions of quantities, being them observable features or mathematical variables, is given an empirical meaning allowing to appreciate their roles in the constructions. In order to follow several of our arguments, it is crucial to keep in mind the empirical meaning of the variables used in the trajectory set construction.
The presentation is organized as follows, Section 2 introduces some notation and basic notions needed from the general framework from Ferrando et al. (2019) and Degano et al. (2018). Section 3 provides an overview of the characteristics of charts that will be modeled by trajectory sets. Section 4 describes the basic operations performed on charts by our class of investors. Section 5 provides the paper basic construction given by a recursive algorithm. Section 5.1 is a first introduction to some of the parameters that are used in the construction of models. Section 5.2 describes an algorithm for the recursive step completing the construction introduced in Section 5. Section 6 establishes rigorous results giving observable conditions implying the validity of the models introduced. Section 7 presents an analysis of trajectory approximation error accumulation. Section 8 sets model parameters to worst case observed estimates. Section 9 completes the specifications from Section 8 by calibrating some remaining parameters, enumerating characteristics of the data employed and providing a simple description of the meaning of worst case. The section also illustrates several characteristics of estimated parameters. Section 9.5 displays price bounds for the different models introduced. Section 10 explains and illustrates the risk-reward tension of the models. Section 11 explains how a particular feature of type Ⅱ models blocks the effect of worst case parameter estimation propagating into every possible node and, in this way, providing tighter option bounds. Section 12 provides an extended discussion of what we believe to be the most important take away from the paper.
The supporting material in Appendix 1 links to a file providing details of Matlab software implementing an algorithm that constructs the trajectory models as well as an algorithm that evaluates the price bounds and optimal hedging. The supporting material in Appendix 2 links to a bundle of files containing Matlab software, data and further output from the software.
2.
Option pricing in trajectory models
This introduces some notation and notions from Degano et al. (2018) (that reference should be consulted for details).
A trajectory set model S, in this article, is given by a set of sequences S={Si≡(Si,Ti,Wi)}i≥0 with S0=s0,T0=0,W0=0,∀S∈S. Of course, other variables/coordinates are also possible. Si models the values of the tradable risky asset at times Ti when an investor rebalances her portfolio and Wi models a variable representing a financial observable that presumably restricts the future possible manifold of asset values.
The financial context is of a risky asset x(t) and a zero interest bank account. The financial goal is to price a European option with time to expiration T. Given this context, our constructions will imply that for each S∈S there exists N(S) satisfying TN(S)=T. The market model is given by M=S×H where H={Hi}∈H are sequences of functions Hi:S→R representing trading strategies. Precise definitions are given below. The following conditional spaces will play a key role. For given k≥0 and S∈S, set:
Notice S(S,0)=S and that if S′∈S(S,k), then S(S′,k)=S(S,k). The tuple (S,k) will be referred to as a node (equivalently, we may refer to a node by Sk as well).
Definition 2.1 (Portfolio Set). A portfolio H is a sequence of (pairs of) functions H={Φi=(Bi,Hi)}i≥0 with Bi,Hi:S→R.
● A portfolio H is said to be admissible for S if for each S∈S there exists a nonnegative integer NH(S)≤N(S) such that Hi(S)=0 for all i≥NH(S).
● A portfolio H is said to be self-financing at S∈S if for all i≥0,
● A portfolio H is called non-anticipative if for all S,S′∈S, satisfying S′k=Sk for all 0≤k≤i, it then follows that Φi(S)=Φi(S′).
Hi(S) and Bi(S) represent the number of shares and the funds in the bank account respectively, held at time Ti. We abuse the notation by writing H={Hi}i≥0 instead of H={(Bi,Hi)}i≥0. Given S∈S and a self-financing portfolio H, the portfolio value defined by VH(i,S)=Bi(S)+Hi(S)Si is equal to VH(i,S)=VH(0,S0)+∑i−1k=0Hk(S)ΔkS, during the period [i,i+1) for i=0,…,NH(S)−1 and ΔkS≡(Sk+1−Sk); notice that VH(0,S0)=B0(S)+H0(S)S0. Clearly, to specify self-financing portfolios, it is enough to provide sequences H={Hi} of non-anticipative functions and an associated real number V0=VH(0,S0), since the corresponding Bi are obtained from (2).
We call M n-bounded (or just simply bounded) if there exists a constant n so that : NH(S)≤N(S)≤n for all S∈S and H∈H.
The models are discrete in the sense that we index potential portfolio rebalances by integer numbers. Otherwise, stock charts and investment amounts can take values in general subsets of the real numbers and time can flow continuously.
Let Z:S→R denote a general function, from time to time, we will refer to such function informally as the derivative or payoff function. Results in the paper mainly apply to path dependent European options but at some points we restrict to path independent options. This choice is to keep developments simple and so avoid getting diverted by inessential complications. Similarly, one could handle American options but doing so will distract from our main focus. The usual dynamic programming approach to pricing American options in discrete time (see for example Cutland and Roux (2012) section 7.6) can be easily adapted to superhedging such type of options.
The quantity ¯Vk(S,Z,M) introduced in the next definition is the minimum capital needed, conditional on a node (S,k), to superhedge Z.
Definition 2.2 (Conditional Minmax Bounds). Given a market M=S×H, k≥0 and S∈S. Let Z be a function defined on S, define:
Also set V_k(S,Z,M)≡−¯Vk(S,−Z,M). Since ¯V0(S,Z,M) and V_0(S,Z,M) depend on S only through S0, we adopt the notation ¯V(S0,Z,M) and V_(S0,Z,M) respectively. These quantities are called price bounds.
Stochastic models imply existence of a fair price interval for the derivative Z if the market does not contain arbitrage strategies. In our context, the arbitrage-free condition is replaced by the following notion of 0-neutral market.
Definition 2.3 (0-Neutral Market). The market M is conditionally 0-neutral at node (S,k) if
For k=0, we will just refer to M as 0-neutral.
The notion of 0-neutral market, taken from Degano et al. (2018), was originally introduced in Britten-Jones and Neuberger (1996) and was considered equivalent to arbitrage-free in the latter reference. In our general setting, it is only a necessary condition for a market to be arbitrage-free while simultaneously allowing for arbitrage opportunities and a well defined theory of option pricing. 0-neutrality is the key condition to obtain a well defined fair price interval (Degano et al. (2018)).
Theorem 2.1 below is stated for a bounded market and H assumed closed under addition. This is done to avoid introducing further notions, the result holds in more generality as indicated in Ferrando et al. (2019).
Theorem 2.1 (Price Interval). Consider a bounded market M=S×H and a function Z defined on S; fix S∈S and k≥0. If H is closed under addition and M is conditionally 0-neutral at (S,k), then: V_k(S,Z,M)≤¯Vk(S,Z,M).
Upper bounds allow to superhedge, namely, for a given ϵ>0, there exists H∈H, an optimal portfolio, with initial capital ¯V(S0,Z,M)+ϵ such that
We emphasize that the superhedging property is the crucial property in applications. An analogous property holds for the lower bound.
It then remains to address the issue of how to guarantee, for a given trajectory set model S, that the conditional 0-neutral property holds at any given node (S,k). For our simple case of zero interest rates and a single risky asset this just means that for any given node (S,k), there exists S′ and S″ in S(S,k) satisfying:
details are found in Degano et al. (2018). Appendix 1 complements the presentation of trajectory based markets describing an algorithm to evaluate option bounds and optimal portfolios.
In the paper we consistently differentiate between chart values (these being observable on a market) and trajectory coordinates (given by the models).
3.
Operational setting
We refer to charts as the market quoted price x(t) at time t of a risky asset x. We formalize this by considering a chart to be a map x:T→ˆδ0N where ˆδ0≡0.01 (of the monetary unit under consideration) and T a time interval. One could naturally accommodate assets that take negative values but, for simplicity, we do not do so. Unless explicitly indicated otherwise, an interval of real numbers [a,b] is understood to mean [a,b]∩ΔZ, for a given Δ>0, when the variable represents time. So, T⊆ΔZ. We will use T, to denote the time length to maturity of a European option contract active in a given interval [t0,t0+T] and written on the asset x. Instead of replacing ˆδ0 by 0.01 in the rest of the paper, we use ˆδ0 for readability.
The following informal enumeration indicates the ingredients that we will use to construct trajectory sets in the paper. In this way, trajectory coordinates will result from a class of investors that rebalance their portfolios based on prescribed operations on chart data. For fixed real numbers δ, δ0, δ≥δ0, and Δ>0:
1. Charts x are sampled at dynamic times rl according to δ0.
2. Time intervals have a lower bound resolution Δ in the sense that (rl+1−rl)≥Δ>0.
3. Times ti, for the i-th portfolio rebalance, satisfy ti∈{rl} and are given by an investor prescribed threshold δ.
4. Sampled variation w(x,t) is accumulated for the samples x(rl).
5. There is a dynamical number of portfolio rebalances N(x,[t0,t0+T]) that take place in [t0,t0+T].
Hence, we deal with a class of investors that will react to chart changes of size δ and observe chart values at a certain time resolution Δ and spatial resolution δ0. From this perspective, these portfolio managers want to evaluate investment opportunities related to a European option. They want to compare market prices relative to their operational portfolio rebalancing.
Given this setup, the operations of sampling and portfolio re-balancing performed on chart samples will create the associations:
For the precise definition of the notion of association, we refer to Definition 8. Notice that w(x,ti) is neglected above; a specific w(x,ti) is introduced in Section 4 and its role is explained elsewhere in the paper. Historical, worst case, values of w(x,t) and the operational setup, will limit the minimum and maximum possible number of samples as well as their ranges. In this way, we will obtain necessary constraints restricting the possible values of Si+1 for given S0,…,Si. Such restrictions are used to define S; therefore, the meaning of Si+1 is that of possible values at which an investor will re-balance her portfolio given a prescribed way of processing the data. Section 6 discusses the reasons why the association x(ti)→Si can fail. More precisely, we provide hypothesis so that the values of an unfolding chart will be associated to a trajectory in S. We also analyze the related issue of the error build up whenever the association x→S is given by an approximation (this is done in Section 7).
An inequality of the form δ≤|x(t′)−x(t)|, t<t′, as well as analogous expressions, will be referred to as a δ-increment (notice the abuse of language as the value of x(t′) could be smaller than x(t)).
4.
Charts and investors' operations
Set
where MT,F,G are positive integers. Our investor will fix δ, by a process of calibration, and will not rebalance her portfolio for changes smaller than δ. Δ is the smallest time resolution at which the investor will observe charts. The parameter δ0 will provide the grid δ0N, we then require, by construction, that coordinates Si∈δ0N and Wi∈δ0N. Taking δ0=ˆδ0 is the natural choice and simplifies the developments. Our only reason to consider δ0>ˆδ0 is to save on computations, something we need to do to produce output for the values of T and Δ we have chosen to illustrate the models.
Definition 4.1. [Dynamic sampling times] Given δ0>0, a chart x and interval [t0,t0+T]; a sequence of increasing dynamic sampled times is given by r=r(x)={rl}Ll=0⊆[t0,t0+T] (so rl∈ΔZ), L=L(x,[t0,t0+T]), r0≡t0, satisfying:
notice that δ0≤|x(rL)−x(rL−1)| may or may not hold. Consistently with these properties, we also require the times rl to satisfy: if rl<t<rl+1,t∈ΔZ, then δ0>|x(t)−x(rl)|.
The collection {rl} as above is referred as sampling times. The measured times {rl} are independent of a monetary unit re-scaling, i.e. after a change of the form δ0 $ →δ′0=cδ0 ȼ.
From a financial point of view, and when dealing with a long period of historical data, it is more reasonable to define the sampling times in terms of proportional changes (x(rl+1)−x(rl))/x(rl) (i.e. returns). Similarly for the rebalancing times ti.
Definition 4.2. [Dynamic rebalancing times] Given δ>0, a chart x and interval [t0,t0+T], a sequence of increasing dynamic rebalancing times is given by t=t(x)={ti}Ni=0⊆{rl}Ll=0, N=N(x,[t0,t0+T]), t0(x)≡t0, satisfying:
The times ti are chosen in a greedy way, namely given ti=rli, ti+1 is the smallest element rli+1 in {rl} satisfying (8) if such element exists, otherwise rli+1=T and N=li+1.
Notice that δ≤|x(tN)−x(tN−1)| may or may not hold. The latter ambiguity will imply that the trajectory set will need to account for a larger set of possible values for x(tN), conditional on given values S0,…,SN−1 (see extended discussion in Section 5.1). N=N(x,[t0,t0+T]) is the number of times a portfolio is rebalanced in the interval [t0,t0+T], it follows that N(x,[t0,t0+T])≤L(x,[t0,t0+T]). Portfolio rebalancing times ti=ti(x) satisfy t0(x)=t0=r0<t1<…<tN−1≤rL−1. Setting tN=rL=t0+T as a rebalancing time, as we do, is inconsequential in the absence of transaction costs (as is our standing assumption in the paper).
We can write for 0≤i≤N−1:
The relevance of using a ^ notation in ˆmi, and in related variables, will be made clear later on in the paper.
where ti=rli<…<rli+si=ti+1, i.e. li+1=li+si and 0≤si. Notice the possibility of si=0, this could happen only for the case i=N−1 and there are no ˆδ0-increments in between ti and ti+1=T and so x(ti+1)−x(ti)=0. Setting w(x,t0)=0 it follows that w(x,ti)=∑li−1l=0|x(rl+1)−x(rl)|.
Also,
Notice that,
Given the above definitions and notation, we can write:
so
Moreover, given that times ti are chosen in a greedy fashion we also have for any1≤R<si,
where G≤|ˆpj| follows from ˆδ0|ˆpj|=|x(rli+j+1)−x(rli+j)|≥δ0. Given that ˆmiˆδ0≡x(ti+1)−x(ti), hence |ˆmi|ˆδ0≥δ is guaranteed for i<N−1 and so
We have introduced the dichotomy between ˆδ0 and δ, the former being an absolute minimun value for chart changes and the latter being investor dependent.
Analogous to the use of δ0, and also to reduce the execution time of a software implementation, one could introduce Δ0≥ˆΔ0 where ˆΔ0 is the smallest time resolution supported by the data (i.e. t∈ˆΔ0Z). In that case one then will require (rl+1−rl)≥Δ0 and rl∈ˆΔ0Z.
To summarize the above:
● rl are the sampling times.
● ti∈{rl} will denote the portfolio rebalancing times.
● si is the number of chart samples in between two portfolio rebalances.
● qi the possible number of time intervals of size Δ in between two consecutive portfolio rebalances.
● ˆmi the possible number of ˆδ0 chart units in between two consecutive portfolio rebalances.
● ˆpj the possible number of ˆδ0 chart units in between two consecutive samples.
● N(x,[t0,t0+T]) total number of portfolio rebalances in [t0,t0+T].
We will rely on si≤qi given by (12), that is, we are taking an upperbound. This does not create any drawbacks as we will be replacing the role of si by J with J≤qi.
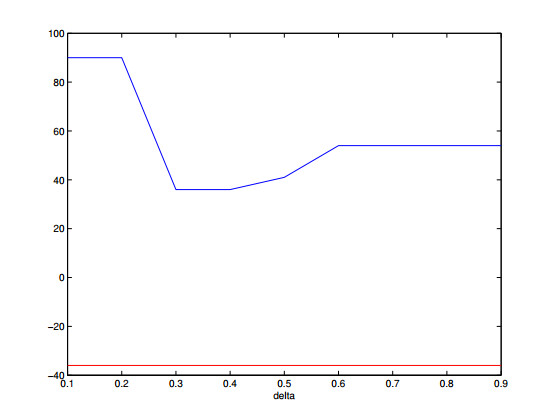
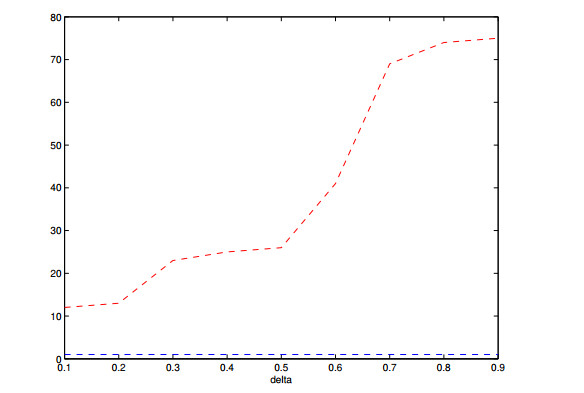
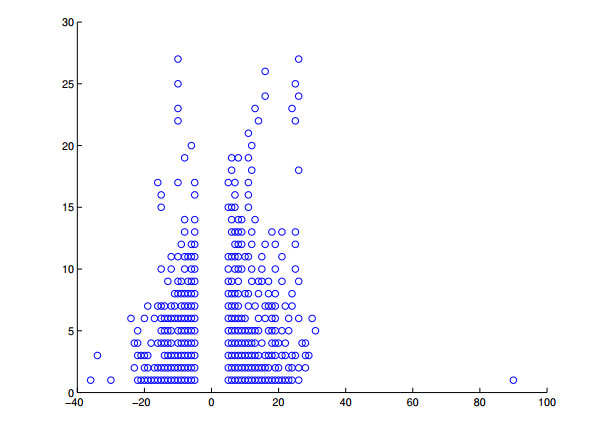
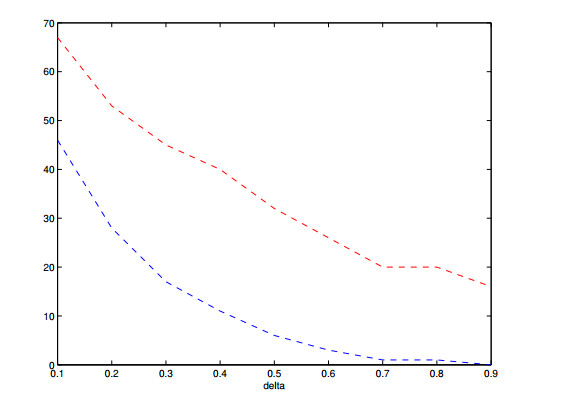
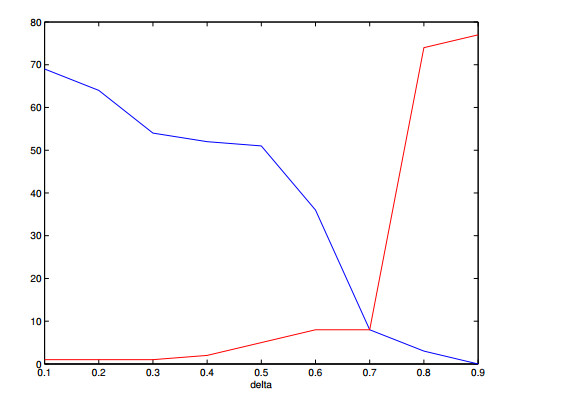
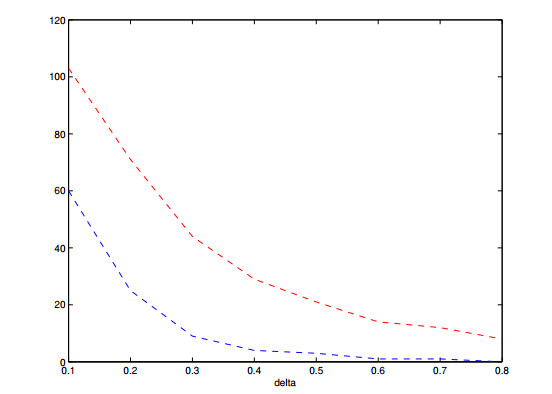
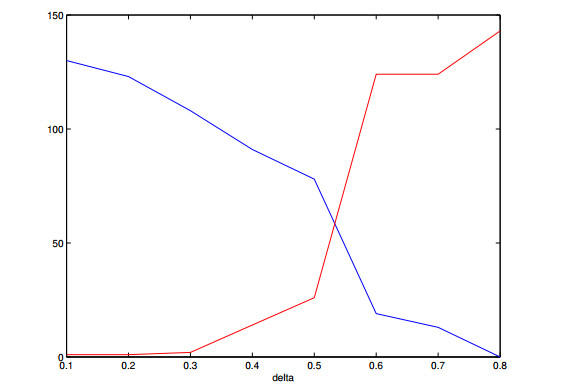
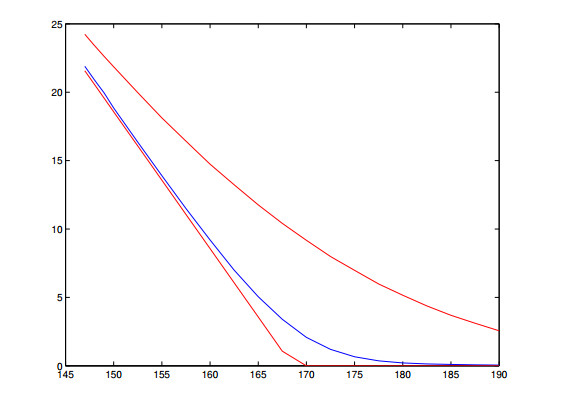
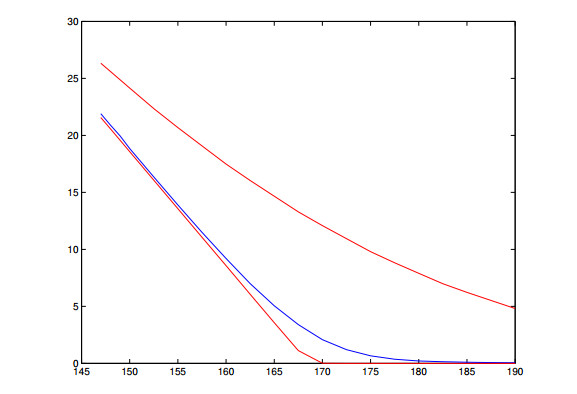
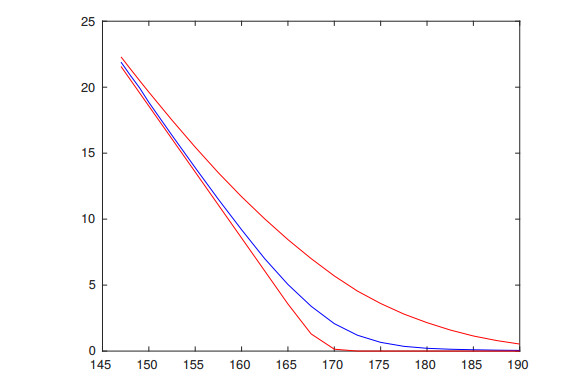
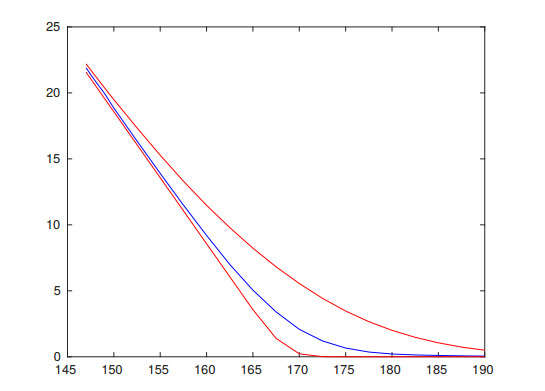
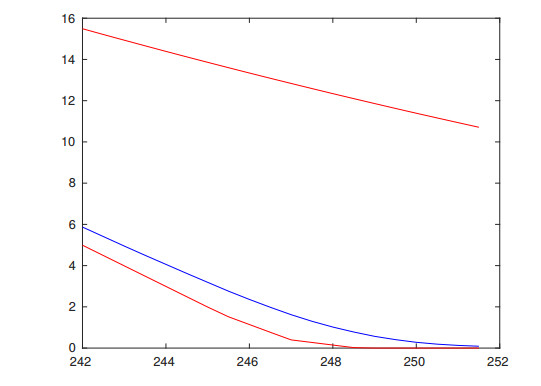
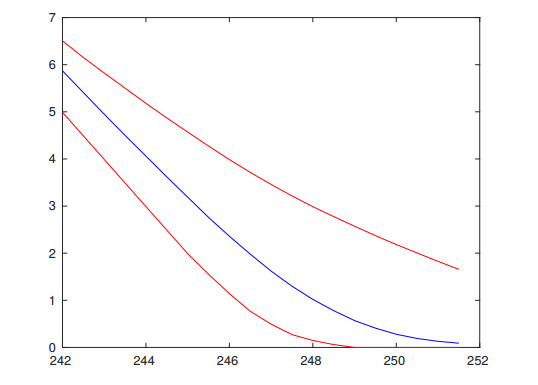
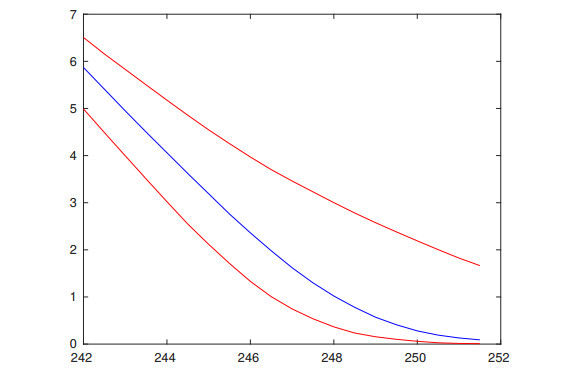
Through the process of calibration, the time and space intervals reflect actions of realistic investors, therefore, we expect the models to reflect features of options' market values. This observation is confirmed for type Ⅱ models, we refer to Figures 13, 14, 16 and 17 for examples.
4.1. Unfolding chart parameters
The definitions in this section are only first required in Section 6; we place the definitions here as they refer to a given chart x and time interval [t0,t0+T]. Moreover, they provide a preliminary meaning to the corresponding parameters used for model building in Section 5.2.
Definition 4.3. (Unfolding S-T Nodes)
where the {ti} are as in Definition (5) and P≡P(x,[t0,t0+T])≡N≡N(x,[t0,t0+T]) (the latter as introduced in Definition 5) if δ≤|x(tN)−x(tN−1)| or P≡P(x,[t0,t0+T])≡N−1 otherwise. Notice the possibility that NE(x,[t0,t0+T])=∅. We also set
notice the possibility τ(x,[t0,t0+T])=(t0−t0)=0 whenever N=1.
Definition 4.4 (Minimal wait for a δ-increment)
That is, Γ(x,[t0,t0+T]) is the smallest length such that for any t satisfying [t,t+Γ(x,[t0,t0+T])]⊆[t0,t0+T] there exists s∈(t,t+Γ(x,[t0,t0+T])] such that δ≤|x(s)−x(t)|. We adopt the usual definition that the minimum over an empty set is equal to T. Clearly, if x has n δ-increments in [t0,t0+T] then Γ(x,[t0,t0+T])≤(T−(n−1)Δ) and if n=1 we may have Γ(x,[t0,t0+T])=T.
5.
Trajectory sets: recursive construction
The previous section assumed the availability of an observable chart x(t) and introduced sequences of integers si,qi,ˆmi,ˆpj, 0≤j<si and N. The integers ˆki, ni and ˆji are derived quantities, in the sense that each set si,qi,ˆmi,ˆpj,0≤j<si gives a triple (ˆki,ni,ˆji). Necessarily, the meaning of the variables impose some constraints obeyed by these sequences. We will construct trajectory models by allowing trajectories to be jointly specified by the mentioned constraints. The end result being the definition of a possible set of chart samples, time rebalances and sampled variation values.
In order to avoid misunderstandings, one should keep in mind that the previously introduced variables: rl,ti,ˆmi,qi,si, N(x,[t0,t0+T]) and ˆpj are either observable or operationally prescribed and, in that way, are a result of acting on unfolding charts. In order to avoid a confusing proliferation of notation, the same symbols will be used to denote the corresponding modeling variables used to define trajectory sets but with the following exemptions: N(x,[t0,t0+T]) will be replaced by N(S), ˆmi for mi, ˆki for ki, ˆji for ji and ˆpj for pj. In the last four cases the reason to drop the ^ notation is due to the fact that x(t)∈ˆδ0N while trajectory coordinates Si,Wi∈δ0N.
The two related, but different, uses of the same notation for charts and trajectories should not be identified of course, doing so will preclude the analysis of how well the model approximates the observational setting. Namely, how relevant are the proposed trajectories to fit the values of the unfolding chart at the re-balancing times.
Trajectory coordinates Si and Wi will take values in δ0N. As already indicated, the possibility to take δ0>ˆδ0 will allow us to save on computations and this is the reason why we introduce δ0. Conceptually, the reader could consider δ0=ˆδ0 but in practical terms we noticed the need for δ0>ˆδ0 due to the time horizons and sampling times we have considered (these choices were dictated by the data we got access to). The choice δ0>ˆδ0 means we will be approximating the values x(ti) which introduces the issue of error accumulation, we deal with this issue in Section 7.
We describe now a formal recursive definition of a generic (abstract) trajectory set S. Section 5.2 completes the formal definition by providing the construction needed in the recursive step. Such constructions are driven by a set of parameters providing a class of trajectory sets. We assume given an interval [t0,t0+T], where a European option of interest is active. We set the notation S={Si≡(Si,t0+Ti,Wi)}≡{(kiδ0+s0,t0+niΔ,jiδ0)}, ki∈Z, ni<ni+1, 0≤ji<ji+1, ni,ji∈N. The recursive step will split into type Ⅰ and type Ⅱ models, in the former case, as already indicated, the variable Wi will be ignored something we remind readers from time to time.
Trajectories S will then be specified by setting s0=x(t0)+k0δ0=x(t0), for x(t0) given, t0+T0=t0+n0Δ=t0, W0=j0δ0=0 and proceeding recursively: given a triple (ki,ni,ji) we should provide a set of admissible values (ki+1,ni+1,ji+1) (these are specified in Section 5.2); for each such admissible triple we set:
Moreover, define
notice that N(S) exists as ΔiT≥Δ for any 0≤i<N(S).
For the case i<N(S)−1 we will also require |mi|≥δδ0=F. Also, for any 1≤R<si and i≤N(S)−1,
Given (Si,Ti,Wi), we introduce the convenient notation for type Ⅱ models:
and for type Ⅰ models:
Notice that the values (pj)si−1j=0,mi,qi need to be prescribed in order to obtain the set of admissible triples (ki+1,ni+1,ji+1) (or tuples (ki+1,ni+1) for type Ⅰ models). This will be done in Section 5.2 for each of the two types of models. Subsequent sections indicate how to estimate the models' parameters. Estimation in this paper involves worst case estimation on historical data. The precise meaning of the latter, we expect, to be quite evident in each instance; specifics are provided in Section 9. It is a simple minded methodology that requires that informative variables have been chosen to define trajectories. Informative here means that the parameters that confine the model variables are contained in worst case ranges that reflect observable and possible financial situations that impact the values of the risky asset and the class of investors under consideration.
Remark: Type Ⅱ models will enforce (historical) constraints on Wi and, in this way, limit the number of possible future trajectories emanating from the node (Si,t0+Ti,Wi). For type Ⅰ models, such historical constraints are not in effect, it follows that the coordinates Wi are irrelevant and so we have only the coordinates (Si,t0+Ti).
5.1. Model Parameters. Last Portfolio Rebalance (accounting for the possibility that δ>|x(tN)−x(tN−1)|)
This section provides informal explanations of some of the parameters that will play a role in the algorithm constructing the two model types.
Recall the notation N=N(x,[t0,t0+T]) from Definition 5. As already hinted, the fact that the last rebalancing time tN does not necessarily satisfy δ≤|x(tN)−x(tN−1)| implies that a node (SN−1,t0+TN−1,WN−1) associated to (x(tN−1),tN−1,w(x,tN−1)) (such association also gives N(S)=N(x,[t0,t0+T])) will be treated differently to other types of nodes. Parameters at nodes (Si,t0+Ti,Wi) (leading to NA(Si,t0+Ti,Wi)), with i<N(S)−1, should prescribe that portfolio rebalances will take place only after the chart has moved by at least an amount δ relative to its present value. At a node with i=N−1 it is not known which of the alternatives: δ≤|x(tN)−x(tN−1)| or δ>|x(tN)−x(tN−1)|, will actually occur. Therefore, at a node (SN−1,t0+TN−1,WN−1) we will need to consider both possibilities. It follows that such a node will lead to a larger admissible set NA(SN−1,t0+TN−1,WN−1).
In fact, the equality i=N−1 is uncertain. In order to deal with this uncertainty, we make use of additional information by means of relevant parameters set to worst case values. In this way we can partially discern if i<N−1 holds and in so doing we reduce the number of cases leading to the enlargement of NA(Si,t0+Ti,Wi) just mentioned. We will make use of a parameter Γ that, when associated to a chart x, will have the following meaning: it is the smallest time length such that for any t (in the historical data set used for estimation), x moves up or down, from its current value x(t), by at least δ in the interval [t,t+Γ]. Γ corresponds to Γ(x,[t0,t0+T]) introduced in Section 4.1; the precise relationship is given by (75).
Another parameter, τ, will also be used for the same purpose. The index i corresponding to (Si,t0+Ti,Wi) is not being encoded in our data structure. This means that we will replace references to i by Ti. This implies the need to introduce τ used to reflect the minimum time length after which δ-increments may stop. τ corresponds to τ(x,[t0,t0+T]) introduced in Section 4.1; the precise relationship is given by (78).
In general, one would like to enforce on S constraints that can be obtained empirically or as a result of further available information. Proceeding in this way will make S smaller, and hence implying more accurate option's bounds, while still obeying our general philosophy of worst case construction.
5.2. Trajectory sets: recursive algorithmic step
This section states the recursive algorithmic construction leading to the two types of trajectory sets to be considered. The specifications complete the general recursive framework introduced in Section 5 where, we recall, an interval [t0,t0+T] was given and only the sets NA(Si,t0+Ti) and NA(Si,t0+Ti,Wi) were missing in order to complete the specifications for type Ⅰ and type Ⅱ models respectively. All models introduced below assume a fixed T and Δ.
The definitions of each of the models below use a list of parameters which enable the construction of each trajectory set. Section 5.3 provides an intuitive explanation of some features of the definitions. Later sections indicate how to set the values of these parameters being by the process of calibration, estimation or by using relationships that relate the parameters.
The notation NE (E for empirical or estimated) represents a given set of pairs (m,q), m∈Z, q∈N. Such set will be estimated as described in Section 9. Define qmin≡min{q:(m,q)∈NE}.
We point out to the appearance below of ∑J−1j=0pj as a replacement for ∑si−1j=0pj (similar comments apply to related quantities). J is needed given that we only know si≤qi (see, (12)); to account for this uncertainty we then consider all J satisfying J≤q for a given (m,q).
As an explanatory comment, we mention that all nodes for which we can ascertain Ti<τ will have the same set of admissible nodes NA(Si,t0+Ti,Wi) for type Ⅱ models (or NA(Si,t0+Ti) for type Ⅰ models). In this case we foresee more δ-increments are forthcoming and construct the trajectory set accordingly.
To repeat, we define possible values recursively, therefore, the cases below assume (Si,t0+Ti,Wi) given (only (Si,t0+Ti) is needed for the type Ⅰ models); the initialization S0=s0,T0=0,W0=0 is in effect.
5.2.1. Type Ⅰ models
Define the statements:
If Ti=T, we terminate.
In case the statements A or C hold, we remark that the condition (m,q)∈NE satisfying qΔ≤(T−Ti) is clearly met and so NA(Si,Ti)≠∅. Obviously, in case B, NA(Si,t0+Ti)≠∅ as well.
The following condition implies that each node (Si,t0+Ti) is 0-neutral as required in (5):
We emphasize that (28) is not required for the construction of the models nor is needed in Proposition 1 below; (28) is needed to obtain meaningful price bounds. Condition (28) holds by construction when case B) executes and, therefore, also when case C) executes. Moreover, as it follows from the definition of type Ⅰ model MIDP in Section 8.5, such models do satisfy (28) when case A) executes (and so MIDP models are 0-neutral).
Condition (28) is a very weak condition indeed, requiring that for any node (Si,t0+Ti), there are at least two children nodes emanating from it such that the stock moves in opposite directions. For general type Ⅰ models one can easily check if the condition holds after the trajectory set has been constructed (as indicated, only case A) needs to be checked).
5.2.2. Type Ⅱ models
The collection {Vρ} will be referred to as the variation constraint sets.
Below we will make use of the statements A, B and C introduced for type Ⅰ models.
For a given (m,q), let z denote a number satisfying z=∑J−1j=0|pj|δ0 where (pj)J−1j=0∈NW(m,q); for any such z set:
For a given (m,q) define:
where Ti+1=Ti+qΔ.
We assume that for any (Si,Ti,Wi) and (m,q)∈NE∪N<S,T(Ti):
equivalently, there exists z∗ satisfying (Wi+z∗)∈VTi+1 such that NA(m,q,z∗)≠∅. In the construction that follows, and for the case Ti+1=T, it will be immaterial which such z∗ is actually chosen.
If Ti=T, we terminate.
If A or C hold, the condition (m,q)∈NE satisfying qΔ≤(T−Ti) is, clearly, non empty and so by (29) NA(Si,t0+Ti,Wi)≠∅. This fact is also true when case B) holds due to (29). A requirement such as (29) is unavoidable as the sets {Vρ} are independent of the sets NE and NW(m,q). Therefore, validity of (29) does depend on the actual estimated values for these sets. Of course, one can also force (29) by construction (i.e. enlarge NW(m,q) or VTi+1 as necessary) but we have chosen not to do so.
The coordinate W′i+1∈VTi+1 in (Si+1,t0+Ti+1,W′i+1) is only used to prune future children nodes. Therefore, once we have arrived at final time t0+T there is no need to keep several of the possible values of Wi+1 for future pruning. For this reason, under case A) with Ti+1=T or case B) (in the latter case Ti+1=T always holds), for a pair (Si+1,t0+T), as long as there exists at least one Wi+1∈VT we then include (Si+1,T,Wi+1) in NA(Si,t0+Ti,Wi). That is, there is no need to consider any other ˜Wi+1∈VT for the given pair (Si+1,t0+T); this explains the freedom to choose any z∗, satisfying (Wi+z∗)∈VTi+1, where Ti+1=T, above.
The following condition implies that each node (Si,t0+Ti,Wi) is 0-neutral as required in (5):
Analogously to the case of type Ⅰ models, (31) is not required for the construction of type Ⅱ models nor is needed in Proposition 2 below. The property stated in (31) is needed to obtain meaningful price bounds. Notice that if (m,q)∈N<S,T(Ti) then, by (29), there exists z∗=z∗(m,q)=∑J−1j=0|pj|δ0, with (pj)∈NW(m,q), it then follows that z∗(−m,q)≡∑J−1j=0|−pj|δ0 and (−pj)∈NW(−m,q). Therefore, given that (−m,q)∈N<S,T(Ti) as well, (Si+mδ0,t0+T,Wi+ΔiW),(Si−mδ0,t0+T,Wi+ΔiW)∈NA(Si,Ti,Wi) and so the node (Si,Ti,Wi) is 0-neutral in case conditions B) or C) execute (this fact always holds for any type Ⅱ model). In case A), one could impose the following condition to imply that (Si,Ti,Wi) is 0-neutral: there exists (m,q),(m′,q′)∈NE with mm′≤0 max(qΔ,q′Δ)≤(T−Ti) and there exists z such that NA(m,q,z)≠∅ or NA(m′,q′,z)≠∅.
5.3. Explanations
Once the parameters are assigned to worst case estimates, the constructed models will capture the intended properties of charts; this is proven in Section 6. In this section we provide a preliminary, informal, interpretation of some of the features and conditions used in the construction of the models.
Condition B models the situation when there is not enough time for the chart to have a (forthcoming) δ-increment. Therefore, when condition B executes the trajectory under construction terminates without a δ-increment. Condition A models the situation when the chart will have a (forthcoming) δ-increment. Therefore, execution of condition A implies that the trajectories constructed will all have a δ-increment. This shows that for any trajectory we have: δ≤|Si+1−Si| if (i+1)<N(S).
Notice that m=0 is possible and could happen only in case B, moreover, it could be that m=0=∑J−1j=0pj with J≥2 (recall that |pj|≥1). This will account for cases where x has a number J of δ0-increments after ti but ends up with ti+1=T, x(T)=x(ti) and so m=0. There is still one more case to consider, namely: x(T)=x(ti) and so m=0 but there are no δ0-increments in between. This case we cover by allowing J=0 (which only has a meaning if m=0 given that the case [m≠0 and J=0] is impossible).
In other words, the pairs (m,q) belonging to NE in case A), represent trajectory changes that replicate historical chart's δ-increments. The pairs (m,q) belonging to N<S,T(Ti) in case B), represent trajectory changes that move directly from t0+Ti to t0+T without moving more than δ relative to Si (but with, possibly, several δ0-increments in between).
The parameter si in (13) represents the number of δ0-increments between two consecutive δ-increments. We have replaced si by q according to (12) and used the variable J≤q to account for all possible cases. The constraint |∑R−1j=0pj|<E,R≤J−1 reflects the fact that there is no δ-increment between the two nodes under consideration. The case J=1 represents the case where there is a single δ0-increment which is in effect a δ-increment, such a case may be referred as a (spatial) jump (as the δ-increment can not be anticipated by observing δ0-increments) and so we may have m=p0 for the case J=1.
Once τ has been set to its estimated value, we will conclude that if Ti<τ, trajectories will move by increments of at least size δ. In case that Ti≥τ, it is uncertain if such increments will be happening, we will then also allow for trajectories to ``difusse'' at δ0 granularity. Notice the disjoint dichotomy: to have one more δ-increment or to δ0-diffuse directly from Ti to T and not to have a δ-increment. Such logic for these events is dictated by the operational arrangement and a worst case point of view which are used here to constraint future possibilities.
A main characteristic of type Ⅰ Models is the fact that the set of admissible nodes is only loosely affected by the current node (Si,t0+Ti), Ti<T. More specifically, the effect of the current node is to differentiate nodes next to expiration or otherwise. Type Ⅱ Models impose a stronger dependency on the current node; actually, the role of the Wi variable is to restrict possible values of (m,q). This comment is explained in Section 11.
To make the description of both types of models more symmetric, one could replace the set of pairs NE for set of triples (m,q,r) where r is used to encode changes in Wi in type Ⅱ models.
6.
Falsifiable models
This section establishes rigorous results requiring conditions that are empirically observable and implying that the models introduced in previous sections succeed. The meaning of the latter is that with the minimal required initial funds the investor can superhedge a given option by trading along the actual chart values x(ti). The results become empirically relevant when model parameters are set to estimated values or are calibrated. This is done in Sections 8 and 9 which also provide the definite meaning for the models' parameters. We emphasize that the said conditions allow the models to be falsifiable, i.e. one can observe if they do not hold and this can be done dynamically (i.e. as chart samples unfold).
The section requires the availability of the trajectory models (and hence of the parameters used for their construction) and chart values x(t),t∈[t0,t0+T]. We rely on notation from Section 4.1.
The following definition is needed to enunciate ours results.
Definition 6.1 (Association relationship). We say that x is associated to S∈S if Xi≡(x(ti),ti,w(x,ti)) (Xi≡(x(ti),ti) for type Ⅰ models) and Si=(Si,t0+Ti,Wi) satisfy (x(ti),ti)=(Si,t0+Ti) for 0≤i≤N(x,[t0,t0+T])=N(S). Of course, the coordinate Wi is dropped for type Ⅰ models and in that case we can write the association simply as Xi=Si for 0≤i≤N(x,[t0,t0+T])=N(S).
We will say that the model M succeeds for the chart x:[t0,t0+T]→R if there is S∈S associated to x. Otherwise, we will say that the model fails for the chart x. If x is associated to S then (4) holds whenever the coordinates Si are replaced by chart values x(ti). That is, given the required initial funds ¯V(S0,Z,M)+ϵ one can superhedge Z by trading on chart values x(ti). Notice that the association definition does not require to match w(x,ti) to Wi as this variable does not appear explicitly in the superhedging property which is the one we want to uphold. Times ti are matched to times t0+Ti as we are dealing with a European option expiring at t0+T.
6.1. Validity of Type Ⅰ models
The notation N<S,T(Ti) used in the proof below was introduced in Section 5.2.1; we also rely on notation from Section 4.1.
Proposition 6.0.1. Consider S to be a trajectory set of type Ⅰ. Assume
Furthermore, assume:
and
Then, there exists S∈S associated to x.
Proof. Consider first the case when τ(x,[t0,t0+T])=0 then, by (32), τ=0 and so condition C holds for (S0,t0+T0) (recall that T0=0). Notice that τ(x,[t0,t0+T])=0 implies x(t),t∈[t0,t0+T], has no δ-increments; therefore N(x)=1 and so t1=t0+T. (34) implies (x(t0+T)−x(t0))∈δ0Z and −F<m≡(x(T)−x(t0))δ0<F, therefore (m,(T−T0)/Δ)∈N<S,T(T0) which shows that S={(S0=x(t0),t0+T0=t0),(S1=x(t0+T),t0+T1=t0+T)} is associated to x and S∈S because (S1=x(t0+T),t0+T1=t0+T)∈NA(S0,t0+T0), the latter set as in case B).
We may then consider τ(x,[t0,t0+T])≥Δ for the remaining of the proof; therefore, there exists t1 such that δ≤|x(t1)−x(t0)|. Moreover (ˆm≡(x(t1)−x(t0))ˆδ0,q≡t1−t0Δ)∈NE(x,[t0,t0+T]), then (33) implies there exists (m,q)∈NE and m=(x(t1)−x(t0))δ0 (recall that δ0=Gˆδ0). Now we continue the proof by induction. For (Si,t0+Ti)=(S0,t0+T0), condition A executes due to Γ≤(T−T0)=T. Given that t1−t0=qΔ≤T−T0 we have (S1=S0+mδ0,t0+T1=t0+qΔ)∈NA(S0,t0+T0). This is the first step in the recursive construction and the latter fact is our base case for the following inductive argument.
Assume, inductively, that we have found S′∈S satisfying Xk=S′k for 0≤k≤i with 0<Ti≤T. In the case that Ti<T, we will show that there exists S∈S(S′,i) and Xi+1=Si+1 with ti+1≤T. One will then conclude that there exists S∈S associated to x. Therefore, we may assume Ti<T in what follows.
Consider first the case when the following holds,
we label this the case a). Then, [(Γ(x,[t0,t0+T])≤(T−Ti))or(Ti<τ(x,[t0,t0+T]))] holds, which implies there exists ti+1, t0+T≥ti+1>ti=t0+Ti satisfying δ≤|x(ti+1)−x(ti)|. Therefore,
from (33) it follows that there exists (m,q)∈NE so that
We remark that qΔ≤(T−Ti) and so qminΔ≤(T−Ti) (so case a) holds if and only if statement A holds). This shows that the construction described in item A) executes and so there exists (ΔiS,ΔiT)=(Δix,(ti+1−ti)) and (Si+1,Ti+1)∈NA(Si,t0+Ti). In view of case a), take Si+1≡Si+mδ0=x(ti+1)=x(ti)+mδ0 and t0+ti+1≡t0+Ti+qΔ=ti+qΔ. In this way the required S is obtained with Sk=S′k for 0≤k≤i and Si+1 as it was just defined. Therefore, the inductive hypothesis for i+1 has been established.
Similarly, assume statement B holds, i.e.: [(T−Ti)<qminΔ] holds, notice this case is potentially non empty as Ti>0. Then, by (33), [(T−Ti)<qmin(x,[t0,t0+T])Δ] where qmin(x,[t0,t0+T])≡min{q:∃(m,q)∈NE(x,[t0,t0+T])}. Therefore, there exists ti+1=t0+T>ti=t0+Ti satisfying δ>|x(ti+1)−x(ti)|, then (34) implies
Notice that |m|<F. This shows that there exists (ΔiS,ΔiT)=(Δix,(ti+1−ti)) and (Si+1,t0+Ti+1)∈NA(Si,t0+Ti) (this latter set as in case B)).
Finally, consider that statement C holds and, we recall, that in this case NA(Si,t0+Ti) is defined as the union of the sets NA(Si,t0+Ti) appearing under the entries A) and B). From our definition of ti+1 (see Definition 5) there are two possibilities: δ≤|x(ti+1)−x(ti)|,ti<ti+1≤t0+T or δ>|x(ti+1)−x(ti)|,ti<ti+1=t0+T. Whichever of these cases holds, the execution of condition C in the recursive construction of S and the arguments employed above for the cases A and B imply the existence of (Si+1,t0+Ti+1)∈NA(Si,t0+Ti) and (Si+1,t0+Ti+1)=(x(ti+1),ti+1). So we have established the validity of the inductive hypothesis for i+1.
Hypothesis (33) implicitly requires (x(ti+1)−x(ti))∈δ0Z for 0≤i<N(x). We weaken this latter requirement in Section 7. Of course, and more substantially, (33) also requires that the chart (ˆm,q) pairs are matched by corresponding trajectory pairs (m,q). The appearence of G in (33) reflects the fact that chart increments are measured in units of ˆδ0 while trajectory increments are measured in δ0 units.
6.2. Validity of Type Ⅱ models
A similar proposition can also be proved for type Ⅱ models; towards this end, we will need to rely on notation introduced in Section 4. The proof follows the same logic as the one of Proposition 1 with the added arguments to handle the coordinate Wi.
The variation constraint sets {Vρ}ρ∈(0,T], introduced in Section 5.2.2, are required to satisfy:
a property that can be easily checked once we assign the sets {Vρ}ρ∈(0,T] to their estimates in Section 8.6. We also introduce the following notation for ρ≤ρ′ and y∈Vρ:
Using (36) we obtain
Proposition 6.0.2. Consider S to be a trajectory set of type Ⅱ. Assume
Furthermore assume:
and
also, (36) holds. Then, there exists S∈S associated to x.
Proof. Consider first the case when τ(x,[t0,t0+T])=0 then, by (38), τ=0 and so condition C holds for (S0,t0+T0,W0) (recall that T0=W0=0). Notice that τ(x,[t0,t0+T])=0 implies x(t),t∈[t0,t0+T], has no δ-increments; therefore N(x)=1 and so t1=t0+T. (40) implies (x(t0+T)−x(t0))∈δ0Z and so −F<m≡(x(T)−x(t0))δ0<F, therefore (m,q≡(T−T0)/Δ)∈N<S,T(T0). From the definitions and notation in Section 4 we can write (here we rely on (40)):
Moreover
(we have dropped the subscript i in ˆmi, li and si appearing in Section 4, we will do the same in the remaining of the proof). Therefore Δ0w≡w(x,t0+T)−w(x,t0)=ˆδ0∑s−1j=0|ˆpj|=δ0∑s−1j=0|pj| (recall that w(x,t0)≡0). By means of the properties listed in (14), and recalling that E=FG, we can check that the properties in (23) hold and by taking J≡s we verify that (p)J−1j=0∈NW(m,q). Therefore z≡δ0∑s−1j=0|pj|=∑l0≤l,l+1≤l1|x(rl+1)−x(rl)|∈Δ0,t1−t0V(w(x,t0)) where we used (41). It then follows from (37) that W1≡w(x,t0)+z=W1∈VT. We emphasize, again, that the property of association in Definition 8 does not involve the coordinate Wi and, given that t1=t0+T, we could then take z∗=z in (30) (more precisely, we have established that there exists z satisfying (W0+z)∈VT such that NA(m,q,z)≠∅; taking z∗ to be any such z will do for our argument). Therefore, S={(S0=x(t0),t0+T0=t0,W0),(S1=x(t0+T),t0+T1=t0+T,W1)}∈S because (S1=x(t0+T),t0+T1=t0+T,W1)∈NA(S0,t0+T0,W0), the latter set as in case B). It then follows that x is associated to S.
In what follows we may not provide as many details on arguments involving z+Wi leading to Wi+1; they are very similar to the arguments for the case τ(x,[t0,t0+T])=0 above.
We may then assume τ(x,[t0,t0+T])≥Δ for the remaining of the proof. Therefore, there exists t1 such that δ≤|x(t1)−x(t0)|. Moreover (ˆm≡(x(t1)−x(t0))ˆδ0,q≡t1−t0Δ)∈NE(x,[t0,t0+T]), then (39) implies there exists (m,q)∈NE and m=(x(t1)−x(t0))δ0 (recall that δ0=Gˆδ0). We continue the proof by induction. For (Si,t0+Ti)=(S0,t0+T0), condition A executes due to Γ≤(T−T0)=T. Notice that x(t1)=x(t0)+mδ0=S1 and t1=t0+qΔ. The same arguments used above for the case τ(x,[t0,t0+T])=0, and the fact that t1−t0=qΔ=T1≤T−T0, show that there exists z+W0=w(x,t1) where z≡δ0∑s−1j=0|pj|=∑l0≤l,l+1≤l1|x(rl+1)−x(rl)|∈Δ0,t1−t0V(w(x,t0)) where we used (41). It then follows from (37) that W1≡w(x,t0)+z∈VT1. If T1<T, it follows that (S1=S0+mδ0,t0+T1=t0+qΔ,W1)∈NA(S0,t0+T0,W0) (this latter set as in case A)). This fact is our base case for the following inductive argument. On the other hand, if T1=T, we could take z∗=z and argue as in the above case τ(x,[t0,t0+T])=0 and conclude there is S associated to x.
Assume, inductively, that we have found S′∈S satisfying Xk=S′k for 0≤k≤i with 0<Ti<T. We will show that there exists S∈S(S′,i) satisfying one of the two alternatives:
One can then conclude that there exists S∈S associated to x.
Consider first the case when the following holds
we label this the case a). Then, [(Γ(x,[t0,t0+T])≤(T−Ti))or(Ti<τ(x,[t0,t0+T]))] holds, which implies there exists ti+1, T≥ti+1>ti=Ti satisfying δ≤|x(ti+1)−x(ti)|. Therefore,
from (39) it follows that there exists (m,q)∈NE so that
We remark that qΔ≤(T−Ti) and so qminΔ≤(T−Ti) (so case a) holds if and only if statement A holds). By case a), take Si+1≡Si+mδ0=x(ti+1)=x(ti)+mδ0 and Ti+1≡t0+Ti+qΔ=ti+qΔ. The same arguments used above for the case τ(x,[t0,t0+T])=0, and the fact that ti+1−ti=qΔ=Ti+1−Ti≤T−Ti, show that there exists z+Wi=w(x,ti+1) where z≡δ0∑s−1j=0|pj|=∑li≤l,l+1≤li+1|x(rl+1)−x(rl)|∈Δti−t0,ti+1−t0V(w(x,ti)) where we used (41) (of course, we have m=∑s−1j=0pj). It then follows from (37) that Wi+1≡w(x,ti)+z∈VTi+1. If Ti+1<T it follows that (Si+1,t0+Ti+1,Wi+1)∈NA(S0,t0+T0,W0) (this set as in case A)). On the other hand, if Ti+1=T, we could take z∗=z and argue as in the above case τ(x,[t0,t0+T])=0 and conclude, in this case, that there is S associated to x.
Similarly, assume statement B holds, i.e.: [(T−Ti)<qminΔ] holds (this is possible as Ti>0). Then [(T−Ti)<qmin(x,[t0,t0+T])Δ] where qmin(x,[t0,t0+T])≡min{q:∃(m,q)∈NE(x,[t0,t0+T])}. Therefore, there exists ti+1=t0+T>ti=t0+Ti satisfying δ>|x(ti+1)−x(ti)|, then (34) implies
Notice that |m|<F. From the definitions and notation in Section 4 we can write (here we rely on (40)):
Moreover
Therefore Δiw≡w(x,t0+T)−w(x,ti)=ˆδ0∑s−1j=0|ˆpj|=δ0∑s−1j=0|pj|. By means of the properties listed in (14), and recalling that E=FG, we can check that the properties in (23) hold and by taking J≡s we verify that (p)J−1j=0∈NW(m,q). Therefore z≡δ0∑s−1j=0|pj|=∑li≤l,l+1≤li+1|x(rl+1)−x(rl)|∈Δti−t0,ti+1−tiV(w(x,ti)) where we used (41). It then follows from (37) that Wi+1≡w(x,ti)+z=Wi+z∈VT (where w(x,ti)=Wi holds by the inductive hypothesis). We emphasize, again, that the property of association in Definition 8 does not involve the coordinate Wi and, given that t1=t0+T, we could then take z∗=z in (30) (more precisely, we have established that there exists z satisfying (Wi+z)∈VT such that NA(m,q,z)≠∅; taking z∗ to be any such z will do for our argument). Therefore (Si+1=x(t0+T),t0+Ti+1=t0+T,Wi+1)∈NA(Si,t0+Ti,Wi), the latter set as in case B). It then follows that x is associated to S.
Finally, consider that statement C holds; we recall that in this case NA(Si,t0+Ti,Wi) is defined as the union of the sets NA(Si,t0+Ti,Wi) appearing under the entries A) and B). From our definition of ti+1 (see Definition 5) there are two possibilities: δ≤|x(ti+1)−x(ti)|,ti<ti+1≤t0+T or δ>|x(ti+1)−x(ti)|,ti<ti+1=t0+T. Whichever of these cases holds, the execution of condition C in the recursive construction of S and the arguments employed above for the cases A and B imply one of the alternatives in (44).
6.3. Discussion of rigurous results
The failure or validity of assumptions in Propositions 1 and 2 can be determined dynamically; that is, when we arrive to the next node that just unfolded. Hypotheses in the two propositions could fail at any node, so the larger N the larger the likelihood of the chart x not being associated to some S∈S. In our setting, the possibility to choose the value of δ with δ>δ0 allows to control the maximum value of N. Restricting N is also crucial when transaction costs are accounted for.
Section 10 defines worst case parameter estimation and risk taking parameter estimation. The mentioned hypotheses failures could be said to happen with uncertainty in the case that all parameters have been estimated in the worst case manner. If, on the other hand, some parameters were estimated in a risk-taking way; the failure may happen with a certain (empirical) frequency.
One special situation, namely the case when there exists l such that
could lead to violation of the assumptions in Propositions 1 or 2. Notice that in practice (50) will occur for our need to take δ0 larger in order to achieve reasonable execution times for our implementation (see Appendix 1). So, it will be a case of a parameter to be considered to be risk taking. It turns out that, under some conditions, one can show that weaker versions of the conclusions in Propositions 1 and 2 are valid under (50). This is argued in Section 7.
Further discussion on the above issues can be found in Sections 9.2 and 9.3.
7.
Trajectory approximation error due to δ0≥0.01
In this section we weaken the assumptions in Proposition 1 to account for the possibility that (x(ti+1)−x(ti))∈δ0Z could fail given that we assume δ0≥0.01. As we remarked previously, (x(ti+1)−x(ti))∈δ0Z is assumed implicitly by (33) and explicitly by (34). In order to afford weaker assumptions, we also need to weaken the conclusion of that proposition while maintaining its practical relevance; this we can achieve by replacing the notion of association between x and S by weak association as defined below. We will establish the existence of a value of δ0≥0.01 for which one can establish a weak association.
For simplicity, we restrict our analysis to type Ⅰ models MIDP. A different error analysis is required to accommodate the coordinate Wi as we will need to account for possible violations of Vti−t0(x,[t0,t0+T])⊆Vti−t0 in Proposition 2 due to δ0≥0.01.
We highlight that the superhedhing property (4) is crucial to deploy the proposed models; the clear financial relevance is explained in Section 10. It is when x is associated to S that such superhedging property becomes relevant as it holds when we replace the values Si for x(ti) (ti=Ti is also essential). Therefore, what really matters is that the superhedging property holds when we use the chart samples x(ti), this observation motivates the definitions and developments that follow.
We modify below the association relationship x→S introduced in Definition 8 (as indicated, we presently restrict ourselves to MIDP models). Also, for simplicity, Z below will be the payoff of a path independent European derivative and so we can consider Z:R→R.
Definition 7.1 (Weak association). Given a chart x:[t0,t0+T]→R, β>0 and option Z, we say that ˆS=ˆS(x)∈S is weakly associated to x (for the given β and Z) if there exists H∈H such that:
where ˆS={ˆSi=(ˆSi,ˆTi)}.
If x is associated to S then, by (4), it will be weakly associated as well for any Z and β. Actually, the dependencies of ˆS on Z and β in Definition 9 are incidental, the crucial point is that there exists ˆS∈S along which we can invest and that such investments will superhedge Z when the actual risky asset unfolds along the values x(t). Given that β is fixed in the above definition, we refer to ˆS as an approximating trajectory.
7.1. Construction of ˆS(x)
We describe below a method to set δ0≥0.01 and to construct ˆS weakly associated to x under weaker assumptions than the ones required in Proposition 1.
To simplify the notation let xi≡x(ti), 0≤i≤N≡N(x). We will assume the following is valid at all nodes (S,i):
where the interval [S−i+1,S+i+1] is considered here as a subset of R (i.e. not as a subset of δ0Z). Property (52) weakens assumptions required in Proposition 1. More precisely, in the present case of models MIDP, assumptions (32), (33) and (34) imply (52) that only requires that we can approximate chart values xi from above and below with trajectory values Si∈δ0Z+x(t0) instead of assuming that chart changes (xi+1−xi) are exactly matched by trajectory coordinates changes (Si+1−Si).
Existence of S+ and S− will be available to our construction of ˆS by the consequent in (52) and the fact that the construction of ˆS (described in this section) is recursive and the antecedent of (52) will be satisfied in the previous step. For the same reason, ˆTi=ti for all i will be trivial by (52) (and the fact that, by construction, either ˆSi+1=S+i+1 or ˆSi+1=S−i+1) hence, we only explicitly describe the construction of the coordinates ˆSi.
We will construct an approximating element ˆS=ˆS(x) in the trajectory set satisfying:
where H is the superhedging optimal portfolio from (4) for Z and ϵ=0 and N=N(ˆS)=NH(ˆS). Notice that for simplicity we have forced ϵ=0 in (4) to avoid introducing a new inessential parameter (this is possible as S is finite and this implies the computation of the optimal H is achieved by an actual minimum in infH∈H). Such H will be fixed for the rest of the discussion. If (53) is fulfilled it guarantees that x is weakly associated to ˆS; this is so because (53) implies
where the last inequality follows because H is the optimal portfolio in (4) with ϵ=0 and ¯V≡¯V(S,Z,M).
So, the question becomes: can one choose δ0≥0.01 so that (53) holds for some approximating trajectory ˆS(x)? The answer is in the affirmative and the developments shed light in how some nodes play a relevant role.
7.2. Upper bound via sign selection
We proceed recursively, fix ˆS0≡S0=x0, so H0(ˆS0)=H0(S0). We describe the construction of ˆSi+1 under the sole assumption that |ˆSi−xi|≤δ0. The construction terminates as soon as ˆTi=T, it will then be clear that the constructed ˆS belongs to S and (53) holds and so ˆS is weakly associated to x.
Our main goal is to find a suitable upper bound for
notice we have joined pairs of terms appearing in (53) and remark that we will have a non paired term, namely Hi+1(ˆS)(xi+2−ˆSi+2) for the case of i+1=N−1. Therefore, that last term has to be considered as a separate case (something we do after first dealing with the paired terms (55)).
Let us analyze (55) with i+1<N−1, and suppose S0,ˆS1(x),…,ˆSi(x) have been already constructed satisfying the antecedent of (52). We attempt to make (55) non positive by choosing a closest (but there is the issue of choosing the approximation from above or below) value of S′i+1, S′∈S(ˆS(x),i), to the given value of xi+1. Notice that the value of Hi+1(ˆS) depends on first choosing the value of ˆSi+1. We have the following possibilities:
● In case there exists S′∈S(ˆS(x),i) satisfying S′i+1=xi+1, we set ˆSi+1=ˆSi+1(x)=S′i+1.
● In case that ˆS+ (recall that ˆS+∈S(ˆS(x),i)) satisfies [Hi+1(ˆS+)−Hi(ˆS)]≥0 we set ˆSi+1=ˆSi+1(x)=ˆS+i+1.
● In case that ˆS− (recall that ˆS−∈S(ˆS(x),i)) satisfies [Hi+1(ˆS−)−Hi(ˆS)]≤0 we we set ˆSi+1=ˆSi+1(x)=ˆS−i+1.
Notice that in all the cases above (55) is non positive and so 0 is, so far, an upperbound for (55).
It remains to define ˆSi+1(x) and bound (55) from above in the following case:
That is, Hi+1(S′)−Hi(ˆS) goes from being negative to being positive when S′=ˆS+→S′=ˆS−.
If (56) holds we define ˆSi+1=ˆSi+1(x)=ˆS+i+1 whenever 0<ˆS+i+1−xi+1≤δ0/2 and set ˆSi+1=ˆSi+1(x)=ˆS−i+1 whenever 0<xi+1−ˆS−i+1<δ0/2. This completes the definition of ˆSi for 0≤i≤N(x)−1.
Notice that in all cases |ˆSi−xi|≤δ0 holds for 0≤i≤N(x)−1 which gives access to the consequent in (52) through the recursion/induction.
We gain some insight by analyzing (56) in some more detail, towards this goal we introduce some notation that will be used shortly. Given a node (S,i), any existing pair S↑ and S↓ satisfying 0<S↑i+1−S↓i+1≤δ0, S↑,S↓∈S(S,i), T↑i+1=T↓i+1 and
will be called a portfolio turning pair for such node. Notice that if the pair S↑=S↑(S) and S↓=S↓(S) exists, then it is unique and that they are analogous to S+(x) and S−(x) introduced earlier.
As an informal remark, notice that a turning pair for a node is expected to happen in isolated circumstances. For example, a plausible continuity of Hi+1 gives Hi+1(S0,…,Si,S↑i+1)≈Hi+1(S0,…,Si,S↓i+1) given that 0<S↑i+1−S↓i+1≤δ0. That is, by taking δ0 small enough any case satisfying (56) disappears by continuity. In the actual discrete case this is clearly always true by taking δ0=0.01 so the portfolio investment is always continuous (independently of the option) with respect to the natural (spatial) proximity of trajectories (by the discrete nature of real trajectories).
For i fixed, let:
and,
For (S,i) given we introduce:
Consider (55), we have already obtained an upperbound by 0 when (56) does not hold. For the upperbound inequality below we then assume the validity of (56), therefore
Adding up terms we obtain the following bound:
The definition of w(δ0) only involves M (and Z indirectly), that is, its evaluation only requires access to S and the optimal portfolio H (for option Z). We comment on the meaning and practicality of (67) in the next section.
7.3. Constraints on δ0 for weak association
Here we put together previous estimates; to sum up, we want to construct a trajectory ˆS(x) which is weakly associated to x. This allows to extend the superhedging property, available in M when using ¯V(S0,Z,M), to the case of using the actual trajectory samples xi. The construction of ˆS(x) described in the previous section works as long as δ0 is small enough, in fact we show below that we obtain constraints on δ0 which depend only on M, β>0 and Z.
To make use of the obtained upperbound, we write (53) as follows
where
and
Bounding a(x) is not problematic as we can always make HN−1(ˆS)(xN−ˆSN)≤0 by choosing ˆSN above or below xN depending on the sign of HN−1(ˆS) (which does not depend on ˆSN). Then, we can bound Z(xN)−Z(ˆSN) by the modulus of continuity of Z as |xN−ˆSN|≤δ0. All this we can do thanks to the fact that the antecedent in (52) holds for i=N(x)−1. In the case of a European call Hi≥0, so we can choose ˆSN≥xN hence Z(xN)−Z(ˆSN)≤0 and so a(x)≤0. Therefore, for a European call option β≥b(x)≥a(x)+b(x) and so, for this reason we concentrate only on b(x) below.
We have seen that b(x)≤w(δ0) (see (67)), therefore we look for a value of δ0 satisfying
As we have argued, taking δ0=0.01 makes w(δ0)=0 and allows the construction of ˆS under the hypothesis (52). This situation is consistent with Proposition 1.
7.4. Meaning of Constraint w(δ0)≤β
Admittedly the computation of w(δ0) is impractical but the analysis leading to this quantity is useful. Actually, to avoid any dependency on ˆS, and so on x, the sets E↑i and E↓i were defined larger than could be necessary if we allow our models to have some extra flexibility. Assume we allow δ0 to depend conditionally on a given node (S,i), in that scenario, we can modify its value iteratively as we construct ˆS0,ˆS1,…. This added flexibility allows us to replace the condition S∈S in the definition of the sets E↑i and E↓i by S∈S(ˆS,i). With such modification wi(δ0,S)=0 if S∉S(ˆS,i); for example, one could identify nodes (S,i) where wi(δ0,S)≠0 and refine δ0 at those nodes only. Crucially, this refinement can be done as the samples xi unfold.
Notice that we have defined weak association in terms of superhedging but we can think in terms of profits as follows: let Profits≡P(t0,K)−¯V(S0,Z,M)−β where P(t0,K) is the market selling price of Z at t0 and β>0. One can then set up parameters in M to risk-taking values so that Profits>0. Then (71) allows to select a value of δ0 such that Profits do not disappear due to errors in trajectory matching (of course with risk taking parameter there is a risk for (52) to fail). This is so as (71) implies (53) which in turn implies (54).
8.
Measurements on charts for estimation
The present and the next sections specify all the inputs required to construct each of the two types of models described in Section 5.2. Actually, by making different instantiations of some of the models' inputs we will be able to describe several specific models.
Towards these tasks we assume the availability of chart values x∗(t) with t∈{kΔ:k∈Z}. We will also use the notation T⊆{kΔ:k∈Z} to denote a historical interval of times for which we have access to values x∗(t), used for estimation. We will specify further characteristics of T whenever relevant. We also assume a given T=MTΔ. Notice that treating T as an interval will incorporate overnight effects that could be best modelled separately (something we neglect to do).
All models rely on the following parameters: τ,Γ, the set NE and the collection of sets {Vρ}0≤ρ≤T (this later collection is only needed for type Ⅱ models). In some cases, for simplicity, we refer to this family of parameters and sets generically as input parameters, they need to be estimated. The remaining parameters are of a different type, they are: δ,δ0,Δ,T. The parameters δ and Δ are investor dependent and they should be calibrated, guidelines to calibrate δ are available in Section 9. The parameter δ0 is a parameter of practical concern discussed in several places in the paper and in particular in Section 7. Finally T depends on the intended financial application.
Our approach relies on worst case estimation and risk taking estimation (see definitions in Section 9). Instead of relying on general notions from the start, we cover first some parameters in a case by case basis. We expect, in this way, to illustrate the straightforward methodology. Hence, for the time being, we will use the word estimate in quite general terms to refer to a computation that uses historical data.
Given historical data x∗(t), t∈T, and a value δ0 we obtain sampling times {rl} that depend on that specific value of δ0. These sample times are evaluated by fixing a window of MT data points (the number of data points in a time window of length T) and then shifting the window by one time unit and starting again. Each set of sampling times {rl}, one for each such window, will have a variable cardinality/length of L(x∗,[t,t+T])+1. Notice that the notation {rl} does not indicate the dependency on the window (which, in these cases, is left implicit for simplicity).
The following sections rely on notation introduced in Section 4.1.
8.1. Rounding
Estimates are evaluated, as much as possible, by manipulating the (exact) data values x(t)∈ˆδ0Z; whenever rounding to the grid δ0Z is required it will take place at the last step of the computations. Rounding is required in two instances, in one case for the estimation of NE and in the other case for the estimation of {Vρ} both quantities are model dependent and so associated to δ0. The quantities NE(x,[t0,t0+T]) (from Definition 6) and ∑li≤l,l+1≤li+1|x(rl+1)−x(rl)| (from (41)) are chart dependent and do not require any rounding. We note in passing that, for the latter quantity, we could have introduced the chart variation notation Vti+1−t0(x,[t0,t0+T])−Vti−t0(x,[t0,t0+T]) but we have not done so.
To emphasize: the sampling times {rl} and transaction times {ti} are evaluated using the exact values x(t). Similarly, the values of τ(x,[t0,t0+T]) and Γ(x,[t0,t0+T]) in (17) and (18) respectively, are in no need of any rounding.
Given y(t)∈ˆδ0Z let ‖y(t)‖∈δ0Z denote the closest value to y(t) (i.e. closest in δ0N). In case of ambiguity, namely when both conditions |⌊y(t)⌋−y(t)|=|⌈y(t)⌉−y(t)|=δ0/2 hold (where ⌊⌋ and ⌈⌉ are floor and ceiling functions rounding in δ0N), any possible disambiguation will be fine.
With some abuse of notation, when compared to Definition 6, we introduce NE(‖x‖,[t0,t0+T]) which is the first instance when we are required to use rounded values:
where the {ti} are as in Definition (5) and P≡P(x,[t0,t0+T])≡N≡N(x,[t0,t0+T]) (the latter as introduced in Definition 5) if δ≤|x(tN)−x(tN−1)| or P≡P(x,[t0,t0+T])≡N−1 otherwise.
The second instance when we rely on rounded values is in (79) below.
8.2. Estimate for NE
Define,
where NE(‖x∗‖,[t,t+T]) was introduced in (72). Define q∗≡min{q:∃(m,q)∈N∗E}, q∗≡max{q:∃(m,q)∈N∗E}, m∗≡min{m:∃(m,q)∈N∗E} and m∗≡max{m:∃(m,q)∈N∗E}.
The set NE will be assigned to two different estimates, doing so for each of the model types gives four different models. This multiplicity illustrates the obvious need to explore the stability/robustness of these alternatives. This is something we do not do in this paper and it may be best approached with machine learning techniques. Notice also that one can detect if the model fails in a dynamic way, this is a very important feature as it could be used to learn or adapt the investor behaviour. We do not pursue such a possibility in the paper.
1. DirectProduct(DP) Choice: NE={m∈Z:m∗≤m≤m∗}×{q∈N:q∗≤q≤q∗}(and soN∗E⊆NE).
2. Observable(OBS) Choice: NE=N∗E.
Either of the two choices for NE is referred to as as a worst case estimate while the sets that remain after removing any arbitrary subset from the worst case estimates are referred to as risk taking estimates.
8.3. Estimate for Γ [Implying: qminΔ≤Γ]
Define
where Γ(x∗,[t,t+T]) is given by (18). That is, Γ∗ is the smallest time duration such that for any t satisfying [t,t+Γ∗]⊆T there exists s∈(t,t+Γ∗] such that δ≤|x∗(s)−x∗(t)|. Unless δ is taken sufficiently small, we will find Γ∗=T which will make the parameter Γ∗ irrelevant. This later remark should be clear from the definitions of the models.
We set
such choice is referred as worst case. One can also consider Γ<Γ∗, this will entail some risk-taking as defined and analyzed in Sections 6 and 10. Notice that the choice Γ≥Γ∗ is possible and is more conservative that the worst case choice.
Given the above definitions and recalling that qmin≡min{q:(m,q)∈NE}, it then follows that qminΔ is the smallest time length, in the historical data set, for x∗ to have a δ-increment. Therefore, the definition of Γ∗ implies
This inequality is an assumption required for the two types of models and is thus established from (75).
8.4. Estimate for τ
Define
where τ(x∗,[t,t+T] was introduced in (17). We then set
One can also consider τ>τ∗ or τ<τ∗, the first choice will entail some risk-taking while the second choice being more conservative (both relative to worst case). Finally, notice that τ∗=0 implies Γ∗=T.
8.5. Models: MIDP,MIOBS
Given the above choices of NE, Γ and τ, we define two models of type Ⅰ which we refer to by MIDP and MIOBS. The former obviously refers to the DP choice for NE and the latter to the OBS choice for NE
8.6. Estimates for {Vρ}, ρ∈[0,T] [Models: MIIDPVAR, MIIOBSVAR]
Here we introduce two models of type Ⅱ. As we did with type Ⅰ models we set NE exactly as in items (1) and (2) in Section 8.2. These choices we label MIIDP and MIIOBS, it remains to specify the estimate for {Vρ}.
For 0≤ρ≤T define
where, as we have done many times before, the sampling times are as in Definition 4 and the notation ||y|| means the rounding of y to the grid δ0Z (already introduced in Section 8.1). Moreover, define
1. We introduce model MIIDPVAR (Model Ⅱ Direct Product with Variation) by setting: NE={m∈δ0Z:m∗≤m≤m∗}×[q∗,q∗]. {Vρ}≡{V∗ρ}, ρ∈[0,T]
2. We introduce model MIIOBSVAR (Model Ⅱ Observed with Variation) by setting: NE=N∗E. {Vρ}≡{V∗ρ}, ρ∈[0,T].
That is, we have set NE as we have done for MIDP and MIOBS. Examples of the sets {Vρ} are displayed in Figures 18 and 19.
9.
Data used, calibration of δ and output for estimates
This section completes the specification of the models introduced by mentioning some criteria to calibrate δ and providing some output for the estimated parameters. We also take the opportunity to introduce some general definitions of worst case estimation, such discussion should provide a perspective to our approach.
The simple estimation methodology used in the paper has been already introduced in Section 8 and we expand on it in the present section. Unless indicated otherwise, whenever we refer to probabilities in relation to parameter estimation or a risk-reward analysis, we mean empirical frequencies. In particular, probabilities are not necessarily given by a probability measure.
The word calibration refers to a process for assigning values to model parameters that can be chosen by the investor, in our case, δ. All other parameters have been set to worst case estimates in Section 8.
At this point in the paper, it seems appropriate to be more specific regarding the data we used and how it affects estimation. We will deploy the models in a setting with Δ=1 hour or Δ=1/2 hour and T of the order of several days. These values were imposed by the data we had access to, a negative side effect is long execution time for pricing. To illustrate how to alleviate this situation, in the case of type Ⅱ models, we have increased the value of δ0 as this choice allows for reasonable fast execution times for our implementation (we have also sub-sampled the sets NE). Notice that δ0 has two usages: i) it represents the discretization used in the model's grid (and it is in this role where δ0 needs to be curtailed to reduce computational time) ii) it defines the sampling times, changing δ0 has then an impact on estimation (in particular for type Ⅱ models which uses the variation coordinate). Details are provided at appropriate places in the paper.
The requirement (29) for type Ⅱ models is enforced in our implementation along the lines described at the end of Section 5.2.2. We also enforce Si≥0 by setting Sj=0, i≤j where i is the smallest index such that Si−1+mδ0<0.
9.1. Data employed
The two sources of data used for calibration and estimation are:
● An approximately 8 month long stretch of hourly data ticks for Facebook Inc (FB) from 2016-12-06 to 2017-07-03. At the end of this period, call option ask prices were captured across a variety of strikes for comparison with an expiration of 15 calendar days into the future.
● The same time interval of the Standard and Poor's Depositary Receipts S & P 500 Trust ETF (SPY) of 30 minutes ticks. Again, at the end of this period, call option ask prices were captured across a variety of strikes for comparison with an expiration of 15 calendar days into the future.
Let |M| be the total number of data points and MT the number of data points corresponding to an interval [t0,t0+T]. Notice we label past data points by M,M+1,…,−1 i.e. M<0.
We neglect overnight and weekend effects in the sense that we do not model any of its characteristics but their peculiarities will impact our estimates. Given that in our data there are 7 hourly samples per business day for the FB stock and there are 11 business days in the 15 calendar days we have T=77Δ, with Δ=1hr (so MT=77). Similarly for the 1/2 hourly data of SPY we have T=154Δ with with Δ=1/2 hr (so MT=154).
We use the notation T={kΔ:k=M,M+1,…,−1} and whenever we indicate historically estimated from chart data below we mean that we made use of data x∗(t) with t∈T.
9.2. Comments on worst case estimation
We hope the previous section's introduction by example of what we mean with worst case estimation has helped to show that our approach is simple minded and should not require, for our purposes, a theoretical justification. The present section and later sections do introduce some definitions on the matter but they are intended to provide due precision and with no intention of complicating the framework.
Worst case estimation as well as calibration (to a lesser extent) depend on a set of historical data. We use 8 months of data and hence, it can be argued, our estimates are not really worst case as it does not contemplate all possible historically available data. Our reasoning and conclusions, for the considered specific models, only depend on the property that the estimated sets NE have finite cardinality (or, more generally, are bounded). So, this should be considered the underlying assumption: these sets of reachable nodes are bounded even in the case of unlimited availability of historical data.
One expects that the worst case estimation as defined will be robust in matching future unfolding trajectories. Failure to match the unfolding chart to a modeling trajectory will only happen if the combined time and stock movements of the unfolding chart are more extreme than any in the past data. As we mentioned previously, a main issue we need to confront is that the presence of extreme price movements (and they do appear in our data set) will translate into non informative bounds for option pricing. Section 11 explains the specific key feature in type Ⅱ models that blocks the effect of extreme parameter values implying unrealistic price bounds.
Informally, parameters associated to an operational setting and used to construct models, should have stable worst case ranges. That is, their ranges should not contain non informative values. For example, our investor can select δ and, up to some extent T as well, so that τ∗>0 and Γ∗<T. The extreme values τ∗=0 and Γ∗=T make these parameters non informative for model construction. The case when a worst case parameter estimate (e.g. N∗) growths unbounded as historical data is agammaegated is a clear indication that some characteristics of the model need to be re-considered. To emphasize: selecting the model variables keeping in mind that their worst case ranges should substantially constrain the trajectory set is central to the proposed methodology.
9.3. Criteria to select δ and δ0
Recall that δ is the minimum chart change before an investor considers rebalancing. The implications of possible choices of δ are worth analyzing.
Choosing δ too large will cause the conditional set to collapse as there will be a value of δ large enough so that NE will contain a single element (in particular, this will create an arbitrage). Increasing δ further means that NE will be empty. Reducing δ from this extreme value could produce a binomial tree which will give a complete model. In this case the upper and lower bounds will coincide but this common value will not be necessarily equal to the market price. Of course, even in our worst case estimation setting, the issue arises of the effect on trajectory matching if we use a large value of δ leading to a small set NE.
For the above reasons we discuss some particular criteria as well as general guidelines to calibrate a value of δ. A general criteria, which we actually use to create our output examples, is to choose a value of δ which gives values of model parameters that constrain the size of of the trajectory set. Towards this end we plot how the parameters τ,Γ,mmax,mmin change with δ. Moreover, we already mentioned that the choice of δ controls the maximum value of N(S). In case we estimate some parameters to risk taking values, there will be a historical frequency of model failure. In this case, controlling the maximum value of N(S) allows to estimate the likelihood of model failure along a trajectory S (which is upperbounded by N(S) times the mentioned frequency of failure). In general terms, one can select a value of δ where observable and operational parameters are in between realistic worst case bounds. For example the minimum number of transactions N∗ and the maximum number of transactions N∗ represent quantities that can be achieved by our investor. Notice that the usual calibration practice will be to try to match the option prices to market prices; we could also use this criteria as a calibration target. Namely we could select δ so that our bounds are tight and contain the observable market value in between. A main benefit of the market models in the paper is the fact that one can use complementary criteria to calibrate given that most features of the models are observable and have a direct operational meaning.
The set NE should become stable before we exhaust all our historical data. In the paper we deal with two dimensions, (m,q), and one can monitor the convex hull of these pairs as a measure of stability. The convex hull could also be used as an alternative to the directproduct construction in order to obtain a solid set NE (as opposed to discrete points).
Given the information we store in the coordinates of the two types of models, and in order to control the maximum value of N(S), we remark that N(S)qminΔ≤MTΔ=T. Therefore, we could select δ so that MTqmin implies at most a few rebalances per day on average (if the value of qmin allows us to do this).
Finally, for type Ⅰ models and FB data, we have provided output for the choice δ=0.5,δ0=0.1. This value of δ is consistent with the above explanations as it follows from Figures 5 and 6. The analogous output for SPY data are Figures 9 and 10. Type Ⅱ models require a larger data structure implying longer computational times. To alleviate this situation we took δ0=0.5 which allows to take δ=1 (for the FB data set) and δ0=0.4,δ=0.8 (for the SPY data set) given smaller sets NE. Furthermore, we also sub-sampled the sets NE (as explained later in the paper). For consistency of comparison, Figure 15 provides pricing bounds for the model MIDP for the SPY data set with the values δ=0.8,δ0=0.4 (this output was produced with the same sub-sampling as the one used for type Ⅱ models).
Based on experimentation, we expect that none of these choices, will significantly alter the price bounds we report (relative to taking δ0=ˆδ0=0.01). Moreover, using sub-sampled sets NE that include the extreme values (as opposed to the full sets) should not alter the price bounds reported as the latter are only affected by the extreme stock value changes (given that the payoffs are convex).
9.4. Output for NE, τ, Γ, N∗ and N∗
As indicated, the output uses Δ=1 hr for FB data and Δ=1/2 hr for SPY data. Figures 2, 3, 5 and 6 illustrate some structure induced in the set of pairs (m,q)∈NE (as well as in τ,Γ,N∗ and N∗) which takes place by changing δ for the FB data. The analogous output for SPY data are Figures 9 and 10 (further output can be found in Appendix 2). In all these cases δ0=0.1. Figures 4 and 7 illustrate the sets NE, with δ=0.5,δ0=0.1 for the FB and SPY data respectively.
As already mentioned, for type Ⅱ models we have taken δ=1,δ0=0.5 for the FB case and δ=0.8,δ0=0.4 for the SPY case. The analogous outputs, to the ones mentioned in the previous paragraph, can be found in Appendix 2; here we only provide Figure 8 that displays NE taking δ=0.8,δ0=0.4 for the SPY data set.
9.5. Price bounds output
Here we comment and explain on the different models' prices obtained as function of the option's strikes. For comparison, the references Britten-Jones and Neuberger (1996) as well as Rebonato (2012), provide output for related models and the same minmax methodology. Figures 11, 12, 13 and 14 provide lower and upper bounds (in red) as functions of the strike for the models: MIOBS, MIDP, MIIDP and MIIOBS respectively for the FB data. In Appendix 2 we have provided more related output, namely output for MIOBS, MIDP but now for δ=1,δ0=0.5 and NE sub-sampled as we do for type Ⅱ models (in this way one can directly compare FB output with the output for type Ⅱ models provided here).
Figures 15, 16 and 17 provide lower and upper bounds (in red) as functions of the strike for the models: MIDP, MIIDP and MIIOBS respectively for the SPY data.
In all the above listed figures, the option market prices are displayed in blue as a function of the strikes.
The values of the relevant parameters are displayed in the captions, notice that for type Ⅱ models the values of δ0,δ are larger than in the case of type Ⅰ models. As explained before, this was done to speed up the execution times from the order of several days to a few hours (details are provided in Appendix 1). In the case of type Ⅱ models we have also sub-sampled NE as follows. For the DP model we skipped every other value of q and kept the extreme values of m. For the OBS model, for every q value we kept only the extreme values of m. Another shortcut we took when generating values for ΔiW=∑s−1j=0|pj|δ0 with the constraints (23) in effect. An explanation of a simple algorithm approximating this computation is described in Appendix 1, the parameter K (not to be confused with the option's strike) in that algorithm was taken to be K=50.
The model MIDP is quite conservative given the construction of NE as a direct product; the model's bounds reflect this fact. In contrast, the effect of using variation for constraining trajectories is illustrated in MIIDP which substantially tightens up the bounds (see Section 11 for the explanation). Consistently, even tighter bounds are given by the model MIIOBS as the historically observed pairs (m,q) are a subset of NE when the latter is given by a direct product. Figures 18 and 19 show the variation values used for the output for type Ⅱ models.
Some details on execution times are provided in Appendix 1, for example the model MIIOBS took 77 minutes in 4 CPU’s at 2.60GHz and 7.5 GiB of RAM plus 4 GB of Swap memory (in a Linux system). Model MIIOBS took 315 minutes (these times are for the SPY data set). While it may seem that compared to classical finite differences and Monte Carlo methods these times are prohibitively long, we would like to point out the following: computing maximal hedging bounds (i.e. the pricing component of our algorithm) is of comparable complexity to the classical pricing algorithm as it can be viewed as a linear dual problem to computing the maximal price in an incomplete discrete time framework. The later problem being itself a convex hull problem with the risk neutral probabilities the hull weights. On the other hand, and as a way of contrast with stochastic models, we have not made any assumptions on the dynamics of the underlying. Correspondingly, we have no assumptions to draw on that will help us find bounds in our models. In addition, our models make use of either every available observed movement or make worse case assumptions and so there is an extra cost to build the graph data structure required to encode the trajectory set. More general stochastic models (e.g. general Levy processes) are often similarly computationally expensive but offering less generality than our setting. Conversely, binomial and trinomial trees often used in industry to calibrate American option prices would obviously have much shorter execution times than the models presented here.
Some details on execution times are provided in Appendix 1.
10.
Risk-reward under worst case
Let us consider the case of an investor selling a European call option Z (with an analogous analysis for the case of buying an option) at time t0 with strike K and expiring at t0+T. She will set up a portfolio that will be rebalanced as described in Section 2 and Appendix 1 with a chosen parameter δ. Let P(t0,K) be the actual market price at which one option contract can be sold and M≡S×H a trajectorial model. If P(t0,K)>¯V(S0,Z,M) and the unfolding chart x(t),t∈[t0,t0+T], is associated to some S∈S, then the investor will profit P(t0,K)−¯V(S0,Z,M) per contract. This profit is guaranteed by (4) under the assumption that worst case estimates are not violated. Under such assumption, if S is one of the two trajectory sets types described in the paper and its parameters are estimated to worst case, then x→S holds. This is so by either the conclusion of Proposition 1 or Proposition 2 which hold given that the assumption that worst case estimates are not violated implies the hypothesis of the said propositions. The conclusion is that P(t0,K)>¯V(S0,Z,M) implies a profit with certainty.
The other logical possibility, in case that P(t0,K)≤¯V(S0,Z,M), is to set the parameters in S to risk taking estimates (all such possibilities were introduced in Section 8). This entails setting parameter values so that P(t0,K)>¯V(S0,Z,M′) holds (here M′ is the model with the said parameters set to risk taking values). It should be clear that the risk being taken is relative to the worst case and that empirical frequencies of failure can be evaluated.
Notice that nothing prevents the models to fail just because the future may not be included in our worst case past estimations. Clearly, distinct models will behave differently regarding this possibility.
The above discussion on profits also applies when we replace the notion of association between x and S by weak association introduced in Section 7.
We have not explored the profit and loss function that results by starting the superhedging portfolio with an initial value v=P(t0,K)≤¯V(S0,Z,M). Our main remark is that our framework permits to take investment decisions that have an objective meaning in terms of risk-reward.
11.
Type Ⅱ models: obstruction for local worst case estimates to propagate to unrealistic bounds
This short section explains why, in the case of type Ⅱ models, extreme parameter values do not translate into unrealistic bounds. It is the effect of the constraints Wi∈VTi that limits the appearance of extreme events. This is easily seen as follows, consider (mmax,q)∈NE and mi=mmax=∑J−1j=0pj. Then |mmax|δ0≤∑J−1j=0|pj|δ0=ΔiW, hence a trajectory S can not have ΔiS=mmaxδ0 at too many coordinates i. Otherwise, WTk∈VTk will not hold at some k (more precisely, this condition will fail as soon as the element S under consideration does not reflect the historical worst case constraint being enforced by VTk). A similar analysis applies to mmin (under the assumption that |mmin| is an extreme value). To summarize: an empirical constraint in variation (i.e. Wk∈VTk) limits the number of nodes (S,i) at which the investor has to account for the worst case possible stock movements (i.e. large values of |mi|). This has the effect of reducing the required funds ¯Vi(S,Z,M), this fact can actually be proven rigorously for convex payoffs Z. The resulting effect is a smaller price interval [V_0,¯V0]. The net effect is to limit the appearance of a large number of extreme values of m along any trajectory, notice that those large moves could appear anywhere in a trajectory and we do not assume any particular distribution. It will be of much interest to find a local condition (i.e. only involving consecutive times Ti,Ti+1) that achieves a similar result.
One could replace our use of variation by quadratic variation.
12.
Discussion
The methodology presented in the paper shows, by example, the possibility to construct models with a financial operational meaning. The elements used to construct the models result from portfolio rebalances and updates of data summaries (i.e. observation and updates for the variables of interest). There is then an association, via operations, between financial events and the model components. In other words, we assume a class of agents that act and react to financial events in a general and well defined manner. This setup allows the agents to obtain prices relative to their operations; the risk and reward characteristic of these prices are then linked to observable events. The price bounds so obtained have an objective meaning for these agents as models' features correspond to specific set of conditions faced by the agents. This charateristic makes the models of great value to investors. Clearly, it is easy to argue about the existence of this type of models without going to the trouble, i.e. analysis and implementation, that we have taken in our paper. The key comment is that the proposed models, when calibrated to worst case conditions (i.e. a robust calibration), can provide tight bounds as shown in the paper. These tight bounds can translate into attractive profit and loss characteristics. The latter type of analysis is a time consuming exercise not developed in the paper and better approached in higher frequency setting with several stocks and with more practical goals in mind. We remark that it is possible to replace the option by another stock and extend the analysis to a multidimensional setting making the whole methodology easier to deploy for testing. This exercise has been performed in Crisci (2019) and will be reported elsewhere. Nonetheless, we should emphasize that, in our opinion, the essential ingredient to obtain useful operational models is the selection of key variables affecting the agent's portfolio rebalances. Profit and loss analysis leading to investment decisions should be reliable and rewarding in relation to the relevance of the variables used in the model's construction.
Acknowledgments
S. Ferrando acknowledges partial financial support from NSERC for the completion of this project.
Conflict of interest
All authors declare no conflicts of interest in this paper.
Supplementary Material
A. Appendix 1
This appendix links to a separate file (Ferrando and et. al. (2019a)) providing details of a Matlab software implementation for the models introduced in the paper.
B. Appendix 2
This appendix links to a separate compressed zip file (Ferrando and et. al. (2019b)). The zip file is named Operational_root and contains a software bundle written in Matlab. The software implements the methods and algorithms described in the paper and can be used to reproduce the output displayed in the main paper. The software bundle also contains a README.pdf file, a copy of Appendix 1, and some other files as described in README.pdf. The data necessary to reproduce the outcomes displayed in the paper is also included in the bundle. There is also the file OutputOperationalModels.pdf, this is the document entitled "Output for Trajectorial Asset Models with Operational Assumptions" and contains extra output beyond the one contained in the main paper.
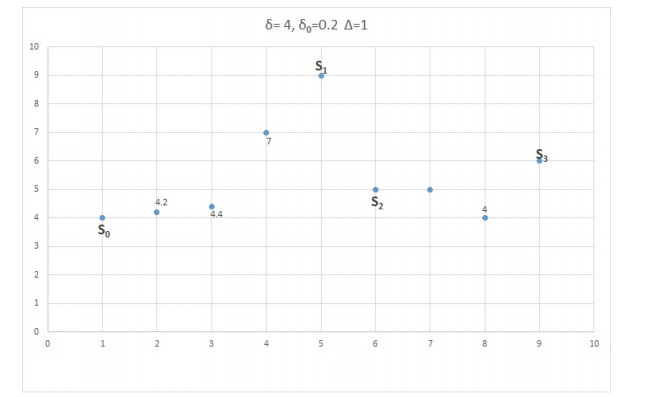









 DownLoad:
DownLoad: