Orbital stability of solitary waves to the coupled compound KdV and MKdV equations with two components

1.   Introduction

The coupled Korteweg-de Vries equations

were presented firstly by Hirota and Satsuma ^[1] in 1981, which indicated Eq.(1.1) exhibited a soliton solution and three basic conserved quantities. System (1.1) is used to describe the interaction of two long waves with different dispersion relations ^[2]. If $v = 0$, then system (1.1) is reduced to the well-known KdV equation. From then on, the coupled nonlinear wave equations draw much more attention from mathematicians. In recent years, system (1.1) has been extensively studied. Many profound results have already been obtained, on the orbital stability of solitary waves, cnoidal waves and dnoidal waves for the system (1.1) and its generalization, see Refereces ^[3,4,5] and the reference therein.

As we known, the following compound KdV and MKdV equation or the Gardner equation

has also been well studied during these decades. This equation is presented as a model for wave propagation in a one-dimensional nonlinear lattice and has widespread applications in the field of solid-state physics, plasma physics, fluid physics, and quantum field theory ^[6,7,8]. In plasma physics, Eq.(1.2) describes the small amplitude propagation of ion acoustic waves without Landau damping. When $\beta = 0$, Eq.(1.2) becomes the famous KdV equation, which is a classical model describing the one-way wave propagating in fluid. When $\lambda = 0$, Eq.(1.2) becomes MKdV equation, which is applied to describe the sonic wave propagating in some non-harmonic lattices and Alfven wave in the plasma free cold collision.

Recently, Eq.(1.2) has been widely studied in physics and mathematics, see for example ^{[9,10,11,12,13,14,15]}. Using Hirota's method, the modified method of full approximation, a special transformation based on the similarity variables, mapping approach and Fan's direct algebraic method, ^{[9,10,11,12,13,14]} studied the conservation laws, N-soliton, exact solitary solution etc. for Eq.(1.2). Zhang and Shi et al. ^[15] presented four explicit exact solitary waves with nonzero asymptotic value and two explicit exact solitary waves with zero asymptotic value for Eq.(1.2), and applied the orbital stability theory presented by Grillakis-Shatah-Strauss ^[16,17] to consider orbital stability of these solitary waves solutions. Alejo ^[18] presented local well-posedness results in the classical Sobolev space $H^{s}(R)$ with $s > \frac{1}{4}$ for the Cauchy problem of the Gardner equation and proved that the soliton was orbitally stable in the energy space using the standard techniques given by Zhidkov ^[19]. Muñoz ^[20] studied the stability of multi-kink solutions of the Gardner equation. Andrade and Pastor ^[21] established sufficient conditions for the orbital stability of periodic traveling wave solutions for one-dimensional dispersive equations by combining Lyapunov stability theorem and GSS orbital stability theory, and gave several applications for well known dispersive equations, such as KdV equation, MKdV euqation and Gardner equation et al. Moreover, Alves et al. ^[22] dealt with sufficient conditions for orbital stability of periodic waves of a general class of evolution equations supporting nonlinear dispersive waves and studied orbital stability of periodic waves for KdV eqaution, generalized KdV equation and Kawahara equation et al. The stability results revealed the behaviour of solution for KdV-type equation, and guided us to understand the evolution mechanism of physical quantity or state of these equations.

As is well known, the coupled nonlinear equations in which a KdV structure are embedded occur naturally in shallow water wave problems. Guha-Roy et al. ^[23,24,25] have studied the coupled nonlinear partial differential equations that can be solved exactly. Even if the stability of solitary waves with zero asymptotic value has been widely studied, few results are known on the orbital stability of solitary waves with nonzero asymptotic value. Moreover, the stability of solitary waves with nonzero asymptotic value cannot be easily obtained. As far as we know, the orbital stability of solitary wave and periodic wave of the coupled version of compound KdV and MKdV equations with two components have not been studied. In this paper, we are concerned with the following coupled version of compound KdV and MKdV equations with two components

where $\alpha, \beta, \lambda \in \mathbb{R}$ are arbitrary constants. The system (1.3) models the physical problem of describing the strong interaction of two-dimensional long internal gravity waves propagating on neighboring pycnoclines in a stratified fluid. It is interesting to point out that for $v = 0$, system (1.3) is reduced to the compounded KdV and MKdV equation (1.2) with $\gamma = 1$. In this paper, we shall focus our attentions on the orbital stability of solitary waves with zero and nonzero asymptotic value for Eqs.(1.3). The study of orbital stability considered in this paper is original and valuable. In addition, our work on Eqs.(1.3) includes and improves the results of Zhang et al. ^[15].

In this paper, we will apply the general theory of orbital stability presented by Grillakis et al. ^[16,17] to study orbital stability and instability of Eqs.(1.3). To overcome the difficulty of studying orbital stability of solitary waves with nonzero asymptotic value for Eqs.(1.3), we use a translation transformation to transfer this problem into solitary waves with zero asymptotic value for a reduced nonlinear coupled equations. Applying the translation transformation $u = \varphi+D$ and $v = \psi+\overline{D}$ to Eqs.(1.3), we have

By direct computation, we obtain that if $u(\xi)$ is a solitary wave with $D$ asymptotic value, and $v(\xi)$ is a solitary wave with $\overline{D}$ asymptotic value of Eqs.(1.3), then $\varphi = u-D$ and $\psi = v-\overline{D}$ are solitary waves with zero asymptotic value of Eqs.(1.4) and (1.5). Therefore, to prove orbital stability of solitary waves with $D$ and $\overline{D}$ asymptotic values for Eqs.(1.3), we only need to verify that solitary waves $\varphi = u-D$ and $\psi = v-\overline{D}$ with zero asymptotic value of Eqs.(1.4) and (1.5) are orbitally stable.

Because the stability in view here refers to perturbations of the solitary wave profile itself, a study of the initial value problem (1.3) is necessary. Similar to Theorem 1–2 in ^[26] and Theorem in ^[27], we can obtain the existence of solutions to the initial value problem of Eqs.(1.4) and (1.5).

Theorem 1.1. For any fixed $(\varphi_{0}, \psi_{0})\in H^{1}(R)\times H^{1}(R)$, there exists a unique solution $(\varphi, \psi)\in C([0, \infty); H^{1}(R)\times H^{1}(R))$ satisfying $(\varphi(0), \psi(0) = (\varphi_{0}, \psi_{0}))$ for Eqs.(1.4) and (1.5).

We define the orbital stability as follows:

Definition 1.1. The solitary waves $T(ct)\Phi(x)$ are orbitally stable if for any $\varepsilon > 0$, there exists $\delta > 0$ with the following property: If $\|U_{0}-\Phi(x)\|_{X} < \delta$ and $U(t)$ is a solution of (1.4) and (1.5) in some interval $[0, t_{0})$ with $U(0) = U_{0}$, then $U(t)$ can be continued to a solution in $0\leq t < +\infty$, and

where $\Phi(x) = (\varphi(x), \psi(x))$. Otherwise $T(ct)\Phi(x)$ are called orbitally unstable.

Then, by applying the extension version of the general theory of orbital stability presented by Grillakis et al. and Bona et al., we obtain the orbital stability of solitary waves for Eqs.(1.4) and (1.5).

Theorem 1.2. The solitary wave $T(ct)\Phi(x)$ of (1.4) and (1.5) are stable in $X$ if the condition $p(d^{\prime\prime}) = n(H_{c})$ holds, where $n(H_{c})$ be the number of negative eigenvalues of $H_{c}$, $p(d^{\prime\prime})$ be the numbers of positive eigenvalue of $d^{\prime\prime}$,

and

More specifically, if $d^{\prime\prime}(c) > 0$, then solitary waves $\Phi(x)$ are orbitally stable. Otherwise, $\Phi(x)$ are orbitally unstable.

This paper is organized as follows. In section 2, we obtain six solitary waves with zero and nonzero asymptotic values of Eqs.(1.3) (see Theorem 2.1 and Corollary 2.1). Section 3 shows that Eqs.(1.4) and (1.5) can be written as a Hamiltonian system and fulfills the conditions of orbital stability theory. In section 4, we show that six solitary waves of the coupled compound KdV and MKdV equations (1.3) are orbital stability and instability under some conditions (see Theorem 4.1). A brief summary is provided in the last section.

2.   Exact solitary waves of the coupled compound KdV and MKdV equations

The method of seeking the solitary wave solutions are various, such as inverse scattering transform, Painlevé analysis, Hirota bilinear transform method, Exp-function method, similarity transformation and so on., but we study the orbital stability for one specific form of solution in this paper. For simplicity, we will seek the solution of sech-type by a direct method.

Considering the traveling wave solutions of Eqs.(1.3)

and substituting (2.1) into Eqs.(1.3), we have

Integrating Eq.(2.3) once with respect to $\xi$ yields

where $E_{1}$ is an integration constant. Then, we obtain from (2.4)

It is to be noted here that $u$ would be regular everywhere (in particular, as $v(\xi)\rightarrow 0$) provided $E_{1}$ vanishes. As a result, Eq.(2.5) yields

Integrating (2.2) once and inserting (2.6), one can eliminate $v$ from (2.2) to get

where $E_{2}$ is an integration constant. Following the idea in ^[15], we seek the solitary wave satisfying

and the asymptotic values $C_{\pm} = \lim_{\xi\rightarrow \pm\infty}u(\xi)$ satisfy the algebraic equation

where $a_{3} = \beta$, $a_{2} = \lambda+\alpha^{3}$, and $a_{1} = (\alpha^{2}+1)c$. We can assume $E_{2} = \frac{\alpha}{2}c^{2}$ in (2.7) without loss of generality. Then, (2.7) reduces to

In what follows, we assume the solutions of (2.10) with the following form

where $A$, $B$, $k$ and $D$ are constants to be determined later. Substitution of (2.11) into (2.10) leads to the simultaneous equations with respect to $A$, $B$, $k$, and $D$

If $D$ satisfies the equality $2a_{3}D^{3}+3a_{2}D^{2}-6a_{1}D = 0$, then system (2.12) has solutions

as $a_{2}+2a_{3}D\neq0$, and

as $a_{2}+2a_{3}D = 0$, $a_{3} > 0$, and $a_{1}-\frac{a_{2}}{2}D > 0$.

Remark 2.1. Since $sechx$ is an even function, we take $k = \sqrt{a_{1}-a_{2}D-a_{3}D^{2}}$ and $k = \sqrt{a_{1}-\frac{a_{2}}{2}D}$ in Eqs.(2.13) and (2.14), respectively.

By combining (2.6), (2.11) with (2.13) and (2.14), respectively, we get the following theorem:

Theorem 2.1. Suppose that $D$ satisfies the equality $a_{3}D^{3}+\frac{3}{2}a_{2}D^{2}-3a_{1}D = 0$.

(1) If $a_{2}+2a_{3}D\neq0$ and $a_{1} > a_{2}D+a_{3}D^{2}$, the coupled compound KdV and MKdV equations (1.3) have the bell-shaped solitary waves $(u^{+}, v^{+})$ and $(u^{-}, v^{-})$, where $u$ is the form of (2.11), $v$ is the form of (2.6), and $A$, $B$, $k$ and $D$ are given by (2.13), $u^{+}$ represents the solution taking $"+"$ in $B$ of (2.13), while $u^{-}$ represents another case.

(2) If $a_{2}+2a_{3}D = 0$, and $a_{1}-\frac{a_{2}}{2}D > 0$, the coupled compound KdV and MKdV equations (1.3) has two solutions of the form (2.6) and (2.11)

where $u^{+}$ denotes the solution taking $"+"$ in front of radical sign in (2.15), $u^{-}$ denotes another case. Also, $v^{+}$ represents the solution taking $"-"$ in front of radical sign in (2.16), $v^{-}$ represents another case.

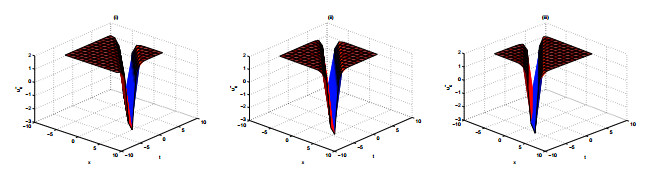
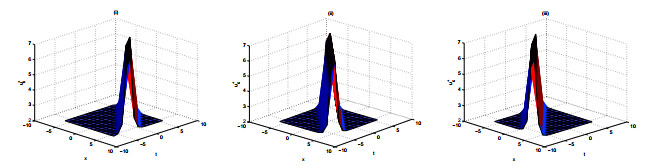
Remark 2.2. As an example, we give the 3D surfaces of $u$ by taking the values $a_1 = 2$, $a_2 = 2$, $a_3 = 0.5$, and $D = -2$ in the following Figures 1 and 2.

Remark 2.3. When $a_{3}\neq0$ and $D = 0$, from Theorem 2.1, system (1.3) has the solitary waves $(u^{\pm}(\xi), v^{\pm}(\xi))$, with $(0, c)$ asymptotic value

Meanwhile, the exact solutions $(u(\xi), v(\xi))$ are the solitary waves with nonzero asymptotic value of Eqs.(1.3) as $D\neq0$ in Theorem 2.1. Since the asymptotic value $D$ is the solution of $a_{3}D^{3}+\frac{3}{2}a_{2}D^{2}-3a_{1}D = 0$, we know that Theorem 2.1 gives the solitary waves $(u(\xi), v(\xi))$ with the following three asymptotic values

where $D_{1} = \frac{-3a_{2}+\sqrt{9a_{2}^{2}+48a_{1}a_{3}}}{4a_{3}}, D_{3} = \frac{-3a_{2}-\sqrt{9a_{2}^{2}+48a_{1}a_{3}}}{4a_{3}}$, in the case of $3a_{2}^{2}+16a_{1}a_{3} > 0$.

For convenience of express, we take $q_{i} = a_{2}+2a_{3}D_{i}$ $(i = 1, 3)$. It follows from Theorem 2.1, $u^{+}_{q_{i} > 0}(\xi)$ represents solitary wave taking $"+"$ in $B$ of (2.13), $u^{-}_{q_{i} > 0}(\xi)$ represents another case, and $v^{\pm}_{q_{i} > 0}(\xi) = c-\alpha u^{\pm}_{q_{i} > 0}$. Meanwhile, we similarly define $u^{+}_{q_{i} < 0}(\xi)$ and $u^{-}_{q_{i} < 0}(\xi)$, where $v^{\pm}_{q_{i} < 0}(\xi) = c-\alpha u^{\pm}_{q_{i} < 0}$. Furthermore, it is easy to see that $u^{+}_{q_{i} > 0}(\xi)$ is equivalent to $u^{-}_{q_{i} < 0}(\xi)$, and $u^{+}_{q_{i} < 0}(\xi)$ is equivalent to $u^{-}_{q_{i} > 0}(\xi)$. By some simple computations, we get the corollary as follows.

Corollary 2.1. (1) For wave speed $c > 0$, the coupled compound KdV and MKdV equations (1.3) have the solitary waves $(u(\xi), v(\xi))$ with $(0, c)$ asymptotic value

In the condition of $\alpha > \frac{c}{M_{1}}$, where $M_{1} = \inf|u_{1}(\xi)|$, we have $v_{1} < 0$. In the condition of $\alpha < -\frac{c}{M_{2}}$, where $M_{2} = \inf|u_{2}|$, we have $v_{2} < 0$.

(2) Suppose that $3(\lambda+\alpha^{3})^{2}+16\beta c(1+\alpha^{2}) > 0$, $(\lambda+\alpha^{3})^{2}+6\beta c(1+\alpha^{2})\neq0$. If $\lambda+\alpha^{3} > 0$ and $c < 0$, the coupled compound KdV and MKdV equations (1.3) have the solitary waves $(u(\xi), v(\xi))$ with $(D_{1}, c-\alpha D_{1})$ asymptotic value

where

In addition, if $c < \min\{\alpha D_{1}, 0, \alpha(\frac{A_{1}}{4+B_{1}}+D_{1})\}$, we have $v_{3}(\xi) < 0$. Also, if $c < \min\{\alpha D_{1}, 0, \alpha(\frac{A_{1}}{B_{1}}+D_{1})\}$, we have $v_{4}(\xi) < 0$.

(3) Assume that $3(\lambda+\alpha^{3})^{2}+16\beta c(1+\alpha^{2}) > 0$, $(\lambda+\alpha^{3})^{2}+6\beta c(1+\alpha^{2})\neq0$. If $\lambda+\alpha^{3} < 0$ and $c < 0$, the coupled compound KdV and MKdV equations (1.3) have the solitary waves $(u(\xi), v(\xi))$ with $(D_{3}, c-\alpha D_{3})$ asymptotic value

where

Moreover, if $c < \min\{\alpha D_{3}, 0, \alpha(\frac{A_{3}}{4+B_{3}}+D_{3})\}$, we have $v_{5}(\xi) < 0$. Also, if $c < \min\{\alpha D_{3}, 0, \alpha(\frac{A_{3}}{B_{3}}+D_{3})\}$, we have $v_{6}(\xi) < 0$.

3.   General conclusion for orbital stability of solitary waves to Eqs.(1.3)

We first employ the translation transformation $u = \varphi+D$ and $v = \psi+\overline{D}$ to Eqs.(1.3). It follows from (1.3) by simple computation

We will prove that system (3.1)–(3.2) are a Hamiltonian system, and satisfies the conditions of the general orbital stability theory proposed by Grillakis et al. ^[16].

Let $U = (\varphi, \psi)$. The function space on which we shall work is defined by $X = H^{1}(R)\times H^{1}(R)$. Let the inner product of $X$ be

for $f = (f_{1}, f_{2}), g = (g_{1}, g_{2})\in X$. The dual space of $X$ is $X^{*} = H^{-1}(R)\times H^{-1}(R)$, there exists a nature isomorphism $I: X\rightarrow X^{*}$ defined by

where $\langle\cdot, \cdot\rangle$ denotes the pairing between $X$ and $X^{*}$

From (3.3)–(3.5), we can see that

Let $T$ be one-parameter groups of unitary operator on $X$ defined by

Differentiating (3.7) with respect to $s$ at $s = 0$, we have

It follows from Theorem 2.1, (3.1) and (3.2) that there exist solitary waves $T(ct)\Phi(x)$ of (3.1) and (3.2) with $\Phi(x)$ defined by

In this and the following sections, we shall consider the orbital stability of solitary waves $T(ct)\Phi(x)$ of (3.1) and (3.2).

Let us define a functional vector on $X$

By (3.7) and (3.10), we can verify that $E(U)$ is invariant under $T$

For any $t\in R$, we get

Note that system (3.1) and (3.2) can be written as the following Hamiltonian system

where $U = (\varphi, \psi)$, $J$ is a skew-symmetrically linear operator defined by

and

is the Frechet derivative of $E$.

Let

such that $T^{\prime}(0) = JB$, and

By (3.7) and (3.15), we can prove that

and

Furthermore, notice that $U(\xi) = (\varphi(\xi), \psi(\xi))$ satisfies system (3.1)–(3.2), where $\xi = x-ct$, we have

We integrate (3.19) and (3.20) once, respectively, then have

Combining (3.14), (3.18), (3.21) and (3.22), we have

Define an operator from $X$ to $X^{*}$

Observe that $H_{c}$ is self-adjoint in the sense that $H_{c}^{*} = H_{c}$. This means that $I^{-1}H_{c}$ is a bounded self-adjoint operator on $X$. The spectrum of $H_{c}$ consists of the real numbers $\lambda$ such that $H_{c}-\lambda I$ is not invertible. By complex calculation with (3.8) and (3.24), we get that

that is, $\lambda = 0$ belongs to the spectrum of $H_{c}$.

For any $y = (y_{1}, y_{2})\in X$, by (3.24), we have

where $L = -\partial^{2}_{x}-(\lambda+2\beta D)\varphi-\beta\varphi^{2}-\beta D^{2}-\lambda D+c+\alpha^{2}(\psi+\overline{D})$. Next, let's study the spectrum structure of the linear operators $L$. For $L$, when $x\rightarrow\infty$, we have $\varphi\rightarrow 0$, $\psi\rightarrow 0$ and $-(\lambda+2\beta D)\varphi-\beta\varphi^{2}+\alpha^{2}\psi\rightarrow 0$. Therefore, by Weyl$^{\prime}$s essential spectral theorem, the essential spectrum of $L$ is $\sigma_{ess} L = [-\beta D^{2}-\lambda D+\alpha^{2}\overline{D}+c, +\infty)$. It follows from (2.6) and (3.19) that

Since $\varphi_{x}$ has a unique zero at $x = 0$, by using the Sturm-Liouville theorem, we know that zero is the second eigenvalue of $L$, and $L$ has exactly one strictly negative eigenvalue $-\sigma^{2}$, with an eigenfunction $\chi$, that is,

According to the Lemma in Appendix of ^[28], for any real functions $y\neq0\in H^{1}(R)$ satisfying $\langle y, \chi\rangle = \langle y, \varphi_{x}\rangle = 0,$ there exists a positive number $\delta > 0$ such that $\langle L y, y\rangle\geq\delta\|y\|^{2}_{H^{1}(R)}.$ Then, we get $\langle L y, y\rangle > 0.$

For any $\Psi = (y^{-}_{1}, y^{-}_{2})\in X$, we choose $y^{-}_{1} = \chi$, $y^{-}_{2} = -\alpha\chi$, $\Psi^{-} = (\chi, -\alpha\chi)$, then

Combining (3.25)–(3.29), the spectrum property of $L$ and the conditions in Corollary 2.1, we know that $H_{c}$ has exactly one strictly negative eigenvalue $-\sigma^{2}$, zero is the second eigenvalue.

Let

Again using the Lemma in Appendix of ^[28], we get that the third eigenvalue of $H_{c}$ is strictly positive, that is, for any $p = (p_{1}, p_{2})\in P, p\neq(0, 0)$, there exist $\delta > 0$ such that $\langle H_{c}p, p\rangle > \delta\|p\|_{X}^{2}$. Let

Then, the assumption 3.3 in ^[16] holds.

Next, we define $d(c): R\rightarrow R$ by

and define $d^{\prime\prime}(c)$ to be the second derivative of function $d$ with respect to $c$. In addition, we use $p(d^{\prime\prime})$ to denote the numbers of positive eigenvalue of $d^{\prime\prime}$.

Then, by applying the extension version of the general theory of orbital stability presented by Grillakis et al., the results obtained in ^[28] or by the similar derivation, we obtain the orbital stability of solitary waves in Theorem 1.2.

4.   Orbital stability of solitary waves for Eqs.(1.3)

In this section, we shall verify that $p(d^{\prime\prime}) = 1$ and give the detailed proof of Theorem 1.2.

Combining (3.8), (3.15) with (3.23) and differentiating (3.33) once with respect to $c$, it follows that

According to the stability theory developed by Grillakis et al. ^[16], we only need to observe the sign of $d^{\prime\prime}$, from which we can obtain the orbital stability of solitary waves $\Phi(\xi)$ with zero asymptotic value for system (3.1)–(3.2). Since orbital stability of $\Phi(\xi)$ is equivalent to that of solitary waves $(u(\xi), v(\xi))$ of Eqs.(1.3), we only need to prove $d^{\prime\prime} > 0$ or $d^{\prime\prime} < 0$ for $\Phi(\xi)$. According to the case of the value $a_{2}+2a_{3}D$, we discuss the orbital stability and instability of the corresponded solutions.

4.1.   Orbital stability of solitary waves for Eqs.(1.3) in the case of $a_{2}+2a_{3}D=0$

In the case of $a_{2}+2a_{3}D = 0$, $k$, $A$, and $B$ are given by (2.14). From (4.1), we have

Let $y = e^{2k\xi}$, we get

since $\beta > 0$ and $2(1+\alpha^{2})c > (\lambda+\alpha^{3})D$. Then, we get conclusion as follows:

Conclusion 4.1. If $a_{2}+2a_{3}D = 0$, and the wave speed $c$ satisfies $c\in E = \{c|c < \min\{-\frac{\alpha(\lambda+\alpha^{3})}{2\beta}, \frac{\alpha(\sqrt{24c(1+\alpha^{2})+6(\lambda+\alpha^{3})^{2}}-\lambda-\alpha^{3})}{2\beta}\}, c > -\frac{(\lambda+\alpha^{3})^{2}}{4(1+\alpha^{2})\beta}\}$, then the solitary waves $u^{+}$ and $v^{+}$ in (2.15) and (2.16) of Eqs.(1.3) are orbitally stable. If $a_{2}+2a_{3}D = 0$, and the wave speed $c$ satisfies $c\in E = \{c|c < \min\{-\frac{\alpha(\lambda+\alpha^{3})}{2\beta}, \frac{-\alpha(\lambda+\alpha^{3}+\sqrt{24c(1+\alpha^{2})+6(\lambda+\alpha^{3})^{2}})}{2\beta}\;\;\;\}, c > -\frac{(\lambda+\alpha^{3})^{2}}{4(1+\alpha^{2})\beta}\}$, then the solitary waves $u^{-}$ and $v^{-}$ in (2.15) and (2.16) of Eqs.(1.3) are orbitally stable.

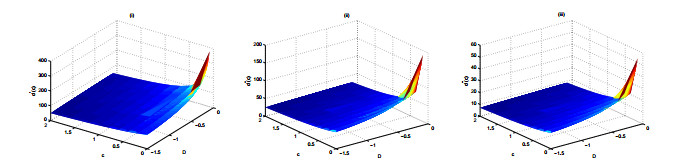
Remark 4.1 We simulate numerically the orbital stability of the solitary wave (2.15) and (2.16) for Eqs.(1.3) by Maple, to show the result obtained visually. Figure 3 is the 3D surface of $d''(c)$ in $(4.3)$ by taking the values $\lambda = 1.2$, $\alpha = 0.3$.

It is shown in Figure 3 that $d''(c)$ is positive when $\beta > 0$ and $D = -\frac{\lambda+\alpha^{3}}{2\beta }$. So there exists a wave speed interval, such that $d''(c)$ is positive.

4.2.   Orbital stability of solitary waves for Eqs.(1.3) in the case of $a_{2}+2a_{3}D\neq0$

In the case of $a_{2}+2a_{3}D\neq0$, $k$, $A$, $B$ are given by (2.13). From (4.1), we have

Let $z = e^{k\xi}$, we get

where $p = \frac{B+2}{2}$. From (2.13), we have $p^{2} = \frac{(a_{2}+2a_{3}D)^{2}}{6a_{3}k^{2}+(a_{2}+2a_{3}D)^{2}} < 1$. Due to

and (4.5), we have

From (2.13) and $p = \frac{B+2}{2}$, we get

Substituting (4.8) into (4.7), we have

where $p$ is a function of $D$ and $D$ is a function of $c$. Hence

Since

and

we have

Substituting (4.11) and (4.15) into (4.10), we have

where $l = 2(a_{2}+2a_{3}D)D^{\prime}_{c}-p^{2}(3(1+\alpha^{2})-(a_{2}+2a_{3}D)D^{\prime}_{c})$.

Furthermore, substituting $p = \pm\frac{|a_{2}+2a_{3}D|}{\sqrt{6a_{3}k^{2}+(a_{2}+2a_{3}D)^{2}}}$ into (4.16), we have

where $a_{1} = c(1+\alpha^{2})$, $a_{2} = \lambda+\alpha^{3}$, $a_{3} = \beta$, and $k$ is given by (2.13). The choice of the signs in parenthesis of (4.17) is the same as that in $B$ of (2.13). From Theorem 2.1, assumption $q = a_{2}+2a_{3}D$ and (4.17), we can get that

(1) the same expression of the discrimination of orbital stability for $u^{+}_{q > 0}(\xi)$ and $u^{-}_{q < 0}(\xi)$ is

(2) the same expression of the discrimination of orbital stability for $u^{+}_{q < 0}(\xi)$ and $u^{-}_{q > 0}(\xi)$ is

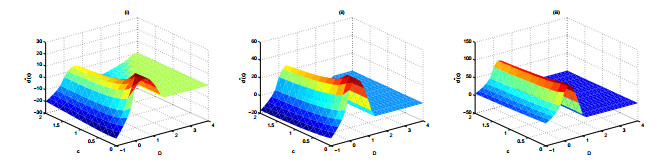
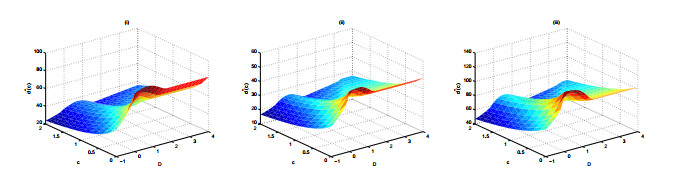
Remark 4.2. Figures 4 and 5 are the 3D surfaces of $d''(c)$ in $(4.18)$ and $(4.19)$ by taking the values $\lambda = 1.2$ and $\beta = 0.3$.

It is shown in Figure 4 that $d''(c)$ may be positive or negative when $\beta > 0$ and $\lambda+\alpha^{3}+2\beta D\neq0$. So there exists a wave speed interval, such that $d''(c)$ is positive or negative for solutions $u^{+}_{q > 0}(\xi)$ and $u^{-}_{q < 0}(\xi)$. Meanwhile, it is shown in Figure 5 that $d''(c)$ is positive when $\beta > 0$ and $\lambda+\alpha^{3}+2\beta D\neq0$. So there exist the wave speed interval, such that $d''(c)$ is positive for solutions $u^{+}_{q < 0}(\xi)$ and $u^{-}_{q > 0}(\xi)$.

Using mathematical analysis methods, we have the following theorem from the discrimination (4.17)–(4.19):

Theorem 4.1. (1) If $(\lambda+\alpha^{3})^{2}+6\beta c(1+\alpha^{2}) > 0$ and $\alpha > \frac{c}{M_{1}}$, where $M_{1} = \inf{|u_{1}(\xi)|}$, then the solitary waves $(u_{1}(\xi), v_{1}(\xi))$ with $(0, c)$ asymptotic value are orbitally stable. If $\alpha < -\frac{c}{M_{2}}$, where $M_{2} = \inf{|u_{2}(\xi)|}$, then the solitary waves $(u_{2}(\xi), v_{2}(\xi))$ with $(0, c)$ asymptotic value are orbitally stable.

(2) If $3a_{2}^{2}+16a_{1}a_{3} > 0$, $a_{2}^{2}+6a_{1}a_{3}\neq0$, $\lambda+\alpha^{3} > 0$, $E_{1} = \{c|c < \min\{\alpha D_{1}, 0, \alpha(D_{1}+\frac{A_{1}}{4+B_{1}})\}$ and $E_{2} = \{c|c < \min\{\alpha D_{1}, 0, \alpha(D_{1}+\frac{A_{1}}{B_{1}})\}$, then the solitary waves $(u_{3}(\xi), v_{3}(\xi))$ and $(u_{4}(\xi), v_{4}(\xi))$ with $(D_{1}, c-\alpha D_{1})$ asymptotic value have the following stability results, respectively.

(2.1) There exist $c_{0}\in(-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}, 0)$ and $c_{1}\in(-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, -\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}})$ such that $(u_{3}(\xi), v_{3}(\xi))$ are orbitally stable as $c\in (c_{1}, c_{0})\cap E_{1}$ and $c\neq-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}$, and they are orbitally unstable as $c\in (-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, c_{1})\cap E_{1}$ or $c\in (c_{0}, 0)\cap E_{1}$.

(2.2) $(u_{4}(\xi), v_{4}(\xi))$ are orbitally stable when the wave speed $c$ satisfies $c\in (-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, 0)\cap E_{2}$ and $c\neq-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}$.

(3) Suppose that $3a_{2}^{2}+16a_{1}a_{3} > 0$, $a_{2}^{2}+6a_{1}a_{3}\neq0$, $\lambda+\alpha^{3} < 0$, $E_{3} = \{c|c < \min\{\alpha D_{3}, 0, \alpha(D_{3}+\frac{A_{3}}{4+B_{3}})\}$ and $E_{4} = \{c|c < \min\{\alpha D_{3}, 0, \alpha(D_{3}+\frac{A_{3}}{B_{3}})\}$, then the solitary waves $(u_{5}(\xi), v_{5}(\xi))$ and $(u_{6}(\xi), v_{6}(\xi))$ with $(D_{3}, c-\alpha D_{3})$ asymptotic value have the following properties, respectively.

(3.1) $(u_{5}(\xi), v_{5}(\xi))$ are orbitally stable when the wave speed $c\in \{-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, 0\}\cap E_{3}$ and $c\neq-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}$.

(3.2) There exist $c_{2}\in(-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}, 0)$ and $c_{3}\in(-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, -\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}})$ such that $(u_{6}(\xi), v_{6}(\xi))$ are orbitally stable as $c\in (c_{3}, c_{2})\cap E_{4}$ and $c\neq-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}$, and they are orbitally unstable as $c\in (-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, c_{3})\cap E_{4}$ or $c\in (c_{2}, 0)\cap E_{4}$.

Proof of Theorem 4.1. (1) Firstly, we show that conclusion (1) in Theorem 4.1 holds.

According to $D_{2} = 0$ and (4.17), we have

when $c > 0$ and $a_{2}^{2}+6a_{1}a_{3} > 0$. Hence, conclusion (1) holds.

(2) Secondly, we prove the orbital stability of $(u_{4}(\xi), v_{4}(\xi))$ in (2.2) of Theorem 4.1.

Since $(u_{4}(\xi), v_{4}(\xi)) = (u_{q_{1} > 0}^{-}, c-\alpha u_{q_{1} > 0}^{-})$ as $q_{1} > 0$, and $(u_{4}(\xi), v_{4}(\xi)) = (u_{q_{1} < 0}^{+}, c-\alpha u_{q_{1} < 0}^{+})$ as $q_{1} < 0$, we only need to show the stabilities of solitary waves $(u_{q_{1} > 0}^{-}, c-\alpha u_{q_{1} > 0}^{-})$ and $(u_{q_{1} < 0}^{+}, c-\alpha u_{q_{1} < 0}^{+})$.

From $D_{1}$ in (2.19), we have

and

Substituting (4.21) and (4.22) into (4.19), we have $d^{\prime\prime}(c) > 0$. Then, $(u_{q_{1} > 0}^{-}, c-\alpha u_{q_{1} > 0}^{-})$ and $(u_{q_{1} < 0}^{+}, c-\alpha u_{q_{1} < 0}^{+})$ are orbitally stable at $D_{1}$. Hence, we get that $(u_{4}, v_{4})$ are orbitally stable.

(3) Thirdly, we prove the orbital stability of $(u_{3}(\xi), v_{3}(\xi))$ in (2.1) of Theorem 4.1.

Similar to proof (2), since $(u_{3}(\xi), v_{3}(\xi)) = (u_{q_{1} > 0}^{+}, c-\alpha u_{q_{1} > 0}^{+})$ as $q_{1} > 0$, and $(u_{3}(\xi), v_{3}(\xi)) = (u_{q_{1} < 0}^{-}, c-\alpha u_{q_{1} < 0}^{-})$ as $q_{1} < 0$, we only need to prove the stabilities of solitary waves $(u_{q_{1} > 0}^{+}, c-\alpha u_{q_{1} > 0}^{+})$ and $(u_{q_{1} < 0}^{-}, c-\alpha u_{q_{1} < 0}^{-})$.

(3.1) Stability and instability of $(u_{q_{1} > 0}^{+}, c-\alpha u_{q_{1} > 0}^{+})$.

From Theorem 2.1, we know that the existence range of $(u_{q_{1} > 0}^{+}, c-\alpha u_{q_{1} > 0}^{+})$ is $a_{2} > 0$ and $c\in(-\frac{(\lambda+\alpha^{3})^{2}}{6(1+\alpha^{2})a_{3}}, 0)\cap E_{1}$. Taking $k = k_{1}$ and $D = D_{1}$, we have

Combining (4.21), (4.23), (4.24) and (4.18), we have

Let

in (4.25), we have

that is, $x = x(c)$ is monotone increasing with respect to c. Therefore, when $c$ changes from $-\frac{a_{2}^{2}}{6a_{3}(1+\alpha^{2})}$ to 0, $x$ changes from 0 to $+\infty$. For convenience, we write the part in curly braces of (4.25) as the following form

where $g = \frac{-a_{2}+\sqrt{9a_{2}^{2}+48a_{1}a_{3}}}{2(a_{2}+\sqrt{9a_{2}^{2}+48a_{1}a_{3}})}$. Since $a_{2}+2a_{3}D_{1} > 0$, $a_{2} > 0$, and $a_{2}^{2}+6a_{1}a_{3} > 0$, we get $0 < g < 1$. In order to determine the sign of $d^{\prime\prime}(c)$ in (4.25), we discuss the sign of $f_{1}(x)$. Differentiating (4.28) with respect to $x$, we have

Solving $(1-g)x^{2}-g = 0$, we have $x_{0} = \sqrt{\frac{g}{1-g}}$ and $x_{1} = -\sqrt{\frac{g}{1-g}}$. By computation, we have $f_{1}(x)$ is monotone decreasing in $(0, \sqrt{\frac{g}{1-g}})$ and monotone increasing in $(\sqrt{\frac{g}{1-g}}, +\infty)$. According to $\lim\limits_{x\rightarrow 0^{+}}f_{1}(x) = +\infty$, $\lim\limits_{x\rightarrow +\infty}f_{1}(x) = 0$ and the intermediate value theorem of continuous functions, we get that there exists $x_{2}\in (0, +\infty)$ such that $f_{1}(x_{2}) = 0$, $f_{1}(x) > 0$ in $(0, x_{2})$, and $f_{1}(x) < 0$ in $(x_{2}, +\infty)$. Therefore, we have that $d^{\prime\prime}(c) > 0$ in $(0, x_{2})$, and $d^{\prime\prime}(c) < 0$ in $(x_{2}, +\infty)$. Since $x = x(c)$ is monotone increasing with respect to c, there exists $c_{0}\in (-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}, 0)$ such that $x(c_{0}) = x_{2}$. Hence, we conclude that there exists $c_{0}\in (-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}, 0)$ such that $(u_{q_{1} > 0}^{+}, c-\alpha u_{q_{1} > 0}^{+})$ are orbitally stable as $c\in (-\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}}, c_{0})\cap E_{1}$ and orbitally unstable as $c\in(c_{0}, 0)\cap E_{1}$.

(3.2) Stability and instability of $(u_{q_{1} < 0}^{-}, c-\alpha u_{q_{1} < 0}^{-})$.

From (4.18), we know that the discrimination $d^{\prime\prime}(c)$ of orbital stability of solitary wave $(u_{q_{1} < 0}^{-}, c-\alpha u_{q_{1} < 0}^{-})$ is also given by (4.25). From Theorem 2.1, we get that the existence range of $(u_{q_{1} < 0}^{-}, c-\alpha u_{q_{1} < 0}^{-})$ is $a_{2} > 0$ and $c\in(-\frac{3(\lambda+\alpha^{3})^{2}}{16(1+\alpha^{2})a_{3}}, -\frac{(\lambda+\alpha^{3})^{2}}{6(1+\alpha^{2})a_{3}})\cap E_{1}$. Taking $k = k_{1}$ and $D = D_{1}$, for $q_{1} < 0$, we have

Let

in (4.25), we have

that is, $x = x(c)$ is monotone increasing with respect to c. Therefore, $x$ changes from $-\infty$ to 0 as $c$ changes from $-\frac{3a_{2}^{2}}{16a_{3}(1+\alpha^{2})}$ to $-\frac{a_{2}^{2}}{6a_{3}(1+\alpha^{2})}$. For convenience, we write the part in curly braces of (4.25) as the following form

where $g = \frac{-a_{2}+\sqrt{9a_{2}^{2}+48a_{1}a_{3}}}{2(a_{2}+\sqrt{9a_{2}^{2}+48a_{1}a_{3}})}$. Since $a_{2}+2a_{3}D_{1} < 0$, $a_{2} > 0$, and $a_{2}^{2}+6a_{1}a_{3} > 0$, we have $g < 0$. In order to determine the sign of $d^{\prime\prime}(c)$ in (4.25), we discuss the sign of $f_{1}(x)$. Differentiating (4.33) with respect to $x$, we have

Then, $f_{2}(x)$ is monotone increasing in $(-\infty, 0)$. According to $\lim\limits_{x\rightarrow 0^{-}}f_{2}(x) = +\infty$, $\lim\limits_{x\rightarrow -\infty}f_{2}(x) = -\pi$ and the intermediate value theorem of continuous functions, we get that there exists $x_{3}\in (-\infty, 0)$ such that $f_{2}(x_{3}) = 0$, $f_{2}(x) < 0$ in $(-\infty, x_{3})$, and $f_{2}(x) > 0$ in $(x_{3}, 0)$. Then, we have that $d^{\prime\prime}(c) < 0$ in $(-\infty, x_{3})$, and $d^{\prime\prime}(c) > 0$ in $(x_{3}, 0)$. Since $x = x(c)$ is monotone increasing with respect to c, there exists $c_{1}\in (-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, -\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}})$ such that $x(c_{1}) = x_{3}$. Hence, we conclude that there exists $c_{1}\in (-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, -\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}})$ such that $(u^{-}_{q_{1}}, c-\alpha u_{q_{1}}^{-}))$ are orbitally unstable as $c\in (-\frac{3a_{2}^{2}}{16(1+\alpha^{2})a_{3}}, c_{1})\cap E_{1}$ and orbitally stable as $c\in(c_{1}, -\frac{a_{2}^{2}}{6(1+\alpha^{2})a_{3}})\cap E_{1}$.

For $(u_{5}(\xi), v_{5}(\xi))$, similar to the proof of orbital stability of $(u_{4}(\xi), v_{4}(\xi))$, by (4.16), we obtain that they are orbitally stable. Also, similar to the proof of orbital stability of $(u_{3}(\xi), v_{3}(\xi))$, by (4.17), we conclude the results on the orbital stability of $(u_{6}(\xi), v_{6}(\xi))$ in Theorem 4.1. In summary, the proof of Theorem 4.1 is finished.

5.   Conclusion

In this article, we are interested in studying the stability of the solitary waves with nonzero asymptotic value for a coupled version of compound KdV and MKdV equations with two components (1.3). In order to overcome the difficulty of studying orbital stability of solitary waves with nonzero asymptotic value for the coupled compound KdV and MKdV equations, we use a translation transformation to transfer this problem into solitary waves with zero asymptotic value for a reduced nonlinear coupled equations. By applying the orbital stability theory presented by Grillakis et al., the results obtained by Bona et al. and detailed spectral analysis, we obtain the orbital stability and instability of solitary waves with zero asymptotic value for a reduced new coupled nonlinear equation. From Conclusion 4.1 and Theorem 4.1, it is easy to see that the orbital stability and instability of solitary waves with zero and nonzero asymptotic value are related to wave speed $c$. The influence regions of stability and instability are given separately in Conclusion 4.1 and Theorem 4.1. As $v = 0$, we can also obtain the stability and instability of solitary waves for the compound KdV equation. Our work not only extends GSS methods to study the orbital stability and instability of solitary wave solutions with nonzero asymptotic value, but also includes and improves the results of Zhang et al. ^[15]. Moreover, the orbital stability of periodic solitary wave is an open problem, we will go on to study this problem.

Acknowledgments

The authors are grateful to the anonymous referees for their useful suggestions which improve the contents of this article. Xiaoxiao Zheng is supported by Natural Science Foundation of Shandong Province (No. ZR2018BA016), Jie Xin is supported by National Natural Science Foundation of China (No. 11371183), Yongyi Gu is supported by National Natural Science Foundation of China (No. 11901111).

Conflict of interest

The authors declare that there is no conflicts of interest in this paper.