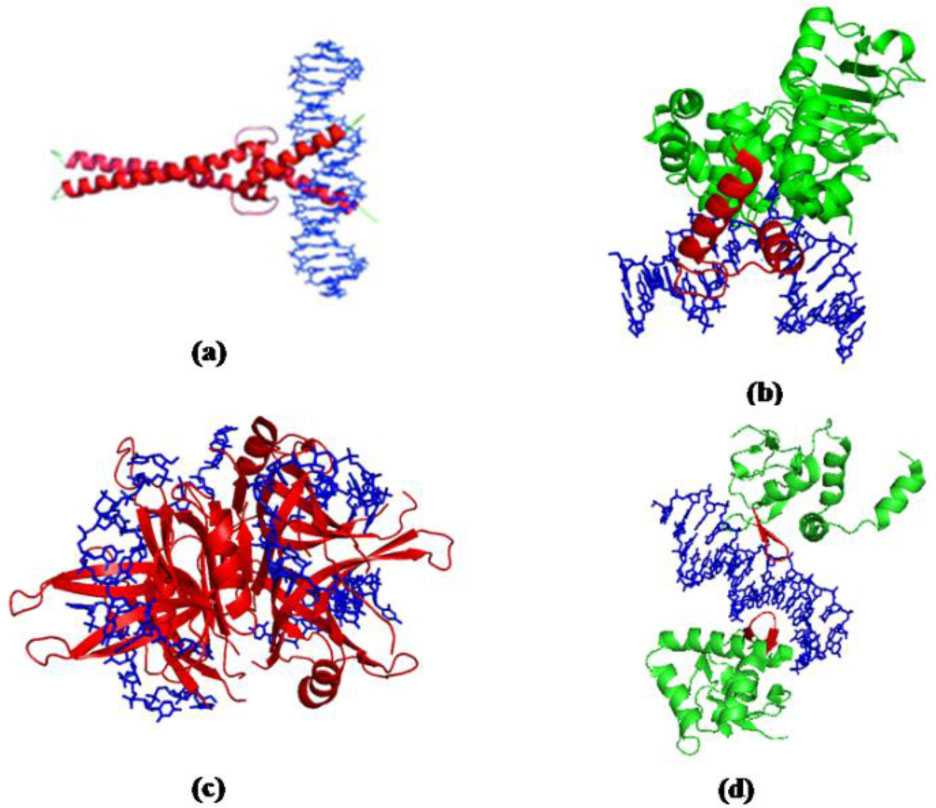
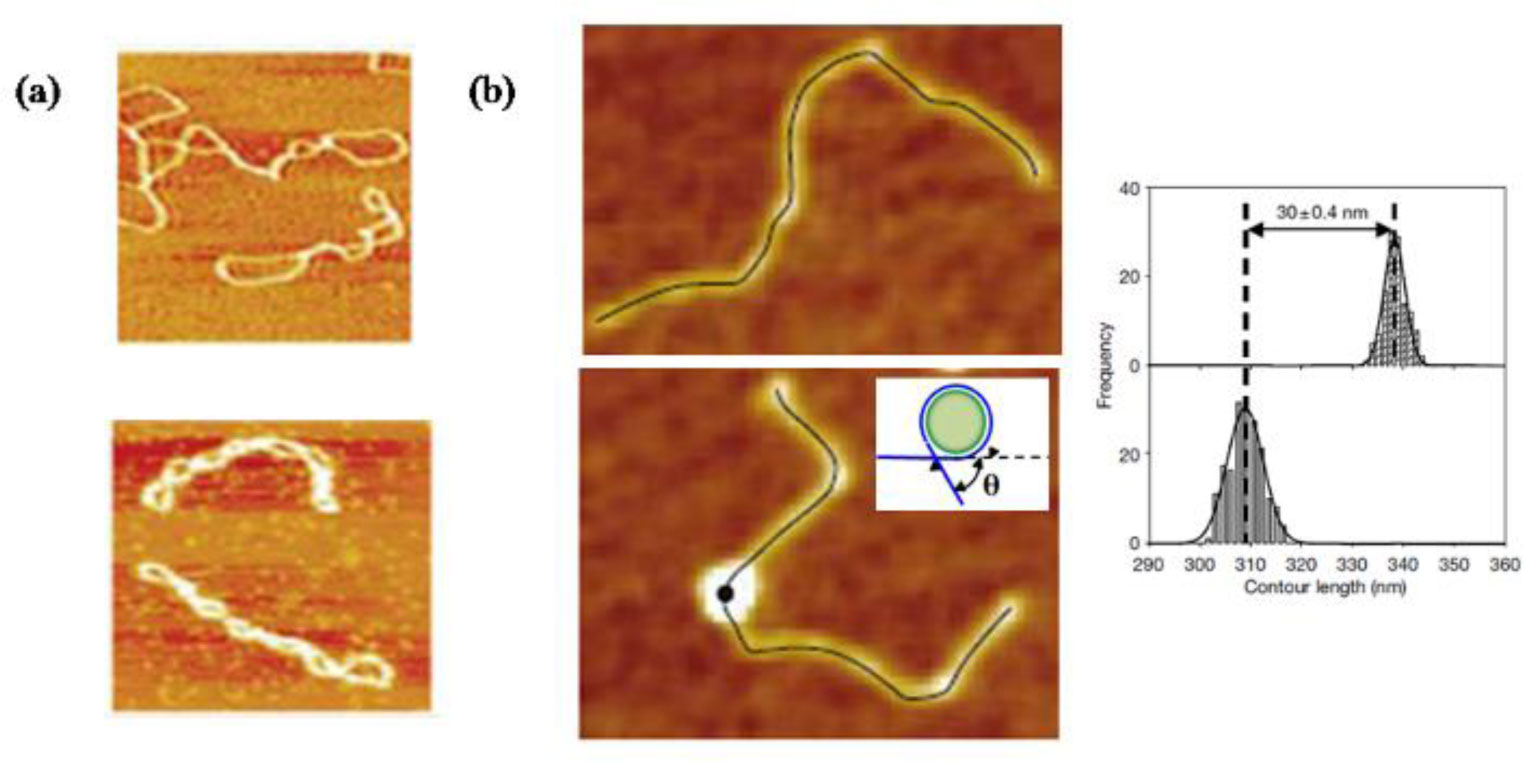
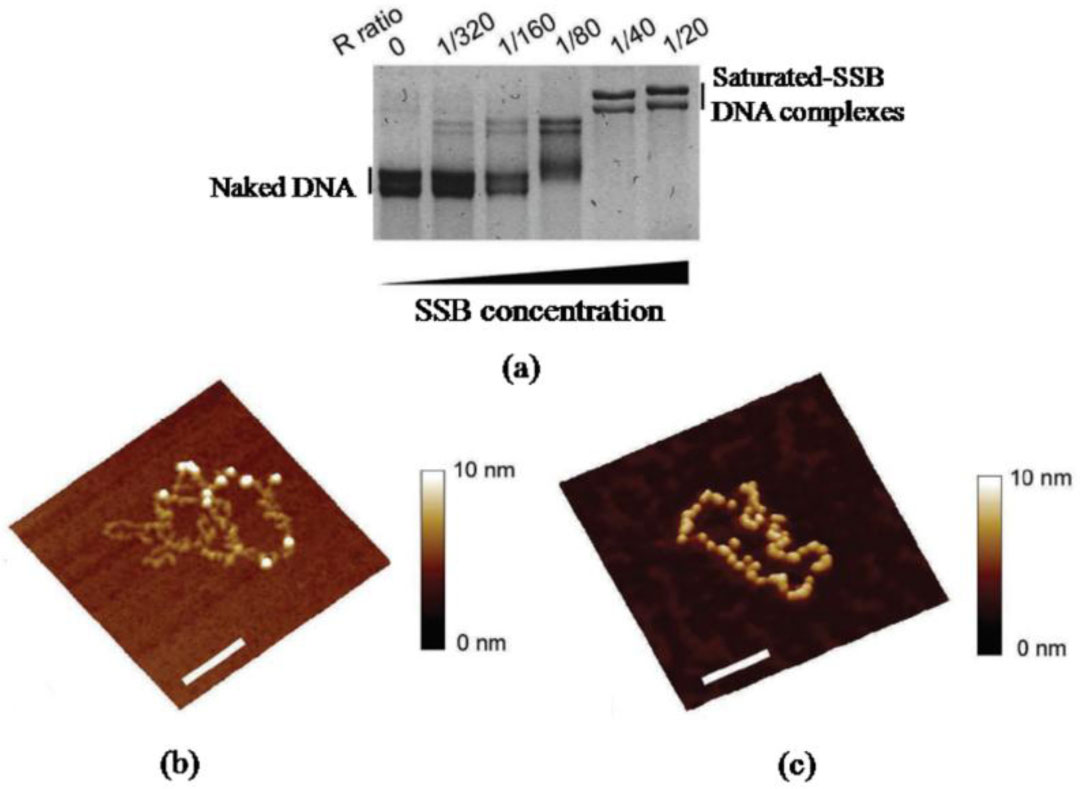
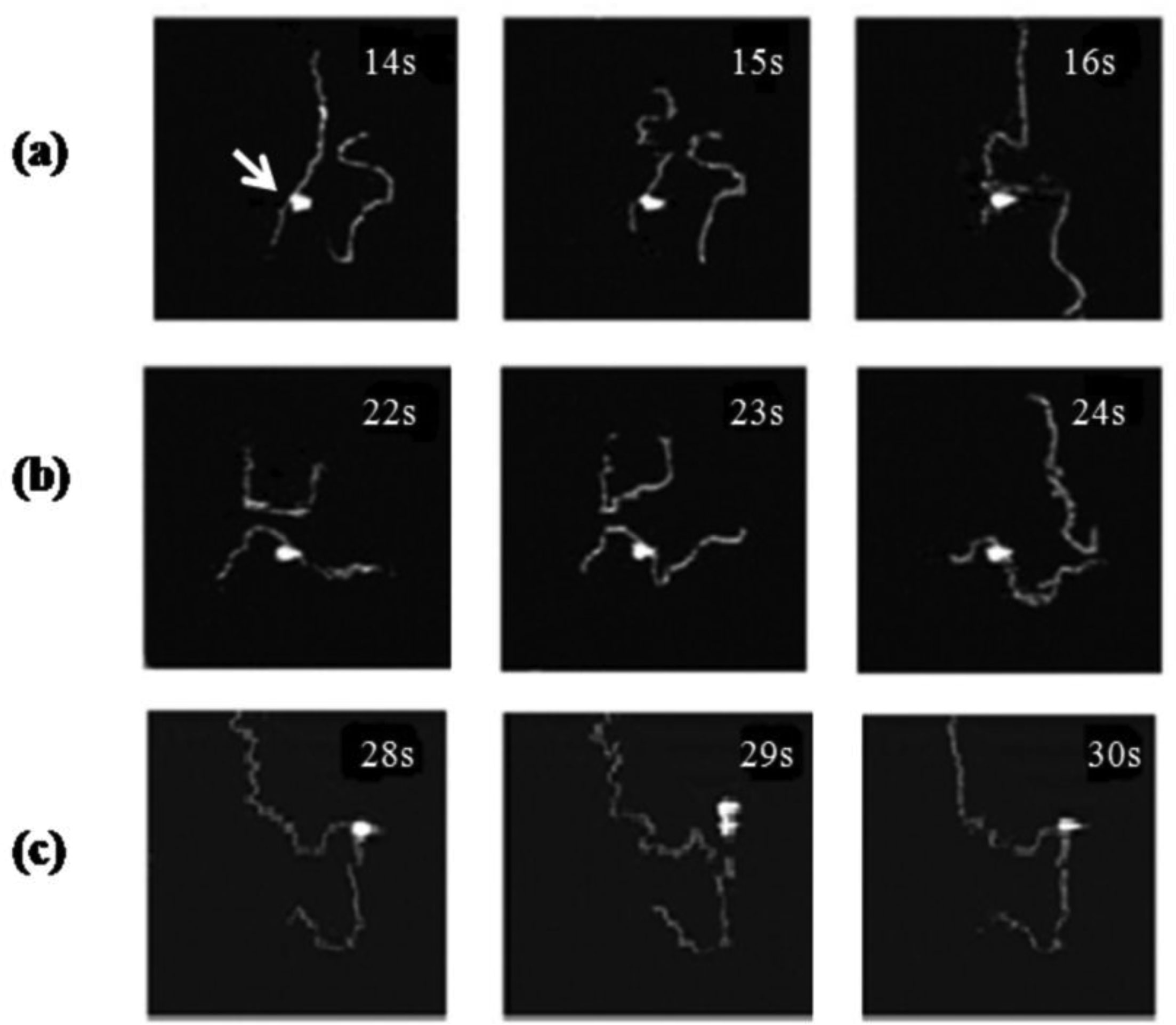
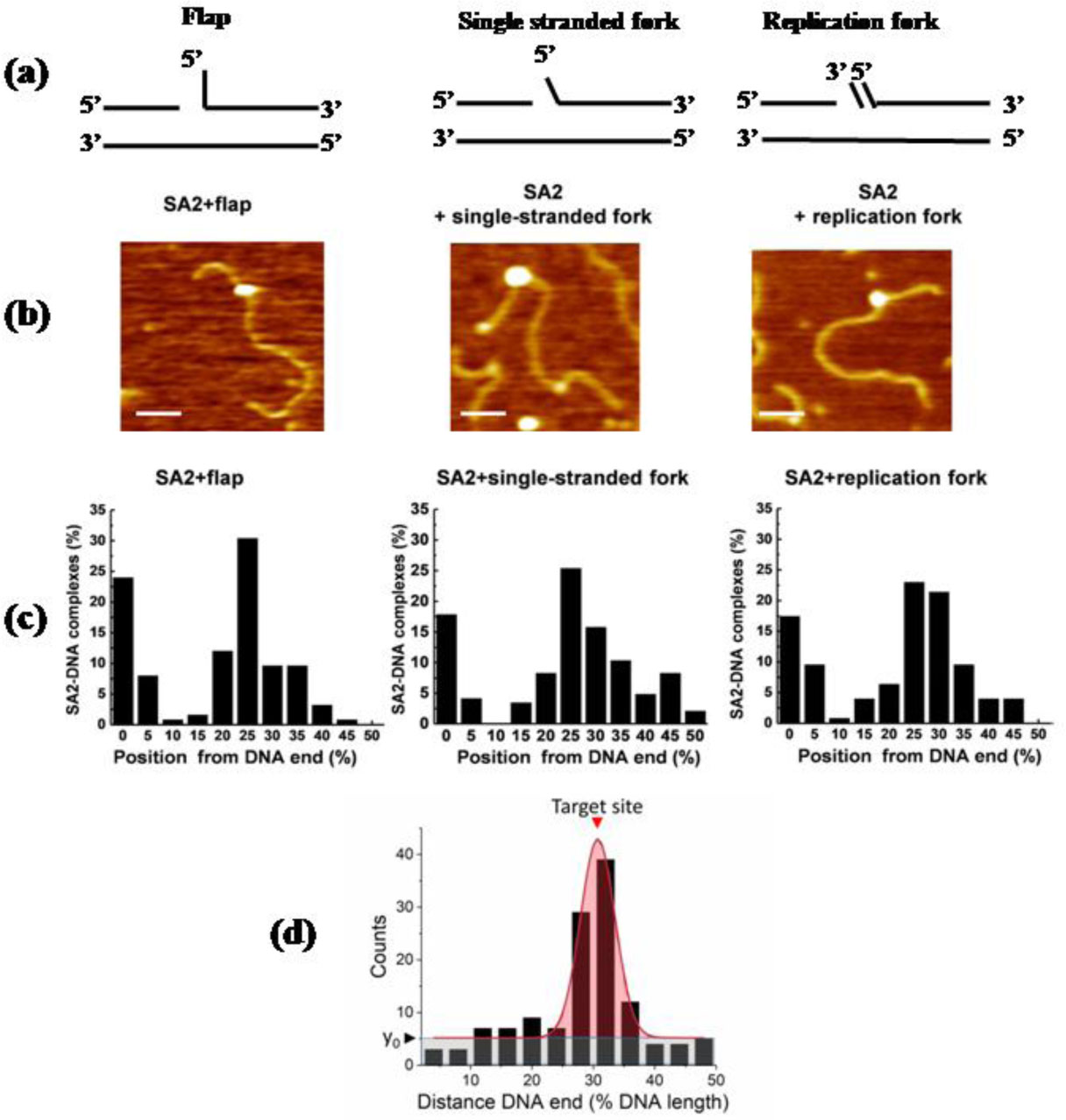
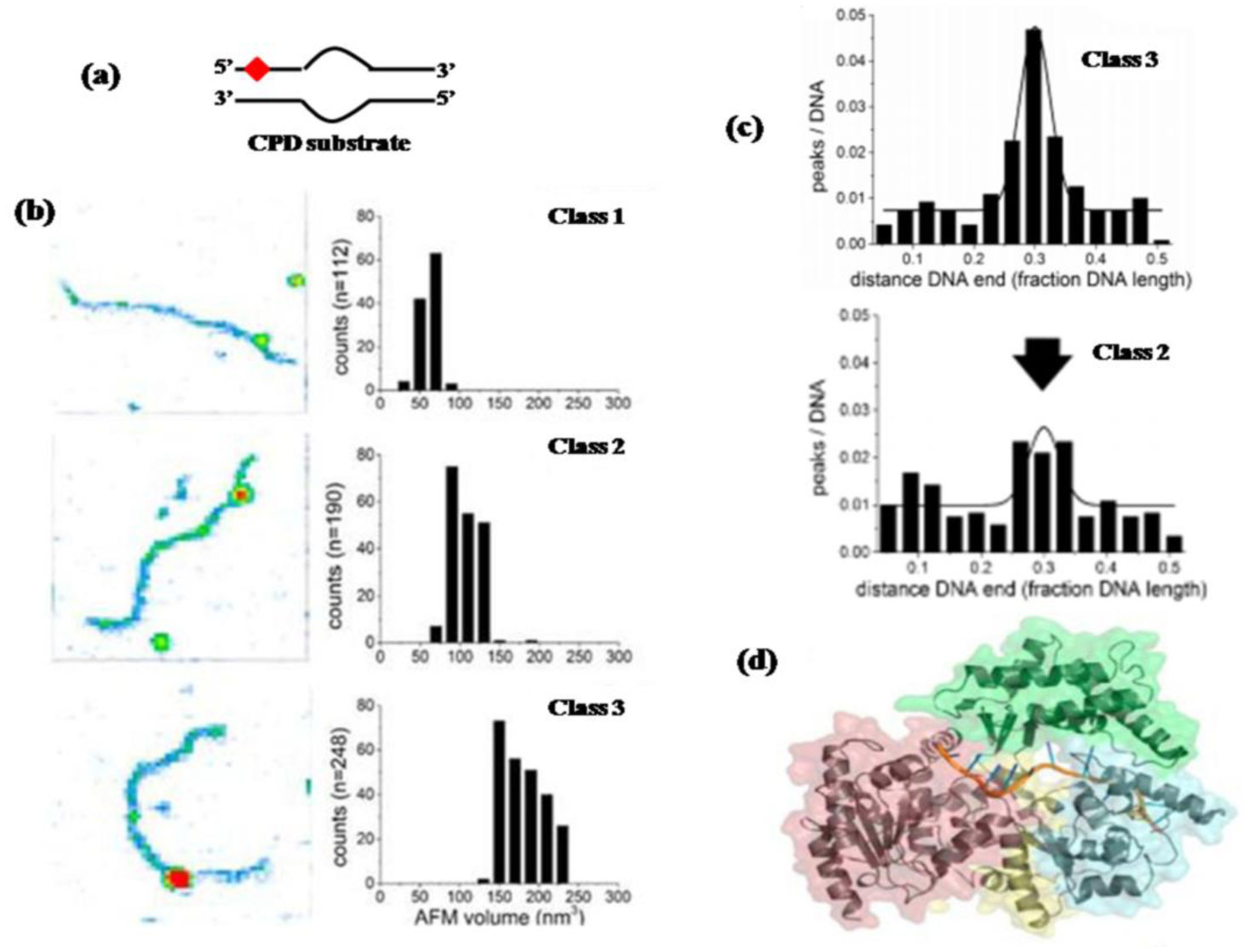
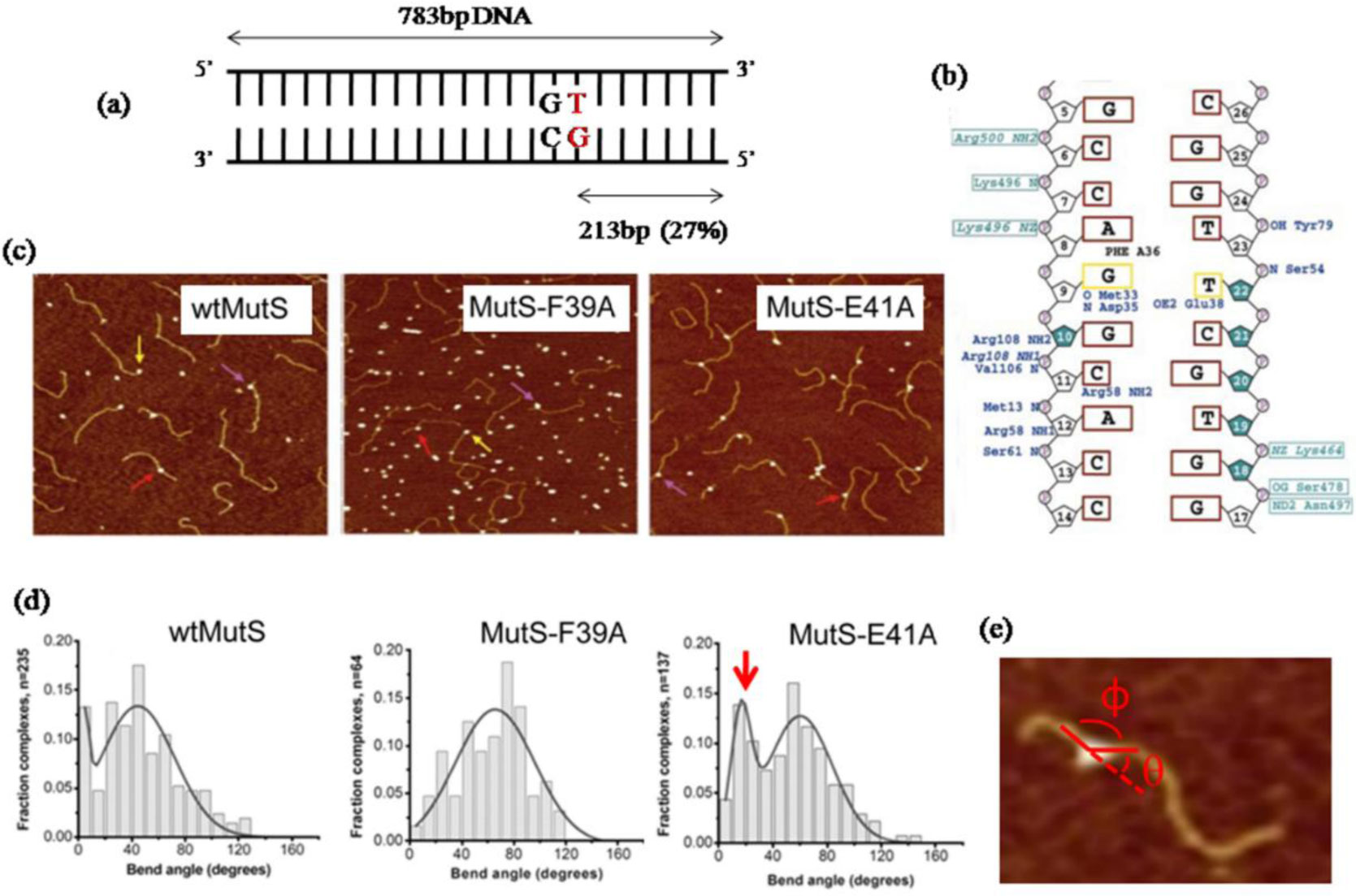
Protein-DNA interactions are pivotal for many essential biological processes. Atomic force microscopy (AFM) imaging of protein-DNA systems involved in DNA target site search, identification, and processing by proteins has contributed invaluable information to our understanding of the underlying mechanisms. The single molecule 3D resolution of AFM enables us to uncover stoichiometries and conformational properties of protein-DNA complexes. Its molecular resolution places AFM at the interface between the atomic resolution achievable by crystallography and the comparably poor (typically > hundred nanometers) spatial resolution of optical microscopy. Furthermore, the transient character of protein interactions with nonspecific DNA sites, for example during their target site search renders these complexes difficult to resolve by standard ensemble methods. Here, we review current applications and capabilities of as well as novel advances in AFM imaging in protein-DNA interaction studies.
1.
Introduction
1.1. Motivation
The PHEV has the characteristics of traditional hybrid electric vehicle and pure electric vehicle, which is an important development direction of new energy vehicles [1]. In order to achieve better energy-saving effect of the PHEV, energy management strategy (EMS) is needed to determine the working mode of various components of the power transmission system and the energy distribution of different power sources to adapt to diverse driving environments [2].
1.2. Literature review
In terms of EMS goals for PHEV, some studies focus on battery aging and its thermal dynamics [3,4], and most studies is devoted to reducing fuel consumption. The way to achieve EMS can be divided into two types: rule-based and optimization-based [5,6]. The rule-based strategy is mainly based on the engineering experience and the characteristics of each component in the power system to design the working mode of the system and the energy distribution of different power sources. The rules are versatile and practical, but the potential for energy saving is limited [6,7,8,9]. Optimization-based strategy can be divided into instantaneous optimization, local optimization and global optimization.
The equivalent consumption minimization strategy (ECMS) is the representative of the instantaneous optimization strategy [7,10,11]. ECMS transforms the electric energy consumption into the equivalent fuel consumption by introducing the EF, so as to optimize the instantaneous equivalent fuel consumption [7,12,13]. This strategy has strong real-time performance, but poor robustness and limited optimization effect.
The EMS of local optimization is mainly based on model predictive control (MPC). This strategy calculates the optimal control parameters in the prediction domain, with small amount of calculation, real-time control and significant optimization effect [8,9].
The global optimization strategy is represented by Reinforcement Learning (RL) and DP. Learning-based EMS has a strong self-learning ability and it is model-free which relies on a mass of real-world sample for training [14,15]. DP can obtain the multi-stage optimization decision and the theoretical global fuel economy optimization, if the global driving cycle is known beforehand. However, the disadvantage is that the calculation amount is large, and the future driving cycle is difficult to obtain in advance, which limits the use of DP in real time [16,17].
In order to apply approximately optimization decision by DP for real-time control, future driving cycles need to be known, which can be obtained by two ways: one is to build a future speed prediction model based on the historical driving cycle data by neural network, Markov or Kalman filter [9,18,19]. And the other is to obtain the traffic information by high-tech [11,16,17], such as Navigation System, Global Positioning System (GPS), Geographic Information System (GIS), Internet of Vehicles and Intelligent Transportation System (ITS). Reference [16] combines GPS and ITS to obtain driving information, and adjusts the EF in A-ECMS accordingly.
The PHEV controller can plan the optimization decision by DP offline to adjust the control parameters in real-time [11]. In reference [17], an EMS of hierarchical control is proposed. The upper layer obtains real-time traffic data with GPS and ITS, and makes long-term planning of SOC optimal consumption trajectory, while the lower layer uses MPC to realize short-term time-domain speed prediction. Some research build A-ECMS based on DP combining initial EF optimized by genetic algorithm [20], or combining driving cycle recognition [21].
When using DP to optimize EMS, it is necessary to recognize driving cycle for more targeted controlling of various driving cycles. In recent years, many researchers [22,23,24] have made great efforts to study the driving cycles of typical cities or specific vehicles. K-means cluster analysis [25], fuzzy c-means (FCM) [26], and neural network [27] are common methods to construct typical driving cycle by historical driving data. Driving cycles directly affect fuel consumption, so how to optimize the energy management of PHEV in combination with driving cycles will be a research trend [17]. Some research uses existing cycles to optimize the EMS, but few combine personalized travel characteristics for a specific driver.
Based on the above studies, it can be seen that current PHEV energy management strategy has achieved multiple research results, a variety of optimization methods have been applied to PHEV energy management. How to make the strategy to get better adaptability to driving cycles and enough real-time optimization ability need to be further resolved.
1.3. Contributions and outline
As discussed above, how to combine ITS to globally optimize PHEV energy management is the research focus. However, long-term traffic flow information from ITS can only reflect the average speed and cannot be adjusted according to the actual speed, lacking robustness. Few studies combine ITS and short-term speed prediction for EMS. Therefore, the main purpose of this study is to improve the performance of A-ECMS by tuning EF instantaneously based on driving cycle prediction and personalized travel characteristics. Two contributions have been realized in this paper, which is: An A-ECMS was proposed, with an EF jointly correction algorithm combining long-term target driving cycle and short-term vehicle speed prediction. Moreover, the DP algorithm is applied to the offline energy optimization process of A-ECMS based on typical driving cycles constructed according to personalized travel characteristics. The improved A-ECMS formulated in this paper can optimize EF in real time based on mileage, SOC, long-term driving cycle and real-time vehicle speed. Meanwhile, the online driving cycle recognition can be practically applied, and the adaptability of A-ECMS to actual driving can be enhanced.
This paper is organized as follows. In Section 2, an A-ECMS with driving cycle prediction and personalized travel characteristics merging DP algorithm is described. In Section 3, the methodology of building typical driving cycles for a specific driver and planning SOC reference trajectory algorithm is introduced. Typical driving cycle construction and simulation verification of A-ECMS are in Section 4. And conclusions are subsequently discussed in Section 5.
2.
Improved adaptive equivalent consumption minimization strategy for PHEV
2.1. PHEV energy management by DP algorithm
2.1.1. PHEV parameters
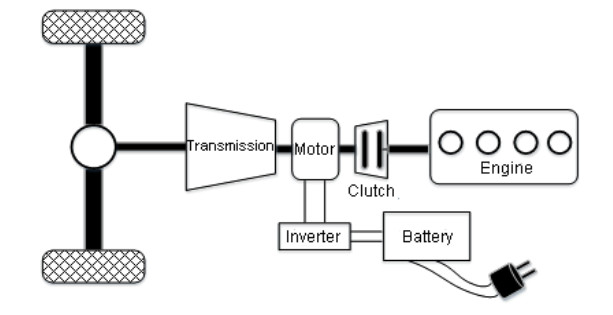
In this paper, the P2 configuration PHEV is taken as the research object. This configuration refers to the coaxial connection of the engine and the motor, while P2 means that the motor is placed at the front end of the transmission, between the engine and the transmission, and using the clutch between the engine and the motor to control the power coupling and disconnection. The structure diagram is shown in Figure 1 and the main parameters are shown in Table 1.
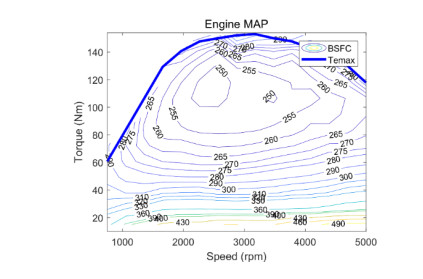
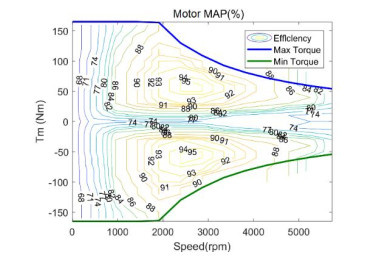
The characteristics of the engine and the motor are shown in Figure 2 and Figure 3 respectively, and the SOC calculation is realized by using the ampere hour integration method [20].
2.1.2. PHEV energy management by DP algorithm
DP, a global optimization algorithm, can calculate the optimal solution of PHEV energy management problem, so as to obtain the optimal fuel economy, but the premise is to know the global driving cycle [12].
In this paper, SOC of battery is selected as the system state variable, motor torque $ {T}_{m} $ and transmission gear $ gear\left(k\right) $ are selected as the system control variables, then the state and control quantity of the system can be given as
According to the dynamic relationship between power assemblies, the engine torque $ {T}_{e} $ obtained from the motor torque $ {T}_{m} $ can be given as follows
where $ {T}_{r} $ is the required torque of the whole vehicle, $ {i}_{0} $ is the main reduction ratio, and $ {i}_{gear\left(k\right)} $ is the transmission ratio of the current gear.
Since the selected state variable is the SOC of battery, the state equation under the dynamic programming algorithm can be given as follows
where $ {U}_{oc} $ is the open circuit voltage, $ {R}_{0} $ is the internal resistance of the battery, $ {Q}_{bat} $ and $ {P}_{bat} $ are the battery capacity and the battery power, respectively.
Since the system takes fuel consumption as the objective function, the objective function under the DP algorithm can be given as
where $ SO{C}_{f} $ is the SOC value at the termination time, $ fue{l}_{k} $ is the fuel consumption of the whole vehicle at the current stage. And $ \alpha \left(SOC\right(k)-SO{C}_{f}{)}^{2} $ is the penalty function of SOC in DP, $ \alpha $ is the penalty coefficient, which is to correct the SOC value of battery and the target SOC value at the termination time when DP calculation ends.
At the same time, when DP algorithm is applied to solve the PHEV energy management problem, it will be limited by the hybrid system itself, so some constraints in the iterative calculation process are shown as follows
where $ {n}_{e}\left(k\right) $ is the engine speed, $ {n}_{m}\left(k\right) $ is the motor speed, $ {n}_{e\_\mathit{min}\mathrm{ }} $ and $ {n}_{e\_\mathit{max}\mathrm{ }} $ are the engine minimum and maximum speed respectively; $ {T}_{e\_\mathit{min}\mathrm{ }} $ and $ {T}_{e\_\mathit{max}\mathrm{ }} $ are the engine minimum and maximum torque respectively; $ {n}_{m\_\mathit{min}\mathrm{ }} $ and $ {n}_{m\_\mathit{max}\mathrm{ }} $ are the motor minimum and maximum speed respectively; $ {T}_{m\_\mathit{min}\mathrm{ }} $ and $ {T}_{m\_\mathit{max}\mathrm{ }} $ are the motor minimum and maximum torque respectively; $ SO{C}_{\mathit{min}} $ and $ SO{C}_{max} $ are the upper and lower limits of battery SOC respectively.
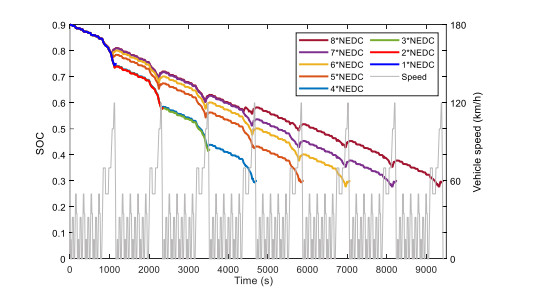
In order to study the optimal SOC trajectory under different driving mileage of PHEV based on DP, this paper selects the different number NEDC driving cycles as test cycles. In the strategy, the initial value of the battery SOC is set to 0.9 and the target value is 0.3. Respectively, simulating under 1 to 8 NEDC driving cycles and result is shown in Figure 4.
The driving range is a key factor affecting the EMS for PHEV. As can be seen from Figure 4, the trajectory of battery SOC will vary with the distance, and SOC presents an approximately linear decline curve. When the trip ends, the SOC value drops to near the target value. But DP algorithm requires a large amount of calculation, so it cannot be applied to real-time control. However, SOC linear descent curve optimized by DP can provide a basis for reference SOC trajectory planning in EMS.
2.1.3. SOC reference trajectory under known driving cycle
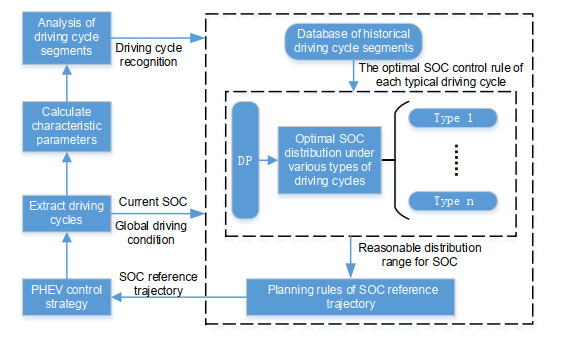
Taking multiple NEDC cycles as an example above, it is found that the optimal SOC reference trajectory is an approximate straight line related to mileage. However, it is difficult to use the SOC trajectory under NEDC or a certain existing driving cycle as a reference for actual driving condition. Therefore, if cluster analysis is performed according to the historical driving data of a specific driver, $ n $ typical driving cycles can be obtained, which can better reflect the personalized travel characteristics of the driver. Then studying the optimal SOC consumption under each typical driving cycle by DP.
As is shown in Figure 5, according to the characteristic parameters, the driving condition is segmented and corresponding classified into different typical driving cycles. The SOC reference trajectory can be linearly composed of the optimal SOC consumption of each section. The specific allocation method and analysis are described in Section 3.2.
2.2. Driving cycle generation and short-term vehicle speed prediction
2.2.1. Long-term target driving cycle generation based on traffic information
SOC reference trajectory described above determines the target driving cycle in advance which requires the use of ITS to generate. This paper extracts the traffic flow based on ITS, generates the target driving cycle of the travel road as the traffic information of the road section, and obtains the average traffic flow speed of the front road section in real time [28].
The actual navigation route is segmented every 200m, and the average traffic speed of each section can be calculated as follows
where $ {V}_{seg}\left(i\right) $ is the average speed of the section marked $ i $ at time $ t $, $ {V}_{k}^{seg\left(i\right)} $ is the average speed of the $ k $ th vehicle passing through the section at time $ t $, and $ N $ is the total number of vehicles recorded in the section at that time.
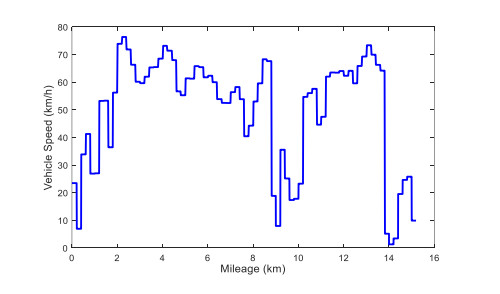
Based on the above method, the route to the destination and the traffic flow speed information can be obtained by the navigation system and ITS, and then the possible vehicle speed information in the next trip can be estimated by fitting according to the traffic flow speed of the sub sections. For a certain section of route, the curve of the average speed and the mileage of each section is shown in Figure 6.
However, the road network only obtains the relationship between mileage and vehicle speed, it also needs to be converted to the time domain, as shown in Eqs. (7).
where $ {L}_{seg\left(i\right)} $ and $ {T}_{seg\left(i\right)} $ are the length and the time of passing through section $ i $.
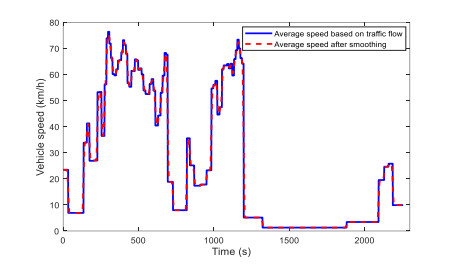
After conversion to time domain, the speed-time curve is a step curve, which does not conform to the continuity characteristics of the vehicle speed, so it cannot be regarded as the real driving cycle. Therefore, this paper uses the LOWESS filter function to smooth the step speed signal, so as to convert it into a driving cycle curve that conforms to the normal driving speed rule, as shown in Figure 7.
In the energy management optimization strategy of PHEV, this is the most likely driving cycle of the vehicle. The speed curve can be taken as the target driving cycle for long-term prediction.
2.2.2. Short-term vehicle speed prediction based on NAR neural network
The long-term target driving cycle based on traffic flow information is the global predicted driving cycle of the travel route, but there may be deviation in the real-time process, and the short-term vehicle speed prediction is more consistent with the real-time driving cycle. Therefore, in the prediction of PHEV driving cycle, the global prediction and short-term prediction can be combined.
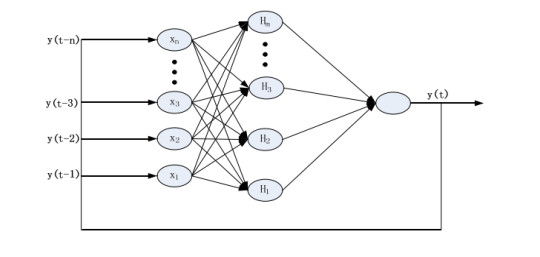
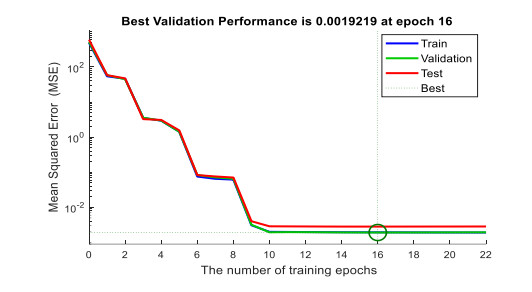
The NAR neural network has advantages of solving time variant and nonlinear problems, making it suitable for vehicle speed prediction [29]. Therefore in this paper, NAR neural network with feedback is built to predict the speed, the structure diagram is shown in Figure 8. Taking the historical driving cycle data as the input sample, through trial-and-error method and repeated tests, the number of neurons in the hidden layer is determined to be 20, and the delay order of the output feedback is determined to be 35 [29,30]. The neural network is trained and the training results are obtained. Figure 9 is the training process, and the ordinate is the mean square error (MSE). It can be seen from the figure that when the number of training reaches 16 times, the mean square error of the verification set is the smallest and converges to 0.0019219, so the training ends.
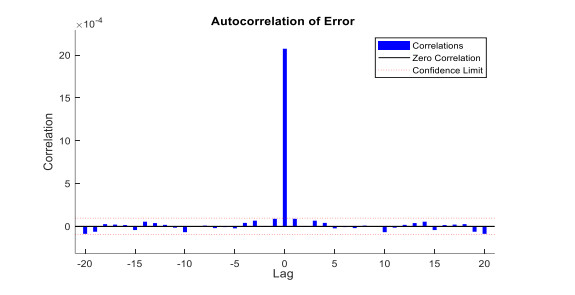
Figure 10 is an error autocorrelation graph of NAR neural network, which describes the correlation of prediction errors in time. Theoretically, the autocorrelation function should have only one maximum value and at Lag = 0, indicating that the prediction error is completely uncorrelated. If there is a significant correlation in the prediction error, the training effect of the network is not good [31]. It can be seen from Figure 10 that the NAR network in this paper has the largest correlation at Lag = 0, and the correlation of other points is within the confidence interval, indicating that the training results and prediction performance of the network are good at this time.
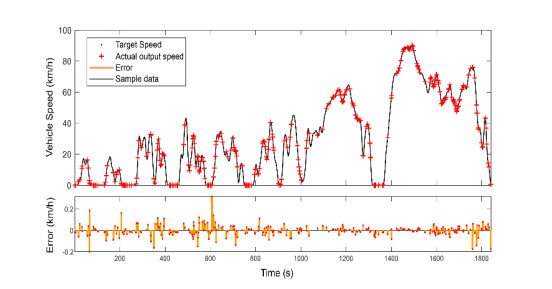
It can be seen from the Figure 11 that most of the error values of single-step prediction are in the interval of [-0.2, 0.2], and the error is very small, indicating that the single-step prediction results are accurate and the selection of neurons number is reasonable.
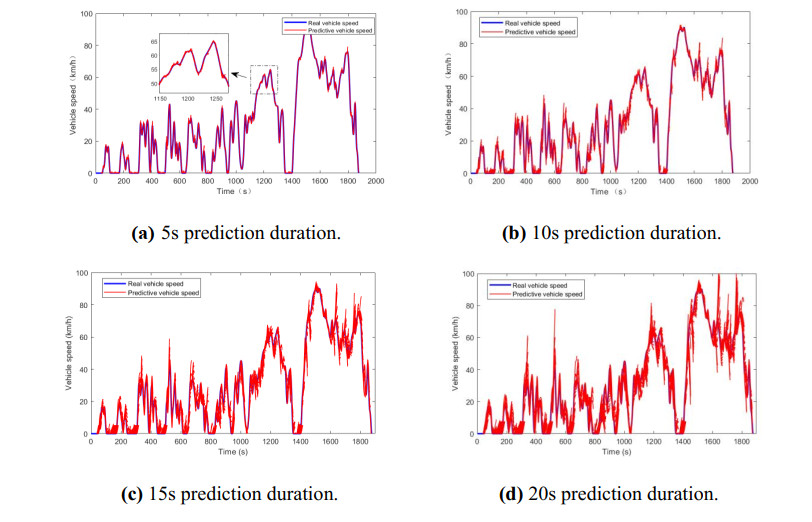
Then the prediction effect of the neural network is studied as follows. Root mean square error (RMSE) is used to evaluate the accuracy of NAR neural network and follow the rule of the higher the RMSE value, the lower the prediction accuracy of the model. In order to evaluate the prediction effects on speed, the results in different prediction duration are shown in Figure 12,and the corresponding RMSE values are shown in Table 2.
It can be seen from Figure 12 and Table 2 that when the prediction time domain is 5 seconds, the overall prediction effect of the test cycle is good, and its RMSE value is also small. With the increase of prediction time domain from 5 to 20 seconds, RMSE increased significantly, while the prediction accuracy decreased gradually. On the whole, vehicle speed prediction time domain is selected for 5 seconds.
2.3. A-ECMS algorithm establishment
The essence of ECMS is to convert the electric energy consumption by the battery into the equivalent fuel consumption through the equivalent factor in each instant. The energy distribution rule with the minimum sum of the instantaneous fuel consumption of the engine and the equivalent fuel consumption of the motor as the optimal solution is conducive to reducing the energy consumption and improving the economy [13].
The instantaneous equivalent fuel consumption of PHEV at a certain time $ t $ can be given as follows
where $ {\dot{m}}_{eq} $ is the total equivalent fuel consumption; $ {\dot{m}}_{fuel} $ is the fuel consumption of the engine; $ {\dot{m}}_{ele} $ is the equivalent fuel consumption after the electric energy conversion of the power battery, and its calculation formula is shown as follows
where $ k = 0.5\times \left(1+sign\left({P}_{m}\left(t\right)\right)\right) $, indicating whether the working state of the motor is discharging or charging; $ {P}_{m}\left(t\right) $ is the power of the motor at time $ t $, $ {Q}_{lhv} $ is the calorific value constant of the gasoline mass, $ {\eta }_{dis} $ and $ {\eta }_{char} $ are the discharge and charge efficiency of the battery, and $ s $ is oil-electricity conversion equivalent factor (EF).
According to the energy management optimization problem of PHEV, the objective function can be obtained as follows
where $ J\left(t\right) $ is the fuel consumption and $ u\left(t\right) $ is the control variable at time $ t $.
For the ECMS strategy, the EF is fixed. However, the driving cycle information and the SOC of the battery also affect the EF. If a fixed EF is adopted globally, the optimization effect may be poor [32,33]. Based on ECMS, an adaptive control strategy based on real-time correction of EF by SOC reference trajectory and vehicle speed is proposed in this section. An adaptive equivalent consumption minimization strategy (A-ECMS) is established by introducing the SOC reference trajectory and short-term driving speed prediction. The formula for changing the EF can be given as follows
where $ {s}_{ref\_i} $ which is the initial equivalent factor of various typical driving cycles under the current vehicle speed, $ {K}_{p} $ is the scale factor, $ SO{C}_{ref} $ is the reference SOC value, and $ SOC\left(t\right) $ is the real SOC value at time $ t $.
SOC reference trajectory can modify the EF in real time through the proportional control method. Constant part of the adaptive equivalent factor $ {s}_{ref\_i} $, or initial EF, is also very important in the method. Therefore, this paper considers the combination of short-term vehicle speed prediction to optimize initial EF of four typical driving cycles under different SOC values. In the application, the constant part of the adaptive EF is modified according to the type of driving cycle, and compared with the EF calculated based on SOC reference trajectory. If there is too much difference between the predicted EF and the current EF, then the constant part of the current EF is modified.
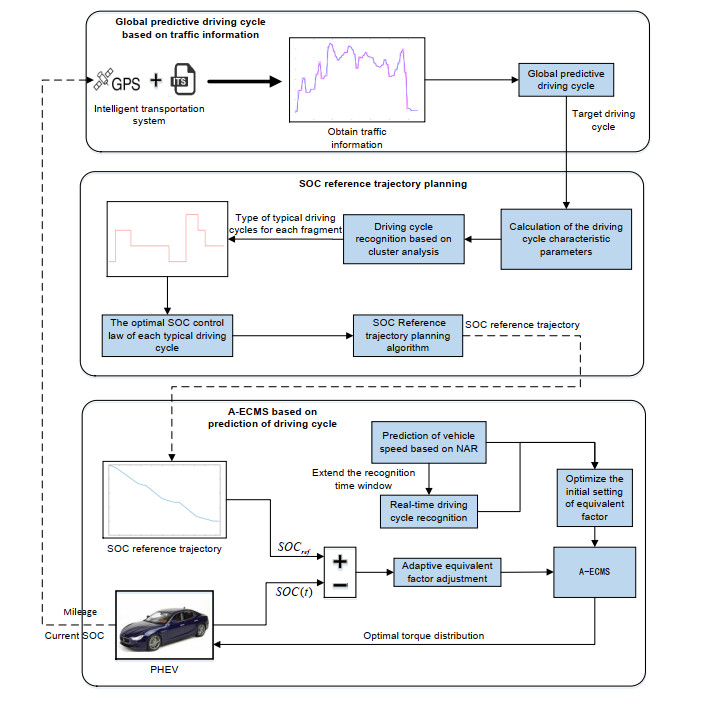
In summary, A-ECMS based on driving cycle prediction and personalized travel characteristics is proposed in this paper and its process is shown in Figure 13. First of all, the driver's historical driving data is clustered and analyzed offline to extract personalized travel characteristics and build the typical driving cycles. Then real-time traffic flow information is obtained through ITS to plan the optimal SOC reference trajectory, and combining the short-term vehicle speed prediction to modify the EF, so as to control the vehicle to achieve the purpose of improving fuel economy.
3.
Methodology of building typical driving cycles and planning SOC trajectory
The development and application of EMS should be able to select appropriate control parameters according to the actual driving cycles of the vehicle, so as to distribute the energy of each power source more reasonably, achieve the best control effect and save energy as much as possible [28,33]. Meanwhile, driving style of each driver and actual driving conditions are diverse. This section will explain the methodology of building typical driving cycles by analyze personalized travel characteristics, and planning the SOC trajectory by driving cycle recognition.
3.1. Typical driving cycle construction based on historical driving data
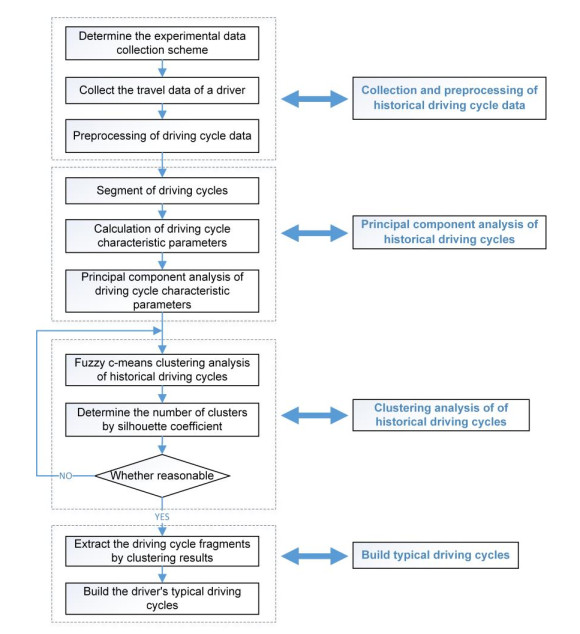
In order to make the PHEV energy management strategy more targeted, the historical driving cycle data by a specific driver should be analyzed firstly, and building the typical driving cycles for the driver which is the basis of SOC reference trajectory analysis. The analysis process is shown in Figure 14.
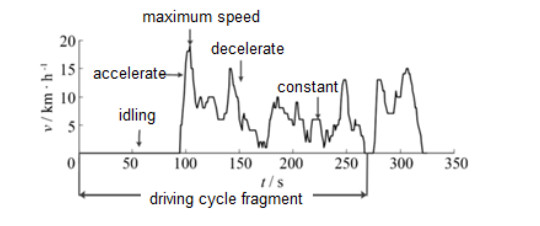
The data of the driver's travel is collected by GPS equipment, and the sampling frequency is 1Hz. And preprocessing is needed to remove the excessively long idle speed section and abnormal section in the data. In the process of driving on urban roads, the driving cycles of vehicles are usually affected by different types of road conditions and traffic environment. There are many idle, acceleration, deceleration and other states [34]. Therefore, after preprocessing the historical data, the next important step is to divide the kinematic segments, also known as short segments. As shown in Figure 15, the kinematic segment is defined as the operating range from one idle to the next [35,36].
By analyzing the driving characteristic parameters of each kinematic segment, the travel characteristics of the vehicle are obtained. There are 13 characteristic parameters representing the characteristics of driving cycles to be selected, as shown in Table 3.
If the 13 characteristic parameters are directly used for clustering analysis, the calculation will be large and affect the clustering results, and there will be information redundancy between the various feature parameters. Therefore, it is necessary to reduce the dimension of the original driving cycle matrix. In this paper, principal component analysis (PCA) method is used for extracting the key ingredients and reducing the dimensionality.
Then by analyzing the principal component of the kinematic segments, they can be clustered into several representative driving cycles for optimization of EMS. In this paper, the fuzzy c-means algorithm (FCM) is used for clustering analysis. If samples $ X = [{x}_{1}, {x}_{2}, ..., {x}_{n}] $ are given, and $ c $ represents the number of clusters, $ [{\mathrm{\alpha }}_{1}, {\mathrm{\alpha }}_{2}, ..., {\mathrm{\alpha }}_{C}] $ represents cluster centers of various categories. Then the objective function can be expressed by Eqs. (12).
where $ b $ is weighting parameters. $ {\delta }_{ik} $ and $ {d}_{ik} $ are membership and Euclidean distance between $ i $ th sample and $ k $ th category. And Euclidean distance can be calculated by Eqs. (2). $ m $ is the dimensions of the sample.
Membership between $ i $ th sample and $ k $ th category can be calculated by Eqs. (3).
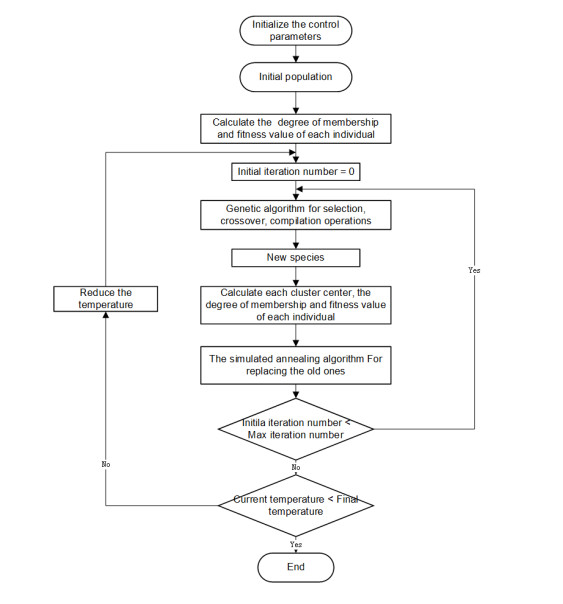
However, if the initial value of FCM is unreasonable, the algorithm may converge to the local minimum point, which will affect the clustering results [25,37]. To solve this problem, this paper applies simulated annealing algorithm (SA) and genetic algorithm (GA) to FCM, making clustering more efficient and accurate [25]. The process of FCM based on genetic simulated annealing algorithm (GA-SA) is shown in Figure 16.
3.2. Driving cycle recognition and SOC reference trajectory planning
3.2.1. Driving cycle recognition
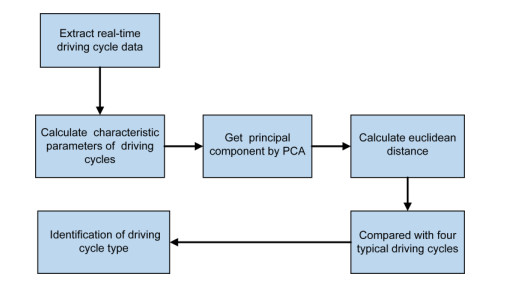
The type of vehicle driving cycle has a great influence on the energy management strategy of PHEV. Therefore, the algorithm of driving cycle recognition is designed based on the results of above clustering analysis, in order to identify the current type of driving cycle in the process of vehicle driving, and provide help for the later SOC reference trajectory planning. The driving cycle recognition process is shown in Figure 17.
The main idea of driving cycle recognition based on cluster analysis is to extract the characteristic parameters of the driving cycle during the actual driving process, to calculate the principal component and the Euclidean proximity of the driving cycle to the clustering center of various typical driving cycles, and to classify the driving cycle as the cluster of a certain category if it is closest to the clustering center of this category [34]. Thus, the classification of the current driving cycle can be recognized.
Let the cluster center of typical driving cycles be $ {Y}_{n}(n = \mathrm{1, 2}, \dots, n) $ and the current actual driving cycle of the vehicle to be identified is $ X $. Then the Euclidean proximity between the current actual driving cycle and the typical driving cycle in the historical driving cycle database can be given as follows
where $ m $ is the number of characteristic parameters of the driving cycle.
According to the Euclidean proximity formula, the approach degree between $ {Y}_{n} $ and $ X $ can be calculated. If there is
It can be considered that the current driving cycle $ X $ and $ {Y}_{n} $ have the highest similarity, that is, the current driving cycle belongs to this kind of driving cycle.
3.2.2. SOC reference trajectory planning
After classifying the driving cycle fragments into typical driving cycles, DP algorithm is needed to solve the optimal SOC consumption law of various typical driving cycles in this paper. By setting different initial value and end value of SOC in the DP algorithm, study the relationship between the SOC consumption per kilometer and the high efficiency utilization rate of engine under typical driving cycles, and the comparison between the SOC consumption per kilometer and the average fuel consumption rate. The calculation of high efficiency area utilization rate is given as follows [21].
where $ N $ represents the length of time when the engine is working, and $ {be}_{min} $ represents the minimum fuel consumption rate of the engine.
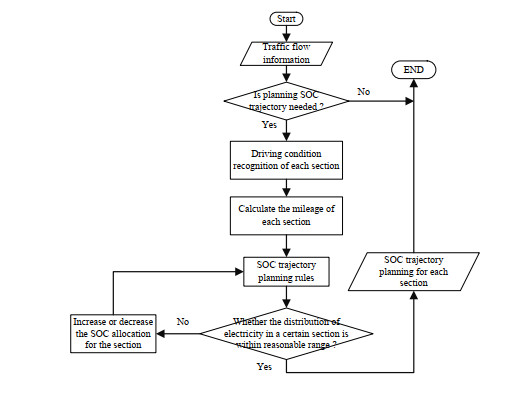
If the whole journey is within the pure electric mileage of PHEV, the pure electric mode is used for the journey without SOC trajectory planning. But if it exceeds the pure electric mileage that can be driven under the current battery state, in order to improve fuel economy, reasonable SOC planning is required. The optimal SOC consumption of each typical driving cycle can be determined according to the relationship between SOC, fuel consumption, and high efficiency utilization rate of engine, so as to formulate SOC trajectory planning rule reasonably. This rule needs to traffic flow information in advance which can be obtained by navigation system and ITS, and then allocate power to each section based on the type of typical driving cycle and the current SOC state. The process of SOC trajectory planning is shown in Figure 18.
4.
Results and discussion
4.1. Building Typical driving cycle for a specific driver
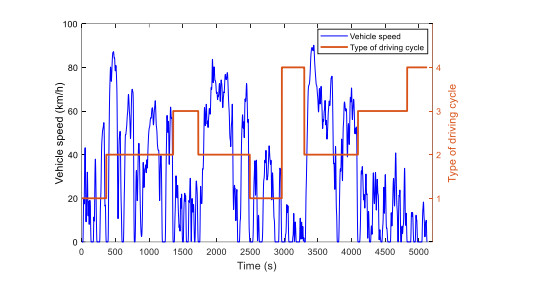
The driving data of a specific driver is collected by GPS and the sampling frequency is 1Hz. The data of vehicle speed and time information is extracted, which is shown in the Figure 19.
There are some abnormal acceleration and deceleration data points caused by GPS equipment or vehicle, abnormal points with discontinuous time, excessive idle data points. These data points need to be eliminated and the historical driving cycle data after preprocessing is shown in Figure 20.
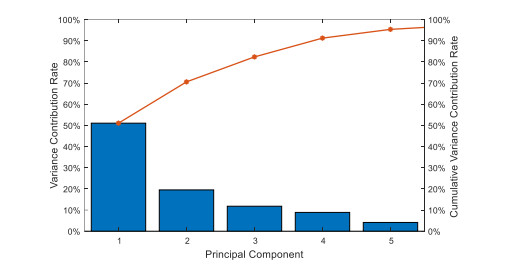
1468 segments of driving cycle are extracted from historical data. 13 driving cycle characteristic parameters, such as average speed, average driving speed and standard deviation of speed, are respectively represented by $ {x}_{1}, {x}_{2}, \dots, {x}_{13} $, and the index of driving cycle segment is represented by $ i = \mathrm{1, 2}, \dots, 1468 $, while the characteristic parameter $ {x}_{1}, {x}_{2}, \dots, {x}_{13} $ of the $ i $ th driving cycle segment is recorded as $ [{x}_{i1}, {x}_{i2}, ..., {x}_{i13}] $. Then there is the full information matrix $ X = ({x}_{ij}{)}_{1468\times 13} $ of the actual driving cycle. Then using PCA regroups the original parameters into a new set of unrelated integrated parameters to reduce dimension and the result is shown in Figure 21.
As a result, the accumulative contribution rate of the first four principal components reached 91.18%. Generally speaking, when it is higher than 85%, it can be considered that the number of principal components selected can retain most of the original data information, and achieve the purpose of dimensionality reduction [34]. Therefore, the first four principal components are selected in this paper. The dimension of historical driving cycle data has been reduced from 13 dimensions to 4 dimensions, which greatly reduces the calculation amount. The principal component score matrix of driving cycle segments obtained by principal component analysis can be used for cluster analysis, as shown in Table 4.
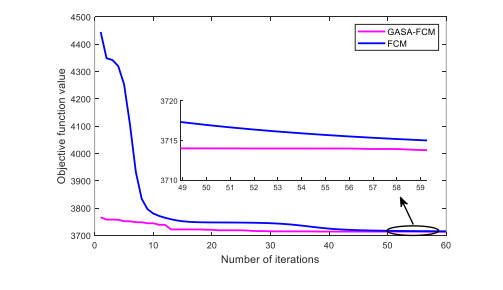
Four principal components of each kinematic segment have obtained above which can be used as the feature vector of FCM samples. And four cluster centers are selected. Iterative process of clustering is shown in Figure 22. It can be seen the convergence speed and objective function value of GASA-FCM are both better than FCM.
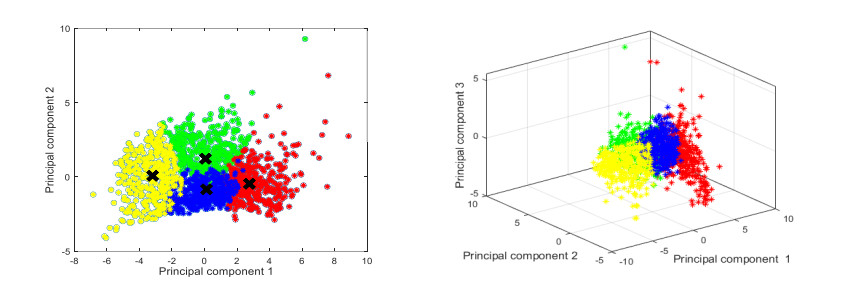
In order to make the clustering results intuitive and clear, the two-dimensional graph composed of principal component 1 and 2 and the three-dimensional graph composed of principal component 1, 2 and 3 are described to show the classification situation, as shown in Figure 23. The black fork in the graph is cluster center.
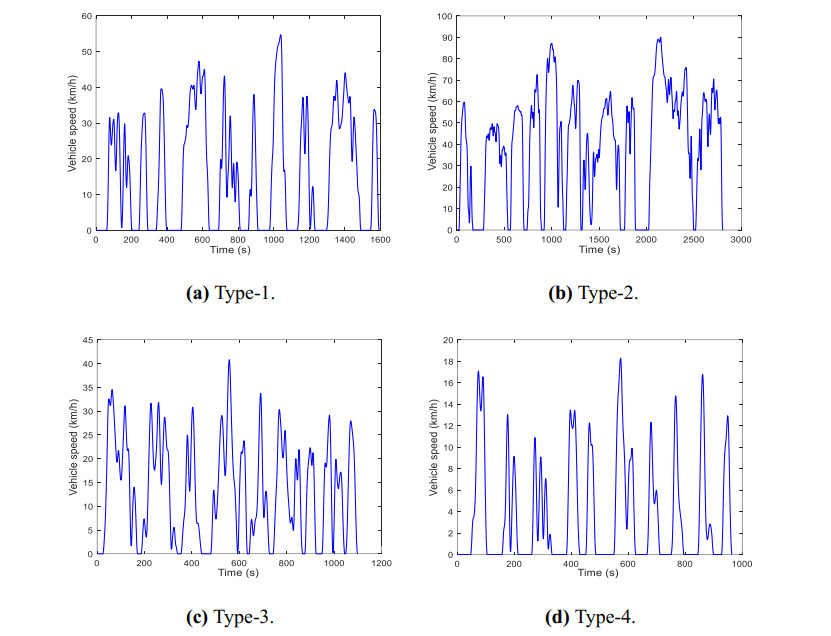
Then it is necessary to extract typical segments of four types of driving cycles. According to the principle that 10 groups of short segments of driving cycles closest to the clustering center are selected as candidate characteristic driving cycles, four types of typical driving cycles are selected, as shown in Figure 24.
Type-1 driving cycle can be defined as medium speed driving cycles. The vehicle speed and the idle time are both moderate, which is generally a relatively smooth urban driving cycle. Type-2 driving cycle can be defined as high-speed driving cycle. The average speed is the highest of the four driving cycle types. Meanwhile, the idle time ratio is the lower of the four driving cycle types, and the maximum speed is also higher, indicating that the road condition of this kind of driving cycle is smooth. Generally, it belongs to the smooth urban expressway section or suburban section. Type-3 driving cycle can be defined as urban medium and low speed driving cycle. It belongs to the urban smooth road condition, which is reflected in the low average driving speed, low idle ratio, and little difference in the proportion of acceleration state, deceleration state and uniform state. Type-4 of driving cycle can also be defined as urban medium and low speed driving cycle. However, the road condition is congested and the start and stop are frequent, which is reflected in the low average driving speed. The idle state accounts for the highest proportion among the four states of acceleration, deceleration, uniform speed and idle.
4.2. SOC trajectory planning
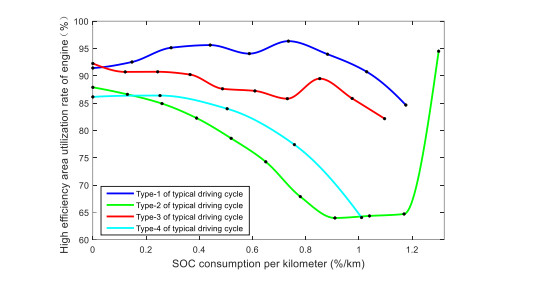
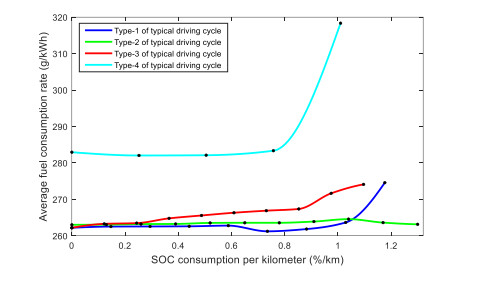
The comparison between the SOC consumption per kilometer and the high efficiency utilization rate of engine under four typical driving cycles, and the comparison between the SOC consumption per kilometer and the average fuel consumption rate are in Figure 25 and Figure 26.
The main purpose of calculating the relationship among SOC consumption per kilometer, engine efficient area utilization rate and average fuel consumption rate under various driving cycles is to provide reasonable SOC distribution value for each driving cycle during SOC trajectory planning. At the same time, calculate the SOC consumption value per kilometer of vehicle under pure electric driving under the condition of sufficient power, as shown in Table 5.
It can be seen that Type-1 typical driving cycles, when the SOC consumption reaches 1.1759% per kilometer, the utilization ratio of the engine efficient area is still over 90%, and the average fuel consumption rate is at the critical point of sudden increase, so this point can be regarded as the critical point of the reasonable SOC distribution range. At the same time, the highest point of high efficiency utilization rate of engine is selected as the optimal SOC distribution value under this driving cycle, which is also at the lowest point of fuel consumption, so $ \Delta SO{C}_{opt\_cycle\_1} = \text{0.7349}\mathrm{\%}/km $.
For Type-2 typical driving cycle, the average speed of this driving cycle is higher, and the start and stop are less. It can be seen the utilization rate of the high-efficiency area of the engine is not high as a whole. In Figure 23, the utilization rate of the high-efficiency area of the engine suddenly rises because it is about to reach the critical value of the pure electric mode, and the engine has little work at this time. Moreover, the change trend of the average fuel consumption rate is not obvious.
For Type-3 typical driving cycle, the critical value shall be selected according to the comprehensive consideration so that the engine efficiency can be as high as possible and the average fuel consumption should not be too high, so the optimal SOC value of this type of driving cycle is $ \Delta SO{C}_{opt\_cycle\_3}=\text{0.8526}\mathrm{\%}/km $.
For Type-4 typical driving cycle, this driving cycle belongs to the congestion driving cycle, with many starts and stops, and the speed is not high, which is not conducive to the engine work. It can be seen engine working efficiency of this kind of driving cycle is not high and the fuel consumption is increased. Therefore, try to operate in pure electric mode under this driving cycle. In conclusion, the reasonable distribution range of SOC under various typical driving cycles is shown in Table 6.
Generally speaking, when the speed is low and the engine starts and stops frequently, the motor should be allowed to work first, because in this case, it is not conducive to the engine working in the efficient area. Therefore, according to the priority order of typical driving cycle 4-3-1-2, the battery power is allocated. This SOC reference trajectory planning rule needs to obtain the road condition information of the trip in advance, and based on the SOC state at this time, then the power allocation of the sub sections can be carried out. The SOC trajectory planning algorithm is shown in Table 7.
The relevant symbolic meanings and calculation methods are shown in Table 8.
In order to verify whether the above SOC trajectory planning algorithm is reasonable and effective, this paper collects a section of data through ITS which only represents the information on a certain route. and uses the method in Section 2.2 to convert to the target driving cycle for simulation and verification. And compares the planned SOC trajectory with the SOC trajectory obtained by DP.
As shown in Figure 27, the driving cycle is divided into 9 sections. Then, it is necessary to calculate the mileage of each driving cycle, and according to the above analysis results of SOC consumption of four typical driving cycle segments, the reasonable SOC distribution value of each typical driving cycle segment can be obtained. The SOC of each driving cycle can be allocated according to the mileage and driving cycle category of each driving cycle, and the detailed information of each driving cycle can be obtained, as shown in Table 9.
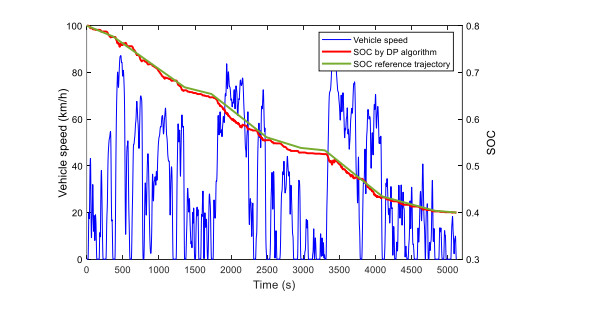
As shown in Figure 28, the reference SOC trajectory is close to the SOC trajectory curve obtained based on DP algorithm, which shows that the SOC reference trajectory obtained by the SOC trajectory planning algorithm is approximately the optimal SOC consumption trajectory.
4.3. A-ECMS simulation verification
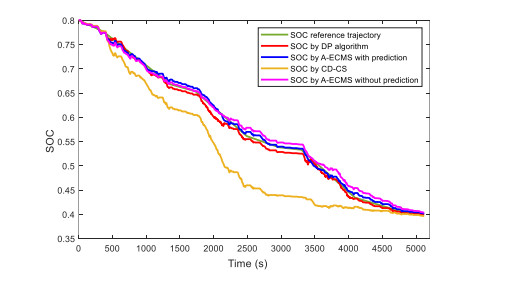
The driving cycle in Figure 27 is taken as the target driving cycle to carry out simulation comparison of different control strategies, mainly including A-ECMS based on vehicle speed prediction, A-ECMS without vehicle speed prediction, DP and CD-CS. The SOC reference trajectory is shown in the Figure 28 and the simulation results are shown in the Figure 29-32 and Table 10.
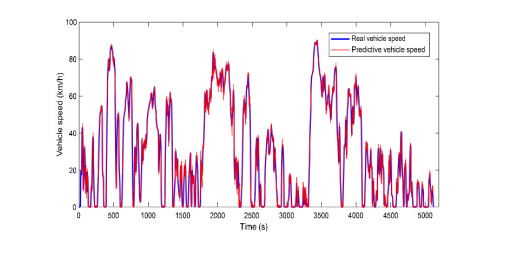
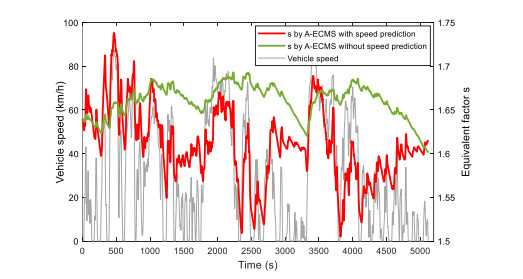
Figure 29 shows vehicle speed prediction in 5s by NAR, the predicted speed and the real speed can be well matched. Figure 30 shows the SOC decline curve under different control strategies. The A-ECMS takes the SOC trajectory obtained from the SOC planning rules mentioned in this paper as the SOC reference trajectory, and modifies the EF in real time. At the same time, combined with the short-term prediction of vehicle speed, when the speed changes greatly in the future, the EF is slightly different from the optimal EF, then the constant part of the adaptive EF is adjusted to the appropriate value. For example, in Figure 31, it can be seen that the EF increases greatly between about 270-500s, which is due to the high-speed driving cycle. The figure also shows that the fluctuation law of the EF is similar to the speed change curve of the simulation driving cycle.
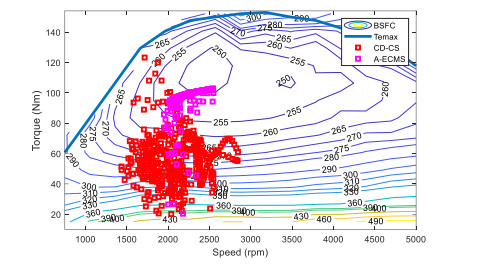
It can also be seen from Figure 30 that the SOC descent trajectory of A-ECMS strategy based on speed prediction is closer to that of DP and can follow the SOC reference trajectory well, while the SOC trajectory of A-ECMS strategy without speed prediction is quite different. It can also be seen from Table 10 that the A-ECMS based on speed prediction and the DP based strategy can better control the SOC terminal value near the target value. For the A-ECMS without speed prediction, the slight difference between the SOC terminal value and the target value is also acceptable. The final value of SOC of CD-CS is more different. It can be seen from the comparison of engine operating points based on the A-ECMS based on speed prediction and CD-CS strategy in Figure 31 that both rotate speeds are concentrated at 1500-3000 rpm, but it is obvious that A-ECMS based on speed prediction engine operating points are more concentrated in the efficient area, which is conducive to the fuel economy of the whole vehicle.
Finally, results in Table 10 show that the fuel saving performance of A-ECMS based on vehicle speed prediction is 8.7% higher than that of CD-CS and same as this is 6.6% in A-ECMS without prediction, which indicates that when the future trip mileage is higher than the pure electric driving mileage under SOC state, the power consumption can be used more reasonably to achieve better fuel saving effect, which is helpful to improve the fuel economy of PHEV.
5.
Conclusion
In order to solve the energy management problems for PHEV, such as the lack of self-adaptability of driving cycle and the inability of real-time online control, the research on the driving cycle prediction and adaptive control strategy of PHEV is carried out.
First of all, this paper proposes an A-ECMS for PHEV energy management, combined with long-term driving cycle recognition by ITS and short-term vehicle speed prediction by NAR neural network to real-time modify EF. Then through the analysis of historical driving cycles by PCA and FCM clustering analysis based on genetic simulated annealing algorithm, this paper obtain four typical driving cycles of the specific driver. Meanwhile, the relationship between SOC consumption, fuel consumption and engine efficiency under typical driving cycle by DP is studied which contributes to establish optimal SOC reference trajectory. Finally, the effect of A-ECMS based on speed prediction proposed in this paper is verified by simulation. Simulation results show that compared with CD-CS and A-ECMS without speed prediction, the fuel consumption of A-ECMS based on speed prediction is reduced by 8.7% and 2.1%. SOC trajectory under A-ECMS basically coincides with SOC trajectory under DP which shows that the algorithm in this paper can apply the optimized results of DP to real-time control and take full advantage of energy saving potential for PHEV.
In this paper, driving data is obtained by the specific driver driving on a substantially fixed route. Then in the further study, it will expand the database and combine Internet of Vehicles and big data analysis to study the versatility of the algorithm and use it for real vehicle control.
Acknowledgments
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the National Key R & D Program of China (2018YFB0106200) and Natural Science Foundation of China (51775229).









 DownLoad:
DownLoad: