Traveling waves for conservation laws with nonlocal flux for traffic flow on rough roads

1.   Introduction

We consider two scalar conservation laws with nonlocal flux, describing traffic flow with varying road condition. To be specific, we consider the integro-differential equations

and

In both equations, $ \rho $ is the main unknown, denoting the density of cars on a road. When $ \rho = 0 $, the road is empty; when $ \rho = 1 $, the road is packed full. The function $ v(\cdot)\in \mathbb{C}^2 $ satisfies

For example, the classical Lighthill-Whitham model [17] uses $ v(\rho) = 1-\rho $.

The function $ \kappa(x) $ denotes the speed limit of the road at $ x $, which represents the road condition. We consider rough road condition where $ \kappa(\cdot) $ can be discontinuous.

The models (M1) and (M2) can be formally derived as the continuum limit of particle models where the speed of each car follows certain rules. For model (M1), the speed of the car at $ x $ is

where a weighted average of car density on an interval of length $ h $ in front of the driver (i.e., downstream) is computed. For model (M2), the speed of the car at $ x $ is

where the weighted average is taken over $ \kappa(\cdot)v(\rho(t, \cdot)) $ over an interval of length $ h $ in front of the driver.

The weight $ w(\cdot) $ is a non-negative function defined on $ x\ge 0 $. For a given $ h $, we assume that $ w(x) $ is continuous and bounded on $ x>0 $ with its support on $ [0, h) $, and satisfies

Here, the assumption $ w' <0 $ indicates that the condition right in front of the driver is more important than those further ahead.

Formally, as $ h\to 0+ $ and $ w(\cdot) $ converges to a Dirac delta, both (M1) and (M2) converge to a scalar conservation law with local flux

Unfortunately rigorous proofs of such convergences have not been established yet in the literature, not even for the case where $ \kappa(\cdot) $ is a constant function.

Non-local conservation laws has gained growing interests in recent years. In the simpler case where $ \kappa(x)\equiv1 $, the existence and well-posedness of solutions of the Cauchy problem for (M1) were established in [6], using numerical approximations generated by the Lax-Friedrich scheme. The same results for (M2) were proved in [15], using numerical approximations generated by a Godunov-type scheme. Other models of conservation laws with nonlocal flux include models for slow erosion of granular flow [3,21], for synchronization [2], for sedimentation [5], for nonlocal crowd dynamics [11], and for material with fading memory [7]. Models with symmetric kernel functions have been studied in [22], and for systems in several space dimensions [1]. Some numerical integrations are studied in [4], and an overview of several nonlinear nonlocal models can be found in [14]. The singular local limit for these equations with nonlocal fluxes is studied in a recent preprint [9], while an interesting counter example where the total variation blows up is constructed in [10].

In this paper we are interested in the traveling wave profiles for (M1) and (M2). We remark that, when the road condition is uniform, say $ \kappa(x) \equiv 1 $, the traveling wave profiles for (M1) and (M2) are studied in a recent work [18], where we established various results on existence, uniqueness and stability of the traveling wave profiles. In this paper, however, we consider rough road condition, where $ \kappa(\cdot) $ is discontinuous. To fix the idea, we consider

The main objective of this paper is to study the stationary wave profiles of (M1) and (M2), crossing the jump in $ \kappa(x) $ at $ x = 0 $. For all possible cases, we show analytical and numerical results on existence (and non-existence), uniqueness (and non-uniqueness) and stability (and instability) of these traveling wave profiles.

Unfortunately, for (M1) and (M2), due to the discontinuity in the coefficient $ \kappa(\cdot) $, a general result on the existence of solutions for the Cauchy problems is not yet available in the literature. They are subjects for possible future studies.

Traveling wave profiles for a local follow-the-leader model for traffic flow was studied in [20] for homogeneous road conditions, and in [19] with rough road condition. We also mention that, for the non-local models for slow erosion of granular flow, traveling waves and their local stability were studied in [16].

The rest of the paper is organized as follows. In Section 2 we consider model (M1) and analyze two cases with $ \kappa^- > \kappa^+ $ and $ \kappa^- < \kappa^+ $, where each case has 4 sub-cases. In Section 3 we analyze model (M2). Final remarks are given in Section 4.

2.   Stationary wave profiles for (M1)

We seek a stationary wave profile $ Q(\cdot) $ for (M1) around $ x = 0 $. To simplify the notation, we introduce an averaging operator

Note that, since $ w(x) $ vanishes outside the interval $ (0, h) $, we could put the upper integration bound to be $ \infty $. Furthermore, as long as $ Q(\cdot) $ is bounded, $ x\mapsto A(Q;x) $ is Lipschitz continuous even if $ Q(\cdot) $ is discontinuous.

Since $ Q $ is a stationary solution for (M1), it must satisfy

where

In the case when

the following constraint on $ \rho^-, \rho^+ $ must be imposed

Differentiating (2.1) in $ x $, we obtain an delay integro-differential equation

Here, $ \delta_0(x) $ denote the dirac delta. For general theory on delay differential equations we refer to [12,13].

Note that $ \kappa(x) $ is discontinuous at $ x = 0 $, therefore the profiles $ Q(x) $ are discontinuous at $ x = 0 $, and extra care must be taken. Note $ A(Q;x) $ is continuous at $ x = 0 $, therefore $ \kappa(x)Q(x) $ must also be continuous at $ x = 0 $. Thus we impose the connecting condition on the traces

Thus, the jump in $ Q(x) $ at $ x = 0 $ is in the opposite direction of the jump in $ \kappa(x) $. In summary, the equation (2.1) with $ \kappa(\cdot) $ in (1.6) is equivalent to

2.1.   Review of previous results

The simpler case where $ \kappa(x)\equiv \bar\kappa = $ constant is studied in a recent work [18]. We review some related results which will be useful in the analysis of this paper.

Under the assumption (1.3), there exists a unique stagnation point $ \hat\rho $ where

Let $ W(\cdot) $ be a stationary profile for (M1) with $ \kappa(x)\equiv \bar\kappa $. It satisfies the following integro-equation

Next Lemma was proved in [18] (Lemma 3.1).

Lemma 2.1 (Asymptotic limits). Assume that $ W $ is a solution of (2.8) which satisfies the asymptotic conditions

Let $ \hat\rho $ be the stagnation point satisfying (2.7). The following holds.

i) As $ x\to+\infty $, $ W(x) $ approaches $ \rho^+ $ with an exponential rate if and only if $ \rho^+ > \hat\rho $;

ii) As $ x\to-\infty $, $ W(x) $ approaches $ \rho^- $ with an exponential rate if and only if $ \rho^- < \hat\rho $.

The following existence and uniqueness result of the profile is proved in Theorem 3.2 of [18].

Theorem 2.2. Let $ W $ satisfy the equation (2.8) and the asymptotic conditions

There exist solutions $ W $ which are monotone increasing. Furthermore, the solution is unique up to horizontal shifts.

In the remaining of this section we let $ W(\cdot) $ denote the smooth and monotone profile for the case with $ \kappa(x)\equiv \kappa^+ $ and the asymptotic boundary conditions

where

By Lemma 2.1, we see that the asymptote $ \lim_{x\to\infty} W(x) = \rho^+ $ is stable if $ \rho^+ > \hat\rho $, while the asymptote $ \lim_{x\to-\infty} W(x) = \rho^- $ is stable if $ \rho^- < \hat\rho $. This implies that if $ \rho^+ \le \hat\rho $ then it is an unstable asymptote for $ x\to\infty $, and if $ \rho^-\ge \hat\rho $ then it is an unstable asymptote for $ x\to-\infty $.

When $ \kappa(\cdot) $ is discontinuous, the profiles $ Q $ are very differently. We discuss two cases in the next two sections, where Case A is for $ \kappa^->\kappa^+ $, and Case B for $ \kappa^-<\kappa^+ $.

For notational convenience, we introduce the functions:

Under the assumptions (1.3), both $ f^-(\rho) $ and $ f^+(\rho) $ are strictly concave functions for $ \rho\in[0, 1] $ with $ (f^\pm)'' <0 $ and $ f^\pm(0) = f^\pm(1) = 0 $.

2.2.   Case A: $ \kappa^- > \kappa^+ $

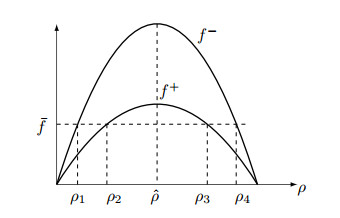
The values $ \rho^-, \rho^+ $ must satisfy (2.3). Given $ \bar f $ that lies in the ranges of both $ f^- $ and $ f^+ $, there exist unique values $ \rho_{1}, \rho_2, \rho_3, \rho_4 $ such that (see Figure 1)

We have 4 sub cases:

$ A1. $ We have $ \rho^- = \rho_1 $, $ \rho^+ = \rho_3 $, with $ \rho^- < \hat \rho < \rho^+ $;

$ A2. $ We have $ \rho^- = \rho_1 $, $ \rho^+ = \rho_2 $, with $ \rho^- <\rho^+ \le \hat\rho $;

$ A3. $ We have $ \rho^- = \rho_4 $, $ \rho^+ = \rho_3 $, with $ \hat\rho \le \rho^+ < \rho^- $;

$ A4. $ We have $ \rho^- = \rho_4 $, $ \rho^+ = \rho_2 $, with $ \rho^+ < \hat\rho <\rho^- $.

We first observe that the cases with $ \bar f = 0 $ are trivial. In this case we have $ \rho_1 = \rho_2 = 0 $ and $ \rho_3 = \rho_4 = 1 $. Then

● For Case A1, we have $ \rho^- = 0, \; \rho^+ = 1 $ and $ Q $ is the unit step function;

● For Case A2, we have $ \rho^- = \rho^+ = 0 $, and we have $ Q(x) \equiv 0 $;

● for Case A3, we have $ \rho^- = \rho^+ = 1 $, and we have $ Q(x)\equiv 1 $;

● For Case A4, we have $ \rho^- = 1, \; \rho^+ = 0 $, there are no profiles. See discussion in Section 2.2.4.

For the rest of the paper we only consider the nontrivial case with $ \bar f >0 $, where $ 0< \rho^\pm<1 $.

2.2.1.   Case A1: $ 0<\rho^-<\hat\rho<\rho^+<1 $

Theorem 2.3 (Existence of profiles). Assume $ \kappa^->\kappa^+ $, and let $ \rho^-, \rho^+ $ satisfy $ 0<\rho^-<\hat\rho<\rho^+<1 $ and (2.3). Then, there exist infinitely many stationary monotone profiles $ Q $ which satisfies the equation (2.1) and the asymptotic boundary conditions

The profiles $ Q $ are discontinuous at $ x = 0 $, but are continuous on $ x>0 $ and $ x<0 $.

Proof. The proof takes several steps.

Step 1. Since $ \rho^+>\hat\rho $ is a stable asymptote as $ x\to\infty $, then on $ x>0 $, the profile $ Q $ can be either the constant function $ Q(x)\equiv \rho^+ $, or some horizontal shift of $ W(\cdot) $. This solution is continuous and monotone increasing on $ x>0 $.

Step 2. At $ x = 0 $ the profile $ Q $ has an upward jump. The traces $ Q(0-) $ and $ Q(0+) $ satisfy

Furthermore, recalling the definition of $ \rho_2 $ in (2.11), we have

Then it holds

Step 3. With this $ Q $ given on $ x\ge 0 $, we solve an ``initial value problem'' backward in $ x $ for $ x<0 $. In order to establish the existence of solutions for the initial value problem, we generate approximate solutions by discretization. Fix the mesh size $ \Delta x $, we have the discretization

On $ x<0 $, the approximate solution $ Q^{\Delta x} $ is reconstructed as the linear interpolation through the discrete values $ Q_i $, i.e.,

The discrete values $ Q_i $ can be generated iteratively. Given a profile $ Q^{\Delta x}(x) $ on $ x\ge x_i $, we compute the value $ Q_{i-1} $ by solving the nonlinear equation

assuming that

Step 4. We now verify that (2.14) has a unique solution. We compute:

Furthermore, for $ {\Delta x} $ sufficiently small, we have

Since

we conclude that

Thus, (2.14) has a unique solution $ Q_{i-1} $, satisfying $ 0<Q_{i-1}<Q_i $. We remark that, numerically, (2.14) can be solved efficiently by Newton iterations, using $ Q_i $ as the initial guess.

By induction we conclude that $ 0<Q_{i-1}<Q_i $ for all $ i<0 $. Thus the approximate solution $ Q^{\Delta x}(\cdot) $ is positive and monotone increasing on $ x<0 $. By construction, it satisfies the equation (2.1) at every grid point $ x_i $. Taking the limit $ {\Delta x}\to0 $, $ Q^{\Delta x}(\cdot) $ converges to a limit function $ Q(\cdot) $, positive and monotone increasing, and satisfies (2.1) for every $ x $.

Step 5. It remains to verify the limit as $ x\to-\infty $. Since $ Q(x) $ is monotone and bounded, it must admit a limit at $ x\to -\infty $. Call it $ \rho^- $. We have

We must also have $ \rho^- < \hat\rho $, since by Lemma 2.1 it is the only stable asymptote as $ x\to-\infty $. This completes the proof.

Several sample profiles are plotted in Figure 2. They are generated by numerical simulation, solving (2.14) by Newton iterations. All profiles are bounded and monotone, continuous except an upward jump at $ x = 0 $. We further note that the profiles do not cross each other. In other words, the profiles are ordered. We have the following Corollary.

Corollary 1 (Ordering of the profiles). Consider the setting of Theorem 2.3, and let $ Q_1 $ and $ Q_2 $ be two distinct profiles. Then, we must have either

Proof. First we observe that on $ x>0 $, the profiles can not cross each other, since they are horizontal shifts of the monotone profile $ W(x) $. Now consider two distinct profiles $ Q_1, Q_2 $, such that $ Q_1(x) > Q_2(x) $ on $ x> 0 $. Then $ Q_1(0+) > Q_2(0+) $, and by the connecting condition (2.5), we have also $ Q_1(0-) > Q_2(0-) $.

We continue by contradiction, and assume that there exists a point $ y<0 $ such that

Then, by equation (2.1) we have

which implies

a contradiction to (2.16). We conclude that the graphs of $ Q_1, Q_2 $ does not cross each other.

Stability. We now show the local stability of these profiles, such that they are local attractors for solutions of the Cauchy problems for (M1) with suitable initial data. When $ \kappa(x)\equiv 1 $ is a constant function, the existence and uniqueness of solutions for the Cauchy problems of (1.1) is established in [6]. In particular, if the initial condition $ \rho(0, \cdot) $ is smooth, so is the solution $ \rho(t, \cdot) $ for $ t>0 $.

However, if $ \kappa(\cdot) $ is discontinuous at $ x = 0 $, then the solution $ \rho(t, \cdot) $ must have a jump at $ x = 0 $ as well. A connecting condition, similar to (2.5), should be imposed:

We have the following definition.

Definition 2.4. We say that a function $ \rho $ is a solution of (1.1) if $ \rho(t, x) $ satisfies (1.1) for all $ x>0 $ and $ x<0 $, and the connecting condition (2.17) at $ x = 0 $, for all $ t> 0 $.

We remark that, a general existence theorem for the Cauchy problem of (M1) with discontinuous coefficient $ \kappa $ is not yet available in the literature. One may speculate that the existence of solutions could be established by the vanishing viscosity approach, a possible topic for future work. In this paper, assuming that solutions exist for the Cauchy problem, we establish the local stability of the traveling wave profiles.

Let $ Q^\sharp $ and $ Q^\flat $ be two profiles such that $ Q^\sharp(x) > Q^\flat(x) $ for every $ x $. Define $ D $ as the region between $ Q^\sharp $ and $ Q^\flat $, i.e.,

By Corollary 1, all these profiles are ordered and they do not intersect with each other. One can parametrize each profile by its trace $ Q(0+) $. For every point $ (x, q)\in D $ with $ x\not = 0 $, there is a unique profile that passes through it. Fix a time $ t\ge 0 $. For each function $ \rho(t, x) $ with $ (x, \rho(t, x))\in D $ and $ x\not = 0 $, we define the mapping:

We have the following stability Theorem.

Theorem 2.5 (Stability of the profiles). Consider (M1) with $ \kappa(\cdot) $ given in (1.6) and $ \kappa^- >\kappa^+ $. Let $ \bar \rho(\cdot) $ be the initial data, smooth except at $ x = 0 $, satisfying

Let $ \rho(\cdot, \cdot) $ be the solution of the Cauchy problem for (M1) with initial data $ \bar\rho(\cdot) $, following Definition 2.4. Then, we have

Furthermore, let $ \Phi(\cdot, \cdot) $ be the mapping for $ \rho(\cdot, \cdot) $, as defined in (2.19). Then

Proof. We first observe that, since the initial data is smooth except at $ x = 0 $, so is the solution for $ t>0 $. We now claim the following:

● If $ \Phi(t, y) $ is a maximum value such that

then $ \Phi_t(t, y) <0 $.

● Symmetrically, if $ \Phi(t, y) $ is a minimum value such that

then $ \Phi_t(t, y) >0 $.

This claim would imply both (2.21) and (2.22).

We provide a proof for the case of a maximum value point, while the minimum value point can be treated in a completely similar way. Fix a time $ t\ge 0 $, and let $ y $ be a point that satisfies (2.23). We discuss 3 cases, for different locations of $ y $.

(1). Consider $ y>0 $ which satisfies (2.23), and let $ Q $ be the profile such that

Since $ v'<0 $, this implies

We also have

Using $ w(h) = 0, Q(y) = \rho(t, y), w'(s)<0 $ and $ Q(y+s) > \rho(t, y+s) $, we get

We now compute:

Here the last inequality holds thanks to (2.25)-(2.26).

(2). Consider $ y = 0 $. By the connecting conditions (2.5) and (2.17), we have

Since the delay differential equation has one-sided delay, then the derivative $ Q'(x) $ in (2.4) at $ x = 0 $ effectively the left limit. We consider $ y = 0- $, and compute

We have similar estimates as those in (2.25)-(2.26), i.e.,

We now compute, by using (2.27)

(3). If $ y<0 $, then the averaging operator could possibly be taken over the jump location at $ x = 0 $. Nevertheless, we still have

The rest of the computation remains the same as in the previous steps.

We perform a numerical simulation with Riemann initial data $ (\rho^-, \rho^+) $, and the plots are shown in Figure 3. We observe that, the solution approaches a traveling wave profile as $ t $ grows. Note also that the Riemann initial data actually do not satisfy the assumptions in Theorem 2.5, but we still observe stability property. This indicates that Theorem 2.5 probably applies to more general initial data.

2.2.2.   Case A2: $ \rho^- < \rho^+\le \hat\rho $

Since $ \rho^+ \le \hat\rho $ is an unstable asymptote for $ x\to\infty $, the solution on $ x>0 $ must be $ Q(x)\equiv \rho^+ $. At $ x = 0 $ the connecting condition (2.5) implies $ Q(0-) < Q(0+) $, therefore the profile has an upward jump. Finally, the solution can be extended to $ x<0 $ by solving an initial value problem for (2.1), with initial data given on $ x>0 $, and a jump at $ x = 0 $. Using the same argument as in Theorem 2.3 for Case A1, we conclude that this unique profile is monotone increasing on $ x<0 $. We have the following Theorem.

Theorem 2.6 (Existence of a unique profile). Let $ \kappa^->\kappa^+ $, and let $ \rho^-, \rho^+ $ be given such that $ \rho^- < \rho^+ \le\hat\rho $ and (2.3) holds. Then, there exists exactly one stationary monotone profile $ Q(x) $, monotone increasing on $ x<0 $, satisfying

See Figure 4 for a sample profile.

Since $ \rho^+\le\hat\rho $ is an unstable asymptote for $ x\to \infty $, the profile is not a local attractor for solutions of the Cauchy problems for (M1). In fact, any perturbation that enters the region $ x>0 $ will persist, as verified by a numerical simulation in Figure 5. We observe that, with Riemann initial data, an oscillation is formed around the origin and then travels into the region $ x>0 $, where it travels further to the right as $ t $ grows.

2.2.3.   Case A3: $ \hat\rho\le \rho^+<\rho^- $

Since $ \rho^- > \hat \rho $, the asymptote $ \rho^- $ is unstable as $ x\to-\infty $. If a profile shall exists, it must be constant $ \rho^- $ on $ x<0 $. There exists no profile on $ x>0 $ that can be connected to this constant solution. In conclusion, no stationary profiles exist for this case.

A numerical simulation with Riemann initial data is performed, and results are plotted in Figure 6. We observe that oscillations are formed around $ x = 0 $, which travel to the left in the region $ x<0 $, where they persist as $ t $ grows.

2.2.4.   Case A4: $ \rho^+ < \hat\rho < \rho^- $

Since both $ \rho^- $ and $ \rho^+ $ are unstable, there does not exist any profiles. We present a numerical simulation with Riemann data, and plot the results in Figure 7. We observe rather wild behavior. Oscillations are formed around $ x = 0 $, and then enter both regions of $ x>0 $ and $ x<0 $, and they persist as $ t $ grows.

2.3.   Case B: $ \kappa^- < \kappa^+ $

Fix $ \bar f > 0 $ which lies in the ranges of $ f^- $ and $ f^+ $, there exist unique values $ \rho_{1}, \rho_2, \rho_3, \rho_4 $ such that

Similar to Case A, there are 4 sub-cases:

B1. We have $ \rho^- = \rho_2, \rho^+ = \rho_4 $ and $ \rho^-<\hat\rho<\rho^+ $;

B2. We have $ \rho^- = \rho_1, \rho^+ = \rho_2 $ and $ \rho^+<\rho^-\le\hat\rho $;

B3. We have $ \rho^- = \rho_3, \rho^+ = \rho_4 $ and $ \hat\rho\le \rho^-<\rho^+ $;

B4. We have $ \rho^- = \rho_1, \rho^+ = \rho_3 $ and $ \rho^+<\hat\rho<\rho^- $.

Note that since $ \kappa^- < \kappa^+ $, the connecting condition (2.5) implies that $ Q(0-)>Q(0+) $, thus $ Q(\cdot) $ has a downward jump at $ x = 0 $. This means that the profiles are no longer monotone increasing. Furthermore, since we seek profiles with $ Q(0-)\le 1 $, this imposes a restriction on the trace $ Q(0+) $,

As previously, we let $ W $ denote a stationary profile for the case $ \kappa(x)\equiv\kappa^+ $, discussed in Section 2.1. Below, we discuss each sub-case in detail. We remark that the overall framework of the discussions is similar to that of Case A, but details (especially for Case B1) are rather different, due to the lack of monotonicity.

2.3.1.   Case B1: $ \rho^-<\hat\rho<\rho^+ $

Theorem 2.7. Given $ \kappa^- <\kappa^+ $, and $ \rho^-, \rho^+ $ satisfying

there exist infinitely many solutions $ Q $ to (2.6) which satisfy the asymptotic boundary conditions

All profiles are monotone increasing on $ x>0 $, but some profiles may be oscillatory on $ x<0 $.

Proof. The proof takes several steps.

(1) On $ x>0 $, $ Q $ could be either the constant function $ Q(x)\equiv \rho^+ $ or some horizontal shift of $ W $. We first claim that the constant solution $ Q(x)\equiv \rho^+ $ on $ x>0 $ will not give a profile on $ x<0 $. Indeed, by the connecting condition (2.5) we have $ Q(0-) > Q(0+) = \rho^+ $. Then one can easily show that $ Q'(0-) <0 $, and furthermore $ Q'(x)<0 $ for $ x<0 $. Thus, $ Q(x) $ reaches 1 for some finite $ x<0 $, and the solution can not be continued further as $ x $ becomes smaller.

In conclusion, on $ x>0 $, $ Q $ is some horizontal shift of $ W $. At $ x = 0 $, the trace $ Q(0+) $ takes value between $ \rho_1 $ and $ \rho^+ $, where $ \rho_1<\rho^-< \hat\rho<\rho^+ $ and $ f^+(\rho_1) = f^+(\rho^+)\;\dot = \;\bar f>0 $.

(2) Furthermore, we consider only the profiles where $ Q(0+) $ satisfies (2.28). At $ x = 0 $, the connecting condition (2.5) applies, which determines the value for the trace $ Q(0-) $. We then solve an initial value problem on $ x<0 $, with initial data given on $ x\ge 0 $. We expect to have infinitely many profiles. From the same argument as in Corollary 1, all profiles are ordered and will never cross each other.

(3) Utilizing the same analysis as in Step 3-4 of Theorem 2.3, we have that, if a profile $ Q $ is monotone on $ [-h, 0] $, then it remains monotone on $ (-\infty, -h] $.

(4) We now construct a lower envelope $ Q^\flat $ for all the profiles on $ x<0 $, by solving the initial value problem with initial data $ Q(x)\equiv \rho_1< \rho^- $ for $ x>0 $. Note that any horizontal shift of the profile $ W $ satisfies $ W(x) > \rho_1 $ for $ x>0 $. Since the profiles can not cross each other, we conclude that, any profiles with $ Q(x) = W(x) $ on $ x>0 $ will lie above $ Q^\flat $.

We claim that, on $ x<0 $ the profile $ Q^\flat $ is monotone decreasing and it lies below $ \rho^- $. Indeed, since $ \kappa^+\rho_1 v(\rho_1) = \kappa^- \rho^- v(\rho^-) = \bar f $, the connecting condition (2.5) gives

Then, by (2.4), we have

where the last inequality holds thanks to $ Q(0-) > Q^\flat(h) = \rho_1 $ and we have $ A(Q^\flat;0-)_x <0 $. A contradiction argument shows that $ (Q^\flat)'(x) <0 $ for every $ x<0 $. Thus, $ Q^\flat $ is monotone decreasing on $ x<0 $.

To show that $ Q^\flat(x) < \rho^- $ on $ x<0 $, we proceed with contradiction. We assume that there exists a $ y<0 $ such that $ Q^\flat(y) = \rho^- $ and $ Q^\flat(x) < \rho^- $ for $ x>y $. By (2.1) we compute

thus

a contradiction which proofs our claim.

Finally, by the same argument as in Step 5 in the proof of Theorem 2.3 one concludes that the profile $ Q^\flat(x) $ approaches $ \rho^- $ asymptotically as $ x\to -\infty $.

(5) By the ordering of the profiles, any profile $ Q $ with $ Q(0-)>\rho_1 $, if it exists, would lie above $ Q^\flat(x) $. However $ Q $ might lose monotonicity and become oscillatory around $ \rho^- $ on $ x<0 $. If this happens, we claim that the local max of an oscillating solution is decreasing and approaches $ \rho^- $ as $ x\to -\infty $.

Indeed, by (2.1), on $ x<0 $ we have

Thus, $ Q'(x) $ has the same sign as $ A(Q;x)_x $. By the assumption $ w(h) = 0 $, we have $ w(0) = -\int_0^h w'(s)\; ds $. Thus, we compute, for $ x<0 $

Since $ w'<0 $, we conclude that, if $ A(Q;x')_x = 0 $ for some $ x' $, then on $ [x', x'+h] $ we have either $ Q(x)\equiv Q(x') $ or $ Q(x) $ oscillated around $ Q(x') $. In particular, this implies that if $ y<-h $ is a local max with $ Q(y) > \rho^- $, such that $ A(Q;y)_x = 0 $, then we must have $ Q(x^*) > Q(y) $ for some $ x^*\in (y, y+h) $. Therefore, there exists a local max on the left of $ y $, with a higher max value.

Thus, there exists a sequence of local maxima $ y_k $ with

The sequence might be finite or infinite. We conclude that there exists an increasing function on $ x<0 $ which serves as an upper envelope for this oscillatory profile. Since the flux equals $ \bar f $, this envelope approaches $ \rho^- $ asymptotically as $ x\to -\infty $.

By continuity there exists an upper profile $ Q^\sharp $, whose graph lies between $ Q^\flat $ and the upper envelope. In particular, $ Q^\sharp $ approaches the limit $ \rho^- $ as $ x\to-\infty $.

We conclude that, in between the profiles $ Q^\flat $ and $ Q^\sharp $, there exist infinitely many profiles $ Q $. These profiles never cross each other, and they all approach $ \rho^- $ as $ x \to -\infty $.

Sample profiles for Case B1 are given in Figure 8. By a similar argument as for Case A1, one concludes that these profiles are time asymptotic limits for solutions of the Cauchy problems for (M1). We omit the details of the proof. Result of a numerical simulation is given in Figure 9, with Riemann initial data. We observe that the solution approaches a certain traveling wave profile as $ t $ grows.

2.3.2.   Case B2, Case B3, and Case B4

For Case B2, we have $ \rho^+<\rho^-\le\hat\rho $, which is the counter part for Case A2. Since $ \rho^+ \le\hat\rho $ is an unstable asymptote as $ x\to\infty $, we must have $ Q(x) \equiv \rho^+ $ on $ x>0 $. At $ x = 0 $ we apply the connecting condition (2.5) to get $ Q(0-) $. We then solve an initial value problem on $ x<0 $. By the same arguments as for Case A2 we prove the existence of a monotone decreasing profile on $ x<0 $. A sample profile is illustrated in Figure 10. Unfortunately, such an profile is not a local attractor for the solutions of the Cauchy problem for (M1). Result of a numerical simulation is given in Figure 11, with Riemann initial data. We observe that an oscillation is formed around $ x = 0 $, which travels into the region $ x>0 $, where it persists as $ t $ grows.

For case B3, we have $ \hat\rho\le \rho^-<\rho^+ $ and for Case B4 we have $ \rho^+<\hat\rho<\rho^- $. These are the counter parts for Case A3 and Case A4 respectively, and there are no profiles. We plot the results of a numerical simulation in Figure 12 for Case B3 and in Figure 13 for Case B4, and observe the oscillations in solutions which persist in time.

3.   Stationary traveling wave profiles for (M2)

Let $ P $ be a stationary profile for (M2). It satisfies the equation

and

In the case where $ \lim_{x\to\pm\infty} P(x) = \rho^\pm $ and $ \kappa $ satisfies (1.6), we have $ \bar f = f^-(\rho^-) = f^+(\rho^+). $

We see that $ V(x) $ is Lipschitz continuous even with discontinuous $ P(x) $. This implies that $ P(x) $ is also Lipschitz continuous, but with a kink at $ x = 0 $.

Previous results. Consider the simpler case where $ \kappa(x)\equiv \bar\kappa $ is a constant function, and let $ \mathcal{W} $ be a stationary profile for (M2). Then, $ \mathcal{W} $ satisfies the integral equation

By the results in [18], Lemma 2.1 and Theorem 2.2 in Section 2.1 hold for the profile $ \mathcal{W} $.

Below we consider two cases, where Case C is for $ \kappa^->\kappa^+ $, and Case D for $ \kappa^-<\kappa^+ $. We assume that $ \bar f>0 $, since the cases with $ \bar f = 0 $ are trivial.

3.1.   Case C: $ \kappa^->\kappa^+ $

Similar to Case A, we let $ \rho_{1}, \rho_2, \rho_3, \rho_4 $ be the unique values that satisfies (2.11). Then, we have 4 sub-cases of C1, C2, C3, C4, which are the corresponding cases of A1, A2, A3, A4, respectively. We also denote by $ \mathcal{W} $ the stationary profile with $ \kappa(x)\equiv\kappa^+ $ and $ \lim_{x\to\infty} \mathcal{W}(x) = \rho^+ $.

3.1.1.   Case C1: $ \rho^- < \hat \rho < \rho^+ $

Theorem 3.1. Let $ \kappa^->\kappa^+ $ and let $ \rho^-, \rho^+ $ be given such that $ 0<\rho^-< \hat\rho < \rho^+<1 $, and assume that (2.10) holds. Then, there exist infinitely many stationary monotone profiles $ P $ which satisfy the equation (3.1) and the boundary conditions (2.12). At $ x = 0 $ the profiles are continuous but not differentiable.

Proof. A proof very similar to the proof of Theorem 2.3 can be carried out here, with small modifications. Here we provide a new approach, utilizing a contractive Picard operator.

On $ x\ge 0 $, the profile matches some horizontal shift of $ \mathcal{W} $. Using this as the initial condition, tt remains to prove existence and uniqueness of the solution for the initial value problem of (3.1). Given a $ \mathcal{W} $, we consider the closed set $ \mathcal{U} $ of functions, as

Let $ u\in\mathcal{U} $. We define a Picard operator on $ \mathcal{U} $ as

Note that a fixed point for $ \mathcal{P} $ is a solution for (3.1).

We claim that $ \mathcal{P} $ maps $ \mathcal{U} $ into itself, i.e., $ \mathcal{P} u \in \mathcal{U} $ if $ u\in\mathcal{U} $. Indeed, since $ \mathcal{W} $ satisfies (3.1) on $ x\ge 0 $, we clearly have $ (\mathcal{P} u )(x) = \mathcal{W}(x) $ for $ x\ge 0 $. Moreover, we have

Furthermore, $ u'\ge 0 $ and $ \kappa^->\kappa^+ $ imply $ V(u;x)_x \le 0 $, and therefore $ (\mathcal{P} u)'(x) \ge 0 $ for $ x\le 0 $. This further implies

Finally, we estimate the Lipschitz constant for $ x \mapsto \mathcal{P} u $. Since

we have

proving the claim.

We introduce a norm which we call the $ \alpha $-norm

We claim that the operator $ \mathcal{P} $ is a strict contraction w.r.t. $ \alpha $-norm. Hence $ \mathcal{P} $ has a unique fixed point in $ \mathcal{U} $. In particular, the fixed point iterations converge point-wise on bounded sets on $ x\le 0 $. Since we also have the asymptotic limit fixed at $ x\to-\infty $, we conclude point-wise convergence for all $ x\le 0 $.

It remains to establish the contractive property. Indeed, let $ u_1, u_2\in\mathcal{U} $. Assume

Then, on $ x\le 0 $ we have

Hence

completing the proof.

We remark that a suitable Picard operator could be defined for the proof of Theorem 2.3 for Case A1.

Sample profiles for case C1 are plotted in Figure 14. We observe that they do not cross each other. The ordering property in Corollary 1 holds for these profile, with a very similar proof.

Stability. In the case when $ \kappa(x)\equiv \bar\kappa $ is a constant function, the existence and well-posedness of solution for (M2) is established in [15], through convergence of approximate solutions generated by a Godunov-type scheme. Unfortunately, when $ \kappa(\cdot) $ is discontinuous, no existence result is yet available. Assuming that the solutions exist, we show that they converge to the traveling wave profile as $ t $ grows, under mild assumptions on the initial data.

Definition 3.2 We say that $ \rho(t, \cdot) $ is a solution of (1.2) if $ \rho(t, \cdot) $ is continuous and satisfies the equation (1.2) for all $ x<0 $ and $ x>0 $, and the connecting condition

With a very similar argument as those for Case A1, one can prove that the profiles $ P $ are time asymptotical limit for the Cauchy problem of (1.2). We omit the details of the proof, and state the following stability Theorem.

Theorem 3.3. Let $ \rho(t, \cdot) $ be the solution to the Cauchy problem for (1.2) with initial data $ \rho(0, \cdot) $, with $ \kappa^- >\kappa^+ $. Assume that the initial data satisfies the connecting condition (3.6) and $ P^\flat (x) \le \rho(0, x) \le P^\sharp(x) $ for all $ x $, for some profiles $ P^\flat $ and $ P^\sharp $. Then, the solution $ \rho(t, \cdot) $ converges to a profile $ P(\cdot) $ as $ t\to\infty $.

We perform a numerical simulation with Riemann initial data, and plot the result in Figure 15. We observe that the solution $ \rho(t, \cdot) $ quickly approaches a profile, confirming Theorem 3.3.

3.1.2.   Case C2, Case C3, and Case C4

For Case C2 we have $ \rho^- <\rho^+ \le \hat\rho $. Since $ \rho^+ $ is an unstable asymptote for $ x\to\infty $, we must have the constant solution $ P(x)\equiv \rho^+ $ for $ x\ge 0 $. A unique monotone profile $ P $ can be obtained by solving this initial value problem backward in $ x $, for $ x<0 $. See a sample graph in Figure 16. Similarly, the profile is not a local attractor for solutions of (1.2), since $ \rho^+ $ is an unstable asymptote. This is further confirmed by the numerical simulation in Figure 17, where we observe oscillation entering the region $ x>0 $ and persisting in time.

For Case C3 with $ \hat\rho \le \rho^+ < \rho^- $ and Case C4 with $ \rho^- > \hat\rho >\rho^+ $, there are no profiles, similar to the results for Case A3 and Case A4. Numerical simulations with Riemann initial data are given in Figure 18 for Case C3, and in Figure 19 for Case C4. In both cases, we observe that oscillations form around $ x = 0 $ and enter the region $ x>0 $ and/or $ x<0 $, and the oscillations persist as $ t $ grows.

3.2.   Case D: $ \kappa^-<\kappa^+ $

This is the counter part for Case B, and similarly we have 4 sub-cases which we discuss in detail in the following sub sections.

3.2.1.   Case D1: $ \rho^- < \hat\rho < \rho^+ $

Theorem 3.4. Let $ \kappa^- < \kappa^+ $, and let $ \rho^-, \rho^+ $ satisfy

Then there exist infinitely many solutions for (3.1) which satisfy the asymptotic boundary conditions

Proof. The proof follows a similar line of argument as those in the proof of Theorem 2.7. Below we briefly outline the adjustments.

Step 1. On $ x\ge 0 $, the profile can be either the constant function $ P(x)\equiv \rho^+ $ or some horizontal shift of $ \mathcal{W}(x) $. At $ x = 0 $, $ P(0) $ takes value between $ \rho_1 $ and $ \rho^+ $, where $ \rho_1 < \hat\rho<\rho^+ $ and $ f^+(\rho_1) = f^+(\rho^+) \;\dot = \; \bar f $.

Step 2. Let $ P^\flat $ denote the solution of the initial value problem with $ P^\flat(x)\equiv \rho_1 $ on $ x\ge 0 $, where $ \rho_1 $ is defined in Step 1. By a similar argument as in Step 4 of the proof for Theorem 2.7, the solution is monotone decreasing and approaches $ \rho^- $ as $ x\to-\infty $. Similarly $ P^\flat $ serves as a lower envelope.

Step 3. Let $ P $ be a profile which equals some horizontal shift of $ \mathcal{W}(\cdot) $ on $ x\ge 0 $. As $ P(0) $ varies from $ \rho_1 $ to $ \rho^+ $, the profile might lose monotonicity and becomes oscillatory. By a similar argument as in Step 5 of the proof for Theorem 2.7, we have, for $ x<-h $,

Thus, if $ V'(x') = 0 $ for some $ x' $, then on $ x\in[x', x'+h] $ we have either $ P(x)\equiv P(x') $, or $ P(\cdot) $ oscillates around $ x = x' $. Following the same argument as in the rest of Step 5 of the proof for Theorem 2.7, we conclude that there exists an upper envelope $ P^\sharp $ for all the profiles that approaches $ \rho^- $ as $ x\to-\infty $. By continuity and the ordering of the profiles, there exist infinitely many profiles between $ P^\flat $ and $ P^\sharp $.

Sample profiles are given in Figure 20. Using a similar argument as for Theorem 2.5 for Case A1, these profiles are time asymptotic limits for the solutions of the the Cauchy problem of (1.2). We omit the details of the proof. A numerical simulation is presented in Figure 21, with Riemann data, where we observe this asymptotic behavior as $ t $ grows.

3.2.2.   Case D2, Case D3, and Case D4

Case D2, D3 and D4 are the counter part of Case B1, B2 and B3, respectively, with similar results. Here we only present the sample plots for Case D2 in Figure 22, and numerical simulations in Figure 23, Figure 24 and Figure 25 for Case D2, D3 and D4, respectively.

4.   Concluding remarks

We study traveling wave profiles for two nonlocal PDE models for traffic flow with rough road condition. For all possible cases, we show that for different cases there can exist infinitely many traveling wave profiles, a unique profile, or no profiles at all, depending on the jump in speed limit and the limits $ \rho^-, \rho^+ $. The stability of these profiles also vary from case to case.

Formally, the non-local PDE models are the macroscopic limits of the corresponding non-local particle models, referred to as the follow-the-leaders (FtLs) model. In the case where $ \kappa(x)\equiv 1 $, the existence of traveling waves and their convergence to the traveling waves for the PDE models were provided in [18]. It is interesting to establish a similar result for the FtLs model where $ \kappa(x) $ has a jump. Details are available in a recent preprint [8].

Codes for all the numerical simulations in this paper can be found at:

http://www.personal.psu.edu/wxs27/TrafficNLRough/