Left: Comparison of solutions of the Scharfetter-Gummel (red line) and upwind (blue, dashed line) schemes at time
Citation: Grégory Faye, Pascal Chossat. A spatialized model of visual texture perception using the structure tensor formalism[J]. Networks and Heterogeneous Media, 2013, 8(1): 211-260. doi: 10.3934/nhm.2013.8.211
| [1] | Luis Almeida, Federica Bubba, Benoît Perthame, Camille Pouchol . Energy and implicit discretization of the Fokker-Planck and Keller-Segel type equations. Networks and Heterogeneous Media, 2019, 14(1): 23-41. doi: 10.3934/nhm.2019002 |
| [2] | Karoline Disser, Matthias Liero . On gradient structures for Markov chains and the passage to Wasserstein gradient flows. Networks and Heterogeneous Media, 2015, 10(2): 233-253. doi: 10.3934/nhm.2015.10.233 |
| [3] | José Antonio Carrillo, Yingping Peng, Aneta Wróblewska-Kamińska . Relative entropy method for the relaxation limit of hydrodynamic models. Networks and Heterogeneous Media, 2020, 15(3): 369-387. doi: 10.3934/nhm.2020023 |
| [4] | Panpan Xu, Yongbin Ge, Lin Zhang . High-order finite difference approximation of the Keller-Segel model with additional self- and cross-diffusion terms and a logistic source. Networks and Heterogeneous Media, 2023, 18(4): 1471-1492. doi: 10.3934/nhm.2023065 |
| [5] | Raul Borsche, Axel Klar, T. N. Ha Pham . Nonlinear flux-limited models for chemotaxis on networks. Networks and Heterogeneous Media, 2017, 12(3): 381-401. doi: 10.3934/nhm.2017017 |
| [6] | Kenneth H. Karlsen, Süleyman Ulusoy . On a hyperbolic Keller-Segel system with degenerate nonlinear fractional diffusion. Networks and Heterogeneous Media, 2016, 11(1): 181-201. doi: 10.3934/nhm.2016.11.181 |
| [7] | Jin Cui, Yayun Fu . A high-order linearly implicit energy-preserving Partitioned Runge-Kutta scheme for a class of nonlinear dispersive equations. Networks and Heterogeneous Media, 2023, 18(1): 399-411. doi: 10.3934/nhm.2023016 |
| [8] | Michael T. Redle, Michael Herty . An asymptotic-preserving scheme for isentropic flow in pipe networks. Networks and Heterogeneous Media, 2025, 20(1): 254-285. doi: 10.3934/nhm.2025013 |
| [9] | Tingting Ma, Yayun Fu, Yuehua He, Wenjie Yang . A linearly implicit energy-preserving exponential time differencing scheme for the fractional nonlinear Schrödinger equation. Networks and Heterogeneous Media, 2023, 18(3): 1105-1117. doi: 10.3934/nhm.2023048 |
| [10] | Yves Achdou, Victor Perez . Iterative strategies for solving linearized discrete mean field games systems. Networks and Heterogeneous Media, 2012, 7(2): 197-217. doi: 10.3934/nhm.2012.7.197 |
Taxis-diffusion and aggregation equations are widely studied in the context of biological populations (see [10,15,16,21] for instance). They describe cell communities which react to external stimuli and form aggregates of organisms (pattern formation), such as bacterial colonies, slime mold or cancer cells. The Patlak-Keller-Segel model [18] is the most famous system and we are interested in the following generalization
| $ {∂u∂t−∂∂x[∂u∂x−φ(u)∂v∂x]=0,x∈(0,1),t>0,∂u∂x−φ(u)∂v∂x=0,for x=0 or 1,u(x,0)=u0(x)≥0,x∈[0,1]. $ | (1) |
Here,
| $ v:=v(x)≥0,∂v∂x∈L∞(0,1), $ | (2) |
or the case of the generalized Keller-Segel (GKS in short) equation, where
| $ v(x,t)=∫K(x,y)u(y,t)dy,K(x,y) a smooth, symmetric kernel. $ | (3) |
Depending on the modeling choice for
| $ u(x,t)≥0, $ | (4) |
| $ ∫10u(x,t)=∫10u0(x)dx, $ | (5) |
| $ g(u)=μ+v,g′(u)=1φ(u), $ | (6) |
where
| $ ddtE(t)≤0,E(t)=∫10[G(u)−κuv]dx, $ | (7) |
where
| $ κ=1(FP case),κ=12(GKS case). $ | (8) |
The aims of our work are first to recall two points of view for the derivation of the above energy inequality, second to use them for the construction of conservative, finite volume numerical schemes preserving energy dissipation to solve equation 1, third to make numerical comparisons in the case of complex patterns in order to distinguish physical instabilities from numerical artifacts. The two different derivations of the energy dissipation use two symmetrization strategies: the gradient flow or the Scharfetter-Gummel approach. It turns out that they lead to two strategies for discretization of problem 1. We prove that the proposed schemes statisfy properties 4-7 and because we build implicit schemes, there is no limitation on the time step in the fully discrete case.
There exist other works which propose schemes for the resolution of problems in the form 1. For instance, finite elements methods are used, see [25] and references therein. Optimal transportation schemes for Keller-Segel systems are introduced in [5]. The papers [8] and [9] propose a finite-volume method able to preserve the above properties, including energy dissipation, at the semi-discrete level or with an explicit in time discretization, using the gradient flow approach, see also [4]. The symmetrization using the Scharfetter-Gummel approach is used in [20] where properties similar to ours are proved. However, the results do not include sensitivity saturation. To the best of our knowledge, our work is the first to propose implicit in time methods, without time step limitation (CFL condition), for which we are able to prove that, under generic conditions, the energy decreases at both semi-discrete and discrete level. Moreover, we build an alternative to the gradient flow approach applying the Scharfetter-Gummel strategy [26] for the discretization of drift-diffusion equations 1 with a general saturation function
The paper is organized as follows. In Section 2, we present in more details our assumptions for the equation 1. We also explain some modeling choices in particular for the nonlinearity
The standard biological interpretation of 1 ([14,21,23]) provides us with some further properties of the nonlinearities which we describe now.
Chemotactic sensitivity. The function
| $ φ(u)=uψ(u),withψ(u)≥0,ψ′(u)≤0. $ | (9) |
More precisely, we consider two cases for the smooth function
| $ ψ(u)>0,∀u>0, $ | (10) |
or
| $ ψ(u)>0for0<u<M,ψ(M)=0. $ | (11) |
In the case 11 we only consider solutions which satisfy
It is convenient to introduce the notations
| $ g(u)=∫ua1φ(v)dv,G(u)=∫u0g(s)ds, $ | (12) |
where
| $ 1φ∉L1(a,+∞),g(u)⟶u→∞+∞, $ | (13) |
an assumption which, as we see it later, appears naturally when it comes to the well-posedness of numerical schemes.
Note that under assumption 10 and if
Expression of the drift
| $ {−∂2v∂x2=u−v,x∈(0,1),∂v∂x=0,x=0 or 1. $ |
This equation leads to 3 using the Green function given by the positive and symmetric kernel
| $ K(x,y)=λ(ex+e−x)(ey+e2−y),x≤y,λ=12(e2−1). $ | (14) |
Energy dissipation is the most difficult property to preserve in a discretization and methods might require corrections [17]. Therefore, it is useful to recall how it can be derived simply for the continuous equation. We focus on two different strategies, that lead to two different discretization approaches, the gradient flow approach and the Scharfetter-Gummel approach.
Using the notations 12, the equation for
| $ ∂u∂t−∂∂x[φ(u)∂(g(u)−v)∂x]=0, $ | (15) |
so that
| $ (g(u)−v)∂u∂t=(g(u)−v)∂∂x[φ(u)∂(g(u)−v)∂x]=12∂∂x[φ(u)∂(g(u)−v)2∂x]−φ(u)[∂(g(u)−v)∂x]2. $ |
Consequently, we find, in the Fokker-Planck case
| $ ddt∫10[G(u)−uv(x)]dx=−∫10φ(u)[∂(g(u)−v)∂x]2dx≤0, $ |
and in the generalized Keller-Segel case
| $ ddt∫10[G(u)−12uv(x,t)]dx=−∫10φ(u)[∂(g(u)−v)∂x]2dx≤0, $ |
because, thanks to the symmetry assumption on
| $ ∫10∫10K(x,y)u(y,t)∂u(x,t)∂t=∫10∫10K(x,y)∂u(y,t)∂tu(x,t)=12ddt∫10∫10K(x,y)u(y,t)u(x,t). $ |
Inspired from the case of electric forces in semi-conductors, the equation for
| $ ∂u∂t−∂∂x[ev−g(u)φ(u)∂eg(u)−v∂x]=0, $ | (16) |
so that
| $ (g(u)−v)∂u∂t=(g(u)−v)∂∂x[ev−g(u)φ(u)∂eg(u)−v∂x]=∂∂x[(g(u)−v)ev−g(u)φ(u)∂eg(u)−v∂x]−ev−g(u)φ(u)∂eg(u)−v∂x∂(g(u)−v)∂x. $ |
It is immediate to see that the last term has the negative sign while the time derivative term is exactly the same as in the gradient flow approach.
At the continuous level, these two calculations are very close to each other. However, they lead to the construction of different discretizations. The gradient flow point of view is used for numerical schemes by [10], the Scharfetter-Gummel approach is used in [20].
We give here our notations for the semi-discretization. We consider a (small) space discretization
| $ Ii=(xi−12,xi+12),i=1,…,I. $ |
The semi-discrete approximation of
| $ ui(t)≈1Δx∫Iiu(x,t)dx,i=1,…,I. $ |
As for the discretization of
| $ K_{ij} : = K(x_i, x_j), \qquad i = 1, \ldots, I, \; j = 1 \ldots, I. $ |
Integration on the interval
The mass conservative form of 1 leads to a finite volume semi-discrete scheme
| $ {dui(t)dt+1Δx[Fi+1/2(t)−Fi−1/2(t)]=0,i=1,…,I,t>0,F1/2(t)=FI+1/2(t)=0. $ | (17) |
We use the definition 8 for
| $ Ei(t)=G(ui(t))−κui(t)vi(t). $ |
The semi-discrete energy is then
| $ Esd(t):=ΔxI∑i=1Ei(t). $ |
Using the form 15 of equation 1, we define the semi-discrete flux as
| $ Fi+1/2(t)=−φi+1/2Δx[g(ui+1)−vi+1−(g(ui)−vi)],i=1,…,I−1. $ | (18) |
The precise expression of
Then, the semi-discrete energy form is obtained after multiplication by
| $ ddtΔxI∑i=1Ei(t)=−I∑i=1(g(ui)−vi)[Fi+1/2−Fi−1/2]=I−1∑i=1Fi+1/2[(g(ui+1)−vi+1)−(g(ui)−vi)]. $ |
Therefore, we find the semi-discrete form of energy dissipation
| $ dEsddt=−ΔxI−1∑i=1φi+1/2[(g(ui+1)−vi+1)−(g(ui)−vi)Δx]2≤0. $ |
We choose to discretize the form 16, defining the semi-discrete flux as
| $ Fi+1/2(t)=−(ev−g(u)φ(u))i+1/2Δx[eg(ui+1)−vi+1−eg(ui)−vi],i=1,…,I−1, $ | (19) |
where, again, the specific form of the interpolant
As above, the semi-discrete energy form follows upon multiplication by
| $ ddtΔxI∑i=1Ei(t)=−I∑i=1(g(ui)−vi)[Fi+1/2−Fi−1/2]=I−1∑i=1Fi+1/2[(g(ui+1)−vi+1)−(g(ui)−vi)]. $ |
Summing up, the semi-discrete form of energy dissipation here writes
| $ dEsddt=−ΔxI−1∑i=1{(ev−g(u)φ(u))i+1/2⋅eg(ui+1)−vi+1−eg(ui)−viΔx⋅(g(ui+1)−vi+1)−(g(ui)−vi)Δx}≤0. $ |
Steady states make the energy derivative vanish which imposes both in the gradient flow and the Scharfetter-Gummel approaches that
| $ g(ui)=vi+μ,i=1,…,I. $ | (20) |
We recall from [24] that in the GKS case, there are several steady states and the constant ones can be unstable.
For the time discretization, we consider (small) time steps
| $ uni≈1Δx∫Iiu(x,tn)dx,i=1,…,I,n∈N. $ |
Integration on the interval
To achieve the time discretization, and restricting our analysis to the Euler scheme, we write the time discretization
| $ {un+1i−uni+ΔtΔx[Fn+1i+1/2−Fn+1i−1/2]=0,i=1,…,I,Fn+11/2=Fn+1I+1/2=0. $ | (21) |
The issue here is to decide which terms (in
We define the energy at the discrete level through
| $ Eni=G(uni)−κunivni,i=1,…,I,n∈N, $ |
and
| $ En:=ΔxI∑i=1Eni,n∈N. $ |
The computation made in the semi-discrete case,
| $ I∑i=1(En+1i−Eni)≤I∑i=1(un+1i−uni)(g(uαni)−vβni). $ |
Here,
| $ G(un+1i)−G(uni)≤g(un+1i)(un+1i−uni). $ |
Regarding the term in
| $ −I∑i=1[un+1ivn+1i−univni]≤−2I∑i=1vβni(un+1i−uni). $ |
It is natural to try and balance the terms by choosing a semi-explicit discretization with
| $ I∑i=12vβni(un+1i−uni)−(un+1ivn+1i−univni)=I∑i=1(un+1ivni−univn+1i)=∑i,jKij(un+1iunj−uniun+1j), $ |
with the last term vanishing due to the symmetry of
However, implicit and explicit time discretizations for
| $ I∑i=12vβni(un+1i−uni)−(un+1ivn+1i−univni)=(1−2β)∑i,jKij(un+1i−uni)(un+1j−unj). $ |
As a consequence, an explicit (resp. implicit) scheme is suitable for the time discretization of
Finally, we note that the interpolant does not play any role for energy discretization and we can use the simplest explicit or implicit discretization (both in
We consider the full discretization of 18 and define the fully discrete flux in 21 as
| $ Fn+1i+1/2=−φ(u)n+1i+1/2Δx[(g(un+1i+1)−vni+1)−(g(un+1i)−vni)],i=1,…,I−1. $ | (22) |
At this level, we need to define the form of the interpolant
| $ φ(u)n+1i+1/2:={un+1iψ(un+1i+1)wheng(un+1i)−g(un+1i+1)+vni+1−vni≥0,un+1i+1ψ(un+1i)wheng(un+1i)−g(un+1i+1)+vni+1−vni<0. $ | (23) |
Proposition 1 (Fully discrete gradient flow scheme). We assume either 10 and 13, or 11 and give the
(ⅰ) the solution
(ⅱ) it satisfies
(ⅲ) the steady states
(ⅳ) the discrete energy dissipation inequality is satisfied
| $ En+1−En≤−ΔtΔxI−1∑i=1φ(u)ni+1/2[(g(un+1i+1)−vni+1)−(g(un+1i)−vni)]2. $ |
Notice that this theorem does not state a uniform bound in the case 10 and 13.
Proof. (ⅰ) We prove that the scheme satisfies the hypotheses of the theorem in Appendix A. We set
| $ Ai+1/2(un+1i,un+1i+1)=ΔtΔxFn+1i+1/2. $ |
Then, the simplest case is when
| $ Fn+1i+1/2=−φ(u)n+1i+1/2Δx[(g(ˉUn+1i+1)−vni+1)−(g(ˉUn+1i)−vni)]=−φ(u)n+1i+1/2Δx[C−C]=0. $ |
Thus
Moreover, the scheme is monotone since
| $ ∂1Ai+12(un+1i,un+1i+1)=−Δt(Δx)2un+1i+1ψ′(un+1i)[g(un+1i+1)−vni+1−(g(un+1i)−vni)]+−Δt(Δx)2ψ(un+1i+1)[g(un+1i+1)−vni+1−(g(un+1i)−vni)]−−Δt(Δx)2φ(u)n+1i+12[−g′(un+1i)]≥0, $ |
where
| $ [x]+={xforx≥0,0forx<0and[x]−={0forx≥0,xforx<0, $ |
so that
(ⅱ) Positivity of discrete solutions and the upper bound in the logistic case follow from the subsolution and supersolution built in step (ⅰ).
(ⅲ) Preservation of steady states at the discrete level follows immediately from the form we have chosen for the fully discrete fluxes.
(ⅳ) For the energy inequality, we remark that the contribution regarding time discretization is treated in the introduction of the present section. The space term is exactly treated as in the corresponding subsection of Section 4.
In 21, the fully discrete Scharfetter-Gummel flux reads
| $ Fn+1i+1/2=−(evn−g(un)φ(un+1))i+1/2[eg(un+1i+1)−vni+1−eg(un+1i)−vni],i=1,…,I−1. $ |
As for the gradient flow approach, we need the upwind technique to get a scheme which satisfies the hypotheses in Appendix A. So, we set for
| $ (evn−g(un)φ(un+1))i+1/2:={un+1i+1ψ(un+1i)evni+1−g(uni+1),ife(g(un+1i+1)−vni+1)−e(g(un+1i)−vni)≥0,un+1iψ(un+1i+1)evni−g(uni),ife(g(un+1i+1)−vni+1)−e(g(un+1i)−vni)<0. $ |
Proposition 2 (Fully discrete Scharfetter-Gummel scheme). We assume either 10 and 13, or 11 and give the
(ⅰ) the solution
(ⅱ) it satisfies
(ⅲ) the steady states
(ⅳ) the discrete energy dissipation inequality is satisfied
| $En+1−En≤−ΔtΔxI−1∑i=1{(evn−g(un)φ(un))i+1/2⋅[eg(un+1i+1)−vni+1−eg(un+1i)−vni]⋅[(g(un+1i+1)−vni+1)−(g(un+1i)−vni)]}≤0.$ |
Proof. We argue exactly as for the gradient flow approach.
The upwind scheme is driven by simplicity and, in 21, the fluxes are defined by
| $ Fn+1i+1/2=−1Δx[un+1i+1−un+1i−φ(u)ni+1/2(vni+1−vni)],i=1,…,I−1, $ |
with
| $ φ(u)n+1i+1/2:={un+1iψ(un+1i+1)whenvni+1−vni≥0,un+1i+1ψ(un+1i)whenvni+1−vni<0, $ | (24) |
as in 23, but this time depending on the sign of
Proposition 3 (Fully discrete upwind scheme). We assume either 10 and 13, or 11 and give the
(i) the solution
(ii) it satisfies
Proof. As for the gradient flow approach, the above choice makes the scheme monotone, because
| $ ΔtΔx∂1Fi+12(un+1i,un+1i+1)=−ΔtΔx2(−1−un+1i+1ψ′(un+1i)[vni+1−vni]−−ψ(un+1i+1)[vni+1−vni]+)≥0. $ |
Thus, arguing as for the gradient flow approach and relying on the results in Appendix A, existence and uniqueness of the discrete solution as well as preservation of the initial bounds follow immediately.
Thus, choice 24 enables to prove that the scheme is well-defined, satisfies
We first present the numerical implementation of the Fokker-Planck equation with
We consider a first case with
| $ v=x(1−x)|x−0.5|. $ |
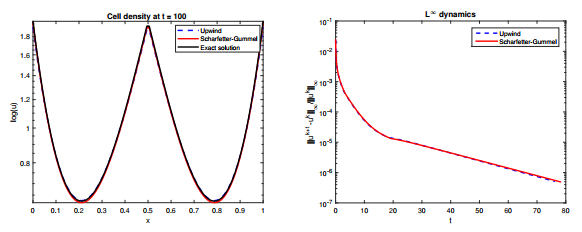
In Figure 1, we compare the approximate stationary solutions obtained with the upwind scheme (blue, dashed line) and the Scharfetter-Gummel scheme (red line) with the exact stationary solution (black line), which in this case has the form

Left: Comparison of solutions of the Scharfetter-Gummel (red line) and upwind (blue, dashed line) schemes at time
We turn to the equation 1 coupled with 3 for two nonlinear forms of the chemotactic sensitivity function: the logistic form
| $ {∂u∂t−∂∂x[D∂u∂x−χφ(u)∂v∂x]=0,x∈(0,1),t>0,D∂u∂x−χφ(u)∂v∂x=0,for x=0 or 1,u(x,0)=u0(x)≥0,x∈[0,1], $ | (25) |
in order to emphasize the coefficients driving the instabilities:
We first consider the logistic case with
Figure 2 shows the evolution in time of the density
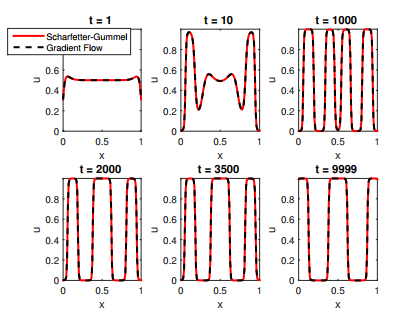
Evolution in time of solutions to (25) in the logistic case
As for the schemes, Figure 2 shows that the Scharfetter-Gummel and the gradient flow approaches give the same solution; no difference can be spotted. This is not true for the upwind approach. In Figure 3, we compare the solutions to the Scharfetter-Gummel (red line) and the upwind (blue, dashed line) schemes. The upwind solution transitions faster from one metastable structure to the following than the Scharfetter-Gummel one. In fact, as proved above, the latter preserves discrete stationary profiles which, using the no-flux boundary conditions, solve the equation
| $ ∂u∂x=χDφ(u)∂v∂x. $ | (26) |
From 26, it is clear that, in the logistic case, the expected stationary solutions are 0-1 plateaus (or "steps") connected by a sigmoid curve which is increasing or decreasing when
Moreover, in Figure 4c we compare the
Next, we consider an exponentially decreasing form of the chemotactic sensitivity function with
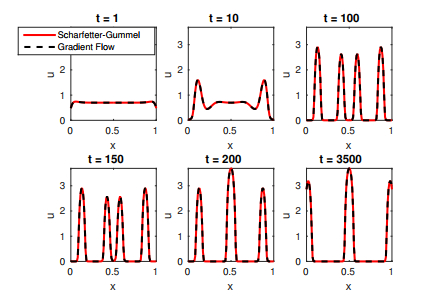
Evolution in time of solutions to 25 in the exponential case
In the context of the Generalized Keller-Segel system, we have presented constructions of numerical schemes which extend previous works [10,20], built on two different views of energy dissipation. Our construction unifies these two views, the gradient flow and Scharfetter-Gummel symmetrizations. Our schemes preserve desirable continuous properties: positivity, mass conservation, exact energy dissipation, discrete steady states. Being correctly tuned between implicit and explicit discretization, they can handle large time steps without CFL condition.
The present work is motivated by experiments of breast cancer cells put in a 3D structure mimicking the conditions they meet in vivo, namely in the extracellular matrix. After a few days, images of 2D sections show that cells have organized as spheroids, a phenomenon believed to be driven by chemotaxis. The spheroids can then be interpreted as Turing patterns for Keller-Segel type models and it is crucial to use appropriate schemes for them to be distinguishable from actual steady states or numerical artifacts. Comparing 2D simulations of such models with these experimental images will be the subject of future work.
In fact, it is important to remark that the schemes we presented here in 1D could be easily extended to rectangular domains, without loss of properties 4-7. However, it remains a perspective to treat more general geometries in a multi-dimensional setting with our approach.
The authors acknowledge partial funding from the "ANR blanche" project Kibord [ANR-13-BS01-0004] funded by the French Ministry of Research.
B.P. has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement No 740623).
We recall sufficient conditions for which an implicit Euler discretization in time can be solved, independently of the step-size. This is the case for a monotone scheme. The proof relies on the existence of sub- and supersolutions, and thus also yields the preservation of positivity and other pertinent bounds as we have used in Section 5.
We consider the problem of finding a unique solution
| $ un+1i−uniΔt+1Δx[F(uni,uni+1,vni,vni+1,un+1i,un+1i+1)⏟Fn+1i+12−Fn+1i−12]=0,i=1,…,I. $ | (27) |
We write a general proof for a scheme of the form
| $ ui+Ai+12(ui,ui+1)−Ai−12(ui−1,ui)=fi,i=1,…,I, $ | (28) |
where we consider the problem of finding a solution
Here we assume that the
| $ ∂1Ai+12(⋅,⋅)≥0,∂2Ai+12(⋅,⋅)≤0,i=1,…,I, $ | (29) |
and there are a supersolution
| $ ˉUi+Ai+12(ˉUi,ˉUi+1)−Ai−12(ˉUi−1,ˉUi)≥fi, $ | (30) |
| $ U_i+Ai+12(U_i,U_i+1)−Ai−12(U_i−1,U_i)≤fi. $ | (31) |
We build a solution of 28 using an evolution equation
| $ dui(t)dt+ui(t)+Ai+12(ui(t),ui+1(t))−Ai−12(ui−1(t),ui(t))=fi,i=1,…,I. $ | (32) |
Theorem A.1. Assume 29 and the existence of a subsolution and of a supersolution. Then,
(ⅰ) For a supersolution (resp. subsolution) initial data, the dynamics 32 satisfies
(ⅱ) A subsolution is smaller than a supersolution.
(ⅲ)
Proof. (ⅰ) We prove the statement with the supersolution. We set
| $ zi(t)=dˉui(t)dt,zi(0)≤0,i=1,…,I. $ |
Since the
Differentiating equation 32, we obtain for
| $ dzi(t)dt+zi(t)+[∂1Ai+12−∂2Ai−12]zi(t)=−∂2Ai+12zi+1(t)+∂1Ai−12zi−1(t). $ |
The solution cannot change sign and thus for
(ⅱ) Consider
We write for
| $ wi+[Ai+12(u_i,u_i+1)−Ai+12(ˉui,u_i+1)]+[Ai+12(ˉui,u_i+1)−Ai+12(ˉui,ˉui+1)]−[Ai−12(u_i−1,u_i)−Ai−12(ˉui−1,u_i)]−[Ai−12(ˉui−1,u_i)−Ai−12(ˉui−1,ˉui)]≤0. $ |
For
| $ I∑i=1(wi)++I−1∑i=1Ji+12+I−1∑i=1Ki+12=0, $ |
with
| $ Ji+12=[Ai+12(u_i,u_i+1)−Ai+12(ˉui,u_i+1)][sgn+(wi)−sgn+(wi+1)],Ki+12=[Ai+12(ˉui,u_i+1)−Ai+12(ˉui,ˉui+1)][sgn+(wi)−sgn+(wi+1)]. $ |
For each of the these terms, we show that
| $ u_i≥ˉui,andu_i+1≤ˉui+1. $ |
Then, we have by assumption 29,
| $ [Ai+12(u_i,u_i+1)−Ai+12(ˉui,u_i+1)]≥0⇒Ji+12≥0,[Ai+12(ˉui,u_i+1)−Ai+12(ˉui,ˉui+1)]≥0⇒Ki+12≥0. $ |
Therefore
(ⅲ) This is clear since the limits are solutions.
| [1] |
R. Aurich and F. Steiner, Periodic-orbit sum rules for the hadamard-gutzwiller model, Physica D, 39 (1989), 169-193. doi: 10.1016/0167-2789(89)90003-1

|
| [2] |
T. I. Baker and J. D. Cowan, Spontaneous pattern formation and pinning in the primary visual cortex, Journal of Physiology-Paris, 103 (2009), 52-68. doi: 10.1016/j.jphysparis.2009.05.011

|
| [3] |
N. L. Balazs and A. Voros, Chaos on the pseudosphere, Physics Reports, 143 (1986), 109-240. doi: 10.1016/0370-1573(86)90159-6

|
| [4] |
R. Ben-Yishai, RL Bar-Or and H. Sompolinsky, Theory of orientation tuning in visual cortex, Proceedings of the National Academy of Sciences, 92 (1995), 3844-3848. doi: 10.1073/pnas.92.9.3844

|
| [5] | J. Bigun and G. Granlund, Optimal orientation detection of linear symmetry, in "Proc. First Int'l Conf. Comput. Vision", pages 433-438. EEE Computer Society Press, (1987). |
| [6] |
B. Blumenfeld, D. Bibitchkov and M. Tsodyks, Neural network model of the primary visual cortex: From functional architecture to lateral connectivity and back, Journal of Computational Neuroscience, 20 (2006), 219-241. doi: 10.1007/s10827-006-6307-y

|
| [7] |
I. Bosch Vivancos, P. Chossat and I. Melbourne, New planforms in systems of partial differential equations with Euclidean symmetry, Archive for Rational Mechanics and Analysis, 131 (1995), 199-224. doi: 10.1007/BF00382886

|
| [8] | W. H. Bosking, Y. Zhang, B. Schofield and D. Fitzpatrick, Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex, The Journal of Neuroscience, 17 (1997), 2112-2127. |
| [9] |
P. C. Bressloff and J. D.Cowan, The functional geometry of local and horizontal connections in a model of v1, Journal of Physiology, Paris, 97 (2003), 221-236. doi: 10.1016/j.jphysparis.2003.09.017

|
| [10] |
P. C. Bressloff and J. D. Cowan, A spherical model for orientation and spatial frequency tuning in a cortical hypercolumn, Philosophical Transactions of the Royal Society B, (2003). doi: 10.1098/rstb.2002.1109

|
| [11] |
P. C. Bressloff, Spatially periodic modulation of cortical patterns by long-range horizontal connections, Physica D: Nonlinear Phenomena, 185 (2003), 131-157. doi: 10.1016/S0167-2789(03)00238-0

|
| [12] |
P. C. Bressloff and J. D. Cowan, The visual cortex as a crystal, Physica D: Nonlinear Phenomena, 173 (2002), 226-258. doi: 10.1016/S0167-2789(02)00677-2

|
| [13] |
P. C. Bressloff, J. D. Cowan, M. Golubitsky and P. J. Thomas, Scalar and pseudoscalar bifurcations motivated by pattern formation on the visual cortex, Nonlinearity, 14 (2001), 739. doi: 10.1088/0951-7715/14/4/305

|
| [14] |
P. C. Bressloff, J. D. Cowan, M. Golubitsky, P. J. Thomas and M. C. Wiener, Geometric visual hallucinations, euclidean symmetry and the functional architecture of striate cortex, Phil. Trans. R. Soc. Lond. B, 306 (2001), 299-330. doi: 10.1098/rstb.2000.0769

|
| [15] |
P. C. Bressloff and A. M. Oster, Theory for the alignment of cortical feature maps during development, Physical Review E, 82 (2010), 021920. doi: 10.1103/PhysRevE.82.021920

|
| [16] | I. Chavel, "Eigenvalues in Riemannian Geometry," 115. Academic Press, 1984. |
| [17] |
S. Chemla and F. Chavane, Voltage-sensitive dye imaging: Technique review and models, Journal of Physiology-Paris, 104 (2010), 40-50. doi: 10.1016/j.jphysparis.2009.11.009

|
| [18] |
P. Chossat, G. Faye and O. Faugeras, Bifurcations of hyperbolic planforms, Journal of Nonlinear Science, February 2011. doi: 10.1007/s00332-010-9089-3

|
| [19] | P. Chossat and R. Lauterbach, "Methods in Equivariant Bifurcations and Dynamical Systems," World Scientific Publishing Company, Singapur, 2000. |
| [20] |
P. Chossat and O. Faugeras, Hyperbolic planforms in relation to visual edges and textures perception, Plos. Comput. Biol., 5 (2009), e1000625. doi: 10.1371/journal.pcbi.1000625

|
| [21] | P. G. Ciarlet and J. L. Lions, "Handbook of Numerical Analysis," II Finite Element Methods (part1). North-Holland, 1991. |
| [22] |
G. Citti and A. Sarti, A cortical based model of perceptual completion in the roto-translation space, J. Math. Imaging Vis., (2006), 307-326. doi: 10.1007/s10851-005-3630-2

|
| [23] | D. P. Edwards, K. P. Purpura and E. Kaplan, Contrast sensitivity and spatial frequency response of primate cortical neurons in and around the cytochrome oxidase blobs, Vision Research, 35 (1995), 1501-1523,. |
| [24] | I. Erdélyi, "Higher Transcendental Functions," 1 Robert E. Krieger Publishing Company, 1985. |
| [25] |
G. B. Ermentrout and J. D. Cowan, A mathematical theory of visual hallucination patterns, Biological Cybernetics, 34 (1979), 137-150. doi: 10.1007/BF00336965

|
| [26] |
G. Faye and P. Chossat, Bifurcation diagrams and heteroclinic networks of octagonal h-planforms, Journal of Nonlinear Science, 22 (2012), 277-326. doi: 10.1007/s00332-011-9118-x

|
| [27] |
G. Faye, P. Chossat and O. Faugeras, Analysis of a hyperbolic geometric model for visual texture perception, The Journal of Mathematical Neuroscience, 1 (2011). doi: 10.1186/2190-8567-1-4

|
| [28] |
M. Golubitsky, L. J. Shiau and A. Török, Bifurcation on the visual cortex with weakly anisotropic lateral coupling, SIAM Journal on Applied Dynamical Systems, 2 (2003), 97-143. doi: 10.1137/S1111111102409882

|
| [29] |
M. Golubitsky, I. Stewart and D. G. Schaeffer, "Singularities and Groups in Bifurcation Theory," volume II. Springer, 1988. doi: 10.1007/978-1-4612-4574-2

|
| [30] | D. Hansel and H. Sompolinsky, Modeling feature selectivity in local cortical circuits, Methods of Neuronal Modeling, (1997), 499-567. |
| [31] |
M. Haragus and G. Iooss, "Local Bifurcations, Center Manifolds, and Normal Forms in Infinite Dimensional Systems," EDP Sci. Springer Verlag UTX Series, 2010. doi: 10.1007/978-0-85729-112-7

|
| [32] | S. Helgason, "Groups and Geometric Analysis," 83 of Mathematical Surveys and Monographs. American Mathematical Society, 2000. |
| [33] |
R. B. Hoyle, "Pattern Formation: an Introduction to Methods," Cambridge Univ Pr, 2006. doi: 10.1017/CBO9780511616051

|
| [34] | D. H. Hubel and T. N. Wiesel, Receptive fields and functional architecture in two nonstriate visual areas (18 and 19) of the cat, Journal of Neurophysiology, 28 (1965), 229-289, |
| [35] | D. H. Hubel and T. N. Wiesel, Receptive fields and functional architecture of monkey striate cortex, The Journal of Physiology, 195 (1968), 215. |
| [36] | D. H. Hubel and T. N. Wiesel, Functional architecture of macaque monkey, Proceedings of the Royal Society, London [B]: (1977), 1-59. |
| [37] | H. Iwaniec, "Spectral Methods of Automorphic Forms," 53 of AMS Graduate Series in Mathematics, AMS Bookstore, 2002. |
| [38] |
M. Kaschube, M. Schnabel, S. Löwel, D. M. Coppola, L. E. White and F. Wolf, Universality in the evolution of orientation columns in the visual cortex, Science, 330 (2010), 1113. doi: 10.1126/science.1194869

|
| [39] |
M. Kaschube, M. Schnabel and F. Wolf, Self-organization and the selection of pinwheel density in visual cortical development, New Journal of Physics, 10 (2008), 015009. doi: 10.1088/1367-2630/10/1/015009

|
| [40] | S. Katok, "Fuchsian Groups," Chicago Lectures in Mathematics. The University of Chicago Press, 1992. |
| [41] | H. Kluver, "Mescal, and Mechanisms of Hallucinations," University of Chicago Press Chicago, 1966. |
| [42] |
H. Knutsson, Representing local structure using tensors, Scandinavian Conference on Image Analysis, (1989), 244-251. doi: 10.1007/978-3-642-21227-7_51

|
| [43] | N. N. Lebedev, "Special Functions and Their Applications," (edited by R. A. Silverman), Dover Pubns, 1972. |
| [44] |
P. S. Leon, I. Vanzetta, G. S. Masson and L. U. Perrinet, Motion Clouds: Model-based stimulus synthesis of natural-like random textures for the study of motion perception, Journal of Neurophysiology, 107 (2012), 3217-3226. doi: 10.1152/jn.00737.2011

|
| [45] | M. S. Livingstone and D. H. Hubel, Anatomy and physiology of a color system in the primate visual cortex, Journal of Neuroscience, 4 (1984), 309-356. |
| [46] |
J. S. Lund, A. Angelucci and P. C. Bressloff, Anatomical substrates for functional columns in macaque monkey primary visual cortex, Cerebral Cortex, 12 (2003), 15-24. doi: 10.1093/cercor/13.1.15

|
| [47] |
I. Melbourne, A singularity theory analysis of bifurcation problems with octahedral symmetry, Dynamics and Stability of Systems, 1 (1986). doi: 10.1080/02681118608806020

|
| [48] | W. Miller, "Symmetry Groups and Their Applications," Academic Press, 1972. |
| [49] |
M. Moakher, A differential geometric approach to the geometric mean of symmetric positie-definite matrices, SIAM J. Matrix Anal. Appl., 26 (2005), 735-747. doi: 10.1137/S0895479803436937

|
| [50] | J. D. Murray, "Mathematical Biology II, Spatial Models and Biomedical Applications," Springer, 2003. |
| [51] | G. A. Orban, H. Kennedy and J. Bullier, Velocity sensitivity and direction selectivity of neurons in areas V1 and V2 of the monkey: Influence of eccentricity, Journal of Neurophysiology, 56 (1986), 462-480. |
| [52] |
G. Oster, Phosphenes, Scientific American, 222 (1970), 82. doi: 10.1038/scientificamerican0270-82

|
| [53] |
A. M. Oster and P. C. Bressloff, A developmental model of ocular dominance column formation on a growing cortex, Bulletin of Mathematical Biology, (2006). doi: 10.1007/s11538-005-9055-7

|
| [54] | J. Petitot, The neurogeometry of pinwheels as a sub-Riemannian contact structure, Journal of Physiology-Paris, 97 (2003), 265-309. |
| [55] | J. Petitot, "Neurogéométrie de la Vision," Les Éditions de l'École Polytechnique, 2009. |
| [56] | G. Sanguinetti, A. Sarti and G. Citti, Implementation of a Model for Perceptual Completion in $\R^2\times S^1$, Computer Vision and Computer Graphics, Communications in Computer and Information Science, 24 (2009), 188-201. |
| [57] | A. Sarti and G. Citti, Non-commutative field theory in the visual cortex, Computer Vision: from Surfaces to 3D Objects, C. Tyler editor, CRC Press, (2010). |
| [58] |
A. Sarti, G. Citti and J. Petitot, The symplectic structure of the primary visual cortex, Biological Cybernetics, 98 (2008), 33-48. doi: 10.1007/s00422-007-0194-9

|
| [59] |
J. Schummers, J. Mariño and M. Sur, Synaptic integration by v1 neurons depends on location within the orientation map, Neuron, 36 (2002), 969-978. doi: 10.1016/S0896-6273(02)01012-7

|
| [60] | J. P. Serre, "Représentations Linéaires des Groupes Finis," Hermann, 1978. |
| [61] | L. C. Sincich and J. C. Horton, Divided by cytochrome oxidase: A map of the projections from V1 to V2 in macaques, Science, 295 (2002), 1734-1737. |
| [62] |
A. Terras, "Harmonic Analysis on Symmetric Spaces and Applications," Springer-Verlag, 2, 1988. doi: 10.1007/978-1-4612-3820-1

|
| [63] | R. B. H. Tootell, S. L. Hamilton, M. S. Silverman, E. Switkes and R. L. De Valois, Functional anatomy of macaque striate cortex. V. Spatial Frequency, Journal of Neuroscience, 8 (1988), 1610-1624. |
| [64] |
R. Veltz and O. Faugeras, Local/global analysis of the stationary solutions of some neural field equations, SIAM Journal on Applied Dynamical Systems, 9 (2010), 954-998. doi: 10.1137/090773611

|
| [65] |
R. Veltz and O. Faugeras, Illusions in the ring model of visual orientation selectivity, Technical Report, arXiv:1007.2493, (2010). doi: 10.1137/090773611

|
| [66] | G. N. Watson, "A Treatise on the Theory of Bessel Functions," Cambridge University Press, 1995. |
| [67] |
H. R. Wilson and J. D. Cowan, Excitatory and inhibitory interactions in localized populations of model neurons, Biophys. Journal, 12 (1972), 1-24. doi: 10.1016/S0006-3495(72)86068-5

|
| [68] |
H. R. Wilson and J. D. Cowan, A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue, Biological Cybernetics, 13 (1973), 55-80. doi: 10.1007/BF00288786

|
| [69] | F. Wolf and T. Geisel, Spontaneous pinwheel annihilation during visual development, Nature, 395 (1998), 73-78. |
| [70] | A. Zettl, "Sturm-Liouville Theory," 121, American Mathematical Society, 2005. |
| 1. | Luis Almeida, Gissell Estrada-Rodriguez, Lisa Oliver, Diane Peurichard, Alexandre Poulain, Francois Vallette, Treatment-induced shrinking of tumour aggregates: a nonlinear volume-filling chemotactic approach, 2021, 83, 0303-6812, 10.1007/s00285-021-01642-x | |
| 2. | Giorgia Ciavolella, Effect of a Membrane on Diffusion-Driven Turing Instability, 2022, 178, 0167-8019, 10.1007/s10440-022-00475-0 | |
| 3. | André Schlichting, Christian Seis, The Scharfetter–Gummel scheme for aggregation–diffusion equations, 2022, 42, 0272-4979, 2361, 10.1093/imanum/drab039 | |
| 4. | Yangyang Qiao, Steinar Evje, A general cell–fluid Navier–Stokes model with inclusion of chemotaxis, 2020, 30, 0218-2025, 1167, 10.1142/S0218202520400096 | |
| 5. | Xueling Huang, Jie Shen, Bound/positivity preserving SAV schemes for the Patlak-Keller-Segel-Navier-Stokes system, 2023, 480, 00219991, 112034, 10.1016/j.jcp.2023.112034 | |
| 6. | Yong Zhang, Yu Zhao, Zhennan Zhou, A Unified Structure Preserving Scheme for a Multispecies Model with a Gradient Flow Structure and Nonlocal Interactions via Singular Kernels, 2021, 43, 1064-8275, B539, 10.1137/20M1348911 | |
| 7. | Federica Bubba, Camille Pouchol, Nathalie Ferrand, Guillaume Vidal, Luis Almeida, Benoît Perthame, Michèle Sabbah, A chemotaxis-based explanation of spheroid formation in 3D cultures of breast cancer cells, 2019, 479, 00225193, 73, 10.1016/j.jtbi.2019.07.002 | |
| 8. | Federica Bubba, Benoit Perthame, Daniele Cerroni, Pasquale Ciarletta, Paolo Zunino, A coupled 3D-1D multiscale Keller-Segel model of chemotaxis and its application to cancer invasion, 2022, 15, 1937-1632, 2053, 10.3934/dcdss.2022044 | |
| 9. | Jingwei Hu, Xiangxiong Zhang, Positivity-preserving and energy-dissipative finite difference schemes for the Fokker–Planck and Keller–Segel equations, 2022, 0272-4979, 10.1093/imanum/drac014 | |
| 10. | Clément Cancès, Thomas O. Gallouët, Gabriele Todeschi, A variational finite volume scheme for Wasserstein gradient flows, 2020, 146, 0029-599X, 437, 10.1007/s00211-020-01153-9 | |
| 11. | Federica Bubba, Alexandre Poulain, A nonnegativity preserving scheme for the relaxed Cahn–Hilliard equation with single-well potential and degenerate mobility, 2022, 56, 2822-7840, 1741, 10.1051/m2an/2022050 | |
| 12. | Jose A. Carrillo, Daniel Matthes, Marie-Therese Wolfram, 2021, 22, 9780444643056, 271, 10.1016/bs.hna.2020.10.002 | |
| 13. | Clément Cancès, Benoît Gaudeul, A Convergent Entropy Diminishing Finite Volume Scheme for a Cross-Diffusion System, 2020, 58, 0036-1429, 2684, 10.1137/20M1316093 | |
| 14. | Noemi David, Xinran Ruan, An asymptotic preserving scheme for a tumor growth model of porous medium type, 2022, 56, 2822-7840, 121, 10.1051/m2an/2021080 | |
| 15. | Clément Cancès, Virginie Ehrlacher, Laurent Monasse, Finite volumes for the Stefan–Maxwell cross-diffusion system, 2024, 44, 0272-4979, 1029, 10.1093/imanum/drad032 | |
| 16. | José A. Carrillo, Katy Craig, Yao Yao, 2019, Chapter 3, 978-3-030-20296-5, 65, 10.1007/978-3-030-20297-2_3 | |
| 17. | Rafael Bailo, José A. Carrillo, Jingwei Hu, Bound-Preserving Finite-Volume Schemes for Systems of Continuity Equations with Saturation, 2023, 83, 0036-1399, 1315, 10.1137/22M1488703 |