American call option pricing under the KoBoL model with Poisson jumps

1.   Introduction

The American option is an important financial tool and is widely used in real market. However, the pricing model of this financial derivative is a free boundary problem so that it is impossible to obtain the analytic pricing formula of this financial derivative. Thus, in the past two decades, the numerical method becomes a mainstream tool to solve the mathematical model.

More and more authors have studied the American option in the case of Black-Scholes model (BS). For example, Geske and Johson ^[1] investigated the American put option, and an analytic solution to this option was derived. Moreover, based on the analytical solution, the risk hedging coefficient for American put was obtained. Based on this literature, Zhu et al. ^[2,3] used the integral transformation method to solve the American Contingent Claims pricing mathematical model, and the price and optimal exercise price of this kind of financial derivatives are obtained. Gyulov and Koleva ^[4] developed a numerical method based on the penalty for American option in the case of the BS model with the regime-switching process. Xiang and Wang ^[5] proposed an efficient quasi-Monte Carlo method for estimating American option sensitivities. Wang et al. ^[6] constructed a high-order deferred correction algorithm combined with penalty iteration for solving American option pricing model. Elettra and Rossella ^[7] use the Recurrent neural network framework for computing prices and deltas of American options in high dimensions. Under the framework of the Cox-Ingersoll-Ross (CIR), Zhang et al. ^[8] proposed an efficient numerical method for the American options pricing. Additionally for the perpetual American put option, an analytical solution is proposed under the framework of BS in ^[9].

However, in the case of the classical BS model, the stock price is assumed to follow the Geometric Brownian motion, which cannot reflect the character of the risk asset in the real market. The conclusions in ^{[10,11,12,13]} show that the risk asset price should appear to be "phenomenon of jumps" and "asymmetric distribution". Thus, the more complex stochastic differential equation should be used to capture the characters of the risk asset by many scholars. Prominent examples, including the FMLS equation ^[14], CGMY equation ^[15], and KoBoL equation ^[16]. Moreover, as described in ^[17], both FMLS and CGMY equations are the special cases of the KoBoL equation, so we consider the American call pricing problem in this paper. Under this framework, the function of the option price value is governed by the fractional partial differential equation free boundary problem, which is proved in ^[18]. Following this work, Chen and Lin ^[19] used the integral transformation method to obtain the analytical solution of the European option pricing model. For the European double barrier option pricing model, the numerical method is set, and the convergence rate and stability of this numerical method are proved in ^[17]. Mohapatra et al. ^[20] considered the numerical solution for the time fractional Black-Scholes model under jump-diffusion involving a Caputo differential operator, and their schemes are investigated for numerous European option pricing jump-diffusion models. Guo et al. ^[21] proposed a numerical method for European and American option pricing under the time fractional jump-diffusion model in Caputo scene. Fan et al. ^[22] considered the values and optimal exercise prices of the American option under the CGMY model with the regime-switching process.

Based on the literature, the American call option pricing problem is investigated in the case of the KoBoL model with the jump process (KoBoLJ) in this paper. Under the framework of the KoBoLJ model, the function of the American call value follows a FPIDE, and the pricing model is a free boundary problem. To obtain a FPIDE boundary value problem over a fixed rectangular domain, a nonlinear penalty term is added to the governing equation. However, it is still impossible to achieve the analytical solution of the new mathematical model. Hence, the finite differential method is essentially considered in this paper. Moreover, a dense coefficient matrix resulted from the fractional derivatives in the final linear system, which requires the computational cost in the order of $\mathcal{O}(M^3)$, where $M$ is the number of spatial grid nodes. This shows that the computational time of numerical method will increase.

The major contributions of this study can be summarized as follows:

ⅰ) The Poisson jumps is introduced into the KoBoL model due to the need to capture the characters of stock price so that the option pricing models can capture market risk;

ⅱ) The preconditioned conjugate gradient normal residual (PCGNR) method with a Strang's circulant pre-conditioner ^[23] and the fast Fourier transform (FFT) technique are used, so that the computational cost reduces significantly from $\mathcal{O}(M^3)$ to $\mathcal{O}(M\log M)$;

ⅲ) Based on the numerical scheme, we prove that the American call option value generated by the penalty method cannot fall below the value obtained when the American call option is exercised early, i.e., $V(x, t)\geq \max (e^x - K, 0)$.

The rest of this article is outlined below. In the next section, the pricing mathematical model of American call under the framework of the KoBoLJ model is derived in detail. In Section 3, the numerical scheme is proposed, and we prove that the American call option value obtained by our numerical method is bigger than the exercising value. In Section 4, we prove the PCGNR method with a circulant pre-conditioner and the FFT technique to calculate the final system. Moreover, the numerical experiments are presented with some discussions in Section 5. We conclude this paper in the last section.

2.   Mathematical formulation

2.1.   The stochastic process

Take $(\Omega, \mathcal{F}_t, \mathbb{P})$ as a filtered probability, where $t\in[0, T]$. The KoBoL model with the jump process is defined on this probability space. Following the assumptions in ^[24], under this model, the logarithmic price of the underlying, i.e., $x_t = \ln(S_t)$, satisfies the following stochastic differential equation

with solution

where $x_t$ is the logarithmic form stock price $x_t = \ln S_t$, $r$ is the risk-free interest rate, $D$ is dividend, $dL_t^{KoBoL}$ is the increment of a $L\acute{e}vy$ process under the equivalent martingale measure, and $\nu = \frac{1}{2}\sigma^\alpha[p(\lambda-1)^\alpha+q(\lambda+1)^\alpha-\lambda^\alpha-\alpha\lambda^{\alpha-1}(q-p)]$ is convexity adjustment so that the expectation of $S_T$ becomes $\mathbb{E}[S_T] = e^{r(T-t)}S_t$. Parameter $\alpha\in(1, 2)$ determines whether the KoBoLJ stochastic process has finite or infinite variation. The relative frequency and overall upwind and downwind movements KoBoLJ stochastic process are controlled by $q > 0, p > 0 (p+q = 1)$. The decay rate of tails of our stochastic process probability density function is controlled by parameter $\lambda > 0$. $\mathcal{N}_t$ is a Poisson process and it is characterized by the jump intensity $\xi\geq0$. $\{Y_i, i = 1, 2, \ldots\}$ is a sequence of independent and identically distributed hyper-exponential random variables with probability density function

Note that $\hat{p}_i$ ($i = 1, 2, ..., m_1$) and $\tilde{p}_j$ ($j = 1, 2, ..., m_2$) denote the probabilities of the ith positive and negative jumps, respectively. They satisfy $\sum_{i = 1}^{m_1}\hat{p_i}+\sum_{j = 1}^{m_2}\tilde{p_j} = 1$. $\hat{\theta}_i > 1$ ($i = 1, ..., m_1$) is the magnitude of the upward jumps and $\tilde{\theta}_j > 0$ ($j = 1, ..., m_2$) is that of the downward random jumps. The average jump size is given by

where $\mathbb{E}_{\mathbb{P}}$ is the expectation operator under probability measure $\mathbb{P}$.

2.2.   The FPIDE system

Now, we turn to formulate mathematically the pricing of the American option under our model. Financially, the payoff function of American call contract can be written as

where $K$ is the strike price. According to the no-arbitrage pricing principle, one can obtain

Then, according to the conclusions in ^[18], it can be obtained that the American call option value $V(x, t)$ satisfies the following equation

where $x\in(-\infty, x_f], t\in [0, T]$, $a = r-\nu-D-\xi\varsigma-\lambda^{\alpha-1}(q-p), b = r+\xi$, and

In fact, the fractional derivative in Eq (2.5) is closely related to the KoBoLJ model. Moreover, the fractional derivatives in the governing Eq (2.5) are non-local in order to describe the American call option value in the holding region $(-\infty, x_f]$.

In this paper, we take American call as the research object, so the function $V(x, t)$ satisfies the following boundary conditions:

To sum up, a complete pricing mathematical model of American call under the KoBoLJ process can be obtained as Eqs (2.5) and (2.6). Moreover, we remark that the above FPIDE system is much more difficult to solve than the corresponding BS case with jumps, with the main difficulty resulting from the free boundary and the non-localness of the fractional-integro differential operator. In the following section, a new numerical scheme is proposed to solve it efficiently.

According to the unique characteristics of the American call option, the value function $V(x, t)$ of this financial derivative should satisfy the following inequality constraint

for all $t\in[0, T]$ and $x\leq x_{f}$.

3.   Numerical method

There are two parts in this section. In the first part, the free boundary problem should be changed as one defined on a fixed interval by introducing a nonlinear penalty term. Both the difference scheme and theoretical analysis are displayed in the second part.

3.1.   Model transformation

Let $0 < \epsilon \ll 1$ and $C > 0$ be a fixed constant, and we will determine its specific value. We construct the following nonlinear penalty term

Then we add it to Eq (2.5)and obtain the following system,

where $x\in(-\infty, x_{\max}], t\in [0, T], 1 < \alpha < 2$,

Moreover, according to the conclusion in ^[25], the maximum value of risk asset equal to 4 times of $K$ value. The subscript $\varepsilon$ of $V_{\varepsilon}(x, t)$ should be omitted for clarity.

3.2.   Difference scheme

Define $\Delta t > 0$ and $\Delta x > 0$ as time and spatial step, respectively. Taking $N, M$ as the positive $N * \Delta t = T$ and $M \Delta x = x_{\max}$. Thus

The forward and backward difference schemes are used for the discrete first-order space. For the time derivative, we use the forward and backward difference schemes, respectively. The approximation of the left-sided and right-sided tempered fractional derivatives given in formula ^[26] can be used to discretize the left-sided and right-sided tempered fractional derivatives as the following:

where $V_j^i$ is the value of function $V(x, t)$ at grid point $(x_j, t_i)$. The coefficients $g_k\; (k = 0, 1, 2, \cdots)$ are used and satisfy the following two equations

In addition, the integral term contained in the governing equation of Eq (3.2) is approximated by the trapezoidal rules ^[24], i.e.,

where

and

To sum up, the fully implicit difference scheme for Eq (3.2) can be obtained as follows:

and the boundary conditions are approximated as

The fact that the values of $V_{j}^{i}$ for all $i, j$) must satisfy the constraint condition (2.7) should be strictly proven. In order to ensure completion of proof, we first give two lemmas as follows

Lemma 3.11. (^[26]) If $\alpha \in (1, 2)$, then the coefficients $g_k$ in Eq (3.6) satisfy

where $m\geq1$.

Lemma 3.2. (^[27]) Both the coefficients $\rho_j^M$ in Eq (3.7) and $R_j$ in Eq (3.8) are bounded and satisfy

Theorem 3.1. If $\Delta t \leq \frac{1}{\left|b+2\xi \sum^{M}_{\ell = 0 }\rho^M_{\ell-j}\right|}$ and the constant $C$ satisfies the following inequality

then $V_{j}^{i}$ obtained by Eq (3.9) satisfies the following inequality $V_{j}^{i}\ge\max(e^{x_j}-K, 0)$. Here, $\mathfrak{K} = \exp(x_{\max})-\; K.$

Proof. We are going to complete the proof in two steps: We first prove $V_{j}^{i}\ge e^{x_j}-K$ and then prove that $V_{j}^{i}\ge 0$ for all $i, \; j$.

Let $Q_j = e^{x_j}-K, u_{j}^{i} = V_{j}^{i}-Q_j$, then we have

where

Since $|\frac{e^{\Delta x}-1}{\Delta x}| \leq \frac{e^{x_{\max}}-1}{x_{\max}}\leq 1$, $\sum^\infty_{k = 0} g_ke^{x_{j-k+1}} = e^{x_{j+1}}\sum^\infty_{k = 0}g_ke^{-k\Delta x}$, and when $|z| < 1$

Hence, we have

Moreover, let $\mathfrak{K} = [\exp(x_{\max})-K]$, then

Therefore,

Let $u_{J}^{i} = \min_{j}u_{j}^{i}$ and $u_{L}^{i+1} = \min_{j}u_{j}^{i+1}$, then

Namely,

On the other hand, according to Lemma 3.2 and $\Delta t \leq \frac{1}{\left|b+2\xi \mathop \sum \nolimits_{\ell = 0}^M \rho^M_{\ell-j}\right|}$, we can obtain

Let

and define a function $H(x)$ as

Then, $H(u^i)\geq0$ if $u^{i+1}\geq0$. Since $H'(x) = A + \frac{\epsilon C\Delta t}{(x+\epsilon)^2}\geq0$, $H(0) = \Delta t(F-C)\leq0$, and $u^{N+1}\geq0$, we obtain $u^i\geq0$. Hence, $u_j^i\geq0$, and consequently $V_j^i\geq Q_j$ is satisfied.

Next, we prove that $V_j^i\geq 0$. We define $V^i = \min_{j}V_{j}^{i}$ and let $J$ satisfy $V_J^i = V^i$. Hence, according to Eq (3.9), the following inequality can be obtained,

Then,

In the first step, $V_j^i \geq Q_j (\forall i, j)$ is proven, so $\frac{\epsilon C\Delta t}{V^i+\epsilon-Q_j}\geq 0$. Thus,

Since, $V_j^{N+1} = \max \left[\exp(x_j)-K, 0\right] \geq 0$, therefore

To sum up, we complete the proof. □

4.   The PCGNR method with a circulant pre-conditioner

In fact, the penalty term should result that the discrete system (3.9) is nonlinear; therefore, the Newton iteration method is employed. However, due to the existence of the fractional-integro differential operator, there is a matrix with a dense form in the final system. Thus, we should enhance the computational efficiency while decreasing the storage space.

In order to facilitate the computer to simulate the algorithm (3.9), the original semi-infinite region $(-\infty, x_{\max}]\times[0, T]$ must be truncated into a limited region $(x, t)\in(x_{\min}, x_{\max}]\times [0, T],$ where $x_{\min} = \ln(0.01)$ in the numerical experiments below. Now, the left boundary condition in the original model is changed to $V(x_{\min}, t) = 0$.

We should redefine the spatial step size $\Delta x = (x_{\max}-x_{\min})/M$, then $x_j = (j-1)\Delta x+x_{\min}$, for $j = 2, \ldots, M+1$. Now, we define

and

Then, system (3.9) can be rewritten as the following matrix form,

where

with

${\bf I}$ is an identity matrix of order $(M-1)$, and ${\bf A}^{\top}$ means matrix transpose of ${\bf A}$. ${\bf A}$, ${\bf B}$, and ${\bf W}$ are Toeplitz matrices, i.e.,

In fact, the nonlinear penalty term shows that the system (4.1) cannot be solved directly; therefore, we first use the Newton iteration method to change it as a linear system,

where $l = 1, 2, 3, \ldots$, $J_{\mathcal{F}}(\mathfrak{w}^{l-1})$ is the Jacobian matrix of the vector $\mathcal{F} (\mathfrak{w}^{l-1})$, and $0 < \kappa < 1$ is the adjustment factor. During the numerical iteration, it is assumed that for the current time layer $t_i$, the information of the previous time layer $t_{i+1}$ is known. Therefore, $V^{i+1}$ can be taken as the initial value of the iterative sequence $\mathfrak{w}^{l}$, i.e., $\mathfrak{w}^{0} = V^{i+1}$. We set $V^i = \mathfrak{w}^l$ once the stopping criterion $\parallel \mathfrak{w}^{l}-\mathfrak{w}^{l-1}\parallel\le tol$ for some $l$ is reached, where $tol$ is the stopping tolerance of the iterative method. Now, by taking

Eq (4.2) can be rewritten as

The most challenging part in solving Eq (4.3) is the high computational cost resulting from the fact that both ${\bf A}$ and ${\bf W}$ are dense matrices. To overcome this difficulty, we first apply the CGNR method ^[28], which is to solve $[\mathfrak{M}-J_{\mathcal{F}}]^{\top}\mathfrak{M}\delta \mathfrak{w}^{l} = [\mathfrak{M}-J_{\mathcal{F}}]^{\top} {\bf b}^{l}$ instead of Eq (4.3).

However, by noticing that the convergence rate of the CGNR method is still quite low due to the fact that the conditional number of the matrix $\mathfrak{M}^{\top}\mathfrak{M}$ is large, a pre-conditioner technique is applied to accelerate the convergence rate of the CGNR method. It is straightforward to find that the matrix $J_{\mathcal{F}}$ is not the Toeplitz matrix, and we should approximate this matrix as $a_0 {\bf I}$, where $a_0$ is the average value of main diagonal elements of matrix $J_{\mathcal{F}}$. Thus, we structure a Toeplitz matrix as follows

Next, the Strang's circulant preconditioner $s(\mathcal{T}) = [s_{j-k}]_{0\leq j, k < M}$ for matrix $\mathcal{T}$ is structured as

Let $\mathfrak{P}$ denote the Strang's circulant preconditioner $s(\mathcal{T}) = [s_{j-k}]_{0\leq j, k < M}$ to simplify the expression.

Mathematically, after the PCGNR method with a pre-conditioner $\mathfrak{P}$ is applied, Eq (4.3) becomes

The pseudo-code of the PCGNR method is displayed in Algorithm 1. The matrix-vector multiplication needs only $\mathcal{O}(MlogM)$ operations via the fast Fourier transform (FFT) method.

5.   Numerical simulations and discussions

Several numerical examples are given to show the computational efficiency of our numerical method in this part. Moreover, the impacts of the key parameter in our model to the option value and optimal exercise boundary are also discussed. All simulations are implemented using MATLAB2014a on a Lenovo T14 laptop with configuration: Intel(R) Core(TM) i7-1260P 2.10 GHz. The CPU time (in seconds) is estimated by using the timing functions tic/toc.

5.1.   Performance of the numerical method

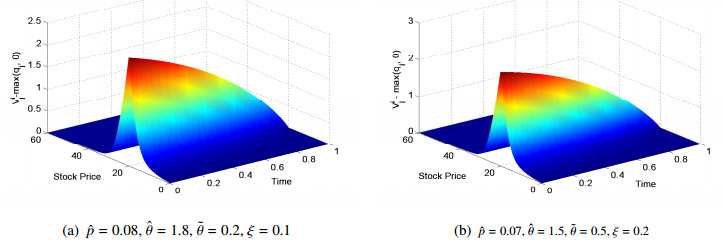
First, we should examine whether or not the numerical solution preserves the basic properties of American call. This could be viewed as a necessary condition for the reliability of the proposed approach. Mathematically, the current numerical solution must satisfy the inequality $V_j^i \geq \max(q_j - K, 0)$. Depicted in Figure 1 are the surfaces of $V_j^i-\max(q_j-K, 0)$ with different parameter settings, which implies that the inequality is preserved.

Figure 2(a), (b) display the American call value surface and option values and payoff function, respectively. First, the curves in the two figures indicate that the American call option price is an increasing function with respect to an underlying asset price, and the 'high contact' condition for American call is also confirmed by such surfaces in Figure 2(a), which shows KoBoLJ model is indeed reasonable. It can be observed from the two figures that the numerical method based on the penalty term produces the smooth and stable approximation solutions. To sum up, both our model and the numerical scheme are reasonable.

To further investigate the performance of the method, we compare the computational efficiency of the Gaussian elimination (GE), the CGNR method, and the PCGNR method, as shown in Table 1. The parameters adopted for computing this table are $K = 20$, $r = 0.05$, $\sigma = 0.24$, $D = 0.06$, $p = 0.6$, $\hat{p} = 0.07$, $\hat{\theta} = 1.5$, $\tilde{\theta} = 0.5$, , $\alpha = 1.52$, $\xi = 0.2$, $\hat{p} = 0.08$, $\hat{\theta} = 1.8$, $\tilde{\theta} = 0.2$, $\xi = 0.1$. Moreover, in this table, $Ite-In$ denotes the average iteration number required in each time step. $OR_{GE}$, $OR_{CGNR}$ and $OR_{PCGNR}$ refer the convergence order in $x$ direction of three different method, respectively. The convergence order is defined as

where $M_i$ is the number of spatial grid nodes employed and

where $\parallel \cdot\parallel_2$ is the $L_2$ norm for matrix, and $V(x, t)_{\mathrm{ref}}$ is the benchmark solution determined directly through matrix operation '$A\backslash b$' in Matlab with $(M, N) = (2^{12}, 1000)$.

We can observe from Table 1 that for a fixed number of nodal points, the total CPU times required by the CGNR and PCGNR to produce the same level of error are significantly less than that of the GE. Furthermore, the average inner iteration numbers required by the PCGNR method are the lowest. These suggest the superiority of the PCGNR method in computational efficiency over the GE and CGNR methods. Moreover, it is clear that the $OR_{GE}$, $OR_{CGNR}$, and $OR_{PCGNR}$ are close to 1, which indicates that the three schemes are of first-order convergence in the spatial direction.

Similarly, the convergence order and error in the $t$ direction of the PCGNR method is also examined. First, the $V(x, t)_{\mathrm{ref}}$ is the benchmark solution that can be determined directly through matrix operation '$A\backslash b$' in Matlab with $(M, N) = (2^{12}+1, 1000)$. We increase the grid number in the $t$ direction from $100$ to $800$. In Table 2, both the $Err$ and $OR$ denote the error and convergence order in the $t$ direction of PCGNR method, respectively. The results are displayed in Table 2. From this table, it is clear that our scheme is first-order convergent.

5.2.   Analysis on parameter impact

We first consider the value of parameter $\alpha$, which affects the optimal exercise boundary of American call. Tow sets of optimal exercise boundary with different $\alpha$ are computed and displayed in Figure 3. From the curves in this figure, one can find that a bigger value of $\alpha$ should show a higher optimal exercise boundary. Financially, the $\alpha$ controls the tail of the distribution of the returns of risk asset, and both tails will be fatter when $\alpha$ becomes bigger. Thus, as $\alpha$ becomes bigger, the possibility of smaller stock price increases, and so does the optimal exercise price.

Next, we consider how the discrete jumps influence the optimal exercise price of American call. As shown in Figure 4 is the optimal exercise price as a function of the time to expiry with different jump intensity $\xi$. One can observe from this figure that the optimal exercise price increases with respect to $\xi$. Financially, a larger jump intensity indicates that the risk asset would change more often so that the American call option contract should be more valuable as it contains more risks. Hence, according to the smooth pasty condition across the free boundary, the monotonicity of $S_f$ with respect to $\xi$ holds automatically.

In Figure 5, the optimal exericse price is plotted against the time to expiry with different probabilities of positive jumps $\hat{p}$. From the curves in this figure, it is straightforward to find that a larger $\hat{p}$ results in a lower optimal exercise boundary curve. In fact, the logarithmic return of the risk asset is decreasing with respect to $\hat{p}$, because the return decreases with respect to $\xi$ from Eq (2.1) and $\xi$ increases with respect to $\hat{p}$ from Eq (2.2). Therefore, an increasing $\hat{p}$ would lower the risk asset value, and thus makes the intermediate American call option less valuable. Therefore, the optimal exercise boundary $e^{x_f}$ of the intermediate American call decreases with respect to $\hat{p}$. Similarly, one could explain the monotonicity of the optimal exercise price with respect to $\hat{\theta}$ and $\tilde{\theta}$. For the length of the paper, we provide those curves in Figure 6 with no detailed explanations.

Next, we should investigate the impacts of parameters $p$ and $q$. In fact, the upward movement frequency of our stochastic process is controlled by parameter $p$. If the value of parameter $p$ becomes bigger, which means that our stochastic process should have increased upward movement, then the American call option price should become bigger. As a rational investor, a higher price should be used to exercise the option. Hence, a bigger value of $p$ should result in a higher optimal exercise price as shown in Figure 7. Similarly, we can analyze the impacts of parameter $q$ on the optimal exercise boundary.

The optimal exercise boundary curves under different parameter $\lambda$ are displayed in Figure 8. As described in Section 3.2, the decay rate of tails of our stochastic process probability density function is controlled by parameter $\lambda > 0$. Thus, a bigger value of this parameter should result in a thinner tail of the stochastic process density function, and the investor should want to gain a bigger price to exercise the American option.

5.3.   An application of the current method

In this subsection, we consider the stock loans based on the finite moment log-stable process (FMLS). Under this framework of FMLS, the stock loans pricing model is ^[25].

where $V(x, t)$ denotes the price of stock loans, $r$, $D$, and $t$ are the risk free interest rate, the dividend and the current time, respectively, $\sigma$ is a constant, and $\nu = -\sigma^{\alpha}\sec\frac{\alpha\pi}{2}$ is a convexity adjustment. $t\in [0, T], x \in(-\infty, x_f), 1 < \alpha < 2, e^{x_f}$ is the optimal redemption price of stock loans. Thus,

In fact, the FMLS model is a special case of the KoBoLJ model. Hence, the method is used to solve model (5.1).

We choose the spatial step size $\Delta x = \frac{x_{\max}-x_{\min}}{2^{11}+1}$ and temporal step size $\Delta t = \frac{2}{1000}$. Thus, we can obtain the following three figures:

The curved surface in Figure 9 and the curve in Figures 10 and 11 show that our numerical method is effective.

6.   Conclusions

In this paper, we consider the American call option pricing based on the KoBoLJ model. The pricing model is a free boundary problem, and the governing equation is a FPIDE. Thus, a numerical scheme based on the penalty function is set. Both the pricing mathematical model and current scheme are very reliable, which is verified by our numerical results. In order to improve computational efficiency, both the PCGNR and fast Fourier transform technique are used to solve the final linear system. Moreover, the impacts of key parameters $\alpha, \; p, \; \hat{p}, \; \hat{\theta}, \; \tilde{\theta}$, and $\lambda$ on optimal exercise price are also analyzed.

At the end of this section, we point out that several issues are not discussed in this paper but the future studies will be implemented for them. First, a risk-free interest rate is a constant in our model. In fact, the constant interest rate cannot describe how the interest rate evolves with respect to the time, especially for the option contracts that have a long time horizon. Second, our numerical results show that the KoBoLJ model is a more comprehensive model than the KoBoJ model; therefore, it should be used to investigate other financial derivative pricing and hedging problems, such as the CDS and Stock Loans. Finally, for the jump processes without the consideration of diffusion processes, we should discuss whether their approaches can be extended to models with jumps and diffusion, such as the stochastic volatility and stochastic liquidity ^[29,30,31].

Authors contribution

The first author is mainly responsible for formula derivation and programming. The second author is primarily responsible for writing the paper and conducting theoretical analysis.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work on this paper is partially supported by the Guizhou University of Commerce Natural Science Projects (No. [2022]ZKZD003). Guizhou University of Commerce Social Science Projects (No. 2024XJSDZD07). Guizhou Provincial Department of Education Natural Science Research Project (No. QJJ[2024]179). And the Disaster Remote Sensing Prevention Workstation of the Academician Innovation Team in Guizhou Province (No. KXJZ[2024]006).

Conflict of interest

The authors declare there is no conflict of interest.