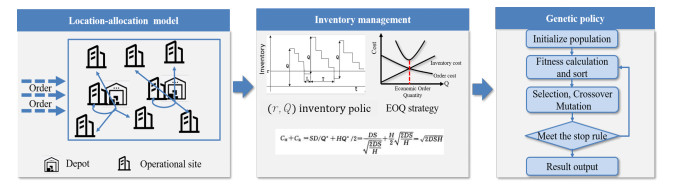
The ability to replace failed spare parts in time directly affects the supportability level of equipment systems. The selection of spare parts' depot locations, inventory mode, and allocation are often separate and independent operations. However, in these situations, the total supply cost is usually relatively high with the consideration of spare parts shortage and maintenance delays. Therefore, this article dealt with a depot location-inventory-allocation problem based on the (r,Q) inventory method and analyzed a combined network of centralized spare part depot locations, inventory, and allocation. Meanwhile, considering the convenience and speed of spare parts transportation brought about by the improvement of transportation capacity, a network is proposed to adopt a centralized storage and point-to-point allocation strategy for parts replacement, which reduces supportability costs without affecting supply efficiency. An optimization model has been developed that reduces the overall cost of support, including inventory, construction, transportation, and logistics. Three equipment support efficiency metrics were used as constraints in this model to assess the location of open depots: selection availability, fill rate, and predicted downtime. Additionally, due to the knowledge asymmetry, there are some shortage issues which always lead to extra expenditure. The model also introduces uncertain distribution to demand measurement and adopts a genetic algorithm for model solving. Ultimately, a numerical instance was developed so as to verify our results.
Citation: Yaojun Liu, Li Jia, Ping Wang, Xiaolin Song. Joint optimization of location and allocation for spare parts depots under (r,Q) inventory policy[J]. Networks and Heterogeneous Media, 2024, 19(3): 1038-1057. doi: 10.3934/nhm.20240046
| [1] | Qinglan Xia, Shaofeng Xu . On the ramified optimal allocation problem. Networks and Heterogeneous Media, 2013, 8(2): 591-624. doi: 10.3934/nhm.2013.8.591 |
| [2] | Eman S. Attia, Ashraf A. M. Khalaf, Fathi E. Abd El-Samie, Saied M. Abd El-atty, Konstantinos A. Lizos, Osama Alfarraj . Performance analysis of nanosystem based on cooperative relay for nanonetworks. Networks and Heterogeneous Media, 2023, 18(4): 1657-1677. doi: 10.3934/nhm.2023072 |
| [3] | Dieter Armbruster, Michael Herty, Xinping Wang, Lindu Zhao . Integrating release and dispatch policies in production models. Networks and Heterogeneous Media, 2015, 10(3): 511-526. doi: 10.3934/nhm.2015.10.511 |
| [4] | Ciro D'Apice, Olha P. Kupenko, Rosanna Manzo . On boundary optimal control problem for an arterial system: First-order optimality conditions. Networks and Heterogeneous Media, 2018, 13(4): 585-607. doi: 10.3934/nhm.2018027 |
| [5] | Ciro D'Apice, Peter I. Kogut, Rosanna Manzo . On relaxation of state constrained optimal control problem for a PDE-ODE model of supply chains. Networks and Heterogeneous Media, 2014, 9(3): 501-518. doi: 10.3934/nhm.2014.9.501 |
| [6] | Giuseppe Buttazzo, Filippo Santambrogio . Asymptotical compliance optimization for connected networks. Networks and Heterogeneous Media, 2007, 2(4): 761-777. doi: 10.3934/nhm.2007.2.761 |
| [7] | Zhi Mao, Dan Luo . A robust adaptive grid method for first-order nonlinear singularly perturbed Fredholm integro-differential equations. Networks and Heterogeneous Media, 2023, 18(3): 1006-1023. doi: 10.3934/nhm.2023044 |
| [8] | Ling Zhang, Xuewen Tan, Jia Li, Fan Yang . Dynamic analysis and optimal control of leptospirosis based on Caputo fractional derivative. Networks and Heterogeneous Media, 2024, 19(3): 1262-1285. doi: 10.3934/nhm.2024054 |
| [9] | Al-hassem Nayam . Asymptotics of an optimal compliance-network problem. Networks and Heterogeneous Media, 2013, 8(2): 573-589. doi: 10.3934/nhm.2013.8.573 |
| [10] | Giulia Cavagnari, Antonio Marigonda, Benedetto Piccoli . Optimal synchronization problem for a multi-agent system. Networks and Heterogeneous Media, 2017, 12(2): 277-295. doi: 10.3934/nhm.2017012 |
The ability to replace failed spare parts in time directly affects the supportability level of equipment systems. The selection of spare parts' depot locations, inventory mode, and allocation are often separate and independent operations. However, in these situations, the total supply cost is usually relatively high with the consideration of spare parts shortage and maintenance delays. Therefore, this article dealt with a depot location-inventory-allocation problem based on the (r,Q) inventory method and analyzed a combined network of centralized spare part depot locations, inventory, and allocation. Meanwhile, considering the convenience and speed of spare parts transportation brought about by the improvement of transportation capacity, a network is proposed to adopt a centralized storage and point-to-point allocation strategy for parts replacement, which reduces supportability costs without affecting supply efficiency. An optimization model has been developed that reduces the overall cost of support, including inventory, construction, transportation, and logistics. Three equipment support efficiency metrics were used as constraints in this model to assess the location of open depots: selection availability, fill rate, and predicted downtime. Additionally, due to the knowledge asymmetry, there are some shortage issues which always lead to extra expenditure. The model also introduces uncertain distribution to demand measurement and adopts a genetic algorithm for model solving. Ultimately, a numerical instance was developed so as to verify our results.
Base-level support systems are crucial to the modern maintenance strategy of complex military and engineering systems because they store, replace, and offer other services related to spare components [1,2].} Furthermore, a number of businesses have observed that, statistically speaking, physical supply site distribution and spare part inventory control account for more than half of the overall cost [2]. Therefore, it is very beneficial for base-level support systems to investigate the best practices for managing supply site locations, inventory techniques, and allocation connections. Liu et al. [3] classified integrated logistics support researches according to the model establishment method and practical application, which emphasized the significance of the spare part support model. For support systems, the supply validity of parts directly impacts the equipment system's degree of support [4]. Maintaining stability and efficiency of spare parts supply becomes a necessary part of integrated logistics support [5].
Traditional spare parts support systems are often characterized by redundancy and cumbersome operations, leading to dispersed inventory locations. While it is common practice to stock fresh spare parts near operational sites (Díaz and Fu [6]), this approach can exacerbate issues related to information asymmetry. The uneven distribution of data can result in inventory shortages and untimely maintenance, causing delays and reducing the availability of spare parts. The existing research has primarily focused on refining demand models (Van der Auweraer and Boute [7], Israe et al. [8], Gupta [9]) to address these inefficiencies. However, these studies have not adequately tackled the fundamental issue of data asymmetry and its impact on the overall system performance. Inventory capacity significantly affects the support level and cost structure of spare parts management. A large portion of support costs is attributed to inventory holding expenses. Previous works, such as those by Kennedy et al. [10] and Wen et al. [11], have explored optimizing stock quantities to improve system availability. Additionally, models like METRIC, developed by Sherbrooke, have been applied to multi-echelon inventory systems. Further research by Turrini and Meissner [12] and Van Horenbeek et al. [13] has focused on inventory modeling and policy analysis. Nonetheless, these studies often concentrate on optimizing inventory levels without fully addressing how the geographical distribution of depots influences these factors.
Selection of optimal depot locations is a key factor in reducing supply times.The problem of facility location has been extensively studied, with comprehensive reviews by Laporte et al. [14] and Farahani et al. [15]. Basic models typically aim to minimize transportation costs by selecting facilities from various alternative locations (Kheybari et al. [16], Uslu and kaya [17], Gebennini et al. [18]). Fernandes et al. [19] extended these models by incorporating the fixed costs associated with opening facilities to determine the optimal number. Rahmaninani et al. [20] highlighted that it is not necessary for all facilities to meet all demands. Hamdan and Diabat [21] advanced this research by developing a two-stage stochastic programming model that simultaneously considers location, inventory, and production decisions in the context of red blood cell manufacturing. Their model aims to minimize the number of out-of-date units, system costs, and delivery times. In the context of enhancing support efficiency, the timely supply of spare parts can be ensured by centralizing resource allocation and constructing spare parts depots with moderate quantities, strategically chosen locations, and reasonable scales. This paper contributes to the existing body of knowledge by emphasizing the importance of depot location in optimizing spare parts supply efficiency, advocating for centralized resource allocation and a robust supply network to reduce delivery times and enhance overall system performance.
In the past decades, there have been a lot of literature that tackles the integrated location-allocation-inventory problems. For example, Wu et al. [22] formulated a complex multi-period location-inventory-routing model with time windows and fuel consumption incorporating both distribution centers and retailers' replenishment decisions, including allowance for stockouts at retailers. Dai et al. [23] attempted to balance the costs, stock capacity, and carbon emissions in managing a supply chain for perishable products. Nevertheless, these models cannot be fully implemented in support systems because they do not take into account the characteristics of support systems, such as supply availability, service level, and balanced allocation laws.
Considering that in the integrated logistics support, the supply of spare parts should meet requirements from many aspects, we make an investigation on support efficiency parameters. Mak and Shen [24] and Topan et al. [25] considered response time in their model to improve service performance. Ozdemir [26] thought that response time could be shortened by optimizing inventory policy. In these works, the Little law was used to calculate the response time. In our model, we call this response time the expected downtime. Basten et al. [27] combined the level of repair analysis with the location-allocation problem, where the availability factor was integrated into the constraints. Then, Basten et al. [28] developed a similar model based on the METRIC method and optimized stock quantity. Gülpınar et al. [29] assumed customer demand followed a normal or an ambiguous distribution. Stockout probability was presented in their model as a chance constraint. Saha and Ray [30] and Küçükyavuz and Jiang [31] also considered stockout in their model. Long et al. [32] analyzed some supply parameters like spare parts support probability, operational availability, supply availability, fill rate, completion rate, and backorder. Then they introduced the concept of an integrated supply performance measure and built an optimization model of spares requisition configuration. Fill rate was used by Sarmah abd Moharana [33] to confirm the number of spare parts. Lad and Kulkarni [34] listed some issues in the integrated system and maintenance schedule including the expected downtime and availability, which addressed customer requirements. Managing the location of depots and allocation to individual sites can be achieved by conducting a thorough analysis of many aspects of supply support.
Furthermore, another crucial issue that has a big impact on supply chain optimization results is the quantification of uncertainty in supply chain variables. Traditionally, probability theory has been used to address these problems [35,36]. However, probability theory is not always suitable, especially in scenarios with limited and sparse observational data. The primary challenge is that frequentist probabilistic methods rely on the law of large numbers, where frequencies approximate probabilities only with a large number of independent trials. In situations with sparse or no data, epistemic uncertainty becomes more significant than aleatory uncertainty. To address this, two mathematical approaches have been introduced for specifying epistemic uncertainty [37]. The uncertainty measurement approachs based on fuzzy theory have been investigated for many years [38]. However, its lack of compliance with the duality axiom has posed challenges for decision-making in supply chains. The other approach involves uncertainty theory, developed by Liu [39], which offers an alternative framework. Integrating uncertainty theory into the optimization of depot locations and inventory policies enhances decision-making in spare parts support systems. This paper demonstrates that uncertainty theory helps accurately model and predict the variability and unpredictability of spare parts demand, which traditional probabilistic models often fail to capture. This improved modeling leads to better demand forecasting, more efficient resource allocation, and more strategic placement of depots.
In general, innovations of the paper cover:
1) Most studies have treated inventory management and depot location decisions separately, while this study contributes to incorporate depot location optimization into the analysis of spare parts support systems, which provides a comprehensive approach that considers the spatial distribution of depots, aiming to minimize delays and costs associated with spare part distribution.
2) Since many studies have integrated stochastic elements into their models, there is limited use of advanced uncertainty theories to rigorously characterize and manage demand variability and asymmetry. With the demand asymmetry taken into account, this paper applies uncertainty theory to characterize demand uncertainty. Inventory and out-of-stock costs are calculated.
3) Because genetic algorithms and other metaheuristic approaches have been widely explored in some areas of logistics and supply chain optimization, the paper attempts to use a genetic algorithm for model solving.
This paper will integrate the support efficiency parameters into the depot location model and make a comprehensive analysis for the inventory and transportation of spare parts. The structure of the paper is as follows. Section 2 gives some basic definitions and theorems from uncertainty theory. Section 3 conveys model assumptions and symbol notations. Section 4.1 determines the overall expense as the function objective and Section 4.2 develops a part location-inventory-allocation model with consideration of (r,Q) inventory policy. In Section 5, the genetic algorithm is outlined to calculate the decision variables. In Section 6, a numerical instance is carried out to prove the model authenticity with conclusions given in Section 7.
We use the uncertainty theory, a revolutionary axiomatic mathematical framework Liu proposed for resolving epistemic uncertainty, in order to accurately forecast the demand quantity based on subjective experience. The definitions and theorems pertaining to uncertainty measure and evaluation are listed below.
Definition 1. (Uncertain variable) An uncertain variable ξ is a function from an uncertainty space (Γ, L, M) to the set of real numbers such that ξ∈B is an event for any Borel set B of real numbers.
Definition 2. (Uncertain distribution) The uncertainty distribution Φ of an uncertain variable ξ is defined by
| Φ(x)=M{ξ≤x}. | (2.1) |
Definition 3. (Normal uncertainty distribution) An uncertain variable ξ is called a normal variable if it has a normal uncertainty distribution
| Φ(x)=(1+exp(π(e−x)√3σ))−1, | (2.2) |
denoted by N(e,σ), where e and σ are real numbers with σ>0.
Definition 4. (Inverse uncertain distribution) Let ξ be an uncertain variable with regular uncertainty distribution Φ(x). Then the inverse function Φ−1(α) is called the inverse uncertainty distribution of ξ. A function Φ−1 is an inverse uncertainty distribution of an uncertain variable ξ if and only if
| M{ξ≤Φ−1(α)}=α, | (2.3) |
for all α∈[0,1].
Definition 5. (Inverse normal uncertain distribution) The inverse uncertainty distribution of normal uncertain variable N(e, σ) is
| Φ−1(α)=e+σ√3πlnα1−α. | (2.4) |
Definition 6. (Expected value) Let ξ be an uncertain variable. Then the expected value of ξ is defined by
| E[ξ]=∫+∞0M{ξ≥x}dx−∫0−∞M{ξ≤x}dx, | (2.5) |
provided that at least one of the two integrals is finite.
Theorem 1. (Inverse uncertain distribution operational law) Let ξ1,ξ2,…,ξn be independent uncertain variables with regular uncertainty distributions Φ1,Φ2,…,Φn, respectively. If f(x1,x2,…,xn) is continuous, strictly increasing with respect to x1,x2,…,xm and strictly decreasing with respect to xm+1,xm+2,…,xn, then ξ=f(ξ1,ξ2,…,ξn) has an inverse uncertainty distribution
| Ψ−1(α)=f(Φ−11(α),…,Φ−1m(α),Φ−1m+1(1−α),…Φ−1n(1−α)). | (2.6) |
Theorem 2. (Normal uncertain distribution operational law) Let ξ1 and ξ2 be independent normal uncertain variables N(e1, σ1) and N(e2, σ2), respectively. Then the sum ξ1+ξ2 is also a normal uncertain variable N(e1+e2, σ1+σ2), i.e.,
| N(e1, σ1)+N(e2, σ2)=N(e1+e2, σ1+σ2). | (2.7) |
The goal of this study is to centralize the allocation of spare components. As Figure 1 shows, depot level stocking exists for every spare part. In the event of an operation level failure, the defective one will be returned and a new one will be despatched right away from the depot. If not, the replacement order is placed on hold until the depot receives the necessary parts. "Demand sites" are operational locations where there is a need for replacement components. As illustrated in Figure 1, the locations of the dotted boxes represent possible depot places. In order to service each of these demand sites, we determine in our model the proper amount and locations of open depots from prospective jobs. Which depots are open is mostly determined by fixed construction costs, transportation costs, and inventory costs. Due to the unpredictable nature of the need for spare parts, inventory levels may not be adequate for every demand site. As a form of punishment, the model also includes the shortage lost. In order to reduce system support costs and maintain the support efficiency parameter within a certain threshold, the objective is to identify depot sites and decide the appropriate inventory policy.
We develop a model based on the following assumptions.
(1) Demand sites, which can be built to serve as central repositories for supplying spare parts to numerous locations, make up the investigated support network.
(2) There is no inventory at operational sites and spare parts are only kept in the depot.
(2) Just one kind of spare part is flowing in the network and each component has an equal and crucial impact at the operational location.
(3) The supply from the designated store can react right away in the event of a failure.
(4) No lateral transshipment occurs between depots and operational sites. There is just one depot per operational site.
(5) Each demand location has independent demands, resulting in an uncertain normal distribution. I=1,2,...,, N(ei,σi).
| Φi(x)=(1+exp(π(ei−x)√3σi))−1. | (3.1) |
(6) All depots have adopted the (r,Q) inventory policy and order acquisition of all depots has constant lead time.
Some notations are defined to present the optimal model. The index sets and model parameters are described below:
I : demand sites set,
J : alternative position for depots set,
i : demand site index, i=1,2,...,I,
j : alternative position for depot index, j=1,2,...,J,
ξi : uncertain demands of site i satisfying an uncertain normal distribution N(ei,σi), i=1,2,...,I,
ei=E[ξi] : the mean value of fill rate requiremented for each demand site i, i=1,2,...,I,
σi=V[ξi] : the standard deviation of fill rate requiremented for each demand site i, i=1,2,...,I,
dij : travel distance from demand site i to depot position j and vice versa, i=1,2,...,I, j=1,2,...,J,
fj : the fixed cost of opening a depot in site j, j=1,2,...,J,
pi : shortage cost coefficient in site j, j=1,2,...,J,
rj : reorder point of inventory position in depot in site j, j=1,2,...,J,
Qj : the fixed order quantity of depot in site j, j=1,2,...,J,
hj : the holding cost per unit time in site j, j=1,2,...,J,
Fj : the fixed cost of placing an order in site j, j=1,2,...,J,
L : the lead time after an order is placed,
α : service level at lead time L,
Ni : the amount of equipment at site i, i=1,2,...,I,
Z : the number of specified item for each piece of equipment,
Ai : availability requirement for each demand site i, i=1,2,...,I,
TDi : the expected downtime requirement for each demand site i, i=1,2,...,I.
Here we set three decision variables:
Transportation amount si from depot to site i, i=1,2,...,I.
Location decision variable Xj is defined as:
| Xj={1, if site j has a depot, 0, if site j does not have a depot, j=1,2,...,J. |
Assignment variable Yij which is defined as follows:
| Yij={1, if sitei is allocated by depotj,0, if sitei is not allocated by depotj,i=1,2,...,I,j=1,2,...,J. |
We set the total cost, which consists of several parts, as our objective function. Inventory cost specifies how inventory policy affects depot location. Fixed construction cost helps limit the number of depots. Transportation cost is calculated to find reasonable routes from demand sites to depots. At last, shortage cost is added as the penalty function for the shortage of spare parts. The specific expressions for these costs are described below:
Inventory cost: In this paper, we suppose that depots conform (r,Q) policies which are widely used in industry. Under these policies, inventory position is continuously reviewed. As soon as it drops to a reorder point rj, a fixed order quantity Qj is placed. Figure 2 shows that the inventory position varies with time.
We consider a single facility whose demand is stochastic, where an order arrives after a given lead time and inventory replenishment is needed. Next, we briefly introduce a working inventory cost model in (r,Q) policies and make further efforts to find the optimal reorder point and order quantity. When demand ξi tends to be steady and has an expected value , the inventory holding cost can be calculated approximately by the EOQ model. As shown below, expected inventory cost includes the order and operational cost
| (4.1) |
The first term of (4.1) represents the order cost. The second term represents the cost of average working inventory. On average, there are items for operational inventory on hand for policies. The optimal policy is obtained when has the following expression:
| (4.2) |
In this case, the minimum inventory cost can be reached and expression (4.1) becomes
| (4.3) |
Reorder point is set to maintain service level in lead time no less than . So reorder point is the minimum integer that satisfies the expression as follows:
| (4.4) |
In our model, depot supplies demand sites. Inventory cost for all open depots is expressed as follows:
| (4.5) |
Fixed construction cost: This cost does not depend on demand or transportation activities. It arises when a supply depot is open. Let be the fixed expense of setting up a depot at position . The total fixed cost of the system is computed as:
| (4.6) |
Transportation cost: Transportation cost is incurred when spare parts are carried from supply depot to demand site . The total transportation cost is expressed as:
| (4.7) |
Shortage cost: This cost is incurred when there is some shortage lost for demand sites. The expected shortage cost is expressed as:
| (4.8) |
The total cost is defined as an aggregation of inventory, fixed, transportation, and shortage costs. The expected total cost is calculated as:
| (4.9) |
Several support efficiency characteristics are employed in our model constraints to guarantee product support ability, which are connected with the support level to ensure timely and sufficient supply. The constraints are discussed as below:
Fill rate constraint: The likelihood that the demand for spare parts can be met on schedule is known as the fill rate. This constraint guarantees that the amount of transportation from the depot to the location will satisfy the demand up to level :
| (4.10) |
Comforming to Definition 5 in Section 2, the deterministic form is written by
| (4.11) |
Availability: Availability is used to evaluate a system that includes equipment, each with spare parts. One particular piece of equipment will not be stopped by the lack of spare components, which is delivered by:
Therefore, the availability constraint of the demand site in our model can be expressed as:
| (4.12) |
The nonequality is transferred into the deterministic form,
| (4.13) |
The expected downtime constraint: The expected downtime refers to the time spent due to the lack of spare parts. According to the Little law, the expected downtime is calculated by:
Expression for the expected downtime constraint is
| (4.14) |
The corresponding deterministic form is given by
| (4.15) |
Other allocation constraints: There can only be one open depot per demand site, thanks to the first constraint below. The second restriction ensures that demand sites can only be served by open depots.
| (4.16) |
The objective is to minimize the overall cost by determining depot locations and allocating resources to each demand site within the restrictions of efficiency standards. Therefore, the inventory-location-allocation model can be summarized as below:
| (4.17) |
The deterministic inventory-location model is formulated as follows:
| (4.18) |
It is challenging to tackle the constrained nonlinear integer programming issue posed by the predicted inventory-location model. Heuristic approaches prove to be quite successful in resolving these issues. The heuristic algorithm is based on algorithms that resemble natural bodies, such as the genetic algorithm, simulated annealing, ant colony algorithm, etc. In this section, we choose a genetic algorithm to solve the predicted inventory-location model by simulating a natural evolutionary process. Global optimization features and probabilistic transfer rules are substituted for deterministic rules in a genetic algorithm. It is helpful when looking for the best answer. The processes shown in Figure 3 define the algorithm:
Step 1. Set the chromosomes to zero. Generate a collection of numbers at random that contain the location and the volume of transit. A chromosome is this collection of numbers. Continue in this manner until chromosomes are generated in total. The set of chromosomes , , represents a population with as the terminal population.
Step 2. Chromosomes on screen with limitations. We verify each chromosome by using the model's constraints to make sure it is feasible. A new generation of viable chromosomes will emerge.
Step 3. Analyze every chromosome. Determine the objective values of each chromosome and arrange them in ascending order. The new order of the rearranged chromosomes is . The superior chromosome is the first chromosome.
Step 4. Choose this set of chromosomes. Based on their order, assign a fitness rating to each chromosome. The definition of the fitness function is
| (5.1) |
Here, is the number ranked in Step 3 and is a parameter in the selection process. Choose chromosomes using a roulette wheel based on the fitness values. We can infer from (5.1) that the likelihood of being chosen increases with decreasing .
Step 5. Crossover a few chromosomes. Set up a crossover operation parameter, . With this likelihood, we choose a few chromosomes () to go through the crossover procedure. After that, is split up into many pairs at random. A portion of each pair's genes are exchanged.
Step 6. Mutate some genes in the chromosomes. Determine the mutation operator and use this probability to choose the chromosomes for the mutation operation. Some of the genes on the selected chromosomes () must be altered. In this case, .
Step 7. Repeat Steps 2–6 until . Report the best chromosome as the optimal result in the support system.
We present a numerical example to evaluate the performance of the evolutionary algorithm. Ten locations are thought to be in need of services. Some of these demand sites' depots will be selected to service other sites for convenience. The location and inventory specifications of the demand sites are displayed in Table 1. We assume that the demand for spare parts follows a Poisson distribution and is stochastic. Each piece of equipment has spare components, and the operational location has equipment. We use the genetic algorithm to identify the answer after including this data into the optimization model. The genetic algorithm uses the following environment parameters: generation , , crossover probability , and mutation probability . and are the set belief levels.
| Site | Position | ||||||
| 1 | (96, 44) | 10 | 3 | 100 | 1 | 1 | 1 |
| 2 | (18, 98) | 6 | 2 | 200 | 2 | 3 | 2 |
| 3 | (16, 21) | 10 | 2 | 300 | 5 | 3 | 1 |
| 4 | (17, 53) | 4 | 1 | 200 | 2 | 2 | 2 |
| 5 | (74, 67) | 18 | 3 | 200 | 3 | 6 | 1 |
| 6 | (19, 49) | 8 | 2 | 100 | 3 | 3 | 1 |
| 7 | (3, 8) | 4 | 1 | 300 | 6 | 6 | 2 |
| 8 | (54, 73) | 8 | 2 | 200 | 5 | 1 | 1 |
| 9 | (64, 48) | 6 | 2 | 100 | 1 | 2 | 2 |
| 10 | (98, 58) | 12 | 3 | 300 | 5 | 5 | 1 |
The constraint parameters and are the same for every site. We compute the overall cost of various constraint settings and alter them for comparison. Every outcome is displayed in Table 2. A base case with , , and is called Case 1. The outcomes of Cases 2 through 5 demonstrate how different parameters can affect both the total cost and the number of depots. The number of depots diminishes as the constraint parameter level drops, suggesting that the outcomes are feasible. Both the number of depots and the cost of support rise as system support requirements do. We display the allocation and location scenario for the optimal solution in instance 1 in Table 3. The ideal solution for instance 2–4 are shown in Figure 4. It is evident that the black squares represent demand sites, the red triangles represent open depots, and the blue line indicates that the depot serves the demand site. Sites 1, 6, 5, and 3 are open as depots according to Table 3; in Figure 4(a), they are shown as red triangles. This depot supports demand sites 8 and 9, as indicated by the links between site 5 (depot) and site 8 (demand), and site 5 (depot) and site 9 (demand) in Figure 4(a). Table 3 displays allocation to additional sites for and . Furthermore, (4.2) and (4.4) are used to compute the inventory policy for open depots.
| Depot number | Overall cost | ||||
| Case 1 | 0.90 | 0.85 | 2 | Four | 434.91 |
| Case 2 | 0.90 | 0.90 | 2 | Four | 431.12 |
| Case 3 | 0.90 | 0.85 | 1 | Four | 431.11 |
| Case 4 | 0.85 | 0.85 | 2 | Three | 396.94 |
| Case 5 | 0.80 | 0.80 | 2 | Three | 368.49 |
| Site index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| (unit) | 15 | 9 | 15 | 6 | 30 | 15 | 7 | 12 | 6 | 18 |
| (6, 33) | (5, 33) | (6, 48) | (5, 30) |
Figures 4(b)–(d) match Cases 2–4. The fill rate and availability bottom values decrease, the open depot in site 7 moves to site 3, and the depot in site 1 cancels when comparing Figures 4(b), (d). By contrasting Figures 4(a), (d), it can be seen that position is significantly influenced by fill rate. In a similar vein, Figures 4(b), (c) demonstrates that the location is less affected by the anticipated downtime constraint.
(1) Belief level analysis
The supportability indexes are changed with the results exhibited in Table 4.
| Inventory policy parameters | Cost | |||
| 0.9 | 0.95 | 0.95 | 1(6, 33), 3(5, 33), 5(6, 48), 6(5, 30) | 434.91 |
| 0.85 | 0.95 | 0.95 | 3(5, 33), 5(8, 52), 6(15, 40) | 396.94 |
| 0.9 | 0.99 | 0.95 | 1(8, 35), 3(9, 36), 5(8, 50), 6(7, 33) | 447.86 |
| 0.9 | 0.95 | 0.99 | 1(7, 34), 3(7, 35), 5(6, 48), 6(6, 30) | 436.62 |
Table 4 summarizes that an increase in belief degree , , or results in a rise in the total cost and an adjustment to inventory parameters. Higher belief degrees indicate higher service level requirements, which will result in higher costs. In a similar vein, an increase in belief degree corresponds to a tougher standard of supply availability at the expense of cost. In actuality, the choice of and determines the balanced degree of cost and supportability. The inventory parameter is unaffected by the decline in stockout risk level , but it does show the decreasing penalty for shortage risk, which lowers the stockout loss and lowers the overall cost.
(2) Inventory policy parameter
Utilizating the calculated parameters from Table 3, the variations of the reorder point and order quantity are investigated with the outcome plotted in Figures 4 and 5.
From Figure 4, we investigate how different depots are affected by the reorder point of inventory capacity. The entire optimal process can be split into the unreliable region and the reliable zone based on the supportability restrictions. The supply system is unreliable in an unreliable zone because the centralized depot is unable to meet the specified supportability criteria. A reliable region shows that the system can meet the needs of the locations. The overall cost rises as the reorder point rises in each of the two zones.
From Figure 5, integrated impacts of inventory cost and stockout caused the overall cost to decrease before a steady increase in total cost, which generates the optimal value.
The timely delivery and commensurate economy of support systems can be guaranteed by deploying backup resources in the right numbers and depot locations, and by creating suitable inventory procedures.
In order to enhance the support system, we created a model in this article that integrates inventory strategy with location-related issues. First, we looked at the support requirement model and the location problem. Next, the link between inventory running costs and the parameters of the strategy was examined. Transportation expenses, scarcity losses, and fixed building costs are all included in the overall cost, which is the ideal objective function. We also included the support efficiency parameter in the placement model and examined the features of the optimization problem. In order to assess the demand quantity in the model, uncertainty theory was presented. The ideal problem was resolved using a genetic algorithm. Finally, numerical examples were used to confirm the algorithm's efficacy. It is important to note that the quantity and locations of spare part depots we locate can meet the requirements of integrated logistical support. The numerical example's results demonstrate how important it is to consider inventory costs and service limitations when choosing depot locations. Our methodology outperforms the standard location model in providing optimal answers under various support conditions.
Future studies will examine the effects of erratic demand or variable lead times on inventory costs and depot locations. Furthermore, multi-item and multi-echelon spare parts depots will be a trend worth watching and will require further work to solve the site optimization issue.
Yaojun Liu: Data analysis and writing; Li Jia: Formal analysis; Ping Wang: Methodology and supervision; Xiaolin Song: Funding acquisition.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
This work was supported by the National Natural Science Foundation of China Grant No. 61873329 and China Postdoctoral Science Foundation Grant No. 2022M710322.
The authors declare there is no conflict of interest.
| [1] |
J. Wu, H. Liu, H. Zuo, Y. Yang, Y. Ma, L. Kong, The demand supply steady-state process-based multi-level spare parts optimization, Sensors, 21 (2021), 8324. https://doi.org/10.3390/s21248324 doi: 10.3390/s21248324

|
| [2] | G. J. Van Houtum, B. Kranenburg, Spare Parts Inventory Control under System Availability Constraints, 227 (2015), Springer: Berlin. |
| [3] | Z. Jia, Z. Zeng, Y. Zhou, Y. Zhou, Configuration optimization methods for multi-echelon and multi-constraints spare parts based on dynamic demands, in 2014 10th International Conference on Reliability, Maintainability and Safety (ICRMS), (2014), 1091–1096. https://doi.org/10.1109/ICRMS.2014.7107372 |
| [4] |
J. Holmström, J. Partanen, J. Tuomi, M. Walter, Rapid manufacturing in the spare parts supply chain: Alternative approaches to capacity deployment, J. Manuf. Technol. Manage., 21 (2010), 687–697. https://doi.org/10.1108/17410381011063996 doi: 10.1108/17410381011063996

|
| [5] |
W. D. Rustenburg, G. J. van Houtum, W. H. M. Zijm, Spare parts management for technical systems: Resupply of spare parts under limited budgets, IIE trans., 32 (2000), 1013–1026. https://doi.org/10.1023/A:1007676901673 doi: 10.1023/A:1007676901673

|
| [6] |
A. Diaz, M. C. Fu, Models for multi-echelon repairable item inventory systems with limited repair capacity, Eur. J. Oper. Res., 97 (1997), 480–492. https://doi.org/10.1016/S0377-2217(96)00279-2 doi: 10.1016/S0377-2217(96)00279-2

|
| [7] |
S. Van der Auweraer, R. Boute, Forecasting spare part demand using service maintenance information, Int. J. Prod. Econ., 213 (2019), 138–149. https://doi.org/10.1016/j.ijpe.2019.03.015 doi: 10.1016/j.ijpe.2019.03.015

|
| [8] |
E. F. Israel, A. Albrecht, E. M. Frazzon, B. Hellingrath, Operational supply chain planning method for integrating spare parts supply chains and intelligent maintenance systems, IFAC-PapersOnLine, 50 (2017), 12428–12433. https://doi.org/10.1016/j.ifacol.2017.08.2432 doi: 10.1016/j.ifacol.2017.08.2432

|
| [9] | S. Gupta, Working capital management through inventory management techniques, Ashok Yakkaldevi, 2020. |
| [10] |
W. J. Kennedy, J. W. Patterson, L. D. Fredendall, An overview of recent literature on spare parts
inventories, Int. J. Prod. Econ., 76 (2002), 201–215. https://doi.org/10.1016/S0925-5273(01)00174-8 doi: 10.1016/S0925-5273(01)00174-8

|
| [11] |
M. Wen, Q. Han, Y. Yang, R. Kang, Uncertain optimization model for multi-echelon spare parts supply system, Appl. Soft Comput., 56 (2017), 646–654. https://doi.org/10.1016/j.asoc.2016.07.057 doi: 10.1016/j.asoc.2016.07.057

|
| [12] |
L. Turrini, J. Meissner, Spare parts inventory management: New evidence from distribution fitting, Eur. J. Oper. Res., 273 (2019), 118–130. https://doi.org/10.1016/j.ejor.2017.09.039 doi: 10.1016/j.ejor.2017.09.039

|
| [13] |
A. Van Horenbeek, J. Buré, D. Cattrysse, L. Pintelon, P. Vansteenwegen, Joint maintenance and inventory optimization systems: A review, Int. J. Prod. Econ., 143 (2013), 499–508. https://doi.org/10.1016/j.ijpe.2012.04.001 doi: 10.1016/j.ijpe.2012.04.001

|
| [14] | G. Laporte, S. Nickel, F. Saldanha-da-Gama, Introduction to Iocation Science, Springer International Publishing, (2019), 1–21. |
| [15] |
R. Z. Farahani, M. Hekmatfar, B. Fahimnia, N. Kazemzadeh, Hierarchical facility location problem: Models, classifications, techniques, and applications, Comput. Ind. Eng., 68 (2014), 104–117. https://doi.org/10.1016/j.cie.2013.12.005 doi: 10.1016/j.cie.2013.12.005

|
| [16] |
S. Kheybari, M. Kazemi, J. Rezaei, Bioethanol facility location selection using best-worst method, Appl. Energy, 242 (2019), 612–623. https://doi.org/10.1016/j.apenergy.2019.03.054 doi: 10.1016/j.apenergy.2019.03.054

|
| [17] |
T. Uslu, O. Kaya, Location and capacity decisions for electric bus charging stations considering waiting times, Transp. Res. Part D Transp. Environ., 90 (2021), 102645. https://doi.org/10.1016/j.trd.2020.102645 doi: 10.1016/j.trd.2020.102645

|
| [18] |
E. Gebennini, R. Gamberini, R. Manzini, An integrated production–distribution model for the dynamic location and allocation problem with safety stock optimization, Int. J. Prod. Econ., 122 (2009), 286–304. https://doi.org/10.1016/j.ijpe.2009.06.027 doi: 10.1016/j.ijpe.2009.06.027

|
| [19] |
D. R. Fernandes, C. Rocha, D. Aloise, G. M. Ribeiro, E. M. Santos, A. Silva, A simple and effective genetic algorithm for the two-stage capacitated facility location problem, Comput. Ind. Eng., 75 (2014), 200–208. https://doi.org/10.1016/j.cie.2014.05.023 doi: 10.1016/j.cie.2014.05.023

|
| [20] | R. Rahmaniani, M. Saidi-Mehrabad, H. Ashouri, Robust capacitated facility location problem optimization model and solution algorithms, J. Uncertain Syst., 7 (2023), 22–35. |
| [21] |
B. Hamdan, A. Diabat, A two-stage multi-echelon stochastic blood supply chain problem, Comput. Oper. Res., 101 (2019), 130–143. https://doi.org/10.1016/j.cor.2018.09.001 doi: 10.1016/j.cor.2018.09.001

|
| [22] |
W. Wu, W. Zhou, Y. Lin, Y. Xie, W. Jin, A hybrid metaheuristic algorithm for location inventory routing problem with time windows and fuel consumption, Expert Syst. Appl., 166 (2021), 114034. https://doi.org/10.1016/j.eswa.2020.114034 doi: 10.1016/j.eswa.2020.114034

|
| [23] |
Z. Dai, F. Aqlan, X. Zheng, K. Gao, A location-inventory supply chain network model using two heuristic algorithms for perishable products with fuzzy constraints, Comput. Ind. Eng., 119 (2018), 338–352. https://doi.org/10.1016/j.cie.2018.04.007 doi: 10.1016/j.cie.2018.04.007

|
| [24] |
H. Y. Mak, Z. J. Shen, Risk diversification and risk pooling in supply chain design, IIE Trans., 44 (2012), 603–621. https://doi.org/10.1080/0740817X.2011.635178 doi: 10.1080/0740817X.2011.635178

|
| [25] | E. Topan, Z. P. Bayındır, T. Tan, An exact solution procedure for multi-item two-echelon spare parts inventory control problem with batch ordering in the central depot, Oper. Res. Lett., 38 (2010), 454–461. |
| [26] | D. Ozdemir, Collaborative Planning and Replenishment Policies, INSEAD (France and Singapore), 2004. |
| [27] |
R. J. Basten, R. J. Schutten, M. C. Van Der Heijden, An efficient model formulation for level of repair analysis, Ann. Oper. Res., 172 (2009), 119–142. https://doi.org/10.1007/s10479-009-0516-5 doi: 10.1007/s10479-009-0516-5

|
| [28] |
R. J. Basten, M. C. Van der Heijden, J. M. Schutten, Joint optimization of level of repair analysis and spare parts stocks, Eur. J. Oper. Res., 222 (2012), 474–483. https://doi.org/10.1016/j.ejor.2012.05.045 doi: 10.1016/j.ejor.2012.05.045

|
| [29] |
N. Gülpınar, D. Pachamanova, E. Çanakoğlu, Robust strategies for facility location under uncertainty, Eur. J. Oper. Res., 225 (2013), 21–35. https://doi.org/10.1016/j.ejor.2012.08.004 doi: 10.1016/j.ejor.2012.08.004

|
| [30] |
E. Saha, P. K. Ray, Modelling and analysis of inventory management systems in healthcare: A review and reflections, Comput. Ind. Eng., 137 (2019), 106051. https://doi.org/10.1016/j.cie.2019.106051 doi: 10.1016/j.cie.2019.106051

|
| [31] |
S. Küçükyavuz, R. Jiang, Chance-constrained optimization under limited distributional information: A review of reformulations based on sampling and distributional robustness, EURO J. Comput. Optim., 10 (2022), 100030. https://doi.org/10.1016/j.ejco.2022.100030 doi: 10.1016/j.ejco.2022.100030

|
| [32] | J. Long, R. Kang, H. L. Cheng, Optimization of spares supply based on integrated supply performance measure, Syst. Eng. Electron., 29 (2007), 2085–2087. |
| [33] | S. P. Sarmah, U. C. Moharana, Spare parts inventory management literature and direction towards the use of data mining technique: A review, Handb. Res. Promoting Bus. Process Improv. Through Inventory Control Tech., 2018,534–558. https://doi.org/10.4018/978-1-5225-3232-3.ch028 |
| [34] |
B. K. Lad, M. S. Kulkarni, Integrated reliability and optimal maintenance schedule design: A life cycle cost based approach, Inter. J. Prod. Lifecycle Manage., 3 (2008), 78–90. https://doi.org/10.1504/IJPLM.2008.019971 doi: 10.1504/IJPLM.2008.019971

|
| [35] |
W. Wu, J. Ma, R. Liu, W. Jin, Multi-class hazmat distribution network design with inventory and superimposed risks, Transp. Res. Part E Logist. Transp. Rev., 161 (2022), 102693. https://doi.org/10.1016/j.tre.2022.102693 doi: 10.1016/j.tre.2022.102693

|
| [36] |
W. Wu, Y. Li, Pareto truck fleet sizing for bike relocation with stochastic demand: Risk-averse multi-stage approximate stochastic programming, Transp. Res. Part E Logist. Transp. Rev., 183 (2024), 103418. https://doi.org/10.1016/j.tre.2024.103418 doi: 10.1016/j.tre.2024.103418

|
| [37] |
P. Li, M. Wen, T. Zu, R. Kang, A joint location–allocation–inventory spare part optimization model for base-level support system with uncertain demands, Axioms, 12 (2023), 46. https://doi.org/10.3390/axioms12010046 doi: 10.3390/axioms12010046

|
| [38] |
A. De, S. P. Singh, Analysis of fuzzy applications in the agri-supply chain: A literature review, J. Cleaner Prod., 283 (2021), 124577. https://doi.org/10.1016/j.jclepro.2020.124577 doi: 10.1016/j.jclepro.2020.124577

|
| [39] | B. Liu, Uncertainty Theory, Springer Berlin Heidelberg, (2010), 1–79. |
| Site | Position | ||||||
| 1 | (96, 44) | 10 | 3 | 100 | 1 | 1 | 1 |
| 2 | (18, 98) | 6 | 2 | 200 | 2 | 3 | 2 |
| 3 | (16, 21) | 10 | 2 | 300 | 5 | 3 | 1 |
| 4 | (17, 53) | 4 | 1 | 200 | 2 | 2 | 2 |
| 5 | (74, 67) | 18 | 3 | 200 | 3 | 6 | 1 |
| 6 | (19, 49) | 8 | 2 | 100 | 3 | 3 | 1 |
| 7 | (3, 8) | 4 | 1 | 300 | 6 | 6 | 2 |
| 8 | (54, 73) | 8 | 2 | 200 | 5 | 1 | 1 |
| 9 | (64, 48) | 6 | 2 | 100 | 1 | 2 | 2 |
| 10 | (98, 58) | 12 | 3 | 300 | 5 | 5 | 1 |
| Depot number | Overall cost | ||||
| Case 1 | 0.90 | 0.85 | 2 | Four | 434.91 |
| Case 2 | 0.90 | 0.90 | 2 | Four | 431.12 |
| Case 3 | 0.90 | 0.85 | 1 | Four | 431.11 |
| Case 4 | 0.85 | 0.85 | 2 | Three | 396.94 |
| Case 5 | 0.80 | 0.80 | 2 | Three | 368.49 |
| Site index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| (unit) | 15 | 9 | 15 | 6 | 30 | 15 | 7 | 12 | 6 | 18 |
| (6, 33) | (5, 33) | (6, 48) | (5, 30) |
| Inventory policy parameters | Cost | |||
| 0.9 | 0.95 | 0.95 | 1(6, 33), 3(5, 33), 5(6, 48), 6(5, 30) | 434.91 |
| 0.85 | 0.95 | 0.95 | 3(5, 33), 5(8, 52), 6(15, 40) | 396.94 |
| 0.9 | 0.99 | 0.95 | 1(8, 35), 3(9, 36), 5(8, 50), 6(7, 33) | 447.86 |
| 0.9 | 0.95 | 0.99 | 1(7, 34), 3(7, 35), 5(6, 48), 6(6, 30) | 436.62 |
| Site | Position | ||||||
| 1 | (96, 44) | 10 | 3 | 100 | 1 | 1 | 1 |
| 2 | (18, 98) | 6 | 2 | 200 | 2 | 3 | 2 |
| 3 | (16, 21) | 10 | 2 | 300 | 5 | 3 | 1 |
| 4 | (17, 53) | 4 | 1 | 200 | 2 | 2 | 2 |
| 5 | (74, 67) | 18 | 3 | 200 | 3 | 6 | 1 |
| 6 | (19, 49) | 8 | 2 | 100 | 3 | 3 | 1 |
| 7 | (3, 8) | 4 | 1 | 300 | 6 | 6 | 2 |
| 8 | (54, 73) | 8 | 2 | 200 | 5 | 1 | 1 |
| 9 | (64, 48) | 6 | 2 | 100 | 1 | 2 | 2 |
| 10 | (98, 58) | 12 | 3 | 300 | 5 | 5 | 1 |
| Depot number | Overall cost | ||||
| Case 1 | 0.90 | 0.85 | 2 | Four | 434.91 |
| Case 2 | 0.90 | 0.90 | 2 | Four | 431.12 |
| Case 3 | 0.90 | 0.85 | 1 | Four | 431.11 |
| Case 4 | 0.85 | 0.85 | 2 | Three | 396.94 |
| Case 5 | 0.80 | 0.80 | 2 | Three | 368.49 |
| Site index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| (unit) | 15 | 9 | 15 | 6 | 30 | 15 | 7 | 12 | 6 | 18 |
| (6, 33) | (5, 33) | (6, 48) | (5, 30) |
| Inventory policy parameters | Cost | |||
| 0.9 | 0.95 | 0.95 | 1(6, 33), 3(5, 33), 5(6, 48), 6(5, 30) | 434.91 |
| 0.85 | 0.95 | 0.95 | 3(5, 33), 5(8, 52), 6(15, 40) | 396.94 |
| 0.9 | 0.99 | 0.95 | 1(8, 35), 3(9, 36), 5(8, 50), 6(7, 33) | 447.86 |
| 0.9 | 0.95 | 0.99 | 1(7, 34), 3(7, 35), 5(6, 48), 6(6, 30) | 436.62 |