Prediction of postoperative recovery in patients with acoustic neuroma using machine learning and SMOTE-ENN techniques

1.   Introduction

We give a biased introduction to generalised Kähler structures based on physics applications. Generalised Kähler or Calabi-Yau geometry ^[10,12] arise from the study of supersymmetric sigma models or super-string compactifications. For example, by placing a super-string theory on $\mathbb{R}^{1, 3}\times X$ where $X$ is a Calabi-Yau 3-fold, one can obtain a gauge theory on $\mathbb{R}^{1, 3}$ that preserves $N = 2$ supersymmetry. For a sigma model based on mappings from a Riemann surface ${\Sigma}$ to a manifold $M$, Zumino showed that one can obtain $N = 2$ supersymmetry if $M$ is Kähler ^[26]. But string theory has an important duality called the $T$-duality (torus duality) that relates the IIA to the IIB super-string and is the local model for mirror symmetry ^[22]. However the two integral ingredients, the Kähler geometry and T-duality are not compatible. The problem is that Kähler geometry is characterised by the covariant constancy of the complex structure under the Levi-Civita connection. But the T-duality will generate a Neveu–Schwarz 3-form $H$. This 3-form modifies the Levi-Civita connection, making it torsionful ^[14,20]. So a more appropriate notion of generalised Kähler structure is formulated as the constancy of complex structure under a torsionful connection $\nabla^H$ (which we will recall in the next section). As for the sigma models, it turns out that Zumino's result can be generalised ^[15] to accommodate a bi-hermitian geometry with torsion connection.

The local geometry of generalised Kähler structure (GKS) has been well understood and used to construct supersymmetric sigma models mentioned above ^[18]. The generalised Kähler potential (GKP) was used to write the action of such models, but the drawback was that the formulation only works at regular points and a more global understanding of the GKP was lacking. A more recent work ^[3] partially answered this question for GKS of the symplectic type, where the GKP was formulated in terms of Morita equivalence of certain holomorphic Poisson structures.

In ^[13] Hitchin gave a construction of GKS on Del Pezzo surfaces using a flow that deforms the original Kähler structure on these surfaces. In general, it can be hard to solve a flow equation due to its non-linear nature. In this work we restrict ourselves to the toric Del Pezzo surfaces, where thanks to the toric symmetry, the flow equations greatly simplify. We show that on $\mathbb{C}P^2$ the flow is solved by the Weierstrass elliptic functions. To present the solution we use the coordinate system $c_3, s$ to parametrise the triangle which is the moment map polygon for $\mathbb{C}P^2$, see Figure 1. If $y^{1, 2}$ are the Euclidean coordinates of $\mathbb{R}^2$, the triangle is the region $1\geq y^{1, 2}\geq 0$, $y^1+y^2\leq 1$, we have

where $\wp$ is the Weierstrass elliptic function satisfying

and with half-periods ${\omega}_{1, 2}$ depending on $c_3$. With the $c_3, s$ coordinates, the flow is simply a shift

with ${\Delta} t$ the flow time. Our main result is that (the details are in Proposition 6.6, 6.4 and 6.9)

Theorem 1.1. On $\mathbb{C}P^2$, Hitchin's construction gives a Generalised Kähler structure with two toric invariant complex structures. The first one $I_-$ is the standard one while $I_+$ is deformed from $I_-$ by a flow $\phi_{{\Delta} t}$: $I_+ = (\phi_{{\Delta} t*})^{-1}I_-\phi_{{\Delta} t*}$, concretely

where the coordinate we use for $\mathbb{C}P^2$ are the two angles ${\theta}_{1, 2}$ in addition to the $c_3, s$. The quantity $\tilde\eta_1$ is introduced in (57) and depends only on $c_3$.

The complex structure $I_+$ is valid for arbitrary flow time ${\Delta} t$, but the bi-hermitian metric is positive definite for small but non-zero ${\Delta} t$. The generalised Kähler potential is given by

The first term is proportional to the Fubini-Study Kähler potential.

We leave the further exploration of our explicit results, such as the relation to certain integrable models ^[19] as well as mirror symmetry for a future work.

2.   Generalised Kähler structure

A generalized Kähler structure (GKS) on a manifold $M$ can be described as a pair of integrable complex structures $I_\pm$ toghether with a Riemannian metric $g$, which is hermitian with respect to both, and a closed 3-form $H$ such that $\nabla^\pm I_\pm = 0$ where $\nabla^\pm$ is the Riemannian connection with skew torsion $\pm H$.

In the case of 4-manifolds, suppose we are given $(M_4, g, I_{\pm})$ with $g$ hermitian with respect to $I_{\pm}$ and $\omega_\pm = I_{\pm}^*g$ are the hermitian forms. We can then define 3-forms $H_\pm$ as

where $\bar\partial_\pm, \partial_\pm$ are defined using the complex structure $I_\pm$. It is proved in ^[1] that if the first Betti number of $M_4$ is even then $H_+ = -H_- = H$ automatically.

Moreover, let $\nabla^\pm$ be the connections on the tangent bundle $TM$ with torsion $\pm H$ defined as

where $X, Y, Z$ are sections of $TM$ and $\langle-, - \rangle$ denotes the pairing using the metric. It can be shown that $\nabla^\pm I_\pm = 0$, (see e.g. ^[9] Proposition 2). This means that constructing a GKS on a 4-manifold with even Betti number is equivalent to finding $I_{\pm}$ and a metric that is hermitian with respect to both.

2.1.   Morita equivalence between holomorphic Poisson structures

What played a crucial role in ^[3] was the formulation of the GKS in terms of holomorphic Poisson structures. One starts with the Hitchin's Poisson structure

It can be shown that this is of type (0, 2)+(2, 0) with respect to both $I_{\pm}$. From $Q$ one can construct two Poisson structures

which are (2, 0) and holomorphic under $I_{\pm}$ respectively. The authors of ^[3] considered the GKS of symplectic type, we refer to ^[3] for the details of this definition, while we only record what would be important for this work. One has a symplectic form $F$, with the following relations to $I_{\pm}$

The solution to such a non-linear pair of equations is encoded in terms of the Morita equivalence of ${\sigma}_{\pm}$ as holomorphic Poisson structures. We recall its definition following Ping Xu, adapted to the holomorphic setting

Definition 2.1. (Definition 2.1 ^[24]) The two holomorphic Poisson structures $(M, {\sigma}_{\pm})$ are Morita equivalent if there is a holomorphic symplectic manifold $(X, J, {\Omega})$ (called the equivalence bi-module) and two maps ${\tt s}$, ${\tt t}$

with the following properties. The source map ${\tt s}$ is holomorphic, anti-Poisson, i.e. ${\tt s}_*{\Omega}^{-1} = -{\sigma}_-$ and complete, while the target map ${\tt t}$ is holomorphic, Poisson i.e. ${\tt t}_*{\Omega}^{-1} = {\sigma}_+$ and complete. Besides, the fibre of $\tt{s}, {\tt t}$ is connected and simply connected. One requires further that $\ker {\tt t}_*$ be symplectic orthogonal complement to $\ker{\tt s}_*$.

Here completeness means that ${\tt s}^*f$ generates a complete Hamiltonian vector field (its flow time extendable to $(-\infty, \infty)$) if the function $f$ on $M$ generates under ${\sigma}_-$ a complete vector field. The same goes for ${\sigma}_+$ and ${\tt t}^*f$. The symplectic orthogonality of $\ker {\tt s}_*$ and $\ker {\tt t}_*$ implies^*

^*For a Poisson structure $\pi$ on $M$, the map $\pi^{\#}:\; T^*M\to TM$ is defined as $(\pi^{\#}dg)\circ f: = \{f, g\}_{\pi}$ where $\circ$ denotes the action of a vector field on a function by derivation, and $f, g\in C^{\infty}(M)$. Then we extend $\pi^{\#}$ to act on 1-forms using $C^{\infty}$-linearity.

This ensures that the hamiltonian vector field generated by a function of type ${\tt t}^*h$ with $h\in C^{\infty}(M)$ has no effect on the image of the source map (and vice versa). Finally that ${\tt s}$ and ${\tt t}$ are holomorphic means that the two complex structures $I_{\pm}$ are 'unified' as one single complex structure up on $X$.

The Morita equivalence is an equivalence relation between integrable Poisson manifolds. In particular, integrable Poisson manifolds are self Morita equivalent with self-equivalence bi-module given by the symplectic groupoid, which we will need next.

In the setting of GKS of symplectic type, this Morita equivalence between $(M, {\sigma}_{\pm})$ can be constructed by deforming a self-Morita equivalence of $(M, {\sigma}_-)$. Let $(X, J_0, {\Omega}_0)$ be a holomorphic symplectic groupoid integrating the Poisson structure ${\sigma}_-$, i.e. a holomorphic symplectic manifold $(X, J_0, {\Omega}_0)$ with maps

satisfying identical conditions as in Definition 2.1 by replacing $I_+, \, {\sigma}_+$ with $I_-, \, {\sigma}_-$. One has again a similar orthogonality

It is helpful to keep in mind that $J_0$ can be expressed as

and that the inverse of ${\Omega}_0$ (as a holomorphic 2-form) is

It turns out that a simple deformation ${\Omega}_0\to {\Omega} = {\Omega}_0+{\tt t}^*F$ gives us the Morita equivalence between ${\sigma}_{\pm}$. For simplicity of discussion we assume that ${\tt t}^*F$ is such that $\operatorname{Re}\, {\Omega}_0+{\tt t}^*F$ remains invertible. First the kernel of ${\Omega}$ defines a distribution $\bar L\subset T_{ \mathbb{C}}X$ which is integrable since ${\Omega}$ is closed. The invertibility of $\operatorname{Re}\, {\Omega}_0+{\tt t}^*F$ ensures that $L\cap \bar L = 0$ and $L\oplus \bar L = T_{ \mathbb{C}}X$. This means that $L$ is spanned by the (1, 0) vector fields in $T_{ \mathbb{C}}X$ but under a different complex structure $J\neq J_0$. The new complex structure can be expressed in the same way as (7)

The source map ${\tt s}$ remains holomorphic $(X, J)\to (M, I_-)$, indeed for any $V\in TX$

where the second term drops thanks to (6). In contrast, for the ${\tt t}$ map we have

where we have used the fact that ${\tt t}$ is a Poisson map sending ${\Omega}_0^{-1}$ to ${\sigma}_- = (I_-Q+iQ)/4$. The last equation says that ${\tt t}_*$ now intertwines $J$ with a certain automorphism $I_+$ of $TM$ with $I_+ = I_–QF = I_-(1+I_-QF)$. This gives (4).

Furthermore, that the lhs of (9) squares to $-1$ gives

which is (5). This also implies $(I_+)^2 = -1$.

The anti-Poisson property of ${\tt s}$, i.e. ${\tt s}_*{\Omega}^{-1} = -{\sigma}_-$ is unaffected. To check that ${\tt t}_*$ sends ${\Omega}^{-1}$ to ${\sigma}_+$, we have

To evaluate the first term we can use a geometric series expansion ^[5] and get

provided $1+I_-QF$ is invertible. So we get

using (4). This shows that ${\tt t}_*$ maps ${\Omega}^{-1}$ to ${\sigma}_+$.

2.2.   Encoding the generalised Kähler potential

The Morita equivalence between ${\sigma}_{\pm}$ encodes the generalised Kähler potential (GKP) as a kind of generating function (see the discussion in Section 4 of ^[3]). Recall that just as the usual Kähler potential is not a globally defined function, the GKP is defined locally, and so the following discussion is local in nature.

From the previous section, one has a holomorphic symplectic form ${\Omega} = {\Omega}_0+{\tt t}^*F$, which can be expressed using local Darboux coordinate as ${\Omega} = i\sum_kdP_k\wedge dQ^k$ where $Q_k, P^k$ are local holomorphic coordinates. The Morita equivalence $(X, {\Omega}, J)$ was constructed out of the symplectic groupoid $(X, {\Omega}_0, J_0)$ integrating ${\sigma}_-$. The space of units is a Lagrangian, denoted $L_0$, with respect to ${\Omega}_0$. Though $L_0$ is no longer Lagrangian under ${\Omega}$, one still has $\operatorname{Im}{\Omega}\big|_{L_0} = 0$ since $F$ is real. Suppose that locally in the $P, Q$ coordinate system $L_0$ is given by $P_k = \eta_k(Q, \bar Q)$ where $\eta = \eta_k dQ^k$ is a 1-form, then one has

This forces $\operatorname{Im} i\eta$ to be a closed 1-form and hence $\operatorname{Re}\, \eta = -d K$ locally for some real function $K(Q, \bar Q)$, as a consequence

The local real function $K$ is the GKP.

As an example, for an actual Kähler manifold $(M, {\omega}, I)$, one has ${\sigma}_{\pm} = 0$ and $I_+ = I_- = I$. Then the Morita equivalence is given simply by the holomorphic cotangent bundle $X = T^{(1, 0)}M$ and ${\Omega}_0$ is the standard holomorphic symplectic form. The maps ${\tt s}$, ${\tt t}$ are the bundle projection $\pi$. The holomorphic symplectic form is then deformed to ${\Omega}_0+\pi^*{\omega}$, for which we can pick the Darboux coordinates as follows. Let $(x^k, \xi_k)$ be the local holomorphic coordinate for $M$ and the fibre coordinate respectively. Let $Q^k = x^k$ and $P_k = \xi_k-2\partial_kK$ with $K$ being the Kähler potential in the usual sense, i.e. $2i\partial\bar\partial K = {\omega}$. We can easily check

Then the zero section $L_0 = M$ is given by the condition $\xi_i = 0$ or $P_i = -2\partial_iK$, which is how the GKP is formulated in the last paragraph.

3.   The Hitchin construction

The pervading theme of the construction of the last section is that one starts from a Kähler manifold with $I_-$ as its complex structure, and one obtains $I_+$ as a deformation of $I_-$. In ^[13] Hitchin used a flow to deform $I_-$ so that for small flow time, one gets a 4D bi-hermitian metric. Note that in this construction the flow time is small but cannot be zero.

3.1.   Overview

Let us give a quick overview of Hitchin's construction, while some proofs are collected in the next section. One starts with the data $(M, I_-, g, {\sigma}_-)$, that is, a Kähler structure on the surface $M$ plus a choice of a holomorphic Poisson tensor ${\sigma}_-$ i.e. any element of $H^0(M, K^{-1})$ with $K$ the canonical bundle. The key observation is that the two holomorphic Poisson structures in (3) encoding the GKS share the same imaginary part $Q$, and so in deforming $I_-$ to reach $I_+$ one has to preserve $Q$. It is thus natural to use a $Q$-Hamiltonian flow $\phi_t$ with $\phi_0 = id$ generated by some Hamiltonian $h$ to deform $I_-$ so that

is the new complex structure. The difficulty is to produce a positive definite bi-hermitian metric.

Hitchin picked the hamiltonian for the flow $h\sim\log ||{\sigma}_-||^2$. Even though $h$ is ill-defined where ${\sigma}_-$ vanishes, the hamiltonian vector field

is globally defined, as demonstrated in ^[13]. This is essentially because $Q$ is zero whenever $h$ diverges, rendering the divergence innocuous. Thus $V$, although not hamiltonian, is Poisson and its flow certainly preserves $Q$.

Take the inverse of ${\sigma}_-$, considered as a meromorphic (2, 0)-form, and denote with ${\omega}_- = \operatorname{Re}\, ({\sigma}_-^{-1})$. It is surely of type (2, 0)+(0, 2) with respect to $I_-$. Also its pull-back ${\omega}_+ = \phi_t^*{\omega}_-$ is by construction of type $(2, 0)+(0, 2)$ with respect to $I_+$. But we consider its (1, 1)-component with respect to $I_-$

This 2-tensor turns out to be well defined (even though ${\omega}_+$ is not), and symmetric (1, 1) with respect to both $I_{\pm}$. But it may not be positive definite. To ensure its positivity, Hitchin studied the first derivative of $g$ with respect to $t$ and showed that

where $\partial$, $\bar\partial$ use the complex structure $I_-$. But the rhs is the curvature of the line bundle $K^{-1}$, thus if the anti-canonical bundle is ample, then the curvature is positive definite. Since positivity is an open condition, for small but nonzero $t$ one has constructed a bi-hermitian metric.

3.2.   Collection of some formulae

For clarity we temporarily denote with $I = I_-$ and $I_t = I_+$. The flow $\phi_t$ is generated by the vector field $V = Q^{\#}dh$, and so $I_t = I_+$ given in (10) can be written as

while $L_VI$ can be written as $L_VI = -Qd(I^*dh)$ which we prove in Lemma 3.1. Comparing with (4) one has

since $Q$ is preserved by $\phi_t$. So we get the formula for $F$

The first time derivative of $F(t)$ is

As for the metric, denote with ${\sigma}_- = {\sigma}$ and ${\sigma}_+ = {\sigma}_t = (\phi_{-t})_*{\sigma}$. Let ${\omega}_+ = {\omega}_t = \operatorname{Re}\, ({\sigma}_t^{-1})$, and set as in (11)

At flow time $t = 0$, ${\omega}_0$ is of type (2, 0)+(0, 2) with respect to $I$ and so $g$ is zero. This is crucial for $g$ to be globally defined for $t > 0$, since the divergence of ${\omega}_t$ resides only in the (2, 0)+(0, 2) component. We observe that

where we used ${\omega}_t = \operatorname{Re}\, ({\sigma}_t^{-1}) = -Q^{-1}I_t$ and that $Q$ is of type $(0, 2)+(2, 0)$ w.r.t. $I$. We see from the last formula that $g_t$ is a symmetric tensor and

c.f. (2). We omit the subscript $t$ in $g$ next. We see a democracy between $I_t$ and $I$, thus if $g$ is (1, 1) under $I$ so will it be under $I_t$. Finally that $g$ is well-defined comes from the relation $I_t-I = -QF$

Taking $t$-derivative at $t = 0$ and using (14), we get the positivity (12).

Lemma 3.1.

Proof. Let $U$ be any (0, 1) vector field we compute $(L_VI)U = [V, IU]-I[V, U] = (-i-I)[V, U]$. To evaluate the rhs we pick a local holomorphic function $f$ so that $df = \partial f$

As $Q^{(2, 0)}$ and $f$ are holomorphic the $U$ derivative passes them by and gives

The case for $U$ being $(1, 0)$ is similar.

4.   Kähler potential under the flow

In this section we combine the two constructions of Section 2 and Section 3.1. Let $(X, {\Omega}_0)$ be holomorphic symplectic groupoid integrating $(M, I_-, {\sigma}_-)$, then the flow $\phi_t$ generated by the vector field $V$ can be lifted up to $\hat\phi_t$ on $X$ generated by

where the minus sign comes from (8) so that $\hat V$ covers $V$. The lifted flow $\hat \phi_t$ satisfies

recall that the symplectic orthogonality (6) ensures that the image of ${\tt s}$ remains fixed, hence the second relation.

We have an expected result

Lemma 4.1. (Proposition 7.2 in ^[3])

Proof. We let ${\Omega}_t = \hat\phi_t^*{\Omega}_0$ be the flow of ${\Omega}_0$, then

One has again the relation $L_{\hat V}J_0 = (\operatorname{Im}{\Omega}_0)^{-1}dJ_0^*{\tt t}^*dh$ (here we understand the 2-form as a map from $T$ to $T^*$ and a bi-vector as a map from $T^*$ to $T$) similar to Lemma 3.1. Thus

where we used (16). Continuing

where $F$ was given in (13).

Next we look for the Darboux coordinates for ${\Omega}_t$. Pictorially the flow looks like Figure 2. If we have found the Darboux coordinates for ${\Omega}_0$

then these will pull back to

and are subsequently the Darboux coordinates of ${\Omega}_t$ since we have shown (17). From this we also see that the new complex structure $J_t$ on $X$ induced from the deformed holomorphic symplectic structure ${\Omega}_t$ is related to $J_0$ by the flow $\hat\phi_t$.

The space of units $L_0$ is flown to $L_t$. Suppose that $L_0$ is described under $Q_t, P_t$ chart as

for some (1, 0)-form $\eta$. Then as discussed earlier

showing that $\operatorname{Im}(i\eta)$ is closed and one has a local real function $K(Q, \bar Q)$ with $i\eta = -2i\partial K$.

There is in general no formula for finding the primitive for $i\eta$, apart from its flow equation.

Lemma 4.2. Assuming that at $t = 0$ the Lagrangian $L_0$ is described by $P = 0$, then $K$ satisfies the flow equation

Proof. Let ${\Omega}_0 = i\sum_kdP_k\wedge dQ^k$ as above and $L_0 = \{P_i = 0\}$. We flow $L_0$ with a Hamiltonian vector field $\hat V = -((\operatorname{Im}{\Omega}_0)^{-1})^{\#}dH$ for some function $H(Q, \bar Q, P, \bar P)$. For small $t$, $L_0$ is described by the graph of a function $K(t, Q_t, \bar Q_t)$: $L_0 = \{P_{t, j} = -2\partial_{Q_t^j}K\}$. Take the $t$-derivative of the equation $P_{t, j} = -2\partial_{Q_t^j}K$ (we temporarily suppress the subscript ${}_t$)

where one can use (8) for the imaginary part of ${\Omega}_0$. Note that the lhs differentiates $H$ first and then sets $P = -2\partial_QK$, so if we combine it with the second and third term on the rhs

Setting $H = {\tt t}^*h$, we get the result.

In the toric case later, we will be able to solve the flow equation for $K$ somewhat more explicitly.

5.   Application for toric Del Pezzo

Hitchin construction applies to Del Pezzo surfaces. Although we will perform the computation on $\mathbb{C}P^2$ certain steps of the construction, for example the description of the symplectic groupoid, are valid more generally for the toric Del Pezzo surfaces. For this reason we recall general facts in this section.

5.1.   Review of some elements of toric surfaces

A good textbook for this is Fulton ^[8], and we shall also make use of the explicit parametrisation of toric manifolds due to Guillemin ^[11].

Our focus of the toric geometry is more on its Kähler aspect, and so it is more appropriate to use the moment map polytope description (the fan description is more adapted for the algebraic aspect).

Definition 5.1. A polytope $\Delta\subset \mathbb{R}^d$ is the convex hull of a finite number of points in $\mathbb{R}^d$, called the vertices. A polytope $\Delta\subset \mathbb{R}^d$ is said to be Delzant if for each vertex $p$ one has

1. there are exactly $d$ edges meeting at $p$;

2. each edge meeting in $p$ is of the form $p+ t u$ with $u\in \mathbb{Z}^d$ and $t\geq 0$ (rationality);

3. the $d$ edges meeting in $p$ form a $\mathbb{Z}$-basis for $\mathbb{Z}^d$. (smoothness)

Theorem 5.2. (Delzant ^[6]) There is a 1-1 correspondence between symplectic toric manifolds (up to $\mathbb{T}^d$ equivariant symplectomorphisms) and Delzant polytopes.

Given a toric symplectic manifold $M$, the image of the moment map for the torus action is a polytope and it is Delzant. While from a Delzant polytope, one can construct a toric symplectic manifold $M_{{\Delta}}$ through symplectic reduction or symplectic cut ^[16], the Delzant condition ensures the smoothness. It is useful to keep in mind the gist of the construction: one can visualise $M_{{\Delta}}$ as a $\mathbb{T}^d$ fibration over the interior of ${\Delta}$, however on a face ${\Delta}_a$ with normal $\vec v^{\, a}$ the torus action

degenerates. Here we use $\phi_i$ to denote the $d$ angle-coordinates of $\mathbb{T}^d$. Condition 3 above says that, each vertex has a neighbourhood of type $\mathbb{C}^d$, and up to an $SL(d, \mathbb{Z})$ the $\phi_i$ are the standard angle coordinates of $\mathbb{C}^d$.

For the remainder of the paper, we let $d = 2$ and all polygons are assumed Delzant. We denote the primitive normal to face ${\Delta}_a$ as $\vec v^{\, a}$. In fact, each face corresponds to an embedded $\mathbb{C}P^1$ in $M_{{\Delta}}$. It is a toric invariant divisor, and all toric invariant divisors are generated (not freely) by the faces. Suppose that the polygon is described by

where $\vec y$ are the coordinates of $\mathbb{R}^2$. Then from ^[11] the Kähler class is expressed as

Since the divisors $[a]$ are not independent and have $n$ relations among them, this expansion is not unique.

Definition 5.3. A smooth surface $M$ is called Del Pezzo if it is birational to $\mathbb{C}P^2$ and the anti-canonical class is ample. The self intersection $d = K\cdotp K$ is called the degree of the Del Pezzo, here $K$ is the canonical divisor.

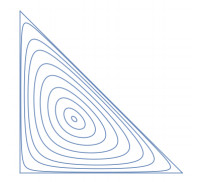
Except for $\mathbb{C}P^1\times \mathbb{C}P^1$, the other Del Pezzo's are obtained from blowing up up to 8 points in general position. But we are interested in toric Del Pezzo's, so one can only blow up toric fixed points on $\mathbb{C}P^2$. The polygon corresponding to $\mathbb{C}P^2$ is a triangle, see Figure 5.1. There are only three toric invariant points located at the three corners of the triangle. We are left with the following polygons

5.2.   Action angle coordinates and complex coordinates

Let $\vec y = (y^1, y^2)$ parametrise ${\Delta}\subset \mathbb{R}^2$, and let ${\theta}_1, {\theta}_2$ be the angle coordinates of $\mathbb{T}^2$. We have

Proposition 5.4. (Guillemin ^[11]) Let $M_{{\Delta}}$ be the toric symplectic manifold corresponding to ${\Delta}$, with normals $\vec v^{\, a}$. The symplectic form of $M_{{\Delta}}$ reads

Further the complex structure and metric read

where

and $G_{ij}\, G^{jk} = \delta_{ik}$. The complex coordinates can be expressed as

Recall from the discussion below Theorem 5.2 that each corner of the polygon corresponds to a $\mathbb{C}^2$ patch, covering the whole $M$.

At a corner with normals $\vec u^1, \vec u^2$, one can take combination of (21) to give local complex coordinates for the $\mathbb{C}^2$ patch

For later use we record how the complex coordinates change from one local patch to another.

Lemma 5.5. Suppose at the two corners of ${\Delta}$ with normals $\vec u^a$ and $\vec v^{\, a}$ respectively, one has complex coordinates $\{z_a, \, a = 1, 2\}$ and $\{\tilde z_a, \, a = 1, 2\}$ defined as in (22) using $\{\vec u^a\}$ and $\{\vec v^{\, a}\}$ respectively, then over the open intersection where both coordinate systems are valid, one has the transformation

The proof is a direct calculation. Of course in the derivation, we used $\vec u^1\times \vec u^2 = 1 = \vec v^1\times \vec v^2$ since ${\Delta}$ is Delzant.

5.3.   Toric invariant holomorphic Poisson tensor

A consequence of (23) is

Lemma 5.6. The unique (up to a constant multiple) toric invariant holomorphic Poisson tensor on a toric surface has local expression

This expression is defined on the $\mathbb{C}^2$ patch corresponding to a corner of ${\Delta}$ with normals $\vec u^1, \vec u^2$, but is in fact globally defined.

Proof. We need only check that if one makes a coordinate transform as in (23), the local expression of ${\sigma}$ remains unchanged, but this follows from $\det A = 1$.

A straightforward calculation gives

Lemma 5.7. When written in the action-angle coordinates, the holomorphic Poisson tensor ${\sigma}$ reads

Its norm computed with the metric (20) is

The determinant $\det(G_{ij})$ can be evaluated as

The concrete expression for $\mathbb{C}P^2$ is given in Section 6.

5.4.   The symplectic groupoid

According to the recipe for constructing the Morita equivalence (see Section 2.1), we need to find $(X, {\Omega}_0)$ integrating ${\sigma}$ which is given in (24). One can use the general construction given in ^[25] for Poisson structures twisted by a solution of the classical Yang–Baxter equation. For the case we are interested in there is an easy description that we discuss in this section. We start from an example on $\mathbb{C}^2$.

Example 5.8. (See Theorem 3.7 of ^[17]) On $\mathbb{C}^2$ with complex coordinates $x, y$, we have a holomorphic Poisson tensor

The pervading trick in finding the integrating object is to notice that $\pi$ is non-degenerate except when $xy = 0$. This means that $(X, {\Omega})$ would look like a pair groupoid $X\sim U\times U$ in an open dense $U = \{xy\neq 0\} = (\mathbb{C}^*)^2$, with

where $x, y$ are the source coordinates and $\hat x, \hat y$ those of the target.

To extend from $U$ to the whole of $\mathbb{C}^2$, we change coordinates to $(x, y, u, v)$ with $(x, y)\in U$ and $(u, v)\in \mathbb{C}^2$. They are related to the old ones as

This trade is meant to reflect the fact that if $xy = 0$ then $\hat x = x, \hat y = y$ necessarily and $u, v, x, y$ are a more fundamental set of coordinates.^† Rewriting ${\Omega}^{-1}$ in the $(x, y, u, v)$ coordinates

^†Note that $u, v$ in (28) are fixed by $(x, \hat x, y, \hat y)$ up to a $\mathbb{Z}\times \mathbb{Z}$ worth of shifts due to the exponential. So one should really call the symplectic groupoid at this stage the path groupoid, with $\mathbb{Z}\times \mathbb{Z}$ reflecting the fundamental group of $\mathbb{C}^*\times \mathbb{C}^*$. We thank the referee for pointing this out to us.

This is invertible, in fact $\det{\Omega} = 1$ everywhere. Its inverse is

The next step is to globalise this construction by regarding $u, v$ as the fibre coordinates of some vector bundle to take into account the non-trivial coordinate change.

Theorem 5.9. Let $M$ be a smooth toric surface associated with a Delzant polygon ${\Delta}$. The holomorphic Poisson structure ${\sigma}$ (24) can be integrated into a symplectic groupoid $(X, {\Omega}_0)$. The space $X$ is diffeomorphic to the holomorphic cotangent bundle of $M$. If $(z^a, \xi_a)$ are the local base and fibre coordinates, then ${\Omega}_0$ reads

Its inverse $\Pi = {\Omega}_0^{-1}$ reads

Let $g = (z^1, z^2;\xi_1, \xi_2)$ be a point in $X$, the source, target maps read

Let $h = (z^1e^{\xi_2z^2}, z^2e^{-\xi_1z^1};\eta_1, \eta_2)$ be another point with ${\tt s}(h) = {\tt t}(g)$ then

Proof. We only need to prove that the local model ex.5.8 globalises under the coordinate change rule Lemma 5.5. If $z^a\to\tilde z^a$ as in (23), then as fibre coordinates of $T^*M$

This means the combination $z^a\xi_a$ (no sum) transforms linearly

Note that $A_{ab}$ is an $SL(2, \mathbb{Z})$ matrix, but recall that for all $SL(2, \mathbb{C})$ matrices $A$ one has

This shows that

transform the same way as $\log z^a$, thus the target $(z^1e^{\xi_2z^2}, z^2e^{-\xi_1 z^1})$ transform the same way as $(z^1, z^2)$. This shows that the ${\tt t}$ map is globally defined.

Using the coordinate transform for $T^* \mathbb{C}^2$ it is straightforward, though tedious, to check that ${\Omega}_0$ is globally well-defined.

Lemma 5.10. The Darboux coordinates for the holomorphic symplectic form (30) are

Under these coordinates, the source, target maps are

The proof is a direct computation.

Remark 5.11. From the Darboux coordinates it is easy to check

which leads to (6).

Lemma 5.10 also gives a simpler check that the symplectic form (30) is well-defined globally. Using the same argument as above, the $q^a, p_b$ transform as

Therefore using $\log q^a$ and $p_aq^a$ as coordinates, it is clear

6.   GKS on $\mathbb{CP}^2$

We put together the ingredients of previous sections and construct a GKS in explicit terms expressed with action-angle coordinates. The polygon is a triangle with normals $\vec v^1 = [1;0]$, $\vec v^2 = [0;1]$ and $\vec v^3 = [-1;-1]$. We fix the Kähler class by fixing ${\lambda}^1 = 0 = {\lambda}^2$ and ${\lambda}^3 = 1$ so that $[{\omega}] = [3]$.

From the general formula Proposition 5.4, we have

where we have let $y^3 = 1-y^1-y^2$ which turns out quite convenient later on. Now

from (26). This is completely expected since ${\sigma}$ vanishes on a cubic curve, which in the toric invariant case is the product of three lines, corresponding to each of the three faces ${\Delta}_a = \{y^a = 0\}$, $a = 1, 2, 3$.

The complex coordinates (21) are

they are in fact the standard inhomogeneous coordinates for $\mathbb{C}P^2$.

The Hitchin Poisson tensor is the imaginary part of ${\sigma}$

6.1.   Solving the flow

We pick the Hamiltonian $h$ as

The pre-factor is for convenience and can always be absorbed by redefining $t$. This gives a vector field

and so the flow equation reads

It pays to keep the symmetry between $y^1, y^2, y^3$ and so we define the symmetric polynomials

It is obvious that $c_3$ is a conserved quantity under the flow since $h\sim\log c_3$.

Proposition 6.1. The flow equation (34) is solved by

with $\wp$ the Weierstrass elliptic function with ${\omega}_{1}\in \mathbb R$ and ${\omega}_{2}\in i\, \mathbb R$ as the $\textrm{half}$ periods of a square lattice in $\mathbb C$ (Figure 3) while ${t_{\infty}} = (2/3){\omega}_1$.

Finally $t$ has constant imaginary part $-i{\omega}_2$ and arbitrary real part^‡.

^‡We made this awkward choice to avoid clutter in later formulae. A more pedantic way would be to write $t$ as $t+{\omega}_2$ for real $t$. But as far as the flow is concerned one only cares about shifts of $t$, which is still real.

Proof. We can solve from $y^2+y^3 = 1-y^1$, $y^2y^3 = c_3/y^1$ that

and hence

The rhs is a quartic polynomial with a root at $y^1 = 0$, which hints at changing variables $y^1 = 1/u$ so one can turn the quartic into a cubic

Further letting $\wp = 1/12-c_3u$ gives

The solution is the celebrated Weierstrass $\wp$ function. It is a doubly periodic meromorphic function with period lattice $2\Lambda$ generated by $2{\omega}_1, 2{\omega}_2\in \mathbb{C}$. It is a convention that the lattice is $2\Lambda$ while ${\omega}_1, {\omega}_2$ are the half periods. We compute the modular invariant (46) (see the appendix), which shows that the lattice is a square lattice and ${\omega}_1$ is real while ${\omega}_2$ is purely imaginary. For such a lattice, the real loci are the lattice lines of $\Lambda$. We have the solution

where $t_i$ is real and fixed using the initial data. In order that $y^i$ be real, the $t$ must have imaginary part equal to 0 or ${\omega}_2$. It cannot be the former option, since then $t+t_i$ can reach the point ${t_{\infty}}$ where $\wp({t_{\infty}}) = 1/12$ (see Lemma A.2) and $y^i$ is unbounded. For the latter option, the solution is bounded and periodic with period $2{\omega}_1$. Indeed starting from $0^+$ (where $\wp = +\infty$) going along straight lines via ${\omega}_1$, ${\omega}_1+{\omega}_2$, ${\omega}_2$ and reaching $i0^+$ (where $\wp = -\infty$), the function $\wp$ is monotonically decreasing. As $1/12$ is reached at $(2/3){\omega}_1$, one has $\wp < 1/12$ along $z = {\omega}_2$. This is reviewed in Section A.1.

To fix the initial values $t_i$, we can analytically continue the solution down to the real axis and then approach $t+t_3 = {t_{\infty}}$ from the right, where $y^3\to\infty$. But the conditions $\sum y^i = 1$, $\prod y^i = c_3$ forces one of $y^1, y^2$ to go to $0^-$ and $-\infty$ respectively. We pick the option $y^1\to-\infty$ and $y^2\to 0^-$ first. In order for this to happen one has to have

Indeed, this way $t+t_1$ approaches $-{t_{\infty}}$ from the right giving $y^1\to-\infty$, and $t+t_2$ approaches $0$ from the right giving $y^2\to 0^-$.

The other option would simply swap $t_1$ and $t_2$, to show that this is not the case, we look at Figure 4. The figure shows the contour of fixed $c_3$, and the flow goes clockwise along this contour, as can be seen from (34). The three red lines cut the triangle into six regions depending on the relative sizes of $y^i$. With the first option, pick, say, $t_3 = 0$, i.e. one starts the flow at $y^1 = y^2 > y^3$ (the red dot). Increasing $t$, one has $y^3, y^1$ increase while $y^2$ decreases until one reaches $t = {\omega}_2+{t_{\infty}}/2$, where $y^1 > y^3 = y^2$. This means one moves down into the east triangle and reaches the boundary with the southeast triangle at $t = {\omega}_2+{t_{\infty}}/2$. However, had one picked the other option, one would swap $y^1, y^2$ and one would be moving up into the north east triangle. This does not agree with the direction of the flow.

Remark 6.2. It is instructive to see that the solution satisfies $\prod y^i = c_3$. Indeed, the product

is doubly periodic without poles or zeros: for example, the first factor has a double pole at $z = 0$, but the other two both have a single zero at $z = 0$. Thus the product must be a constant, which can be obtained by setting $z$ at a convenient point. We choose $z = w_1$ and in Lemma A.4 we show that the constant is $c_3^2$.

The solution involves the inversion of $\wp$ function, we would like to avoid that by expressing elliptic functions with Weierstrass zeta functions. These are recalled briefly in the appendix.

Lemma 6.3. One can express $y^i$ as Weierstrass zeta functions (where ${t_{\infty}} = 2/3\, {\omega}_1$)

Proof. We use the inversion formula (48.2 ^[7])

This is a special case of a broader formula that expresses any elliptic function using the Weierstrass $\zeta$ function, see Theorem 6.2 ^[7]. We show in Lemma A.2 that $\wp({t_{\infty}}) = 1/12$, and $\wp'({t_{\infty}}) = -c_3$, the result for $y^3$ follows. For $y^1$, one would get from the same formula that $y^1(t) = \zeta(t)-\zeta(t+2{t_{\infty}})+2\zeta({t_{\infty}})$. Then one uses the periodicity $\zeta(z+2{\omega}_i) = \zeta(z)+2\eta_i$ and also $\zeta({t_{\infty}}) = 1/6+2/3\, \eta_1$ from Lemma A.5.

6.2.   The generalised Kähler potential

Proposition 6.4. The GKP reads

where $y^i(z)$ is given in (35) and we write $y^i_0 = y^i(t_0)$, $y^i_t = y^i(t+t_0)$.

Recall from Proposition 6.1 that for fixed $c_3$, the value of $t$ fixes the $y^i$'s. Here $t_0$ is chosen to correspond to the initial values of $y^i$ in the flow through (35).

Proof. ^§ In the proof, we exploit the fact that in an open dense subset, we can use the source and target coordinates $z, \hat z$ to parametrise $X$, making the flow easier to write down. With these coordinates, the space of units is $L_0 = \{z = \hat z\}$. The Darboux coordinates $Q, P$ for ${\Omega}_0$ are related to $z, \hat z$ as

^§ We thank the referee for the suggestion about summarising the relations between the various coordinates that improved the readability of the proof.

as can be read from Lemma 5.10.

Referring to Figure 2, under the flow $\hat\phi_t$, the $Q, P$ coordinates pullback to $Q_t, P_t$, the Darboux coordinates for ${\Omega}_t$. As the flow is generated by the function ${\tt t}^*h$, only $\hat z$ will experience this flow: $(z, \hat z)\rightsquigarrow(z, \hat z_t)$. The coordinates $Q_t, P_t$ are related to $z, \hat z_t$ in the same way as (38), only with the addition of a subscript ${}_t$. Also $L_0$ is described in the $z, \hat z_t$ coordinates by setting $\hat z_t = z_t$, where $z_t$ is the flow of $z$ under $\phi_t$ generated by $h$.

Now to the GKP, ${\Omega}_t$ is written as

We know that $\operatorname{Re}\, \eta_t$ is closed when restricted to $L_0$. The goal is to find its local primitive. As laid out above, to do this efficiently, we use the source and target coordinates $z$ and $\hat z_t$ to parametrise $X$

where $[a\cdots b]$ means anti-symmetrisation of indices $a, b$.

The second term in $\eta_t$ is already exact, we focus on the first term and its real part

Now restrict $\operatorname{Re}\, \eta_t$ to $L_0$ by setting $\hat z_t = z_t$, and keeping in mind that $z_t$ and $z$ have the same phase as can be seen from the flow equation (34) and (32)

We focus on finding the primitive of the first term. We denote by

and the first term on the rhs of (39) is just $\phi_t^*\xi-\xi$. We have

We can evaluate explicitly

In the computation we have used

where $\circ$ denotes the action of a vector field on a function by derivation. Altogether

recall that the product $y^1y^2y^3$ is a conserved quantity under the flow.

The second term of (39) is already exact, but we can write it also as an integral. Let

Now use the same trick by differentiating and integrating

Putting everything together

Remembering the convention that $\operatorname{Re}\, \eta_t|_{L_0} = -dK$, we get the GKP (37). Note the leading term of (37) agrees with Lemma 4.2.

Remark 6.5. First, the generalised Kähler potential is not a global function, indeed our expression (37) is ill-defined whenever $y^i = 0$. However the ill-defined term resides only in the leading term which is proportional to the Kähler potential of the Fubini-Study metric. The correction term can be extended to $y^i = 0$ because the log always contains the combination $y^i_t/y^i_0$.

Second, just knowing the GKP is not enough, one needs to know the local complex coordinates $Q_t, \bar Q_t$ on $L_t$. Again in the complement of the anti-canonical divisor where ${\sigma}$ vanishes, we have

These can be read off from the relation between $z, \hat z$ and $Q$ in (38) and how $z$ is related with $y$-coordinates given in (32). Note when $t = 0$, they revert back to the standard complex coordinates.

Lastly, unfortunately we did not manage to perform the integral in the GKP. A possible strategy is to relate ${\sigma}$ to the theta functions as in (54) and use the infinite product formula for the latter to deal with the logarithm.

6.3.   Explicit complex structures

Our flow $\phi_t$ is solved by elliptic functions, so to compute e.g. the pullback map $\phi_t^*$, one needs to differentiate $\phi_t$ with respect to the initial points $y^{1, 2}_0$, where the notation is as in Proposition 6.4. These initial values determine $c_3$ and so affect the flow in two ways

1. through $c_3$ dependence of the shift ${t_{\infty}} = 2/3{\omega}_1$ given in (56)

2. through the dependence of $\wp, \zeta, {\sigma}$ on $c_3$ (via $g_2$ and $g_3$ as in (45)) given in (55).

To compute these derivatives, it is beneficial to preserve the symmetry between $y^{1, 2, 3}$. So we opt to use the coordinates $c_3$ and the $t$ to parametrise the triangle base of $\mathbb{C}P^2$, see Figure 4, where $c_3$ determines the contours and $t$ parametrises each contour. However, the $t$-variable has a $c_3$-dependent period $2{\omega}_1$, so we re-scale $t$ in order that all the contours be of period $2\pi$

This has a small price since $s$ is not a good variable when $c_3 = 0$ or $1/27$ where the ${\omega}_1$ or ${\omega}_2$ goes to infinity. To summarise, the $c_3$ and $s$ coordinates are the 'polar' coordinates of the triangle, with $c_3\in[0, 1/27]$ being the radius while $s\in[0, 2\pi]$ being the angle coordinate.

The initial values $y^1_0, y^2_0$ of the flow will be expressed in terms of the new coordinates $c_3, s_0$. We compute the following partial derivatives in the appendix (see Lemma A.10)

where the index $i$ is taken mod 3 and the function ${\varsigma}(z)$ is defined as

It is real of period $2\pi$ for real $z$. See Definition A.7 for further properties of this function. With these we have

Proposition 6.6. In the $c_3, s$ coordinate system, the Hitchin Poisson structure (33) reads

The standard complex structure reads

where $y^k(s)$ read

Proof. The first statement is trivial, since $h = -1/4\log c_3$ is the hamiltonian that generates the flow $\partial_t$. Nonetheless, we can calculate it explicitly. The angular part of $Q$ is not affected, while the radial part is

and the Jacobian can be computed using the explicit expressions $\partial_{c_3}y^i(s)$ given above. It turns out that the Jacobian equals

which reflects the fact that when ${\omega}_1 = 0$ (which happens when $c_3 = 1/27$, the contour in Figure 4 is the centre point), the $s$-coordinate is not defined, indeed the $s$ variable is like the angle coordinate of the contours in the triangle.

For the complex structure, since we have

We only need to focus on the first term, since the second is the inverse of the first. Evaluating the derivatives we get

while

The components $\langle ds, J\partial_{{\theta}_i} \rangle$ and $\langle dc_3, J\partial_{{\theta}_i} \rangle$ are fixed by demanding $J^2 = -1$, giving

Remark 6.7. With the explicit Poisson vector field $Q$ given above, the flow $\phi_t$ is simply

It is also crucial to remember that the flow time is measured in $t$, not in $s$. Even though $s$ and $t$ differ only by a factor of ${\omega}_1$, the half period depends on $c_3$ in a quite complicated way (56). As a concrete instance where this can cause confusion we state the next corollary.

Corollary 6.8. The two complex structures of the generalised Kähler structure of $\mathbb{C}P^2$ are explicitly given by $I_-(c_3, s) = J(c_3, s)$ and

where ${\Delta} t$ is the flow time and $J(c_3, s)$ is given in the proposition above. The terms proportional to ${\Delta} t$ above comes from the $c_3$-derivative of $s+\pi{\Delta} t/{\omega}_1$.

Next let us investigate the 2-form $F$ more closely.

Proposition 6.9. For fixed flow time ${\Delta} t$, the 2-form $F$ in (4) reads

with $I_{\pm}$ given in the last corollary.

This result provides an explicit check for (4).

Proof. Fixing ${\Delta} t$ we have from (13)

where the factor 3 is expected since $dd^ch$ is proportional to the curvature of the canonical class which is $3$ times the Kähler class. The integral

can be worked out using Lemma 6.3 and the fact that the integral of $\zeta$ is $\log{\sigma}$, see (52).

And so $F$ is simply

It is straightforward to compute $dY^i$ i.e. $\partial_{c_3}Y^i, \, \partial_sY^i$, though rather tedious. So we record only one intermediate step

where $\tilde \eta_i = \eta_i+{\omega}_i(1/12-3c_3)$ and we have discarded any $s$-independent term.

The reason we can disregard such terms is that to get $\partial_{c_3}Y^i$ we need only take the difference of the above expression at $s+\pi{\Delta} t/{\omega}_1$ and at $s$, so the $s$-independent terms drop. However we must not forget the $c_3$-dependence in the shift $\pi{\Delta} t/{\omega}_1$, which produces $3y^i{\Delta} t\tilde\eta_1/(c_3(1-27c_3){\omega}_1)$. This is another instance where the remark 6.7 is important.

where we have used cor.6.8. The $s$-derivatives are much easier

Now the assembling is straightforward

A.   Some facts of the elliptic functions

Our primary source of reference is the book ^[7].

A.1.   The Weierstrass $\wp$ function

Given a lattice $\Lambda = \operatorname{span}_{ \mathbb{Z}} \langle{\omega}_1, {\omega}_2 \rangle$, the function $\wp(z)$ is double periodic with period $2\Lambda$. It can be expressed as a sum

where ${\Sigma}'$ means excluding the origin in the sum. The series is absolutely and uniformly convergent, once this is secured the double periodicity is immediate since one can shift the summation.

The function $\wp$ satisfies the well-known differential equation

This function is even with a double pole with zero residue at $u = 0+2\Lambda$. This fact plus Liouville's theorem show that the equation $\wp(u) = c$ has two roots (in one fundamental region). In particular, the three half periods ${\omega}_1, {\omega}_2, {\omega}_3 = {\omega}_1+{\omega}_2$ are the only points mod $2\Lambda$ where $\wp' = 0$, if we denote

then the equation $\wp(u)-e_i = 0$ has a double root at $u = {\omega}_i$.

From (36), the value of $g_2, g_3$ corresponding to our lattice is

The discriminant of the cubic $4x^3-g_2x-g_3$ is

One can compute the modular invariant

with the lowest value assumed at $c_3 = (1/12 - \sqrt3/36)$.

If the $j$-invariant is between $(1, \infty)$, then the modular parameter $\tau$ corresponds to a square lattice (see Figure 5), which turns degenerate when $j(\tau)\to+\infty$. For us this happens at $c_3 = 0$ or $c_3 = 1/27$, i.e. either $y^i = 0$ (at the $i^{th}$ face of the polygon) or $y^{1, 2, 3} = 1/3$ at the very centre.

We assume from now on a square lattice ${\omega}_1\in \mathbb{R}_{ > 0}$ and ${\omega}_2\in i \mathbb{R}_{ > 0}$. In such case the real locus of $\wp$ is along the lines $\operatorname{Re}\, z = 0, {\omega}_1$ or $\operatorname{Im} z = 0, -i{\omega}_2$ mod $2\Lambda$, which is easy to see from the summation (42).

Lemma A.1. (Section 19 ^[7]) Along the segment $[0, {\omega}_1]$ along the real axis, the function $\wp$ goes from $+\infty$ to $e_1$ monotonically, while along the segment $[0, {\omega}_2]$ along the imaginary axis, the function $\wp$ goes from $-\infty$ to $e_2$ monotonically. Further

Proof. As $\wp' = 0$ only at ${\omega}_1, {\omega}_2, {\omega}_3 = {\omega}_1+{\omega}_2$ mod $2\Lambda$, the monotonicity will be clear once we figure out the relative sizes of $e_{1, 2, 3}$.

From the pole $u^{-2}$ in (42), one knows that going from $0$ to ${\omega}_1$ along the $x$-axis $\wp$ decreases from $+\infty$ to $e_1$. Similarly going from 0 to ${\omega}_2$ along the $y$-axis $\wp$ increases from $-\infty$ to $e_2$.

Suppose $e_2 > e_1$, then there is a value $c\in[e_1, e_2]$ where $\wp(u) = c$ has one root $u_1\in[0, {\omega}_1]$ and another $u_2\in[0, {\omega}_2]$. These are the only solutions. But $u_1+u_2$ should be $0\mod(2\Lambda)$ by Theorem 1.5 ^[7], but this is impossible since $u_1$ is real and $u_2$ is imaginary. Thus $e_1 > e_2$.

By considering a path from ${\omega}_1$ to ${\omega}_3$ then to ${\omega}_2$, if, say, $e_3 > e_1 > e_2$, then again there is $c\in[e_1, e_3]$ and (only) two roots to $\wp = c$ one in $[{\omega}_1, {\omega}_3]$, and another in $[{\omega}_2, {\omega}_3]$. This is again impossible using the same argument.

We will need the value of $\wp$ at tertiary periods.

Lemma A.2.

Proof. The four values

are the four roots of

For the proof see 15.1 ^[7]. This is true for arbitrary $g_2, g_3$, but if we plug in the concrete expression (45), one gets

Thus one of $\wp(2/3{\omega}_i)$ must be the root $1/12$. But $\wp(2/3{\omega}_i)$ is not real for $i = 3, 4$, so we have either $\wp(2/3{\omega}_1) = 1/12$ with $1/12 > e_1 > e_3 > e_2$, or $\wp(2/3{\omega}_2) = 1/12$ with $e_1 > e_3 > e_2 > 1/12$. But the last case would force $e_1+e_2+e_3 > 1/4$, but the sum should be zero. So we have $\wp(2/3{\omega}_1) = 1/12$. Note the case $e_1 > 1/12 > e_2$ is impossible, since this would mean that $\wp = 1/12$ must have a two roots $[{\omega}_2, {\omega}_2+2{\omega}_1]$ or $[{\omega}_1, {\omega}_1+2{\omega}_2]$, but $2/3{\omega}_{1, 2}$ are not in these segments.

As for the statement about the derivative, we use (43) to get $\wp'(2{\omega}_1/3))^2 = c_3^2$. We need to take the minus sign from Lemma A.1.

Lemma A.3. Letting ${t_{\infty}} = 2{\omega}_1/3$, we have

Proof. Apply the addition formula to ${t_{\infty}}+(-{\omega}_1)$

As everything on the rhs is known, we get

To simplify (48), we note that $g_{2, 3}$ are real, the $e_i$'s are algebraic over $\mathbb{R}$. By some elementary field theory, for any polynomial $f(e_i)$, one can express $1/f(e_i)$ as a polynomial of $e_i$. For example

Applying this to (48) we get

As for the derivative, one can use directly (34), (35). Since $\wp({t_{\infty}}/2) = 1/12-c_3/y^1(-{t_{\infty}}/2)$ and so $\wp'({t_{\infty}}/2) = c_3(y^2-y^3)/y^1\big|_{t = -{t_{\infty}}/2}$. But at $-{t_{\infty}}/2$, one has $y^1 = y^3$ and $y^2 = 1-2y^1$

The calculation for $\wp({\omega}_2+{t_{\infty}})$ unfolds by using the addition formula on ${\omega}_2+{t_{\infty}}$, while for $\wp'({\omega}_2+{t_{\infty}})$ we have $\wp'({\omega}_2+{t_{\infty}}) = c_3(y^2-y^3)/y^1\big|_{t = {\omega}_2}$. At ${\omega}_2$, one has $y^1 = y^2$ and $y^3 = 1-2y^1$

Lemma A.4. Assuming (45), then

Proof. This follows from the explicit values of $\wp({t_{\infty}}/2)$ from Lemma A.3 and a direct calculation.

A.2.   The Weierstrass $\zeta$ function

The $\zeta$ function is defined as

This definition is independent of the choice of the integral path, since $\wp$ has only double pole with zero residue at $z = 0\mod2\Lambda$.

Unlike $\wp$, the function $\zeta$ is an odd function, and it is not periodic. One has instead (see Theorem 6.1 ^[7])

Lemma A.5. We have the value of $\zeta$ at some special points

where $\eta_{1, 2} = \zeta({\omega}_{1, 2})$.

Proof. To compute $\zeta({t_{\infty}})$, we use the duplication formula

where we computed $\wp''$ by differentiating $(\wp')^2 = 4\wp^3-g_2\wp-g_3$:

But since $2{t_{\infty}} = 2{\omega}_1-{t_{\infty}}$, one gets $\zeta(2{t_{\infty}}) = 2\eta_1+\zeta(-{t_{\infty}}) = 2\eta_1-\zeta({t_{\infty}})$ as $\zeta$ is odd. Thus $(2\eta_1-\zeta({t_{\infty}}))-2\zeta({t_{\infty}}) = -1/2$.

For the last statement, use again the addition formula

Definition A.6. (54.1 ^[7]) Define a new function

This is odd and periodic along the real axis.

Definition A.7. The function

is real of period $2\pi$ for real $z$. It satisfies the shift relations

Proof. For the reality of $\varsigma$ at real $z$, we note that $\eta_1$ is real and so we need only check the reality for the first two terms in the expression of $\varsigma(z)$, which can be computed from the addition formula

The lhs and the first term on the rhs of (51) are real for real $z$, showing that the remainder of the rhs are also real for real $z$, as desired.

The periodicity follows from that of $\zeta^*$ defined earlier. For the shift relations, we only show one of them,

A.3.   The Weierstrass ${\sigma}$ function and theta function

Since $\zeta$ has a simple pole at $0\mod 2\Lambda$, if one integrates $\zeta$, one gets a branching behaviour similar to that of a log. Indeed $\int\zeta$ is the logarithm of an analytic function

It follows trivially that

Clearly ${\sigma}$ is not periodic

In fact, from this non-periodicity, one can relate ${\sigma}$ function to the more familiar theta functions according to 18.10.8 ^[2]

The ${\vartheta}_1$ function is the solution to the heat equation with $\tau$ serving as the time, and so one has the important property

which helps us to compute the derivation of ${\sigma}$ function with respect to the modular parameter $\tau$, and also $g_2, g_3$.

A.4.   Derivation with respect to $g_{2, 3}$

From the relation between ${\sigma}$ and ${\vartheta}_1$ plus the heat equation satisfied by ${\vartheta}_1$, one can derive

Lemma A.8. (18.6.23-18.6.24 ^[2]) The derivative of ${\sigma}$ with respect to $g_{2, 3}$ reads

The same expression for $\wp, \zeta$ can be obtained by taking derivatives and using (49) and (52).

In our situation $g_{2, 3}$ depend only on $c_3$, and $\partial_{c_3} = (-2\partial_{g_2}+(1/6-2c_3)\partial_{g_3})$. We record for the readers convenience

where $\gamma = g_2^3-27g_3^2 = c_3^3(1-27c_3)$.

Lemma A.9. We have

Note the matrix above is traceless and so it will preserve the condition (50).

Proof. For ${\omega}_1$, since ${t_{\infty}} = 2/3{\omega}_1$, we can differentiate $\wp({t_{\infty}}) = 1/12$ and get $\partial_{c_3}\wp|_{t = {t_{\infty}}}+\wp'({t_{\infty}})\partial_{c_3}{t_{\infty}} = 0$, then we get from (55)

and we get the result.

For $\eta_1$, one can differentiate $\zeta({t_{\infty}}) = 1/6+2/3\eta_1$, while for ${\omega}_2$ and $\eta$ one differentiates $\wp({\omega}_2) = e_2$ and the second equation of Lemma A.5.

One can define the combination

then (56) reads

In particular ${\omega}_1$ satisfies $\partial_{c_3}(c_3(1-27c_3)\partial_{c_3}{\omega}_1) = 6{\omega}_1$ and the solution is given by the hyper-geometric functions

We will not dig further into the hyper-geometric functions here, but the solution to (56) bears heavy resemblance to the torus fibration picture of the Seiberg-Witten solution to the $N = 2$ super-symmetric gauge theory ^[21] in that (50) works as the Dirac quantisation condition for the electric and magnetic charge and both quantities are solved by the hyper-geometric functions. We list however the values of $\tilde \eta_{1, 2}$ and ${\omega}_{1, 2}$ at $c_3 = 0, 1/27$ for completeness

If we write $c_3 = \epsilon$ then ${\omega}_1\sim \epsilon^{-1/2}$ in the first line, or if we write $1/27-c_3 = \epsilon$ then ${\omega}_2\sim i\epsilon^{-1/4}$ for the second line.

Finally we compute the $c_3$ derivative of the functions $y^i$. We have demonstrated in the main text that, in order to exploit the symmetry between $y^i$, we should use the $c_3$ and $t$ coordinate to parametrise the contour in Figure 4. In particular we introduce the time coordinate $s$

so that $s\in \mathbb{R}$ and is of period $2\pi$ regardless of $c_3$.

Lemma A.10. Holding $s$ in (61) fixed, and differentiate with respect to $c_3$

where the index $i$ is taken mod 3 and ${\varsigma}(s)$ is given in Definition A.7.

By using the shift relation in Definition A.7, one can check that $\partial_{c_3}(y^1+y^2+y^3) = 0$ and $\partial_{c_3}(y^1y^2y^3) = 1$.

Proof. We hold $s$ fixed when taking the partial derivative with respect to $c_3$.

One plugs in (55) for $\partial_{c_3}\wp$ and (56) for $\partial_{c_3}{\omega}_i$,

We replace the last term with the function ${\varsigma}$ given in Definition A.7. The computation for $y^{1, 2}$ are similar since they are obtained from $y^3$ by shifting $s\to s\pm 2/3\pi$.

The Jacobian can be computed as

Finally we perform an amusing calculation of the area of the triangle ${\Delta} = \{y^{1, 2}\in[0, 1], \; y^1+y^2\leq 1\}$

This is admittedly a pretentious way of doing some grade school level maths, though a reassuring check of the extensive computations involving elliptic functions.

Acknowledgments

We thank Maxim Zabzine for help over many issues in the draft. Our paper has some overlap with the work of Francis Bischoff and Marco Gualtieri, and we thank the former for sharing with us his thesis ^[4] and both for many interesting discussions. The work of J. Q is supported in part by the grant "Geometry and Physics" from the Knut and Alice Wallenberg foundation.

Conflict of interest

All authors declare no conflicts of interest in this paper.