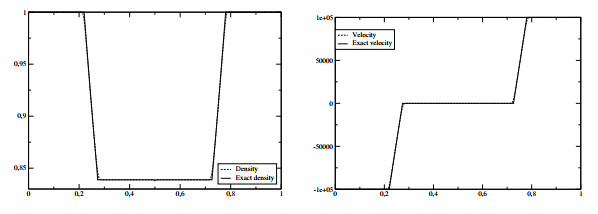
Double rarefaction. Left: density. Right: velocity
.This paper is devoted to the study of the bitemperature Euler system in a polyatomic setting. Physically, this model describes a mixture of one species of ions and one species of electrons in the quasi-neutral regime. We firstly derive the model starting from a kinetic polyatomic model and performing next a fluid limit. This kinetic model is shown to satisfy fundamental properties. Some exact solutions are presented. Finally, a numerical scheme is derived and proved to coincide with an approximation designed in [
Citation: Denise Aregba-Driollet, Stéphane Brull. Modelling and numerical study of the polyatomic bitemperature Euler system[J]. Networks and Heterogeneous Media, 2022, 17(4): 593-611. doi: 10.3934/nhm.2022018
| [1] | Nora Aïssiouene, Marie-Odile Bristeau, Edwige Godlewski, Jacques Sainte-Marie . A combined finite volume - finite element scheme for a dispersive shallow water system. Networks and Heterogeneous Media, 2016, 11(1): 1-27. doi: 10.3934/nhm.2016.11.1 |
| [2] | Young-Pil Choi, Seok-Bae Yun . A BGK kinetic model with local velocity alignment forces. Networks and Heterogeneous Media, 2020, 15(3): 389-404. doi: 10.3934/nhm.2020024 |
| [3] | José Antonio Carrillo, Yingping Peng, Aneta Wróblewska-Kamińska . Relative entropy method for the relaxation limit of hydrodynamic models. Networks and Heterogeneous Media, 2020, 15(3): 369-387. doi: 10.3934/nhm.2020023 |
| [4] | Steinar Evje, Kenneth H. Karlsen . Hyperbolic-elliptic models for well-reservoir flow. Networks and Heterogeneous Media, 2006, 1(4): 639-673. doi: 10.3934/nhm.2006.1.639 |
| [5] | John D. Towers . The Lax-Friedrichs scheme for interaction between the inviscid Burgers equation and multiple particles. Networks and Heterogeneous Media, 2020, 15(1): 143-169. doi: 10.3934/nhm.2020007 |
| [6] | Piotr Gwiazda, Karolina Kropielnicka, Anna Marciniak-Czochra . The Escalator Boxcar Train method for a system of age-structured equations. Networks and Heterogeneous Media, 2016, 11(1): 123-143. doi: 10.3934/nhm.2016.11.123 |
| [7] | Maya Briani, Emiliano Cristiani . An easy-to-use algorithm for simulating traffic flow on networks: Theoretical study. Networks and Heterogeneous Media, 2014, 9(3): 519-552. doi: 10.3934/nhm.2014.9.519 |
| [8] | Raimund Bürger, Kenneth H. Karlsen, John D. Towers . On some difference schemes and entropy conditions for a class of multi-species kinematic flow models with discontinuous flux. Networks and Heterogeneous Media, 2010, 5(3): 461-485. doi: 10.3934/nhm.2010.5.461 |
| [9] | Huanhuan Li, Meiling Ding, Xianbing Luo, Shuwen Xiang . Convergence analysis of finite element approximations for a nonlinear second order hyperbolic optimal control problems. Networks and Heterogeneous Media, 2024, 19(2): 842-866. doi: 10.3934/nhm.2024038 |
| [10] | Caterina Balzotti, Simone Göttlich . A two-dimensional multi-class traffic flow model. Networks and Heterogeneous Media, 2021, 16(1): 69-90. doi: 10.3934/nhm.2020034 |
This paper is devoted to the study of the bitemperature Euler system in a polyatomic setting. Physically, this model describes a mixture of one species of ions and one species of electrons in the quasi-neutral regime. We firstly derive the model starting from a kinetic polyatomic model and performing next a fluid limit. This kinetic model is shown to satisfy fundamental properties. Some exact solutions are presented. Finally, a numerical scheme is derived and proved to coincide with an approximation designed in [
This work is devoted to the modelling and the numerical approximation of the nonconservative polyatomic bitemperature Euler system in the context of plasma physics. Physically, this model describes the interaction of one species of ions and one species of electrons, under the quasi-neutrality assumption.
The aim of this paper is more precisely to provide a construction and an approximation of the polyatomic Euler bitemperature system. This model is constituted of conservative equations for the mass and the momentum and two nonconservative equations for ionic and electronic energies. It is a variant of the system considered in [23]. The nonconservativity is due to source-terms but also to the presence of products of the velocity by pressure gradients. In Inertial Confinement Fusion applications, high temperature solutions involve shocks, for which those nonconservative products have to be determined. This can be done by defining paths, as proposed by Dal Maso, Le Floc'h and Murat ([24]). However, it is shown in [1] that the numerical adaptation of this theory given in [36] is delicate.
In order to compute physically consistent shocks, one can use an underlying kinetic system. This approach was usefully adopted in [3] for the monoatomic case. The model is constituted by a kinetic system coupled with Ampère and Poisson equations. Moreover, this construction leads to a kinetic numerical scheme starting from a semi-discretization in space and time of the kinetic model. A DVM approach of this model has also been considered in [20] together with an asymptotic preserving discretisation toward the bitemperature Euler system. However relaxation schemes and discrete BGK schemes have been developed in the polytropic situation for a general
We construct in this paper an extension of the model developed in [3] to a polyatomic setting with a continuous energy variable. This model is based on the use of several attractors like in [15] and is shown to satisfy an H theorem. We refer to [10], [13], [14], [19], [11], [34] for other BGK models for polyatomic gas mixtures.
In the present paper, the derivation is based again on an hydrodynamic limit performed from an underlying polyatomic kinetic model. In the present case, the unknowns of the kinetic equations are the distribution functions
As observed in [37], [3], it is possible to find an underlying kinetic model where the force term is related to the nonconservative terms. One advantage of the kinetic model, is its conservative form. In the present paper, the kinetic model describing the interspecies interaction is a two component polyatomic BGK model based on one continuous internal energy variable coupled with Ampère and Poisson equations. Hence starting from a standard semi-discretization of this model, the hydrodynamic limit leads to a numerical scheme for the bitemperature model. It must be noted that the obtained scheme is the same as the one obtained in section 3.2 of [3]. In this article however the scheme was obtained by a very different method involving models developed in [7] which are not based on a physically realistic kinetic approximation of the equations. The novelty here is that our polyatomic BGK model gives a physical justification to it in the general case where
The plan of the paper is the following. Section
The bitemperature Euler system reads
| {∂tρ+∂x(ρu)=0,∂t(ρu)+∂x(ρu2+pe+pi)=0,∂tEe+∂x(u(Ee+pe))−u(ci∂xpe−ce∂xpi)=νei(Ti−Te),∂tEi+∂x(u(Ei+pi))+u(ci∂xpe−ce∂xpi)=−νei(Ti−Te), | (1) |
where
One has
| ρ=ρe+ρi | (2) |
where
| cβ=ρβρ,β=e,i | (3) |
are then constant and
| ce=Zmemi+Zme,ci=1−ce. | (4) |
The total energies are linked to the internal electronic and ionic energies by
| Eβ=ρβεβ+12ρβu2,β∈{e,i}. |
The electronic and ionic pressures and temperatures are related by
| εe=kB(γe−1)meTe,εi=kB(γi−1)miTi, |
where
In the following we denote
We complete here the calculations presented in [5]. The system is rewritten by using the variables
| {∂tρ+u∂xρ+ρ∂xu=0,∂tu+u∂xu+ρ−1∂ρ(pe+pi)∂xρ+ρ−1∂εepe∂xεe+ρ−1∂εipi∂xεi=0,∂tεe+u∂xεe+ρ−1epe∂xu=ρ−1eνei(Ti−Te),∂tεi+u∂xεi+ρ−1ipi∂xu=ρ−1iνei(Te−Ti). | (5) |
The matrix of the system (5) writes
| A(V)=uI4+(0ρ00ρ−1∂ρ(pe+pi)0ρ−1∂εepeρ−1∂εipi0ρ−1epe000ρ−1ipi00). | (6) |
We get
| λ1=u−a,λ2=λ3=u,λ4=u+a, |
where
| a=√∑β=e,iγβ(γβ−1)cβεβ. | (7) |
The value of
| r2=(00−(γi−1)ci(γe−1)ce),r3=(−ρ0εeεi). |
This system is then hyperbolic diagonalisable. The fields 2 and 3 are linearly degenerate. Consider now the fields
| r1(V)=(−ρa−(γe−1)εe−(γi−1)εi),r4(V)=(ρa(γe−1)εe(γi−1)εi) |
and
| λ′1(V)⋅r1(V)=λ′4(V)⋅r4(V)=12a∑β=e,i(γβ(γβ−1)(γβ+1)cβεβ)>0. | (8) |
Hence the fields
In this section, we generalize the BGK model considered in [3] to a polyatomic setting with a continuous energy variable. We firstly precise the notations and next introduce the BGK model that is proved to satisfy the right conservation properties and an H theorem.
Kinetic models for a mixture of two polyatomic gases are described by two distribution functions
Hydrodynamic quantities of species
| nβ=∫R3×R+fβIαβdvdI,uβ=1nβ∫R3×R+vfβIαβdvdI,Eβ=∫R3×R+(mβv22+I)fβIαβdvdI, |
and
| Eβ=12ρβu2β+(52+αβ)nβkBTβ,β=e,i. |
Velocities and temperatures of the mixture
| u=1ρ(ρeue+ρiui), | (9) |
| T=(52+αe)nekBTe+(52+αi)nikBTi+12ρeu2e+12ρiu2i−12ρu2(52+αe)nekB+(52+αi)nikB. | (10) |
The parameters
| γe=152+αe+1,γi=152+αi+1. |
For example in the diatomic case, we have
Define the entropy of the mixture by
| H(fe,fi)=Hs(fe)+Hs(fi),withHs(fβ)=∫R3×R+(fβln(fβ)−fβ)IαβdvdI | (11) |
and the entropy flux by
| Φ(fe,fi)=Φs(fe)+Φs(fi),withΦs(fβ)=∫R3×R+v(fβln(fβ)−fβ)IαβdvdI. | (12) |
In this section we consider the following kinetic model for
| ∂tfβ(t,x,v,I)+v⋅∇xfβ(t,x,v,I)+qβmβE⋅∇vfβ(t,x,v,I)=1τβ(Mβ−fβ(t,x,v,I))+1τβδ(¯Mβ(fe,fi)−fβ(t,x,v,I)), | (13) |
with
| Mβ=nβ(2πkBmβTβ)321Qβ(Tβ)exp(−(v−uβ)22kBTβmβ−IkBTβ), | (14) |
| ¯Mβ(fe,fi)=nβ(2πkBmβT#)321Qβ(T#)exp(−(v−u#)22kBT#mβ−IkBT#), | (15) |
where
| Qβ(T)=∫+∞0Iαβexp(−IkBT)dI,αβ≥0. |
As suggested in [32] and developed in [3] the definition of
| u#=1τeiρeue+1τieρiui1τeiρe+1τieρi | (16) |
and
| T#=1τei(52+αe)nekBTe+1τie(52+αi)nikBTi1τei(52+αe)nekB+1τie(52+αi)nikB+121τeiρeu2e+1τieρiu2i−(1τeiρe+1τieρi)(u#)21τei(52+αe)nekB+1τie(52+αi)nikB | (17) |
gives the conservations of impulsion and total energy for the model (13, 14, 15). These definitions allow in particular to consider a model such that the molecular mass ratios of the species are different. This situation corresponds to the case
The model (13, 14, 15, 16, 17) is coupled to Ampère and Poisson equations through the electric field
| ∂tE=−jε0, | (18) |
| ∇x⋅E=¯ρε0. | (19) |
| ¯ρ=∫R3×R+(qefeIαe+qifiIαi)dvdI=neqe+niqi, | (20) |
| j=∫R3×R+v(qefeIαe+qifiIαi)dvdI=neqeue+niqiui. | (21) |
When one of the two components is monoatomic the model has to be slightly modified. In [8], the authors study for moments systems the link beween polyatomic and monoatomic models. The connexion between monoatomic and polyatomic models can be made by passing to the limit in some parameters. When the two components are monoatomic we refer to [3].
In the case of one monoatomic component and one polyatomic component the model has to be clearly written. Consider for example that electrons are monoatomic whereas ions remain polyatomic. In that case, the model is described with the distributions
| ∂tfe(t,x,v)+v⋅∇xfe(t,x,v)+qemeE⋅∇vfe(t,x,v)=1τe(Me−fe(t,x,v))+1τei(¯Me(fe,fi)−fe(t,x,v)), | (22) |
| ∂tfi(t,x,v,I)+v⋅∇xfi(t,x,v,I)+qimiE⋅∇vfi(t,x,v,I)=1τi(Mi−fi(t,x,v,I))+1τie(¯Mi(fe,fi)−fi(t,x,v,I)), | (23) |
with
| Me=ne(2πkBmeTe)32exp(−(v−ue)22kBTeme), | (24) |
| ¯Me(fe,fi)=ne(2πkBmαT#)32exp(−(v−u#)22kBT#me). | (25) |
The hydrodynamic quantities of the monoatomic species are computed as
| ne=∫R3fedv,ue=1ne∫R3vfedv,Ee=∫R3mev22fedv. |
The total impulsion
| ρu=∫R3mevfedv+∫R3×R+mivfiIαidvdI,E=∫R3mev22fedv+∫R3×R+(miv22+I)fiIαidvdI. |
In that case
| T#=1τei32nekBTe+1τie(52+αβ)nikBTi1τei32nekB+1τie(52+αi)nikB+121τeiρeu2e+1τieρiu2i−(1τeiρe+1τieρi)(u#)21τei32nekB+1τie(52+αi)nikB. | (26) |
As previously,
In the present case the definitions of
| ¯ρ=∫R3qefedv+∫R3×R+qifiIαidvdI,j=∫R3vqefedv+∫R3×R+vqifiIαidvdI |
and the electric field is still given by (18, 19). For the sake of conciseness, we continue the presentation only for a two polyatomic species mixture. However, the following steps can be easily adapted when one of the components is monoatomic.
Proposition 1. The model (13, 14, 15, 16, 17) conservesthe mass per species, the total impulsion and the total energy.
The proof is straighforward and based as in [3] on the definition of the fictitious quantities (16, 17).
Theorem 2.1. The model (13, 14, 15, 16, 17) satisfiesan H theorem. The model satisfies the entropic inequality
| 1τe∫R3×R+(Me(fe)−fe)ln(fe)IαedvdI+1τi∫R3×R+(Mi(fi)−fi)ln(fi)IαidvdI+1τei∫R3×R+(¯Me(fe,fi)−fe)ln(fe)IαedvdI+1τie∫R3×R+(¯Mi(fe,fi)−fi)ln(fi)IαidvdI≤0. |
The equality holds in the above equation if and only if there exists(
| Mβ=nβ(2πkBmβT)321Qβ(T)exp(−(v−u)22kBTmβ−IkBT),β∈{e,i}. |
An important feature of the polyatomic model (13, 14, 15, 16, 17) is that it satisfies an entropy dissipation property that is compatible with the macroscopic one. The entropy dissipation property has already been obtained in [3] for the system (1), starting directly from the fluid system. In the present case, we are able to show that the entropy of the system (1) is compatible with the Boltzmann entropy, see subsection 3.3.
Suppose that the system (13, 14, 15, 16, 17) is space homogeneous in two directions. So we assume that the system is even in
| {∂tfβ+v1∂xfβ+qβmβE∂v1fβ=1ε(Mβ−fβ)+1τβδ(¯Mβ−fβ),β≠δ∂tE=−jε2,∂xE=¯ρε2, | (27) |
where
| Mβ=nβ(2πkBmβTβ)321Qβ(Tβ)exp(−(v1−uβ)2+v22+v332kBTβmβ−IkBTβ), | (28) |
| ¯Mβ(fe,fi)=nβ(2πkBmβT#)321Qβ(T#)exp(−(v1−u#β)2+v22+v232kBT#mβ−IkBT#) | (29) |
where
Proposition 2. The system (27, 28, 29, 16, 17) convergesformally to the nonconservative bitemperature Euler system where
| 1ρe∂xpe−1ρi∂xpi=(neqeρe−niqiρi)E=ρρeρineqeE=−ρρeρiniqiE | (30) |
and
| νei=kB(52+αe)(52+αi)neniτie(52+αe)ne+τei(52+αi)ni. | (31) |
Proof. Performing a Chapman-Enskog expansion, it comes that each component of the species is expanded as
| fβ=Mβ+εgβ,β∈{e,i} | (32) |
so that
| ∫R3×R+gβIαβdvdI=0,∫R3×R+v1gβIαβdvdI=0, | (33) |
| ∫R3×R+(12mβv2+I)gβIαβdvdI=0. | (34) |
Moreover, Gauss equation in (27) implies that
| ∂tMβ+v1∂xMβ+qβmβE∂v1Mβ=−gβ+1τβδ(¯Mβ−Mβ)+O(ε) | (35) |
for
Mass conservation equation is obtained by integrating w.r.t
| ∫R3×R+(∂tMe+v1∂xMe)(12mev2+I)IαedvdI+∫R3×R+qemβE∂v1Me(12mev2+I)IαedvdI=1τei∫R3×R+(¯Me−Me)(12mev2+I)IαedvdI. |
Moreover a direct computation gives
| ∫R3×R+(¯Me−Me)(12mev2+I)IαedvdI=(52+αe)nekB(T#−Te). |
So, according to the relation (10) defining
| ∫R3×R+(¯Me−Me)(12mev2+I)IαedvdI=(52+αe)ne(52+αi)niτie(52+αe)ne+τei(52+αi)nikB(Ti−Te) |
and
As proved in [3], the system (1) owns a dissipative entropy-entropy flux pair
| η=ηe+ηi,Q=uη | (36) |
where
| ηβ=−ρβmβ(γβ−1)[ln((γβ−1)ρβεβργββ)+C],β=e,i. | (37) |
Here,
Theorem 3.1. Let
| ∂tη(U)+∂xQ(U)=−νeikBTiTe(Ti−Te)2. | (38) |
If
| ∂tη(U)+∂xQ(U)≤−νeikBTiTe(Ti−Te)2. | (39) |
As in [3], the inequality (39) is obtained by using the proof of the H theorem (Theorem 2.1).
We compute contact discontinuities and rarefaction waves for system (1) in the homogeneous case
A contact discontinuity is a weak solution
| ρ(x,t)=|ρLifx<ut,ρRifx>utEβ(x,t)=|Eβ,Lifx<ut,Eβ,Rifx>utβ=e,i. |
Here,
| {∂tρ+∂x(ρu)=0,∂t(ρu)+∂x(ρu2+pe+pi)=0,∂tEe+∂x(u(Ee+ce(pe+pi)))=0,∂tEi+∂x(u(Ei+ci(pe+pi)))=0. | (40) |
Rankine-Hugoniot jump conditions are
| [u]=0,[pe+pi]=0. |
One can realize those conditions by taking
For contact discontinuities there is no entropy dissipation:
| ∂tη(U)+∂xQ(U)=0. |
A rarefaction wave is a selfsimilar continuous, piecewise
| {−yI+A(W(y))}W′(y)=0 | (41) |
where
| Φ′(ξ)=r4(Φ(ξ)),Φ(0)=WL. |
We set
| W(y)=|WLsiy≤λ+(WL),Φ(Ψ−1(y))ifλ+(WL)≤y≤λ+(WR),WRsiy≥λ+(WR). |
We have
| {ρ′(ξ)=ρ(ξ),u′(ξ)=a(ξ),ε′β(ξ)=(γβ−1)εβ(ξ),β=e,i.(ρ(0),u(0),εe(0),εi(0))=WL. |
We find
| {ρ(ξ)=ρLeξ,u′(ξ)=√∑βγβ(γβ−1)cβεβ,Le(γβ−1)ξ,εβ(ξ)=εβ,Le(γβ−1)ξ,β=e,i. | (42) |
As
| Tβ=(γβ−1)mβkBεβandpβ=(γβ−1)ρβεβ, |
we have also:
| Tβ(ξ)=Tβ,Le(γβ−1)ξetpβ(ξ)=pβ,Leγβξ,β=e,i. |
If
| ξ=ln(ρρL),εβ=εβ,L(ρρL)γβ−1. |
So
| Tβ=Tβ,L(ρρL)γβ−1. |
We retrieve the fact that
| Sβ=pβργββ. |
For all
| Sβ(ξ)=Sβ(0),β=e,i |
hence
| Sβ,L=Sβ,R,β=e,i. |
In this section we derive a numerical scheme starting from a semi-discretization of the kinetic model. In [3], this approach has been developed for a monoatomic gas mixture. We follow the lines of [3] and obtain the scheme for the polyatomic case. For the sake of completeness we give the details.
First we recall that for
| Pβ(fβ)=∫R3×R+(mβmβv1(mβv22+I))fβIαβdvdI | (43) |
one has
| Pβ(fnβ)=Unβ,j,Pβ(v1Mβ(Unβ,j))=Fβ(Unβ,j), | (44) |
where
The spatial discretisation is defined by the step
We use a finite volume approach: for any unknown
First step. For
| ρnβ,j=cβρnj | (45) |
and
| ∀j,fnβ,j(v,I)=Mβ(Unβ,j,v,I),β=e,i. | (46) |
Second step. We solve the transport equations
| hβ(f,g,v,I)=v1(λ2λ2−λ1f(v,I)−λ1λ2−λ1g(v,I))+λ1λ2λ2−λ1(g(v,I)−f(v,I)), | (47) |
where
| fn+12β,j(v,I)=fnβ,j(v,I)−ΔtΔx(hnβ,j+12(v,I)−hnβ,j−12(v,I)). |
Remark 1. This scheme is stable for
We apply
| Un+12β,j=Pβ(fn+12β,j)=(ρn+12β,jρn+12β,jun+12β,jEn+12β,j) |
Denoting for
| Fβ,j+12=Fβ(Uβ,j,Uβ,j+1),Fβ(Uβ,Vβ)=Pβ(hβ(Mβ(Uβ),Mβ(Vβ),⋅)), | (48) |
we have by using (44), (46) and (47)
| Fβ(Uβ,Vβ)=λ2λ2−λ1Fβ(Uβ)−λ1λ2−λ1Fβ(Vβ)+λ1λ2λ2−λ1(Vβ−Uβ), |
and
| Un+12β,j=Unβ,j−ΔtΔx(Fnβ,j+12−Fnβ,j−12). |
Hence
Remark 2. We could have chosen the upwind scheme to approximate the transport equations, but it is more difficult to integrate the formulas w.r.t.
It is easy to prove the following result.
Proposition 3. For
| ρn+12β,j=cβρn+12j | (49) |
where
Third step. We take into account the force terms and the source terms. For all
| fn+34β,j(v,I)=fn+12β,j−ΔtqβmβEn+1j∇vfn+34β,j+Δtτβδ(¯Mβ(fn+34e,j,fn+34i,j)−fn+34β,j) | (50) |
and
| Un+1β,j=Pβ(fn+34β,j). | (51) |
One obtains the following equations for
| {ρn+1β,j=cβρn+12jρn+1β,jun+1β,j=ρnβ,junβ,j−ΔtΔx(Fnβ,j+12,2−Fnβ,j−12,2)−ΔtqβmβEn+1jρn+1β,jEn+1β,j=Enβ,j−ΔtΔx(Fnβ,j+12,3−Fnβ,j−12,3)−En+1jun+1β,jΔtqβmβρn+1β,j+Δtνei(Tn+1β′,j−Tn+1β,j),β′≠β. | (52) |
Subsequently, it is necessary to ensure that the quasineutrality constraints are satisfied, which correspond to Maxwell-Gauss and Maxwell-Ampère equations in the limit
| qemeρn+1e,j+qimiρn+1i,j=0,qemeρn+1e,jun+1e,j+qimiρn+1i,jun+1i,j=0. |
By proposition 3 the first condition is satisfied and
| ceρn+1jun+1j=ceρnjunj−ΔtΔx(Fne,j+12,2−Fne,j−12,2)−ΔtqemeEn+1jρn+1e,j,ciρn+1jun+1j=ciρnjunj−ΔtΔx(Fni,j+12,2−Fi,nj−12,2)−ΔtqimiEn+1jρn+1i,j. |
Hence, by multiplying the first equation by
| En+1jqimiρn+1i,j=−En+1jqemeρn+1e,j=1Δx(δnj+12−δnj−12), |
where
| δnj+12=−ciFne,j+12,2+ceFni,j+12,2. | (53) |
Finally, defining
| Fj+12=(Fe,j+12,1+Fi,j+12,1Fe,j+12,2+Fi,j+12,2Fe,j+12,3Fi,j+12,3), | (54) |
we get a scheme that is consistent with the Euler system (1):
Proposition 4. For any
| Unβ,j=(cβρnj,cβρnjunj,Eβ),β=e,i. | (55) |
The kinetic flux
| {ρn+1j=ρnj−ΔtΔx(Fnj+12,1−Fnj−12,1),ρn+1jun+1j=ρnjunj−ΔtΔx(Fnj+12,2−Fnj−12,2),En+1e,j=Ene,j−ΔtΔx(Fne,j+12,3−Fne,j−12,3)−un+1jΔtΔx(δnj+12−δnj−12)+Δtνei(Tn+1i,j−Tn+1e,j),En+1i,j=Eni,j−ΔtΔx(Fni,j+12,3−Fni,j−12,3)+un+1jΔtΔx(δnj+12−δnj−12)−Δtνei(Tn+1i,j−Tn+1e,j). | (56) |
Remark 3. The scheme is implicit but easy to implement because the first two equations of (56) give
This numerical scheme is the same as the one obtained in section 3.2 of [3] and for which a second order two-dimensional extension is presented in [6], (
We recall that stability and entropy properties where proved in these references. In particular, a discrete entropy inequality holds under appropriate choices of
| λ1≤min(u−a)≤max(u+a)≤λ2,max(|λ1|,|λ2|)ΔtΔx≤1. | (57) |
As pointed out in section 5, the presented scheme has already been tested in [3] and [6]. The aim of this section is to investigate more precisely the polyatomic case with two tests where
We solve the bitemperature Euler system with the following Riemann data, whose orders of magnitude are those encountered in physical situations:
| ρ−=1,ρ+=ρ−,u−=−100000,u+=−u−,Te,−=2.3×107,Te,+=Te,−,Ti,−=2.3×106,Ti,+=Ti,−. |
We set
| {ρ=ρ±e−ξu=u−+∫ξ0a(s)ds=u+−∫ξ0a(s)dsεβ=e−(γβ−1)ξεβ,±,β=e,i, |
with
| a(s)=(∑βγβ(γβ−1)cβεβ,±e−(γβ−1)s)1/2. |
Hence we find numerically
| u+=∫ξ0a(s)ds. |
The numerical results are depicted in Figures 1 and 2. We compare the exact and computed results for density, velocity and temperatures. As already observed in [3] for
In this test case, we consider an implosion problem, introduced in [28] in the monoatomic case
| Te(x1,x2,0)=2,3×106K,Ti(x1,x2,0)=1.7406×106Kif(x1)2+(x2)2<14,Te(x1,x2,0)=2,3×107K,Ti(x1,x2,0)=1.7406×107Kotherwise. |
The relaxation frequency
Thanks to symmetry properties of the problem, it is only necessary to solve it on the quarter domain
On Figure 3, are given the isovalues of the total density and of the electronic temperature at time
When the shock front reaches the center, a peak of density occurs. This peak occurs at time
Double rarefaction. Left: density. Right: velocity
Double rarefaction. Left: electronic temperature. Right : ionic temperature
Total density (left) and electronic temperature (right) at time
Implosion test case with
Implosion test case with