Citation: Christelle Dleuna Nyoumbi, Antoine Tambue. A fitted finite volume method for stochastic optimal control problems in finance[J]. AIMS Mathematics, 2021, 6(4): 3053-3079. doi: 10.3934/math.2021186
| [1] | Zuliang Lu, Ruixiang Xu, Chunjuan Hou, Lu Xing . A priori error estimates of finite volume element method for bilinear parabolic optimal control problem. AIMS Mathematics, 2023, 8(8): 19374-19390. doi: 10.3934/math.2023988 |
| [2] | Zui-Cha Deng, Fan-Li Liu, Liu Yang . Numerical simulations for initial value inversion problem in a two-dimensional degenerate parabolic equation. AIMS Mathematics, 2021, 6(4): 3080-3104. doi: 10.3934/math.2021187 |
| [3] | Dennis Llemit, Jose Maria Escaner IV . Value functions in a regime switching jump diffusion with delay market model. AIMS Mathematics, 2021, 6(10): 11595-11609. doi: 10.3934/math.2021673 |
| [4] | Tiantian Zhang, Wenwen Xu, Xindong Li, Yan Wang . Multipoint flux mixed finite element method for parabolic optimal control problems. AIMS Mathematics, 2022, 7(9): 17461-17474. doi: 10.3934/math.2022962 |
| [5] | Yu Xu, Youjun Deng, Dong Wei . Numerical solution of forward and inverse problems of heat conduction in multi-layered media. AIMS Mathematics, 2025, 10(3): 6144-6167. doi: 10.3934/math.2025280 |
| [6] | Shuangbing Guo, Xiliang Lu, Zhiyue Zhang . Finite element method for an eigenvalue optimization problem of the Schrödinger operator. AIMS Mathematics, 2022, 7(4): 5049-5071. doi: 10.3934/math.2022281 |
| [7] | Lidiya Melnikova, Valeriy Rozenberg . One dynamical input reconstruction problem: tuning of solving algorithm via numerical experiments. AIMS Mathematics, 2019, 4(3): 699-713. doi: 10.3934/math.2019.3.699 |
| [8] | Zuliang Lu, Fei Cai, Ruixiang Xu, Chunjuan Hou, Xiankui Wu, Yin Yang . A posteriori error estimates of hp spectral element method for parabolic optimal control problems. AIMS Mathematics, 2022, 7(4): 5220-5240. doi: 10.3934/math.2022291 |
| [9] | Yuelong Tang . Error estimates of mixed finite elements combined with Crank-Nicolson scheme for parabolic control problems. AIMS Mathematics, 2023, 8(5): 12506-12519. doi: 10.3934/math.2023628 |
| [10] | Jiali Wu, Maoning Tang, Qingxin Meng . A stochastic linear-quadratic optimal control problem with jumps in an infinite horizon. AIMS Mathematics, 2023, 8(2): 4042-4078. doi: 10.3934/math.2023202 |
We consider the numerical approximation of the following controlled Stochastic Differential Equation (SDE) defined in $ \mathbb{R}^{ n} $ ($ n\geq 1 $) by
| $ \begin{equation} \begin{split} & dx_s = b(s, x_s, \alpha_s) ds + \sigma (s, x_s, \alpha_s) dW_s,\,\,s\,\in\,(t,T]\\ & x_t = x \end{split} \end{equation} $ | (1.1) |
where
| $ \begin{equation} \begin{split} b&: [0, T] \times \mathbb{R}^n \times \mathcal{A} \rightarrow \mathbb{R}^n \nonumber\\ & (t,x_t, \alpha_t)) \rightarrow b(t,x_t,\alpha_t) \end{split} \end{equation} $ |
is the drift term and
| $ \begin{equation} \begin{split} \sigma &:[0, T] \times \mathbb{R}^n\times \mathcal{A} \rightarrow \mathbb{R}^{n\times d} \nonumber \\ & (t,x_t,\alpha_t) ) \rightarrow \sigma(t,x_t,\alpha_t) \end{split} \end{equation} $ |
the $ d $-dimensional diffusion coefficients. Note that $ W_t $ are $ d $-dimensional independent Brownian motion on $ \left(\Omega, \mathcal{F}, (\mathcal{F}_t)_{t \geq 0}, \mathbb{P} \right) $, $ \alpha = (\alpha_t)_{t \geq 0} $ is an $ \mathbb{F} $-adapted process, valued in $ \mathcal{A} $ compact convex subset of $ \mathbb{R}^m \, (m \geq 1) $ is the set of admissible controls satisfying some integrability conditions and/or state constraints. Precise assumptions on $ b $ and $ \sigma $ to ensure the existence of the uniqueness solution $ x_t $ of (1.1) can be found in [9].
Given a function $ g :\mathbb{R}^n \rightarrow \mathbb{R} $ and $ f :[0, T]\times \mathbb{R}^n \times \mathcal{A} \rightarrow \mathbb{R} $, the value function is defined by
| $ \begin{equation} v(t, x) = \underset{\alpha \in \mathcal{A}}{\sup}\, \mathbb{E}\, \left[ \int_{t}^T f(s, x_s, \alpha) \,ds +g (x_T)\right], \,\,\,(t,x) \in [0, T]\times \mathbb{R}^n. \end{equation} $ | (1.2) |
Remember that $ x $ is the initial condition in (1.1). Using the dynamic programming approach, the problem (1.2) can be transformed into the following Hamilton-Jacobi-Bellman (HJB) equation (see [5,12] for more explanations)
| $ \begin{align} \begin{cases} v_t(t, x) + \underset{\alpha \in \mathcal{A}}{\sup} \left[L^{\alpha} v(t, x) + f(t, x,\alpha)\right] = 0 \quad\text{on} \ [0,T)\times \mathbb{R}^n\\ v(T,x) = g(x), \,\,\,\,x \,\in \mathbb{R}^n \end{cases} \end{align} $ | (1.3) |
where
| $ \begin{equation} L^{\alpha} v(t, x) = \sum\limits_{i = 1}^n (b(t, x,\alpha))_i \dfrac{\partial v(t,x)}{\partial x_i} + \sum\limits_{i,j = 1}^n ( a (t,x,\alpha))_{i,j}\,\dfrac{\partial^2 v(t,x)}{\partial x_i\,\partial x_j}, \end{equation} $ | (1.4) |
where $ a(t, x, \alpha) = (\dfrac{1}{2}(\sigma (t, x, \alpha))(\sigma(t, x, \alpha))^T)_{i, j} $ the symmetric positive semi-definite diffusion coefficient matrix. Eq (1.3) is a initial value problem. Although this initial value problem (1.3) is defined on the unbounded region $ \mathbb{R}^n $, often it is restricted to a bounded region
| $ \begin{equation} \mathcal{U} = (p_1,q_1)\times(p_1,q_1)\times \cdots \times(p_n,q_n), \end{equation} $ | (1.5) |
with $ p_k $ and $ q_k $ are constants for $ k = 1, 2, \cdots, n $ for computational reasons. This initial value problem with $ \mathbb{R}^n $ in (1.3) being replaced by $ \mathcal{U} $ has been discussed in the literature (see for example [11,21]). There are two unknown functions in this equation, the value function $ v $ and the optimal control $ \alpha $. However, in most practical situations, it is not analytically solvable therefore numerical approximations are the only tools appropriate to provide reasonable approximations. Numerical approximation of HJB-equation of type (1.3) is therefore an active research area and has attracted a lot of attentions [11,13,14,18,20]. When solving numerically HJB equation, the keys challenge are the low regularity of the solution of HJB equation and the lack of appropriate numerical methods to tackle the degeneracy of the differential operator in HJB equation. Indeed adding to the standard issue that we usually have when solving degenerate PDE, we need to couple with an optimization problem at every grid point and every time step. In practice, a feedback optimal control solution is defined in a region containing the optimal trajectory is much preferred. This feedback solution gives a global optimal control defined over a time-space region.
In terms of existing numerical methods, there are three basic threads of literature concerning HJB equations. A standard approach is based on Markov chain approximation. In financial terms, this approach is equivalent to an explicit finite difference method. However, these methods are well-known to suffer from time step limitations due to stability issues [7]. A more recent approach is called semi-Lagrangian schemes, these schemes work for general diffusions with coefficient matrices that may be nondiagonal dominant and arbitrarily degenerate but also use finite difference approximations [22].
For many stochastic optimal control problems such as Merton's control problem, the linear operator is degenerated when the spatial variables approach the region near to zero. This degeneracy has an adverse impact on the accuracy when the finite difference method is used to solve the PDE (see [8], chapter 26) as the monotonicity of the scheme is usually lost. However, when solving HJB equation, the monotonicity also plays a key role to ensure the convergence of the numerical scheme toward the viscosity solution. Indeed in the two dimensional Merton's control problem, the matrix in the diffusion part is of rank 1 near the origin and it has been found in [2,3] that the standard finite difference schemes become non monotone and may not converge to the viscosity solution of the HJB.
The current work aims to propose an alternative novel monotone scheme based on fitted technique in dimensions $ 1 $ and $ 2 $. This fitting technique is based on the idea proposed by [1] for convection-diffusion equations and was upgraded in [4] to solve simple degenerated Black Scholes equations. The fitted technique has for feature to tackle the degeneracy in the HJB equation. Our method is coupled with implicit time-stepping method for temporal discretization method and the iterative method presented in [11] for optimization problem at every time step. Note that to the best of our knowledge, such method has not been used to solve the stochastic optimal control problem (1.3). The merit of the method is that it is absolutely stable in time because of the implicit nature of the time discretization, easy to understand and implement, and the corresponding matrices after spatial and temporal discretization are positive-definite $ M $-matrices. Therefore our alternative scheme is monotone. Numerical simulations prove that our proposed method can be more accurate than the standard method based on finite difference spatial discretization, thanks to the monotonicity properties of our scheme. The novel contribution of our paper over the existing literature can be summarized as
● We have upgraded the fitted finite volume technique to spatial discretization of a more generalized HJB equation coupled with the implicit time-stepping method for temporal discretization method and the iterative method for the optimization problem at every time step. To best of our knowledge such combination has not yet proposed so far to solve stochastic optimal control problems in the literature.
● We have proved that the corresponding matrices after spatial and temporal discretization are positive-definite $ M $-matrices, then our scheme is monotone. Indeed this is the key feature of our novel scheme comparing to standard finite difference scheme where the monotonicity is lost because of degeneracy and the convergence toward the viscosity solution is not longer guarantee [2,3].
● We have demonstrated by numerical experiments that the proposed scheme can be more accurate than the standard finite difference scheme, and that accuracy increase in two dimensional domain where the matrix in the diffusion part is of rank $ 1 $ near the origin. We have also applied our method to approximate realistic optimal problem in finance, more precisely the optimal cash management problem.
The rest of this article is organized as follows. In section 2, we will recall some results about the well posedness problem. In section 3, we present the finite volume method with the fitting technique for dimensions $ 1 $ and $ 2 $. We will also show that the system matrix of the resulting discrete equations is an $ M $-matrix. In section 4, we will present the temporal discretization and optimization problem in dimensions $ 1 $ and $ 2 $. Numerical experiments using Matlab software will be performed in section 5 to demonstrate the accuracy of the proposed numerical method. We conclude the work at section 6 by summarizing our finding.
In this part, we will present results about existence and uniqueness of the value function. Firstly, assume that $ b $ and $ \sigma $ are continuous and for every $ \alpha \, \in\, \mathcal{A} $, $ b(\cdot, \cdot, \alpha) $ and $ \sigma(\cdot, \cdot, \alpha) $ are in $ C^1([0, T] \times \mathbb{R}^n) $. To ensure the existence and uniqueness of the value function solution, we make the following assumptions.
Assumption 1. We assume that there exists $ C \geq 0 $ such that for all $ \alpha \, \in\, \mathcal{A} $, $ x, y \, \in\, \mathbb{R}^n $ and $ t, s \, \in\, [0, T], $
| $ \begin{equation} \begin{split} \vert b(t,x,\alpha)-b(s,y,\alpha)\vert &\leq C\left(\vert x-y\vert + \vert t-s\vert \right)\\ \vert \sigma(t,x,\alpha)-\sigma(s,y,\alpha)\vert &\leq C\left(\vert x-y\vert + \vert t-s\vert \right) \end{split} \end{equation} $ | (2.1) |
Assumption 2. We assume that there exists $ C \geq 0 $ such that for every $ \alpha \, \in\, \mathcal{A} $, $ x \, \in\, \mathbb{R}^n $ and $ t, s \, \in\, [0, T], $
| $ \begin{equation} \begin{split} \vert b(t,x,\alpha)\vert &\leq C\left(1 + \vert x \vert \right)\\ \vert \sigma(t,x,\alpha)\vert &\leq C\left(1+ \vert x\vert \right). \end{split} \end{equation} $ | (2.2) |
Let $ T > 0 $, $ \mathcal{U}\subset \mathbb{R}^n $ be an open bounded set and $ S(n, \mathbb{R}) $ the set of symmetric matrix $ n\times n $. We set $ \mathcal{O} = (0, T) \times\mathcal{U} $ and $ \partial\mathcal{O} $ the parabolic boundary of $ \mathcal{O} $ defined by : $ \partial\mathcal{O} = \partial \mathcal{U}\times (0, T)\cup (\overline{\mathcal{U}})\times \left\lbrace T \right\rbrace $.
Assumption 3. Let $ f : \overline{\mathcal{O}} \times \mathcal{A} \longrightarrow \mathbb{R} $ and $ g :\overline{\mathcal{O}} \longrightarrow \mathbb{R} $ be two continuous functions such that there exists $ C \geq 0 $ such that, for all $ (t, x), \, (s, y)\, \in\, \overline{\mathcal{O}} $, $ \alpha\, \in\, \mathcal{A} $
| $ \begin{equation} \begin{split} \vert f(t, x,\alpha)-f(s, y, \alpha)\vert &\leq C\left(\vert x-y\vert + \vert t-s\vert \right) \\ \vert f(t, x, \alpha)\vert &\leq C\left( 1 + \vert x \vert \right)\\ \vert g (t, x)\vert &\leq C\left(1 + \vert x \vert \right). \end{split} \end{equation} $ | (2.3) |
The value function $ v $ from $ \overline{\mathcal{O}} \rightarrow \mathbb{R} $ is now given by
| $ \begin{equation} v(t,x,\alpha) = \sup\limits_{\alpha\,\in\,\mathcal{A}}\mathbb{E}\left[ \int_{t}^\tau\,f (s, x_s, \alpha(s))\, ds + g (\tau, x_\tau)\right], \end{equation} $ | (2.4) |
where the diffusion process $ x_s $ is on the form (1.1). Using the dynamic programming approach (see [12]), the value function $ v $ leads to the following HJB equation
| $ \begin{equation} \begin{cases} v_t(t, x) + \underset{\alpha \in \mathcal{A}}{\sup} \left[L^{\alpha} v(t, x) + f(t, x,\alpha)\right] = 0 \quad\text{on} \ \,\mathcal{O}\\ v(T,x) = g(x)\quad\text{on} \ \, \,\,\,\partial \mathcal{O}, \end{cases} \end{equation} $ | (2.5) |
where
| $ \begin{equation} L^{\alpha} v(t, x) = \sum\limits_{i = 1}^n (b(t, x,\alpha))_i \dfrac{\partial v(t,x)}{\partial x_i} + \sum\limits_{i,j = 1}^n ( a (t,x,\alpha))_{i,j}\,\dfrac{\partial^2 v(t,x)}{\partial x_i\,\partial x_j},\,\,\, \end{equation} $ | (2.6) |
$ a(t, x, \alpha) = \bigg(\dfrac{1}{2}(\sigma (t, x, \alpha))(\sigma(t, x, \alpha))^T \bigg)_{i, j} $ the symmetric positive semi definite diffusion coefficient matrix.
Let us consider the following equation without final condition
| $ \begin{equation} v_t(t, x) + \underset{\alpha \in \mathcal{A}}{\sup} \left[L^{\alpha} v(t, x) + f(t, x,\alpha)\right] = 0 \quad\text{on} \ \,\mathcal{O} \end{equation} $ | (2.7) |
We denote
| $ \begin{equation} \begin{split} USC(\bar{\mathcal{O}}) = \left\lbrace v: \overline{\mathcal{O}} \rightarrow \mathbb{R} \vert \,v \,\mbox{upper semi-continuous on}\, \overline{\mathcal{O}}\right\rbrace,\\ LSC(\overline{\mathcal{O}}) = \left\lbrace v: \overline{\mathcal{O}} \rightarrow \mathbb{R} \vert \,v \,\mbox{lower semi-continuous on}\, \overline{\mathcal{O}}\right\rbrace. \end{split} \end{equation} $ | (2.8) |
Definition 1. [17] A function $ u\, \in\, USC \left(\overline{\mathcal{O}}\right) $ is a viscosity subsolution of Eq (2.7) if and only if $ u $ is such that for every test function $ \rho \in C^{\infty} \left(\overline{\mathcal{O}}\right) $, $ u-\rho $ has a strict local maximum at $ (t, x) \in \mathcal{O} $ with $ u(t, x) = \rho(t, x) $, implies
| $ \begin{equation} \partial_t \rho(t, x) + \underset{\alpha \in \mathcal{A}}{\sup} \left[L^{\alpha} \rho(t, x) + f(t, x,\alpha)\right] \leq 0, \end{equation} $ | (2.9) |
A function $ u\, \in\, LSC \left(\overline{\mathcal{O}}\right) $ is a viscosity supersolution of Eq (2.7) if and only if $ u $ is such that for every test function $ \rho \in C^{\infty} \left(\overline{\mathcal{O}}\right) $, $ u-\rho $ has a strict local minimum at $ (t, x) \in \mathcal{O} $ with $ u(t, x) = \rho(t, x) $, implies
| $ \begin{align} \partial_t \rho(t, x) + \underset{\alpha \in \mathcal{A}}{\sup} \left[L^{\alpha} \rho(t, x) + f(t,x,\alpha)\right] \geq 0, \end{align} $ | (2.10) |
A function $ u\, \in\, C\left(\overline{\mathcal{O}}\right) $ is a viscosity solution of Eq (2.7) if it is both, a viscosity subsolution and a viscosity supersolution.
Having stated the notion of a viscosity solution to a parabolic PDE, we now turn towards the notion of a viscosity solution to a parabolic final value problem with Dirichlet boundary data on the parabolic boundary.
| $ \begin{align} v_t(t, x) + \underset{\alpha \in \mathcal{A}}{\sup} \left[L^{\alpha} v(t, x) + f(t, x,\alpha)\right] = 0 \quad\text{on} \ \,\mathcal{O} \end{align} $ | (2.11) |
| $ \begin{align} v(T,x) = g(x)\quad\text{on} \ \, \,\,\,\partial \mathcal{O}, \end{align} $ | (2.12) |
Definition 2. A function $ v\, \in\, USC \left(\overline{\mathcal{O}}\right) $ is a viscosity subsolution of (2.11) if $ v $ is a viscosity subsolution in the sense of the definition (1) and $ v \leq g $.
Likewise, a function $ v\, \in\, LSC \left(\overline{\mathcal{O}}\right) $ is a viscosity supersolution of (2.11) if $ v $ is a viscosity subsolution in the sense of the definition (1) and $ v \geq g $ on $ \partial \mathcal{O} $.
A function $ v $ on $ C\left(\overline{\mathcal{O}}\right) $ is a viscosity solution if $ v $ is a viscosity supersolution and a viscosity subsolution.
Theorem 1. Let assumptions (1), (2) and (3) hold, there is at most one viscosity solution in the sense of definition (2) to the HJB final value problem.
| $ \begin{equation} \begin{cases} v_t(t, x) + \underset{\alpha \in \mathcal{A}}{\sup} \left[L^{\alpha} v(t, x) + f(t, x,\alpha)\right] = 0 \quad\mathit{\text{on}} \ \ \mathcal{O}\\ v(T,x) = g(x), \,\,\,\,\,\mathit{\text{on}}\,\, \partial \mathcal{O}. \end{cases} \end{equation} $ | (2.13) |
Proof. The proof of existence and uniqueness can be found in [15,17,19].
As we already know, the resolution of the HJB Eq (2.13) involves a spatial discretization, a temporal discretization and an optimisation problem at every grid point and each time step. The goal of this section is to provide the spatial discretization of the HJB Eq (2.13) solving our stochastic optimal control problem. Details in this section can be found in [6], where such methods have been used to solve the degenerated Black Scholes equation for option pricing with constant coefficients.
Consider the more generalized HJB Eq (2.13) in dimensions 1 ($ n = 1 $) which can be written in the form
| $ \begin{equation} \begin{split} & \dfrac{ \partial v(t, x)}{\partial t} \\ &+ \sup\limits_{\alpha \in \mathcal{A}}\left[ \dfrac{\partial }{\partial x} \left(a (t, x,\alpha)\,x^2 \dfrac{\partial v(t, x)}{\partial x}+ b (t, x,\alpha)\,x\,v(t, x) \right)+c(t, x,\alpha)\,v(t, x)\right] = 0\, \end{split} \end{equation} $ | (3.1) |
where $ a(t, x, \alpha) > 0 $ is bounded. Indeed this divergence form is not a restriction as the differentiation is respect to $ x $ and not respect to the control $ \alpha $, which may be discontinuous in some applications.
As usual, we truncate the problem in the finite interval $ I = [0, x_{\text{max}}] $. Let the interval $ I = [0, x_{\text{max}}] $ be divided into $ N_1 $ sub-intervals $ I_i : = (x_i, x_{i+1}), \, \, \, \, \, i = 0\cdots N_1-1 $ with $ 0 = x_0 < x_1 < \cdots \cdots < x_{N_1} = x_\text{max} $. We also set $ x_{i+1/2} = \dfrac{x_{i} +x_{i+1} }{2} $ and $ x_{i-1/2} = \dfrac{x_{i-1} +x_{i} }{2} $ for each $ i = 1\cdots N_1-1 $. These mid-points form a second partition of $ [0, x_{\text{max}}] $ if we define $ x_{-1/2} = x_0 $ and $ x_{N_1+1/2} = x_\text{max} $. Integrating both size of (3.1) over $ J_i = \left(x_{i-1/2}, \, x_{i+1/2}\;\right) $ and taking $ \alpha_i = \alpha(x_i, t) $, we have
| $ \begin{equation} \int_{x_{i-1/2}}^{x_{i+1/2}}\dfrac{\partial v }{ \partial t} dx + \int_{x_{i-1/2}}^{x_{i+1/2}} \sup\limits_{\alpha_i \in \mathcal{A}}\left[ \dfrac{\partial }{\partial x} x \left(a(t, x,\alpha_i)\,x \dfrac{\partial v}{\partial x}+ b(t, x,\alpha_i) \,v \right)+c(t,x,\alpha_i)\,v\right]dx = 0 \end{equation} $ | (3.2) |
Applying the mid-points quadrature rule to the first and the last point terms, we obtain the above
| $ \begin{equation} \dfrac{\partial v_i(t)}{ \partial t} l_i + \sup\limits_{\alpha_i \in \mathcal{A}}\left[\left[x_{i+1/2}\rho(v)\left|_{x_{i+1/2}}-x_{i-1/2} \rho(v)\right|_{x_{i-1/2}}\right]+c(t,x_i,\alpha_i)\, v_i\, l_i \right] = 0, \end{equation} $ | (3.3) |
for $ i = 1, 2, \cdots N_1-1 $, where $ l_i = x_{i+1/2} - x_{i-1/2} $ is the length of $ J_i $. Note that $ v_i $ denotes the nodal approximation to $ v(t, x_i) $ and $ \rho(v) $ is the flux associated with $ v $ defined by
| $ \begin{equation} \rho(v) : = a(t,x,\alpha_i)\,x\,\dfrac{\partial v}{\partial x} + b(t,x,\alpha_i)\,v. \end{equation} $ | (3.4) |
Clearly, we now need to derive approximation of the flux defined above at the mid-point $ x_{i+1/2} $, of the interval $ I_i $ for $ i = 0, 1, \cdots N_1-1. $ This discussion is divided into two cases for $ i \geq 1 $ and $ i = 0 $ on $ I_0 = [0, x_1] $.
$\underline{\bf Case\; I}:$ Approximation of $ \rho $ at $ x_{i+1/2} $ for $ i\geq 1 $.
The term $ \left(a (t, x, \alpha_i)\, x \dfrac{\partial v}{\partial x}+ b(t, x, \alpha_i)\, v \right) $ is approximated by solving the two point boundary value problem
| $ \begin{equation} \left(a(t,x_{i+1/2}\;,\alpha_i)\,x \dfrac{\partial v}{\partial x}+ b(t,x_{i+1/2}\;,\alpha_i)\,v \right)' = 0,\, \,\,\, x \in I_i \\ v(x_i) = v_i(t),\,\, v(x_{i+1}) = v_{i+1}(t). \end{equation} $ | (3.5) |
Integrating (3.5) yields the first-order linear equations
| $ \begin{equation} \rho_i(v)(t) = a(t,x_{i+1/2}\;,\alpha_i)\,x \dfrac{\partial v}{\partial x}+ b(t, x_{i+1/2}\;,\alpha_i)\,v = C_1 \end{equation} $ | (3.6) |
where $ C_1 $ denotes an additive constant. As in [6], the solution is given by
| $ \begin{equation} v (t) = \dfrac{C_1}{b(t, x_{i+1/2}\;,\alpha_i)} + C_2\, x^{-\dfrac{b(t, x_{i+1/2}\;,\alpha_i)}{a(t, x_{i+1/2}\;,\alpha_i)}}. \end{equation} $ | (3.7) |
Note that in this deduction we have assumed that $ b(t, x_{i+1/2}\;, \alpha_i) \neq 0 $. By setting $ \beta_i(t) = \dfrac{b(t, x_{i+1/2}\;, \alpha_i)}{a(t, x_{i+1/2}\;, \alpha_i)} $, using the boundary conditions in (3.5) yields
| $ \begin{equation} v_i (t) = \dfrac{C_1}{b(t, x_{i+1/2}\;,\alpha_i)} + C_2\, x_i^{-\beta_i(t)}\,\,\, \text{and} \,\,\,v_{i+1} (t) = \dfrac{C_1}{b(t, x_{i+1/2}\;,\alpha_i)} + C_2\, x_{i+1}^{-\beta_i(t)}. \end{equation} $ | (3.8) |
Solving the following linear system with respect to $ C_1 $ and $ C_2 $ yields
| $ \begin{equation} \begin{cases} v_i (t) = \dfrac{C_1}{b(t, x_{i+1/2}\;,\alpha_i)} + C_2\, x_i^{-\beta_i(t)} \\ v_{i+1}(t) = \dfrac{C_1}{b(t, x_{i+1/2}\;,\alpha_i)} + C_2\, x_{i+1}^{-\beta_i(t)} \end{cases} \end{equation} $ | (3.9) |
yields
| $ \begin{equation} \rho_i(v)(t) = C_1 = \dfrac{b(t, x_{i+1/2}\;,\alpha_i)\,\left(x_{i+1}^{\beta_i(t)}v_{i+1}(t)-x_{i}^{\beta_i(t)}v_i (t)\right)}{x_{i+1}^{\beta_i(t)}-x_{i}^{\beta_i(t)}} \end{equation} $ | (3.10) |
$ \rho_i (v)(t) $ provides an approximation to the $ \rho(v)(t) $ at $ x_{i+1/2} $. Similarly the approximation of $ \rho(v)(t) $ at $ x_{i-1/2} $ is given by
| $ \begin{align} \rho(v)(t)\bigg|_{x_{i-1/2}} = \dfrac{b(t, x_{i-1/2},\alpha_i)\,\left(x_{i}^{\beta_{i-1}\;(t)}v_{i}(t)-x_{i-1}^{\beta_{i-1}\;(t)}v_{i-1} (t)\right)}{x_{i}^{\beta_{i-1}\;(t)}-x_{i-1}^{\beta_{i-1}\;(t)}} \end{align} $ | (3.11) |
$\underline{\bf Case\; II}:$ This is the degenerated zone. The aims here is to approximate $ \rho $ at $ x_{1/2} $ in the sub-interval $ I_0 = [0, x_1] $ for $ i = 0 $. In this case, the following problem is considered
| $ \begin{equation} \begin{split} \bigg(a(t, x_{1/2},\alpha_1)\,x \dfrac{\partial v}{\partial x}+b(t, x_{1/2},\alpha_1)\,v \bigg)' = C_2\,\,\,\textbf{in}\,\,[0,x_1] \\ v(0) = v_0(t),\,\,\,v(x_1) = v_1(t) \end{split} \end{equation} $ | (3.12) |
where $ C_2 $ is an unknown constant to be determined. Following [6], integrating (3.12) yields
| $ \begin{eqnarray} \rho_0(v)\vert_{1/2} (t) = a(t, x_{1/2},\alpha_i)\,x_{1/2} \dfrac{\partial v}{\partial x}+ b(t, x_{1/2},\alpha_1)\,v = b(t, x_{1/2},\alpha_1)\,v_0(t) +C_2\,x_{1/2}. \end{eqnarray} $ | (3.13) |
Since $ x_{1/2} = \dfrac{x_1+ x_0}{2} $ with $ x_0 = 0 $, we have $ C_2\, x_1 = (a(x_{1/2}, t, \alpha_1)+b(t, x_{1/2}, \alpha_1))(v_1(t)-v_0(t)) $. Therefore we have
| $ \begin{equation} \begin{split} &\rho_0(v)\vert_{1/2} (t)\\ & = \dfrac{1}{2}\bigg[ (a(t, x_{1/2},\alpha_1)+ b(t, x_{1/2},\alpha_1))v_1(t)-(a(t, x_{1/2},\alpha_1)-b(x_{1/2},t,\alpha_1))v_0(t)\bigg]. \end{split} \end{equation} $ | (3.14) |
By replacing $ \rho $ by its approximated value 3.10, 3.11 and 3.14, (3.3) becomes for $ i = 0, 1, \cdots, N_1-1 $
| $ \begin{equation} \dfrac{d v_i(t) }{d t} + \sup\limits_{\alpha_i \in \mathcal{A}} \dfrac{1}{l_i}\,\left[x_{i+1/2}\rho_i(v)(t)\bigg|_{x_{i+1/2}} -x_{i-1/2}\rho_i(v)(t)\bigg|_{x_{i-1/2}}+c_i(t,\alpha_i)\, v_i (t)\,l_i \right] = 0 \end{equation} $ | (3.15) |
By setting $ \tau = T-t $ and including the boundary conditions, we have the following system of Ordinary Differential Equation (ODE) coupled with optimisation problem.
| $ \left\{\begin{array}{l} \frac{-d \mathbf{v}(\tau)}{d \tau}+\sup\limits_{\alpha \in \mathcal{A}^{N_{1}-1\;\;}}[A(\alpha, \tau) \mathbf{v}(\tau)+G(\alpha, \tau)]=0 \\ \mathbf{v}(0) \text { given }, \end{array}\right. $ | (3.16) |
which can be rewritten as
| $ \left\{\begin{array}{l} \frac{d \mathbf{v}(\tau)}{d \tau}+\inf\limits_{\alpha \in \mathcal{A}^{N_{1}-1\;\;}}[E(\alpha, \tau) \mathbf{v}(\tau)+F(\alpha, \tau)]=0 \\ \mathbf{v}(0) \text { given, } \end{array}\right. $ | (3.17) |
where $ \mathcal{A}^{N_{1}-1} = \underset{N_{1}-1}{\underbrace{\mathcal{A} \times \mathcal{A}\times \cdots \times \mathcal{A}}} $, $ \textbf{v}(\tau) = (v_1(\tau), \cdots, v_{N_1-1}(\tau)) $ and $ F(\alpha, \tau) = (F_1(\alpha_1, \tau), \cdots, F_{N_1-1}(\alpha_{N_1-1}, \tau)) $ includes all Dirichlet boundary and final conditions, $ A (\alpha, \tau) = -E(\alpha, \tau) $ and $ G(\alpha, \tau) = - F(\alpha, \tau) $ are defined as for $ i = 1, \cdots, N_1-1 $
| $ \begin{align} E_{i,i+1}(\alpha_i, \tau)& = -x_{i+1/2}\dfrac{b_{i+1/2}(\tau,\alpha_i)\,x_{i+1}^{\beta_i(\tau)} }{l_i\,(x_{i+1}^{\beta_i(\tau)}-x_{i}^{\beta_i(\tau)})}, \end{align} $ | (3.18) |
| $ \begin{align} E_{i,i}(\alpha_i, \tau) & = \left(x_{i+1/2}\dfrac{b_{i+1/2}(\tau,\alpha_i)\,x_{i}^{\beta_i(\tau)} }{l_i\,(x_{i+1}^{\beta_i(\tau)}-x_{i}^{\beta_i(\tau)})}+ x_{i-1/2}\dfrac{b_{i-1/2}(\tau,\alpha_i)\,x_{i}^{\beta_{i-1}\;(\tau)} }{l_i\,(x_{i}^{\beta_{i-1}\;(\tau)}-x_{i-1}^{\beta_{i-1}\;(\tau)})}- c_i(\tau,\alpha_i) \right), \end{align} $ | (3.19) |
| $ \begin{align} E_{i,i-1}(\alpha_i, \tau)& = -x_{i-1/2}\dfrac{b_{i-1/2}(\tau,\alpha_i)\,x_{i-1}^{\beta_{i-1}\;(\tau)} }{l_i\,(x_{i}^{\beta_{i-1}\;(\tau)}-x_{i-1}^{\beta_{i-1}\;(\tau)})}, \end{align} $ | (3.20) |
| $ \begin{align} E_{1,1}(\alpha_1, \tau)& = x_{1+1/2}\dfrac{b_{1+1/2}(\tau,\alpha_1)\,x_{1}^{\beta_1(\tau)} }{l_1\,(x_{2}^{\beta_1(\tau)}-x_{1}^{\beta_1(\tau)})} + \dfrac{1}{4\,l_1} x_{1}(a_{1/2}(\tau,\alpha_1)+b_{1/2(\tau,\alpha_1)}) - c_1(\tau,\alpha_1) \end{align} $ | (3.21) |
| $ \begin{align} E_{1,2}(\alpha_1, \tau)& = - x_{1+1/2}\dfrac{b_{1+1/2}(\tau,\alpha_1)\,x_{2}^{\beta_1(\tau)} }{l_1\,(x_{2}^{\beta_1(\tau)}-x_{1}^{\beta_1(\tau)})} \end{align} $ | (3.22) |
$ G(\alpha, \tau) = \left[\begin{array}{c} -\dfrac{1}{4\, l_1}\, x_{1}(a_{1/2}(\tau, \alpha_1)-b_{1/2}(\tau, \alpha_1))\, v_0 \\ 0\\ \vdots\\ 0\\ -x_{N_1-1/2}\dfrac{b_{N_1-1/2}(\tau, \alpha_{N_1-1})\, x_{N_1}^{\beta_{N_1-1}\; (\tau)} }{l_{N_1-1}\, (x_{N_1}^{\beta_{N_1-1}\; (\tau)}-x_{N_1-1}^{\beta_{N_1-1}\; (\tau)})}v_{N_1} \end{array} \right]. $
Theorem 2. Assume that $ c $ given in (3.1) is negative and let $ h = \underset{1\leq i\leq N_1} {\max} l_i $. If $ h $ is relatively small then the matrix $ E (\alpha, \tau) $ in the system (3.17) is an M-matrix for any $ \alpha \, \in\, \mathcal{A}^{N_{1}-1} $.
Proof. Let us show that $ E(\alpha, \tau) $ has positive diagonal, non-positive off diagonal, and is diagonally dominant. We first note that
| $ \begin{equation} \dfrac{b_{i+1/2}(\tau,\alpha)}{x_{i+1}^{\beta_i(\tau)}- x_{i}^{\beta_i(\tau)}} = \dfrac{a_{i+1/2}(\tau,\alpha)\,\beta_i(\tau) }{x_{i+1}^{\beta_i(\tau)}- x_{i}^{\beta_i(\tau)}} \gt 0, \end{equation} $ | (3.23) |
for $ i = 1, \cdots, N_1-1 $, and all $ b_{i+1/2}(\tau, \alpha) \neq 0, \; b_{i-1/2}(\tau, \alpha) \neq 0, $ with $ a_{i+1/2}(\tau, \alpha) > 0 $ and $ a_{i-1/2}(\tau, \alpha) > 0 $.
This also holds when $ b_{i+1/2}(\tau, \alpha) \rightarrow 0 $ and $ b_{i-1/2}(\tau, \alpha) \rightarrow 0 $, that is
| $ \begin{equation} \begin{split} &\lim\limits_{b_{i+1/2}\;\;(\tau,\alpha)\rightarrow 0} \dfrac{b_{i+1/2}(\tau,\alpha)}{x_{i+1}^{\beta_i(\tau)}- x_{i}^{\beta_i(\tau)}} = \dfrac{b_{i+1/2}(\tau,\alpha) }{e^{\beta_{i}(\tau)\ln(x_{i+1}\;)}-e^{\beta_{i}(\tau)\ln(x_{i})}} = \dfrac{b_{i+1/2}(\tau,\alpha) }{\beta_{i}(\tau)\ln(x_{i+1})-\beta_{i}(\tau)\ln(x_{i})} \\ & = a_{i+1/2}(\tau,\alpha)\left(\ln \dfrac{ x_{i+1}}{x_{i}}\right)^{-1} \gt 0,\\ & \,\lim\limits_{b_{i-1/2}\;\;(\tau,\alpha)\rightarrow 0} \dfrac{b_{i-1/2}(\tau)}{x_{i}^{\beta_{i-1}\;(\tau)}- x_{i-1}^{\beta_{i-1}\;(\tau)}} = \dfrac{b_{i-1/2}(\tau,\alpha) }{e^{\beta_{i-1}\;(\tau)\ln(x_{i})}-e^{\beta_{i-1}\;(\tau)\ln(x_{i-1}\;)}}\\ & = \dfrac{b_{i-1/2}(\tau,\alpha) }{\beta_{i-1}(\tau)\ln(x_{i})-\beta_{i-1}(\tau)\ln(x_{i-1})} = a_{i-1/2}(\tau,\alpha) \left(\ln \dfrac{ x_{i}}{x_{i-1}}\right)^{-1} \gt 0. \end{split} \end{equation} $ | (3.24) |
Using the definition of $ E (\alpha, \tau) $ given above, we see that
| $ \begin{equation*} E_{i,i} \geqslant 0,\,\,\,E_{i,i+1} \leqslant 0,\,\,\, E_{i,i-1}\leqslant 0\;\;\; i = 2,\cdots,N_1-1, \end{equation*} $ |
| $ \begin{equation*} \left|E_{i,i}\right| \geq \left|E_{i,i-1}\right|+\left|E_{i,i+1}\right| \end{equation*} $ |
because $ x_{i+1}^{\beta_i(\tau)} \approx x_{i}^{\beta_i(\tau)} + x_{i}^{\beta_i(\tau)-1}\, {\beta_i(\tau)}\, h $, $ x_{i-1}^{\beta_{i-1}\;(\tau)} \approx x_{i}^{\beta_{i-1}\;(\tau)} - x_{i}^{\beta_{i-1}\;(\tau)-1}\, {\beta_{i-1}(\tau)}\, h $ and
| $ \begin{equation*} \begin{split} & \left|E_{i,i}\right| - \left|E_{i,i+1}\right|-\left|E_{i,i-1}\right|\\ & = -\underset{\rightarrow 0}{\underbrace{\underset{ \gt 0}{\underbrace{\left(\dfrac{b_{i+1/2}(\tau)}{x_{i+1}^{\beta_i(\tau)}-x_{i}^{\beta_i(\tau)}}\right)}} \underset{\rightarrow 0}{\underbrace{\left(h^{\beta_i}\,\beta_i\,x_{i}^{\beta_{i}-1}\right)}} }}+ \underset{\rightarrow 0}{\underbrace{\underset{ \gt 0}{\underbrace{\left(\dfrac{b_{i-1/2}(\tau,\alpha)}{x_{i}^{\beta_{i-1}\;(\tau)}-x_{i-1}^{\beta_{i-1}\;(\tau)}}\right)}} \underset{\rightarrow 0}{\underbrace{\left(h^{\beta_{i-1}}\,\beta_{i-1}\,x_{i}^{\beta_{i-1}\;-1}\right)}} }} - c_i(\tau,\alpha_i). \end{split} \end{equation*} $ |
Note that for $ i = 1 $, we have $ E_{1, 1}\geq 0 $ if $ {a_{1/2}(\tau, \alpha_1)} + b_{1/2}(\tau, \alpha_1) $, are nonnegative and $ c_1(\tau, \alpha_1) < 0 $. So $ E(\alpha, \tau) $ is diagonally dominant and is therefore an $ \textbf{M} $-matrix.
Indeed the assumption $ c < 0 $ can be relaxed, but if positive it should not be more that a certain threshold $ c_{0} > 0 $ depending of our numerical scheme. Indeed this is not restrictive as from numerical experiments the threshold $ c_{0} > 0 $ is always the best comparing to finite difference scheme where its not monotonicity does not depend on coefficients.
Here we consider the generalized HJB Eq (2.13) in dimension 2 which can be written in the form
| $ \begin{equation} \dfrac{\partial v(t,x,y) }{ \partial t} + \sup\limits_{\alpha \in \mathcal{A}}\left[ \nabla\cdot \left( k(t,x,y,\alpha) \right) + c(t,x,y,\alpha)\,v(t,x,y) \right] = 0, \end{equation} $ | (3.25) |
where $ k (t, x, y, \alpha) = A(t, x, y, \alpha)\cdot\nabla v(t, x, y)+ b\, v(t, x, y) $ is the flux,
| $ \begin{equation} b = (x\,b_1(t,x,y,\alpha), y\, b_2(t,x,y,\alpha))^T \,\,\text{and} \,\,A = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right), \end{equation} $ | (3.26) |
We will assume that $ a_{21} = a_{12} $. We also define the following coefficients, which will help us to build our scheme smoothly $ a_{11}(t, x, y, \alpha) = a(t, x, y, \alpha)\, x^2, a_{22}(t, x, y, \alpha) = \overline{a}(t, x, y, \alpha) y^2 $ and $ a_{1 2} = a_{2 1} = d_1(t, x, y, \alpha)\, x\, y $. Although this initial value problem (3.25) is defined on the unbounded region $ \mathbb{R}^2 $, we often restrict our consideration to a bounded region. As usual the two dimensional domain is truncated to $ I_{x} \times I_{y} $, where $ I_{x} = [0, x_{\text{max}}] $ and $ I_{y} = [0, y_{\text{max}}] $ be divided into $ N_1 $ and $ N_2 $ sub-intervals:
| $ I_{x_{i}} : = (x_{i}, x_{i+1}),\,\, I_{y_j} : = (y_{j}, y_{j+1}),\,\,\,\, i = 0,\cdots ,N_1-1,\,\,j = 0,\cdots, N_2-1 $ |
with $ 0 = x_{0} < x_{1} < \cdots \cdots < x_{N_1} = x_{\text{max}} $ and $ 0 = y_{0} < y_1 < \cdots \cdots < y_{N_2} = y_{\text{max}} $. This defines a mesh on $ I_{x} \times I_{y} $ with all the mesh lines perpendicular to one of the axes.
We also set
| $ x_{i+1/2} = \dfrac{x_{i} + x_{i+1} }{2},\, x_{i-1/2} = \dfrac{x_{i-1} + x_{i} }{2},\, y_{j+1/2} = \dfrac{y_{j} + y_{j+1} }{2},\, \; y_{j-1/2} = \dfrac{y_{j-1} + y_{j} }{2}, $ |
for each $ i = 1, \cdots, N_1-1 $ and each $ j = 1, \cdots, N_2-1 $. We denote $ N = (N_1-1)\times (N_2-1) $. These mid-points form a second partition of $ I_{x} \times I_{y} $ if we define $ x_{-1/2} = x_{0} $, $ x_{N_1+1/2} = x_{\text{max}} $, $ y_{-1/2} = y_{0} $ and $ y_{N_2+1/2} = y_{\text{max}} $. For each $ i = 0, 1, \cdots, N_1 $ and $ j = 0, 1, \cdots, N_2 $, we set $ h_{x_i} = x_{i+1/2} - x_{i-1/2} $ and $ h_{y_j} = y_{j+1/2} - y_{j-1/2} $.
We now discuss the finite volume method for (3.25). Integrating both size of (3.25) over $ \mathcal{R}_{i, j} = \left[ x_{i-1/2}, x_{i+1/2} \right] \times \left[ y_{j-1/2}, y_{j+1/2}\right] $, we have
| $ \begin{equation} \begin{split} & \int_{x_{i-1/2}}^{x_{i+1/2}} \int_{y_{j-1/2}}^{y_{j+1/2}}\dfrac{\partial v (t,x,y)}{ \partial t}\, dx\, dy \\ & + \int_{x_{i-1/2}}^{x_{i+1/2}}\int_{y_{j-1/2}}^{y_{j+1/2}} \sup\limits_{\alpha \in \mathcal{A}} \left[ \nabla \cdot \left( k(v (t,x,y,\alpha))\right) + c(t,x,y,\alpha)\,v(t,x,y) \right]\, dx\,dy = 0, \end{split} \end{equation} $ | (3.27) |
for $ i = 1, 2, \cdots, N_1-1 $, $ j = 1, 2, \cdots, N_2-1 $. Applying the mid-points quadrature rule to the first and the last point terms, we obtain the above
| $ \begin{equation} \dfrac{d v_{i,j} (t) }{d t}\,l_{i,j} + \sup\limits_{\alpha_{i,j} \in \mathcal{A}} \left[ \int_{ \mathcal{R}_{i,j}}\nabla \cdot \left( k(v(t,x,y,\alpha_{i,j} )\right)\,dx\,dy + c_{i,j}(t,\alpha_{i,j} )\, v_{i,j}(t)\,l_{i,j}\right] = 0 \end{equation} $ | (3.28) |
for $ i = 1, 2, \cdots N_1-1 $, $ j = 1, 2, \cdots N_2-1 $ where $ l_{i, j} = \left(x_{i+1/2}-x_{i-1/2}\; \right) \times \left(y_{j+1/2}-y_{j-1/2}\right) $ is the length of $ \mathcal{R}_{i, j} $, and $ v_{i, j}(t) $ denotes the nodal approximation to $ v(t, x_{i}, y_{j}) $. We now consider the approximation of the middle term in (3.28). Let $ \bf n $ denote the unit vector outward-normal to $ \partial \mathcal{R}_{i, j} $. By Ostrogradski Theorem, integrating by parts and using the definition of flux $ k(v) $, we have
| $ \begin{equation} \begin{split} \int_{\mathcal{R}_{i,j}} \nabla \cdot \left( k(v)\right) \,dx\,dy& = \int_{\partial \mathcal{R}_{i,j}} k(v(t,x,y,\alpha_{i,j})) \cdot \bf n \, ds \\ & = \int_{\left(x_{i+1/2}\;,y_{j-1/2} \;\right)}^{\left(x_{i+1/2}\;,y_{j+1/2} \;\right)} \left(a_{11}\,\dfrac{\partial v }{\partial x}+ a_{12}\,\dfrac{\partial v }{\partial y}+ x\,b_1\,v \right)d y \\ &- \int_{\left(x_{i-1/2}\;,y_{j-1/2} \;\right)}^{\left(x_{i-1/2}\;,y_{j+1/2} \;\right)} \left(a_{11}\,\dfrac{\partial v }{\partial x}+a_{12}\,\dfrac{\partial v }{\partial y}+ x b_1\,v \right)d y \\ & + \int_{\left(x_{i-1/2}\;,y_{j+1/2} \;\right)}^{\left(x_{i+1/2}\;,y_{j+1/2} \;\right)} \left(a_{21}\,\dfrac{\partial v }{\partial x}+a_{22}\,\dfrac{\partial v }{\partial y} + y\, b_2\,v \right)d x\\ &- \int_{\left(x_{i-1/2}\;,y_{j-1/2} \;\right)}^{\left(x_{i+1/2}\;,y_{j-1/2} \;\right)} \left(a_{21}\,\dfrac{\partial v }{\partial x}+ a_{22}\,\dfrac{\partial v }{\partial y}+y\, b_2\,v \right)d x. \end{split} \end{equation} $ | (3.29) |
We shall look at (3.29) term by term. For the first term we want to approximate the integral by a constant as
| $ \begin{equation} \begin{split} &\int_{\left(x_{i+1/2}\;,y_{j-1/2} \;\right)}^{\left(x_{i+1/2}\;,y_{j+1/2} \;\right)} \left(a_{11}\,\dfrac{\partial v }{\partial x}+ a_{12}\,\dfrac{\partial v }{\partial y}+ x \,b_1\,v \right)d y \\ & \approx \left(a_{11}\,\dfrac{\partial v }{\partial x}+ a_{12}\,\dfrac{\partial v}{\partial y}+x\, b_1\,v \right)|_{\left(x_{i+1/2}\;,y_{j} \right)} \cdot h_{y_j}. \end{split} \end{equation} $ | (3.30) |
To achieve this, it is clear that we now need to derive approximations of the $ k(v(x, y, t, \alpha_{i, j})) \cdot \bf n $ defined above at the mid-point $ \left(x_{i+1/2}\;, y_{j} \right) $, of the interval $ I_{x_{i}} $ for $ i = 0, 1, \cdots N_1-1 $. This discussion is divided into two cases for $ i \geq 1 $ and $ i = 0 $ on $ I_0 = [0, x_{1}] $. This is really an extension of the one dimensional fitted finite volume presented in the previous section.
$\underline{\bf Case\; I}:$ For $ i\geq 1 $.
Remember that $ a_{11}(t, x, y, \alpha) = a(t, x, y, \alpha)\, x^2 $, we approximate the term $ \left(a_{11} \dfrac{\partial v}{\partial x}+ x\, b_1\, v \right) $ by solving the following two points boundary value problem
| $ \begin{equation} \begin{split} &\left({a} (t, x_{i+1/2}\;, y_j,\alpha_{i,j})\,x \dfrac{\partial v}{\partial x} + b_1 (t, x_{i+1/2}\;,y_{j},\alpha_{i,j})\,v \right)' = 0, \\ & v(t,x_i,y_j) = v_{i,j}(t),\,\,\,\, v(t, x_{i+1},y_j) = v_{i+1,j}(t). \end{split} \end{equation} $ | (3.31) |
Integrating (3.31) yields the first-order linear equations
| $ \begin{equation} {a} (t,x_{i+1/2}\;,y_j,\alpha_{i,j})\,x \dfrac{\partial v}{\partial x}+ b_1 (t,x_{i+1/2}\;,y_j,\alpha_{i,j})\,v = C_1 \end{equation} $ | (3.32) |
where $ C_1 $ denotes an additive constant. Following the one dimensional fitted finite volume presented in the previous section, we have
| $ \begin{equation} C_1 = \dfrac{{b_1}_{i+1/2,j}(t,\alpha_{i,j})\,\left(x_{i+1}^{\beta_{i,j}\;(t)}\,v_{i+1,j}-x_{i}^{\beta_{i,j}\;(t)}v_{i,j} \right)}{x_{i+1}^{\beta_{i,j}\;(t)}-x_{i}^{\beta_{i,j}\;(t)}}. \end{equation} $ | (3.33) |
Therefore,
| $ \begin{equation} \begin{split} & a_{11}\,\dfrac{\partial v }{\partial x} + a_{12}\,\dfrac{\partial v }{\partial y}+ x\,b_1\,v\\ & \approx x_{i+1/2}\left( \dfrac{{b_1}_{i+1/2,j}(t,\alpha_{i,j})\,\left(x_{i+1}^{\beta_{i,j}\;(t)}v_{i+1,j}-x_{i}^{\beta_{i,j}\;(t)}\,v_{i,j} \right)}{x_{i+1}^{\beta_{i,j}\;(t)}-x_{i}^{\beta_{i,j}\;(t)}} + d_1\,y\,\,\dfrac{\partial v }{\partial y}\right), \end{split} \end{equation} $ | (3.34) |
where $ {b_1}(t, x_{i+1/2}\;, y_j, \alpha_{i, j}) = {b_1}_{i+1/2, j}(t, \alpha_{i, j}) $, $ {a}(t, x_{i+1/2}\;, y_j, \alpha_{i, j}) = {a}_{i+1/2, j}(t, \alpha_{i, j}) $, $ \beta_{i, j}(t) = \dfrac{{b_1}_{i+1/2, j}(t, \alpha_{i, j})}{{a}_{i+1/2, j}(t, \alpha_{i, j})} $ and $ a_{12} = a_{21} = d_{1}(t, x, y, \alpha)\, x\, y $. Finally, we use the forward difference,
| $ \begin{equation*} \dfrac{\partial v }{\partial y}\bigg|_{(x_{i+1/2}\;,y_{j})} \approx\dfrac{v_{i,j+1}-v_{i,j}}{h_{y_j}} \end{equation*} $ |
Finally,
| $ \begin{equation} \begin{split} &\left[a_{11}\,\dfrac{\partial v }{\partial x} + a_{12}\,\dfrac{\partial v}{\partial y}+ x\,b_1\,v \right]_{\left(x_{i+1/2}\;,y_j \right)} \cdot h_{y_j} \approx x_{i+1/2} \times\\ &\left( \dfrac{{b_1}_{i+1/2,j}(t,\alpha_{i,j})\,\left(x_{i+1}^{\beta_{i,j}\;(t)}v_{i+1,j}-x_{i}^{\beta_{i,j}\;(t)}\,v_{i,j} \right)}{x_{i+1}^{\beta_{i,j}\;(t)}- x_{i}^{\beta_{i,j}\;(t)}} + {d_1}_{i,j}(t,\alpha_{i,j})\,y_j\,\dfrac{v_{i,j+1}-v_{i,j}}{h_{y_j}} \right) \cdot h_{y_j}. \end{split} \end{equation} $ | (3.35) |
Similarly, the second term in (3.29) can be approximated by
| $ \begin{equation} \begin{split} &\left[a_{11}\,\dfrac{\partial v }{\partial x}+ a_{12}\,\dfrac{\partial v}{\partial y}+x\,b_1\,v \right]_{\left(x_{i-1/2},{y_{j}} \right)} \cdot h_{y_j} \approx x_{i-1/2} \times\\ & \left( \dfrac{{b_1}_{i-1/2,j}(t,\alpha_{i,j})\,\left(x_{i}^{\beta_{i-1,j}(t)}v_{i,j}-x_{i-1}^{\beta_{i-1,j}(t)}v_{i-1,j} \right)}{x_{i}^{\beta_{i-1,j}(t)}- x_{i-1}^{\beta_{i-1,j}(t)}} + {d_1}_{i,j}(t,\alpha_{i,j})\,y_j\,\dfrac{v_{i,j+1}-v_{i,j}}{h_{{y_j}}} \right) \cdot h_{y_j}. \end{split} \end{equation} $ | (3.36) |
$\underline{\bf Case\; II}:$ For $ j\geq 1 $.
For the third term we want to approximate the integral by a constant, that is
| $ \begin{equation} \begin{split} &\int_{\left(x_{i-1/2},y_{j+1/2}\; \right)}^{\left(x_{i+1/2}\;,y_{j+1/2}\;\right)} \left(a_{21}\,\dfrac{\partial v }{\partial x}+ a_{22}\,\dfrac{\partial v }{\partial y}+ y\,b_2\,v \right)d x \\ & \approx \left(a_{21}\,\dfrac{\partial v }{\partial x}+ a_{22}\,\dfrac{\partial v}{\partial y}+ y\,b_2\,v \right)|_{\left({y_{j+1/2}}\;,x_{i} \right)} \cdot h_{x_i}. \end{split} \end{equation} $ | (3.37) |
Following the first case of this section, we have
| $ \begin{equation} \label{vol3} \begin{split} &\left[a_{21}\,\dfrac{\partial v }{\partial x}+ a_{22}\,\dfrac{\partial v}{\partial x_2}+ y\,b_2\,v \right]_{\left(x_{i},{y_{j+1/2}} \right)} \cdot h_{x_i} \approx y_{j+1/2} \times\nonumber\\ & \left( \dfrac{{b_2}_{i,j+1/2}(t,\alpha_{i,j})\,\left({y_{j+1}}^{\bar{\beta}_{i,j}(t)}v_{i,j+1}-{y_{j}}^{\bar{\beta}_{i,j} (t)}\,v_{i,j} \right)}{{y_{j+1}}^{\bar{\beta}_{i,j}(t)}- {y_{j}}^{\bar{\beta}_{i,j}(t)}} + {d_1}_{i,j}(t,\alpha_{i,j})\,x_i\,\dfrac{v_{i+1,j}-v_{i,j}}{h_{x_i}} \right) \cdot h_{x_i}. \end{split} \end{equation} $ |
Similarly, the fourth term in (3.29) can be approximated by
| $ \begin{equation} \begin{split} &\left[a_{21}\,\dfrac{\partial v }{\partial x}+ a_{22}\,\dfrac{\partial v}{\partial y}+y\,b_2\,v \right]_{\left(x_{i},y_{j-1/2}\; \right)} \cdot h_{x_i} \approx y_{j-1/2} \times \\ & \left( \dfrac{{b_2}_{i,j-1/2}(t,\alpha_{i,j})\,\left(y_{j}^{\bar{\beta}_{i,j-1}(t)}\,v_{i,j}-y_{j-1}^{\bar{\beta}_{i,j-1}(t)}\,v_{i,j-1} \right)}{y_{j}^{\bar{\beta}_{i,j-1}(t)}- y_{j-1}^{\bar{\beta}_{i,j-1}(t)}} + {d_1}_{i,j}(t,\alpha_{i,j})\,x_i\,\dfrac{v_{i+1,j}-v_{i,j}}{h_{x_i}} \right) \cdot h_{x_i}, \end{split} \end{equation} $ | (3.38) |
for $ j = 1, \cdots, N_2-1 $, where $ \bar{\beta}_{i, j}(t) = \dfrac{{b_2}_{i, j+1/2}(t, \alpha_{i, j})}{\bar{a}_{i, j+1/2}(t, \alpha_{i, j})} $ with $ a_{22}(t, x, y, \alpha) = \bar{a}(t, x, y, \alpha)\, y^2 $.
$\underline{\bf Case\; III}:$ Approximation of the flux at $ I_0 $. Note that the analysis in case I does not apply to the approximation of the flux on $ [0, x_1] $ because (3.31) is degenerated. Therefore, we reconsider the following form
| $ \begin{align} \left(a(t,x_{1/2},y_j,\alpha_{1,j})\,x \dfrac{\partial v}{\partial x}+{b_1}(t,x_{1/2},y,\alpha_{1,j})\,v \right)' \equiv C_2\,\,\,\textbf{in}\,\,[0,x_{1}] \\ v(x_0,y_j) = v_{0,j},\,\,\,\, v(x_{1},{y_j}) = v_{1,j}, \end{align} $ | (3.39) |
where $ C_2 $ is an unknown constant to be determined. Integrating (3.39), we can deduce that
| $ \begin{equation} \begin{split} &\left[a_{11}\,\dfrac{\partial v }{\partial x} + a_{12}\,\dfrac{\partial v}{\partial y}+ x\,b_1\,v \right]_{\left(x_{1/2},{y_{j}} \right)} \cdot h_{y_j} \\ &\approx x_{1/2}\left( \dfrac{1}{2}\left[ (a_{x_{1/2},\;j}(t,\alpha_{1,j}) + {b_1}_{x_{1/2},\;j}(t,\alpha))\,v_{1,j}-(a_{x_{1/2},\;j}(t,\alpha_{1,j}) - {b_1}_{x_{1/2},\;j}(t,\alpha_{1,j}))\,v_{0,j}\right]\right. \\ &\left.+ {d_1}_{1,j}(t,\alpha_{1,j})\,y_j\,\dfrac{v_{1,j+1}-v_{1,j}}{h_{y_j}} \right) \cdot h_{y_j}. \end{split} \end{equation} $ | (3.40) |
$\underline{\bf Case\; IV}:$ Approximation of the flux at $ J_0 $.
Using the same procedure for the approximation of the flux at $ I_0 $, we deduce that
| $ \begin{align} &\left[a_{21}\,\dfrac{\partial v }{\partial x}+ a_{22}\,\dfrac{\partial v}{\partial y}+ y\,b_2\,v \right]_{\left(x_{i},{y_{1/2}} \right)} \cdot h_{x_{i}}\approx \\ & y_{1/2}\left( \dfrac{1}{2}\left[(\bar{a}_{i,y_{1/2}}(t,\alpha_{i,1}) +{b_2}_{i,y_{1/2}}(t,\alpha))\,v_{i,1}-(\bar{a}_{i,y_{1/2}}(t,\alpha_{i,1}) -{b_2}_{i,y_{1/2}}(t,\alpha_{i,1}))\,v_{i,0}\right] \right. \\ &\left. +{d_1}_{i,1}(t,\alpha_{i,1})\,x_i\,\dfrac{v_{i+1,1}-v_{i,1}}{h_{x_i}} \right) \cdot h_{x_i}. \end{align} $ | (3.41) |
By replacing the flux by his value for $ i = 1, \cdots, N_1-1 $ and $ j = 1, \cdots, N_2-1 $, Eq (3.28) becomes
| $ \begin{equation} \begin{split} &\dfrac{d v_{i,j} }{d t} +\\ & \sup\limits_{\alpha_{i,j} \in \mathcal{A}} \dfrac{1}{l_{i,j}}\,\left[x_{{i+1/2}}\left( \dfrac{{b_1}_{i+1/2,j}(t,\alpha)\,\left(x_{{i+1}}^{\beta_{i,j}\;(t)}\,v_{i+1,j}-x_{{i}}^{\beta_{i,j}\;(t)}\,v_{i,j} \right)}{x_{{i+1}}^{\beta_{i,j}\;(t)}- x_{{i}}^{\beta_{i,j}\;(t)}}\right){h_{y_j}} \right. \\ &\left. + x_{{i+1/2}}\left( {d_1}_{i,j}(t,\alpha_{i,j})\,y_j\,\dfrac{v_{i,j+1}-v_{i,j}}{h_{y_j}} \right) \cdot h_{y_j} \right. \\ & \left.- x_{{i-1/2}}\left( \dfrac{{b_1}_{i-1/2,j}(t,\alpha_{i,j})\,\left(x_{i}^{\beta_{i-1,j}}\,v_{i,j}-x_{{i-1}}^{\beta_{i-1,j}(t)}\,v_{i-1,j} \right)}{x_{{i}}^{\beta_{i-1,j}(t)}- x_{{i-1}}^{\beta_{i-1,j}(t)}} + {d_1}_{i,j}(t,\alpha_{i,j})\,y_j\,\dfrac{v_{i,j+1}-v_{i,j}}{h_{{y_j}}} \right) \cdot h_{{y_j}} \right.\\ & \left. + {y_{j+1/2}}\left( \dfrac{{b_2}_{i,j+1/2}(t,\alpha_{i,j})\,\left({y_{j+1}}^{\bar{\beta}_{i,j}(t)}\,v_{i,j+1}-{y_{j}}^{\bar{\beta}_{i,j}(t)}v_{i,j} \right)}{{y_{j+1}}^{\bar{\beta}_{i,j}(t)} - {y_{j}}^{\bar{\beta}_{i,j}(t)}} + {d_1}_{i,j}(t,\alpha_{i,j})\,x_i\,\dfrac{v_{i+1,j}-v_{i,j}}{h_{x_{i}}} \right) \cdot h_{x_{i}} \right. \\ & \left. - {y_{j-1/2}}\left( \dfrac{{b_2}_{i,j-1/2}(t,\alpha_{i,j})\,\left({y_{j}}^{\bar{\beta}_{i,j-1}(t)}v_{i,j}-{y_{j-1}}^{\bar{\beta}_{i,j-1}(t)}\,v_{i,j-1} \right)}{{y_{j}}^{\bar{\beta}_{i,j-1}(t)}- {y_{j-1}}^{\bar{\beta}_{i,j-1}(t)}} \right.\right. \\ &\left.\left. + {d_1}_{i,j}(t,\alpha_{i,j})\,x_i\,\dfrac{v_{i+1,j}-v_{i,j}}{h_{x_{i}}} \right) \cdot h_{x_{i}} + c_{i,j}(t,\alpha_{i,j})\, v_{i,j}\,l_{i,j}\right] = 0 \end{split} \end{equation} $ | (3.42) |
By setting $ \tau = T-t $ and including the boundary conditions, we have the following system
| $ \begin{equation} \label{p5} \begin{cases} & \underset{\alpha \in \mathcal{A}^N}{\sup}\, \left[e_{i-1,j}^{i,j}(\tau,\alpha)\, v_{i-1,j} +e_{i,j}^{i,j}(\tau,\alpha)\, v_{i,j} + e_{i+1,j}^{i,j}(\tau,\alpha)\, v_{i+1,j}+ e_{i,j-1}^{i,j} (\tau,\alpha)v_{i,j-1}\right.\\ \nonumber & \left.+e_{i,j+1}^{i,j} (\tau,\alpha)v_{i,j+1}\right] -\dfrac{d v_{i,j} }{d \tau} = 0,\,\,\mbox{with}\; \; \,\,\,\, v_{i,j}(0) \,\,\,\text{given}, \end{cases} \end{equation} $ |
where for $ i = 1, \cdots, N_1-1 $, $ j = 1, \cdots, N_2-1 $ and $ N = (N_1-1)\times(N_2-1) $, $ \mathcal{A}^{N} = \underset{(N_{1}-1)\times(N_2-1)}{\underbrace{\mathcal{A} \times \mathcal{A}\times \cdots \times \mathcal{A}}} $. We have
| $ \begin{equation} \begin{split} e_{0,j}^{1,j}& = - \dfrac{1}{4\,l_{1,j} } h_{{y_j}}\,x_{1}(a_{x_{1/2},\;j}(\tau,\alpha_{1,j})- {b_1}_{x_{1/2},\;j}(\tau,\alpha_{1,j}))\,v_{0,j}\\ e_{1,j}^{1,j} & = \dfrac{1}{4\,l_{1,j} } h_{{y_j}}\,x_{1}(a_{x_{1/2},\;j}(\tau,\alpha_{1,j}) + {b_1}_{x_{1/2},\;j}(\tau,\alpha_{1,j})) - \dfrac{1}{2}\,c_{1,j}(\tau,\alpha_{1,j}) \\ & + {d_1}_{1,j}(\tau,\alpha_{1,j})\,x_i\dfrac{h_{{y_j}}}{l_{1,j}} + x_{{1+1/2}} h_{{y_j}} \dfrac{{b_1}_{1+1/2,j}(\tau,\alpha_{1,j})\,x_{{1}}^{\beta_{1,j}\;(\tau)} }{l_{1,j}\left(x_{{2}}^{\beta_{1,j}\;(\tau)}- x_{{1}}^{\beta_{1,j}\;(\tau)}\right)} \\ e_{2,j}^{1,j} & = -{d_1}_{1,j}(\tau,\alpha_{1,j})\,x_i\,\dfrac{h_{{y_j}}}{l_{1,j}} - x_{{1+1/2}} h_{{y_j}} \dfrac{{b_1}_{1+1/2,j}(\tau,\alpha_{1,j})\,x_{{2}}^{\beta_{1,j}\;(\tau)} }{l_{1,j}\left(x_{{2}}^{\beta_{1,j}\;(\tau)}- x_{{1}}^{\beta_{1,j}\;(\tau)}\right)}\\ e_{i,0}^{i,1}& = -\dfrac{1}{4\,l_{i,1} } h_{x_{i}}\,y_{1}( \bar{a}_{i,y_{1/2}}\;(\tau,\alpha_{i,1}) - {b_2}_{i,y_{1/2}}\;(\tau,\alpha_{i,1})) \,v_{i,0}\\ e_{i,1}^{i,1}& = \dfrac{1}{4\,l_{i,1} } h_{x_{i}}\,y_{1}( \bar{a}_{i,y_{1/2}}\;(\tau,\alpha_{i,1}) +{b_2}_{i,y_{1/2}}\;(\tau,\alpha_{i,1}) - \dfrac{1}{2}\,c_{i,1}(\tau,\alpha_{i,1}) \\ & + {d_1}_{i,1} (\tau,\alpha_{i,1})\,y_j\,\dfrac{h_{x_{i}}}{l_{i,1}} + y_{{1+1/2}} h_{x_{i}} \dfrac{{b_2}_{i,1+1/2}(\tau,\alpha_{i,1})\,y_{{1}}^{\bar{\beta}_{i,1}\;(\tau)} }{l_{i,1}\left(y_{{2}}^{\bar{\beta}_{i,1}\;(\tau)}- y_{{1}}^{\bar{\beta}_{i,1}\;(\tau)}\right)} \\ e_{i,2}^{i,1}& = -{d_1}_{i,1}(\tau,\alpha_{i,1}) \,y_j\,\dfrac{h_{x_{i}}}{l_{i,1}} - {y_{1+1/2}} h_{x_{i}} \dfrac{{b_2}_{i,1+1/2}(\tau,\alpha_{i,1})\,{y_{2}}^{\bar{\beta}_{i,1}\;(\tau)} }{l_{i,1}\left({y_{2}}^{\bar{\beta}_{i,1}\;(\tau)}- {y_{1}}^{\bar{\beta}_{i,1}\;(\tau)}\right)}\\ e_{i+1,j}^{i,j} & = - {d_1}_{i,j}(\tau, \alpha_{i,j})\,x_i\,\dfrac{h_{{y_j}}}{l_{i,j}} - x_{{i+1/2}} h_{{y_j}} \dfrac{{b_1}_{i+1/2,j}(\tau, \alpha_{i,j})\,x_{{i+1}}^{\beta_{i,j}\;(\tau)} }{l_{i,j}\left(x_{{i+1}}^{\beta_{i,j}\;(\tau)}- x_{{i}}^{\beta_{i,j}\;(\tau)}\right)}\\ e_{i-1,j}^{i,j}& = - x_{{i-1/2}} h_{{y_j}} \dfrac{{b_1}_{{i-1/2,j}}(\tau, \alpha_{i,j})\,x_{{i-1}}^{\beta_{i-1,j}\;(\tau)} }{l_{i,j}\left(x_{{i}}^{\beta_{i-1,j}\;(\tau)}- x_{{i-1}}^{\beta_{i-1,j}\;(\tau)}\right)}\\ e_{i,j+1}^{i,j} & = - {d_1}_{i,j}(\tau,\alpha_{i,j})) \,y_j\,\dfrac{h_{x_{i}}}{l_{i,j}} - y_{{j+1/2}} h_{x_{i}} \dfrac{{b_2}_{{i,j+1/2}}(\tau,\alpha_{i,j}))\,{y_{j+1}}^{\bar{\beta}_{i,j}\;(\tau)} }{l_{i,j}\left({y_{j+1}}^{\bar{\beta}_{i,j}\;(\tau)}- {y_{j}}^{\bar{\beta}_{i,j}\;(\tau)}\right)}\\ e_{i,j-1}^{i,j}& = - {y_{j-1/2}} h_{x_{i}} \dfrac{{b_2}_{i,j-1/2}(\tau,\alpha_{i,j}))\,{y_{j-1}}^{\bar{\beta}_{i,j-1}\;(\tau)} }{l_{i,j}\left({y_{j}}^{\bar{\beta}_{i,j-1}\;(\tau)}- {y_{j-1}}^{\bar{\beta}_{i,j-1}\;(\tau)}\right)},\\ e_{i,j}^{i,j}& = {d_1}_{i,j}(\tau, \alpha_{i,j}))\,x_i\,\dfrac{h_{{y_j}}}{l_{i,j}} + x_{{i+1/2}} h_{{y_j}} \dfrac{{b_1}_{{i+1/2,j}}(\tau,\alpha_{i,j}))\,x_{{i}}^{\beta_{i,j}\;(\tau)} }{l_{i,j}\left(x_{{i+1}}^{\beta_{i,j}\;(\tau)}- x_{{i}}^{\beta_{i,j}\;(\tau)}\right)} \\ & + x_{{i-1/2}} h_{{y_j}} \dfrac{{b_1}_{{i-1/2,j}}(\tau,\alpha_{i,j}))\,x_{{i}}^{\beta_{i-1,j}\;(\tau)} }{l_{i,j}\left(x_{{i}}^{\beta_{i-1,j}\;(\tau)}- x_{{i-1}}^{\beta_{i-1,j}\;(\tau)}\right)}-c_{i,j}(\tau,\alpha_{i,j})) \\ & {d_1}_{i,j}(\tau,\alpha_{i,j})) \,y_j\,\dfrac{h_{x_{i}}}{l_{i,j}} + {y_{j+1/2}} h_{x_{i}} \dfrac{{b_2}_{i,j+1/2}(\tau,\alpha_{i,j}))\,{y_{j}}^{\bar{\beta}_{i,j}\;(\tau)} }{l_{i,j}\left({y_{j+1}}^{\bar{\beta}_{i,j}\;(\tau)}- {y_{j}}^{\bar{\beta}_{i,j}\;(\tau)}\right)} \\ & +{y_{j-1/2}} h_{x_{i}} \dfrac{{b_2}_{i,j-1/2}(\tau,\alpha_{i,j}))\,{y_{j}}^{{\bar{\beta}}_{i,j-1}\;(\tau)} }{l_{i,j}\left({y_{j}}^{\bar{\beta}_{i,j-1}\;(\tau)}- {y_{j-1}}^{\bar{\beta}_{i,j-1}\;(\tau)}\right)}. \end{split} \end{equation} $ | (3.43) |
As for one dimension case, (3.43) can be rewritten as the ODE coupled with optimization problem
| $ \begin{equation} \begin{cases} \dfrac{d \textbf{v}(\tau)}{d \tau} + \underset{\alpha \in \mathcal{A}^N}{\inf}\,\left[E (\tau, \alpha)\,\textbf{v}(\tau) + F(\tau,\alpha) \right] = 0, \\ \; \; \; \mbox{with}\; \; \,\,\,\, \textbf{v}(0)\,\,\,\text{given}, \end{cases} \end{equation} $ | (3.44) |
or
| $ \begin{equation} \begin{cases} \dfrac{d \textbf{v}(\tau)}{d \tau} = \underset{\alpha \in \mathcal{A}^N}{\sup}\,\left[A (\tau,\alpha)\,\textbf{v}(\tau) + G(\tau, \alpha) \right] \\ \; \; \; \mbox{with}\; \; \,\,\,\, \textbf{v}(0) \,\,\,\text{given}, \end{cases} \end{equation} $ | (3.45) |
where $ A(\tau, \alpha) = - E (\tau, \alpha) $, $ E (\tau, \alpha) (I, J) = \left(e_{i', j'}^{i, j}\right) $, $ i', i = 1, \cdots, N_1-1 $, $ j', j = 1, \cdots, N_2-1 $, $ n_1 = N_1-1, \; n_2 = N_2-1; \; \; I: = I (i, j) = i + (j-1)n_1 $ and $ J: = J (i', j') = i' + (j'-1)n_1 $, $ \textbf{v} = \left({v}_{1, 1}, \cdots, {v}_{1, N_2-1}, \cdots, {v}_{N_1-1, 1}, \cdots, {v}_{N_1-1, N_2-1}\right) $ and $ G (\tau, \alpha) = -F(\tau, \alpha) $ includes boundary condition.
Theorem 3. Assume that the coefficients of $ A $ given by (3.26) are positive, $ c < 0 $ and let $ h = \underset{\underset{1\leq j\leq N_2}{1\leq i\leq N_1}} {\max} \{ h_{x_i}, \, h_{y_j} \} $. If $ h $ is relatively small then the matrix $ E (\tau, \alpha) = \left(e_{i, j}^{i, j}\right)_{\underset{j = 1, \cdots, N_2-1, }{i = 1, \cdots, N_1-1}} $ in (3.44) is an M-matrix for any $ \alpha\, \in\, \mathcal{A}^N $.
Proof. The Proof follows the same lines of that of Theorem 2.
This section is devoted to the numerical time discretization method for the spatially discretized optimization problem using the fitted finite volume method. Let us re-consider the differential equation coupled with optimization problem given in (3.16) or (3.45) by
| $ \begin{align} \dfrac{d\textbf{v}(\tau) }{d\tau} = \sup\limits_{\alpha \in \mathcal{A}^N} \left[ A (\tau,\alpha) \textbf{v}(\tau)+ G(\tau,\alpha) \right],\\ \; \; \,\,\,\textbf{v}(0)\,\,\,\text{given}. \end{align} $ | (4.1) |
For temporal discretization, we use a constant time step $ \Delta t > 0 $, of course variable time steps can be used. The temporal grid points given by $ \Delta t = \tau_{n+1}-\tau_n $ for $ n = 1, 2, \ldots m-1 $. We denote $ \textbf{v}(\tau_n) \approx \textbf{v}^n $, $ A^n (\alpha) = A(\tau_n, \alpha) $ and $ G^n (\alpha) = G(\tau_n, \alpha). $
For $ \theta \, \in \left[\frac{1}{2}, 1\right] $, following [11], the $ \theta $-Method approximation of (4.1) in time is given by
| $ \begin{equation} \label{scheme} \begin{split} & \textbf{v}^{n+1} - \textbf{v}^{n} = \Delta t \,\sup\limits_{\alpha \in \mathcal{A}^N} \left( \theta\, [A^{n+1} (\alpha)\,\textbf{v}^{n+1} + G^{n+1}(\alpha)] \right. \\ \nonumber &\left. + (1-\theta)\, [A^{n} (\alpha)\,\textbf{v}^{n} + G^{n}(\alpha)]\right), \end{split} \end{equation} $ |
this also can be written as
| $ \begin{equation} \begin{split} \inf\limits_{\alpha \in \mathcal{A}^N} \left( [I + \Delta t \,\theta\, E^{n+1}]\textbf{v}^{n+1} +F^{n+1}(\alpha) + [I + \Delta t \,\theta\, E^{n}]\textbf{v}^{n} + F^{n}(\alpha)\right) = 0. \end{split} \end{equation} $ | (4.2) |
As we can notice, to find the unknown $ \textbf{v}^{n+1} $ we need also to solve an optimization problem. Let
| $ \begin{equation} \alpha^{n+1} \in \left(\underset{\alpha \in \mathcal{A}^N }{arg \sup} \left\lbrace \theta \,\Delta t \left[ A^{n+1}(\alpha)\,\textbf{v}^{n+1} + G^{n+1}(\alpha )\right] + (1-\theta)\,\Delta t \left[A^{n} (\alpha )\,\textbf{v}^{n} + G^{n}(\alpha)\right] \right\rbrace\right). \end{equation} $ | (4.3) |
Then, the unknown $ \textbf{v}^{n+1} $ is solution of the following equation
| $ \begin{equation} \begin{split} & [ I - \theta\, \Delta t \,A^{n+1} (\alpha^{n+1})]\,\textbf{v}^{n+1} = [I + (1-\theta)\,\Delta t\, A^{n} (\alpha^{n+1})]\,\textbf{v}^{n} \\ &+[\theta\, \Delta t \, G^{n+1}(\alpha^{n+1})+(1-\theta) \Delta t\, G^{n}(\alpha^{n+1})], \end{split} \end{equation} $ | (4.4) |
Note that when $ \theta = \frac{1}{2} $ the time-stepping scheme becomes the Crank-Nicolson scheme and when $ \theta = 1 $ it is the Implicit scheme. Both of these schemes are unconditionally stable, and they are second and first-order accuracy respectively. Unfortunately (4.2) and (4.3) are nonlinear and coupled and we need to iterate at every time step. The following iterative scheme close to the one in [11] is used.
1. Let $ \left(\textbf{v}^{n+1}\right)^0 = \textbf{v}^{n} $,
2. Let $ \hat{\textbf{v}}^{k} = \left(\textbf{v}^{n+1}\right)^k $,
3. For $ k = 0, 1, 2 \cdots $ until convergence ($ \Vert \hat{\textbf{v}}^{k+1}-\hat{\textbf{v}}^{k}\Vert \leq \epsilon $, given tolerance) solve
| $ \begin{align} &\alpha^{k}_i \in \end{align} $ | (4.5) |
| $ \begin{align} &\left(\underset{\alpha \in \mathcal{A}^N }{arg \sup} \left\lbrace \theta \,\Delta t \left[ A^{n+1} (\alpha)\,\hat{\textbf{v}}^k+ G^{n+1}(\alpha) \right]_i + (1-\theta)\,\Delta t \, \left[A^{n} (\alpha )\,\textbf{v}^{n} + G^{n}(\alpha)\right]_i \right\rbrace\right)&\\ & \alpha^{k} = (\alpha^{k})_i& \end{align} $ | (4.6) |
| $ \begin{align} & [ I - \theta\, \Delta t\,A^{n+1} (\alpha^{k})]\,\hat{\textbf{v}}^{k+1} = [I + (1-\theta)\,\Delta t \, A ^{n}(\alpha^{k})] \textbf{v}^{n} \end{align} $ | (4.7) |
| $ \begin{align} &+[\theta\, \Delta t \, G^{n+1}(\alpha^{k})+(1-\theta) \Delta t \, G^{n}(\alpha^{k})] \nonumber, \end{align} $ |
4. Let $ k_l $ being the last iteration in step 3, set $ \textbf{v}^{n+1}: = \hat{\textbf{v}}^{k_l} $, $ \alpha^{n+1}: = \alpha^{k_l} $.
Indeed to find the solution at time $ \tau_{n+1} $, we use the solution at time $ \tau_n $ and the iterations in our algorithm. We have used the Matlab optimisation toolbox and more precisely the Matlab function " fminbnd" in (4.5). Note that the optimization problem (4.5) is solved in each grid point at every iteration.
The monotonicity of system matrix of (4.2), more precisely $ [I + \Delta t \, \theta E^{n+1}] $ is given in the following theorem.
Theorem 4. Under the same assumptions as in Theorem 2 and 3, for any given $ n = 1, 2, \cdots, m - 1 $, the system matrix $ [I + \Delta t \, \theta E^{n+1}] $ in (4.2) is an M–matrix for each $ \alpha \in \mathcal{A}^N. $
Proof. The proof is obvious. Indeed as in Theorem 2 and 3, $ [I + \Delta t \, \theta E^{n+1}] $ is (strictly) diagonally dominant since $ \Delta t > 0 $. Then, it is an $ M $–matrix.
Note that a simple finite difference scheme generally does not give an M-matrix. The merit of the proposed method is that it is unconditionally stable in time because of the implicit nature of the time discretization. More precisely, following [10,Theorem 6 and Lemma 3], we can easily prove that the scheme (4.4) is stable and consistent, so the convergence of the scheme is ensured (see [23]).
The goal of this section is carried out test problems in both $ 1 $ and $ 2 $ spatial dimensions to validate the numerical scheme presented in the previous section. All computations were performed in Matlab 2013. In our numerical experiments, we found that the fitted finite volume method and the finite difference method converge after $ 2 $ or $ 3 $ iterations in our algorithm (4.5). We have used for tolerance $ \epsilon = 10^{-6} $ in our iterative algorithm.
We will present two problems with exact solution and one problem without exact solution modelling cash management in finance.
Problem 1. Consider the following Merton's stochastic control problem such that $ \alpha = \alpha(t) $ is a feedback control belongs in $ [0, 1] $
| $ \begin{equation} v(t, x) = \underset{\alpha \in\, [0,1]}{\max} \mathbb{E}\left\lbrace \dfrac{1}{p}\,x^p(T)\right\rbrace. \end{equation} $ | (5.1) |
subject to
| $ \begin{equation*} dx_t = b^{\alpha_t}(t,x_t)\, dt + \sigma^{\alpha_t} (t,x_t)\,dW_t, \end{equation*} $ |
where $ b^{\alpha_t}(t, x_t) = x_t\, \left[ r + \alpha_t\, (\mu-r)\right] $, $ \sigma^{\alpha_t} (t, x_t) = x_t\, \alpha_t \, \sigma $, $ 0 < p < 1 $ is coefficient of risk aversion, $ r $, $ \mu $, $ \sigma $ are constants, $ x_t\, \in\, \mathbb{R} $ and $ W_t $ Brownian motion. We assume $ \mu > r $. For this problem, using dynamic programming the corresponding HJB equation is given by
| $ \begin{equation} \begin{cases} v_t(t, x) + \underset{\alpha \in [0,1]}{\sup} \left[L^{\alpha} v(t, x)\right] = 0 \quad\mathit{\text{on}} \ [0,T)\times \mathbb{R}_+\\ v(T, x) = \dfrac{x^p}{p}, \,\, \,x \,\in \mathbb{R}_+ \end{cases} \end{equation} $ | (5.2) |
where
| $ \begin{equation} L^{\alpha} v(t, x) = (b^{\alpha}(t, x)) \dfrac{\partial v(t,x)}{\partial x} + ( a^{\alpha} (t,x)) \,\dfrac{\partial^2 v(t,x)}{\partial x^2}, \end{equation} $ | (5.3) |
and $ a^\alpha (t, x) = \dfrac{1}{2}\bigg(\sigma^{\alpha}(t, x)\bigg)^2 $.
The divergence form of the HJB (5.2) is given by
| $ \begin{equation} \begin{split} &\dfrac{\partial v (t, x)}{\partial t}\\ & + \sup\limits_{\alpha \in \,[0,1]}\left[ \dfrac{\partial }{\partial x} \left(a (t,x,\alpha)\,x^2 \dfrac{\partial v(t, x)}{\partial x}+ b (t,x,\alpha)\,x\,v(t, x) \right)+c(t, x,\alpha)\,v(t, x)\right] = 0,\,\,\,\mathit{\text{where}} \end{split} \end{equation} $ | (5.4) |
| $ \begin{equation*} \begin{split} a(t, x, \alpha) & = \dfrac{1}{2}\sigma^2\alpha^2\\ b(t, x,\alpha)& = r+ (\mu-r)\,\alpha-\sigma^2\alpha^2\\ c(t, x, \alpha)& = -(r+\alpha\, (\mu-r)-\sigma^2\,\alpha^2). \end{split} \end{equation*} $ |
The domain where we compare the solution is $ \Omega = \left[0, x_{{max}}\right] $, where Dirichlet boundary conditions is used at the boundaries. Of course the value of the boundary conditions are taken to be equal to the exact solution. The exact solution given in [9] is given at every $ (\tau^n, x_i) $ by
| $ \begin{eqnarray} v\left(\tau^n, x_i\right) & = & \exp\left(p \times (n \times \Delta t- T) \times \rho\right) \times \dfrac{(x_i)^p}{p}, \end{eqnarray} $ | (5.5) |
| $ \begin{eqnarray} \rho & = & \left( r+\dfrac{(\mu-r)^2}{\sigma^2\,(1-p)} + \dfrac{1}{2}(p-1)\,\sigma^2\,\left(\dfrac{(\mu-r)}{\sigma^2\,(1-p)}\right)^2 \right),\,\,\,\,0 \lt p \lt 1 \end{eqnarray} $ | (5.6) |
We use the following $ L^2([0, T]\times \Omega) $ norm of the absolute error
| $ \begin{eqnarray} \ \left\| v^m-v\right\|_{L^2[[0,T]\times \Omega]} = \left(\sum\limits_{n = 0}^{m-1} \sum\limits_{i = 1}^{N_1-1} (\tau_{n+1}-\tau_n)\times l_{i}\times (v_{i}^n - v\left( \tau^n, x_{i}, \right))^2 \right)^{1/2}, \end{eqnarray} $ | (5.7) |
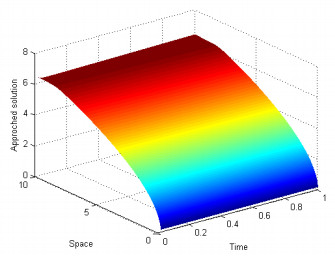
where $ v^m $ is the numerical approximation of $ v $ computed from our numerical scheme. The 3 D graphs of the implicit fitted finite volume ($ \theta = 1 $) with its corresponding exact solution are given at Figures 1 and 2 with parameters coming from [16]. For our computation, we have $ [0, 10] $ for computational domain with $ N = 1500 $, $ r = 0.0449 $, $ \mu = 0.0657 $, $ \sigma = 0.2537 $, $ p = 0.5255 $ and $ T = 1 $.
We compare the fitted finite volume method and the finite difference method in Table 1.
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 3.34 E-01 | 6.81 E-01 | 1.01 E-00 | 1.33 E-00 |
| Error of finite difference method | 3.37 E-01 | 6.89 E-01 | 1.02 E-00 | 1.34 E-00 |
From Tables 1–3, we can observe that the implicit fitted finite volume is slightly accurate comparing to the implicit finite difference method. Both fitted finite volume and finite difference method converge with order $ 0.9 $ in time.
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 1.64 E-01 | 3.35 E-01 | 4.97 E-01 | 6.53 E-01 |
| Error of finite difference method | 1.66 E-01 | 3.38 E-01 | 5.03 E-01 | 6.61 E-01 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 2.97 E-01 | 5.99 E-01 | 8.83 E-01 | 1.15 E-01 |
| Error of finite difference method | 3.00 E-01 | 6.05 E-01 | 8.91 E-01 | 1.17 E-01 |
Problem 2. Consider the following two dimensional Merton's stochastic control model such that $ \alpha_1 = \alpha_1(t) $ and $ \alpha_2 = \alpha_2(t) $ are a feedback control in $ [0, 1] $
| $ \begin{equation} v(t,x,y) = \underset{(\alpha_1, \alpha_2) \in\, [0,1]\times [0,1]}{\max} \mathbb{E}\left\lbrace \dfrac{1}{p}\,x^p(T) \times \dfrac{1}{p}\,y^p(T)\right\rbrace, \end{equation} $ | (5.8) |
| $ \begin{equation} \mathit{\mbox{subject}}\,\,\mathit{\text{to}}\,\, \begin{cases} dx_t = {b_1}^{{\alpha_1}_t}(t,x_t)\, dt + \sigma^{{\alpha_1}_t} (t,x_t)\,d{W_1}_t\\ dy_t = {b_2}^{{\alpha_2}_t}(t,y_t)\, dt + \sigma^{{\alpha_2}_t} (t,y_t)\,d{W_2}_t\\ \end{cases} \end{equation} $ | (5.9) |
where
| $ \begin{equation*} \begin{split} & {b_1}^{{\alpha_1}_t}(t,x_t) = x_t\,\left[ r_1 + {\alpha_1}_t\, (\mu_1-r_1)\right],\\ & {b_2}^{{\alpha_2}_t}(t,y_t) = y_t\,\left[ r_2 + {\alpha_2}_t\, (\mu_2-r_2)\right],\\ &\sigma^{{\alpha_1}_t} (t, x_t) = x_t\, {\alpha_1}_t \,\sigma,\,\quad \quad \sigma^{{\alpha_2}_t} (t, y_t) = y_t\, {\alpha_2}_t \,\sigma, \end{split} \end{equation*} $ |
$ 0 < p < 1 $ is coefficient of risk aversion, $ r_1 $, $ \mu_1 $, $ r_2 $, $ \mu_2 \; \sigma $ are constants, $ x_t, \, y_t\, \in\, \mathbb{R} $ and $ \rho_{12} \in [0, 1) $ the correlation of the two Brownian motion. We assume that $ \mu_1 > r_1 $ and $ \mu_2 > r_2 $. For this problem, using dynamic programming the corresponding HJB equation is given by
| $ \begin{equation} \begin{cases} v_t(t, x, y) + \underset{(\alpha_1, \alpha_2) \in [0,1]\times [0,1]}{\sup} \left[L^{\alpha_1,\alpha_2} v(t, x, y)\right] = 0 \quad\mathit{\text{on}} \ [0,T)\times \mathbb{R}_+\times \mathbb{R}_+\\ v(T, x , y) = \dfrac{x^p}{p}\times \dfrac{y^p}{p}, \,\, \,x,\, \,y\,\in \mathbb{R}_+ \end{cases} \end{equation} $ | (5.10) |
where
| $ \begin{equation*} \begin{split} & L^{\alpha} v(t, x, y) = ({b_1}^{\alpha_1}(t, x)) \dfrac{\partial v(t, x, y)}{\partial x} + ({b_2}^{\alpha_2}(t, y)) \dfrac{\partial v(t, x, y)}{\partial y} + \dfrac{1}{2}(\sigma^{\alpha_1}(t,x))^2\,\dfrac{\partial^2 v(t, x, y )}{\partial x^2}\\ & + \dfrac{1}{2}(\sigma^{\alpha_2}(t, y))^2\,\dfrac{\partial^2 v(t,x ,y )}{\partial y^2} + (\sigma^{\alpha_1}(t,x))\,(\sigma^{\alpha_2}(t, y))\,\rho_{12}\,\dfrac{\partial^2 v(t, x, y )}{\partial x \partial y}, \end{split} \end{equation*} $ |
and the two dimensional divergence form is given by
| $ \begin{equation} \dfrac{\partial v(t, x, y ) }{\partial t} + \sup\limits_{\alpha \in \,[0,1]\times[0,1]}\left[ \nabla\cdot \left( k(t, x, y,\alpha)\right) + c(t,x,y,\alpha)\,v(t,x,y) \right] = 0, \end{equation} $ | (5.11) |
where $ k(t, x, y, \alpha) = A(t, x, y, \alpha)\nabla v(t, x, y)+ b(t, x, y, \alpha) v(t, x, y) $
| $ A = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right), $ |
| $ \begin{eqnarray*} && a_{11}(t,x,y,\alpha) = \dfrac{1}{2}\sigma^2\,\alpha_1^2 \,x^2 ,\; a_{22}(t,x,y,\alpha) = \dfrac{1}{2} \,\sigma^2\,\alpha_2^2 \,y^2, \\ && a_{12}(t,x,y,\alpha) = a_{21}(x,y,t,\alpha) = \dfrac{1}{2} \sigma^2\,\alpha_1 \,\alpha_2 \,\rho_{12}\,x\,y. \end{eqnarray*} $ |
By identification,
| $ \begin{eqnarray*} a(t,x,y,\alpha) & = & \dfrac{1}{2}\sigma^2\,\alpha_1^2\\ \bar{a}(t,x,y,\alpha)& = & \dfrac{1}{2} \,\sigma^2\,\alpha_2^2\\ b_1(t,x,y,\alpha) & = & r_1 + \alpha_1\, (\mu_1-r_1) - \dfrac{1}{2}\sigma^2\,\alpha_1\,\alpha_2 \, \rho_{12} - \sigma^2\,\alpha_1^2, \\ b_2(t,x,y,\alpha) & = & r_2 + \alpha_2\, (\mu_2-r_2) -\dfrac{1}{2}\sigma^2\,\alpha_1\,\alpha_2\, \rho_{12} -\sigma^2\,\alpha_2^2,\\ c (t,x,y,\alpha)& = & -\left[ r_1 + (\mu_1-r_1)\,\alpha_1\right]- \left[ r_2 + (\mu_2-r_2)\,\alpha_2 \right] +\sigma^2\left(\alpha_1^2 +\alpha_2^2 + \alpha_1 \,\alpha_2 \, \rho_{12}\right),\\ d_1(t,x,y,\alpha)& = &\dfrac{1}{2} \sigma^2\,\alpha_1 \alpha_2\, \rho_{12}. \end{eqnarray*} $ |
The two dimensional Ansatz exact solution [9] at $ \left(\tau^n, x_i, y_j\right) $ is given by
| $ \begin{eqnarray*} && v\left(\tau^n, x_i, y_j\right) = \exp\left(p \times (n \times \Delta t - T) \times \rho\right) \times \dfrac{(x_i)^p}{p} \times \dfrac{(y_j)^p}{p},\\ &&\rho = \underset{\alpha_1,\alpha_2 \,\in [0,1]\times[0,1]}{\sup}\left[ r_1 + r_2 + (\mu_1-r_1)\,\alpha_1 + (\mu_2-r_2)\,\alpha_2\right.\\ &&\left. +\dfrac{1}{2} \sigma^2\,\alpha_1^2\,(p-1) + \dfrac{1}{2} \sigma^2\,\alpha_2^2\,(p-1) + \sigma^2\,\alpha_1\,\alpha_2\,\rho_{12}\,p \right], \,\,\,\,\,0 \lt p \lt 1/2. \end{eqnarray*} $ |
We use the following $ L^2([0, T]\times \Omega), \, \, \Omega = [0, x_{{\text{max}}}] \times [0, y_{{\text{max}}}] $ norm of the absolute error
| $ \begin{equation} \begin{split} & \left\| v^m-v\right\|_{L^2[\Omega \times [0,T]]} \\ & = \left(\sum\limits_{n = 0}^{m-1} \sum\limits_{i = 1}^{N_1-1} \sum\limits_{j = 1}^{N_2-1} (\tau_{n+1}-\tau_n)\times h_{x_{i}}\times h_{y_{j}}\times (v_{i,j}^n - v\left( \tau^n, x_{i}, x_{j},\right))^2 \right)^{1/2}, \end{split} \end{equation} $ | (5.12) |
where $ v^m $ is the numerical approximation of $ v $ computed from our numerical scheme.
The 3 D graphs of the implicit fitted finite volume ($ \theta = 1 $ at the final time $ T = 1 $) with its corresponding exact solution are given at Figures 3 and 4, with $ N_1 = 25 $, $ N_2 = 20 $, $ r_1 = 0.0449/2 $, $ \mu_1 = 0.0657/2 $, $ r_2 = 0.0448/2 $, $ \mu_2 = 0.0656/2 $, $ \sigma = 0.2537/2 $, $ p = 0.5255/2 $ and $ \rho_{12} = 0.9 $.
We compare the fitted finite volume method and the finite difference method in Table 4. As in dimension 1, we can observe the accuracy of the fitted scheme comparing to the finite difference scheme, thanks to the fitted technique. We can also observe that the accuracy is high when the number of time subdivisions is small. For $ \rho_{12} = 0.9 $ the fitted finite volume and the finite difference converge with order $ 1.3 $ in time.
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 2.90 E-03 | 6.50 E-03 | 1.15 E-02 | 2.09 E-02 |
| Error of finite difference method | 3.01 E-03 | 6.52 E-02 | 1.16 E-02 | 2.10 E-01 |
Problem 3. We consider a optimal cash management under a stochastic volatility Model problem coming from [21]. We assume that the firm invests its cash in a bank account and a stock in a portfolio of value $ w_t $ at time $ t $, and the proportion of wealth invested in the stock at time $ t $ is $ u_t $. The interest rate earned in the bank account is $ r_1 $, the return from the stock at time $ t $ has two components, the cash dividend rate $ r_2 $, the capital gain rate $ R_t $. The dynamic of the capital gain rate $ R_t $ is assumed to be governed by the stochastic process
| $ \begin{equation} dR_t = [\beta_1\, R_t + f]\, dt + \sigma_t \,d{W_{1}}_t, \end{equation} $ | (5.13) |
and the volatility $ \sigma_t $ with modeled by
| $ \begin{equation} d\sigma_t = \alpha\,\sigma_t\, dt + \beta\,\sigma_t \, d{W_{2}}_t. \end{equation} $ | (5.14) |
Suppose that the firm has a demand rate $ d(t) $ for cash at time $ t $, and that the demand rate $ d(t) $ is normally distributed with mean $ 0 $ and variance $ 0.2 $. We assume that $ u_t\, \in\, [0, 1] $ and the wealth dynamics for this cash management problem is given by
| $ \begin{equation} dw_t = w_t \,u_t\,r_2\,dt +w_t\,(1-u_t)\,r_1\,dt + w_t\,R_t\,dt -d(t)\,w_t\,dt. \end{equation} $ | (5.15) |
The objective of the firm is to maximize the expectation of the total holdings at the terminal time $ T $. The portfolio optimization problem is given by
| $ \begin{equation} J(T, w, R, \sigma) = \underset{u \in [0,1]}{\max} \mathbb{E}\left\lbrace w_T\right\rbrace. \end{equation} $ | (5.16) |
| $ \begin{equation} \mathit{\mbox{subject}}\,\,\mathit{\text{to}}\,\, \begin{cases} dw_t & = w_t \,u_t\,r_2\,dt +w_t\,(1-u_t)\,r_1\,dt + w_t\,R_t\,dt -d(t)\,w_t\,dt,\,\,\\ \nonumber dR_t & = [\beta_1\, R_t + f]\, dt + \sigma_t \,d{W_{1}}_t\\ \nonumber d\sigma_t & = \alpha\,\sigma_t\, dt + \beta\,\sigma_t \, d{W_{2}}_t \nonumber \end{cases} \end{equation} $ |
We assume that the two Brownian motions are correlated, that is $ d{W_{1}}_t\, d{W_{2}}_t = \rho\, dt $. For this problem of optimal cash management the analytical solution is not available, so our numerical scheme will to provide approximated solution. Using dynamic programming, the corresponding HJB equation for this optimal cash management problem (5.16) is given by
| $ \begin{equation} \begin{split} & J_t + \underset{u \in [0,1]}{\max} \left\lbrace (f + \beta_1\,R)\,J_R + w\,(u\,r_2 + (1-u)\,r_1 + u\,R - d(t )\,J_w + \right.\\ & \left. 1/2\,\left(\sigma^2\,J_{RR} +\beta^2\,\sigma^2 \,J_{\sigma \sigma} + 2\,\rho\,\beta\,\sigma^2\,J_{\sigma\,R} \right) + \alpha\,\sigma\,J_\sigma \right\rbrace = 0, \end{split} \end{equation} $ | (5.17) |
with terminal condition $ J(T, \cdot) = w_T. $ To simplify the problem, we assume that
| $ J(t, w, R, \sigma) = w H( t, R, \sigma). $ |
Therefore (5.17) is equivalent to
| $ \begin{equation} \begin{split} & H_t + \underset{u \in [0,1]}{\max} \left\lbrace (f + \beta_1\,R)\,H_R + (u\,r_2 + (1-u)\,r_1 + u\,R - d (t))\,H + \right.\\ & \left. 1/2\,\left(\sigma^2\,J_{RR} +\beta^2\,\sigma^2 \,H_{\sigma \sigma} + 2\,\rho\,\beta\,\sigma^2\,H_{\sigma\,R} \right) + (\alpha\,\sigma)\,H_\sigma \right\rbrace = 0 \end{split} \end{equation} $ | (5.18) |
with terminal condition $ H(T, R, \sigma) = 1 $. The HJB Eq (5.18) is a problem with two state variables $ R $ and $ \sigma $. The divergence form of the problem (5.18) is then given by
| $ \begin{equation} \dfrac{\partial H(t, R,\sigma) }{\partial t} + \sup\limits_{u \,\in \,[0,1]}\left[ \nabla\cdot \left( k(t,R,\sigma,u)\right) + c(t,R,\sigma,u)\,H(t,R,\sigma) \right] = 0, \end{equation} $ | (5.19) |
where $ k(t, R, \sigma, u) = A(t, R, \sigma, u)\nabla H(t, R, \sigma)+ b(t, R, \sigma) H(t, R, \sigma) $
| $ A = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right), $ |
| $ \begin{equation*} a_{11} = \dfrac{1}{2}\sigma^2 ,\; a_{22} = \dfrac{1}{2} \,\beta^2\, \,\sigma^2, \; a_{12} = a_{21} = \dfrac{1}{2}\, \sigma^2\,\rho\, \beta. \end{equation*} $ |
By identification,
| $ \begin{equation*} \begin{split} a(t,R,\sigma) & = \dfrac{\sigma^2}{2\,R^2},\,\,\, \bar{a}(t,R,\sigma) = \dfrac{\beta^2}{2}\\ b_1(t,R,\sigma) & = \dfrac{f}{R} + \beta_1 - \sigma\,\dfrac{ \rho\,\beta}{\,R},\,\,\,\, b_2(t,R,\sigma) = \alpha -\beta^2 \\ c (t,R,\sigma,u)& = u\,r_2 + (1-u)\,r_1 +u\,R -d(t) -\beta_1-\alpha +\beta^2. \end{split} \end{equation*} $ |
Because we have a stochastic volatility model, to solve the PDE equation, we have considered the following boundary conditions of Heston model
| $ \begin{equation} \begin{split} H(t, 0, \sigma)& = 0,\\ H(t, R, \sigma_{\text{max}}) & = R,\\ \dfrac{\partial H }{\partial R} (t, R_{\text{max}}, \sigma) & = 1. \end{split} \end{equation} $ | (5.20) |
Because the PDE has two second derivatives in the two spatial directions, four boundary conditions are needed. This comes from the fact that the two second order derivatives give rise to two unknown integration constants. To meet this requirement, at the boundary $ \sigma = 0 $ it is considered inserting $ \sigma = 0 $ into the PDE to complete the set of four boundary conditions:
| $ \begin{equation} \begin{split} & H_t(t, R, 0) \\ &+ \underset{u \in [0,1]}{\max} \left\lbrace (f + \beta_1\,R)\,H_R(t, R, 0) + (u\,r_2 + (1-u)\,r_1 + u\,R - d )\,H(R,0,t) \right\rbrace = 0 \end{split} \end{equation} $ | (5.21) |
The HJB equation is solved using some parameters values in [21] given in the following tabular
| $ f $ | $ \beta_1 $ | $ \beta $ | $ \alpha $ | $ r_1 $ | $ r_2 $ | $ \rho $ |
| $ 0.12 $ | $ 0.96 $ | $ 0.3 $ | $ -0.85 $ | $ 0.024 $ | $ 0.01 $ | $ 0.5 $ |
Figure 5 shows a sample of fitted finite volume solution of the wealth rate $ H $ at the point $ (1/2, 1/2) $ from $ t = 1 $ to $ t = 10 $ with $ N_1 = 10 $, $ N_2 = 10 $, $ R_{\text{max}} = 1/2 $, $ \sigma_{\text{max}} = 1/2 $. We can estimate the mean and moment of $ H $ using Monte Carlo Method by generating many samples of $ H $. Table 6 presents the optimal investment policy from $ t = 1 $ to $ t = 10 $.
| Time | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | $ 6 $ | $ 7 $ | $ 8 $ | $ 9 $ | $ 10 $ |
| Optimal choice using fitted scheme | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ |
| Optimal choice using finite difference | $ 1 $ | $ 0 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 0 $ | $ 0 $ | $ 1 $ | $ 1 $ |
We presented a fitted finite volume method to solve the HJB equation from stochastic optimal control problems coupled with implicit temporal discretization. It was shown that the corresponding system matrices are M-matrices, so the maximum principle is preserved for the discrete system. Numerical experiments in $ 1 $ and $ 2 $ dimensions are performed to prove that the fitted scheme can be more accurate comparing to the standard finite difference methods. We intent to extend our method in high dimension.
The first author was supported by the project African Center of Excellence in Mathematical Sciences and Applications (ACE-MSA) at IMSP Benin and the European Mathematical Society (EMS).
The authors declare no potential conflict of interests.
| [1] |
D. N. DE G. Allen, R. V. Southwell, Relaxation methods applied to determine the motion, in two dimensions, of a viscous fluid past a fixed cylinder, Q. J. Mech. Appl. Math., 8 (1955), 129–145. doi: 10.1093/qjmam/8.2.129

|
| [2] | C. Benezet, J. Chassagneux, C. Reisinger, A numerical scheme for the quantile hedging problem. Available from: https://arXiv.org/abs/1902.11228v1. |
| [3] | V. Henderson, K. Kladvko, M. Monoyios, C. Reisinger, Executive stock option exercise with full and partial information on a drift change point. Available from: arXiv: 1709.10141v4. |
| [4] |
C. S. Huang, C. H. Hung, S. Wang, A fitted finite volume method for the valuation of options on assets with stochastic volatilities, Computing, 77 (2006), 297–320. doi: 10.1007/s00607-006-0164-4

|
| [5] | N. V. Krylov, Controlled Diffusion Processes, Applications of Mathematics, Springer-Verlag, New York, 1980. |
| [6] |
S. Wang, A Novel fitted finite volume method for the Black-Scholes equation governing option pricing, IMA J. Numer. Anal., 24 (2004), 699–720. doi: 10.1093/imanum/24.4.699

|
| [7] | P. Forsyth, G. Labahn, Numerical methods for controlled Hamilton-Jacobi-Bellman PDEs in finance, J. Comput. Finance, 11 (2007), 1–43. |
| [8] | P. Wilmott, The Best of Wilmott 1: Incorporating the Quantitative Finance Review, John Wiley & Sons, 2005. |
| [9] | H. Pham, Optimisation et contrôle stochastique appliqués à la finance, Mathématiques et applications, Springer-Verlag, New York, 2000. |
| [10] |
L. Angermann, S. Wang, Convergence of a fitted finite volume method for the penalized Black–Scholes equation governing European and American Option pricing, Numerische Math., 106 (2007), 1–40. doi: 10.1007/s00211-006-0057-7

|
| [11] | H. Peyrl, F. Herzog, H. P. Geering, Numerical solution of the Hamilton-Jacobi-Bellman equation for stochastic optimal control problems, WSEAS international conference on Dynamical systems and control, 2005. |
| [12] |
N. V. Krylov, On the rate of convergence of finite-difference approximations for Bellman's equations with variable coefficients, Probab. Theory Relat. Fields, 117 (2000), 1–16. doi: 10.1007/s004400050264

|
| [13] |
N. V. Krylov, The rate of convergence of finite-difference approximations for Bellman equations with Lipschitz coefficients, Appl. Math. Optim., 52 (2005), 365–399. doi: 10.1007/s00245-005-0832-3

|
| [14] |
E. R. Jakobsen, On the rate of convergence of approximations schemes for Bellman equations associated with optimal stopping time problems, Math. Models Methods Appl. Sci., 13 (2003), 613–644. doi: 10.1142/S0218202503002660

|
| [15] |
M. G. Crandall, P. L. Lions, Viscosity solutions of Hamilton-Jacobi equations, Trans. Am. Math. Soc., 277 (1983), 1–42. doi: 10.1090/S0002-9947-1983-0690039-8

|
| [16] | J. Holth, Merton's portfolio problem, constant fraction investment strategy and frequency of portfolio rebalancing, Master Thesis, University of Oslo, 2011. Available from: http://hdl.handle.net/10852/10798. |
| [17] | Iain Smears, Hamilton-Jacobi-Bellman Equations, Analysis and Numerical Analysis, Research report, 2011. Available from: http://fourier.dur.ac.uk/Ug/projects/highlights/PR4/Smears_HJB_report.pdf |
| [18] |
N. Krylov, Approximating value functions for controlled degenerate diffusion processes by using piece-wise constant policies, Electron. J. Probab., 4 (1999), 1–19. doi: 10.1214/ECP.v4-999

|
| [19] |
M. G. Crandall, H. Ishii, P. L. Lions, User's guide to viscosity solutions of second order partial differential equations, Bull. Am. Math. Soc., 27 (1992), 1–67. doi: 10.1090/S0273-0979-1992-00266-5

|
| [20] | C. S. Huang, S. Wang, K. L. Teo, On application of an alternating direction method to Hamilton-Jacobi-Bellman equations, J. Comput. Appl. Math., 27 (2004), 153–166. |
| [21] |
N. Song, W. K. Ching, T. K. Siu, C. K. F. Yiu, On optimal cash management under a stochastic volatility model, East Asian J. Appl. Math., 3 (2013), 81–92. doi: 10.4208/eajam.070313.220413a

|
| [22] | K. Debrabant, Espen R. Jakobsen, Semi-Lagrangian schemes for linear and fully non-linear diffusion equations, Math. Comput., 82 (2013), 1433–1462. |
| [23] |
G. Barles, P. E. Souganidis, Convergence of approximation schemesfor fully nonlinear second order equations, Asymptot. Anal., 4 (1991), 271–283. doi: 10.3233/ASY-1991-4305

|
| 1. | Mohammad Shirazian, Optimal control design for linear time-varying systems by interpolated variational iteration method, 2022, 1077-5463, 107754632211277, 10.1177/10775463221127739 | |
| 2. | Christelle Dleuna Nyoumbi, Antoine Tambue, A Novel High Dimensional Fitted Scheme for Stochastic Optimal Control Problems, 2023, 61, 0927-7099, 1, 10.1007/s10614-021-10197-4 | |
| 3. | Zifu Fan, Youpeng Tao, Wei Zhang, Kexin Fan, Jiaojiao Cheng, Research on open and shared data from government-enterprise cooperation based on a stochastic differential game, 2023, 8, 2473-6988, 4726, 10.3934/math.2023234 | |
| 4. | Jiamian Lin, Xi Li, SingRu (Celine) Hoe, Zhongfeng Yan, A Generalized Finite Difference Method for Solving Hamilton–Jacobi–Bellman Equations in Optimal Investment, 2023, 11, 2227-7390, 2346, 10.3390/math11102346 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 3.34 E-01 | 6.81 E-01 | 1.01 E-00 | 1.33 E-00 |
| Error of finite difference method | 3.37 E-01 | 6.89 E-01 | 1.02 E-00 | 1.34 E-00 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 1.64 E-01 | 3.35 E-01 | 4.97 E-01 | 6.53 E-01 |
| Error of finite difference method | 1.66 E-01 | 3.38 E-01 | 5.03 E-01 | 6.61 E-01 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 2.97 E-01 | 5.99 E-01 | 8.83 E-01 | 1.15 E-01 |
| Error of finite difference method | 3.00 E-01 | 6.05 E-01 | 8.91 E-01 | 1.17 E-01 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 2.90 E-03 | 6.50 E-03 | 1.15 E-02 | 2.09 E-02 |
| Error of finite difference method | 3.01 E-03 | 6.52 E-02 | 1.16 E-02 | 2.10 E-01 |
| $ f $ | $ \beta_1 $ | $ \beta $ | $ \alpha $ | $ r_1 $ | $ r_2 $ | $ \rho $ |
| $ 0.12 $ | $ 0.96 $ | $ 0.3 $ | $ -0.85 $ | $ 0.024 $ | $ 0.01 $ | $ 0.5 $ |
| Time | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | $ 6 $ | $ 7 $ | $ 8 $ | $ 9 $ | $ 10 $ |
| Optimal choice using fitted scheme | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ |
| Optimal choice using finite difference | $ 1 $ | $ 0 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 0 $ | $ 0 $ | $ 1 $ | $ 1 $ |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 3.34 E-01 | 6.81 E-01 | 1.01 E-00 | 1.33 E-00 |
| Error of finite difference method | 3.37 E-01 | 6.89 E-01 | 1.02 E-00 | 1.34 E-00 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 1.64 E-01 | 3.35 E-01 | 4.97 E-01 | 6.53 E-01 |
| Error of finite difference method | 1.66 E-01 | 3.38 E-01 | 5.03 E-01 | 6.61 E-01 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 2.97 E-01 | 5.99 E-01 | 8.83 E-01 | 1.15 E-01 |
| Error of finite difference method | 3.00 E-01 | 6.05 E-01 | 8.91 E-01 | 1.17 E-01 |
| Time subdivision | $ 200 $ | $ 150 $ | $ 100 $ | $ 50 $ |
| Error of fitted finite volume method | 2.90 E-03 | 6.50 E-03 | 1.15 E-02 | 2.09 E-02 |
| Error of finite difference method | 3.01 E-03 | 6.52 E-02 | 1.16 E-02 | 2.10 E-01 |
| $ f $ | $ \beta_1 $ | $ \beta $ | $ \alpha $ | $ r_1 $ | $ r_2 $ | $ \rho $ |
| $ 0.12 $ | $ 0.96 $ | $ 0.3 $ | $ -0.85 $ | $ 0.024 $ | $ 0.01 $ | $ 0.5 $ |
| Time | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | $ 6 $ | $ 7 $ | $ 8 $ | $ 9 $ | $ 10 $ |
| Optimal choice using fitted scheme | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ |
| Optimal choice using finite difference | $ 1 $ | $ 0 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 1 $ | $ 0 $ | $ 0 $ | $ 1 $ | $ 1 $ |