1.
Introduction
1.1. Scope
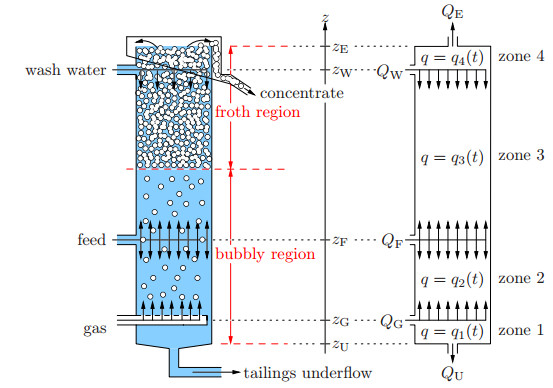
Flotation is a unit operation that is extensively used in the recovery of valuable minerals and coals in mineral processing but also in many other applications in environmental and chemical engineering [12,21,33,36,42]. It is a physico-chemical separation process that utilizes the difference in surface properties of the valuable hydrophobic minerals and the unwanted hydrophilic gangue material. The theory of froth flotation is complex and involves three phases (solids, water, and froth or gas) with many subprocesses [42]. The principle of the conventional flotation process is roughly as follows. Gas is introduced close to the bottom of a flotation column (see Figure 1), and the bubbles generated then rise upward throughout the pulp that contains hydrophobic and hydrophilic solid particles. The hydrophobic particles in the pulp attach to the bubbles. Since the overall density of the bubble-particle aggregates is less than that of the medium, the aggregates then float to the top of the column, where the desired product, the foam or froth carrying the valuable material (the concentrate in mining) is removed, usually through a launder. Additionally, close to the top wash water is injected to assist with the rejection of entrained impurities [39] and to increase the froth stability and improve recovery [31,21]. Once the hydrophobic particles have attached to the air bubbles, flotation can be considered as a separation between relatively large low-density entities, called air bubbles, and a suspension of liquid and gangue.Consequently, flotation can be described as a gas-liquid separation process by buoyancy analogous to the solid-liquid separation by gravity sedimentation in clarifier-thickeners [8,10,15].
Well-established spatially one-dimensional models of clarifier-thickeners can be formulated as a scalar conservation law for the local solids concentration as a function of depth and time, where the flux is discontinuous as a function of spatial position due to upward- and downward-directed bulk flows, transitions to overflow and underflow transport, and a singular source term marking the feed [8,10,15].Clarifier-thickener models have motivated in part the mathematical research on conservation laws with discontinuous flux [3,4,6,10,14,15,16,17,18,19,20].
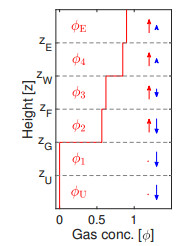
It is the purpose of this paper to formulate, partially analyze, solve for steady states, and numerically simulate a related model for a flotation column, where we follow [13] and limit ourselves to a one-dimensional two-phase system of gas bubbles dispersed in a fluid, or rather a suspension of liquid and gangue. Hence, we do not model any sedimentation of solid particles in the suspension. The final form of the model (cf. Figure 1) is the conservation law with multiply discontinuous flux
where $\phi$ is the sought volume fraction of gas bubbles as a function of height $z$ and time $t$, and $F(z, t, \phi)$ is a flux function, made precise in later parts of the paper, that is nonlinear in $\phi$ and discontinuous in $z$ at five different positions. Three of these positions, $z_{{\rm{G}}}$, $z_{{\rm{F}}}$ and $z_{{\rm{W}}}$, are associated with singular feed sources of gas, feed slurry, and wash water, respectively, at given rates $q_S$ and volume fractions $\phi_S$, where $\delta (\cdot)$ denotes the Dirac symbol. The model (1.1) is posed for $z \in \mathbb{R}$ without boundary conditions, and is therefore supplied solely with initial data
While the time-dependent partial differential equation (PDE) (1.1) describes transient variations of $\phi$ as a function of position and time, a property of practical interest in applications are the stationary solutions to the model that correspond to undisturbed normal states of operation. A steady-state solution of (1.1) is generally a piecewise constant function, with possible jump discontinuities both within the four zones of Figure 1, and across the five spatial discontinuities $z = z_{\rm E}$, etc.
The main outcomes of this work are to a classification of all steady-state solutions by means of diagrams and tables, and numerical simulations of dynamic behaviour. The variety of real-world applications of conservation laws with discontinuous flux is hereby widened to include flotation.
1.2. Related work
Our model formulation is based on the description of a flotation column by Stevenson et al. [38], Dickinson and Galvin [13], and Galvin and Dickinson [22] that is based on algebraic expressions for the gas and liquid fluxes, velocities and volume fractions. The description of one-dimensional two-phase flows based on the continuity equations for both phases and closed by defining a relative flux, or drift flux, between both phases as a function of volume fraction was introduced by Wallis [40], as is elaborated in [35]. Treatments that invoke this drift-flux analysis to describe flotation processes include [25,27,31,39,43,44]. However, all these works utilize these variables for steady-state analyses, but do not incorporate the drift-flux variables into one solvable PDE model for transient simulations, which is precisely the main contribution of the present paper.
As stated above, the theory of conservation laws with discontinuous flux has seen a vast amount of interest in recent years, where the typical model equation is
or equivalently, in terms of the Heaviside step function $H(z)$,
The basic difficulty associated with (1.3) is as follows. Suppose, for simplicity, that $\phi = \phi(z, t)$, $z \in \mathbb{R}$, $t >0$ is a piecewise constant solution of (1.3) having traces $\phi_-(t) : = \lim_{z \uparrow 0} \phi(z, t)$ and $\phi_+(t) : = \lim_{z \downarrow 0} \phi(z, t)$ at $z = 0$. Then the fluxes to both sides of $z = 0$ must be equal at any time, which compels the jump condition
This single equation does not define the two traces uniquely and one needs to specify a selection principle or jump entropy condition to single out pairs that besides satisfying (1.4) are admissible. This selection principle usually depends on the particular physical reality (1.3) is supposed to model. For instance, applications of (1.3) also include traffic flow with discontinuously changing road surface conditions, ion etching, two-phase flow in heterogeneous porous media, and medical applications (see [5], [24,Ch. 8], and [28] for overviews and references). We use here the admissibility condition from [14], which has proved to be the natural one for the related problem of continuous sedimentation [15]. Furthermore, its generalization [18] to the case of a scalar convection-diffusion equation with spatial discontinuity in both the flux and diffusion functions implies the physically relevant solution in the case of the well-established model of continuous sedimentation with compression [10]. As is stated in [24,p. 426], there are different "recipes" to select unique solutions of the Riemann problem of (1.3), and all of them eventually lead to uniqueness of the initial value problem for (1.3), according to the unified treatment in [1].
1.3. Outline of the paper
In Section 2, we derive the model equations for the local fraction of gas bubbles, detailing the definition of the flux density functions in each zone of the spatial domain and the treatment of the feed inlets. Some notation necessary for the description of the steady-state solutions is also introduced. In Section 3, we focus on the characterization of all possible steady states for the flotation model previously defined, providing a detailed study of the derivation process at the different spatial discontinuities introduced by the feed inlets. Some steady states exist only under certain conditions on the injection rates and to get an overview of all possibilities, we present operating charts and tables for the categorization of all steady states. In Section 4, we briefly review the numerical method to approximately solve the flotation model. Some numerical examples are provided in Section 5 and, finally, we present some conclusions in Section 6.
2.
Mathematical model
2.1. Phase velocities and drift flux
Assume that we consider a region of space that is free of sources and sinks, that $\phi$ is the local fraction of gas bubbles, and that $\boldsymbol{v}_{\rm{f}}$ and $\boldsymbol{v}_{\rm{g}}$ are the phase velocities of the gas and fluid, respectively. Then the conservation of mass equations for both can be written in local form as
where we assume that the gas bubbles are incompressible and do not coalesce. Then, defining the volume average velocity, or bulk flux of the suspension,
and the gas-fluid relative velocity $\boldsymbol{v}_{\rm{r}}: = \boldsymbol{v}_{\rm{g}} - \boldsymbol{v}_{\rm{f}}$, we may rewrite the first equation in (2.1) and replace the second by the sum of both to obtain
It is assumed that $\boldsymbol{v}_{\rm{r}} = {v}_{\rm{r}} \boldsymbol{e}_z$, where $\boldsymbol{e}_z$ is the upward-pointing unit vector and ${v}_{\rm{r}}$ is given as a function of $\phi$ so that the gas drift-flux function is
The drift-flux function $j_{\rm{g}}(\phi)$ gives the gas flux in a closed column relative to the column. Here, $v_{\rm{term}}$ is the terminal velocity of a single bubble in an unbounded fluid. As is stated in [38], there exists a number of methods to calculate $v_{\rm{term}}$, and Wallis' generalized correlation [41] leading to $v_{\rm{term}}$ is recommended, see [38,Appendix A] for details. This correlation involves additional quantities such as equilibrium surface tension and the viscosity of the fluid. Its detailed discussion is beyond the focus of this paper; for the present analysis it suffices to assume that $v_{\rm{term}}$ is a set constant for a given material and equipment.
Furthermore, in (2.3), $V(\phi)$ is a dimensionless hindered-bubbling function that can, for instance, be given by the Richardson-Zaki expression [34]
The maximum possible volume fraction of bubbles is $\phi_{\rm{max}} = 1$. Realistic values of $n_{\rm{RZ}}$ range from $n_{\rm{RZ}} = 2$ to $n_{\rm{RZ}} = 3.2$ (cf., e.g., [13,22,25,31,39]).
Finally, in one space dimension (in the $z$-direction) and away from sinks or sources, $\nabla \cdot \boldsymbol{q} = 0$ reduces to $\partial q / \partial z = 0$, so $q$ will depend on $t$ only, and the only equation that needs to be solved is the nonlinear first-order conservation law
Hence, $j(\phi, t)$ is the total flux of gas. If we denote the total fluid flux by $\varphi: = (1-\phi)v_{\rm{f}}$, then (2.2) yields the simple relation $q = j+\varphi$ between the three fluxes, which all generally may have any sign.
2.2. Volumetric flows, bulk velocities and flux functions
It is assumed that the unit has a constant cross-sectional area $A$, and that concentrations are horizontally constant so that all variables depend on height $z$ and time $t$ only. The unit is fed at heights $z = z_{{\rm{W}}}$, $z = z_{{\rm{F}}}$ and $z = z_{{\rm{G}}}$, with wash water, fluid (feed slurry), and gas, respectively (see Figure 1), where we assume that $z_{{\rm{W}}} > z_{{\rm{F}}}> z_{{\rm{G}}}$. The corresponding volumetric flows $Q_{{\rm{W}}} \geq 0$, $Q_{{\rm{F}}} \geq 0$ and $Q_{{\rm{G}}} \geq 0$ are assumed to be given functions of time, as is the volumetric underflow rate $Q_{\rm{U}} \geq 0$. Furthermore, $Q_{\rm{E}}$ is the resulting effluent volumetric overflow, which is assumed to be nonnegative, i.e., the mixture is conserved and the vessel is always completely filled with mixture.
The spatially piecewise constant bulk velocity $q = q(z, t)$ is defined by the values $q_1(t)$ to $q_4(t)$ in the corresponding four zones in the vessel; see Figure 1.To simplify notation, we define the velocities $q_{S}(t) : = Q_{S}(t) / A$ for $S \in \{ {\rm{E}}, {\rm{F}}, {\rm{G}}, {\rm{U}}, {\rm{W}} \}$.
Starting from the bottom of the vessel, we have $q_1 = - {q_{\rm{U}}}$, $q_2 = q_1+q_{{\rm{G}}}$, etc. and we obtain the total bulk velocity function
Hence, we always have $q_{\rm{E}} = q_4 \geq 0$ and $q_1 = - {q_{\rm{U}}} \leq 0$, whereas $q_2$ and $q_3$ may have any sign.
We denote the intervals $z>z_{\rm{E}}$ and $z<z_{\rm{U}}$ by the effluent and underflow zone, respectively. During normal operation, zone 1 contains only liquid. Above $z = z_{\rm{G}}$ there is a region of bubbles rising with a high velocity up to an upper region of froth with a high volume fraction of gas; see Figure 1. The large discontinuity between the bubbly and froth regions is usually located in the interval $[z_{{\rm{F}}}, z_{{\rm{W}}}]$, either at the location of one injection point or within a zone. As we will see, discontinuities in $\phi$ are possible at every injection point and inside some zones. Usually, zone 4 is small, and sometimes $z_{{\rm{G}}} = z_{{\rm{F}}}$, i.e., gas and feed slurry are injected at the same location.
We assume that in the effluent and underflow zones, the gas and the fluid move at the same velocity, so we set $v_{\rm{r}}: = 0$, and therefore $j_{\rm{g}}: = 0$ in these zones. The total flux function is then defined as
2.3. Feed sources and governing equation in final form
The conservation law (2.5) is completed by including the feed of material at levels $z_{{\rm{W}}}$, $z_{{\rm{F}}}$ and $z_{{\rm{G}}}$ at volume rates $Q_{{\rm{W}}}$, $Q_{{\rm{F}}}$ and $Q_{{\rm{G}}}$. The feed mechanisms give rise to singular source terms that extend (2.5) to the final governing model equation (1.1). The given gas volume fraction of the three time-dependent feed streams is denoted by $\phi_{{\rm{W}}}$, $\phi_{{\rm{F}}}$ and $\phi_{{\rm{G}}}$, respectively. In agreement to common practice, we assume that either pure gas or pure liquid is injected through the respective singular sources, so we assume from now on $\phi_{{\rm{G}}} \equiv 1$ and $\phi_{{\rm{F}}} = \phi_{{\rm{W}}} \equiv 0$.
2.4. Entropy solutions
Within each zone, the governing equation (1.1), (2.7) reduces to (2.5), and we consider the Cauchy problem of this equation. A piecewise smooth function $\phi = \phi(x, t)$ is defined to be an entropy solution of the problem if $\phi$ is continuously differentiable everywhere with the exception of a finite number of curves $z = z_{\rm d}(t)\in C^1$ of discontinuities. At each point $(z_{\rm d}(t), t)$ of discontinuity, the (non-equal) values $\smash{\phi^{\pm}: = \phi(z_{\rm d}(t)^{\pm}, t)}$ satisfy the jump condition
and the jump entropy condition
It is well known that entropy solutions in the sense of Oleinik [30] are also the unique entropy solutions in the sense of Kružkov-type [26] integral inequalities (cf., e.g., [24]). On the other hand and as mentioned in Section 1.2, at the five spatial discontinuities of problem (1.1), a generalized entropy is needed [14,18]. Since we only construct steady-state solutions, we review that condition in Section 3.1 for this purpose, which means less notation than for the dynamic case.
2.5. Properties of the zone flux functions
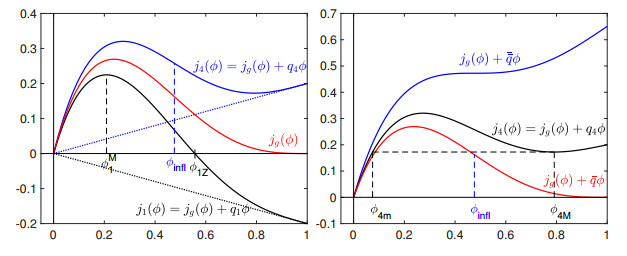
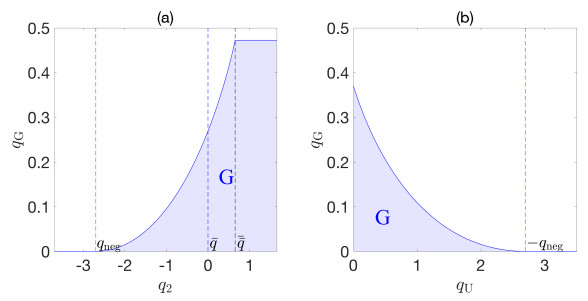
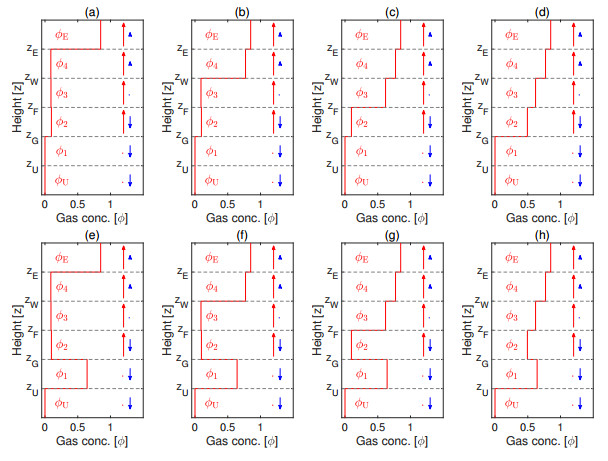
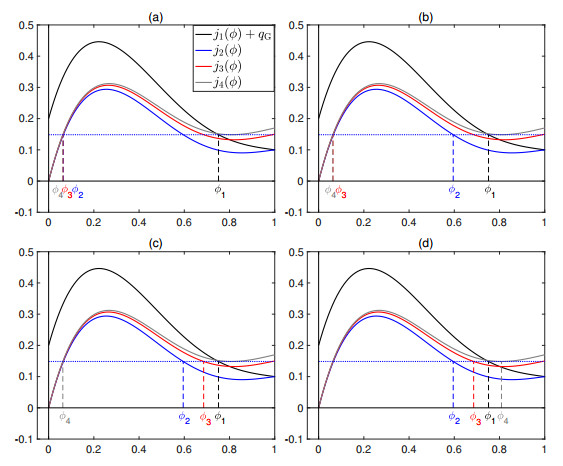
We assume that the drift-flux function $j_{\rm{g}}(\phi)\geq 0$ is continuously differentiable, satisfies $j_{\rm{g}}(0) = j_{\rm{g}}(1) = 0$, and is concave-convex with an inflection point $\phi_{\rm infl}\in(0, 1)$; see Figure 2. (Drawings have been made for $j_{\rm{g}}$ given by (2.3) and (2.4), with $v_{\rm{term}} = 2.7 \, {\rm{cm/s}}$ and $n_{\rm{RZ}} = 3.2$. These values are also utilized in [13].) The form of $j_{\rm{g}}$ singles out certain distinguished values of the volume fraction that appear in the steady-state solution (see Figure 2). The same values appear in the related problem of continuous sedimentation [16,17].
Since we will mostly refer to steady-state situations, we often supress the dependence on $t$ in $j_1, \dots, j_4$. The functions $j_1, \dots, j_4$ and $j_{\rm{g}}$ have the same inflection point $\phi_{\rm infl}$, since they only differ by a linear term. If $j_k(\phi)$ has a zero in $(0, 1]$, which can happen only for $k = 1, 2, 3$ and $q_k<0$, then we denote it by $\phi_{k{\rm{Z}}}$. If $j_k(\phi)<0$ for all $\phi\in(0, 1]$, we set $\phi_{k{\rm{Z}}}: = 0$. We define
which are the bulk velocities such that the slope of $j_k(\phi)$ is zero at $\phi_{\rm max} = 1$ and $\phi_{\rm infl}$, respectively. To reduce the number of cases to investigate, we assume in this work that
in accordance with the common Richardson-Zaki function (2.4). For intermediate values of $q_k$, i.e., $\bar q<q_k<{\bar {\bar{q}}}$, there is a local minimizer $\phi_{k{\rm{M}}}$ of $j_k(\phi)$ ($k = 2, 3, 4$) on the right of $\phi_{\rm{infl}}$. Then $\smash{0 = j_k'(\phi_{k{\rm{M}}}) = j_{\rm{g}}'(\phi_{k{\rm{M}}})+q_k}$. To obtain a definition for all values of $q_k$, we note that the restriction $\smash{(j_{\rm{g}}|_{(\phi_{\rm infl}, 1)})'}$ is a decreasing function so that we can define
Given $\phi_{k{\rm{M}}}$ and $q_k\geq 0$, we define $\phi_{k{\rm{m}}}$ as the unique value satisfying
For $q_k<{\bar {\bar{q}}}$, $j_k(\phi)$ assumes a local maximum point at $\smash{\phi_k^{\rm{M}}} \in[0, \phi_{\rm infl})$. Let $\smash{q_{\text{neg}}}: = \smash{-j_{\rm{g}}'}(0)$ be the value below which $j_k$ is a decreasing function. For $q_k\leq q_{\text{neg}}$, the local maximum is $\smash{\phi_k^{\rm{M}}: = 0}$. For $\smash{q_k\geq {\bar {\bar{q}}}}$, we set $\smash{\phi_k^{\rm{M}}}: = \phi_{\rm infl}$.
In some instances it is convenient to write out the dependence on $q$ of the flux function, i.e., $j_k(\phi;q_k)$, and of the specific concentrations, e.g., $\smash{\phi_k^{\rm{M}}(q_k)}$. The following properties follow directly from the definitions above (cf. [16,Lemma 2]).
Lemma 2.1. The following properties hold:
3.
Steady-state solutions
In order to completely describe all possible steady states of model (1.1) (under the assumptions of Section 2.5), we here extract from the theory of conservation laws with discontinuous flux function [14,18] what is necessary to construct steady-state solutions in a neighbourhood of a spatial discontinuity.
To start with, we investigate the case when the steady-state solution is constant $\phi_k$ in zone $k = 1, 2, 3, 4$, and constant $\phi_{\rm{U}}$ and $\phi_{\rm{E}}$ in the underflow and effluent zones, respectively. In Section 3.9, we describe the general solution, having also discontinuities within one or several zones. First, we review the necessary theory and notation, and then go through the possible couplings between zones 1 to 4 and the effluent and underflow zones.
3.1. Construction of steady-state solutions for a conservation law with discontinuous flux function
We consider the conservation law with discontinuous flux function (1.3). The equation should be interpreted in the weak sense and we seek steady-state solutions of the form
where $\phi_{\pm}$ are constants. The conservation law across $z = 0$ implies the jump condition $g(\phi_-) = f(\phi_+)$ (see (1.4)). This single equation has two unknowns. The generalized entropy condition [14] selects the physically relevant solution in a neighbourhood of $z = 0$ for a dynamic solution of (1.3) for given initial data at $t = 0$. We define the auxiliary functions
Since ${\check g}(\cdot;\phi_-)$ is non-increasing and ${\hat f}(\cdot;\phi_+)$ is non-decreasing, the intersection of the graphs of these functions occurs at a unique flux value, if there exists an intersection. For the model of flotation, this is always the case; the proof of this statement can be made in the same way as for the problem of continuous sedimentation; see [15].
We define the set of possible $\phi$-values of the intersection as
and the corresponding unique flux value $\eta(\phi_+, \phi_-): = {\hat f}(\bar{\Phi};\phi_+)$. Since we are here only interested in stationary solutions, the generalized entropy condition can be stated as
where we note that ${\hat f}(\phi_+;\phi_+) = f(\phi_+)$ and ${\check g}(\phi_-;\phi_-) = g(\phi_-)$.
3.2. Couplings at the underflow location $z=z_{\rm{U}}$
In a neighbourhood of ${z = z_{\rm{U}}}$, the PDE (1.1) becomes
where
We now suppress the time dependence and seek possible constant solutions $\phi_1$ and $\phi_{\rm U}$ in the two neighbouring zones so that the entropy condition (3.1) is satisfied. With the notation of Section 3.1, we have $g(\phi) = j_{\rm{U}}(\phi) = q_1\phi$ and $f(\phi) = j_1(\phi) = q_1\phi+j_{\rm{g}}(\phi)$. The task is to find a pair $\phi_{\rm U}$ and $\phi_1$ so that the entropy condition (3.1) is satisfied. This condition now reads
where $\eta(\phi_1, \phi_{\rm U})$ denotes the flux value of the intersection of ${\hat{\jmath}}_U(\cdot;\phi_{\rm U})$ and ${\hat{\jmath}}(\cdot;\phi_1)$. As $j_{\rm{U}}(\phi) = -q_{\rm{U}}\phi$ is a linear decreasing function, we have $\check{\jmath}_{\rm{U}}(\cdot;\phi_{\rm{U}}) = j_{\rm{U}}$ for any $\phi_{\rm U}\in[0, 1]$. The function $j_1$ has two monotonicity intervals separated by the maximum point $\phi_{1}^{\rm{M}}$, which leads to the following cases:
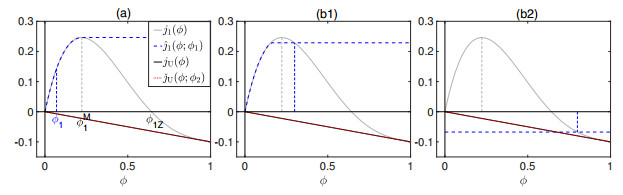
(a) $\phi_1\in[0, \phi_1^{\rm{M}}]$, see Fig. 3(a). The only possible intersection between $\hat{\jmath}_1$ and $\check{\jmath}_{\rm{U}}$ is $\phi_1 = 0$; hence $\phi_{\rm{U}} = 0$. Thus, the zero solution on both sides is the only possible steady-state coupling in this case.
(b) $\phi_1\in(\phi_1^{\rm{M}}, 1]$, see Fig. 3(b1) and (b2). If $\phi_1\in(\phi_1^{\rm{M}}, \phi_{1{\rm{Z}}})$, the middle plot shows that the only possible intersection is, as in the previous case, ${\phi_1 = 0}$, but is outside the interval of definition of $\phi_1$, i.e., there is no possible steady state with $\phi_1\in(\phi_1^{\rm{M}}, \phi_{1{\rm{Z}}})$. If $\phi_1\in[\phi_{1{\rm{Z}}}, 1]$ (right plot), then there is always a possible intersection between $\hat{\jmath}_1(\cdot;\phi_1)$ and $\check{\jmath}_{\rm{U}}(\cdot;\phi_{\rm{U}})$ satisfying (3.2). Consequently, the possible steady states satisfy $\phi_1\in[\phi_{1{\rm{Z}}}, 1]$ and $\phi_{\rm{U}}\in[0, 1]$.
We conclude this subsection by stating the possible steady-state values in the underflow and the first zone:
3.3. Couplings at the effluent location $z=z_{{\rm{E}}}$
Here, $j_{\rm{E}}(\phi) = q_{\rm{E}}\phi$ is an increasing linear function. The procedure is analogous to the coupling at $z = z_{\rm{U}}$. In fact, this case is the same as the one at the underflow level in the problem of continuous sedimentation. Details can be found in [15,Section 9], and we state here directly the possible steady-state values in zone 4 and the effluent zone:
3.4. Couplings at $z=z_{{\rm{G}}}$
In a neighbourhood of $z = z_{\rm{G}}$, the PDE (1.1) is
which, with $\phi_{\rm{G}}(t)\equiv 1$, is formally equivalent to
The flux functions to consider for the steady-state coupling are thus
which intersect only at $\phi = 1$, and the entropy condition is
We have $q_1 = -q_{\rm{U}}\leq0$, but $q_2$ may have any sign. We will make a main division depending on the sign of $q_2$. From (3.3), we know that a steady state in zone 1 satisfies $\phi_1\in\{0\}\cup[\phi_{1{\rm{Z}}}, 1]$. These two intervals should be coupled with the three monotonicity intervals of $j_2$, which are separated by $\phi_{2}^{\rm{M}}$ and $\phi_{2{\rm{M}}}$. We will get conditions on $q_{\rm{G}}$ in the subcases.
Remark 1. In the division into subcases further on, we will sometimes let such overlap in the following way. Instead of having disjoint intervals defining two subcases, e.g., $\phi_2\in[0, \phi_2^{\rm{M}}]$ and $\phi_2\in(\phi_2^{\rm{M}}, \phi_{2{\rm{M}}})$, the second subcase will instead be $\phi_2\in[\phi_2^{\rm{M}}, \phi_{2{\rm{M}}}]$. This overlap will reduce the number of conditions in terms of inequalities. Then the same steady-state solution can occur in two subcases, but the final number of steady-state solutions is not affected.
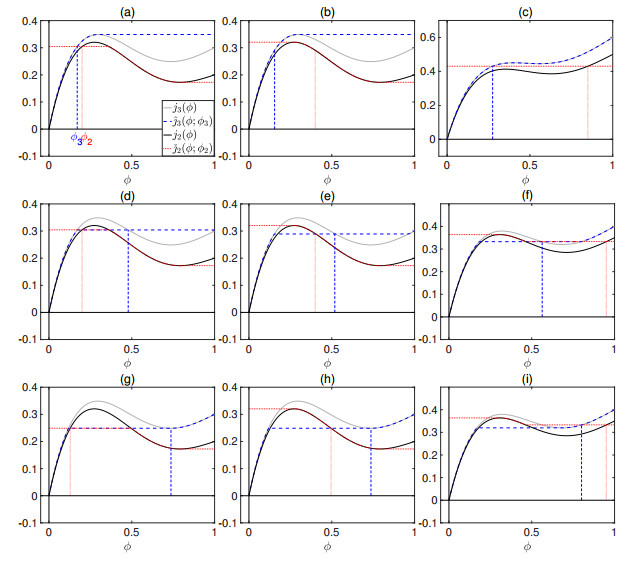
1. Case G1. $q_1\leq 0\leq q_2$.
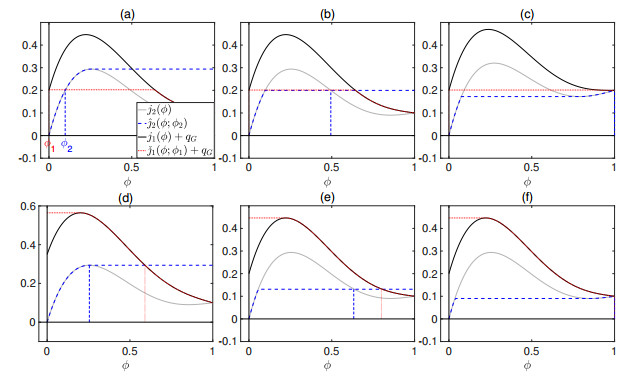
(a) $\phi_1 = 0$, $\phi_2\in[0, \phi_2^{\rm{M}}]$; see Fig. 4(a). A necessary condition for a steady-state solution is
(b) $\phi_1 = 0$, $\phi_2\in[\phi_2^{\rm{M}}, \phi_{2{\rm{M}}}]$; see Fig. 4(b). A necessary condition for a steady-state solution is (G).
(c) $\phi_1 = 0$, $\phi_2\in(\phi_{2{\rm{M}}}, 1]$; see Fig. 4(c). The only possible solution is $\phi_2 = 1$ when $q_1 = 0$.
(d) $\phi_1\in[\phi_{1{\rm{Z}}}, 1]$, $\phi_2\in[0, \phi_2^{\rm{M}}]$; see Fig. 4(d). The only possible steady-state solution satisfies $\phi_2 = \phi_2^{\rm{M}}<\phi_1$.
(e) $\phi_1\in[\phi_{1{\rm{Z}}}, 1]$, $\phi_2\in(\phi_2^{\rm{M}}, \phi_{2{\rm{M}}})$; see Fig. 4(e). A steady-state coupling is possible with $\phi_2\leq\phi_1$ with equality if and only if $q_1 = q_2$, i.e., $q_{\rm{G}} = 0$.
(f) $\phi_1\in[\phi_{1{\rm{Z}}}, 1]$, $\phi_2\in[\phi_{2{\rm{M}}}, 1]$; see Fig. 4(f). The only possible coupling is $\phi_1 = \phi_2 = 1$.
2. Case G2. $q_1\leq q_2\leq 0$.
(a) $\phi_1 = 0$, $\phi_2\in[0, \phi_2^{\rm{M}}]$; see Fig. 5(a). The same as Case G1(a) with condition (G).
(b) $\phi_1 = 0$, $\phi_2\in[\phi_2^{\rm{M}}, 1]$; see Fig. 5(b1) and (b2). As in Case G1(b) a necessary condition is (G). The largest value in zone 2 is $\phi_2 = \phi_{2{\rm{Z}}}$ and then $q_1 = q_2$, i.e., $q_{\rm{G}} = 0$, see plot (b2).
(c) $\phi_1\in[\phi_{1{\rm{Z}}}, 1]$, $\phi_2\in[0, \phi_2^{\rm{M}}]$; see Fig. 5(c). The same as Case G1(d): $\phi_2 = \phi_2^{\rm{M}}<\phi_1$.
(d) $\phi_1\in[\phi_{1{\rm{Z}}}, 1]$, $\phi_2\in(\phi_2^{\rm{M}}, 1]$. Solution exists with either a positive, see Fig. 5(d1) or a negative flux (d2).
3.5. Couplings at $z=z_{\rm{F}}$
We derive the possible constant steady states in zones 2 and 3 considering their coupling at $z = z_{\rm{F}}$. This is the most complicated case where both bulk velocities, hence both fluxes, can be either positive or negative. Since there is no injection of bubbles, $\phi_{\rm{F}} = 0$, the fluxes to consider are
where $q_2 = q_{\rm{G}}-q_{\rm{U}}\leq q_{\rm{G}}+q_{\rm{F}}-q_{\rm{U}} = q_3$. We require that the entropy condition (3.1) holds, which now reads
We now study the possible intersections between $\check{\jmath}_2(\cdot;\phi_2)$ and $\hat{\jmath}_3(\cdot;\phi_3)$ and make a division into three main cases F1-F3 depending on the signs of the two bulk velocities $q_2$ and $q_3$. Subdivisions are then made according to the intervals of monotonicity of the flux functions $j_2$ and $j_3$, which give qualitatively different intersections of $\check{\jmath}_2(\cdot;\phi_2)$ and $\hat{\jmath}_3(\cdot;\phi_3)$ because of their strictly monotone parts and plateaus. Some cases will be empty, i.e., no steady-state solution is possible and this may depend on $q_2$ and $q_3$. When a steady-state solution is possible, it always satisfies $j_2(\phi_2) = j_3(\phi_3)$.
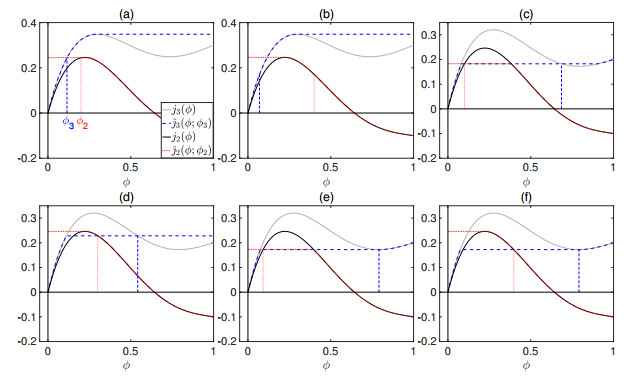
1. Case F1. $0\leq q_2\leq q_3$.
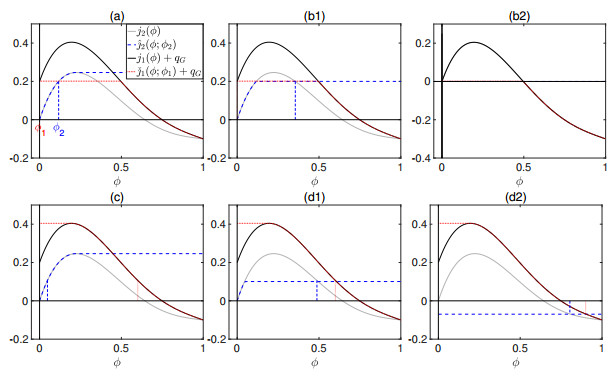
(a) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in[0, \phi_3^{\rm{M}}]$; see Fig. 6(a). In this case there is a possible intersection point between $\check{\jmath}_2(\cdot;\phi_2)$ and $\hat{\jmath}_3(\cdot;\phi_3)$. We have $q_2\leq q_3\Leftrightarrow\phi_3\leq\phi_2$.
(b) $\phi_2\in(\phi_2^{\rm{M}}, \phi_{2{\rm{M}}})$, $\phi_3\in[0, \phi_3^{\rm{M}}]$. The flux value of the intersection of ${\check{\jmath}}_2$ and ${\hat \jmath}_3$ is $\eta = j_2(\phi_2^{\rm{M}}) = {\check{\jmath}}_2(\phi_2^{\rm{M}};\phi_2)$. Since this case requires $\phi_2^{\rm{M}}<\phi_2$, (3.5) is not satisfied and there is no possible stationary solution.
(c) $\phi_2\in[\phi_{2{\rm{M}}}, 1]$, $\phi_3\in[0, \phi_3^{\rm{M}}]$; see Fig. 6(c). The only possibility for the plateau of ${\check{\jmath}}_2(\cdot;\phi_2)$ to intersect the increasing part of ${\hat \jmath}_3(\cdot;\phi_3)$ is that the plateau lies above the value of the local maximum of $j_2$. In other words, this case is empty unless the following condition is satisfied:
(d) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in(\phi_3^{\rm{M}}, \phi_{3{\rm{M}}}]$; see Fig. 6(d). For (3.5) to be satisfied, two plateaus are involved in the intersection. A necessary condition for this is that the flux value of the local maximum of $j_2$ is larger than or equal to the flux value of the local minimum of $j_3$, i.e.,
(e) $\phi_2\in[\phi_2^{\rm{M}}, \phi_{2{\rm{M}}})$, $\phi_3\in(\phi_3^{\rm{M}}, \phi_{3{\rm{M}}}]$. An intersection occurs between the decreasing part of ${\check{\jmath}}_2(\cdot;\phi_2)$ and the plateau of ${\hat \jmath}_3(\cdot;\phi_3)$ only if (FⅡ) holds. We have $q_2\leq q_3\Leftrightarrow\phi_2\leq\phi_3$.
(f) $\phi_2\in[\phi_{2{\rm{M}}}, 1]$, $\phi_3\in(\phi_3^{\rm{M}}, \phi_{3{\rm{M}}}]$. Two plateaus are necessarily involved in the intersection, which occurs only if the following condition is satisfied:
(g) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in(\phi_{3{\rm{M}}}, 1]$. The intersection occurs at the flux level $j_3(\phi_{3{\rm{M}}}) = {\hat \jmath}_3(\phi_{3{\rm{M}}};\phi_3)$. However, $\phi_3 = \phi_{3{\rm{M}}}$ is not allowed in this subcase, so (3.5) is not satisfied and this case is therefore empty.
(h) $\phi_2\in(\phi_2^{\rm{M}}, \phi_{2{\rm{M}}})$, $\phi_3\in(\phi_{3{\rm{M}}}, 1]$. This case is empty with the same motivation as in subcase (g).
(i) $\phi_2\in[\phi_{2{\rm{M}}}, 1]$, $\phi_3\in[\phi_{3{\rm{M}}}, 1]$. Similarly to subcase (f), a steady-state solution is possible only if (FⅢ) holds. We have $q_2\leq q_3\Leftrightarrow\phi_2\leq\phi_3$.
2. Case F2. $q_2\leq 0\leq q_3$. We use the same principle of subdivision as in Case F1. However, when $q_2\leq 0$, the local minimizer of $j_2(\cdot;q_2)$ is $\phi_{2{\rm{M}}} = 1$, so the domain of $j_2(\cdot;q_2)$ consists of two disjoint intervals where $j_2$ is monotone. Together with the three intervals of $j_3$, we get six subcases.
(a) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in[0, \phi_3^{\rm{M}}]$. As can be seen in Fig. 7(a), there is always a possible intersection between $\check{\jmath}_2(\cdot;\phi_2)$ and $\hat{\jmath}_3(\cdot;\phi_3)$. We have either $q_2<q_3\Leftrightarrow\phi_3<\phi_2$, or $q_2 = q_3 = 0\Leftrightarrow\phi_2 = \phi_3$. This subcase is thus similar to Case F1(a).
(b) $\phi_2\in(\phi_2^{\rm{M}}, 1]$, $\phi_3\in[0, \phi_3^{\rm{M}}]$. This case is empty with analogous arguments as in Case F1(b).
(c) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in(\phi_3^{\rm{M}}, \phi_{3{\rm{M}}}]$. The intersection of $\check{\jmath}_2(\cdot;\phi_2)$ and $\hat{\jmath}_3(\cdot;\phi_3)$ is qualitatively the same as in Case F1(d) and (e) and the steady state represented in Fig. 7(c) is possible only if (FⅡ) holds.
(d) $\phi_2\in(\phi_2^{\rm{M}}, 1]$, $\phi_3\in(\phi_3^{\rm{M}}, \phi_{3{\rm{M}}}]$. By analogy with subcase (c), (FⅡ) has to be satisfied.
(e) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in(\phi_{3{\rm{M}}}, 1]$. This case is analogous to Case F1(g), and is consequently empty.
(f) $\phi_2\in(\phi_2^{\rm{M}}, 1]$, $\phi_3\in(\phi_{3{\rm{M}}}, 1]$. Analogous to Case F1(h) and empty case.
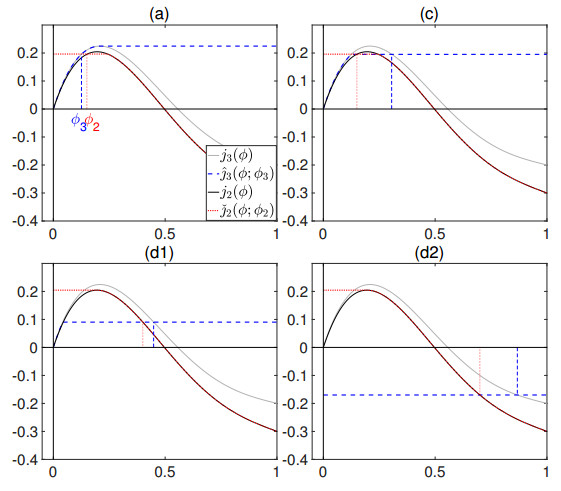
3. Case F3. $q_2\leq q_3\leq0$. In this case $\phi_{2{\rm{M}}} = \phi_{3{\rm{M}}} = 1$, so there are only four subcases with the maximum point of each flux function as the point of division of two monotonicity intervals.
(a) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in[0, \phi_3^{\rm{M}}]$. This is qualitatively the same as Case F2(a) with steady-state solution possible.
(b) $\phi_2\in(\phi_2^{\rm{M}}, 1]$, $\phi_3\in[0, \phi_3^{\rm{M}}]$. This case is empty with analogous arguments as in Case F1(b) or F2(b) (no plot is shown).
(c) $\phi_2\in[0, \phi_2^{\rm{M}}]$, $\phi_3\in(\phi_3^{\rm{M}}, 1]$. There is a possible intersection only at a non-negative flux value. Then bubbles flow upwards and we have $\phi_3\in[\phi_3^{\rm{M}}, \phi_{3{\rm{Z}}}]$, see Fig. 8(c).
(d) $\phi_2\in(\phi_2^{\rm{M}}, 1]$, $\phi_3\in(\phi_3^{\rm{M}}, 1]$. Intersection may occur at a positive or negative flux value (bubbles moving downwards or upwards), see Fig. 8(d1) and (d2), respectively.
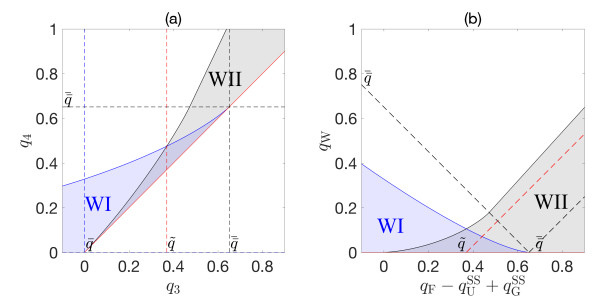
3.6. Couplings at $z=z_{{\rm{W}}}$
Since $\phi_{{\rm{W}}} = 0$, the fluxes to consider for the entropy condition are ${\check \jmath}_3(\cdot;\phi_3)$ and ${\hat \jmath}_4(\cdot;\phi_4)$. From (3.4) we know that only $\phi_4\in[0, \phi_{4{\rm{m}}}] \cup [\phi_{4{\rm{M}}}, 1]$ are possible steady states in zone 4. In these two intervals, $j_4$ is increasing and we combine these intervals with the three monotone parts of $j_3$.
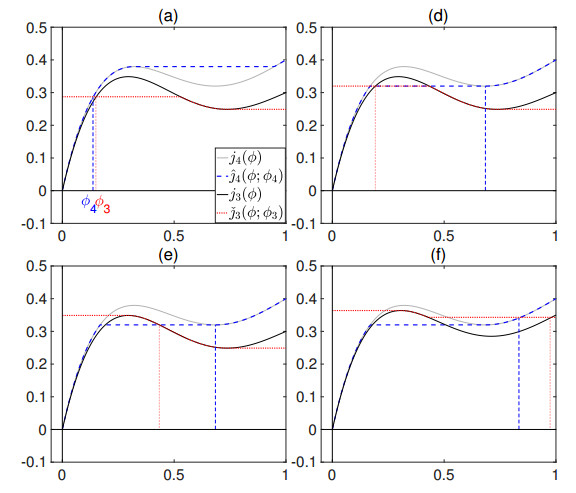
1. Case W1. $0\leq q_3\leq q_4$.
(a) $\phi_3\in[0, \phi_3^{\rm{M}}]$, $\phi_4\in[0, \phi_{4{\rm{m}}}]$; see Fig. 9(a).
(b) $\phi_3\in(\phi_3^{\rm{M}}, \phi_{3{\rm{M}}})$, $\phi_4\in[0, \phi_{4{\rm{m}}}]$ is an empty case (no plot is shown).
(c) $\phi_3\in[\phi_{3{\rm{M}}}, 1]$, $\phi_4\in[0, \phi_{4{\rm{m}}}]$ is an empty case (no plot is shown).
(d) $\phi_3\in[0, \phi_3^{\rm{M}}]$, $\phi_4\in[\phi_{4{\rm{M}}}, 1]$; see Fig. 9(d). Necessarily, $\phi_4 = \phi_{4{\rm{M}}}$ holds. Another necessary condition for this steady state is that the flux value of the local maximum of $j_3$ is larger than or equal to the flux value of the local minimum of $j_4$, i.e.,
(e) $\phi_3\in[\phi_3^{\rm{M}}, \phi_{3{\rm{M}}})$, $\phi_4\in[\phi_{4{\rm{M}}}, 1]$; see Fig. 9(e). In this case $\phi_4 = \phi_{4{\rm{M}}}$ and the necessary condition is (WⅠ).
(f) $\phi_3\in[\phi_{3{\rm{M}}}, 1]$, $\phi_4\in[\phi_{4{\rm{M}}}, 1]$; see Fig. 9(f). This case is empty unless the following condition holds:
2. Case W2. $q_3\leq 0\leq q_4$. The conclusions are the same as in Case W1.
3.7. Operating charts for bulk velocities
The different necessary conditions on the fluxes that appear in the derivation of possible steady states can be visualized in operating charts. These are two-dimensional diagrams involving the bulk velocities at an injection point.
Condition (G) can be written as
where the dependence on $q_2$ is written out as in Lemma 2.1. This lemma gives that $j_2(\phi_2^{\rm{M}}(q_2);q_2)$ is an increasing function of intermediate (normal) values of $q_2$ and otherwise constant (for $q_2<q_{\rm{neg}}$ and $q_2>{\bar {\bar q}}$). Its graph, and consequently the region in $(q_2, q_{\rm{G}})$-space where (G) is satisfied, are shown in Fig. 10(a). In Fig. 10(b), the corresponding region in $(q_{\rm{U}}, q_{\rm{G}})$-space is shown. This has been obtained by the linear mapping of the curve $q_{\rm{G}} = j_2(\phi_2^{\rm{M}}(q_2);q_2)$ (since $q_{\rm{U}} = q_{\rm{G}}-q_2$):
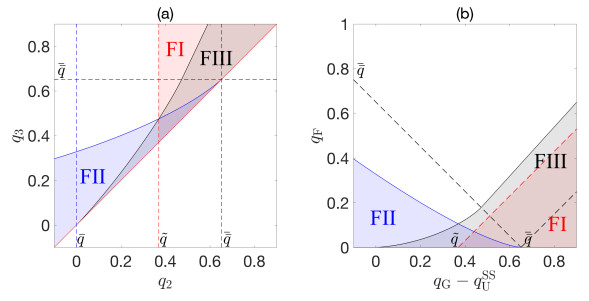
We will now do the same for the coupling at $z = z_{\rm{F}}$ and conditions (FⅠ)-(FⅢ). These lead to overlapping regions in the $(q_2, q_3)$-plane leading to different numbers of possible steady states in different regions. In Fig. 11, the regions are shadowed in which (FⅠ) (red), (FⅡ) (blue) and (FⅢ) (grey) hold.
To obtain these regions, we define the following functions with respect to conditions (FⅠ)-(FⅡ):
These functions are continuously differentiable by Lemma 2.1. The following lemma gives the qualitative properties of the boundaries of the regions.
Lemma 3.1. There exists a unique $\tilde{q}\in(0, {\bar {\bar q}})$ and a unique continuously differentiable function ${\tilde h}_{\rm{II}}$ such that $\tilde{q} = j_3(\phi_{\rm{3M}}(\tilde{q});\tilde{q})$ and the following hold:
Proof. Using Lemma 2.1, we get
where the last inequality follows from the fact that $j_2(\cdot;{\bar {\bar q}})$ is an increasing function. Hence, ${h_{\rm{I}}}$ is a continuous increasing function and (3.6) follows. For condition (FⅡ), we have (by means of Lemma 2.1)
Since the latter derivative is always non-zero, the implicit function theorem implies the existence of a continuously differentiable function ${\tilde h}_{\rm{II}}$ satisfying
For $q_2\leq q_{\rm{neg}}$ and $q_3 = 0$, we have
and for $q_3 = q_2\geq{\bar {\bar q}}$, we have
Condition (FⅢ) can directly be rewritten by using the identity $j_2(1;q_2) = q_2$. Hence, the boundary of the region where condition (FⅢ) holds is given by the curve $j_3(\phi_{\rm{3M}}(q_3);q_3)$, and its properties follow from Lemma 2.1 and the definition of $\phi_{\rm{3M}}(q_3)$. Finally, the definition of $\tilde{q}$ gives that
As we did for the gas injection point, we now transform the boundary curves of conditions (FⅠ)-(FⅢ) from the $(q_2, q_3)$-plane to the $(q_{\rm{G}}, q_{\rm{F}})$-plane with the linear mapping
This mapping depends on the chosen steady-state value of $q_{\rm{U}}$, denoted by $q_{\rm{U}}^{\rm{SS}}$, from the chart in Fig. 10(b). For a given value of $q_{\rm{U}}^{\rm{SS}}$, we therefore use the scale $q_{\rm{G}}-q_{\rm{U}}^{\rm{SS}}$ on the horizontal axis; see Fig. 11(b).
For the coupling at $z = z_{\rm{W}}$, we note that conditions (WⅠ) and (WⅡ) are the same as conditions (FⅡ) and (FⅢ) except for the zone index increased by one. Hence, the analogous statements of Lemma 3.1 hold, except for those involving $\tilde{q}$. We can draw the operating chart in the $(q_3, q_4)$-plane, and with the mapping
the chart in the $(q_{\rm{F}}, q_{\rm{W}})$-plane, where the steady-state values $q_{\rm{U}}^{\rm{SS}}$ and $q_{\rm{G}}^{\rm{SS}}$ have been chosen from the previous operating charts; see Fig. 12.
It seems logical that when working with steady states, it is necessary to restrict the amount of gas, fluid or water pumped into the tank. Moreover, from the desliming point of view, situations as huge quantities of fluid leaving at the top of the column, loosening the froth or washing it in excess, or gas bubbles flowing down and out of the tank through the bottom tailings underflow, are not convenient. Conditions (G), (FⅠ)-(FⅢ) and (WⅠ)-(WⅡ) set a theoretical upper limit for the values of $q_{\rm{G}}$, $q_{\rm{F}}$ and $q_{\rm{W}}$, respectively, for a fixed given value of $q_{\rm{U}}^{\rm{SS}}$, as Figures 10-12 show. For instance, Fig. 11(b) shows that if we want any condition (FⅠ)-(FⅢ) to be satisfied for $\smash{q_{\rm{G}}-q_{\rm{U}}^{\rm{SS}}\in[-0.1, 0.9] \, {\rm{cm/s}}}$, then we should set $q_{\rm{F}}<0.7 \, {\rm{cm/s}}$.
3.8. Tables and visualization of steady states
Whereas the operating charts in Section 3.7 give an overview on how to choose the bulk velocities with respect to conditions for certain steady-state couplings at the points of injection and outlets, we here collect in Tables 1 and 3 all possible steady-state combinations between these couplings for the cases $q_3\geq q_2\geq0$ and $q_2<0$, respectively. Some of the couplings made locally, for example for $\phi_2$ and $\phi_3$ in Section 3.5, do not appear in the tables because they are not possible when taking into account also the couplings with $\phi_1$ and $\phi_4$.
The tables should be read as follows. A possible steady-state solution with constant concentration in each zone is obtained by connecting adjacent rectangles passing only over vertical lines (and no corners), from the left column $\phi_{\rm{U}}$ to the right $\phi_{\rm{E}}$. In Table 2 we show some examples of admissible and inadmissible paths, in green and red respectively, for steady states for the case $q_3\geq q_2\geq0$ in Table 1. As it can be seen, the inadmissible path passes over a horizontal line in the $\phi_2$-column, yielding two different possible intervals of definition for $\phi_2$, which is not allowed.
Table 3 shows the possible steady states when $q_2<0$ and the sign restrictions of $q_3$ are given in the table. The appearance of conditions (G), (FⅠ), etc. in the tables means that the corresponding steady state is possible only if the corresponding conditions are satisfied. As can be seen in the first and the last columns of the tables, the values of $\phi_{\rm{U}}$ and $\phi_{\rm{E}}$ are uniquely given by the chosen value of $\phi_{1}$ and $\phi_4$, respectively. Also notice that although in the derivation of the cases we allow the intervals of definition of $\phi_i$ to overlap, we do not do this in the construction of the tables, to avoid the appearance of a possible steady state more than once and keep the tables as simple as possible.
3.9. Steady states having discontinuities within zones
Despite the diversity of possible steady states with a constant value in each zone, which are categorized in Tables 1 and 3, there exist further steady states with possible stationary discontinuities within the zones. For example, in zone 1, the constant solutions $\phi_1 = 0$ and $\phi_{1{\rm{Z}}}$ have the same flux value, i.e., $j_1(0) = j_1(\phi_{1{\rm{Z}}})$. This means that there may be a stationary discontinuity from $\phi_1 = 0$ below to $\phi_{1{\rm{Z}}}$ above the discontinuity, which may be located anywhere in the interval $(z_{\rm{U}}, z_{\rm{G}})$, since the entropy condition (2.9) is satisfied. If such a discontinuity exists in zone 1, then the value $\phi_{1{\rm{Z}}}$ can be coupled with admissible values of $\phi_2$ according to Table 1 or 3.
In the same way, stationary discontinuities from a lower to a higher value are possible in zones 2, 3 and 4 for all bulk velocities $q_k$ that imply that the drift-flux function in the zone is not monotone; hence, $q_k>q_{\rm{neg}}$ should hold. Analogously, there may be discontinuities from higher gas volume fraction below a standing discontinuity than above, if the drift flux has its local minimum point $\phi_{k{\rm{M}}}(q_k)\in(\phi_{\rm infl}, 1)$, which is equivalent to $q_k\in({\bar q}, {\bar {\bar q}})$. We provide examples of such discontinuities in Section 5.
4.
Numerical method
For the discretization of the model, we follow the procedure of [3] for the sedimentation process in a clarifier-thickener.
We subdivide the tank into $N$ internal layers, or cells, and four external layers, two at the top and two at the bottom, corresponding to the overflow and underflow zones, respectively, each of them with depth $\Delta z = 1/N$. We let $\phi^i(t)\approx\phi(z_i, t)$ denote the average of the exact solution over layer $i$, i.e. $(z_{i-1}, z_i)$, at time $t$, i.e.,
For each layer $i$, we use the balance law corresponding to (1.1) to obtain
where the flux $F(z, t, \phi)$ is defined by (2.7). This is approximated by Godunov's numerical flux [23], which is
where $k\in\{{\rm{E}}, 1, 2, 3, 4, {\rm{U}}\}$ denotes the present zone of the vessel ($k$ depends on $i$). We define the indices $i_{\rm{G}}$, $i_{\rm{F}}$, $i_{\rm{W}}$ to indicate that the gas inlet is located in the layer $\smash{(z_{i_{{\rm{G}}}-1}, z_{i_{{\rm{G}}}})}$, and the fluid and wash water inlets in $\smash{(z_{i_{\rm{F}}-1}, z_{i_{\rm{F}}})}$ and $\smash{(z_{i_{\rm{W}}-1}, z_{i_{\rm{W}}})}$, respectively. For instance, the numerical fluxes $\mathcal{F}_i$ between layers $\smash{(z_{i_{\rm{G}}-1}, z_{i_{\rm{G}}})}$ and $\smash{(z_{i_{\rm{F}}-1}, z_{i_{\rm{F}}})}$ will be computed using the function ${j_{2}(\phi)}$.
Substituting the numerical fluxes into the exact version of the conservation law (4.1), we get the following method-of-lines formula:
where $\delta_{i, i_S} = 1$ if $i = i_S$ and $0$ otherwise. Since we utilize the Godunov flux, the following is valid. For given piecewise constant (in each cell) initial data at $t = 0$, equation (4.3) is in fact exact for the cell average of the solution of PDE (1.1) for small times until any wave from a cell boundary hits another cell boundary.
Using an explicit Euler step for the approximation of the time derivative and the CFL condition
we obtain the following fully discrete method for $\phi^{i, n}\approx \phi^i(t_n)$, where the upper index $n$ stands for evaluation at time $t = t_n$:
5.
Numerical examples
The examples demonstrate the dynamic and steady-state behaviour of a flotation column and we use dimensionless numbers. The drift-flux function $j_{\rm{g}}(\phi) = v_{\rm{term}}\phi(1-\phi)^{3.2}$ has been applied. We chose $v_{\rm{term}} = 2.7 \, {\rm{cm}}/{\rm{s}}$ in agreement with [13]. Furthermore, the height of the vessel is $100\, {\rm{cm}}$ and we have placed the injection points equidistantly: $z_{\rm{G}} = 25\, {\rm{cm}}$, $z_{\rm{F}} = 50\, {\rm{cm}}$ and $z_{\rm{W}} = 75\, {\rm{cm}}$. From now on the following units are used: $q \, [{\rm{cm}}/{\rm{s}}]$, $z \, [{\rm{cm}}]$ and $t \, [{\rm{s}}]$.
5.1. Examples 1 and 2: Transition between steady states
First, we define an initial set of velocities for the inlets and the outlets. In order to maximize the number of possible steady states, and also satisfying conditions (G), (FⅡ), (FⅢ), (WⅠ) and (WⅡ), we use the operating charts in Figures 10-12 to first choose $q_{\rm{U}} = 0.1$ and $q_{\rm{G}} = 0.2$, and then $q_{{\rm{F}}} = 0.1$ and $q_{{\rm{W}}} = 0.0353$, which satisfy $j_{1}(\phi_1)+q_{\rm{G}} = j_4(\phi_{4{\rm{M}}})$. With these values, the velocities in the column are
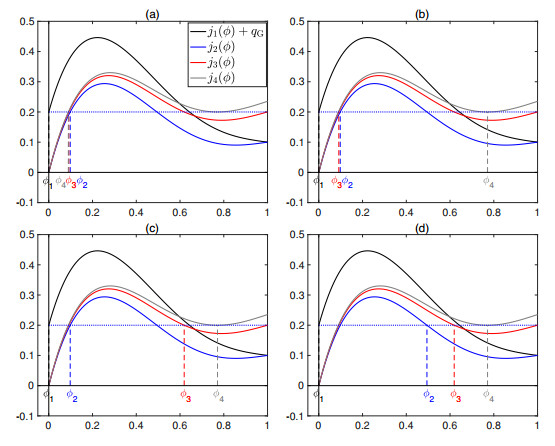
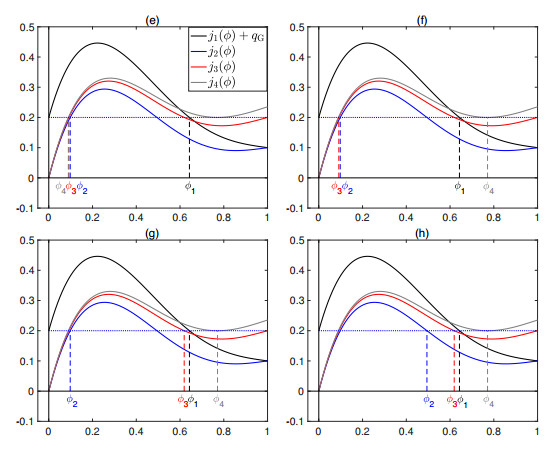
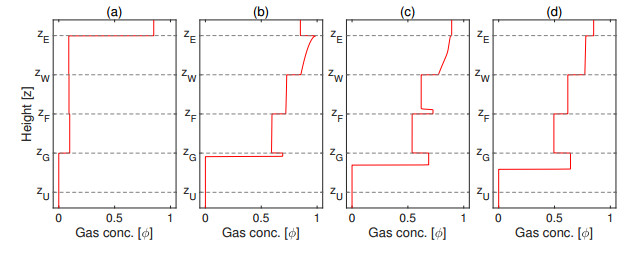
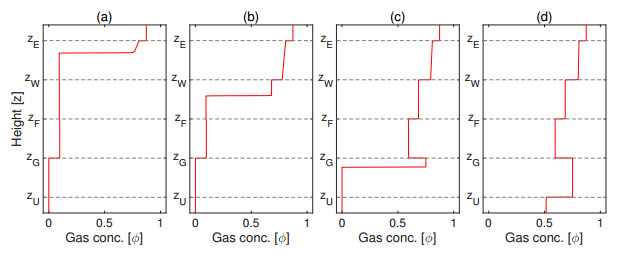
and hence $q_{\rm{U}} = q_1 = -0.1$ and $q_{\rm{E}} = q_4 = 0.2353$. Using Table 1 we know that, for these values satisfying conditions (G), (FⅡ), (FⅢ), (WⅠ) and (WⅡ), there are eight possible steady states with a constant volume fraction in each zone. In Table 4, the admissible paths for the case $\phi_1 = 0$ can be seen, corresponding to steady states (a)-(d) in Figure 13. The paths with $\phi_1\in[\phi_{1 {\rm{Z}}}, 1]$ can be obtained analogously, starting from the corresponding rectangle in Table 1. A detailed description of all steady states is provided by Figures 13-15.
In addition to the volume fractions $\phi_k$, $k\in\{{\rm{U}}, 1, 2, 3, 4, {\rm{E}}\}$, Figure 15 shows the gas and fluid fluxes ($j_k$ and $\varphi_k$) in each zone $k$ represented by red and blue arrows, respectively. In all eight cases, the gas flux is zero below $z = z_{\rm{G}}$, since $j_1(\phi_1) = 0$, and equal to the constant value $j_4(\phi_{4{\rm{M}}})$ above. The flux of water in zone $k$ is then $\varphi_k = q_k-j_k(\phi_k)$.
Let us now run two simulations.
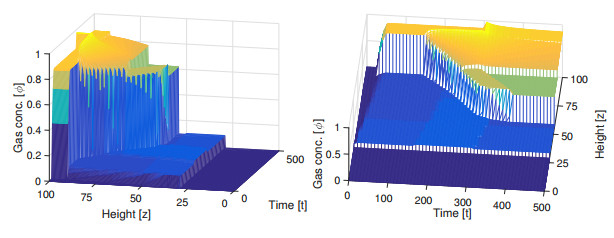
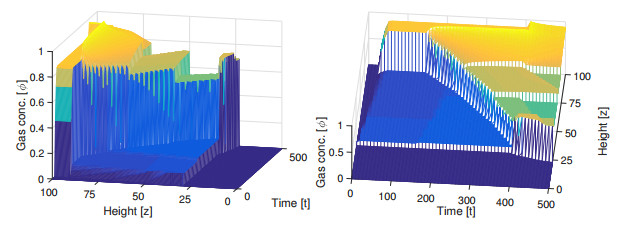
Example 1. Initially, we consider a column filled with only fluid, i.e., $\phi(z, 0) = 0$ for all $z$, and we start pumping gas, fluid and wash water into it, with the velocities stated above. The gas rises fast and reaches the top of the vessel in a short time; see Figure 16, which shows the time evolution of the gas concentration. As can be seen in Figure 17(a), at $t = 150$, the first steady state, see Figure 15(a), has been reached. Then we close the top of the vessel by setting $q_{\rm{E}} = 0$ and $q_{\rm{U}} = -0.3353$ and let the gas accumulate at the top until $t = 300$, see Figure 17(b), when we open the top again (the previous values are used). As can be seen in Figures 17(c) and (d), after opening the top, a discontinuity arises within zone 3 between the fluid and wash water inlets, and becomes stationary at $z\approx 55$; see the explanation in Section 3.9. The new steady state is thus not among the eight ones shown in Figure 15, but can be seen as combination of cases (b) and (c) of both Figures 13 and 15.
Example 2. Figures 18 and 19 show the results when we close the top of the tank for a longer period, in this case until $t = 400$. Then, still another steady state is reached, namely the intermediate one of Figure 15(d) and (h) having a discontinuity in zone 1. The flux of gas is zero in zone 1, which means that there is a region of bubbles standing still with the concentration $\phi\approx 0.65$ just below the gas inlet $z_{\rm{G}} = 25$.
5.2. Example 3: Overloaded tank
We now define an initial set of velocities for the inlets and the outlets for which no steady state with $\phi_1 = 0$ is possible. Consequently, the system is overloaded and gas has to leave also through the underflow, so that $\phi_1>0$. The velocities in the column chosen are
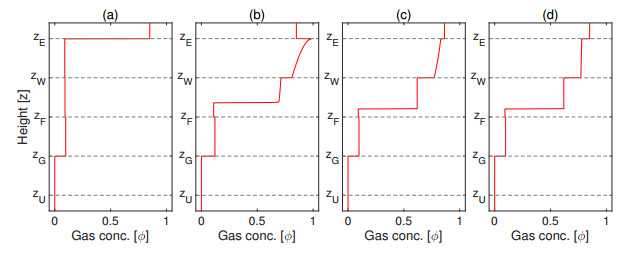
and hence $q_{\rm{U}} = q_1 = -0.1$ and $q_{\rm{E}} = q_4 = 0.17$. A detailed description of the possible steady states is provided by Figure 20.
As in Examples 1 and 2, we start with a column filled with only fluid, i.e., $\phi(z, 0) = 0$ for all $z$, and we start pumping gas, fluid and wash water into it, with the velocities stated above. In Figure 21, we can see how the gas rises and reaches the top of the column in a short time. A steady state, corresponding to case (d) in Figure 20, has been reached by $t = 2000$, as it can be seen in Figure 21(d). Clearly this is not an acceptable set of parameters for the desliming process: an unnecessary excess of gas is flowing downwards and leaving the tank through the bottom.
5.3. Example 4: Desliming
A flotation column is generally operated so that there are two regions: one with bubbles (intermediate gas volume fraction) and one with froth. In the bubbly region, usually in zone 2 and sometimes the lower part of zone 3, the hydrophobic particles of the pulp slurry attach to the air bubbles. In the froth region, located above the bubbly region, further enrichment takes place and the foam is efficient for promoting water rejection. The injection of wash water into the foam assists with rejection of entrained slimes. This is, however, effective only if the wash water flows downwards through the foam and bubbly regions, as stated by Dickinson and Galvin in [13]. Then the the foam is washed properly. In all steady states of Experiment 1, the wash water flows upwards.
To achieve a proper wash, the flux of water in zone 3, and consequently in zones 1 and 2, should be negative, while in zone 4, it should remain relatively small. We set $q_{\rm{U}} = 0.11$ and $q_{\rm{G}} = 0.1$, and choose $q_{{\rm{F}}} = 0.05$ and $q_{{\rm{W}}} = 0.0714$, satisfying $j_{1}(\phi_1)+q_{\rm{G}} = j_4(\phi_{4{\rm{M}}})$ to ensure that the steady state with the higher concentration of bubbles in zone 4, and hence the most ideal scenario for desliming, can be achieved. With these values, the average bulk velocities in the vessel are the following:
hence $q_{\rm{U}} = -0.11$ and $q_{\rm{E}} = 0.1114$. The bulk velocity in zone 2 is negative and relatively small compared with the velocity in zone 1. Figure 22 shows the steady state with maximum concentration of gas in zones 2, 3 and 4 for the conditions given, along with the gas and water fluxes in each zone. Despite the bulk velocity in zone 3 is positive, most of the wash water injected at $z = z_{\rm{W}}$ flows downwards through zone 3, with $\varphi_3 = -0.06$, while the flux of fluid flowing up in zone 4 and the effluent zone remains small, $\varphi_4 = 0.0114$, compared with the flux of fluid in other zones.
6.
Conclusions
The present work has shown how the available drift-flux theory for flotation columns, to the authors' knowledge so far utilized in the engineering literature for stationary analyses only, can be combined with results coming from the mathematical and numerical analysis of conservation laws with discontinuous flux to obtain a model for transient simulations as well as prediction of steady states.
The well-posedness established in [10] for the problem of continuous sedimentation, which has one flux discontinuity, covers the case here with flotation with several (but finite number of) discontinuities. In [10], a Kružkov-type of entropy condition was used together with a crossing condition for the fluxes for the proof of uniqueness. It is worth noting that the flux discontinuities within the present model do satisfy this condition. The entropy condition used here implies, however, the Kružkov-type and uniqueness is obtained without the crossing condition [18].
One-dimensional models such as the one treated herein are easier to solve than multi-dimensional multiphase flow models, and may be useful to model a flotation cell within plant-wide simulators [2]. Nevertheless, for practical use, the present model should be improved and refined in future work. Some suggested directions of future work are as follows. Starting with a property of the model in its present formulation, we recall that the present analysis is limited to drift flux functions $j_{\rm{g}}$ that satisfy (2.10), i.e., that have a horizontal tangent at $\phi = 1$, for which the Richardson-Zaki expression (2.3), (2.4) is the most common example. Results of the steady-state analysis will be more complicated, but can be obtained by similar techniques to those of Section 3, whenever $\bar{q} = -j_{\rm{g}} '(1) >0$. To underline that this case is relevant for investigation we mention that Pal and Masliyah [31] come to the conclusion that the Richardson-Zaki expression (2.4), with $\bar{q} = 0$, is suitable with $n_{\rm{RZ}} = 2.39$. However, their Figures 10 and 11, displaying drift flux data obtained by their own experiments and from the literature, including those obtained within the froth region, strongly indicate that a function $j_{\rm{g}}$ with $\bar{q} >0$ is more suitable. In fact, in their next paper [32] they modify the expression for $V$ to $V(\phi) = 0.8(1-\phi) \exp ( -2.9 \phi^{2.1})$, such that indeed $-j_{\rm{g}}'(1) = 0.8 \exp(-2.9) >0$.
With respect to the hydrodynamical setup of the flotation column and its conceptual counterpart as drawn in Figure 1, we mention that Vandenberghe et al. [39] propose an interesting recirculation: according to their Figure 1, mixture is sucked from the column at a determined level, aerated, and re-injected at another position. The extraction of material at a given rate but whose composition is part of the solution gives rise to a singular sink term whose mathematical treatment is more involved than that of a singular source term (as those appearing in (1.1)). The basic difficulty is that the sink term cannot be incorporated into the flux function; rather, the sink is represented by a new non-conservative transport term (see [6]).
In several instances, our analyses invoke available mathematical and numerical results for clarifier-thickener models. If sediment compressibility is included in a clarifier-thickener model, an effect that arises if the solid-liquid suspension is flocculated, then the governing equation for such models features an additional strongly degenerating diffusion term [10] whose appropriate treatment, roughly speaking, arises from handling it as part of the convective flux. Such a term may also be motivated in the application to flotation in future works: for instance, Narsimhan [29] derives such a term to account for gradual compressibility of the foam layer that is caused by flow of liquid through a network of plateau borders due to gravitational and capillary forces [29]. On the other hand, Stevenson et al. [37] propose a convection-diffusion model for the transport of gangue in flotation froth.
Clearly, an obvious shortcoming of the present description, although it is in line with the cited treatments of literature [13,22,25,27,31,32,38,39,43,44], is that it does not explicitly model the transport and settling of solid particles. It would be highly desirable to extend the model by solids phases, for example of hydrophobic and hydrophilic particles (of minerals and gangue material), and to include their attachment to bubble and transport via the liquid and gas components. The likely outcome of such a description is a convection-diffusion-reaction system with discontinuous flux akin to a recently advanced model of continuous sedimentation with reactions [4]. On the other hand, several gas or solid phases representing size classes that segregate and form areas of different composition can be included, and lead to first-order hyperbolic systems of conservation laws with discontinuous flux, under determined circumstances (see, e.g., [11] and the references cited in that paper).
Within the present work the emphasis has been on the construction of stationary solutions. The numerical scheme utilized, Godunov's scheme with suitable modifications to handle the flux discontinuities (see Section 4), is monotone provided that $\Delta t$ and $\Delta z$ satisfy the CFL condition (4.4), and therefore delivers approximate solutions that converge to the unique entropy solution of the problem (1.1), (1.2). However, formally second-order accurate solvers are possible for instance by techniques of variable extrapolation, see e.g. [7,9].
Acknowledgments
R.B. is supported by Fondecyt project 1170473; Fondef project ID15I10291; and CRHIAM, Proyecto Conicyt Fondap 15130015. In addition, R.B. and M.C.M. are supported by BASAL project PFB 03, CMM, Universidad de Chile and CI2MA, Universidad de Concepción. M.C.M. was also supported by Conicyt Fondecyt/Postdoctorado/3150140.









 DownLoad:
DownLoad: