Incompressible limit of a continuum model of tissue growth for two cell populations

1.   Introduction

Diversity is key in biology. It appears at all kind of level from the human scale to the microscopic scale, with million of cells types; each scales impacting on the others. During development, the coexistence of different cells types following different rules impact on the growth of tissue and then on the global structures. In a more specific case, this can be observed in cancerous tissue with the invasion of tumour cells in an healthy tissue creating abnormal growth. Furthermore, not all cancerous cells play the same role. They can be proliferative or quiescent depending on their positions, ages, ... To study the influence of these diverse cells on each others from a theoretical view, we introduce mathematical model for multiple populations. In this paper we are interesting in the global dynamics and interactions of the two populations, meaning that we focus specifically on continuous models.

In the already existing literature on macroscopic model, we distinguish two categories. The most common ones involved partial differential equations (PDE) in which cells are represented by densities. These models have been widely used to model growth of tissue [10,31], in particular for tumor growth [1,7,11,16]. Another way to model tissue growth is by considering free boundary models [17,18,21]. In these models the tissue is described by a domain and its growth and movement are driven by the motion of the boundary. The link between these two types of model has been been made via an incompressible limit in [23,24,26,28,29,30]. This link is interesting as both models have their advantages. On the one hand PDE relying models, also called mechanical models, are widely studied with many numerical and analytical tools. On the other hand free boundary models are closer to the biologic vision of the tissue and allow to study motion and dynamics of the tissue. This paper aims to extend the link between the mechanical and the free boundary models, in the case of multiple populations system.

In the specific case of multiple populations, several mathematical models have been already introduced. In particular in population dynamics, the famous Lotka-Volterra system [25] models the dynamics of a predator-prey system. This model has been extended to nonlinear diffusion Lotka-Volterra systems [3,4,5,9]. For the tumor growth modelling (see e.g. [14]), some models focus on mechanical property of tissues such as contact inhibition [2,6,20] and mutation [19]. They have been extended to multiple populations [19,32]. Solutions to these models may have some interesting spatial pattern known as segregation [3,12,27,32].

The two cell populations system under investigation in this paper is an extension on a simplest cell population model proposed in [10,29]. Let $n(x, t)$ be the density of a single category of cell depending on the position $x \in \mathbb{R}^d$ and the time $t>0$, and let $p(x, t)$ be the mechanical pressure of the system. The pressure is generated by the cell density and is defined via a pressure law $p = P(n)$. This pressure exerted on cells induces a motion with a velocity field $v = v(x, t)$ related to the pressure through the Darcy's law. The proliferation is modelled by a growth term $G(p)$ which is pressure dependent. In order to model the competition for space, the function $G$ is taken nonincreasing. Moreover, to model apoptosis, this function takes negative values when the pressure is higher to some pressure value $P_M$ which is often referred to as the homeostatic pressure [31]. With these assumptions, the mathematical model reads

In [24,26,28,29,30], the pressure law is given by $P(n) = \frac{\gamma}{\gamma -1}n^{\gamma-1}$ which allows to recover the porous medium equation. However, in many tissues, cells may not overlap, implying that the maximal packing density should be bounded by $1$. To take into account this non-overlapping constraint, the pressure law $P(n) = \epsilon \frac{n}{1-n}$ has been taken in [23]. This latter choice of pressure law has also been taken in the present paper. For this one population model, it has been shown in [23] that, in the incompressible limit $\epsilon \rightarrow 0$ (or $\gamma\to +\infty$ depending on the pressure expression), the model converges towards a Hele-Shaw free boundary problem defined by:

with the relations $(1-n_0)p_0 = 0$, $1\leq n_0 \leq 1$ and the complementary relation

In the region where $p_0>0$ the limit density $n_0$ is uniform equal to $1$ which means that the fluid cannot be further compressed. For this reason, we refer to this limit as the incompressible limit.

The previous model has the particularity to derive from the free energy

as a gradient flow for the Wasserstein metric. Using this property a model for two species of cells has been derived in the appendix of [15]. Let us denote $n_1(x, t)$ and $n_2(x, t)$ the two cell densities depending on the position $x \in \mathbb{R}^d$ and the time $t>0$. We assume that the pressure depends on the total density $n = n_1 +n_2$. As the pressure depends on a parameter $\epsilon$, we introduce this dependancy in the notation. We define the free energy for the two cell populations by,

Restricting to the one dimensional case, the system of equation deriving from this free energy is then defined by,

with $G_1, G_2$ the growth functions, and $p_{\epsilon}$ the pressure. The proposed system models two different types of cells which have identical cell volumes and identical mechanical properties. This assumption results in the two species having the same pressure laws. Tissues consisting of different types of cells having roughly identical cell volumes and mechanical properties are commonplace. Thanks to this assumption, the gradient flow structure of the one-species model can be extended to the two-species case. This would not be possible if different pressure laws were considered. Here, the differences between the considered cell species lie in the growth terms. Indeed, growth rates may differ significantly between different cell types. This is well documented as growth rates can be easily measured (by e.g. recording the size increase of the colony in time). On the other hand, it is much more difficult to make pressure measurements in the tissue and to determine the exponent in the pressure law.

The model (2)-(5) has been first introduced in [14]. An interesting feature of this model is the preservation of the segregation of the species if they are initially segregated. Recently, in [22], the existence of solutions on $\mathbb{R}^d$ has been shown but not the segregation property. The existence of solutions with segregation for system (2)-(5) has been proven in [2,6] for a compact domain $[-L, L]$ with $L>0$, with Neumann homogeneous boundary condition.

More precisely, we recall the precise statement of the main result in [2]:

Theorem 1.1 (Theorem 1.1 of [2]). Let $\epsilon>0$ be fixed. Given initial conditions ${n_1}^{\mathit{\mbox{ini}}}_{\epsilon}$ and ${n_2}^{\mathit{\mbox{ini}}}_{\epsilon}$ satisfying,

and

then there exists $\zeta_{\epsilon} \in C([0, \infty)) \cap C^1( (0, \infty))$ such that

and ${n_1}_{\epsilon}$ and ${n_2}_{\epsilon}$ respectively satisfy (2) on $\Omega_-: = \{ (t, x), x< \zeta_{\epsilon}(t)\}$ and (3) on $\Omega_+: = \{ (t, x), x> \zeta_{\epsilon}(t)\}$. Moreover, we have ${n_1}_\epsilon, {n_2}_\epsilon \in C^{2, 1}(\Omega_-\cup\Omega_+)$, and ${n_1}_\epsilon \in C^1(\Omega_-\cup\{(t, \zeta_\epsilon(t)); t>0\})$, ${n_2}_\epsilon \in C^1(\Omega_+\cup\{(t, \zeta_\epsilon(t)); t>0\})$. Here, for an open subset $\omega$ of ${\mathbb R}^2$, $C^k(\bar \omega)$ denotes the space of functions which are restrictions to $\omega$ of functions having continuous derivatives up to the order $k$ on an open set $\omega' \supset \bar \omega$ and $C^{k, 1}(\omega)$ is the space of functions having continuous derivative up to the order $k$ in $\omega$ and such that the $k$th partial derivatives are Lipschitz continuous. In addition ${n}_{\epsilon} = {n_1}_{\epsilon} +{n_2}_{\epsilon}$ is a solution to:

In [2], the reaction terms are chosen to be affine decreasing. However, as mentioned by the authors, it is easy to verify that their proof can be extended to our system under a set of assumptions for the growth functions which will be defined later in this paper. We also mention that Theorem 1.1 above has been proved in [2] for a smooth pressure law whereas here we have to deal with a possible singularity when the density reaches the value $1$. However, it is proved below that the solution of the above system is always bounded away from $1$, which allows us to extend the result of [2] to the current framework.

The aim of this paper is is to study the incompressible limit $\epsilon \rightarrow 0$ for the two populations systems. In dimension 1, the incompressible limit for a system with different pressure laws and reaction terms is investigated in [8] through regularity results obtained using Aronson-Benilan type estimates and methods similar to [22]. In the present paper we restrict the domain to a compact interval $(-L, L)$ with $L>0$ and assume (6) and (7) are verified, in order to set ourself in the framework of [2]. Then the two populations are initially in contact, which is reasonable. In fact, when there is no contact, the system is equivalent to the one population model [23]. In addition, outside the domain $(-L, L)$, the system corresponds to the single population model. Then our approach relies strongly on the description of the solutions obtained in [2].

When the two species are not in contact, the system is equivalent to the one population model [23], this is why we limit ourself in this paper to the case where the two populations are initially in contact. To use the solutions defined in [2], we restrict the space to a compact domain $(-L, L)$ with $L>0$ and assume (6) and (7) are verified. Outside the domain $(-L, L)$, the system will be equivalent to the one population model.

We firstly remark that by adding (2) and (3), we get,

Multiplying by $P'(n_\epsilon)$ we find an equation for the pressure,

Formally, passing at the limit $\epsilon \rightarrow 0$, we expect the relation,

In addition, passing formally to the limit $\epsilon\to 0$ into (4), it appears clearly that $(1-n_0) p_0 = 0$. We consider the domain $\Omega_0(t) = \{x \in (-L, L), p_0(x, t)>0\}$, then, from the latter identity, $n_0 = 1$ on $\Omega_0$. Moreover, from the segregation property, we have ${n_1}_{\epsilon}{n_2}_{\epsilon} = 0$ when the two densities are initially segregated. Passing to the limit $\epsilon\to 0$ into this relation implies ${n_1}_{0} {n_2}_{0} = 0$. Then we may split $\Omega_0(t)$ into two disjoint sets $\Omega_1(t) = \{x \in (-L, L), {n_1}_{0}(x, t) = 1\}$ and $\Omega_2(t) = \{x\in (-L, L), {n_2}_{0}(x, t) = 1\}$. Formally, it is not difficult to deduce from (11) that when $\epsilon\to 0$, we expect to have the relation

Then we obtain a free boundary problem of Hele-Shaw type: On $\Omega_1(t)$, we have ${n_1}_{0} = 1$ and $-\partial_{xx} p_0 = G_1(p_0)$, on $\Omega_2(t)$, we have ${n_2}_{0} = 1$ and $-\partial_{xx} p_0 = G_2(p_0)$.

The outline of the paper is the following. In Section 2 we expose the main results of this paper, which are the convergence of the continuous model (2)-(5) when $\epsilon \rightarrow 0$ to a Hele-Shaw free boundary model, and uniqueness for this limiting model. Section 3 is devoted to the proof of these main results. The proof on the convergence relies on some a priori estimate and compactness techniques. We use Hilbert duality method to establish uniqueness of solution to the limiting system. Finally in Section 4, we present some numerical simulations of the system (2)-(5) when $\epsilon$ is going to 0 and simulations of a specific application on tumor spheroid growth.

2.   Main results

In this paper we aim to prove the incompressible limit $\epsilon \rightarrow 0$ of the two populations model with non overlapping constraint (2)-(5) in one dimension. We first introduce a list of assumptions on the growth terms and the initial conditions. For the growth, we consider the following set of assumptions:

The set of assumptions on the growth rate is standard and similar to the one in e.g. [23]. Notice that the boundedness and the decay of $G_1$, $G_2$ comes from the modelling assumptions as explained in the introduction. For some technical reasons in our computations, we add some additional smoothness assumptions and bounds on the derivatives. The parameters $P_M^1$ and $P_M^2$ are called homeostatic pressures which represent the maximal pressure that the tissue can handle before starting dying. For the initial datas, we assume that there exists $\epsilon_0>0$ such that, for all $\epsilon\in (0, \epsilon_0)$, for all $x\in(-L, L)$,

These initial conditions imply that ${n_1}^{ini}_{\epsilon}$ and ${n_2}^{ini}_{\epsilon}$ are uniformly bounded in $W^{1, 1}(-L, L)$. Notice also that the existence of $\zeta^0$ being the interface between the two species implies that the two populations are initially segregated.

From [2], we recover that at a fix $\epsilon>0$ under assumption (12), given initial conditions ${n_1}^{\mbox{ ini}}_{\epsilon}$ and ${n_2}^{\mbox{ ini}}_{\epsilon}$ satisfying (13), then there exists $\zeta_{\epsilon} \in C([0, \infty)) \cap C^1( (0, \infty))$ such that ${n_1}_{\epsilon}$ and ${n_2}_{\epsilon}$ verify (8) and ${n_1}_{\epsilon}$ and ${n_2}_{\epsilon}$ respectively satisfy (2) on $\{ (t, x), x\leq \zeta_{\epsilon}(t)\}$ and (3) on $\{ (t, x), x\geq \zeta_{\epsilon}(t)\}$. In addition ${n}_{\epsilon} = {n_1}_{\epsilon} +{n_2}_{\epsilon}$ is solution to (9).

Remark 1. Considering ${n_1}_\epsilon$ and ${n_2}_\epsilon$ defined previously, we have for $i = 1, 2$

Given (9), for all $\varphi \in C_c^{\infty} (-L, L)$ we compute, for $i = 1, 2$

Hence ${n_1}_\epsilon$ and ${n_2}_\epsilon$ are weak solutions to (2) and (3) on $(-L, L)$ respectively. This result will be used in the following.

Considering this particular solution, we are going to show the incompressible limit $\epsilon \rightarrow 0$ for system (2)-(5). The main result is the following

Theorem 2.1. Let $T>0$, $Q_T = (0, T)\times(-L, L)$ and $\mathcal{D}'(Q_T)$ denote the space of distributions on $Q_T$. Let $G_1$, $G_2$ and $({n_1}^{\mathit{\mbox{ini}}}_{\epsilon})$, $({n_2}^{\mathit{\mbox{ini}}}_{\epsilon})$ satisfy assumptions (12)–(13). After extraction of subsequences, the densities ${n_1}_{\epsilon}$, ${n_2}_{\epsilon}$ and the pressure $p_{\epsilon}$, solutions defined in (8)-(9), converge strongly in $L^1(Q_T)$ as $\epsilon \rightarrow 0$ towards the respective limit ${n_1}_0, {n_2}_0 \in L^\infty([0, T];L^1(-L, L))\cap BV(Q_T)$, and $p_0 \in BV(Q_T)\cap L^2([0, T];H^1(-L, L))$. Moreover, these functions satisfy:

where $n_0 = {n_1}_0 +{n_2}_0$, and

complemented with Neumann boundary conditions $\partial_x p_0(\pm L) = 0$. Moreover, we have the relations

and

and the complementary relation

Thanks to (19), we may consider the domain $\Omega_0(t)$ where the pressure is nonnegative and the total density is equal to 1. The segregation pressure (20) leads us to divide this domain in two subdomains where either the density ${n_1}_0$ is equal to 1 or the density ${n_2}_0$ is equal to 1. The complementary relation (21) describes the evolution of the pressure inside these domains.

The proof of this convergence result is given in Section 3. It is straightforward to observe that adding (2) and (3) provides an equation on the total density similar to the one found in the one species case [23,29]. Then we use a similar strategy for the proof relying on a compatness method. However the presence of the two populations generate some technical difficulties. To overcome them, we use the segregation property. Notice that this paper is written in the specific case where the two species are separated by one interface, but could be generalised to many interfaces. Using the segregation of the species we are able to obtain a priori estimates on the densities, the pressure and their spatial derivatives. The proof of convergence follows from these new estimates. In order to obtain the complementary relation (21), we follow the approach proposed in [8] which allows us to obtained further regularity.

To complete the results on the asymptotic limit of the model, an uniqueness result for the Hele-Shaw free boundary model for two populations is provided in Proposition 1 in §3.4. The proof of this uniqueness result for the limiting problem is based on Hilbert's duality method.

3.   Proof of the main results

This section is devoted to the proof of Theorem 2.1, whereas in Section 3.4 the uniqueness of the solution to the Hele Shaw system is established. We first establish some a priori estimates.

3.1.   A priori estimates

3.1.1.   Nonnegativity principle

The following Lemma establishes the nonnegativity of the densities.

Lemma 3.1. Let $({n_1}_\epsilon, {n_2}_\epsilon, p_\epsilon)$ be a solution to (2) and (3) such that ${n_1}_\epsilon^{\mathit{\mbox{ini}}}\geq 0$, ${n_2}_\epsilon^{\mathit{\mbox{ini}}}\geq 0$ and $G_m <\infty$. Then, for all $t\geq 0$, ${n_1}_\epsilon(t)\geq 0$ and ${n_2}_\epsilon(t)\geq 0$.

Proof. To show the nonnegativity we use the Stampaccchia method. We multiply (2) by $\mathbf{1}_{{n_1}_\epsilon<0}$ and denote $n_- = \max(0, -n)$ for the negative part, we get

With the above notation, it reads

We may integrate in space thanks to the continuity of ${n_1}_\epsilon$ on $\Omega_-\cup\{(t, \zeta_\epsilon(t)); t>0\})$ and the fact that it is identically zero on $\Omega_+$ (as recalled in Theorem 1.1), which implies its boundedness on $[-L, L]$. Using assumption (12) and $\partial_x p_\epsilon (\pm L, t) = p'_{\epsilon}(n_\epsilon) \partial_x n_\epsilon (\pm L, t) = 0$, we deduce

Then we integrate in time,

With the initial condition ${n_1}_{\epsilon}^{\mbox{ ini }} > 0$ we deduce ${n_1}_{\epsilon} > 0$. With the same method we can show that if ${n_2}_{\epsilon}^{\mbox{ ini }} > 0$ we have ${n_2}_{\epsilon}> 0$.

Remark 2. We notice that the positivity gives a formal proof of the segregation of any solution of (2)-(5). Indeed, defining $r_{\epsilon} = {n_1}_{\epsilon} {n_2}_{\epsilon}$ and multiplying (2) by ${n_2}_{\epsilon}$, (3) by ${n_1}_{\epsilon}$ and adding, we obtain the following equation for $r_{\epsilon}$,

Multiplying by $\mathbf{1}_{{r}_\epsilon<0}$ and formally integrating in time (using the same steps as for the non negativity principle) gives, after an integration by parts,

Given that $r^{\mbox{ ini}}_\epsilon = 0$, under regularity assumptions on the pressure, it is clear that $r_\epsilon = 0$ at all time. Hence, at least formally, the segregation property applies to any solution of the system, provided that the initial conditions are segregated. However, in the present work, we will not need this remark as we use a stronger structural property namely the existence of a single curve $\zeta_\varepsilon(t)$ that separates the support of $n_{1 \epsilon}$ (to the left of $\zeta_\varepsilon(t)$) with that of $n_{2 \epsilon}$ (to the right of $\zeta_\varepsilon(t)$) which is provided by [2,6].

3.1.2.   A priori estimates

To show the compactness result we establish a priori estimate on the densities, pressure and their derivatives. We first compute the equation on the total density. As shown earlier ${n_1}_\epsilon$ and ${n_2}_\epsilon$ are respectively weak solutions of (2) and (3). By summing the two equations we deduce that ${n}_\epsilon$ is a weak solution of (10). Notice that this equation can be rewritten as,

with $H(n) = \int_0^{n} u P'(u)du = P(n)-\epsilon \ln (P(n)+\epsilon) + \epsilon \ln \epsilon$.

We establish the following a priori estimates

Lemma 3.2. Let us assume that (12) and (13) hold. Let $({n_1}_\epsilon, {n_2}_\epsilon, p_\epsilon)$ be a solution to (2)–(5). Then, for all $T>0$, and $t\in (0, T)$, we have the uniform bounds in $\epsilon\in(0, \epsilon_0)$,

Moreover, we have that $({n_1}_\epsilon)_\epsilon$ and $({n_2}_\epsilon)_\epsilon$ are uniformly bounded in $L^\infty([0, T], W^{1, 1}(-L, L))$ and $(p_\epsilon)_\epsilon$ is uniformly bounded in $L^1([0, T], W^{1, 1}(-L, L))$.

Proof. Comparison principle.

The usual comparison principle is not true for this system of equations. However we are able to show some comparison between the total density and $n_M$ defined by $n_M = \frac{P_M}{\epsilon+P_M}$ where $P_M$ is defined in (13). We deduce from (22) that

where we use the monotonicity of $G_1$ and $G_2$ from assumption (12).

Notice that, since the function $H$ is nondecreasing, the sign of $n_{\epsilon}-n_M$ is the same as the sign of $H(n_{\epsilon})-H(n_M)$. Moreover,

so for $y = H(n_{\epsilon})-H(n_M)$ and $f(y) = y_+$ the positive part, the so-called Kato inequality reads $\partial_{xx} f(y) \geq f'(y) \partial_{xx} y$. Thus multiplying the latter equation by $\mathbf{1}_{n_\epsilon-n_M>0}$ and given (8) we obtain (denoting $n_+ = \max(n, 0)$)

Since the function $P$ is increasing and $G_1$ and $G_2$ are decreasing (see (12)), we deduce that the last term is nonpositive. Then, integrating on $(-L, L)$ and using $\partial_x n_\epsilon (\pm L, t) = 0$, we deduce

Given that $n_{\epsilon} \leq n_M$ implies $P(n_{\epsilon}) \leq P_M = \max(P_M^1, P_M^2)$, it follows that the two last terms are nonpositive. Then, we deduce

$L^{\infty}$ bounds.

With the above comparison principle, we conclude that $n_\epsilon \leq n_M$. Since the function $P$ is inscreasing, we deduce easily with the non-negativity principle (3.1) that $0 \leq p_\epsilon \leq P_M$, $0 \leq {n_1}_\epsilon\leq n_M$ and $0 \leq {n_2}_\epsilon \leq n_M$.

Estimates from below.

From above, we deduce that the pressure is bounded by $P_M$. Hence, using assumption (12) we deduce

Let us introduce $n_m : = A_0 e^{-g_m t}$. We deduce

As above, for the comparison principle, we may use the positive part and the Kato inequality to deduce

Integrating in space and in time as above, we deduce that $(n_m-n_\epsilon)_+ = 0$.

$L^{1}$ bounds of $n_{\epsilon}$, ${n_1}_{\epsilon}$, ${n_2}_{\epsilon}$ and ${p}_{\epsilon}$.

Integrating (22) on $(-L, L)$ and using the nonnegativity of the densities from Lemma 3.1 as well as the Neumann boundary conditions, we deduce

Integrating in time, we deduce

Since ${n_1}_{\epsilon} \geq 0$ and ${n_2}_{\epsilon} \geq 0$, we deduce the uniform bounds on $\| {n_1}_{\epsilon}\|_{L^1(-L, L)}$ and on $\| {n_2}_{\epsilon}\|_{L^1(-L, L)}$.

From the relation (4), we deduce $p_{\epsilon} = n_{\epsilon} (\epsilon+p_{\epsilon})$. Moreover, the bound $p_{\epsilon} \leq P_M: = \max (P^1_M, P^2_M)$ implies

$L^{1}$ estimates on the $x$ derivatives.

Recalling (8), we can refomulate (10) by

with $G(p, t, x) = G_1(p) \mathbf{1}_{x \leq \zeta_{\epsilon}(t) }+G_2(p)\mathbf{1}_{x \geq \zeta_{\epsilon}(t) }$. The space derivative of this growth function is given by,

We derive (23) with respect to $x$,

We multiply by $sign(\partial_{x} n_{\epsilon}) = sign(\partial_{x} p_{\epsilon})$ and use the Kato inequality,

We integrate in space on $(-L, L)$. Using the fact that $\max_{[0, P^1_M]} G_1' \leq -\gamma <0$ and $\max_{[0, P^2_M]} G_2' \leq -\gamma <0$ (see (12)) and that $\partial_x H(n_{\epsilon}) (\pm L, t) = H'(n_{\epsilon}) \partial_x n_{\epsilon} (\pm L, t) = 0$,

Using Gronwall's lemma and the uniform bound on $n_\epsilon$ and $G_1$ and $G_2$ (see (12)), we deduce that, for all $t>0$,

Given the estimate from below from Lemma 3.2, namely $A_0 e^{-g_mT} \leq n_{\epsilon}(t)$, and using (24), we recover

Hence we have a uniform bound on $\partial_x p_\epsilon$ in $L^1(Q_T)$. To recover the estimate on $\partial_{x} {n_1}_{\epsilon}$ and $\partial_{x} {n_2}_{\epsilon}$ we deduce from (8),

So

and

This concludes the proof.

3.1.3.   $L^2$ estimate for $\partial_x p$

Lemma 3.3 ($L^2$ estimate for $\partial_x p$). Let us assume that (12) and (13) hold. Let $({n_1}_\epsilon, {n_2}_\epsilon, p_\epsilon)$ be a solution to (2)–(5). Then, for all $T>0$ we have a uniform bound on $\partial_x p_\epsilon$ in $L^2(Q_T)$.

Proof. For a given function $\psi$ we have, multiplying (5) by $\psi(n_\epsilon)$,

Integrating on $(-L, L)$, we have

where $\Psi$ is an antiderivative of $\psi$. We choose $\psi(n) = \epsilon (\ln(n)-\ln(1-n)+\frac{1}{1-n})$ so that $n_{\epsilon} \psi'(n_{\epsilon}) = P'(n_{\epsilon})$. Inserting the expression of $\psi$, we get

After integrating in time and using the expression of the pressure (4), we have

Then, to prove that $\partial_x p_\epsilon \in L^2(Q_T)$, we are left to find a uniform bound on $\int_{-L}^L \epsilon n_{\epsilon} |\ln(\frac{p_{\epsilon}}{\epsilon})|dx$. Using the expression of $p_\epsilon$ in (4), we have

Since $n_\epsilon$ is bounded in $L^1$, the second term of the right hand side is uniformly bounded with respect to $\epsilon$. Moreover given that $0\leq p_\epsilon \leq P_M$ and $x\mapsto x|\ln x|$ is uniformly bounded on $[0, P_M]$, we get

This concludes the proof.

3.1.4.   $L^1$ estimate for $\partial_t p$

Lemma 3.4 ($L^1$ estimate for $\partial_t p$). Let us assume that (12) and (13) hold. Let $({n_1}_\epsilon, {n_2}_\epsilon, p_\epsilon)$ be a solution to (2)–(5). Then, for all $T>0$ we have the uniform bound: $\|\partial_t p_\epsilon\|_{L^1(Q_T)} \leq C_T$.

Proof. Introduce $w_\epsilon = \partial_{xx} p_\epsilon + G(p_\epsilon, t, x)$. The equation on the pressure (11) can be rewritten as

As for all $T>0$ we have a uniform bound on $\partial_x p_\epsilon$ in $L^2(Q_T)$, we are left to find an estimate for the term $(\frac{p_{\epsilon}^2}{\epsilon}+p_{\epsilon})w_\epsilon$. The control of this term is based on the previous work [23] and the recent publication [8]. We consider the equation satisfied by $w_\epsilon$,

We recall that $\zeta_{\epsilon}'(t) = -\partial_{x} p_{\epsilon} (\zeta_{\epsilon}(t))$. Therefore, using also the definition of $w_\epsilon$, we get

Moreover, we have

Then inserting (28) in (27), we get

Since $G_1$ and $G_2$ are decreasing functions, the last term of the equality is positive. By multiplying (29) by $- \mathbf{1}_{ w_{\epsilon} \leq 0}$, we get

Using assumption (12), we get

We want to integrate on $(-L, L)$, we first observe that at any time $t\in[0, T]$,

Besides, by differentiating the equation of the pressure (26) we have

Then, given that the pressure is subject to homogeneous Neumann boundary conditions,

and so

Therefore, integrating (30) on $(-L, L)$, we obtain

Note that we may integrate in space thanks to the regularity of the pressure given in Theorem 1.1. Indeed, thanks to the interface conditions at $\zeta_\varepsilon(t)$, $\partial_x p_{\epsilon}$ is continuous on $[-L, L]$ and continuously differentiable on $[-L, \zeta_\varepsilon(t))$ and $(\zeta_\varepsilon(t), L]$. Then, $\partial_{xx} p_{\epsilon}$ is a bounded function. Then, from its definition, it follows that $w_{\epsilon}$ is bounded on $[-L, L]$ and therefore is in $L^1(-L, L)$. Moreover, we observe that

Moreover, since $| w_{\epsilon} | = w_{\epsilon} + 2 ( w_{\epsilon} )_-$, we have

where we use Neumann boundary condition and (12) for the last inequality. Then we get

with $C$ a constant. Thanks to (13), we have $\|\partial_{xx} p_{\epsilon}^{ini}\|_{L^1(-L, L)} \leq C$ and thus $\| w_{\epsilon}(t = 0)\|_{L^1(-L, L)}\leq C$. Then using Gronwall Lemma we get $\int_{-L}^{L} (w_\epsilon)_- \leq C$ with $C$ independent of $\epsilon$. Besides, we also have

Since $\partial_t p_{\epsilon} = (\frac{p_{\epsilon}^2}{\epsilon}+p_{\epsilon})w_\epsilon + |\partial_x p_{\epsilon}|^2 \geq (\frac{p_{\epsilon}^2}{\epsilon}+p_{\epsilon})w_\epsilon$, it is clear that $(\partial_t p_{\epsilon})_- \leq (\frac{p_{\epsilon}^2}{\epsilon}+p_{\epsilon})(w_\epsilon)_-$. Then,

This concludes the proof.

3.2.   Proof of theorem 1

3.2.1.   Convergence

In the last paragraph we have found a priori estimates for the densities and their space derivatives. To use a compactness argument, we need to obtain estimates on the time derivative. To do so, we are going to use the Aubin Lions theorem [33]. More precisely, we have

Lemma 3.5. Assume that (12) and (13) hold. Let $({n_1}_\epsilon, {n_2}_\epsilon, p_\epsilon)$ be a solution to (2)–(5). Then, there exist ${n_1}_0$, ${n_2}_0$, $p_0$ belonging to $BV(Q_T)$ and satisfying (14)–(15), such that, up to extraction of subsequences, $({n_1}_\epsilon)_\epsilon$, $({n_2}_\epsilon)_\epsilon$, $(p_\epsilon)_\epsilon$ converge strongly in $L^1(Q_T)$ and almost everywhere in $Q_T$ towards ${n_1}_0$, ${n_2}_0$, $p_0$, respectively, and $(\partial_x p_\epsilon)_\epsilon$ converges weakly in $L^2(Q_T)$ towards $\partial_x p_0$.

Proof. According to Lemma 3.3, ${n_1}_{\epsilon}\partial_x p_\epsilon$ and ${n_2}_{\epsilon}\partial_x p_\epsilon$ are in $L^2(Q_T)$. Moreover thanks to Lemma 3.2, we have that ${n_1}_{\epsilon} G_1(p_{\epsilon})$ and ${n_2}_{\epsilon} G_2(p_{\epsilon})$ are uniformly bounded in $L^\infty([0, T];L^1\cap L^\infty(-L, L))$, so $\partial_t {n_1}_{\epsilon}$ and $\partial_t {n_2}_{\epsilon}$ are uniformly bounded in $L^2([0, T], W^{-1, 2}(-L, L))$. We also have ${n_1}_{\epsilon}$ and ${n_2}_{\epsilon}$ bounded in $L^1([0, T], W^{1, 1}(-L, L))$. Since we are working in one dimension, we have the following embeddings

The Aubin Lions theorem implies that $\{u \in L^1([0, T], W_{loc}^{1, 1}(-L, L)); \dot{u} \in L^2([0, T], W^{-1, 2}(-L, L)) \}$ is compactly embedded in $L^1([0, T], L^1(-L, L))$. So we can extract strongly converging subsequences ${n_1}_{\epsilon}$ and ${n_2}_{\epsilon}$ in $L^1(Q_T)$. Thanks to Lemma 3.2 and 3.4 we know that $p_{\epsilon}$ is bounded in $W^{1, 1}(Q_T)$. Therefore we may apply Helly's theorem and recover strong convergence in $L^1(Q_T)$.

As a consequence, up to extraction of subsequences, $(n_{1\epsilon})_\epsilon$, $(n_{2\epsilon})_\epsilon$, and $(p_\epsilon)_\epsilon$ converge strongly in $L^1(Q_T)$ and a.e. towards some limits denoted $n_{10}$, $n_{20}$, and $p_0$, respectively. Moreover, due to the uniform estimate on $(\partial_x p_\epsilon)_\epsilon$ in $L^2(Q_T)$ from Lemma 3.3, we may extract a subsequence, still denoted $(\partial_x p_\epsilon)_\epsilon$, which converges weakly in $L^2(Q_T)$ towards $\partial_x p_0$. Passing to the limit in the uniform estimates of Lemma 3.2 gives (14) and (15) and ${n_1}_0, {n_2}_0, n_0, p_0$ belongs to $BV(Q_T)$.

3.2.2.   Limit model

From Lemma 3.5, we have the convergence, up to subsequences, of $({n_1}_\epsilon)_\epsilon$, $({n_2}_\epsilon)_\epsilon$, and $(p_\epsilon)_\epsilon$. In this section we look for the equations satisfied by these limits. In particular we have

Lemma 3.6. Assume that(12) and (13) hold. Let $({n_1}_\epsilon, {n_2}_\epsilon, p_\epsilon)$ be a solution to (2)–(5) and $({n_1}_0, {n_2}_0, p_0)$ its limit given by Lemma 3.5. Then ${n_1}_0$, ${n_2}_0$ are solutions to Eqs. (17) and (18) respectively and relations (19) and (20) are verified.

Proof. We recall that

From the uniform bounds on $p_\epsilon$, we get,

Thus, the term in the Laplacian converges strongly to $p_0$. Then, thanks to the strong convergence of $n_\epsilon$ and $p_\epsilon$, we deduce that in the sense of distributions

Moreover, let $\phi\in W^{1, \alpha}(Q_T)$ with $\phi(T, x) = 0$ ($\alpha>2$) be a test function. We multiply equation (2) by $\phi$ and integrate using the Neumann boundary conditions, we get

Due to the strong convergence of ${n_1}_\epsilon$ and $p_\epsilon$, we can pass easily to the limit $\epsilon\to 0$ into the first term of the left hand side and into the term in the right hand side. For the second term, we use the assumptions on the initial data to pass into the limit. For the third term, we can pass to the limit in a product of a weak-strong convergence from standard arguments, then we arrive at

for any test function $\phi\in W^{1, \alpha}(Q_T)$. Then we obtain the weak formulation of (17) with Neumann boundary conditions on $p_0$. We proceed by the same token to recover (18).

Passing into the limit in the relation $(1-n_\epsilon) p_\epsilon = \epsilon n_\epsilon$ implies

We can also pass to the limit for the segregation and deduce ${n_1}_0 {n_2}_0 = 0$.

To conclude the proof of Theorem 2.1, we are left to establish the relation (21).

3.3.   Complementary relation

In this section we prove the following results.

Lemma 3.7. Assume that (12) and (13) hold. Let ${(n_1}_\epsilon, {n_2}_\epsilon, p_\epsilon)$ be a solution to (2)–(5) and let $({n_1}_0, {n_2}_0, p_0)$ be its limit as in Lemma 3.5. Then $({n_1}_0, {n_2}_0, p_0)$ satisfies the complementary relation (21).

Proof. The approach is based on the previous work [23] and the recent publication [8]. In the weak sense, the complementary relation is equivalent to

Multiplying the pressure equation (11) by $\epsilon$, recalling the relation $p_\epsilon = n_\epsilon (p_\epsilon + \epsilon)$ from (4), we get

where we recall the definition $n_\epsilon G(p_\epsilon) = {n_1}_\epsilon G_1(p_\epsilon) + {n_2}_\epsilon G_2(p_\epsilon)$. We multiply this last equation by a test function $\phi\in \mathcal{D}((0, T)\times \mathbb{R}^d)$ and integrate on $(-L, L)$ and obtain:

Therefore, the estimates of Lemmas 3.2 and 3.4 yield

Moreover, we have

We want to study the convergence of the terms $I_{\epsilon}$ and $II_{\epsilon}$. The convergence of the term $II_{\epsilon}$ is obtained from the strong convergence of $p_{\epsilon}$ and the weak convergence of $\partial_x p_{\epsilon}$ (see Lemma 3.5). We have

The convergence of the term $I_{\epsilon}$ requires the strong convergence of (a subsequence of) $\partial_x p_{\epsilon}$ and hence, some compactness of $\partial_x p_{\epsilon}$. The control of the space derivative follows from Eq. (31). Indeed given the boundary conditions $\partial_{x} p_{\epsilon}(t, \pm L) = 0$, we have

Therefore $\|\partial_{xx} p_{\epsilon}(t)\|_{L^1(-L, L)} \leq C$ and $\sup_{0\leq t \leq T} \|\partial_{xx} p_{\epsilon}(t)\|_{L^1(-L, L)} \leq C$ uniformly with respect to $\epsilon$. The control of the time derivative of $\partial_x p_{\epsilon}$ requires further analysis. We will use the Fréchet-Kolmogorov compactness method and proves that

uniformly when $\epsilon \to 0$. Let us denote, for $h>0$, $u_{h, \epsilon} = \partial_x p_\epsilon(t+h, x) - \partial_x p_\epsilon(t, x)$. Let us consider $0\leq \omega\in C^\infty_c(\mathbb{R})$, compactly supported, with $\|\omega\|_{L^1(\mathbb{R})} = 1$. We introduce the mollifiers $(\omega_\eta)_{\{\eta>0\}}$ defined by $\omega_{\eta}(x) = \frac{1}{\eta}\omega(\frac{x}{\eta})$, such that, for any $\eta>0$, $\|\omega_\eta\|_{L^1(\mathbb{R})} = \|\omega\|_{L^1(\mathbb{R})} = 1$ and

Moreover, for any $f\in W^{1, 1}(-L, L)$, we have

Then, we compute,

For the first term of the right hand side, we get with (36),

uniformly with respect to $\epsilon$, thanks to the estimate (34). To estimate the second term of the right hand side, we compute

which is uniformly bounded with respect to $\epsilon$ thanks to Lemma 3.4. Choosing $\eta = \sqrt{h}$ and letting $h$ going to $0$, we deduce from the above consideration that (35) holds true. From the Fréchet-Kolmogorov compactness, we deduce that the sequence $(\partial_x p_{\epsilon})_\epsilon$ is precompact in $L^1(Q_T)$. Passing in the limit in (33) we recover (32). This concludes the proof of Theorem 2.1.

3.4.   Uniqueness of solutions

In this section, we focus on the uniqueness of solutions to the limiting problem (16)–(20). We first observe that from (16) and (20), we have

Since we have the segregation property given by (20), we deduce that the support of $n_{10}$ and of $n_{20}$ are disjoints. Then, by taking test functions with support included in the support of $n_{10}$ or of $n_{20}$ in the weak formulation of (37), we deduce that

We are going to prove that system (38)–(39) complemented with the segregation property (20) and the relation (19) admits an unique solution. More precisely our result reads:

Proposition 1. Let us assume that assumptions (12) on $G_i$, $i = 1, 2$ holds. There exists a unique solution $(n_{10}, n_{20}, p_0)$ to the problem (38)-(39)-(19)-(20) with $0\leq n_{i0}\leq 1$ for $i = 1, 2$.

Proof. We follow the idea developped in [29] and adapt the Hilbert's duality method. Consider two solutions $(n_{10}, n_{20}, p_0)$ and $(\widetilde{n_{10}}, \widetilde{n_{20}}, \widetilde{p_0})$ of the system (38)-(39)-(19)-(20). Making the difference and denoting $q_i = n_{i0} p_0$ and $\widetilde{q_i} = \widetilde{n_{i0}} \widetilde{p_0}$, for $i = 1, 2$, we have

We first observe that on the set $\{n_{10}>0\}\cap\{p_0>0\}$, we have $q_1 = p_0$ from (19). Hence we have $n_{10} G_1(p_0) = n_{10} G_1(q_1)$. The same observation holds for the other terms in the right hand side of these latter equations. For any suitable test functions $\psi_1$ and $\psi_2$, we have, for $i = 1, 2$,

This can be rewritten as, for $i = 1, 2$,

where

and we define $A_i = 0$ as soon as $n_{i0} = \widetilde{n_{i0}}$ and $B_i = 0$ as soon as $q_i = \widetilde{q_i}$, whatever is the value of their denominators. It is shown in Lemma 3.8 below that, for $i = 1, 2$, we have $0\leq A_i\leq 1$, $0\leq B_i \leq 1$, $0\leq C_i \leq \gamma$.

The idea of the Hilbert's duality method consists in solving the dual problem, which is defined here by, for any smooth function $\Phi_i$, $i = 1, 2$,

If such a system admits a smooth solution, then, by choosing $\psi_i$ as a test function in (41), we get

From the expression of $A_i$, we deduce

for any smooth function $\Phi_i$, $i = 1, 2$. It is obvious to deduce the uniqueness for the density. Uniqueness for the pressure will follow from (40).

However, the dual problem (42) is not uniformly parabolic and its coefficients are not smooth. Then, in order to make this step rigorous, a regularization procedure is required. It can be done exactly as in [29,p 109-110]. For the sake of completeness of this paper, this regularizing procedure is recalled in Appendix A.

Lemma 3.8. Under assumptions (12), we have $0\leq A_i\leq 1$, $0\leq B_i \leq 1$, $0\leq C_i \leq \gamma$, for $i = 1, 2$.

Proof. We observe that, for $i = 1, 2$, $n_{i0}>\widetilde{n_{i0}}$ implies $q_i \geq \widetilde{q_i}$. Indeed, either $\widetilde{n_{i0}} = 0$ and then $\widetilde{q_{i}} = 0\leq q_i$, or $0<\widetilde{n_{i0}}<1$ and then from the segregation property (20) we have $\widetilde{n_0} = \widetilde{n_{i0}}$ and from the relation $(1-\widetilde{n_0})\widetilde{p_0} = 0$ we deduce that $\widetilde{p_0} = 0$, thus $\widetilde{q_{i}} = 0\leq q_i$. Similarly, for $i = 1, 2$, $\widetilde{n_{i0}}>n_{i0}$ implies $\widetilde{q_i} \geq q_i$. By setting $A_i = 0$ whenever $\widetilde{n_{i0}} = n_{i0}$, we conclude that $0\leq A_i \leq 1$.

By the same token, we show that, for $i = 1, 2$, $q_i \geq \widetilde{q_i}$ implies $n_{i0} \geq \widetilde{n_{i0}}$. Indeed, from $q_i = n_{i0} p_0 >0$, we deduce that $n_{i0}>0$ which implies $n_0 = n_{i0}$, and then $p_0>0$ implies from (19) that $n_{i0} = 1\geq \widetilde{n_{i0}}$. Hence, $0\leq B_i\leq 1$.

Finally, the bound on $C_i$ is a direct consequence of the fact that $G_i$ is nonincreasing and Lipschitz (see (12)) and that $0\leq \widetilde{n_{i0}} \leq 1$.

4.   Numerical simulations

4.1.   Numerical scheme

The numerical simulations are performed using a finite volume method similar as the one proposed in [13,15]. The scheme used for the conservative part is a classical explicit upwind scheme. To facilitate the reading of this paper, we recall here the scheme used. We divide the computational domain into finite-volume cells $C_j = [x_{j-1/2} , x_{j+1/2} ]$ of uniform size $\Delta x$ with $x_j = j\Delta x$, $j\in \{1, ..., M_x\}$, and $x_{j} = \frac{x_{j-1/2} +x_{j+1/2} }{2}$ so that

and define the cell average of functions $n_1(t, x)$ and $n_2(t, x)$ on the cell $C_j$ by

The scheme is obtained by integrating system (2)-(3) over $C_j$ and is given by

where $F^k_{\beta, j+1/2}$ are numerical fluxes approximating $-n^k_{\beta} u^k_{\beta}: = -n^k_{\beta} \partial_x(p^k_{\beta})$ and defined by:

where

with the discretized pressure

We use the usual notation $(u)^+ = \max(u, 0)$ and $(u)^- = \min(u, 0)$ for the positive part and, respectively, the negative part of $u$. Neumann boundary conditions are also implemented at the boundaries of the computational model.

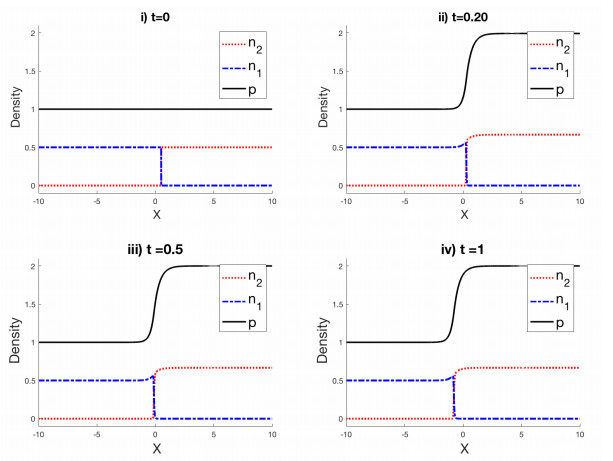
In order to illustrate the time dynamics for the model, we plot in Fig 1 the densities computed thanks to the above scheme for $\epsilon = 1$ at different times : (a) $t = 0$, (b) $t = 0.1$, (c) $t = 0.3$, (d) $t = 0.6$, (e) $t = 1$ and (f) $t = 2$. For this numerical simulation, the densities are initialized by

with $L = 5$, and the growth rates are defined by

We recall that we have defined the parameters $P_M^1$ and $P_M^2$ as the values of the pressure for which the growth functions vanish (see (12)). In this case their numerical values are given by $P_M^1 = 2$ and $P_M^2 = 1$. Then, we define

Since the growth functions are different, clearly ${N_M^2}_\epsilon<{N_M^1}_\epsilon$.

In Fig 1 the red and blue species are initially segregated and equal to 0.5. At first the dynamics is driven by the growth term, so the two species grow and reach their respective maximal packing values ${N_M^1}_{\epsilon}$ and ${N_M^2}_{\epsilon}$. Once this value is reached ($t = 1, 2$ on both panel (ⅱ), (ⅲ) and (ⅳ)), we observe two phenomena. First a bump is created on the left side of the interface, in the domain of $n_2$. This bump help the total densities to stay continuous, as it joins the two maximal densities. It also means that, at the interface, the pressure is going to be higher than the limit pressure $P_M^2$. Then the derivative of the pressure at the interface is positive, which induces a motion of the interface representing the fact that the red species $n_1$ pushes the blue species $n_2$. This motion of the interface is the second phenomenon which is observed.

4.2.   Influence of the parameter $\epsilon$

In order to illustrate our main result on the limit $\epsilon\to 0$, we show, in this section, some numerical simulations of the model (2)-(3) when $\epsilon$ goes to $0$. We also compare with the analytical solution of the limiting Hele-Shaw free boundary model. To perform these simulations we use the numerical scheme (43) complemented with the initial condition (44) and the growth function (45). For the limiting model, we use the initial conditions

and the growth function (45). The analytical expressions of the solution to the limiting Hele-Shaw system is computed in [15].

Fig 2 displays the time dynamics of the densities for different values of $\epsilon$: (a) $\epsilon = 1$, (b) $\epsilon = 0.1$, (c) $\epsilon = 0.01$, and (d) $\epsilon = 0.001$, along with solution to the Hele-Shaw system (e). For all simulations, the densities are plotted at times $t = 0.5$, $t = 1$ and $t = 1.5$.

We observe in Fig. 2 that the time dynamics of the numerical solutions is similar for each case and follows the dynamics presented above for the case $\epsilon = 1$. The main difference observed is the maximal packing value ${N_M^1}_{\epsilon}$ and ${N_M^2}_{\epsilon}$. Indeed since the maximal packing values are given by (46), when $\epsilon \rightarrow 0$, the maximal packing value converges to $1$. This is consistent with the numerical results shown in Fig. 2. In addition we observe that as $\epsilon$ decreases the stiffness of the densities increases. In overall we observe that as $\epsilon \rightarrow 0$ densities converge to Heaviside functions.

4.3.   Particular solutions: Tumor spheroid

One interested application of this study is tissue development. Since we consider a system with two populations of cells, we can for example consider the case of tumour with proliferative cells, whose density is denoted $n_2$, and quiescent cells, whose density is denoted $n_1$.

Solution of the limiting Hele-Shaw problem. We assume that initially the tumor is a spheroid centered in 0 and is composed by a spherical core representing the quiescent cells surrounded by a ring representing the proliferative cells. Then, we are looking for particular solution of the limiting Hele-Shaw problem (2)-(3) under the form:

The radius $R_1(t)$, with $R_1(t)<L$, is computed according to the geometric motion rules

where $p$ is the solution of

Such functions $n_1$ and $n_2$ are solutions to the limiting Hele-Shaw problem (2)-(3). Indeed by differentiating the densities, in the distributional sense, we get,

Since $R_1'(t) = -\partial_{x}p(R_1(t))$, it follows that

By applying the same computation on $n_2$ we get,

Analytical solution. As this paper is reduced to the case of dimension 1, we can compute the exact solution of the limiting Hele-Shaw problem (2)-(3) with this initial configuration for some simple expression of the growth terms $G_1$ and $G_2$. For instance, let us suppose that the growth terms are linear,

This choice means that as the pressure increases, the tumor will grow more slowly, until the pressure reach a critical value ($P_M^1$ or $P_M^2$ depending of the species) where the growth rate takes negative values, modelling the apoptosis of cells. The solution of the pressure equation is given by,

with

Computing the derivatives at the interface $R_1(t)$ we deduce that,

We are interested in the study of the evolution of $R_1$ in time, in function of the parameters $g_1, g_2, P_M^1, P_M^2$. Given that $0 \leq R_1(t) \leq L$, it is straightfoward that $\lambda \leq 0$. From (47), we deduce that the sign of $R_1'(t) \geq 0$ is the same as the sign of $P_M^1-P_M^2$.

Numerical simulations. Finally we show some simulations of the mechanical problem for the case of spheroid tumor growth. We run the simulations with $\epsilon = 0.01$ as we have shown in Section 4.2 that the simulations are close enough from the free boundary model. We consider two populations with the same space configuration as at the beginning of this section,

with

We fix the parameter $\epsilon$ to the value 1. The growth rates are going to defined the dynamics of the two populations. In the first example, we choose growth functions such that we observe death of the inner species $n_1$, which corresponds to the apoptosis of one population of cells. The growth functions are defined by

In a second example we display an example where the species $n_1$ grows and pushes the surrounding species $n_2$.

In Fig 3, we display the time dynamics of the densities of these two examples at different time step: (ⅰ) $t = 0$, (ⅱ) $t = 0.1$, (ⅲ) $t = 0.3$, (ⅳ) $t = 0.6$, (ⅴ) $t = 1$. It illustrates the two different behaviours mentionned above by (48) and (49). In Fig 3 (a) the red species grows and the blue species disappears since the pressure in the domain is bigger that $P_M^1$. In Fig 3 (b), the blue species pushes the red species and propagates.

Appendix A.   Uniqueness of solutions: Regularized dual problem

In this appendix we prove rigorously Proposition 1 using a regularization procedure for the dual problem 42. We follow closely the ideas in [29,p 109-110] which are recall here for the sake of completness of this paper. Since the coefficients $A_i$, $B_i$ are not strictly positive and not smooth, then we need to regularize the problem 42. For $i = 1, 2$, let ${A^k_i}$, ${B^k_i}$, ${C^k_i}$ and ${G^k_i}$ be sequences of smooth functions such that,

for some constant $\alpha_i, \beta_i, \delta_{1, i}, \delta_{2, i}, M_{1, i}, M_{2, i}, K_{1, i}, K_{2, i}$. For any smooth function $\Phi_i$, $i = 1, 2$, we consider the following regularised dual system,

As the coefficients $\frac{B^k_i}{A^k_i}$ for $i = 1, 2$, are positive, continuous and bounded below away from zero, the dual equation is uniformly parabolic in $Q_T$. Then we can solve it and we denote $\psi^k_i$ the solution of (50). This solution $\psi^k_i$ is smooth and can be used as a test function in (41).

Using (41) and (50), for $i = 1, 2$,

where

We intend to show that at the limit $k \rightarrow +\infty$, $I_{j, i}$ converges to 0 for $j = 1, 2, 3, 4$ and $i = 1, 2$. To show the convergence, we are going to find estimates on $\psi^k_i$ and its derivative:

● As $\psi^k_i$ is solution of (50) with $C_i^k$ nonnegative and $G_{i}^k$ uniformly bounded, from the maximum principle we get,

where $\kappa_1$ is independent of $k$.

● Multipling (50) by $\partial_{xx} \psi^k_i- C_i^k \psi^k_i$ and integrating on $\Omega \times (t, T)$, we get

with $K$ a constant independent of $k$. By using Gronwall lemma we get the following bound,

with $\kappa_2$ independent of $k$.

● Using (51), we get

with $\kappa_3$ independent of $k$.

We use these bounds to prove the convergence of the integrals $I_{j, i}$ for $j = 1, 2, 3, 4$ and $i = 1, 2$. We get,

where $\tilde{K}$ is a contant independent of of $k$. It justifies that $\lim_{k \rightarrow +\infty} I_{j, i} = 0$ for $j = 1, 2, 3, 4$ and $i = 1, 2$. Then

for any smooth function $\Phi_i$ for $i = 1, 2$. This implies that ${n_{10}} = \widetilde{n_{10}}$ and ${n_{20}} = \widetilde{n_{20}}$. Then, we deduce from (40),

By using $\psi_i = q_i - \widetilde{q_i}$, we recover $q_i = \widetilde{q_i}$ for $i = 1, 2$. It concludes the proof.

Acknowledgments

PD acknowledges support by the Engineering and Physical Sciences Research Council (EPSRC) under grants no. EP/M006883/1, EP/N014529/1 and EP/P013651/1, by the Royal Society and the Wolfson Foundation through a Royal Society Wolfson Research Merit Award no. WM130048 and by the National Science Foundation (NSF) under grant no. RNMS11-07444 (KI-Net). PD is on leave from CNRS, Institut de Mathématiques de Toulouse, France. SH acknowledge support from the Francis Crick Institute which receives its core funding from Cancer Research UK (FC001204), the UK Medical Research Council (FC001204), and the Well- come Trust (FC001204). N.V. acknowledges partial support from the ANR blanche project Kibord No ANR-13-BS01-0004 funded by the French Ministry of Research. Part of this work has been done while N.V. was a CNRS fellow at Imperial College, he is really grateful to the CNRS and to Imperial College for the opportunity of this visit. PD, SH and NV would like to thanks Jean-Paul Vincent for stimulating discussion.

Data statement

No new data was collected in the course of this research.