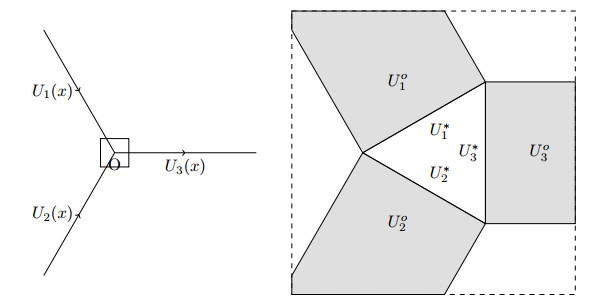
Intersection of three pipes at junction O. Right-Zoomed view of the junction with old traces
Gas flow through pipeline networks can be described using $ 2\times 2 $ hyperbolic balance laws along with coupling conditions at nodes. The numerical solution at steady state is highly sensitive to these coupling conditions and also to the balance between flux and source terms within the pipes. To avoid spurious oscillations for near equilibrium flows, it is essential to design well-balanced schemes. Recently Chertock, Herty & Özcan[
Citation: Yogiraj Mantri, Michael Herty, Sebastian Noelle. Well-balanced scheme for gas-flow in pipeline networks[J]. Networks and Heterogeneous Media, 2019, 14(4): 659-676. doi: 10.3934/nhm.2019026
| [1] | Yogiraj Mantri, Michael Herty, Sebastian Noelle . Well-balanced scheme for gas-flow in pipeline networks. Networks and Heterogeneous Media, 2019, 14(4): 659-676. doi: 10.3934/nhm.2019026 |
| [2] | Steinar Evje, Kenneth H. Karlsen . Hyperbolic-elliptic models for well-reservoir flow. Networks and Heterogeneous Media, 2006, 1(4): 639-673. doi: 10.3934/nhm.2006.1.639 |
| [3] | Fabian Rüffler, Volker Mehrmann, Falk M. Hante . Optimal model switching for gas flow in pipe networks. Networks and Heterogeneous Media, 2018, 13(4): 641-661. doi: 10.3934/nhm.2018029 |
| [4] | Felisia Angela Chiarello, Harold Deivi Contreras, Luis Miguel Villada . Nonlocal reaction traffic flow model with on-off ramps. Networks and Heterogeneous Media, 2022, 17(2): 203-226. doi: 10.3934/nhm.2022003 |
| [5] | Maya Briani, Benedetto Piccoli . Fluvial to torrential phase transition in open canals. Networks and Heterogeneous Media, 2018, 13(4): 663-690. doi: 10.3934/nhm.2018030 |
| [6] | Michael Herty, Niklas Kolbe, Siegfried Müller . Central schemes for networked scalar conservation laws. Networks and Heterogeneous Media, 2023, 18(1): 310-340. doi: 10.3934/nhm.2023012 |
| [7] | Tong Li, Nitesh Mathur . Global well-posedness and asymptotic behavior of $ BV $ solutions to a system of balance laws arising in traffic flow. Networks and Heterogeneous Media, 2023, 18(2): 581-600. doi: 10.3934/nhm.2023025 |
| [8] | Raul Borsche, Axel Klar, T. N. Ha Pham . Nonlinear flux-limited models for chemotaxis on networks. Networks and Heterogeneous Media, 2017, 12(3): 381-401. doi: 10.3934/nhm.2017017 |
| [9] | Maya Briani, Emiliano Cristiani . An easy-to-use algorithm for simulating traffic flow on networks: Theoretical study. Networks and Heterogeneous Media, 2014, 9(3): 519-552. doi: 10.3934/nhm.2014.9.519 |
| [10] | Mapundi K. Banda, Michael Herty, Axel Klar . Gas flow in pipeline networks. Networks and Heterogeneous Media, 2006, 1(1): 41-56. doi: 10.3934/nhm.2006.1.41 |
Gas flow through pipeline networks can be described using $ 2\times 2 $ hyperbolic balance laws along with coupling conditions at nodes. The numerical solution at steady state is highly sensitive to these coupling conditions and also to the balance between flux and source terms within the pipes. To avoid spurious oscillations for near equilibrium flows, it is essential to design well-balanced schemes. Recently Chertock, Herty & Özcan[
The study of mathematical models for gas flow in pipe networks has recently gained interest in the mathematical community, see e.g. [3,4,9,12,27]. While in the engineering literature [31] the topic has been discussed some decades ago, a complete mathematical theory has only emerged recently, see e.g. [16] for the Euler system on networks, [14] for the p–system on networks and [8] for a recent review article on general mathematical models on networks. Depending on the scale of phenomena of interest, different mathematical models for gas flow might be useful. A complete hierarchy of fluid–dynamic models has been developed and discussed in [9]. Therein, typical flow rates and pressure conditions are given and it is shown that a steady state algebraic model can be sufficient to describe average states in a gas network. Models based on an asymptotic expansion of the pressure may lead to further improvements in case of typical, slowly varying, temporal flow patterns [23,18]. If a finer resolution of the spatial and temporal dynamics is required, the isothermal Euler equations (1) provide a suitable model [3]. Here we focus on schemes which capture both steady states and small temporal and spatial perturbations.
Schemes which preserve a steady state exactly are called well-balanced, and their development is a lively topic in the field of hyperbolic balance laws, see e.g. the monograph [32]. Usually, these schemes use specific knowledge of an equilibrium state. As a consequence, well-balanced schemes for still water such as [1,29], or for moving water, [30], or for wet-dry fronts such as [6,10], which all approximate solutions to the shallow water equations, use different discretization techniques. A unified approach to well-balancing in one space dimension was recently proposed by Chertock, Herty and Özcan [11], who integrate the source term in space and subtract it from the numerical flux. This results in a new set of so-called equilibrium variables. The equilibrium variables are then reconstructed, and their values at the cell interfaces are used to compute numerical fluxes, which involve a new equilibrium limiter. Chertock et al. demonstrated the feasibility of this approach using a second order scheme for subsonic gas flow in a pipe with wall friction.
To the best of our knowledge, there is currently no well-balanced scheme for hyperbolic flows on networks. Here spurious oscillations may not only be caused by an imbalance of numerical fluxes and source terms, but also by discretization errors at junctions and compressors. In the present paper, we extend the equilibrium variable approach and develop a second order well-balanced scheme on a network. We also simplify the numerical fluxes introduced in [11] by removing the equilibrium limiter. High-order schemes for gas networks have been introduced only recently in [2,7,28]. A challenging question would be to extend our new well-balancing method to these more accurate schemes.
In the following we introduce the mathematical model for the temporal and spatial dynamics of gas flow in pipe networks. For simplicity, we study a single node
|
$ (Ui)t+F(Ui)x=S(Ui) $
|
(1) |
with conservative variables
|
$ Ui=[ρiqi],F(Ui)=[qiq2iρi+p(ρi)],S(Ui)=[0−fg,i2Diqi|qi|ρi]. $
|
(2) |
Here
|
$ p(ρ)=κργ for γ≥1. $
|
(3) |
For the numerical tests we focus on the special case of isothermal pressure,
|
$ p(ρ)=ρRT=a2ρ, $
|
(4) |
with speed of sound
|
$ ϕ(U1,U2,...,UM)=0,ϕ:R2M→RM. $
|
(5) |
In [12,13,35] general conditions are identified which guarantee a well–posed problem for initial data with suitable small total variation. If at a node the conservation of mass and equality of adjacent pressures is assumed, then existence, uniqueness and continuous dependence on the initial data for the p–system was shown in [15].
For pipes with a junction, a flow which is steady within each pipe, and fulfills the coupling conditions at the junction is called a steady state [22]. The coupling conditions are further detailed in Sections 2 and 3.
Our construction of well-balanced schemes is based upon analytical results for the isothermal Euler equations which have already been established (see e.g. [3,15] and the references therein). For completeness, and to fix the notation, we would like to give a brief summary.
When we study the coupling condition, we set the source terms
|
$ λ1(Ui)<0<λ2(Ui) for i=1…M. $
|
(6) |
This assumption is satisfied for typical gas flow conditions in high–pressure gas transmission systems. We denote the set of all incoming (respectively outgoing) pipes by
|
$ Uoi:=limx↑xolimt↓toUi(x,t) for i∈I−, $
|
(7) |
|
$ U∗i:=limt↓tolimx↑xoUi(x,t) for i∈I−, $
|
(8) |
|
$ Uoj:=limx↓xolimt↓toUj(x,t) for j∈I+. $
|
(9) |
|
$ U∗j:=limt↓tolimx↓xoUj(x,t) for j∈I+, $
|
(10) |
Note that the limits are exchanged in (8) and (7) (respectively (10) and (9)), so
The construction of the coupling conditions starts by connecting, within each pipe, the old with the new trace by a Lax curve entering the pipe. For an incoming pipe, this will be a curve
|
$ 1−R:¯Ui(σi):=ρleσi[1ul−aσi] for σi≤0,1−S:¯Ui(σi):=ρl(1+σi)[1ul−aσi√1+σi] for σi>0. $
|
(11) |
Analogously, for an outgoing pipe, we use curves of the second family with right state
|
$ 2−R:¯Uj(σj):=ρreσj[1ur+aσj] for σj≤0,2−S:¯Uj(σj):=ρr(1+σj)[1ur+aσj√1+σj] for σj>0. $
|
(12) |
We refer to [17] for case
The parameters
|
$ ¯ϕ(σ1,…,σM):=ϕ(¯U1(σ1),…,¯UM(σM))=0. $
|
(13) |
Now we set
|
$ U∗i:=¯Ui(σi). $
|
(14) |
By construction, the new traces satisfy the coupling conditions (5). Note that the number of unknowns in (13) are halved compared to (5) as each conservative variable,
So far, we have reviewed the general framework which was established and applied in [3,15,33]. In the following we focus on a particular coupling condition for which we design a well-balanced scheme. Let
|
$ ∑i∈I−Aiq∗i=∑j∈I+Ajq∗j, $
|
(15) |
since mass should not be accumulated or lost at the junction. Various approaches have been studied in order to model the other
|
$ h(ρ∗i,q∗i)=h∗(to) for all i∈I−∪I+. $
|
(16) |
In [35], Reigstad et al. showed that the coupling conditions are well-posed if the function
|
$ ddσh(ˉρi(σ),ˉqi(σ))>0 for all i∈I−∪I+. $
|
(17) |
Our analytical results are obtained under the general coupling condition (16) (respectively (16)), together with the monotonicity condition (17). In the numerical experiments, we use the following pressure-coupling condition: we require that the traces of the pressures should take one and the same value
|
$ p(ρ∗i)=p∗(to) for all i∈I−∪I+. $
|
(18) |
This condition is common in the engineering literature, and for a certain regime it is indeed a suitable approximation of the two-dimensional situation [24].
Thus the coupling function (5) at a junction reads
|
$ ϕ(U1,…,UM)=[∑i∈I−Aiqi−∑j∈I+Ajqjp(ρ2)−p(ρ1)⋮p(ρM)−p(ρM−1)]. $
|
(19) |
We now turn to a junction which models a compressor between the incoming pipe
|
$ q∗1=q∗2,p(ρ∗2)=CRp(ρ∗1). $
|
(20) |
Here
|
$ ϕ(U1,…,UM)=[q2−q1p(ρ2)−CRp(ρ1)]. $
|
(21) |
Summarizing, the analytical problem at the nodes is to connect the old traces
If the old traces are subsonic, and their variation is small enough, then the new traces will be subsonic as well. The new traces serve as initial data in the Riemann solver which determines the numerical flux.
In this paper, we show the analytical results of well-balancing for the case of multiple pipes meeting at the junction. However the scheme is valid for the case of compressor as well, as can be seen from the numerical results in Section 5.2.
The difficulty in preserving steady states is that the divergence of the conservative fluxes is approximated by a flux-difference, while the source is usually integrated by a quadrature over the cell. If this is not tuned carefully, the equilibrium state is not maintained, and spurious oscillations may be created. Chertock, Herty and Özcan [11] resolved this difficulty for one-dimensional balance laws by integrating the source term and hence writing it in conservative form. They applied this approach to the Cauchy problem for
|
$ (ρi)t+(Ki)x=0,(qi)t+(Li)x=0 $
|
(22) |
where the flux variable,
|
$ Vi(Ui,Ri)=[KiLi]=F(Ui)+[0Ri] $
|
(23) |
and fluxes
|
$ Ki:=qi,Li:=q2iρi+p(ρi)+Ri(x),Ri(x):=∫x~xifg,i2Diqi|qi|ρidx. $
|
(24) |
The point
|
$ ρp−ρ(L−R)=−K2. $
|
In other words, our task is to find the non-negative real roots of
|
$ φ(ρ)=c $
|
(25) |
with
|
$ φ(ρ):=ργ+1−bρ,b:=L−Rκ≥0,c:=−K2κ≤0. $
|
(26) |
For
|
$ ρ∗=(bγ+1)1/γ $
|
with corresponding minimum value
|
$ φ∗=−γ(bγ+1)1+1/γ. $
|
An elementary calculation shows that if
|
$ 0≤ρ−<ρ∗<ρ+<ρ1. $
|
We find the supersonic root
|
$ ρi(Vi,Ri)=Li−Ri+√(Li−Ri)2−4K2ia22a2, $
|
(27) |
and hence
|
$ Pi(Vi,Ri)=a2ρi(Vi,Ri). $
|
(28) |
Note that
|
$ ∑i∈I−AiK∗i=∑j∈I+AjK∗j, $
|
(29) |
|
$ P(K∗i,L∗i)=p∗ for all i∈I±, $
|
(30) |
or more generally
|
$ H(K∗i,L∗i)=h∗ for all i∈I± $
|
(31) |
where
|
$ P(K∗2,L∗2)=CRP(K∗1,L∗1). $
|
(32) |
For subsonic states, the coupling conditions (29), (30), (32) are equivalent to the coupling conditions (15), (18), (20).
For steady states,
|
$ 1−R:¯Vi(σi):=ρleσi[ul−aσi(ul−aσi)2+a2]+[0Rl]for σi≤0,1−S:¯Vi(σi):=ρl(1+σi)[ul−aσi√1+σi(ul−aσi√1+σi)2+a2]+[0Rl]for σi>0. $
|
(33) |
Similarly for the admissible boundary states on the pipes
|
$ 2−R:¯Vj(σj):=ρreσj[ur+aσj(ur+aσj)2+a2]+[0Rr]for σj≤0,2−S:¯Vj(σj):=ρr(1+σj)[ur+aσj√1+σj(ur+aσj√1+σj)2+a2]+[0Rr]for σj>0. $
|
(34) |
The equilibrium variables satisfying the coupling condition (29) and (30) are given by
|
$ K∗i:=¯Ki(σi) and L∗i:=¯Li(σi). $
|
(35) |
Note that all variables defined along the Lax-curves also depend on the old traces and the integrated source terms as parameters, e.g.
Theorem 3.1. Consider a nodal point with
Then there exists an open neighborhood
Proof. Denote by
|
$ Ψ(V,(Vo,Ro)):=[∑i∈I−AiKi−∑j∈I+AjKjH(V1)−H(V2)⋮H(VM−1)−H(VM)] $
|
(36) |
where
| $ \overline{\Psi}( \sigma, (V^o, R^o)): = {\Psi}(\overline{V}(\sigma), (V^o, R^o)):\mathbb{R}^{M } \times \mathbb{R}^{ 2 M }\times \mathbb{R}^M \to \mathbb{R}^{M } $ |
where
| $ \overline{V}(\sigma): = (\overline{V}_i(\sigma_i))_{i \in I^\pm} $ |
and the components of
|
$ Dσ¯Ψ=[A1dK1dσ1…A|I−|dK|I−|dσ|I−|−A|I−|+jdK|I−|+jdσ|I−|+j…j=1,...|I+|dH1dσ1−dH2dσ20……00dH2dσ2−dH3dσ3……0⋱⋱⋱⋱0……0dHM−1dσM−1−dHMdσM] $
|
and therefore
|
$ det(Dσ¯Ψ)=(−1)M−1∑i∈I−(AidKidσi∏k∈I−,k≠idHkdσk)+(−1)M∑j∈I+(AjdKjdσj∏k∈I−,k≠jdHkdσk), $
|
(37) |
From equations (33) and (34), we obtain at
|
$ dKidσi(0)=qoi−aρoi<0,dLidσi(0)=(qoi−aρoi)2ρoi>0,∀i∈I−,dKidσi(0)=qoi+aρoi>0,dLidσi(0)=(qoi+aρoi)2ρoi>0,∀i∈I+. $
|
Hence,
|
$ sign(det(Dσ¯Ψ))=(−1)M∑isign(dHidσi). $
|
Thus for any monotonic coupling condition, we see that
For example, for the pressure coupling condition (using
Hence,  and therefore
and therefore 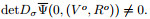
Similarly for coupling condition given by continuity of momentum flux,
| $ \frac{dH_i}{d\sigma_i}(0) = \frac{dL_i}{d\sigma_i}(0) > 0. $ |
Thus, by the implicit function theorem there exists an open neighborhood
| $ \Psi(V^*, (V^o, R^o)) = \overline{\Psi}(\sigma^*, (V^o, R^o)) = 0. $ |
Since the corresponding state of
Using the same technique, we can also treat the compressor, because the pressure changes monotonically along the Lax curves.
Corollary 1. Consider a nodal point with
Proof. The corollary follows from the proof of Theorem 3.1. One can also check that the pressure for a general Gamma law is also monotonic, i.e.,
In case of a compressor the pressure of the gas is multiplied by the compression ratio
Remark 1. Note that we have omitted the source term when computing the solution along the Lax curves. This is justified by the semi-discrete formulation of the finite volume scheme in the next section, which implies that we are evaluating the coupling condition at a set of measure zero in space-time. Since the source term is bounded, it does not contribute to the integral over the cells.
Remark 2. Another possibility is to reformulate system (22) as a system of three equations in
| $ \partial_t R_i = 0. $ |
Therefore, the corresponding hyperbolic field has a zero eigenvalue in an independent subspace. This yields a characteristic boundary at each adjacent pipe. Hence in phase space, at each pipe
We compute the evolution of the conservative variables using the second–order central upwind scheme [26,25]. The computational domain
| $ U_{{i}}^{{j}}(t) = \frac{1}{\Delta x} \int_{x_{j-\frac{1}2}}^{x_{j+\frac{1}2}} U_i(x, t) dx, , \; i \in I^\pm, j = 1, \ldots , N. $ |
The evolution of conservative variables, density and momentum using central upwind scheme [25,26] reads
|
$ dUjidt=−Vj+1/2i−Vj−1/2iΔx $
|
(38) |
where
|
$ VN+1/2i=V∗i,i∈I−, $
|
(39) |
|
$ V1/2i=V∗i,i∈I+. $
|
(40) |
The new traces
|
$ R1/2i=RN+1/2k=0∀i∈I+,k∈I−,Rj+1/2i=Rj−1/2i+Δxfg,i2Diqji|qji|ρji,Rj−1/2k=Rj+1/2k+Δxfg,k2Dkqjk|qjk|ρjk. $
|
The equilibrium variables
|
$ Wj,Ei=Wji+Δx2(Wx)ji,Wj,Wi=Wji−Δx2(Wx)ji $
|
(41) |
with numerical derivatives
|
$ (Wx)ji={Wj+1i−WjiΔx,j=1Wji−Wj−1iΔx,j=Nminmod(θWj+1i−WjiΔx,Wj+1i−Wj−1i2Δx,θWji−Wj−1iΔx),otherwise, $
|
(42) |
|
$ minmod(w1,w2,…,wn)={min(w1,w2,…,wn)if wi>0,∀imax(w1,w2,…,wn)if wi<0,∀i0otherwise $
|
(43) |
For interior interfaces, we may use any conservative numerical flux functions whose numerical diffusion vanishes at equilibrium states. Here we choose the central upwind flux,
|
$ Vj+1/2i=aj+1/2i,+Vj,Ei−aj+1/2i,−Vj+1,Wiaj+1/2i,+−aj+1/2i,−+αj+1/2i(Uj+1,Wi−Uj,Ei), $
|
(44) |
where
|
$ aj+1/2i,+=max(λ(Uj,Ei),λ(Uj+1,Wi),0),aj+1/2i,−=min(λ(Uj,Ei),λ(Uj+1,Wi),0) $
|
(45) |
and
Remark 3. Note that in [11] an additional limiter was introduced to suppress the numerical viscosity in (44) at equilibrium and assure well-balancing:in particular, the numerical viscosity
|
$ H(ϕ)=(Cϕ)m1+(Cϕ)m $
|
(46) |
where
The following theorem shows that well-balancing is already assured by the continuity of the integrated source terms
Theorem 4.1. The numerical scheme given by (38) and flux defined by (44) preserves the steady state across a node of
Proof. Consider steady state
Since the equilibrium variables
At the nodal point the flux variables satisfy the coupling conditions (29) and (30). Then, the boundary data
| Data: Given discretized initial conditions |
| while: terminal time not reached do |

|
| end |
Some remarks are in order. The algorithm uses the same time step for all adjacent pipes. This is not necessary but simplifies the computation of the coupling condition. Also, the algorithm is second–order in the pipe but it may reduce to first order at the coupling condition. The algorithm can be extended to second–order across the nodal point using techniques presented in [2]. However, note that the steady state is constant and therefore the scheme preserves the steady state to any order across the nodal point.
In this section, we test the well-balanced(WB) scheme with numerical examples for steady state and near steady state flows. The results of this WB method have been compared with a second order non well-balanced method(NWB). The NWB scheme is given by,
|
$ dUjidt=−Fj+1/2i−Fj−1/2iΔx+Sji $
|
(47) |
where
|
$ Fj+1/2i=aj+1/2i,+F(Uj,Ei)−aj+1/2i,−F(Uj+1,Wi)aj+1/2i,+−aj+1/2i,−+αj+1/2i(Uj+1,Wi−Uj,Ei) $
|
where the flux terms are as defined in (2) and
We run the tests at CFL number = 0.4 and minmod parameter,
In the first example, we study the WB scheme for steady state at a node with three types of pipe combinations–1 incoming and 1 outgoing pipes; 1 incoming and 2 outgoing pipe; and 2 incoming and 1 outgoing pipe. The initial conditions are selected in such a way that the node is at steady state with the equilibrium variables constant in each pipe and satisfying the coupling conditions at the node.
The initial condition for first case with 1 incoming and 1 outgoing pipe are
The L-1 error for the three cases are given in Table 1,
Comparison of L-1 errors between well-balanced(WB) and non well-balanced(NWB) scheme at steady state for a junction at time T = 1
.| No. of cells in each pipe | L1-error for variable | 1 Incoming, 1 Outgoing | 1 Incoming, 2 Outgoing | 2 Incoming, 1 Outgoing | |||||
| WB | NWB | WB | NWB | WB | NWB | ||||
| 50 | K | $2.83\text{x}10^{-17}$ | $6.19\text{x}10^{-7}$ | $6.91\text{x}10^{-17}$ | $3.78\text{x}10^{-7}$ | $9.02\text{x}10^{-17}$ | $3.45\text{x}10^{-7}$ | ||
| L | $3.44\text{x}10^{-17}$ | $9.48\text{x}10^{-7}$ | $5.16\text{x}10^{-17}$ | $3.57\text{x}10^{-7}$ | $9.21\text{x}10^{-17}$ | $7.38\text{x}10^{-7}$ | |||
| 100 | K | $3.95\text{x}10^{-17}$ | $1.56\text{x}10^{-7}$ | $8.12\text{x}10^{-17}$ | $9.63\text{x}10^{-8}$ | $8.60\text{x}10^{-17}$ | $8.67\text{x}10^{-8}$ | ||
| L | $4.86\text{x}10^{-17}$ | $2.43\text{x}10^{-7}$ | $7.38\text{x}10^{-17}$ | $8.94\text{x}10^{-8}$ | $8.24\text{x}10^{-17}$ | $1.87\text{x}10^{-7}$ | |||
| 200 | K | $5.11\text{x}10^{-17}$ | $3.88\text{x}10^{-8}$ | $8.69\text{x}10^{-17}$ | $2.62\text{x}10^{-8}$ | $1.04\text{x}10^{-16}$ | $2.69\text{x}10^{-8}$ | ||
| L | $5.85\text{x}10^{-17}$ | $6.13\text{x}10^{-8}$ | $7.06\text{x}10^{-17}$ | $2.32\text{x}10^{-8}$ | $9.49\text{x}10^{-17}$ | $5.03\text{x}10^{-8}$ | |||
As can be seen from the results in Table 1, the L-1 error
In the second example, we study the well-balancing at steady state for compressor connecting two pipes with compression ratios
Comparison of L-1 errors between well-balanced(WB) and non well-balanced(NWB) scheme at steady state with a compressor at different compression ratios at time T = 1
.| No. of cells in each pipe | L1-error for variable | CR=1.5 | CR=2.0 | CR=2.5 | |||||
| WB | NWB | WB | NWB | WB | NWB | ||||
| 50 | K | $1.11\text{x}10^{-17}$ | $4.16\text{x}10^{-7}$ | $5.30\text{x}10^{-17}$ | $3.78\text{x}10^{-7}$ | $1.97\text{x}10^{-17}$ | $3.77\text{x}10^{-7}$ | ||
| L | $2.66\text{x}10^{-17}$ | $4.00\text{x}10^{-7}$ | $5.38\text{x}10^{-17}$ | $3.57\text{x}10^{-7}$ | $1.39\text{x}10^{-17}$ | $3.54\text{x}10^{-7}$ | |||
| 100 | K | $2.90\text{x}10^{-17}$ | $1.05\text{x}10^{-7}$ | $7.28\text{x}10^{-17}$ | $9.63\text{x}10^{-8}$ | $4.22\text{x}10^{-17}$ | $9.68\text{x}10^{-8}$ | ||
| L | $4.08\text{x}10^{-17}$ | $1.01\text{x}10^{-7}$ | $7.24\text{x}10^{-17}$ | $8.94\text{x}10^{-8}$ | $4.66\text{x}10^{-17}$ | $8.89\text{x}10^{-7}$ | |||
| 200 | K | $4.26\text{x}10^{-17}$ | $2.64\text{x}10^{-8}$ | $8.15\text{x}10^{-17}$ | $2.62\text{x}10^{-8}$ | $5.02\text{x}10^{-17}$ | $2.84\text{x}10^{-8}$ | ||
| L | $4.69\text{x}10^{-17}$ | $2.53\text{x}10^{-8}$ | $7.45\text{x}10^{-17}$ | $2.32\text{x}10^{-8}$ | $5.76\text{x}10^{-17}$ | $2.59\text{x}10^{-8}$ | |||
Similar to the first example, we see that the L1 errors using the WB scheme are accurate up to machine precision. Also the coupling conditions for the compressor do not affect the well-balancing of the scheme.
From the first two examples, we can see that the WB scheme preserves steady state. We now compare the WB and NWB scheme for initial conditions given by perturbations to momentum at steady state. The initial conditions for the perturbed state are given by,
|
$ Ki(x)=ˆKi+ηie−100(x−x0)2,Li=ˆLi∀i=1,2…M $
|
(48) |
where
At first, we consider a node connecting two pipes. The equilibrium variables for this case are given by,
We can see from the results that both the WB and NWB schemes provide similar solutions for the perturbation of order
From Figure 4 we can see that the NWB scheme develops oscillations for N = 100 when the perturbation is of order
We now do a similar test for a node connected to 1 incoming and 2 outgoing pipes. The equilibrium states are given by,
We see from the results that even for the perturbations of order
So far we have tested the scheme for smooth near-equilibrium solutions. Now we consider a discontinuity at a junction of 1 incoming and 2 outgoing pipes, i.e.
From the above test, we can see that the scheme is able to capture shocks. The solution shows a 1-wave moving towards left into the first pipe from the junction and a 2-wave towards right into the second and third pipes. Similar solutions were obtained by Egger[19] using a conservative mixed finite element method with a stagnation enthalpy coupling condition. In Figures 7 and 8, we use the classical, non-well -balanced scheme (using
In this paper we have extended the recent, equilibrium variable based approach to well-balancing, developed by Chertock, Herty and Özcan[11] for one-dimensional systems, to a network of gas pipelines with friction. In particular we studied intersections of pipes at a node and compressors within a pipeline network. We prove well-posedness and well-balancing of the new scheme. For compressors and for junctions of three pipes, numerical experiments demonstrate that equilibria are resolved up to machine accuracy. Most interestingly, near equilibrium flows are resolved robustly and accurately, even in cases where a standard non-balanced scheme fails. For flows away from equilibrium, including shocks emanating from a junction, the scheme is as good as a standard scheme using conservative instead of equilibrium variables.
This work has been supported by HE5386/13–15, BMBF ENets Project, and DFG Research Training Group 2326: Energy, Entropy, and Dissipative Dynamics, RWTH Aachen University.
| 1. | Martin Gugat, Michael Herty, 2022, 23, 9780323850599, 59, 10.1016/bs.hna.2021.12.002 | |
| 2. | Yogiraj Mantri, Sebastian Noelle, Well-balanced discontinuous Galerkin scheme for 2 × 2 hyperbolic balance law, 2021, 429, 00219991, 110011, 10.1016/j.jcp.2020.110011 | |
| 3. | Sara Grundel, Michael Herty, Hyperbolic discretization of simplified Euler equation via Riemann invariants, 2022, 106, 0307904X, 60, 10.1016/j.apm.2022.01.006 | |
| 4. | Michael Herty, Niklas Kolbe, Siegfried Müller, Central schemes for networked scalar conservation laws, 2022, 18, 1556-1801, 310, 10.3934/nhm.2023012 | |
| 5. | Zlatinka Dimitrova, Flows of Substances in Networks and Network Channels: Selected Results and Applications, 2022, 24, 1099-4300, 1485, 10.3390/e24101485 | |
| 6. | Sonia Valbuena, Carlos A. Vega, Numerical approximation of living-man steady state solutions for blood flow in arteries using a well-balanced discontinuous Galerkin scheme, 2023, 18, 25900374, 100375, 10.1016/j.rinam.2023.100375 | |
| 7. | Andrea Corli, Massimiliano D. Rosini, Ulrich Razafison, 2024, Mathematical Modeling of Chattering and the Optimal Design of a Valve*, 979-8-3503-1633-9, 76, 10.1109/CDC56724.2024.10886245 |
| Data: Given discretized initial conditions |
| while: terminal time not reached do |

|
| end |
Comparison of L-1 errors between well-balanced(WB) and non well-balanced(NWB) scheme at steady state for a junction at time T = 1
.| No. of cells in each pipe | L1-error for variable | 1 Incoming, 1 Outgoing | 1 Incoming, 2 Outgoing | 2 Incoming, 1 Outgoing | |||||
| WB | NWB | WB | NWB | WB | NWB | ||||
| 50 | K | $2.83\text{x}10^{-17}$ | $6.19\text{x}10^{-7}$ | $6.91\text{x}10^{-17}$ | $3.78\text{x}10^{-7}$ | $9.02\text{x}10^{-17}$ | $3.45\text{x}10^{-7}$ | ||
| L | $3.44\text{x}10^{-17}$ | $9.48\text{x}10^{-7}$ | $5.16\text{x}10^{-17}$ | $3.57\text{x}10^{-7}$ | $9.21\text{x}10^{-17}$ | $7.38\text{x}10^{-7}$ | |||
| 100 | K | $3.95\text{x}10^{-17}$ | $1.56\text{x}10^{-7}$ | $8.12\text{x}10^{-17}$ | $9.63\text{x}10^{-8}$ | $8.60\text{x}10^{-17}$ | $8.67\text{x}10^{-8}$ | ||
| L | $4.86\text{x}10^{-17}$ | $2.43\text{x}10^{-7}$ | $7.38\text{x}10^{-17}$ | $8.94\text{x}10^{-8}$ | $8.24\text{x}10^{-17}$ | $1.87\text{x}10^{-7}$ | |||
| 200 | K | $5.11\text{x}10^{-17}$ | $3.88\text{x}10^{-8}$ | $8.69\text{x}10^{-17}$ | $2.62\text{x}10^{-8}$ | $1.04\text{x}10^{-16}$ | $2.69\text{x}10^{-8}$ | ||
| L | $5.85\text{x}10^{-17}$ | $6.13\text{x}10^{-8}$ | $7.06\text{x}10^{-17}$ | $2.32\text{x}10^{-8}$ | $9.49\text{x}10^{-17}$ | $5.03\text{x}10^{-8}$ | |||
Comparison of L-1 errors between well-balanced(WB) and non well-balanced(NWB) scheme at steady state with a compressor at different compression ratios at time T = 1
.| No. of cells in each pipe | L1-error for variable | CR=1.5 | CR=2.0 | CR=2.5 | |||||
| WB | NWB | WB | NWB | WB | NWB | ||||
| 50 | K | $1.11\text{x}10^{-17}$ | $4.16\text{x}10^{-7}$ | $5.30\text{x}10^{-17}$ | $3.78\text{x}10^{-7}$ | $1.97\text{x}10^{-17}$ | $3.77\text{x}10^{-7}$ | ||
| L | $2.66\text{x}10^{-17}$ | $4.00\text{x}10^{-7}$ | $5.38\text{x}10^{-17}$ | $3.57\text{x}10^{-7}$ | $1.39\text{x}10^{-17}$ | $3.54\text{x}10^{-7}$ | |||
| 100 | K | $2.90\text{x}10^{-17}$ | $1.05\text{x}10^{-7}$ | $7.28\text{x}10^{-17}$ | $9.63\text{x}10^{-8}$ | $4.22\text{x}10^{-17}$ | $9.68\text{x}10^{-8}$ | ||
| L | $4.08\text{x}10^{-17}$ | $1.01\text{x}10^{-7}$ | $7.24\text{x}10^{-17}$ | $8.94\text{x}10^{-8}$ | $4.66\text{x}10^{-17}$ | $8.89\text{x}10^{-7}$ | |||
| 200 | K | $4.26\text{x}10^{-17}$ | $2.64\text{x}10^{-8}$ | $8.15\text{x}10^{-17}$ | $2.62\text{x}10^{-8}$ | $5.02\text{x}10^{-17}$ | $2.84\text{x}10^{-8}$ | ||
| L | $4.69\text{x}10^{-17}$ | $2.53\text{x}10^{-8}$ | $7.45\text{x}10^{-17}$ | $2.32\text{x}10^{-8}$ | $5.76\text{x}10^{-17}$ | $2.59\text{x}10^{-8}$ | |||
| Data: Given discretized initial conditions |
| while: terminal time not reached do |

|
| end |
| No. of cells in each pipe | L1-error for variable | 1 Incoming, 1 Outgoing | 1 Incoming, 2 Outgoing | 2 Incoming, 1 Outgoing | |||||
| WB | NWB | WB | NWB | WB | NWB | ||||
| 50 | K | $2.83\text{x}10^{-17}$ | $6.19\text{x}10^{-7}$ | $6.91\text{x}10^{-17}$ | $3.78\text{x}10^{-7}$ | $9.02\text{x}10^{-17}$ | $3.45\text{x}10^{-7}$ | ||
| L | $3.44\text{x}10^{-17}$ | $9.48\text{x}10^{-7}$ | $5.16\text{x}10^{-17}$ | $3.57\text{x}10^{-7}$ | $9.21\text{x}10^{-17}$ | $7.38\text{x}10^{-7}$ | |||
| 100 | K | $3.95\text{x}10^{-17}$ | $1.56\text{x}10^{-7}$ | $8.12\text{x}10^{-17}$ | $9.63\text{x}10^{-8}$ | $8.60\text{x}10^{-17}$ | $8.67\text{x}10^{-8}$ | ||
| L | $4.86\text{x}10^{-17}$ | $2.43\text{x}10^{-7}$ | $7.38\text{x}10^{-17}$ | $8.94\text{x}10^{-8}$ | $8.24\text{x}10^{-17}$ | $1.87\text{x}10^{-7}$ | |||
| 200 | K | $5.11\text{x}10^{-17}$ | $3.88\text{x}10^{-8}$ | $8.69\text{x}10^{-17}$ | $2.62\text{x}10^{-8}$ | $1.04\text{x}10^{-16}$ | $2.69\text{x}10^{-8}$ | ||
| L | $5.85\text{x}10^{-17}$ | $6.13\text{x}10^{-8}$ | $7.06\text{x}10^{-17}$ | $2.32\text{x}10^{-8}$ | $9.49\text{x}10^{-17}$ | $5.03\text{x}10^{-8}$ | |||
| No. of cells in each pipe | L1-error for variable | CR=1.5 | CR=2.0 | CR=2.5 | |||||
| WB | NWB | WB | NWB | WB | NWB | ||||
| 50 | K | $1.11\text{x}10^{-17}$ | $4.16\text{x}10^{-7}$ | $5.30\text{x}10^{-17}$ | $3.78\text{x}10^{-7}$ | $1.97\text{x}10^{-17}$ | $3.77\text{x}10^{-7}$ | ||
| L | $2.66\text{x}10^{-17}$ | $4.00\text{x}10^{-7}$ | $5.38\text{x}10^{-17}$ | $3.57\text{x}10^{-7}$ | $1.39\text{x}10^{-17}$ | $3.54\text{x}10^{-7}$ | |||
| 100 | K | $2.90\text{x}10^{-17}$ | $1.05\text{x}10^{-7}$ | $7.28\text{x}10^{-17}$ | $9.63\text{x}10^{-8}$ | $4.22\text{x}10^{-17}$ | $9.68\text{x}10^{-8}$ | ||
| L | $4.08\text{x}10^{-17}$ | $1.01\text{x}10^{-7}$ | $7.24\text{x}10^{-17}$ | $8.94\text{x}10^{-8}$ | $4.66\text{x}10^{-17}$ | $8.89\text{x}10^{-7}$ | |||
| 200 | K | $4.26\text{x}10^{-17}$ | $2.64\text{x}10^{-8}$ | $8.15\text{x}10^{-17}$ | $2.62\text{x}10^{-8}$ | $5.02\text{x}10^{-17}$ | $2.84\text{x}10^{-8}$ | ||
| L | $4.69\text{x}10^{-17}$ | $2.53\text{x}10^{-8}$ | $7.45\text{x}10^{-17}$ | $2.32\text{x}10^{-8}$ | $5.76\text{x}10^{-17}$ | $2.59\text{x}10^{-8}$ | |||
Intersection of three pipes at junction O. Right-Zoomed view of the junction with old traces
Phase plot in terms of equilibrium variables with initial state
Momentum for perturbation of order
Momentum for perturbation of order
Momentum for perturbation of order
Momentum for perturbation of order
Conservative variables,
Conservative variables,