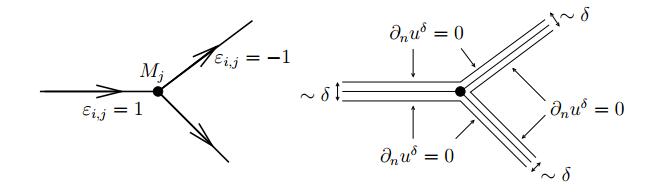Wave propagation in fractal trees. Mathematical and numerical issues

1.   Introduction

This paper deals with the initial boundary value problem for the phase transition model introduced in [9], consisting of the following $2\times 2$ system of conservation laws:

where $\rho$ is the traffic density, $\eta$ is a generalized momentum and $v=v(\rho,\eta)$ is the speed. This system is non-smooth since $v(\rho, \eta) = \min \left\{ V_{\max}, \frac{\eta}{\rho}\, \psi(\rho) \right\}$ is not a $\mathbf{C^1}$ function; $V_{\max}$ is a uniform bound on the speed and $\psi$ is a decreasing function.

The system in (1.1) belongs to the class of macroscopic second order traffic models, see [3,23], and it is characterized by two different phases: the Free one and the Congested one. A peculiarity of $2-$phases models is the existence of a free regime where the single density characterizes the state of the system, while in congested regime it is necessary the use of two variables. Thus, in the free phase the model reduces to a single conservation law, the classical Lighthill-Whitham [20] and Richards [22] (LWR) model, where the speed is constantly equal to $V_{\max}$, while in the congested phase the model is a strictly hyperbolic system of two conservation laws, see Section 2. In 2002, Colombo proposed the first second order model with two phases, see [6,7]. For other $2-$phases and phase transition models see [4,8,17,19,21].

In this paper we consider an initial boundary value problem for the model in (1.1) and we prove existence of solutions, provided the initial data and the boundary conditions have finite total variation. More precisely, we fix $a, b \in \mathbb{R}$ with $a < b$ and we consider the following problem:

The initial datum is $\left(\rho_0, \eta_0\right): (a,b) \to F \cup C$ and the boundary conditions are $\left(\rho_a, q_a\right): (0, +\infty) \to F \cup C$ and $\left(\rho_b, q_b\right): (0,+\infty) \to F \cup C$. The sets $F$ and $C$, respectively the free and the congested phase, will be defined in the next section.

In [12] Garavello considered an IBVP for the phase transition model introduced in [4]. We remark here that the model in [9], considered in this paper, and that one in [4], although similar, are different. Indeed Riemann problems for the two systems are solved, in general, in a different way and with a different number of waves. Another difference relies in the derivation: the model in [4] is based on the two phases, the free and the congested, while in [9] the two phases are a consequence of the model by imposing the speed limit $V_{\max}$, see Remark 1.

In this paper we use the wave front tracking technique, that is we explicitly construct a piecewise constant approximate solution, we prove that there exists an uniform bound on a functional measuring the strength of the waves and then, we conclude with the existence of a solution obtained by a compactness argument. We remark that, as in [12], the phase transition system with boundary considered in this paper is characteristic, since there are phase transitions waves with zero speed. In general, as usual in conservation laws, imposing characteristic boundary conditions is a delicate topic, see [1,2,11] and Remark 2.

The paper is organized as follows: in the next section we briefly recall the phase transition traffic model introduced in [9]. In Section 3, following the approach in [12], we state and prove the main result concerning the boundary value problem; the proof is divided into three different subsections.

2.   Description of the phase transition model

We recall at first the phase transition model introduced in [9]. This model has been derived as an extension of the LWR model, given by the following single conservation law:

where $\rho$ is the traffic density and $V=V(t,x,\rho)$ is a general speed. We assume that $V = w \, \psi(\rho)$, where $\psi$ is a decreasing function and $w = w(t,x)$ is the maximal speed of each driver. Moreover, introducing a uniform bound $V_{\max}$ on the speed, we get the following system:

where $v = \min \left\{V_{\max} ,\, w \, \psi(\rho) \right\}$. Note that the maximal speed $w$ is a peculiar characteristic of (2.2), being a specific feature of every single driver. With the change of variable $\eta=\rho w$ we get the system in (1.1), where the conserved variables are $\rho$ and $\eta$.

As in [9,14], we recall the following assumptions:

(H-1): $R,\check w, \hat w, V_{\max}$ are positive constants, with $V_{\max} < \check w < \hat w$.

(H-2): $\psi \in \mathbf{C^2} \left( [0,R];[0,1]\right)$ is such that $\psi(0) = 1$, $\psi(R) = 0$, and, for every $\rho \in [0,R]$, $\psi'(\rho) \le 0$, $\frac{d^2\ }{d\rho^2} \left( \rho\, \psi(\rho) \right) \le 0$.

(H-3): $\eta\, \psi'(\rho) + \frac{\eta}{\rho}\psi(\rho)<0$, for every $(\rho,\eta) \in C$.

Here, $R$ is the maximal possible density, typically $R=1$; $\check w$, respectively, $\hat w$, is the minimum, respectively, maximum, of the maximal speeds of each vehicle. The latter condition means that waves of the first family in the congested phase $C$ have negative speed.

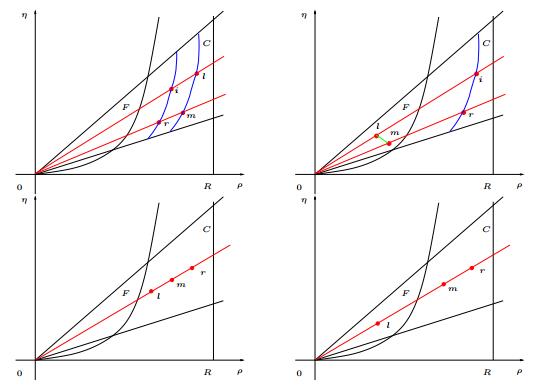
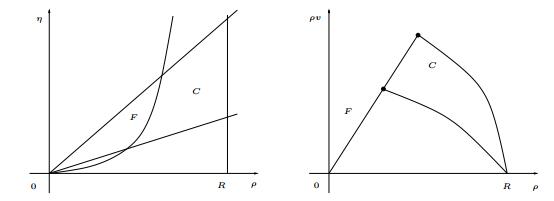
In (1.1), the two phases, free and congested, are described by the sets

represented in Figure 1. Note that $F$ and $C$ are closed sets and $F\cap C \neq \emptyset$. Note also that $F$ is a one-dimensional manifold in the $(\rho, \rho v)$ plane of the fundamental diagram, while it is a two-dimensional manifold in the $(\rho,\eta)$ coordinates.

We remark that, in the free phase $F$, the model (1.1) reduces to the degenerate linear system

while, in the congested phase $C$, it is given by

We recall also the eigenvalues, right eigenvectors, and Lax curves $\eta=\mathcal{L}_i(\rho;\rho_o,\eta_o)$ in $C$:

When $\rho_o = R$, the 2-Lax curve through $(\rho_o, \eta_o)$ is the segment $\rho=R$, $\eta \in [R \check w, R \hat w]$.

Finally, we list the waves and the notations that we will use in the present paper.

● First family wave: a wave connecting a left state $\left(\rho_l, \eta_l\right) \in C$ with a right state $\left(\rho_r, \eta_r\right) \in C$ such that $\frac{\eta_l}{\rho_l} = \frac{\eta_r}{\rho_r}$.

● Second family wave: a wave connecting a left state $\left(\rho_l, \eta_l\right) \in C$ with a right state $\left(\rho_r, \eta_r\right) \in C$ such that $v\left(\rho_l, \eta_l\right) = v\left(\rho_r, \eta_r\right)$.

● Linear wave: a wave connecting two states in the free phase.

● Phase transition wave: a wave connecting a left state $\left(\rho_l, \eta_l\right) \in F$ with a right state $\left(\rho_r, \eta_r\right) \in C$ satisfying $\frac{\eta_l}{\rho_l} = \frac{\eta_r}{\rho_r}$.

Remark 1. We remark hare that model (1.1), considered in this paper, and that one in [4], although similar, are different.

Both models are described by two intersecting phases: the free phase and the two-dimensional congested phase. Note however that, in the model (1.1) the free phase is two-dimensional in the conserved quantity coordinates $(\rho,\eta)$.

The main diffference lies in the solution of the Riemann problem, in particular when the left state belongs to the free phase and the right state to the congested one. In this case the Riemann problem for model (1.1) is solved with at most two waves, while the Riemann problem for the model considered in [4] is solved with at most three waves. See [13,Proposition 3.1,Proposition 3.2].

Also the derivation of the two models is completely different: the construction of the model in [4] is done imposing a priori two phases, the free and the congested one, while in [9] the two phases are obtained as a consequence of the speed limit $V_{\max}$.

3.   Main result

Before stating the main result, we introduce the definition of solution to the initial boundary value problem (1.2).

Definition 3.1. The function

is a solution to (1.2) if

1. the function $(\rho^{*}, \eta^{*})$ is a weak solution to (1.1), for $(t,x) \in (0,+\infty) \times (a,b)$;

2. for a.e. $t>0$, the function $x \mapsto \left(\rho^{*}(t, x), \eta^{*}(t, x)\right)$ has bounded total variation;

3. for a.e. $t>0$, the Riemann problem

admits a self similar solution $\left(\tilde \rho, \tilde \eta\right)$ such that, for a.e. $\tau > 0$,

4. for a.e. $t>0$, the Riemann problem

admits a self similar solution $\left(\tilde \rho, \tilde \eta\right)$ such that, for a.e. $\tau > 0$,

5. $\left(\rho^{*}(0, x), \eta^{*}(0, x)\right) = \left(\rho_0(x), \eta_0(x)\right)$, for a.e. $x \in (a,b)$.

Remark 2. The boundaries treated in this paper are characteristic, since there are phase transition waves with zero speed. Conditions 3 and 4 of Definition 3.1 are exactly the same as the boundary condition in the characteristic case in [1].

We can now state the main result of the paper:

Theorem 3.2. Let assumptions (H-1), (H-2) and (H-3) hold. Fix the initial condition $(\rho_0, \eta_0) \in \mathbf{BV} ((a,b); F \cup C)$ and the boundary data $(\rho_a,\eta_a), (\rho_b,\eta_b) \in \left(\mathbf{BV} \cap \mathbf{L^1}\right) ((0, +\infty); F \cup C)$. Assume that $\rho_0 (x) \geq C$ a.e. $x\in (a,b)$ and $\rho_a(t)\geq C,\rho_b(t)\geq C$ a.e. $t>0$ for some $C>0$. Then there exists $\left(\rho^{*}, \eta^{*}\right)$, a solution to (1.2) in the sense of Definition 3.1.

The proof is contained in the following subsections.

3.1.   Wave-front tracking approximate solution

In this subsection we construct piecewise constant approximations via the wave-front tracking algoritm, which is a set of techniques to obtain approximate solutions to hyperbolic conservation laws in one space dimension. These tools were first introduced by Dafermos [10], see also [5,18] for the general theory. We show that every limit point is indeed a solution of the differential problem. The key estimate for compactness of the approximated solutions is a uniform bound of a functional measuring the strength of waves.

At first, we give the following definition of an $\varepsilon$-approximate wave-front tracking solution to (1.2).

Definition 3.3. Given $\varepsilon > 0$, the map $\bar u_\varepsilon = \left(\bar \rho_{\varepsilon}, \bar \eta_{\varepsilon}\right)$ is an $\varepsilon$-approximate wave-front tracking solution to (1.2) if there exist $\bar u_{a,\varepsilon} = \left(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon}\right)$ and $\bar u_{b,\varepsilon} = \left(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon}\right)$ such that the following conditions hold.

1. $\bar u_{\varepsilon} \in \mathbf{C^0} \left( (0,+\infty);\mathbf{L^1}((a,b);F \cup C)\right) $ and $\bar u_{a,\varepsilon}, \bar u_{b,\varepsilon} \in \mathbf{L^1}\left((0,+\infty); F \cup C \right)$.

2. $\left(\bar\rho_{\varepsilon}, \bar \eta_{\varepsilon}\right)$ is picewise constant, with discontinuities along finitely many straight lines in $(0, +\infty) \times (a,b)$. Moreover the jumps can be of the first family, of the second family, linear waves or phase transition waves.

3. $\bar u_{a,\varepsilon}$ and $\bar u_{b,\varepsilon}$ are piecewise constant with a finite number of discontinuities.

4. It holds that

5. It holds that, for a.e. $t > 0$, the Riemann problem with initial condition

is solved with waves with negative speed.

6. It holds that, for a.e. $t > 0$, the Riemann problem with initial condition

is solved with waves with positive speed.

We consider now three sequences $(\rho_{0,\nu}, \eta_{0,\nu})$, $(\rho_{a,\nu}, \eta_{a,\nu})$ and $(\rho_{b,\nu}, \eta_{b,\nu})$ of piecewise constant functions with a finite number of discontinuities such that the following conditions hold.

1. $(\rho_{0,\nu}, \eta_{0,\nu}):(a,b) \to F \cup C$ and $(\rho_{a,\nu}, \eta_{a,\nu}), (\rho_{b,\nu}, \eta_{b,\nu}):(0,+\infty) \to F \cup C$;

2. the following limits hold

3. the following inequalities hold

Next, for every $\nu \in \mathbb{N} \setminus \{0\}$, we proceed with the following method. At time $t=0$, we solve all the Riemann problems for $x \in (a,b)$ and the boundary Riemann problems at $x = a$ and at $x = b$. At every interaction between two waves, we solve the corresponding Riemann problem and at every discontinuity time for $(\rho_{a,\nu}, q_{a,\nu})$ or for $(\rho_{b,\nu}, q_{b,\nu})$, we solve the corresponding Riemann problem at $x=a$ or $x=b$. Finally, when a wave interacts with the boundary $x=a$ or $x=b$, we solve the corresponding boundary Riemann problem.

Remark 3. We may assume that, at every positive time $t$, at most one of the following possibilities happens:

1. two waves interact together at a point $x \in (a,b)$;

2. a wave interacts with the boundary $x=a$ or with the boundary $x=b$;

3. $t$ is a point of discontinuity either for $(\rho_{a,\nu}, \eta_{a,\nu})$ or for $(\rho_{b,\nu}, \eta_{b,\nu})$.

Given an $\varepsilon$-approximate wave-front tracking solution $\bar u_\varepsilon = \left(\bar \rho_{\varepsilon}, \bar \eta_{\varepsilon}\right)$ with boundary data $\bar u_{a,\varepsilon} = \left(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon}\right)$ and $\bar u_{b,\varepsilon} = \left(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon}\right)$ in the union of the free phase $F$ and the congested phase $C$, define, for a.e. $t > 0$, the following functionals

where, we denote by $\tilde v$ the function $\tilde v(\rho, \eta) =\frac{\eta \psi(\omega)}{\rho}$. Note that the previous functionals may vary only at times at which the boundary datum changes or at times $\bar t$ when two waves interact or a wave reaches the boundary.

The functional $\mathcal F(t)$ is composed by $4$ terms. The first term measures the strength of waves of second family. The second term measures the strength of waves of first family and of phase transition waves. Moreover both of the first two terms measure the strength of linear waves. Finally, the last two terms measure the distance of the boundary term from the trace at the boundary of the approximate solution.

3.2.   Interaction estimates

Next we consider interactions estimates of waves. We describe wave interactions by the nature of the involved waves, see [15,16]. For example, if a wave of the second family hits a wave of the first family producing a phase-transition wave, we write $2-1/\mathcal{PT}$. Here the symbol "/" divides the waves before and after the interaction.

Lemma 3.4. Assume that the wave $((\rho^l, \eta^l), (\rho^m, \eta^m))$ interacts with the wave $((\rho^m, \eta^m), (\rho^r, \eta^r))$ at the point $(\bar t, \bar x)$ with $\bar t > 0$ and $\bar x \in (a,b)$. Then $\mathcal F (\bar t+) \le \mathcal F(\bar t-)$. The possible interactions are: $2-1/1-2$, $\mathcal{LW}-\mathcal{PT}/\mathcal{PT}-2$, $1-1/1$, $\mathcal{PT}-1/\mathcal{PT}$.

Proof. For simplicity, we define

We have four different cases.

1. The case $2-1/1-2$. In this case, a wave $((\rho^l, \eta^l), (\rho^m, \eta^m))$ of the second family interacts with a wave $((\rho^m, \eta^m), (\rho^r, \eta^r))$ of the first family producing a wave $((\rho^l, \eta^l), (\rho^i, \eta^i))$ of the first family and a wave $((\rho^i, \eta^i), (\rho^r, \eta^r))$ of the second family. The only possible case is that all the states $(\rho^l, \eta^l), (\rho^m, \eta^m),(\rho^r, \eta^r)$ and $(\rho^i, \eta^i)$ are in the congested phase $C$, see Figure 2, above, left. For the functional (3.1) we have

Now $w^l=w^i$ since $(\rho^l, \eta^l)$ and $(\rho^i, \eta^i)$ belong to the Lax curve of the first family. Analogously $w^m=w^r$. Thus

Analogously for the functional (3.2), we have that

and since $v^i=v^r$ and $v^l=v^m$, because the states $(\rho^i, \eta^i),(\rho^r, \eta^r)$ and the states $(\rho^l, \eta^l),(\rho^m, \eta^m)$ respectively belong to the same Lax curve of the second family,

Since $\Delta\mathcal F_a (\bar t)=\Delta\mathcal F_b (\bar t)=0$, we have that $\Delta\mathcal F (\bar t)=0$.

2. The case $\mathcal{LW}-\mathcal{PT}/\mathcal{PT}-2$. In this case, a linear wave $((\rho^l, \eta^l), (\rho^m, \eta^m))$ interacts with a phase transition wave $((\rho^m, \eta^m), (\rho^r, \eta^r))$ producing a phase transition wave $((\rho^l, \eta^l), (\rho^i, \eta^i))$ and a wave $( (\rho^i, \eta^i), (\rho^r, \eta^r))$ of the second family. The only possible case is that the states $(\rho^l, \eta^l)$, $(\rho^m, \eta^m)$ are in the free phase $F$ and the states $(\rho^i, \eta^i),(\rho^r, \eta^r)$ are in the congested phase $C$, see Figure 2, above, right. For the functional (3.1) we have

Similarly as before, $w^l=w^i$ and $w^m=w^r$. Thus

For the functional (3.2), we have that

Since $v^i=v^r$, and by the triangular inequality:

Since $\Delta\mathcal F_a (\bar t)=\Delta\mathcal F_b (\bar t)=0$, we have that $\Delta\mathcal F (\bar t)\leq0$.

3. The case $1-1/1$. In this case, a wave $((\rho^l, \eta^l), (\rho^m, \eta^m))$ of the first family interacts with another wave $((\rho^m, \eta^m), (\rho^r, \eta^r))$ of the first family producing again a wave $((\rho^l, \eta^l), (\rho^r, \eta^r))$ of the first family. The only possible case is that all the states $(\rho^l, \eta^l)$, $(\rho^m, \eta^m), (\rho^r, \eta^r)$ are in the congested phase $C$, see Figure 2, below, left. For the functional (3.1) we have

since $w^l = w^m = w^r$. For the functional (3.2), by the triangular inequality we have that

Since $\Delta\mathcal F_a (\bar t)=\Delta\mathcal F_b (\bar t)=0$, we have that $\Delta\mathcal F (\bar t)\leq0$.

4. The case $\mathcal{PT}-1/\mathcal{PT}$. A phase transition wave $((\rho^l, \eta^l), (\rho^m, \eta^m))$ interacts with a wave $((\rho^m, \eta^m), (\rho^r, \eta^r))$ of the first family producing a phase transition wave $((\rho^l, \eta^l), (\rho^r, \eta^r))$. The only possible case is that the state $(\rho^l, \eta^l)$ is in the free phase $F$ and the states $(\rho^m, \eta^m), (\rho^r, \eta^r)$ are in the congested phase $C$, see Figure 2, below, right. For the functional (3.1) we have

since $w^l = w^m = w^r$. For the functional (3.2), by the triangular inequality we have that

Since $\Delta\mathcal F_a (\bar t)=\Delta\mathcal F_b (\bar t)=0$, we have that $\Delta\mathcal F (\bar t)\leq0$.

The proof is thus completed.

Lemma 3.5. Assume that the wave $((\rho^l, q^l), (\rho^r, \eta^r))$ interacts with the boundary at the point $(\bar t, a)$, with $\bar t > 0$. Then $\mathcal F (\bar t+) \le \mathcal F (\bar t-)$. The only possible interaction, producing one wave, is $1/\mathcal{PT}$.

Proof. First note that $\Delta\mathcal F_b (\bar t)=0$, since the interaction happens at $x = a$. Moreover, since the boundary Riemann problem does not generate waves, then the states $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(t)$ and $(\rho^l, \eta^l)$ are connected through waves with negative speed. For simplicity, we use the notations in (3.6), moreover we define

We have the following cases.

1. The case $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(t) = (\rho^l, \eta^l)$.

Since the wave $((\rho^l, \eta^l), (\rho^r, \eta^r))$ has negative speed, then, at time $\bar t$, it is absorbed and no other wave is generated. If $((\rho^l, \eta^l), (\rho^r, \eta^r))$ is a wave of the first family or a phase transition wave with negative speed, anyway we have $\Delta\mathcal F _w (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)= -|v^l-v^r|$ and $\Delta \mathcal F _a (\bar t)=|v^l-v^r|$. Consequentely

2. The case when the states $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(\bar t)$ and $(\rho^l, \eta^l)$ are connected by a wave of the first family.

In this situation both the states $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(\bar t)$ and $(\rho^l, \eta^l)$ are in the congested phase $C$ and so the interacting wave also is of the first family; at time $\bar t$, it is absorbed and no other wave is generated.

Thus we have $\Delta\mathcal F _w (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)= -|v^l-v^r|$ and $\Delta\mathcal F_a(\bar t) = |v^{a,\varepsilon}-v^r|-|v^{a,\varepsilon}-v^l|$. Then, by the triangular inequality

3. The case when the states $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(\bar t)$ and $(\rho^l, \eta^l)$ are connected by a phase-transition wave with negtive speed.

In this situation the state $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(\bar t)$ is in the free phase $F$ and $(\rho^l, \eta^l)$ is in the congested phase $C$ and so the interacting wave is of the first family. The only possible cases are that no wave is produced at time $\bar t$ or a phase transition wave is produced at time $\bar t$.

In the case no wave is produced at time $\bar t$, the situation is analogous to the previous case.

In the case a phase transition wave with positive speed, connecting the states $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(\bar t)$ to $(\rho^r, \eta^r)$, is produced at time $\bar t$, then $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(\bar t)$ is in the free phase $F$ and $(\rho^r, \eta^r)$ is in the congested phase $C$. Thus we have that $\Delta\mathcal F _w (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)=|v^{a,\varepsilon} -v^r|-|v^l-v^r|$ and $\Delta\mathcal F_a(\bar t) = - |v^{a,\varepsilon} -v^l|$. Then

The proof is thus completed.

Lemma 3.6. Assume that the wave $((\rho^l, \eta^l), (\rho^r, \eta^r))$ interacts with the boundary at the point $(\bar t, b)$, with $\bar t >0$. Then $\mathcal F (\bar t+) \le \mathcal F (\bar t-)$. The only possible interaction, producing one wave, is $\mathcal{LW}/\mathcal{PT}$.

Proof. First note that $\Delta\mathcal F_a (\bar t)=0$, since the interaction happens at $x = b$. Moreover, since the boundary Riemann problem does not generate waves, then the states $(\bar \rho_{a,\varepsilon}, \bar \eta_{a,\varepsilon})(t)$ and $(\rho^l, \eta^l)$ are connected through waves with positive speed. For simplicity, we use the notations in (3.6), (3.7). We have the following cases.

1. The case $(\rho^r, \eta^r)=(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(t)$.

Since the wave $((\rho^l, \eta^l), (\rho^r, \eta^r))$ has positive speed, then, at time $\bar t$, it is absorbed and no other wave is generated.

If $((\rho^l, \eta^l), (\rho^r, \eta^r))$ is a wave of the second family, we have $\Delta\mathcal F _{\tilde v} (\bar t) =0$, $\Delta\mathcal F _{w} (\bar t)= -|w^l-w^r|$ and $\Delta \mathcal F _b (\bar t)=|w^l-w^r|$. Consequentely

If $((\rho^l, \eta^l), (\rho^r, \eta^r))$ is a phase transition wave with positive speed, we have $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)= -|v^l-v^r|$ and $\Delta \mathcal F _b (\bar t)=|v^l-v^r|$. Consequentely

2. The case when the states $(\rho^r, \eta^r)$ and $(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(\bar t)$ are connected by a wave of the second family.

In this situation both the states $(\rho^r, \eta^r)$ and $(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(\bar t)$ are in the congested phase $C$ and the interacting wave could be a wave of the second family or a phase transition with positive speed.

If the interacting wave is of the second family, then no wave is generated at time $\bar t$. Thus we have $\Delta\mathcal F _{\tilde v} (\bar t) =0$, $\Delta\mathcal F _{w} (\bar t)= -|w^l-w^r|$ and $\Delta\mathcal F_b(\bar t) = |w^l-w^{b,\varepsilon}|-|w^r-w^{b,\varepsilon}|$. Then,

If the interacting wave is a phase transition wave with positive speed, then no wave is generated at time $\bar t$. Thus we have $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)= -|v^l-v^r|$ and $\Delta\mathcal F_b(\bar t) =|v^l-v^r|+ |w^r-w^{b,\varepsilon}|-|w^r-w^{b,\varepsilon}|$. Then,

3. The case when the states $(\rho^r, \eta^r)$ and $(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(\bar t)$ are connected by a phase transition wave with positive speed.

In this situation the state $(\rho^r, \eta^r)$ is in the free phase $F$ and the state $(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(\bar t)$ is in the congested phase $C$ and so, the interacting wave is a linear wave.

In this case a phase transition wave with negative speed between the states $(\rho^l, \eta^l)$ and $(\bar \rho_{b,\varepsilon'}, \bar \eta_{b,\varepsilon'})(\bar t)$, possibly followed by a wave of the second family between the states $(\bar \rho_{b,\varepsilon'}, \bar \eta_{b,\varepsilon'})(\bar t)$ and $(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(\bar t)$, are generated at time $\bar t$. Following the usual notations, define $v^{a,\varepsilon'}=\tilde v\left(\bar u_{a,\varepsilon'}(t)\right)$ and $w^{a,\varepsilon'}=w \left(\bar u_{a,\varepsilon'}(t)\right)$. Then $\Delta\mathcal F _{w} (\bar t) =-|w^l-w^r|$, $\Delta\mathcal F _{\tilde v} (\bar t)= |v^l-v^{b,\varepsilon'}|-|v^l-v^r|$ and $\Delta\mathcal F_b(\bar t) = |w^{b,\varepsilon}-w^{b,\varepsilon'}|-|v^{b,\varepsilon}-v^r|$. Since $w^l=w^{b,\varepsilon'}$, $w^r=w^{b,\varepsilon}$ and $v^{b,\varepsilon'}=v^{b,\varepsilon}$, we have

4. The case when the states $(\rho^r, \eta^r)$ and $(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(\bar t)$ are connected by a linear wave.

In this situation both the states $(\rho^r, \eta^r)$ and $(\bar \rho_{b,\varepsilon}, \bar \eta_{b,\varepsilon})(\bar t)$ are in the free phase $F$ and so, the interacting wave is also a linear wave.

In this case no wave is generated at time $\bar t$, then $\Delta\mathcal F _{w} (\bar t) =-|w^l-w^r|$, $\Delta\mathcal F _{\tilde v} (\bar t)= -|v^l-v^r|$ and $\Delta\mathcal F_b(\bar t) =|v^l-v^{b,\varepsilon}|+|w^l-w^{b,\varepsilon}| -|v^r-v^{b,\varepsilon}|-|w^r-w^{b,\varepsilon}|$. Then, by applying twice the triangular inequality,

The proof is thus completed.

Lemma 3.7. Assume that $\bar t$ is a point of discontinuity for the boundary datum at $x=a$. Then,

Proof. In general, at time $\bar t$, a wave with positive speed emerges from the boundary $x=a$. We denote with $u^r =\left(\rho^{r}, \eta^{r}\right)$ the trace of the approximate solution before time $\bar t$ at $x=a+$ and we solve the Riemann problem at time $\bar t$ between the states $\bar u_{a,\varepsilon}(t+)$ and $u^r$. For simplicity, we define

where $u^m =\left(\rho^{m}, \eta^{m}\right)$ is a middle state in the solution of the Riemann problem between the states $\bar u_{a,\varepsilon}(t+)$ and $u^r$. We have the following cases.

1. The states $\bar u_{a,\varepsilon}(t+)$ and $\bar u_{a,\varepsilon}(t-)$ are both in the congested phase $C$.

If $u^r$ belongs to the curve of the first family passing through $\bar u_{a,\varepsilon}(t-)$, then the Riemann problem produces a wave of the first family between $\bar u_{a,\varepsilon}(t+)$ and $u^m$ and a wave of the second family between $u^m$ and $u^r$. Consequentely $\Delta\mathcal F _{w} (\bar t) =|w^m-w^r|$, $\Delta\mathcal F _{\tilde v} (\bar t)= 0$ and $\Delta\mathcal F_a(\bar t) =|v^+ - v^m|-|v^- - v^r|$. Then, since $w^m=w^+, w^r=w^-, v^r=v^m$ and by the triangular inequality,

If $u^r=\bar u_{a,\varepsilon}(t-)$, then the Riemann problem between $\bar u_{a,\varepsilon}(t+)$ and $\bar u_{a,\varepsilon}(t-)$ produces a wave of the first family between $\bar u_{a,\varepsilon}(t+)$ and $u^m$ and a wave of the second family between $u^m$ and $\bar u_{a,\varepsilon}(t-)$. Consequentely $\Delta\mathcal F _{w} (\bar t) =|w^m-w^-|$, $\Delta\mathcal F _{\tilde v} (\bar t)= 0$ and $\Delta\mathcal F_a(\bar t) =|v^+ - v^m|$. Then, since $w^m=w^+, v^m=v^+$,

2. The states $\bar u_{a,\varepsilon}(t+)$ and $\bar u_{a,\varepsilon}(t-)$ are both in the free phase $F$.

If $u^r$ belongs to the phase transition passing through $\bar u_{a,\varepsilon}(t-)$, then $u^r$ is in the congested phase $C$. The Riemann problem produces a phase transition, with positive or negative speed, between $\bar u_{a,\varepsilon}(t+)$ and $u^m$ (which is in $C$) and a wave of the second family between $u^m$ and $u^r$. Thus $\Delta\mathcal F _{w} (\bar t) =|w^m-w^r|$ and $\Delta\mathcal F _{\tilde v} (\bar t)+\Delta\mathcal F_a(\bar t) =|v^+ - v^m|-|v^- - v^r|$. Then, since $w^m=w^+, w^r=w^-, v^r=v^m$ and by the triangular inequality,

If $u^r=\bar u_{a,\varepsilon}(t-)$, then the Riemann problem between $\bar u_{a,\varepsilon}(t+)$ and $\bar u_{a,\varepsilon}(t-)$ produces a linear wave between $\bar u_{a,\varepsilon}(t+)$ and $\bar u_{a,\varepsilon}(t-)$. Thus $\Delta\mathcal F _{w} (\bar t) =|w^+-w^-|$, $\Delta\mathcal F _{\tilde v} (\bar t) =|v^+ - v^-|$ and $\Delta\mathcal F_a(\bar t) =0$. Then,

3. The state $\left(\bar u_{a,\varepsilon}\right)(t-)$ is in the free phase $F$ and the state $\left(\bar u_{a,\varepsilon}\right)(t+)$ is in the congested phase $C$.

If $u^r$ belongs to the phase transition passing through $\bar u_{a,\varepsilon}(t-)$, then $u^r$ is in the congested phase $C$. The Riemann problem produces a wave of the first family between $\bar u_{a,\varepsilon}(t+)$ and $u^m$ and a wave of the second family between $u^m$ and $u^r$. Thus $\Delta\mathcal F _{w} (\bar t) =|w^m-w^r|$, $\Delta\mathcal F_v(\bar t) =0$ and $\Delta\mathcal F_a(\bar t) =|v^+ - v^m|-|v^- - v^r|$. Then, since $w^m=w^+, w^r=w^-, v^r=v^m$,

If $u^r=\bar u_{a,\varepsilon}(t-)$, then the Riemann problem between $\bar u_{a,\varepsilon}(t+)$ and $\bar u_{a,\varepsilon}(t-)$ produces a wave of the first family between $\bar u_{a,\varepsilon}(t+)$ and $u^m$ (which is in $F \cap C$) and a linear wave between $u^m$ and $\bar u_{a,\varepsilon}(t-)$. Thus $\Delta\mathcal F _{w} (\bar t) =|w^m-w^-|$, $\Delta\mathcal F _{\tilde v} (\bar t) =|v^m - v^-|$ and $\Delta\mathcal F_a(\bar t) =|v^+ - v^m|$. Then, since $w^m=w^+$ and by the triangualar inequality,

4. The state $\left(\bar u_{a,\varepsilon}\right)(t-)$ is in the congested phase $C$ and the state $\left(\bar u_{a,\varepsilon}\right)(t+)$ is in the free phase $F$.

If $u^r$ belongs to the curve of the first family passing through $\bar u_{a,\varepsilon}(t-)$, then the Riemann problem produces a phase transition, with positive or negative speed, between $\bar u_{a,\varepsilon}(t+)$ and $u^m$ (which is in $C$) and a wave of the second family between $u^m$ and $u^r$. Thus $\Delta\mathcal F _{w} (\bar t) =|w^m-w^r|$ and $\Delta\mathcal F _{\tilde v} (\bar t)+\Delta\mathcal F_a(\bar t) =|v^+ - v^m|-|v^- - v^r|$. Then, as before,

If $u^r=\bar u_{a,\varepsilon}(t-)$, then the Riemann problem between $\bar u_{a,\varepsilon}(t+)$ and $\bar u_{a,\varepsilon}(t-)$ produces a phase transition between $\bar u_{a,\varepsilon}(t+)$ and $u^m$ and a wave of the second family between $u^m$ and $\bar u_{a,\varepsilon}(t-)$. Thus $\Delta\mathcal F _{w} (\bar t) =|w^m-w^-|$, $\Delta\mathcal F _{\tilde v} (\bar t)+ \Delta\mathcal F_a(\bar t)=|v^+ - v^m|$. Then, since $w^m=w^+$ and $v^m=v^+$,

The proof is so concluded.

Lemma 3.8. Assume that $\bar t$ is a point of discontinuity for the boundary datum at $x=b$. Then,

Proof. In general, at time $\bar t$, a wave with negative speed emerges from the boundary $x=b$. We denote with $u^l=(\rho^{l}, \eta^{l})$ the trace of the approximate solution before time $\bar t$ at $x=b-$ and we solve the Riemann problem at time $\bar t$ between the states $u^l$ and $\bar u_{b,\varepsilon}(t+)$. For simplicity, we define

where $u^m=(\rho^{m}, \eta^{m})$ is a middle state in the solution of the Riemann problem between the states $u^l$ and $\bar u_{b,\varepsilon}(t+)$. We have the following cases.

1. The states $\bar u_{b,\varepsilon}(t+)$ and $\bar u_{b,\varepsilon}(t-)$ are both in the congested phase $C$.

If $u^l$ belongs to the curve of the second family passing through $\bar u_{b,\varepsilon}(t-)$, then we have a wave of the first family between $u^l$ and $u^m$ and a wave of the second family between $u^m$ and $\bar u_{b,\varepsilon}(t+)$. Consequentely $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)= |v^l - v^m|$ and $\Delta\mathcal F_b(\bar t) =|w^m - w^+|-|w^l - w^-|$. Then, since $w^l=w^m, v^l=v^-, v^m=v^+$ and by the triangular inequality,

If $u^l$ belongs to the phase transition passing through $\bar u_{b,\varepsilon}(t-)$, then $u^l$ is in the free phase $F$. We have a phase transition between $u^l$ and $u^m$ and a wave of the second family between $u^m$ and $\bar u_{b,\varepsilon}(t+)$. Consequentely $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t) + \Delta\mathcal F_b(\bar t) = $$ |v^l - v^m|+|w^m - w^+|-|v^l - v^-| $. Then, since $w^m=w^-$ and $v^m=v^+$,

If $u^l=\bar u_{b,\varepsilon}(t-)$, the Riemann problem between $\bar u_{b,\varepsilon}(t-)$ and $\bar u_{b,\varepsilon}(t+)$ produces a wave of the first family between $\bar u_{b,\varepsilon}(t-)$ and $u^m$ and a wave of the second family between $u^m$ and $\bar u_{b,\varepsilon}(t+)$. Consequentely $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)= |v^- - v^m|$ and $\Delta\mathcal F_b(\bar t) =|w^m - w^+|$. Then, since $w^m=w^-$ and $v^m=v^+$,

2. The states $\bar u_{b,\varepsilon}(t+)$ and $\bar u_{b,\varepsilon}(t-)$ are both in the free phase $F$.

If $u^l$ belongs to the phase transition passing through $\bar u_{b,\varepsilon}(t-)$, then $u^l$ is in the congested phase $C$. The Riemann problem produces a wave of the first family between $u^l$ and $u^m$ (which is in $F \cap C$) and a linear wave between $u^m$ and $\bar u_{b,\varepsilon}(t+)$. Thus $\Delta\mathcal F _{w} (\bar t) =0$ and $\Delta\mathcal F _{\tilde v} (\bar t)=|v^l - v^m|$ and $\Delta\mathcal F_b(\bar t) =|v^m - v^+|+|w^m- w^+|-|v^l - v^-|$. Then, since $v^m=v^-$ and $w^m=w^-$,

If $u^l$ belongs to the linear wave passing through $\bar u_{b,\varepsilon}(t-)$, then the Riemann problem produces a linear wave between $u^l$ and $\bar u_{b,\varepsilon}(t+)$. Thus $\Delta\mathcal F _{w} (\bar t) =0$ and $\Delta\mathcal F _{\tilde v} (\bar t)=0$ and $\Delta\mathcal F_b(\bar t) =|v^l - v^+|+|w^l- w^+|-|v^l - v^-|-|w^l - w^-|$. Then,

If $u^l=\bar u_{b,\varepsilon}(t-)$, then the Riemann problem between $\bar u_{b,\varepsilon}(t-)$ and $\bar u_{b,\varepsilon}(t+)$ produces a linear wave between $\bar u_{b,\varepsilon}(t+)$ and $\bar u_{b,\varepsilon}(t-)$. Thus $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t) =0$ and $\Delta\mathcal F_b(\bar t) =|w^+-w^-|+|v^+ - v^-|$. Then,

3. The state $\left(\bar u_{b,\varepsilon}\right)(t-)$ is in the free phase $F$ and the state $\left(\bar u_{b,\varepsilon}\right)(t+)$ is in the congested phase $C$.

If $u^l$ belongs to the phase transition passing through $\bar u_{b,\varepsilon}(t-)$, then $u^l$ is in the congested phase $C$. The Riemann problem produces a wave of the first family between $u^l$ and $u^m$ and a wave of the second family between $u^m$ and $\left(\bar u_{b,\varepsilon}\right)(t+)$. Thus $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F_v(\bar t) =|v^l - v^m|$ and $\Delta\mathcal F_b(\bar t) =|w^m - w^+|-|v^l - v^-|$. Then, since $w^m=w^-$ and $v^m=v^+$,

If $u^l$ belongs to the linear wave passing through $\bar u_{b,\varepsilon}(t-)$, then the Riemann problem produces a phase transition between $u^l$ and $u^m$ and a wave of the second family between $u^m$ and $\left(\bar u_{b,\varepsilon}\right)(t+)$. Thus $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F_v(\bar t)+ \Delta\mathcal F_b(\bar t) = |v^l - v^m|+$$|w^m - w^+|-|v^l - v^-|-|w^l - w^-| $. Then, since $w^m=w^l$ and $v^m=v^+$,

If $u^l=\bar u_{b,\varepsilon}(t-)$, the Riemann problem between $\bar u_{b,\varepsilon}(t-)$ and $\bar u_{b,\varepsilon}(t+)$ produces a phase transition between $\bar u_{b,\varepsilon}(t-)$ and $u^m$ and wave of the second family between $u^m$ and $\bar u_{b,\varepsilon}(t+)$. Thus $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t) + \Delta\mathcal F_b(\bar t) = |v^m - v^-|+|w^+ - w^m|$. Then, since $w^m=w^+$ and $v^m=v^+$,

4. The state $\left(\bar u_{b,\varepsilon}\right)(t-)$ is in the congested phase $C$ and the state $\left(\bar u_{b,\varepsilon}\right)(t+)$ is in the free phase $F$.

If $u^l$ belongs to the curve of the second family passing through $\bar u_{b,\varepsilon}(t-)$, then the Riemann problem produces a wave of the first family between $u^l$ and $u^m$ (which is in $F \cap C$) and a linear wave between $u^m$ and $\left(\bar u_{b,\varepsilon}\right)(t+)$. Consequentely $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)= |v^l - v^m|$ and $\Delta\mathcal F_b(\bar t) =|v^m - v^+|+|w^m-w^+|-|w^l - w^-|$. Then, since $w^l=w^m$ and $v^l=v^-$,

If $u^l$ belongs to the phase transition passing through $\bar u_{b,\varepsilon}(t-)$, then $u^l$ is in the free phase $F$. The Riemann problem produces a linear wave between $u^l$ and $\left(\bar u_{b,\varepsilon}\right)(t+)$. Consequentely $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)=0$ and $\Delta\mathcal F_b(\bar t) =|v^l - v^+|+$$|w^l-w^+|-|v^l - v^-| $. Then, since $w^l=w^-$,

If $u^l=\bar u_{b,\varepsilon}(t-)$, the Riemann problem between $\bar u_{b,\varepsilon}(t-)$ and $\bar u_{b,\varepsilon}(t+)$ produces a wave of the first family between $\bar u_{b,\varepsilon}(t-)$ and $u^m$ and a linear wave between $u^m$ and $\bar u_{a,\varepsilon}(t+)$. Thus $\Delta\mathcal F _{w} (\bar t) =0$, $\Delta\mathcal F _{\tilde v} (\bar t)=|v^- - v^m|$ and $\Delta\mathcal F_b(\bar t) =|w^m-w^+|+ |v^m - v^+|$. Then, since $w^m=w^-$,

The proof is so concluded.

Proposition 1. The following estimate holds

where $M=\mathcal F (0)+ {\rm{TV}} (\rho_{a},\eta_{a})+ {\rm{TV}} (\rho_{b},\eta_{b})$.

Proof. This is a consequence of the previous Lemmas 3.4, 3.5, 3.6, 3.7, and 3.8.

3.3.   Existence of solutions

Next we aim to bound the number of waves and of interactions. The following result holds.

Proposition 2. The construction in Subsection 3.1 can be done for every positive time and, for every $\nu \in \mathbb{N} \setminus \{0\}$, it produces a $\frac{1}{\nu}$-approximate wave-front tracking solution to (1.2).

Proof. We consider the construction in Subsection 3.1 and the function $u_\nu =\left(\rho_{\nu}, \eta_{\nu}\right)$ there built, for $\nu \in \mathbb{N} \setminus \{0\}$. It is sufficient to prove that the number of waves and interactions generated is finite. We define the functional $N_{\nu}(t)$, which counts the number of discontinuities of $(\rho_{\nu}, \eta_{\nu})$. Note that the functional $N_{\nu}(t)$ is piecewise constant and can vary at interaction times in the following way.

1. If at time $\bar t > 0$ two waves interact at $\bar x \in (a,b)$, then $\Delta N_{\nu}(\bar t) \le 0$. More precisely, $\Delta N_{\nu}(\bar t) = 0$ if and only if the interaction is either $2-1/1-2$ or $\mathcal{LW}-\mathcal{PT}/\mathcal{PT}-2$; see Lemma 3.4.

2. If at time $\bar t > 0$ a wave interacts with the boundary at $x=a$, then $\Delta N_{\nu}(\bar t) \le 0$. In the case $\Delta N_{\nu}(\bar t) = 0$ the interaction is $1/\mathcal{PT}$; see Lemma 3.5.

3. If at time $\bar t > 0$ a wave interacts with the boundary at $x=b$, then $\Delta N_{\nu}(\bar t) \le 0$. In the case $\Delta N_{\nu}(\bar t) = 0$ the interaction is $\mathcal{LW}/\mathcal{PT}$; see Lemma 3.6.

4. If the time $\bar t > 0$ is a point of discontinuity for the boundary value $\left(\rho_{a, \nu}, \eta_{a, \nu}\right)$, then $\Delta N_{\nu}(\bar t) \le 2$; see Lemma 3.7.

5. If the time $\bar t > 0$ is a point of discontinuity for the boundary value $\left(\rho_{b, \nu}, \eta_{b, \nu}\right)$, then $\Delta N_{\nu}(\bar t) \le 2$; see Lemma 3.8.

The number of waves can increase only in the cases 4., and 5. By construction, theese cases happen at most a finite number of times.

The interactions inside the domain $(a,b)$, $1-1/1$ and $\mathcal{PT}-1/\mathcal{PT}$, can happen at most a finite number of times, since we have a uniform bound on the number of waves.

To prove that the number of interactions is finite, we have to consider and to bound the number of interactions of the following types:

1. Inside the domain: $2-1/1-2$ and $\mathcal{LW}-\mathcal{PT}/\mathcal{PT}-2$.

2. Left boundary: $1/\mathcal{PT}$.

3. Right boundary: $\mathcal{LW}/\mathcal{PT}$.

Consider first the interaction $\mathcal{LW}/\mathcal{PT}$ that can happen a finite number of times, since the interacting wave is a linear wave and it is not generated in any other interaction. Then, we consider the interactions $2-1/1-2$ and $1/\mathcal{PT}$. The combination of theese interactions can not happen an infinite number of times. Indeed $2-1/1-2$ can not happen an infinite number of times since one of the interacting waves, the wave of the first family, is not generated in any other interaction; consequentely also $1/\mathcal{PT}$ can happen a finite number of times. Finally, it remains to consider only the interaction $\mathcal{LW}-\mathcal{PT}/\mathcal{PT}-2$, that can happen a finite number of times, since no other interaction produces a linear wave. The proof is so concluded.

We can next conclude the proof of the Theorem 3.2.

Proof of Theorem 3.2. Fix an $\varepsilon$-approximate wave-front tracking solution $\bar u_\varepsilon$ to (1.2), in the sense of Definition 3.3. By Proposition 1, we deduce that there exists a constant $M>0$, depending on the total variation of the flux of the initial datum, such that, for a.e. $t > 0$,

The above inequality states that the functional ${\rm{TV}} \left((\bar \rho_{\varepsilon}, \bar \eta_{\varepsilon}) (t, \cdot)\right)$ is uniformly bounded for a.e. $t>0$. Hence, up to a subsequence, it converges to a function $(\bar \rho, \bar \eta)$, which is a solution to (1.2) in the sense of Definition 3.1. The proof is so concluded.

Acknowledgments

The author thanks Mauro Garavello for useful discussions. The author was partial supported by the INdAM-GNAMPA 2016 project "Balance Laws: Theory and Applications".