Thyroid nodule segmentation in ultrasound images using U-Net with ResNet encoder: achieving state-of-the-art performance on all public datasets

1.   Introduction

Ultrasound (US) imaging, typically ranging from 7.5 to 15 MHz, holds significant importance in the evaluation of thyroid nodules. The superficial nature of the thyroid gland makes it highly amenable to US imaging, thus providing us with detailed and clear images with very good spatial resolution. US imaging assumes a critical role in evaluating the malignity risk of nodules in the thyroid gland, monitoring their progression, and serving as a control imaging modality for nodule biopsies.

Thyroid nodules are abnormal growths in the thyroid gland. Most thyroid nodules are benign, though some of thyroid nodules may be cancerous, thus necessitating further evaluation and treatment. Thyroid cancer has seen a significant increase in diagnosis rates worldwide, ranking seventh among the most common cancers in women and fifteenth in men [1],[2]. Due to this growing incidence, there is a need for effective diagnostic tools, and B-mode ultrasound imaging has emerged as the first choice. Thyroid nodules can be categorized as solid, cystic, or a combination of both solid and cystic components. Epidemiological studies indicate that palpable thyroid nodules are present in approximately 5% in women and 1% in men [3]. However, when ultrasound examinations are conducted, the incidental detection rate of thyroid nodules significantly increases to a range of 19% to 67% [4],[5].

There has been significant research focused on evaluating and ranking the ultrasound risk features used by endocrinologists to predict the malignant potential of thyroid nodules. Several studies have investigated these risk features, and two meta-analyses were conducted by Remonti et al. [6] and Brito et al. [7] synthesized the findings from a large number of studies. Remonti et al. included over 12,500 nodules from 54 studies in their meta-analysis, while Brito et al. analyzed a total of 18,288 nodules. The results from these meta-analyses indicate that certain US features are associated with an increased risk of malignancy. These features include calcifications, a taller-than-wide shape, irregular margins, absence of elasticity, hypoechogenicity (reduced echogenicity), increased blood flow, absence of a halo, and/or larger nodule size. The research conducted on thyroid nodules and their sonographic features have contributed to the development of the Thyroid Imaging, Reporting, and Data System (TI-RADS) by the American College of Radiology [8].

In addition to research focused on the visual inspection of ultrasound images by endocrinologists, computer-aided diagnosis (CAD) systems have emerged to assist in diagnosing thyroid lesions and reducing unnecessary biopsies. These CAD systems [9]–[14] utilize US images to facilitate the accurate and efficient classification of benign and malignant thyroid nodules. Typically, CAD systems for thyroid nodules consist of two main components: segmentation and classification. The segmentation part of the system is responsible for accurately identifying and delineating the boundaries of the nodule within the ultrasound image of the thyroid gland. Once the nodule is successfully segmented, the classification component analyzes the extracted features and provides an estimation of the nodule's malignant potential. The segmentation process plays a crucial role in CAD systems as it enables the system to specifically focus on the nodule region of interest. This step helps in excluding irrelevant structures and background noise from the analysis, thus allowing for more accurate classifications. By accurately delineating the nodule boundaries, the CAD system can concentrate on the specific characteristics and features of the nodule that are indicative of its malignancy.

Although conventional ultrasound provides valuable insights into thyroid nodules, it remains a two-dimensional (2D) imaging modality, which presents limitations in tracking nodule changes over time. Three-dimensional (3D) US imaging has the potential to improve the diagnostic accuracy by offering volumetric information, thus allowing clinicians to more effectively assess nodule growth, changes in structure, and spatial relationships. Tracking nodule volumes over time is essential in clinical decision-making, as volume changes may indicate malignant transformations or nodule regression. Future advancements in segmentation models should explore their applicability in 3D US imaging to enhance the longitudinal assessment and ensure a robust diagnostic performance.

1.1.   Segmentation

Before the emergence of deep learning, US image segmentation for thyroid nodules primarily relied on conventional image processing techniques. These techniques can be broadly categorized into three groups: contour and shape-based methods, region-based methods, and traditional machine learning methods. While these conventional techniques made valuable contributions to thyroid nodule segmentation, deep learning-based approaches has revolutionized thyroid nodule segmentation in US images, thus offering improved accuracy on larger datasets by automatically learning features directly from the data. In the review paper authored by Chen et al. [15], these conventional image processing techniques were extensively examined. However, in our current discussion, we will solely focus on deep learning, as the method proposed in our paper specifically pertains to this approach.

1.2.   Deep learning methods in segmentation of thyroid nodules

Deep neural networks, particularly convolutional neural networks (CNNs), have demonstrated remarkable performances in various computer vision tasks including segmentation. Several studies reported using them on the segmentation of thyroid nodules with very promising results. The following overview reports results of image segmentation methods, whether employed individually or as a part of the entire CAD system. Unfortunately, direct comparisons are challenging since, in the majority of cases, the authors employed private datasets. An exception to this trend is the study conducted by Gong et al. [16] and few others [17]–[19]. We explicitly mention when the authors utilized a public dataset, such as the Thyroid Digital Image Database (TDID) [20].

Ma et al. [21] developed a CNN model with 15 convolutional layers and 2 max pooling layers. The input image size of CNN model was 353 × 353 and the output image size was 44 × 44. Using a dataset of 22,123 US images, the model achieved a mean overlap value of 86.83% on a test set. Another approach, proposed by Ying et al. [22], employed a cascaded convolutional neural network (CCNN). The CCNN consisted of three phases: using a U-Net-based [23] and VGG- based [24] model to extract regions of interest (ROIs) containing thyroid nodules, followed by artificial marks and a fully CNN for segmentation. With 1,000 ultrasound images (800 in training set and 200 the testing), the CCNN achieved a mean overlap value of 87.00% on a test set. Kumar et al. [25] proposed an approach based on dilated convolutional layers that accurately segmented thyroid nodules, cystic components, and normal thyroid gland from ultrasound scans. The algorithm achieved a mean Dice coefficient of 0.76 and demonstrated high detection rates for thyroid nodules and cystic components. Pan et al. [17] proposed a thyroid nodule segmentation approach called SGUNet, that utilized a pixel-wise semantic map to guide low-level features, thus resulting in improved nodule representation. The evaluation on the Thyroid Digital Image Database (TDID) demonstrated SGUNet's superiority over traditional UNet and UNet++ with a 72.9% Dice coefficient. Sun et al. [26] proposed a dual-path CNN with soft shape supervision for the accurate segmentation of thyroid nodules on US images. The network achieved a high accuracy of 95.81% and a Dice coefficient of 85.33%. Song et al. [27] proposed FDnet, a feature-enhanced dual-branch network. By incorporating a semantic segmentation branch and a feature enhancement mechanism, FDnet improved the proposal scores and reduced the false positives segmentation. The Boundary Attention Transformer Network (BTNet), introduced by Li et al. [18], integrated a segmentation network with a boundary attention mechanism, thus combining the advantages of a convolutional neural network and transformer. The results were an IoU of 0.81 and a Dice score of 0.89 on a private dataset and an IoU 65.4 and a Dice score 75.7 on a TDID dataset. Ataide et al. [28] compared UNet, SUMNET, Attention UNet, and a combination of ResNet and UNet. They found that the combination of ResNet and UNet had the highest Dice score on the private dataset. Gong et al. [16] published TRFE+, a network that utilized the thyroid region prior guided attention for accurate thyroid nodule segmentation in US images with an IoU of 0.71 and a Dice score of 0.83.

1.3.   Motivation

The last-mentioned noteworthy paper presented a comprehensive comparison of various architectures, although it overlooked a particularly robust one—the combination of ResNet and UNet. This combined architecture (ResUNet) has established itself as one of the leading state-of-the-art approaches for US image segmentation. Additionally, the authors introduced TN3K, an open-access dataset consisting of high-quality nodule masks, which was strictly divided into the train and test sets. Therefore, it can be used for the direct comparison of segmentation models. Our research aims to implement ResUNet and evaluate its performance in comparison to the results reported by Gong et al. This combination of ResNet and UNet shows the promising results in different segmentation tasks in biomedical area [29]–[34]. It is important to note the inherent distinctions between US images and images from other biomedical imaging modalities, such as computed tomography (CT) or magnetic resonance (MR) scans. Unlike the latter methods, US image formation relies on different physical quantities, specifically the acoustic impedance of tissues and its differences on tissue boundaries. The process of image formation introduces challenges, as certain boundaries may not be visible (those parallel to the ultrasound waves), or that US creates so called shadows, which are artefacts that can be caused by a strong reflection from a boundary. Additionally, there may be a diffraction of ultrasound waves on boundaries which introduce a significant noise in the US images. Moreover, there are limitations in terms of brightness and contrast in comparison to CT, which uses Hounsfield units to code the overall brightness scale that can be viewed by separate windowed images. Therefore, we assert that optimizing the segmentation of US images needs a more generalized methodology to effectively address the aforementioned challenges. In the context of US image segmentation, the utilization of the ResNet and UNet combination is an area that has yet to be extensively explored. Nevertheless, existing literature suggests that it holds promise as one of the top-performing options. In several studies [28],[35],[36], it has been found that the combination of ResNet and UNet is the most effective for segmentation in US images. The initial study that compared architectures on US images was conducted by Cai et al. [35]. In this study, the authors assessed the combination of ResNet and UNet, thereby incorporating an attention layer after the ResNet encoder. They conclude that this architecture is more precise than TransUnet [37], which utilizes transformers to encode tokenized image patches from a feature map as the input sequence to extract the global contexts in the neural network. The second paper, authored by Song et al. [36], compared architectures for the segmentation of US images of the kidney. The study concluded that the combination of ResNet and UNet achieved the second-best dice score, following DeepLabV3+ (which also incorporates the ResNet backbone). The third paper [28] corresponds to the previously mentioned study, where various architectures were used on a private dataset of the thyroid gland. The authors' results indicated that ResUNet achieved the highest Dice score.

2.   Materials and methods

2.1.   Architecture

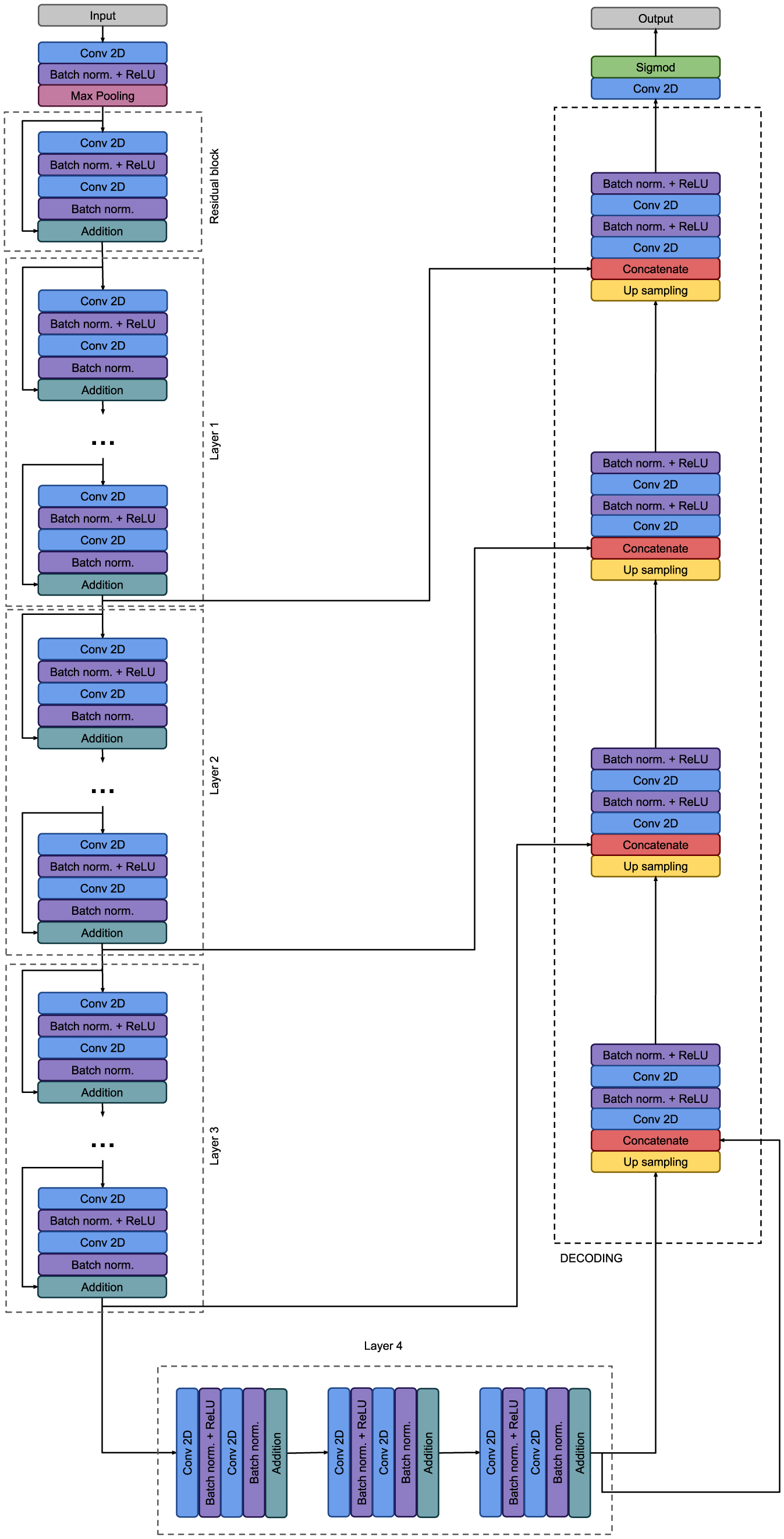
The architecture of our model combines UNet with a ResNet34 used as an encoder. This integrated design, referred to as ResUNet, represents a synthesis of ResNet and UNet, strategically devised to leverage the advantages of both architectures. In this design, the traditional UNet's encoder, composed of convolutional layers and max-pooling, is replaced by ResNet34, which uses a series of residual blocks. Each residual block contains two 3×3 convolutions with batch normalization and ReLU, and also adds the block's input to its output via a shortcut connection. This mechanism not only facilitates the training of deeper networks by improving the gradient flow, but also constrains the learned modifications to be minor, thus preserving critical information. Following the encoding phase, the decoder mirrors the UNet structure. It upsamples the feature maps using 2 × 2 convolutions and employs skip connections to concatenate the corresponding encoder features. This blend of high-level contextual information with fine-grained spatial details allows for precise localization, culminating in a segmentation head that applies a final convolution and sigmoid activation to produce the output map. The use of residual connections in the encoder mitigates vanishing gradients and allows for deeper, more robust network designs. Skip connections from the encoder to the decoder facilitate the combination of contextual and detailed spatial features, which can potentially enhance the segmentation accuracy. By combining ResNet's powerful feature extraction with UNet's efficient localization strategy, ResUNet offers a compelling balance that is well-suited for complex segmentation tasks.

However, ResUNet has some limitations, particularly in terms of data sensitivity and hyperparameter sensitivity. The deeper architecture and increased parameter count can lead to overfitting if the model is not trained on sufficiently large and diverse datasets, thus making effective data augmentation and hyperparameter optimization crucial to ensure that ResUNet reaches its full potential in image segmentation tasks. The architecture of our ResUNet is show in the Figure 1.

2.2.   Dataset

As far as we know, all publicly available datasets of images of thyroid nodules are used in this study. They are three in total: the TN3K dataset, the Thyroid Digital image Database (TDID) dataset, and the Thyroid Ultrasound Cine-clip dataset.

2.2.1.   TN3K dataset

This dataset¹ was published by Gong et al. [16] and is divided into a training set and a test set based on the criterion that images from the same patient only appear in one specific subset. The training set consists of 2,879 images, while the test set contains 614 images. We adhered to this data partitioning and utilized the TN3K test set to evaluate the performance of our models. This enabled us to make direct comparisons between our results and those published by Gong et al.

2.2.2.   Thyroid Digital Image Database (TDID) dataset

This dataset² was published by Pedraza et al. [20] and it was used in several studies for segmentation [17]–[19] and classification [38],[39]. This dataset is comprised of images along with corresponding XML files containing coordinates. However, during the conversion process from coordinates to binary masks, we encountered several issues. Specifically, not all the coordinates were present in the XML files, and some problems arose with the masks themselves (e.g., some of them are outside of ultrasound image area). As a result, it was necessary to either adjust the coordinates of certain masks or remove certain images entirely. A comprehensive list of deleted or modified images is provided in Appendix A.

2.2.3.   Thyroid Ultrasound Cine-clip dataset

This dataset³ is comprised of 167 patients who have been biopsy-confirmed to have thyroid nodules (n = 192) at Stanford. The dataset includes US cine-clip images, segmentations annotated by radiologists, patient demographics, lesion size and location, TI-RADS descriptors, and histopathological diagnoses. The total number of cine-clip frames is 17,412. The dataset is comprised of thyroid nodule cine-clip sequences with frame counts ranging from a minimum of 11 frames to a maximum of 442 frames per nodule. The dataset distribution is shown in Figure 2. Given that the dataset is comprised of multiple images (frames) per thyroid nodule, our objective is to investigate how the evaluation metrics are influenced by the number of frames (images) assigned to each thyroid nodule. Since the number of frames is not constant for each nodule, we employed the following sampling strategy. When extracting n frames from the dataset, we address nodules with frame numbers below n by incorporating all available frames. Conversely, for nodules with occurrences in the dataset where the frame counts exceed n, we opt for a random selection of n frames corresponding to the specific nodule.

Image examples from the 3 datasets and the corresponding ground truth masks are shown in Figure 3.

2.3.   Data augmentation

Data augmentation is employed in image segmentation to increase the diversity and quantity of the training data. By applying transformations such as resizing, flipping, rotation, and contrast adjustments to the original images, the augmented dataset provides the model with more varied samples to learn from. This process helps improve the segmentation model's robustness, generalization ability, and performance on unseen data. We implement augmentations using Albumentations library [40] on each image and its mask in the training data (after division to training and validation set), including random adjustments of brightness and contrast (up to 35%, with probability of 50%), shifts, scales, and rotations (limited by 35%, 35%, and 35 degrees, respectively) with a probability of 50% and a horizontal flip with a probability of 50%. Each image and its mask undergo augmentations, giving it a 50% chance of being modified by one of the augmentation functions. Consequently, there is a 12.5% probability that an image will remain unaltered. If shifts, scales, and rotations affect the integrity of the original reference region, then the same adjustments are applied to the corresponding masks. This might result in the nodule being positioned at the edge of the image, which is a scenario that is not uncommon in original datasets where nodules can naturally appear at the image edge. It's important to note that we do not generate new images through augmentations: we solely modify the existing ones. We avoid applying these modifications to the validation and test data.

2.4.   Evaluations metrics

To quantitatively assess the segmentation performance of our proposed method, we have chosen several metrics as follows (where TP, FP, TN, FN indicate true positive, false positive, true negative, and false negative, respectively):

While human interpretation remains the gold standard, intraobserver and interobserver variability among radiologists is a well-known issue. Automated systems with a high Dice coefficient can help reduce observer-dependent inconsistencies and standardize diagnoses, particularly in large-scale screening applications. To compare the studies that assess interobserver variability—typically using the percentage difference and Bland-Altman limits of agreement (LOA), which measure the percentage agreement between two observers regarding two dimensions of a nodule—we introduce a novel approximation between the percentage difference and the Dice score for elliptic shapes. Let's consider a reference ellipse with axes a and b. Its area is as follows:

If a second observer measures an ellipse with axes that are scaled versions of the reference, as defined by the scaling factors αa and βb (where α and β represent the percentage of the reference measurements), then

Assuming that both ellipses are concentric (i.e., the second ellipse is entirely contained within the reference ellipse), the area of their intersection is simply S₂.

Then, the Dice coefficient (DSC) is calculated as follows:

By canceling out S₁ from the numerator and denominator, we obtain the following general formula:

This should be considered as an approximation because thyroid nodules do not necessarily have an elliptic shape, and in some cases, the two shapes delineated by observers may not be in the same location, meaning these nodules cannot be considered concentric.

2.5.   Setup

We used the Google Colab platform for training and testing, thereby utilizing the NVIDIA Tesla V100 GPUs with a memory capacity of 16 GB. The implementation framework chosen was PyTorch 2.0.1, integrated with CUDA 12.0. Pre-trained encoders from the ImageNet dataset were employed to initialize the model weights. Optimization of the models was accomplished using the Adam algorithm, and a total of 100 epochs were executed during the training phase. We used the Cosine Annealing Learning Rate strategy with a maximal learning rate 0.0005. The Cosine Annealing Learning Rate strategy is defined as follows [41]:

where lr is learning rate to be used in the current epoch, lr_min is the minimum learning rate, lr_max is the maximum learning rate, T_cur is the current epoch, and T_max is the total number of epochs in the training process. For each epoch, a batch size of 64 was used, and all input images were resized to dimensions of 224 × 224 pixels. For model prediction, all images were simply resized to 224 × 224 without any additional augmentation. The data was divided into training and validation sets in an 80:20 ratio when the training set was only the TN3K dataset; alternatively, the data was in a 70:30 ratio when we utilized other datasets for training. This adjustment aimed to ensure that the validation set encompassed a more diverse range of images, thereby preventing the risk of overfitting.

3.   Results

We trained ResUNet solely on the TN3K train set and evaluated its performance on the TN3K test set. Our findings demonstrated superior scores compared to the results published by Gong et al. Specifically, our mean Dice score, mean IoU, and mean accuracy reached 83.77%, 75.09%, and 97.18%, respectively. Moreover, the proposed method involves the direct segmentation of thyroid nodules from thyroid images. In contrast, the TEFE+ method relies on the processing of both thyroid gland and thyroid nodule images. Both types of images pass through a shared encoder; then, they diverge into separate decoders for thyroid nodule segmentation and thyroid gland segmentation. This implies that thyroid gland images are required for training the TEFE+ architecture. In the proposed method, we only use thyroid nodule images. The results are shown in Table 2.

Moreover, we explored different augmentation techniques and hyperparameter settings. When no data augmentation was applied, the mean IoU score was 69.71% ± 23.73% and the mean Dice score was 79.46% ± 22.60%. When only horizontal flip was used, the mean IoU score was 70.53% ± 23.21% and the mean Dice score was 80.51% ± 21.23%. When the Cosine Annealing Learning Rate was not applied, the mean IoU score was 73.09% ± 22.51% and the mean Dice score was 82.31% ± 21.77%. These results are reported on the TN3K test set. Our findings indicate that appropriate augmentation and hyperparameter tuning can improve the segmentation scores by up to 3% on the Dice score and up to 4.5% IoU in our case.

Additionally, we trained ResUNet solely on the TDID dataset, where we evaluated it using 5-fold cross validation (same technique as was reported in Pan et al. publication [17]), and achieved an IoU of 0.7281 and a Dice score of 0.8329. The comparison of the existing results on the TDID dataset is shown in Table 3. It is essential to emphasize that performing a direct comparison on the TDID dataset presents challenges due to variations in the data cleaning process. Throughout the conversion from coordinates to binary masks, we encountered several issues, as detailed in the Datasets section. The issues in the conversion process, as also reported by Pan et al. [17], resulted in a decreased number of images. A comprehensive list of deleted or modified images is provided in Appendix A.

After conducting the initial tests on the TDID and TN3K datasets, we proceeded with further training on other datasets. First, we added the TDID dataset to the training set, and then progressively added the clip frames from the Thyroid Ultrasound Cine-clip dataset. Our objective was to evaluate the model's performance on all known publicly available datasets and assess its performance on the TN3K test dataset to enable a comparison with previously published results. The results are shown in Table 4. For these combined datasets, considering that the Cine-clip dataset contains numerous images (frames) of 192 thyroid nodules, we opted to randomly select a variable number of frames (denoted as “n”) from the Cine-clip dataset for each thyroid nodule. In the clarification, we conducted a random sampling process to select one image for each thyroid nodule for the specific case where n = 1. The employed sampling methodology is detailed in the Datasets section.

At the end of training, our model achieved a Dice score of 87.95% on the training set and 86.95% on the validation set, with corresponding IoU scores of 78.59% and 76.98%, respectively. On the test set, it maintained a robust performance with a Dice score of 84.24% and an IoU score of 75.48%. The slight drop of approximately 2.7% in the Dice score and 1.5% in the IoU score from the validation set to the test set indicates a minimal generalization gap, thus suggesting that the model learns robust features that generalize well to unseen data without a significant overfitting.

4.   Discussion

The comparison of our implementation of ResUNet on TN3K dataset with previously published works is presented in Table 2. With a different augmentation approach, ResUNet outperforms the other methods. The comparison of ResUNet on the TDID datasets is presented in Table 3. Both results demonstrate that ResNet serves as a powerful encoder for UNet, thereby achieving state-of-the-art results in US image segmentation. Additionally, we explored the possibility of training ResUNet on all publicly available datasets known to us, thus resulting in even better metrics than those achieved solely on the TN3K and TDID datasets. The results are presented in Table 4. From the findings, it is evident that the highest Dice score or IoU were attained by the combined dataset of TN3K and TDID, along with one randomly selected image (n = 1) for each thyroid nodule in the Thyroid Ultrasound Cine-clip dataset.

Despite the application of brightness and contrast augmentation, the final model has incorrectly segmented images with varying the overall intensity. However, it is important to note that some of the images are excessively bright, thus leading to a loss of detail in the bright regions. Another incorrectly segmented images were related to the number of nodules present in the images. When the images contained multiple nodules, the model very often exhibited inaccuracies in its predictions. The model's capability is limited to detecting one or two nodules. The ability to detect up to two nodules can be attributed to the fact that the training data lacked a sufficient number of thyroid glands with 3 or more nodules, thus leading to the limited exposure of the model to such cases. Examples of correctly segmented images are displayed in Figure 4. On the other hand, Figure 5 showcases examples of incorrectly segmented images. In our experiments, we encountered several challenging cases where our segmentation algorithm failed to perform as expected. Specifically, the model struggled with images that exhibited high brightness, multiple nodules, and interference from measurement tools, which resulted in inaccurate segmentation outcomes. We plan to implement optimal augmentation strategies in the future, including controlled variations in the brightness and contrast as well as the simulation of synthetic artifacts, to expand the diversity and representativeness of our training dataset. We plan to develop methods to detect interfering objects, such as measurement tools and noise, and include similar examples in our training set through data augmentation.

Moreover, the results demonstrated that using a significant number of almost identical images does not lead to better results when working with a large dataset containing repeated images (Thyroid Ultrasound Cine-clip dataset). We initially hypothesized that augmenting the training set with a larger number of similar but not identical images would result in better performance. Contrary to our expectations, we observed that the trend was opposite. With an increasing number of frames, the Dice score and other metrics were more likely to decrease.

Although CAD systems do not directly challenge human experts, they can ensure a high segmentation performance, thus minimizing the variability and enhancing the reproducibility. In clinical practice, CAD systems are designed to support rather than replace human experts, and higher Dice coefficients indicate a closer alignment between the segmentation outputs and expert annotations. Several studies have assessed the performance of human experts in delineating thyroid nodules. Brauer et al. [47] reported interobserver differences in the mediolateral (21.21%), anteroposterior (20.99%), and craniocaudal (19.89%) diameters. The corresponding interobserver Dice scores, as calculated using the proposed method described in Section 2.4, were approximately 0.77 and 0.78 for the axial and longitudinal planes, respectively. Lee et al. [48] used a Bland-Altman analysis to evaluate the intraobserver and interobserver variability in US measurements of thyroid nodules, thereby reporting percentage differences and the 95% limits of agreement (LOA). When converted to Dice scores using the proposed calculation, the intraobserver Dice scores were identical in both planes: 0.93 for the axial plane and 0.94 for the longitudinal plane. The interobserver Dice scores were 0.92 for the axial plane and 0.91 for the longitudinal plane. Another study [49] focused on the thyroid gland in children. The authors reported that, when taking the mean value of the left and right thyroid lobes, the interobserver differences in lobe measurements (not the nodules) were as follows: a mediolateral difference of 9.7%, an anteroposterior difference of 11.0%, and a craniocaudal difference of 13.7%. The corresponding Dice scores were 0.89 for the axial plane and 0.87 for the longitudinal plane. Our segmentation algorithm achieved a Dice score of 0.84 on a mix of axial and longitudinal images (when compared with expert-annotated ground truth masks in the test set of Gong et al. study [16]). While this result does not fully reach the intraobserver agreement levels, it is within the range of reported interobserver variability among human experts.

5.   Conclusions

In this study, we implemented and evaluated a deep learning-based segmentation model, ResUNet, for thyroid nodule segmentation in US images. By leveraging the advantages of both ResNet and UNet architectures, our model achieved state-of-the-art performance, thus surpassing previously published methods. We demonstrated the effectiveness of our approach through extensive experiments using all publicly available thyroid ultrasound datasets, with our model achieving the highest Dice score and IoU metrics on the TN3K test set.

Our findings highlight that training on a diverse dataset significantly improves the segmentation performance on the TN3K test set, particularly when utilizing a combination of TN3K, TDID, and the Thyroid Ultrasound Cine-clip datasets. However, we observed diminishing results when incorporating a large number of near-identical images from cine-clip sequences, thus suggesting that an optimal balance between dataset diversity and redundancy is essential. The diverse and complex nature of thyroid nodules and US image quality highlight the importance of collecting and publishing further datasets. Having access to diverse datasets amplifies a researchers' ability to evaluate and improve their future models, thus enhancing the generalization and robustness to real-world clinical challenges.

In light of this, we acknowledge the novel dataset published by Gong et al. This dataset is originally divided into train and test subsets which is excellent for a direct comparison of studies. We conducted experiments using this dataset, along with other publicly available datasets, and obtained the following mean evaluation metrics (± standard deviations) on the published test set: Dice score, IoU score, accuracy, precision, and recall of 84.24% ± 0.19, 75.48% ± 0.21, 97.24% ± 0.32, 82.75% ± 0.20, and 88.98% ± 0.19, respectively. These results represent the most advanced state-of-the-art scores compared to previously published studies and demonstrate that UNet with the ResNet encoder has the capability to accurately segment thyroid nodules in ultrasound images.

Our results achieved scores comparable to interobserver studies, suggesting that automated thyroid nodule segmentation using deep learning can reach expert-level performance. While CAD systems are not intended to replace human expertise, they can serve as valuable tools for supporting clinical decision-making and improving diagnostic consistency. Our results show that data augmentation has a significant impact, and raises the question of whether it has a greater influence than the architecture used. Considering that the dataset remains small even with all publicly available data on thyroid nodules (and that data augmentation considerably affects the outcomes), we plan to focus our future work on optimizing data augmentation.

Author contributions

This manuscript was collaboratively prepared by both authors, who have contributed to its focus and content. Antonin Prochazka wrote the main part of the manuscript and the Python script. Both authors have reviewed and approved the final version for publication.

Use of AI tools declaration

During the preparation of this work the author(s) used ChatGPT 4 and Grammarly in order to improve readability and language of the text. After using this tool/service, the author(s) reviewed and edited the content as needed and take(s) full responsibility for the content of the publication.