Comparative analysis of phenomenological growth models applied to epidemic outbreaks

1.   Introduction

1.1.   Scope

Dynamic growth models provide an important quantitative framework for characterizing epidemic trajectories, generating estimates of key transmission parameters, assessing the impact of control interventions, gaining insight to the contribution of different transmission pathways, and producing short- and long-term forecasts ^[1]. A natural question is that of the choice of the best suitable growth model for a given epidemic. It is the purpose of this paper to shed light on the performance of different growth models in describing different real epidemic outbreaks. Specifically, we employ four different growth models based on differential equations (two of them with two parameters, and two with three parameters), and apply them to a total of 37 infectious disease outbreak datasets consisting of time series of case incidence for different historic outbreaks comprising different diseases and settings.

The two-parameter models are the well-known logistic model (LM) ^[2] and Gompertz model (GoM) ^[3], and the three-parameter models are generalizations for both models which we refer to as the generalized logistic model (GLM) and the generalized Gompertz model (GGoM), respectively. These models incorporate a parameter $p$, which is an exponent that provides a criterion about the type of early growth dynamics, namely sub-exponential ($0 < p < 1$) or exponential ($p = 1$) growth. (For $p = 1$, the GLM and GGoM models reduce to the LM and GoM models, respectively.) We explored the performance of these models in describing the trajectory of 37 outbreaks by applying the methodology described by Chowell ^[1] to estimate parameters with their confidence intervals. In this analysis, we analyzed how well models fitted the 37 outbreaks using the root mean squared error (RMSE).

The particular choice of parametric models complements that of ^[1], where the well-known exponential and Richards ^[4,5] growth models are employed along with their generalized counterparts. Moreover, since that work is focused in detailing the methodology, the data set in ^[1] is limited to the 2013–2016 Ebola outbreak in Sierra Leone, and no mechanism of choice between two or more alternative models for the same data set is established. In this paper we are particularly interested in gaining insight into the types of outbreaks where the different model variants provide an enhanced description of the epidemic outbreaks.

1.2.   Related work

This paper is focused on models given by ordinary differential equations (ODEs) to describe the temporal dynamics of epidemic outbreaks. The properties of ODEs as models of growth are treated in numerous monographs, see e.g. ^{[6,7,8,9,10,11,12]}. On the other hand, the presence of the nonlinearity caused by the growth rate exponent $p$ precludes in some cases solutions of the corresponding ODE in closed form. Nevertheless, we mention that for $p = 1$, the properties of the Richards, logistic, Gompertz, and related (e.g., von Bertalanffy ^[13,14]) models are broadly discussed in terms of closed algebraic expressions in ^[15,16,17] (see also the references cited in these papers).

We use phenomenological models within an empirical approach (without an explicit basis of physical laws or mechanisms) that are useful to reproduce the patterns observed in the time series data ^[18]. The result is a fairly simple temporal description of epidemic growth patterns ^[1]. For instance, epidemics display variable epidemic growth scaling (e.g., from sub-exponential to exponential). Here we are particularly interested in the contribution of the parameter $p$ as a corrector in the fit and the possible improvement in the forecasts. The relevance of this parameter was recently highlighted by Chowell and Viboud ^[19] who demonstrated that a generalized-growth model is a simple tool that can be used to characterize the early epidemic growth profile from case incidence data as well as from synthetic data derived from transmission models via stochastic simulation ^[18]. Related references to early epidemic growth models also include ^[20,21]. For the connection between the growth rate and the reproductive number of an epidemic, an aspect that is not discussed herein, we refer to ^{[22,23,24,25]}.

Finally, we mention that there are also stochastic models built to study sigmoidal behaviours. In particular, in recent years there have been many advances in stochastic models based on diffusion processes, particularly associated with the Gompertz and logistic curves. A general procedure for obtaining and estimating this type of models is considered in ^[26], where also further references can be found (see also ^[27]). As is discussed in the introduction of ^[26], considering particular choices of the time functions that define the exogenous factors has enabled researchers to define diffusion processes associated to alternative expressions of already-known growth curves ^[26]. These processes include a Gompertz-type process ^[28] (applied to the study of rabbit growth), a generalized von Bertalanffy diffusion process (with an application to the growth of fish species) ^[29], a logistic-type process ^[30] (applied to the growth of a microorganism culture), and a Richards-type diffusion process ^[31]. More recent contributions to this line of research are ^[32] and ^[33].

1.3.   Outline of the paper

The remainder of the paper is organized as follows. In Section 2 the mathematical growth models that we employ to investigate the trajectory of epidemic outbreaks are described. Specifically, we employ two growth models with two parameters and two models with three parameters, which are generalizations of the first models that incorporate a third parameter to model varying degrees of early growth profiles (from sub-exponential to exponential growth). The materials and methods employed in our analyses are presented in the Section 3, including the descriptions of the datasets for the 37 epidemic outbreaks, the concept of the RMSE, and the methods for the parameter estimation and confidence interval generation using the parametric bootstrap approach. The results of applying the methodology developed in Section 3 to the datasets are presented in Section 4. Finally, some conclusions and possible directions of future work are collected in Section 5.

2.   Mathematical models

The general form of a phenomenological model is

where $\mathrm{d} x_i / \mathrm{d}t$ denotes the rate of change of the system state $x_i$, $i = 1, \dots, n$, and $\Theta = (\theta_1, \dots, \theta_m)$ is the set of model parameters, where the complexity of a model depends on the number $m$ of parameters that are needed to characterize the states of the system and the spectrum of the dynamics that can be recovered from the model ^[1]. In this contribution we highlight the logistic growth model (LM) and the Gompertz model (GoM) and their respective generalizations, namely the generalized logistic model (GLM) and the generalized Gompertz model (GGoM). The last two models incorporate a parameter $p$ that indicates the kind of scaling of growth. These models can be described as follows.

The logistic growth model (LM) relies on two parameters to characterize the trajectory of an epidemic, where the model is given by the differential equation

where $t$ is time, $C'(t)$ describes the incidence curve over time, $C(t)$ is the cumulative number of cases at time $t$, while the parameter $r > 0$ indicates the growth rate (its dimension is $1/\mathrm{time}$), and $K$ is the size of the epidemic. During the initial stages of disease propagation, when $C(t) \ll K$, this model assumes an exponential growth phase, as can be inferred from the well-known explicit solution of (2.2),

The two-parameter Gompertz model (GoM) is given by the ODE

where the parameter $b > 0$ describes the exponential decay of the growth rate $r$, and the quantities $C$ and $C'$ have the same meaning as for the LM model. If $C(0)$ is the initial number of cases, then the solution of (2.3) is

We generalize the logistic and Gompertz models by incorporating a growth scaling parameter $p\in [0, 1]$ that indicates the kind of growth, where $p = 0$ corresponds to a constant incidence over time, $p = 1$ corresponds to the exponential growth and recovers the logistic model, and any value $0 < p < 1$ leads to a model that describes a sub-exponential growth, a property that leads to potentially more realistic models as shown in ^[18]. The model is given by the differential equation

Similarly, the Gompertz model leads to the following ODE that defines the Generalized Gompertz Model (GGoM), where $p$ plays the same role as in the GLM:

It is worth noting that for general values $p \in (0, 1)$, (2.5) does not possess an explicit solution in closed algebraic form. (For a detailed discussion of this point and further references we refer to Ohnishi et al. ^[34], who deal with the Pütter-von Bertalanffy equation $\mathrm{d} C / \mathrm{d} t = \alpha C^A - \beta C^B$ with positive constants $\alpha$, $\beta$, $A$ and $B$, which includes (2.5). Nevertheless, this equation admits an analytical solution given in implicit form ^[34]HY__HY, Eq. (9)].)

In contrast to the GLM equation (2.5), one may easily integrate the GGoM equation (2.6) for these values of $p$ to get

For this expression we get

It is interesting to note that for the Gompertz model with $p = 1$, (2.3), the expression (2.4) implies that $C(t) \to C(0) \exp (r/b)$ as $t \to \infty$ so the limit value depends linearly on $C(0)$ (unless the initial population is absorbed into $b$ or $r$), while for $0 < p < 1$, (2.7) means that the limit of $C(t)$ still depends on $C(0)$ but does so in a nonlinear fashion.

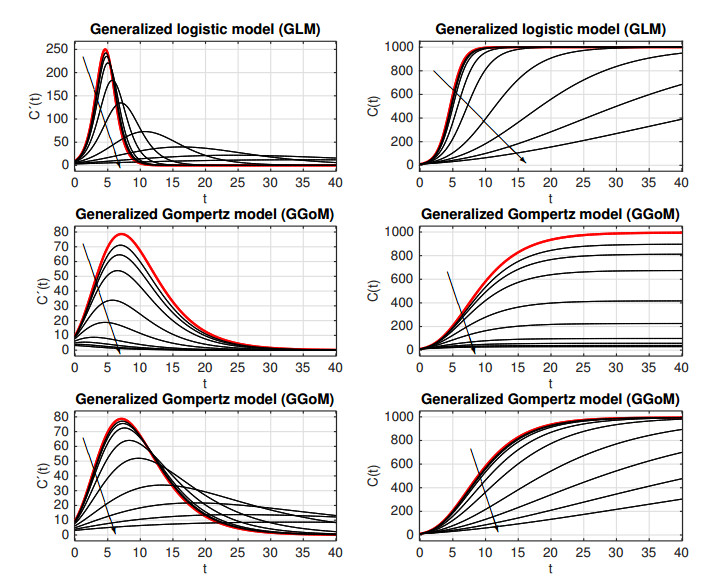
Summarizing, we have two two-parameter models with their respective generalizations that are three-parameter models, where the third parameter is the growth scaling parameter $p\in [0, 1]$, as we show in Table 1. Before we proceed, we illustrate by an example the effect of varying $p$ within the GLM and GGoM, see Figure 1. We start with the logistic model (2.2) setting $r = 1$, $C(0) = 10$ and $K = 1000$. The solid red curve in Figure 1 (top left) shows the incidence curve $t \mapsto C'(t)$ corresponding to the solution $t \mapsto C(t)$ (Figure 1, top right). This solution approximates the maximum ($K = 1000$). Now we pass to the GLM (2.5) by gradually decreasing $p$ from one to $p = 0.995$, $p = 0.99$, and so on (see the caption of Figure 1). We observe that the maxima of the incidence $C'(t)$ decrease (as follows easily from discussing the extrema of $C \mapsto C^p (1- C/K)$), but their time of occurrence increases, as $p$ is decreased. Furthermore, the incidence curves stay fairly close to the curve for $p = 1$ for values of $p$ close to one, and all solutions behave like $C(t) \to K$ as $t \to \infty$.

Table 1.  Summary of information about models and parameters.

Growth model	Parameters
Logistic growth model (LM)	$\Theta = \{ \theta_1= r, \theta_2=K\}; \ r, K > 0$
Gompertz model (GoM)	$\Theta = \{ \theta_1= r, \theta_2=b \}; \ r, b > 0$
Generalized Logistic growth model (GLM)	$\Theta=\{ \theta_1=r, \theta_2=p, \theta_3=K\}; \ r, K > 0, \ p\in[0, 1]$
Generalized Gompertz model (GGoM)	$\Theta=\{ \theta_1=r, \theta_2= b, \theta_3=p\}; \ r, b > 0, \ p\in[0, 1]$

---

 | Show Table

DownLoad: CSV

Figure 1.  Illustration of the GLM model (top) and the GGoM model (middle and bottom), showing in each case $C'(t)$ (left) and $C(t)$ (right). The solid red curve corresponds to $p = 1$. The arrow indicates decreasing values of $p = 0.995$, $0.99$, $0.98$, $0.95$, $0.9$, $0.8$, $0.7$, $0.6$, and $0.5$, corresponding to the thin black curves. The plots in the middle correspond to fixed values of $r$ and $b$ (see (2.8)), while in the bottom $r$ is fixed but $b$ is variable (see (2.9)).

DownLoad: Full-Size Img PowerPoint

In order to compare these observations with those for the Gompertz and GGoM models, we plot in Figure 1 (middle left) the incidence curve $t \mapsto C'(t)$ corresponding to the solution $t \mapsto C(t)$ (Figure 1, middle right) for the Gompertz model (2.3) with parameters $C(0) = 10$,

which have been chosen in such a way that $C'(0)$ is the same as for the GLM as well as that $C(t) \to K$ as $t \to \infty$ (cf. (2.4)) for $p = 1$. Note that the maximum of $C'(t)$ is smaller than for the logistic model. As $p$ is decreased, but all other parameters are kept, these maxima become smaller (as with the GLM), but they appear each time earlier (in contrast to the GLM). However, for $t \to \infty$ we observe that consistently with (2.7), $C(t)$ approaches smaller values than $K$ as $t \to \infty$. If we wish to ensure that the GGoM with $p \in (0, 1)$ has the same value of $C'(0)$ as the GLM (for the corresponding value of $p$) and $C(t) \to K$ as $t \to \infty$, then we must also adjust $b$ by setting

(which results from equating the limit in (2.7) with $K$). From the bottom plots of Figure 1 we observe that the joint variation of $p$ and $b$ produces curves similar to those of the GLM.

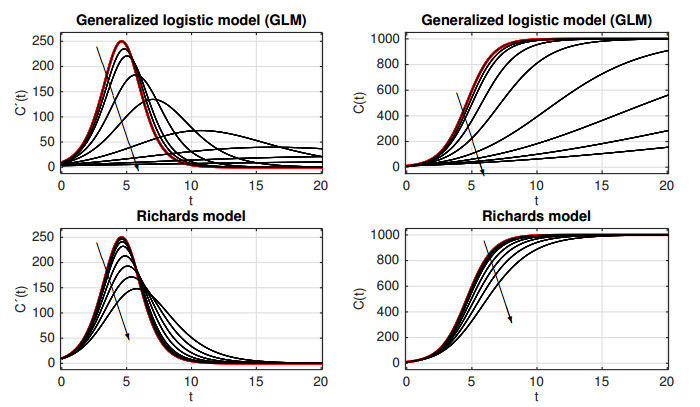
Finally, let us emphasize once again that the exponent $p$ is introduced in both (2.5) and (2.6) in such a way that it affects the initial growth rate, corresponding to the early stage when $C(t)/K \ll 1$ and therefore $C' (t) \approx r C^p (t)$, so that $p$ characterizes sub-exponential growth dynamics ^[18]. In particular, the identification of $p$ at early stage of an epidemic is fundamental for forecasting the outbreak ^[19]. It is therefore instructive to provide an example to compare (2.5) with an alternative way of introducing an exponent $p$ into (2.2), namely the well-known Richards equation ^[4]

Figure 2 displays the incidence curves $t \mapsto C'(t)$ and the solution $t \mapsto C(t)$ for selected values of $p$ for both the GLM model (2.5) and the Richards equation (2.10). We observe that since $C(0)/K \ll 1$, the initial growth rates for (2.10) are very similar for all values of $p$, in contrast to those of the GLM model. Thus, the variability of the exponent $p$ in the Richards equation (2.10) is not suitable for capturing sub-exponential initial growth.

Figure 2.  Illustration of the GLM model (top) and the Richards model (bottom), showing in each case $C'(t)$ (left) and $C(t)$ (right), starting from $C(0) = 10$ with $K = 1000$. The solid red curve corresponds to $p = 1$. The arrow indicates decreasing values of $p = 0.99$, $0.98$, $0.95$, $0.9$, $0.8$, $0.7$, $0.6$, and $0.5$, corresponding to the thin black curves.

DownLoad: Full-Size Img PowerPoint

On a similar note, we mention that the traditional form of the Gompertz ODE (cf., e.g., ^[28]) is

with a constant $\alpha > 0$, which is a nonlinear differential equation, in contrast to the linear ODE (2.3) utilized herein. Our preference of (2.3) is based on the fact that this equation can easily be equipped with the exponent $p$ to give (2.6). Furthermore it is fairly easily possible to compare (2.6) and its solutions with those of the sub-exponential growth equation $\mathrm{d} C / \mathrm{d} t = r C(t)^p$ analyzed in ^[18,19], while the multiple, and nonlinear occurrence of $C(t)$ makes such a generalization at least more complicated.

3.   Materials and methods

In order to compare the mathematical models, we need time series data that describe the temporal changes in one or more states of the system, whose temporal resolution varies among daily, weekly or yearly and by the frequency at which the state of the system is measured. We herein employ a data set for 37 different epidemic trajectories with different temporal resolutions (see Table 2). Additionally we present the method for fitting the model to the data, that is, to estimate the parameters as in ^[1]. Finally, to compare the models, we conduct a comparative analysis of RMSEs for all models and epidemics. Then, to continue we present the materials and methods that allow us to understand the methodology.

Table 2.  Information on the 37 data sets of epidemic outbreaks obtained from the following sources: Cases 1 to 23: ^[38], Case 24: ^[39,40], Case 25: ^[41,42], Case 26: ^[43], Case 27: ^[44], Case 28: ^[45], Case 29: ^[46], Case 30: ^[47], Cases 31 and 32: ^[48,49], Case 33: ^[50], Case 34: ^[51], Cases 35 and 36: ^[52,53], Case 37: ^[54].

Case	Disease	Outbreak	Temporal	Total	Case	Disease	Outbreak	Temporal	Total
No.			resolution	data	No.			resolution	data
1	Ebola	Forecariah (GIN)	weeks	51	20	Ebola	Tonkolili (SLE)	weeks	29
2	Ebola	Gueckedou (GIN)	weeks	49	21	Ebola	Western Area Rural (SLE)	weeks	51
3	Ebola	Keroune (GIN)	weeks	14	22	Ebola	Western Area Urban (SLE))	weeks	55
4	Ebola	Kindia (GIN)	weeks	30	23	Ebola	Grand Bassa (LBR)	weeks	30
5	Ebola	Macenta (GIN)	weeks	32	24	Ebola	Congo (1976)	days	52
6	Ebola	N'Zerekore (GIN)	weeks	24	25	Ebola	Uganda (2000)	weeks	18
7	Ebola	Bomi (LBR)	weeks	33	26	Measles	London (ING) (1948)	weeks	40
8	Ebola	Bong (LBR)	weeks	17	27	Plague	Bombay (IND) (1905-06)	weeks	41
9	Ebola	Grand Cape Mount (LBR)	weeks	29	28	Plague	Madagascar (2017)	weeks	50
10	Ebola	Lofa (LBR)	weeks	24	29	Smallpox	Khulna (BGD) (1972)	weeks	13
11	Ebola	Margibi (LBR)	weeks	40	30	Yellow fever	Luanda (AGO) (2016)	weeks	28
12	Ebola	Montserrado (LBR)	weeks	42	31	FMD	UK (2001)	days	121
13	Ebola	Bo (SLE) (2014)	weeks	39	32	FMD	Uruguay (2001)	days	27
14	Ebola	Kailahun (SLE)	weeks	33	33	Pandemic Influenza	San Francisco (USA) (1918)	days	63
15	Ebola	Kambia (SLE)	weeks	45	34	Zika	Antioquia (COL)(2016)	days	105
16	Ebola	Kenema (SLE)	weeks	39	35	VIH-AIDS	Japan (1985-2012)	years	21
17	Ebola	Kono (SLE)	weeks	30	36	VIH-AIDS	NYC (1982-2002)	years	70
18	Ebola	Moyamba (SLE)	weeks	37	37	Cholera	Aalborg (DNK) (1853)	days	105
19	Ebola	Port Loko (SLE) (2014)	weeks	54

---

 | Show Table

DownLoad: CSV

3.1.   Datasets

Table 2 summarizes the information of the 37 epidemic outbreaks analyzed, including the name of the disease associated with each epidemic, the location where the outbreak occurred, the temporal resolution (by days, weeks, or years) of the time series, and the number of data points. For each outbreak, the onset corresponds to the first observation associated with a monotonic increase in incident cases, up to the peak incidence. We notice that for Ebola we have more information about the outbreak in West Africa (see also ^[35,36,37]).

3.2.   The root mean square error (RMSE)

As in ^[1], besides using the residuals for any systematic deviations for the model fit to the data, it is also possible to quantify the error of the model fit to the data using performance metrics ^[55]. These metrics are also useful to quantify the error associated with a forecast. A widely used performance metric is the root mean squared error (RMSE) given by

where $\hat{\Theta}$ is the set of parameter estimates, $f(t_i, \hat{\Theta})$ denotes the best-fit model, and $y_{t_i}$ ($i = 1, \dots, n$) is the time series data (for that specific epidemic outbreak) and $n$ is the total number of data points. In this work we employ the RMSE since this quantity naturally arises in the context of least-squares methods. Other applicable performance metrics ^[1] include the mean absolute error (MAE) and the mean absolute percentage error (MAPE), given by the respective expressions

While we have not applied any special treatment on outliers when calculating the RSME, the sensitivity of each of these performance metrics to anomalous data is left as a topic for future study.

3.3.   Parameter estimation and confidence interval generation

Based on the description of the determination of the best fit in ^[1], we use the built-in Matlab (The Mathworks, Inc.) function LSQCURVEFIT to obtain parameter estimates via least-square fitting of the model solution to the observed data. This is achieved by searching for the set of parameters $\smash{\hat{\Theta} = (\hat{\theta}_1, \dots, \hat{\theta}_m)}$ that minimizes the sum of squared differences between the observed data $\smash{y_{t_i} = y_{t_1}, \dots, y_{t_n}}$ and the corresponding model solution denoted by $f(t_i, \Theta)$. For the implementation for this function, we need the initial parameter guesses and the upper and lower bounds for these parameters as well as the initial data point C(0). The process for the parameter estimation is summarized in the next steps:

$1.$ Define the upper and lower bounds for each parameter.

$2.$ Consider $m$ sets of initial parameters defined with the Matlab function LSHDESING and the upper and lower bounds defined in step 1.

$3.$ Calculate the parameter estimation for each set of initial parameters with the function LSQCURVEFIT.

$4.$ Measure the error RMSE and select the parameter estimates with lowest RMSE, in order to ensure that the global minimum rather than a local minimum was found.

On the other hand, to generate the confidence interval, we use the parametric bootstrap method ^[56] (see also ^[57,58]) with Poisson error structure that was implemented to generate 250 model realizations. This process can be summarized in the following steps:

$1.$ With the parameter estimations $\hat{\Theta}$ obtained by the least-squares fit of the model $f(t_i, \Theta)$ to the time series data $y_{t_1}, \dots, y_{t n}$, we achieve the best-fit model $\smash{f(t_i, \hat{\Theta})}$.

$2.$ Then, we generate $S$-times replicated simulated datasets, using the best-fit model, which we denote by $\smash{f_1^{*}(t_j, \hat{\Theta})}, \dots, \smash{f_S^{*}(t_j, \hat{\Theta}})$. To generate these simulated data sets, we first use the best-fit model $\smash{f(t_i, \hat{\Theta})}$ to calculate the corresponding cumulative curve function $\smash{F(t_j, \hat{\Theta})}$ defined as

Moreover, $f_k^{*}(t_1, \hat{\Theta}) = f(t_1, \hat{\Theta})$ for $k = 1, \dots, S$. Besides, these data are generated assuming a Poisson error structure as follows: we assume that

where $\operatorname*{Po} (\lambda)$ denotes the Poisson distribution with mean $\lambda$.

$3.$ We re-estimate parameters for each of the $S$ simulated realizations, which are denoted by $\hat{\Theta}_i$ for $i = 1, \dots, S$.

$4.$ Finally, using the set of re-estimated parameters $\hat{\Theta}_i$, $i = 1, \dots, S$, we construct the confidence interval, so the resulting uncertainty around the model fit is given by $f(t, \hat{\Theta}_1), f(t, \hat{\Theta}_2), \dots, f(t, \hat{\Theta}_S)$.

Then, for our case, from these $S = 250$ realizations, we calculate $95\%$ confidence intervals for model parameters.

3.4.   Methodology: Analysis of the RMSE

In this section we summarize the methodology used to decide which is the best model for a given outbreak, and to analyze the contribution of the parameter $p$. The definitions and theory are taken from ^[1]. The methodology consists in an analysis of the RMSE error with the help of bar and scatter charts.

For this purpose, we first explore the initial parameters for each model and epidemic in order to ensure that the best fit of the model yields the smallest RMSE following the steps defined in the Section 3.3 for parameter estimation and considering $r, b \in [0, 5]$, $K \in [0, 10^7]$ and the known $p\in [0, 1]$. The above is an important process in order to ensure that we are obtaining the best fit to the data using the LSQCURVEFIT function in Matlab. We then with the best fits for each model and epidemic, we have their incidence curves and the lower RMSE. With these values we obtain graphs that compare the fit with the data, bar charts and scatter plots, which will be used for the error analysis (see Figure 3).

Figure 3.  Methodology for error analysis.

DownLoad: Full-Size Img PowerPoint

4.   Results

4.1.   Error analysis and comparison of fits for each epidemic

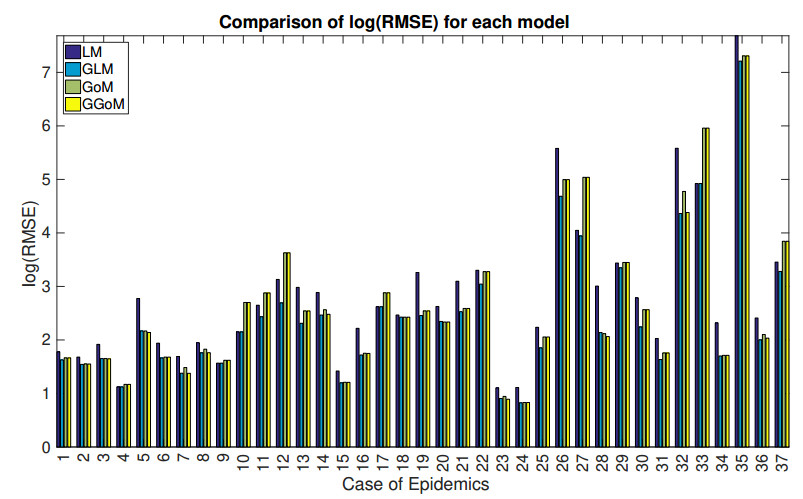
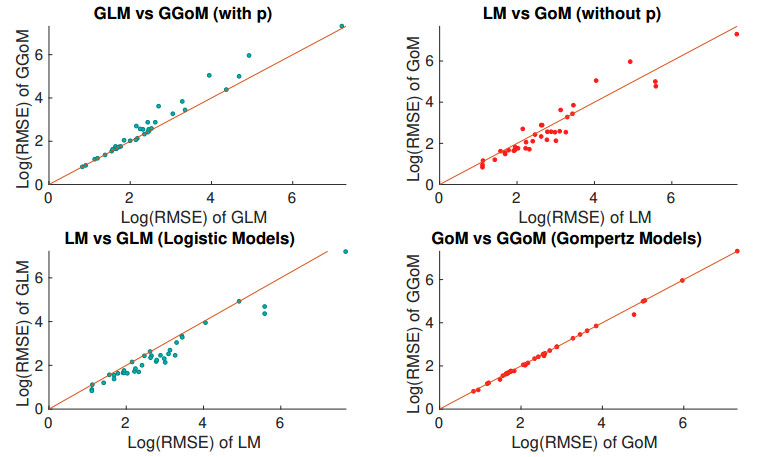
With the RMSE and the best fits obtained for each model, we obtain tables and graphics (see Table 3 and Figures 4 to 8) to compare the sizes of the errors for each model and epidemic outbreak, where the numbers from $1$ to $37$ in Table 3 identify the cases of outbreak (see Table 2). In Table 3 we observe that (independently of the epidemic) the GLM method yields the lowest RMSE in most of the cases (highlighted in green), and the LM yields the larger errors (highlighted in yellow). Besides, whenever the GLM is not the "best'' model, the GGoM follows.

Table 3.  RMSE using the total data for each model. For each outbreak, we highlight the lowest RMSE (green) and the highest value (yellow) for the error sizes.

Case	LM	GLM	GoM	GGoM	Case	LM	GLM	GoM	GGoM
No.					No.
1	5.91840	5.08749	5.28578	5.28578	20	13.81574	10.44249	10.33338	10.33338
2	5.36334	4.68065	4.72246	4.71404	21	22.13303	12.51529	13.31396	13.31396
3	6.80378	5.21596	5.21959	5.19461	22	27.16583	20.98778	26.48861	26.48861
4	3.07198	3.06934	3.22175	3.22175	23	3.01595	2.47452	2.57271	2.43990
5	16.02456	8.74242	8.73707	8.49820	24	3.03925	2.28213	2.29532	2.29498
6	6.95680	5.27913	5.36135	5.36135	25	9.36028	6.37029	7.81157	7.81157
7	5.42450	3.96942	4.41215	3.96139	26	264.91368	108.36306	147.87904	147.87904
8	7.01087	5.81503	6.21805	5.81937	27	57.27638	51.60129	154.36235	154.36234
9	4.79101	4.79101	5.05457	5.05457	28	20.21720	8.50542	8.31521	7.87152
10	8.58955	8.58955	14.88488	14.88488	29	31.10051	28.45452	31.44816	31.44816
11	14.13951	11.40156	17.78045	17.78045	30	16.22091	9.42127	13.00660	13.00660
12	22.89522	14.77254	37.63692	37.63692	31	7.59491	5.12274	5.79428	5.79428
13	19.73810	10.08899	12.70424	12.70424	32	265.53459	78.47628	118.53622	79.95863
14	17.94184	11.77214	12.98507	11.93256	33	137.38697	137.38697	387.23469	387.23464
15	4.13574	3.31649	3.35153	3.34541	34	10.15666	5.47679	5.54259	5.54259
16	9.18180	5.58002	5.76447	5.74384	35	2174.08795	1354.63027	1493.07521	1493.07521
17	13.74655	13.74655	17.83847	17.83847	36	11.13642	7.40159	8.17479	7.64371
18	11.77779	11.32307	11.31585	11.31585	37	31.65064	26.58298	46.71374	46.71374
19	26.11925	11.66119	12.71813	12.71813

---

 | Show Table

DownLoad: CSV

Figure 4.  Bar chart for comparison of the errors of each methods, where we observed that among the best results are for the GLM and GGoM.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Scatter plots for RMSE, where we verify that the pair of Gompertz models have a closer behavior than the logistic models, where the variations are more marked. Additionally, we also verify that the models incorporating the parameter $p$ yield similar errors, in contrast to the models with $p = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Results of fits for epidemic outbreaks (Cases 1 to 12).

DownLoad: Full-Size Img PowerPoint

Figure 7.  Results of fits for epidemic outbreaks (Cases 13 to 24).

DownLoad: Full-Size Img PowerPoint

Figure 8.  Results of fits for epidemic outbreaks (Cases to 37).

DownLoad: Full-Size Img PowerPoint

Furthermore, we also observe that between LM and GoM, the GoM is better, because the dynamics of this model are more closely aligned to the dynamics of the GGoM. Furthermore, the LM is associated with the largest errors in the great majority of the cases of outbreaks.

Figures 4 and 5 display the RMSE for each model and dataset. In Figure 4 we can see that although the GLM outperforms in most cases, we note that the error for the GLM is higher for Cases 3, 5, 7, 18, 20, 23, and 28 compared to the GGoM. Yet, those error differences are very small.

We also employ scatter plots to compare the errors yielded by a pair of models across all of the epidemics (Figure 5). Therefore, we compare the models with or without the para-meter $p$, and then between the logistic and Gompertz models. For the first comparison we verify that the GGoM has errors with sizes larger than the GLM, unlike the models without $p$, where the behavior is different, since the LM has the errors with more scatter and below the line with slope one. Moreover, for the second group of cases, we note that the logistic models have a more scattered behavior above the diagonal line, where LM has errors with sizes greater than the sizes for the GLM's errors. This contrasts with the Gompertz models, where the scatter is closer to the diagonal. This shows that the errors yielded by both Gompertz models are very similar, and we can readily observe that these models are stable or closer to each other.

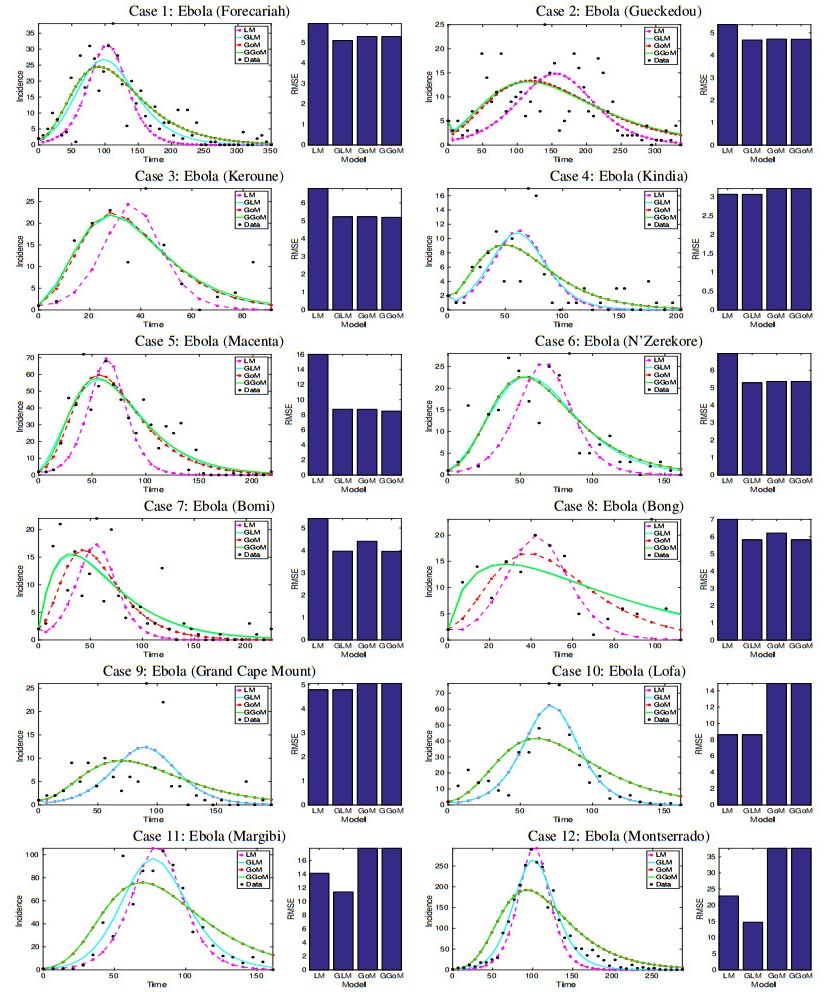
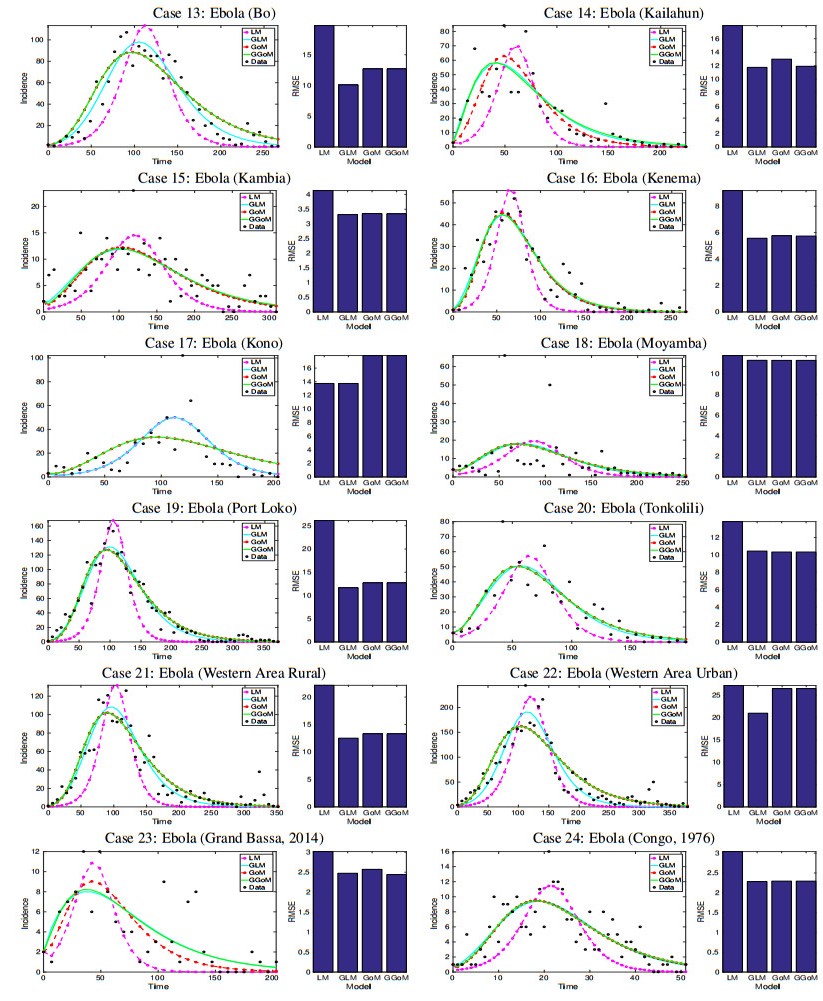
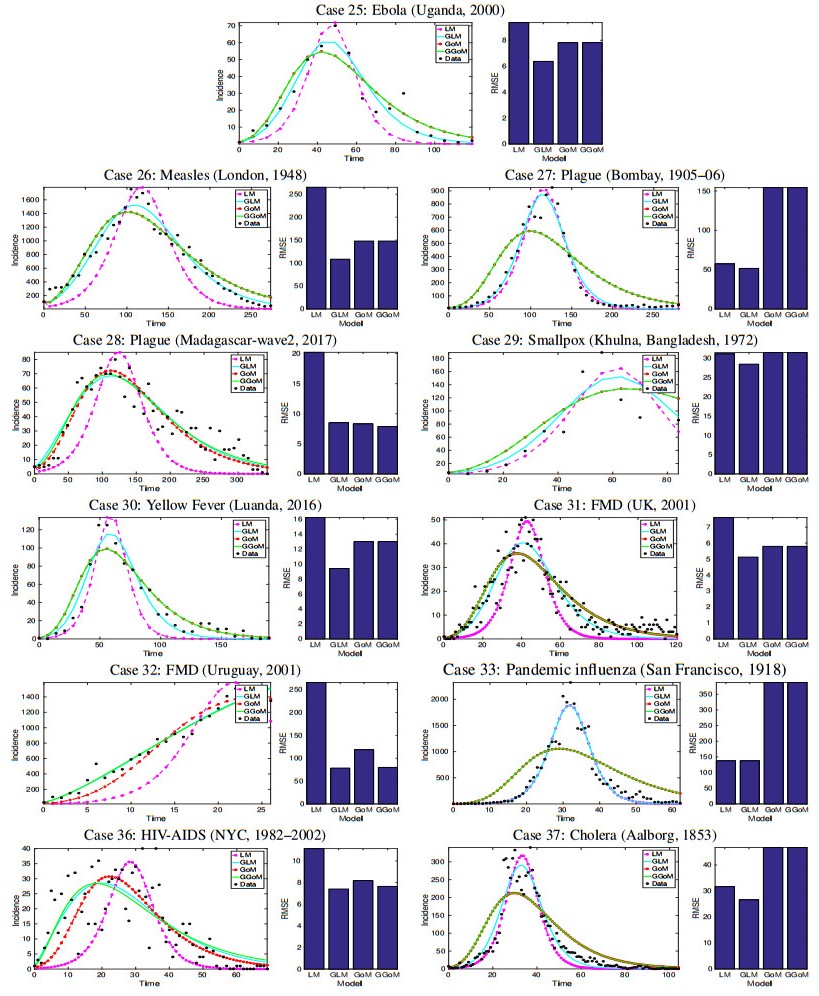
Having analyzed the RMSE for each model, now we study their respective fits for each epidemic outbreak, where we obtain a graphic sample of the best fit that corresponds to the RMSE, i.e., we will plot the best fits. These results are plotted in Figures 6 to 8. In these figures we can observe and compare the quality of the fits and their erorrs, where can note that the best fits to the data correspond to the smaller errors in terms of the RMSE.

Having finalized our comparative analysis of the model fits and their corresponding errors, we point out that for the Ebola epidemics (Cases 1 to 25), the GLM tends to yield an improved description to the data because in those cases where the GGoM wins (in terms of smallness of the RMSE), the corresponding errors do not differ by more than $0.6399$. However, for the rest of the cases of epidemic outbreaks, the best model remains the GLM which yields smaller errors compared to the GGoM.

4.2.   Parameter estimation

These results were obtained from the fits calculated in the previous section with the use of the Matlab function LSDCURVEFIT. We summarize the results for all cases in Table 4. We note that for the GGoM, there are 24 cases with $p = 1$, which means that these exhibit an initial exponential growth, where moreover the Gompertz and GGoM models yield equal RSMEs for that value of $p$. On the other hand for this same period of time and for the logistic models, we notice that only for four epidemics we have $p = 1$ (exponential initial growth), and the others give rise to initial sub-exponential growth with $p \in (0, 1)$. There were a number of outbreaks where the Gompertz models yield $p = 1$ (Gompertz and GGoM models are equivalent), for which the differences between the corresponding RMSEs are negligible.

Table 4.  Parameter estimation for LM, GLM, GoM and GGoM with total data.

Case	LM		GLM			GoM		GGoM
no.	$\hat{r}$	$\hat{K}$	$\hat{r}$	$\hat{p}$	$\hat{K}$	$\hat{r}$	$\hat{b}$	$\hat{r}$	$\hat{b}$	$\hat{p}$
1	0.0515	349.7231	0.1166	0.7713	444.2758	0.1074	0.0195	0.1074	0.0195	1.0000
2	0.0272	312.0756	0.1333	0.6196	407.0675	0.0716	0.0129	0.0716	0.0119	0.9199
3	0.1395	103.0945	0.4286	0.6217	140.4582	0.3545	0.0636	0.3545	0.0580	0.9182
4	0.0661	96.5409	0.0761	0.9502	99.1794	0.1245	0.0307	0.1245	0.0307	1.0000
5	0.0895	447.7870	0.4231	0.6114	725.6594	0.2533	0.0334	0.2533	0.0293	0.8988
6	0.0824	181.5802	0.2410	0.6776	248.1927	0.1937	0.0350	0.1937	0.0350	1.0000
7	0.0794	125.5729	0.6590	0.3822	197.6517	0.5303	0.0376	0.5303	0.0229	0.5241
8	0.1022	112.4554	0.8366	0.3050	197.8649	0.7161	0.0421	0.7161	0.0188	0.3987
9	0.0563	126.3540	0.0563	1.0000	126.3550	0.1222	0.0243	0.1222	0.0243	1.0000
10	0.0801	449.7942	0.0801	1.0000	449.7945	0.1680	0.0300	0.1680	0.0300	1.0000
11	0.0860	717.8667	0.1321	0.8856	835.4420	0.2037	0.0295	0.2037	0.0295	1.0000
12	0.0781	2186.2506	0.1151	0.9075	2558.8591	0.1891	0.0234	0.1891	0.0234	1.0000
13	0.0580	1120.3306	0.1510	0.7861	1516.9220	0.1379	0.0205	0.1379	0.0205	1.0000
14	0.0881	460.4146	0.8746	0.4820	743.9952	0.5880	0.0371	0.5880	0.0249	0.6606
15	0.0397	209.5318	0.1488	0.6165	297.9425	0.0931	0.0162	0.0931	0.0151	0.9355
16	0.0937	348.5524	0.3352	0.6473	521.6719	0.2350	0.0344	0.2350	0.0324	0.9540
17	0.0488	588.5557	0.0488	1.0000	588.5585	0.1001	0.0183	0.1001	0.0183	1.0000
18	0.0481	233.1384	0.1574	0.6929	299.3579	0.0975	0.0224	0.0975	0.0224	1.0000
19	0.0704	1367.5564	0.2398	0.7224	2117.9765	0.1731	0.0225	0.1731	0.0225	1.0000
20	0.0713	462.3494	0.2765	0.6858	621.0968	0.1428	0.0306	0.1428	0.0306	1.0000
21	0.0704	1081.3964	0.2051	0.7484	1597.3617	0.1728	0.0232	0.1728	0.0232	1.0000
22	0.0544	2333.8907	0.1257	0.8349	2869.5270	0.1282	0.0191	0.1282	0.0191	1.0000
23	0.0881	71.3732	0.3692	0.4182	117.6898	0.2726	0.0351	0.2726	0.0219	0.6261
24	0.2489	184.6402	0.7254	0.6591	264.8534	0.5537	0.0970	0.5537	0.0955	0.9869
25	0.1320	321.0079	0.2531	0.7975	405.2692	0.2883	0.0471	0.2883	0.0471	1.0000
26	0.0464	22036.2242	0.3110	0.7547	28828.6606	0.1004	0.0178	0.1004	0.0178	1.0000
27	0.0619	8469.9885	0.0785	0.9599	8953.5581	0.1488	0.0205	0.1488	0.0205	1.0000
28	0.0447	1092.7766	0.2944	0.6104	1794.4156	0.1352	0.0163	0.1352	0.0141	0.8972
29	0.0897	1066.4611	0.1540	0.8772	1248.9623	0.1622	0.0283	0.1622	0.0283	1.0000
30	0.1175	676.3573	0.2210	0.8228	881.6454	0.2617	0.0378	0.2617	0.0378	1.0000
31	0.1672	1183.5522	0.3987	0.7918	1613.2740	0.4063	0.0542	0.4063	0.0542	1.0000
32	0.3065	20755.6167	5.8972	0.5830	95304.7125	4.9103	0.0845	4.9103	0.0178	0.6244
33	0.2818	26871.5921	0.2818	1.0000	26871.5957	0.7090	0.0776	0.7090	0.0776	1.0000
34	0.1643	1138.8055	0.6332	0.6874	1847.4319	0.3922	0.0521	0.3922	0.0521	1.0000
35	0.4780	108372.6501	3.6817	0.7742	144496.6825	1.0171	0.1613	1.0171	0.1613	1.0000
36	0.2301	621.0656	1.8679	0.5341	1057.3185	1.4274	0.0886	1.4274	0.0607	0.7021
37	0.2067	6151.3786	0.3366	0.9132	7000.0555	0.4765	0.0670	0.4765	0.0670	1.0000

---

 | Show Table

DownLoad: CSV

Additionally, we observe that for the cases of Ebola in Grand Cape Mount, Lofa, Kono and Pandemic Influenza (Cases 9, 10, 17, and 33), we obtained $p = 1$ for the two generalized models. Also, for epidemics when the value of $p$ for GLM is near one, the corresponding value of the parameter for the GGoM is one including the epidemics of Ebola (Kindia, Montserrado; Cases 4 and 12), Plague (Bombay; Case 27) and Cholera (Aalborg; Case 37), in Table 4. We also observe that when the value of the parameter for GLM is small, for example the cases of Ebola (Bomi, Bong; Cases 7 and 8), the value for the GGoM is also small, and for all cases when the value of $p = 1$ en GGoM, the values of $p$ for GLM is greater than $0.6$.

4.3.   Confidence intervals

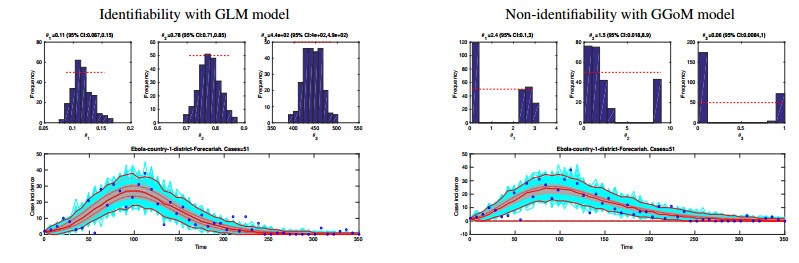
In this part, for the calculation of confidence intervals, we consider the generalized models (GLM and GGoM), for which we can obtain another piece of information to compare both models, and to decide which models best fit a given dataset. To this end we take the same initial parameters obtained for the RMSE calculation, and we use the parametric bootstrap process with 250 simulations with Poisson error structure, defined in Section 3, and summarize the results in Tables 5 and 6. In these results we note that the intervals are narrower and contain the mean value, suggesting that the parameters are identifiable (see ^[1]) for the GLM model. On the other hand, for the GGoM model, this situation occurs in some cases, for example, see Figure 9, where for Case 1 the confidence interval obtained with GLM model has a bar chart that is centred, while that for the GGoM model, the bar chart displays a distribution with two modes. This behavior displayed by the GGoM model can be due to dependency or correlations (presented in Section 2) between the parameters $b$ and $p$.

Table 5.  Confidence intervals for GLM parameters.

Case	$r$		$p$		$K$
no.	mean	95$\%$CI	mean	$95\%$CI	mean	$95\%$CI
1	0.115	(0.086, 0.158)	0.776	(0.696, 0.846)	443.49	(394.90,487.00)
2	0.131	(0.089, 0.200)	0.626	(0.526, 0.717)	406.78	(365.07,452.51)
3	0.423	(0.257, 0.704)	0.627	(0.471, 0.777)	139.71	(119.44,163.74)
4	0.073	(0.062, 0.121)	0.965	(0.790, 1.000)	98.86	(82.50,116.37)
5	0.431	(0.323, 0.548)	0.605	(0.559, 0.671)	726.36	(668.81,778.98)
6	0.240	(0.175, 0.320)	0.678	(0.606, 0.773)	246.65	(218.27,274.52)
7	0.642	(0.378, 1.147)	0.384	(0.227, 0.523)	196.30	(166.86,220.68)
8	0.840	(0.423, 2.038)	0.313	(0.005, 0.499)	199.49	(160.34,283.75)
9	0.058	(0.053, 0.077)	1.000	(0.885, 1.000)	129.27	(108.47,150.70)
10	0.081	(0.078, 0.096)	1.000	(0.950, 1.000)	451.77	(417.50,494.91)
11	0.132	(0.115, 0.149)	0.885	(0.853, 0.922)	833.39	(775.85,894.77)
12	0.115	(0.105, 0.122)	0.908	(0.894, 0.928)	2556.08	(2451.96, 2652.82)
13	0.152	(0.129, 0.176)	0.785	(0.755, 0.818)	1516.06	(1437.87, 1598.21)
14	0.858	(0.638, 1.192)	0.487	(0.418, 0.547)	742.15	(691.23,794.99)
15	0.153	(0.098, 0.216)	0.614	(0.521, 0.729)	299.04	(262.92,333.23)
16	0.329	(0.252, 0.443)	0.652	(0.587, 0.714)	518.72	(473.90,565.42)
17	0.049	(0.047, 0.059)	1.000	(0.954, 1.000)	594.39	(551.33,647.65)
18	0.156	(0.100, 0.235)	0.693	(0.597, 0.813)	300.69	(267.36,329.84)
19	0.240	(0.216, 0.265)	0.722	(0.703, 0.744)	2123.24	(2028.54, 2209.52)
20	0.274	(0.194, 0.374)	0.688	(0.618, 0.760)	620.20	(570.91,671.19)
21	0.205	(0.183, 0.232)	0.749	(0.720, 0.771)	1598.77	(1509.05, 1682.88)
22	0.126	(0.113, 0.139)	0.835	(0.815, 0.855)	2869.41	(2750.68, 2980.44)
23	0.356	(0.161, 0.796)	0.433	(0.162, 0.683)	116.16	(94.65,141.21)
24	0.719	(0.514, 1.012)	0.663	(0.567, 0.761)	263.51	(227.52,299.68)
25	0.256	(0.196, 0.308)	0.796	(0.740, 0.873)	405.35	(361.75,440.83)
26	0.310	(0.289, 0.330)	0.755	(0.747, 0.764)	28794.12	(28454.39, 29171.09)
27	0.078	(0.074, 0.083)	0.961	(0.951, 0.970)	8950.33	(8758.74, 9158.87)
28	0.295	(0.245, 0.353)	0.609	(0.576, 0.645)	1794.21	(1700.83, 1870.10)
29	0.153	(0.118, 0.201)	0.879	(0.819, 0.938)	1250.05	(1145.82, 1369.44)
30	0.221	(0.185, 0.260)	0.824	(0.786, 0.869)	878.98	(821.33,929.29)
31	0.400	(0.353, 0.452)	0.791	(0.765, 0.820)	1618.73	(1522.17, 1682.63)
32	5.899	(5.227, 6.851)	0.583	(0.562, 0.600)	93958.96	(73179.88, 139505.38)
33	3.288	(2.811, 3.494)	0.639	(0.627, 0.663)	26899.66	(23324.67, 28492.81)
34	0.629	(0.552, 0.716)	0.689	(0.665, 0.714)	1848.41	(1745.74, 1928.95)
35	3.700	(3.567, 3.819)	0.774	(0.767, 0.778)	144499.22	(88406.56, 145514.69)
36	1.862	(1.483, 2.435)	0.536	(0.482, 0.585)	1057.80	(986.65, 1116.99)
37	0.338	(0.312, 0.358)	0.912	(0.902, 0.927)	7016.81	(6840.94, 7162.10)

---

 | Show Table

DownLoad: CSV

Table 6.  Confidence intervals for GGoM parameters.

Case	$r$		$b$		$p$
no.	mean	95$\%$CI	mean	$95\%$CI	mean	$95\%$CI)
1	2.399	(0.103, 2.934)	1.489	(0.017, 8.886)	0.061	(0.008, 1.000)
2	0.069	(0.016, 0.178)	0.012	(0.010, 9.034)	0.901	(0.010, 1.000)
3	0.355	(0.292, 0.670)	0.058	(0.043, 0.074)	0.900	(0.589, 1.000)
4	0.129	(0.050, 0.302)	0.030	(0.020, 9.357)	0.977	(0.041, 1.000)
5	0.254	(0.193, 0.327)	0.029	(0.026, 0.033)	0.900	(0.806, 1.000)
6	0.200	(0.175, 0.265)	0.034	(0.028, 0.040)	1.000	(0.716, 1.000)
7	0.523	(0.264, 1.014)	0.023	(0.018, 0.032)	0.535	(0.284, 0.795)
8	0.687	(0.341, 1.479)	0.020	(0.011, 0.032)	0.416	(0.134, 0.718)
9	0.125	(0.082, 1.620)	0.025	(0.018, 8.948)	0.877	(0.068, 1.000)
10	0.174	(0.159, 0.219)	0.029	(0.026, 0.032)	1.000	(0.886, 1.000)
11	0.208	(0.195, 0.270)	0.029	(0.027, 3.012)	0.994	(0.408, 1.000)
12	0.191	(0.185, 0.205)	0.023	(0.022, 0.024)	0.999	(0.971, 1.000)
13	0.139	(0.134, 0.166)	0.020	(0.019, 0.021)	1.000	(0.935, 1.000)
14	0.570	(0.391, 0.814)	0.025	(0.022, 0.029)	0.667	(0.569, 0.784)
15	3.424	(0.071, 4.404)	3.847	(0.014, 9.774)	0.130	(0.005, 0.943)
16	0.236	(0.206, 0.294)	0.032	(0.029, 0.036)	0.951	(0.858, 1.000)
17	0.106	(0.096, 0.983)	0.018	(0.015, 5.936)	0.979	(0.260, 1.000)
18	0.114	(0.091, 3.443)	0.023	(0.018, 9.747)	0.931	(0.004, 1.000)
19	0.175	(0.170, 0.195)	0.022	(0.021, 0.023)	1.000	(0.955, 1.000)
20	0.148	(0.136, 0.215)	0.030	(0.026, 0.032)	1.000	(0.871, 1.000)
21	0.175	(0.169, 0.193)	0.023	(0.021, 0.024)	0.999	(0.948, 1.000)
22	0.130	(0.126, 0.146)	0.019	(0.018, 0.019)	1.000	(0.963, 1.000)
23	0.256	(0.122, 0.671)	0.023	(0.014, 0.035)	0.648	(0.242, 1.000)
24	0.560	(0.109, 3.233)	0.096	(0.077, 9.604)	0.953	(0.037, 1.000)
25	0.297	(0.273, 0.363)	0.046	(0.040, 0.050)	1.000	(0.890, 1.000)
26	0.101	(0.100, 0.112)	0.018	(0.017, 0.018)	1.000	(0.984, 1.000)
27	0.150	(0.148, 0.162)	0.020	(0.020, 0.021)	1.000	(0.980, 1.000)
28	0.134	(0.104, 0.168)	0.014	(0.013, 0.016)	0.899	(0.839, 0.973)
29	0.169	(0.155, 0.268)	0.027	(0.019, 0.030)	0.998	(0.830, 1.000)
30	0.267	(0.253, 0.306)	0.037	(0.034, 0.039)	1.000	(0.929, 1.000)
31	0.409	(0.006, 3.851)	0.055	(0.050, 9.469)	0.973	(0.005, 1.000)
32	4.891	(3.893, 6.247)	0.018	(0.011, 0.025)	0.625	(0.584, 0.664)
33	0.712	(0.705, 0.744)	0.077	(0.076, 0.078)	1.000	(0.989, 1.000)
34	0.559	(0.386, 3.960)	5.605	(0.049, 7.869)	0.305	(0.292, 1.000)
35	1.020	(1.014, 1.096)	0.161	(0.159, 0.162)	1.000	(0.990, 1.000)
36	1.424	(1.114, 1.798)	0.061	(0.054, 0.069)	0.704	(0.632, 0.774)
37	0.481	(0.471, 0.542)	0.067	(0.065, 0.068)	0.999	(0.970, 1.000)

---

 | Show Table

DownLoad: CSV

Figure 9.  Identifiability vs. non-identifiability of parameters for Case No 1.

DownLoad: Full-Size Img PowerPoint

Another observation is that the non-identifiability can be present in the results where the upper and lower limit of the $95\%$CI intervals are not so close, and the mean is not a central value inside the interval. This is observed for the GGoM in the Cases 1 and 24, and the opposite situation can be observed, for instance, for Cases 12 and 19, where the mean value is a central value inside the interval which has the extremes very close. This last situation also appears in all the results derived from the GLM.

5.   Discussion and conclusion

Our systematic comparison of a number of epidemic outbreaks using phenomenological growth models indicates that the GLM outperformed the other models in describing the great majority of the epidemic trajectories. In a few cases (such as Cases 3, 4, 23, and 28) the GGoM outperformed the other models. These findings indicate that the parameter $p$ plays a much more significant role in shaping the dynamic trajectories supported by the GLM compared to the GoM since we observed that the errors of the GoM and GGoM models stay fairly close to each other and the contribution of the adjustment of $p$ remains subtle in some cases. In fact, a closer examination of the parameter estimates derived from both models GoM and GGoM indicates that parameter $p$ is close to 1 in these models, which explains the similarity in the fits derived from these models. So the GGoM model could be reduced to GoM without much impact on the model fit. This is in sharp contrast to what is happening with the logistic models where both the LM and GLM models only yield similar fits for three epidemics. Future research could be directed at determining which of the models equipped with generalized growth are easier to calibrate than the other, considering the initial or final parts of the dynamics and with the aim to improve predictions.

Referring to the parameter estimation procedure and the need to provide an initial solution to the optimization numerical methods, we have found that Matlab functions and the steps defined in the section 3.3, are sufficient for the present study, in agreement with the experience made in ^[1,18]. However, since there is a limited range for some of the parameters (as is the case of parameter $p$, but not of the others) it might be interesting future work to use metaheuristic procedures to the parameter estimation that possibly guarantee in an appropriate form that the parameters found are indeed optimal globally. As is mentioned in ^[26], such procedures include simulated annealing (see, e.g., ^[27,31,59]), variable neighborhood search (VNS) ^[27,31], and the so-called firefly algorithm ^[33].

While we compared phenomenological growth models based on their ability to describe empirical trajectories of real epidemics, our methodology could be extended to assess the "distance" between models in terms of the range of dynamics supported by model A that can also be supported by model B and vice versa. For instance, based on our empirical findings we hypothesize that the distance between the LM and GLM models is larger compared to the distance between the GoM and GGoM models. Importantly such distance could be derived for any pair of models regardless of model complexity. Future work could explore this research direction by analyzing a larger set of dynamic models including phenomenological and mechanistic models.

Acknowledgements

RB is supported by Fondecyt project 1170473; CONICYT/PIA/Concurso Apoyo a Centros Científicos y Tecnológicos de Excelencia con Financiamiento Basal AFB170001; and CRHIAM, project CONICYT/FONDAP/15130015. GC acknowledges financial support from grants NSF-IIS RAPID award #1518939, NSF grant 1318788 Ⅲ: Small: Data Management for Real-Time Data Driven Epidemic simulation, and Conicyt (Chile), project MEC80170119. LYLD is supported by CONICYT scholarship CONICYT-PCHA/Doctorado Nacional/2019-21190640.

Conflict of interest

All authors declare no conflicts of interest in this paper.