1.
Introduction
The investigation of partially ordered algebraic systems was initiated by Conrad[16,17]. Particularly, an ordered semigroup (also called a partially ordered semigroup or a po-semigroup) is a well-known example of the partially ordered algebraic systems, which is a semigroup together with a compatible partial order. The notion of ideals and filters on ordered semigroups play a significant role in studying the structure of ordered semigroups, especially the decompositions of ordered semigroups see [2,23,34], and there are many applications in various branches of mathematics and computer science. Many mathematicians have studied different aspects of ideals and filters on ordered semigroups. For examples, see [2,22,23,24,25,34].
The theory of algebraic hyperstructures have been originated by Marty[28] in 1934 when he studied hypergroups, which are considered as a generalization of groups, by using hyperoperations. Later on, several kinds of hyperstructures were studied by many mathematicians, for instance, see [4,5,6,7,19,20,26]. In 2011, Davvaz and Heidari[18] applied the notion of ordered semigroups to hyperstructures and presented a new class of hyperstructures called ordered semihypergroups. Such hyperstructure can be considered as an extension and a generalization of ordered semigroups. The relationships between ordered semihypergroups and ordered semigroups were described by Davvaz et al.[11]. Some properties of hyperideals on ordered semihypergroups were investigated by Changphas and Davvaz[3]. Next, Tang et al.[32] introduced the concept of a (right, left) hyperfilter on ordered semihypergroups and discussed their related properties. Omidi and Davvaz[29] generalized the concept of the relation N on ordered semigroups into ordered semihypergroups and proved some remarkable results. Note that, in an ordered semihypergroup S, the relation N on S is defined by N:={(x,y)∈S×S:N(x)=N(y)} where N(x) is the hyperfilter generated by the element x of S. Kehayopulu[21] proved that the relation N is the least semilattice congruence on semihypergroups. Meanwhile, Kehayopulu illustrate by counterexample that N is not the least semilattice congruence on ordered semihypergroups in general. The author introduced the concept of complete semilattice congruence on ordered semihypergroups and proved that N is the smallest complete semilattice congruence. Recently, Tang and Davvaz[31] studied the relation N and Green's relations, especially the relations L,R and J, on ordered semihypergroups. They showed that every (respectively, right, left) hyperideal can be decomposable into its (R-, L-)J-classes and posed a problem: " Can every prime hyperideal be decomposable into its N-classes?"
On the other hand, the investigation of algebraic hyperstructures have been widely expanded. In 2006, Davvaz and Vougiouklis[14] applied the notion of hypergroups to n-ary algebras and presented the notion of n-ary hypergroups for n≥2. Leoreanu-Fotea and Davvaz [27] studied some binary relations on n-ary hypergroups. Anvariyeh and Momeni [1] investigated the interesting properties of n-ary relations on n-ary hypergroups. In 2009, Davvaz et al.[13] introduced a new class of hyperstructure called n-ary semihypergroups. This new class can be considered as a natural extension of semigroups, semihypergroups, ternary semigroups, ternary semihypergroups and n-ary semigroups. The interesting results of n-ary semigroups and n-ary semihypergroups, the readers can be referred to [8,12,13,15,30]. Recently, Daengsaen and Leeratanavalee [9] applied the theory of n-ary algebras to ordered semihypergroups and introduced the notion of ordered n-ary semihypergroups for n≥2. Such new notion is a natural generalization of ordered semigroups, ordered semihypergroups, ordered ternary semigroups and ordered ternary semihypergroups. Also, they characterized several kinds of regularities of ordered n-ary semihypergroups. In this paper, we attempt to study the notion of hyperfilters on ordered n-ary semihypergroups. In particular, we introduce the concept of j-hyperfilters, for all positive integers 1≤j≤n and n≥2, of ordered n-ary semihypergroups and use such concept to construct the relation N for studying the properties of semilattice congruence on ordered n-ary semihypergroups where n≥2.
The present paper is organized as follows. In Section 2, we recall some basic notions and elementary results of algebraic hyperstructures. In Section 3, we introduce the concept of j-hyperfilters, which is a generalization of left and right hyperfilters of ordered semihypergroups and discuss the connection between j-hyperfilters and completely prime j-hyperideals on ordered n-ary semihypergroups where n≥2. In Section 4, we investigate some properties of the relation N on n-ary semihypergroups. We illustrate by counterexample that N does not necessarily to be the least semilattice congruence on n-ary semihypergroup, where n≥3, in general. At the meantime, we provide a sufficient condition that makes the previous result true. In Section 5, we introduce the concept of a complete ∗-semilattice (strongly) regular relation on ordered n-ary semihypergroups, where n≥3, and prove that N is the smallest complete ∗-semilattice strongly regular relation. In the last section, we give an example to show that a prime hyperideal of ordered n-ary semihypergroups cannot be decomposable into its N-classes in general. However, we provide some special condition for prime hyperideals that lead to be decomposable into its N-classes. As an application of our results, the related problem posed by Tang and Davvaz is solved.
2.
Preliminaries
In this section, we recall some elementary results of algebraic hyperstructures. For more detail, we refer to [8,9,12,13,14].
Let S be a nonempty set and let P∗(S) denote the set of all nonempty subsets of S. A mapping f:S×⋯×S⏟S appearsn≥2times→P∗(S) is called an n-ary hyperoperation. A structure (S,f) is called an n-ary hypergroupoid [14]. Throughout this paper, we use the symbol akj to denote a sequence of elements aj,aj+1,...,ak of S. For the case k<j, akj is the empty symbol. Then f(a1,a2,...,an)=f(an1) and
In case a1=...=aj=a and ck+1=...=cn=c, we write the second expression in the form f(aj,bkj+1,cn−k). For the symbols of a sequence of subsets of S, we denote analogously. For X1,...,Xn∈P∗(S), we define
If X1={a1}, then we write f({a1},Xn2) as f(a1,Xn2) and analogously in other cases. In case X1=...=Xj=Y and Xj+1=...=Xn=Z, we write f(Xn1) as f(Yj,Zn−j). The hyperoperation f is associative[13] if
hold for all a2n−11∈S and for all 1<j≤n. In this case, the n-ary hypergroupoid (S,f) is called an n-ary semihypergroup (also called an n-ary hypersemigroup)[13].
An ordered n-ary semihypergroup (S,f,≤) (also called a partially ordered n-ary semihypergroup or a po-n-ary semihypergroup)[9] is an n-ary semihypergroup (S,f) and a partially ordered set (S,≤) such that a partial order ≤ is compatible with f. Indeed, for any a,b∈S,
for all cn1∈S and for all 1≤j≤n. Note that, for any X,Y∈P∗(S), X⪯Y means for every x∈X there exists y∈Y such that x≤y. If H is an n-ary subsemihypergroup of an ordered n-ary semihypergroup (S,f,≤), i.e f(Hn)⊆H, then (H,f,≤) is an ordered n-ary semihypergroup.
Definition 2.1. [9] Let (S,f,≤) be an ordered n-ary semihypergroup. For any positive integer 1≤j≤n and n≥2, a nonempty subset I of S is called a j-hyperideal of S if it satisfies the following two conditions:
(I1)I is a j-hyperideal of an n-ary semihypergroup (S,f), i.e., f(aj−11,b,anj+1)⊆I for all b∈I and aj−11,anj+1∈S.
(I2) If b∈I and c∈S such that c≤b then c∈I.
If I is a j-hyperideal, for all 1≤j≤n, then I is said to be a hyperideal.
Here, 1-hyperideal (n-hyperideal) is called a right hyperideal (left hyperideal), respectively. Throughout this paper, we let S stand for an ordered n-ary semihypergroup (S,f,≤). By applying Lemma 4 in [8], the following lemma is obtained.
Lemma 2.2. [8] For any positive integer 1≤j≤n, let {Ik:k∈J} be a collection of j-hyperideals (hyperideals) of S. Then ⋃k∈JIk is a j-hyperideal (hyperideal) of S and ⋂k∈JIk is also a j-hyperideal (hyperideal) of S if ⋂k∈JIk≠∅.
A nonempty subset P of S is called prime[31] if, for every an1∈S, f(an1)⊆P implies ak∈P for some 1≤k≤n. Equivalently, if an1∉P then f(an1)⊈P.
P is called completely prime[32] if, for every an1∈S, f(an1)∩P≠∅ implies ak∈P for some 1≤k≤n. Equivalently, if an1∉P then f(an1)∩P=∅.
A (j-)hyperideal I of S is called a prime (j-)hyperideal (completely prime (j-)hyperideal) of S if I is a prime (completely prime) subset of S. Clearly, every completely prime (j-)hyperideal of S is a prime (j-)hyperideal of S.
Example 2.3. Let Z be the set of all integers. Define f:Zn→P∗(Z) by
for all xn1∈Z. Then (Z,f,≤) is an ordered n-ary semihypergroup where ≤ is a usual partial order on Z. Let N be the set of all natural numbers. Then (N,f,≤) is an ordered n-ary subsemihypergroup of Z.
Example 2.4. Let S={w,x,y,z}. Define f:Sn→P∗(S) by f(xn1)=((...(x1∘x2)∘...)∘xn), for all xn1∈S, where ∘ is defined by the following table.
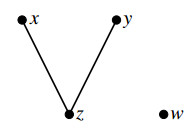
By applying Example 2 in [31], (S,f) is an n-ary semihypergroup. Define a partial order ≤ on S as follows:
Such relation can be presented by the following diagram.
Then (S,f,≤) is an ordered n-ary semihypergroup. It is easy to verify that the sets A1={x,z}, A2={y,z}, A3={w,x,z} and A4={x,y,z} are all proper 2-hyperideals of S. Then we obtain the results as follows:
(1) A1 and A4 are not prime since there exists w∈S∖Ak such that f(wn)⊆Ak for all k=1,4. It follows that A1,A4 are also not completely prime.
(2) A2 is prime since f(xn1)⊈A2 for all xn1∈S∖A2. But, it is not completely prime since there exists w∈S∖A2 such that f(wn)∩A2≠∅.
(3) A3 is completely prime since f(xn1)∩A3=∅ for all xn1∈S∖A3. It follows that A3 is prime.
3.
Hyperfilters on ordered n-ary semihypergroups
In this section, we introduce the concept of j-hyperfilters on ordered n-ary semihypergroups, which generalizes the notion of right and left hyperfilters on ordered semihypergroups[32], and investigate their related properties.
Definition 3.1. Let (S,f,≤) be an ordered n-ary semihypergroup. For any positive integer 1≤j≤n and n≥2, an n-ary subsemihypergroup K of S is said to be a j-hyperfilter of S if it satisfies the following two conditions:
(F1)K is a j-hyperfilter of an n-ary semihypergroup (S,f), i.e., for all an1∈S, f(an1)∩K≠∅ implies aj∈K.
(F2) If for any a∈K and b∈S such that a≤b then b∈K.
If K is a j-hyperfilter, for all 1≤j≤n, then K is called a hyperfilter.
Here, 1-hyperfilter (n-hyperfilter) is said to be a right hyperfilter (left hyperfilter, respectively). For any a∈S and 1≤j≤n, we denote by Nj(a)(N(a)) the j-hyperfilter (hyperfilter) of S generated by a and called the principal j-hyperfilter (hyperfilter) generated by a. A j-hyperfilter (hyperfilter) K of S is said to be proper if K≠S. Clearly, Definition 3.1 coincides with Definition 3.1 given in [32] if n=2.
Example 3.2. Let S={w,x,y,z}. Define f:Sn→P∗(S) by f(xn1)=((...(x1∘x2)∘...)∘xn), for all xn1∈S, where ∘ is defined by the following table
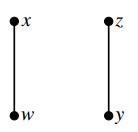
and a partial order ≤ is defined as follows:
Such relation can be presented by the following diagram.
By applying Example 3.3 in [33], (S,f,≤) is an ordered n-ary semihypergroup. Clearly, the sets {w,x} and S are all 1-hyperfilters of S.
Proposition 3.3. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2. For any 1≤j≤n, let K1,K2 be two j-hyperfilters of S. Then K1∩K2 is a j-hyperfilter of S if K1∩K2≠∅.
Proof. Let an1∈K1∩K2. Then an1∈Ki for all i=1,2. Since Ki is an n-ary subsemihypergroup, we obtain f(an1)⊆K1∩K2. Thus K1∩K2 is an n-ary semihypergroup of S. Next, let bn1∈S and c∈f(bn1)∩(K1∩K2). Then c∈f(bn1)∩Ki for all i=1,2. Since Ki is a j-hyperfilter of S, we have bj∈Ki for all i=1,2. So bj∈K1∩K2. Finally, let a∈K1∩K2 such that a≤b∈S. Since Ki is a j-hyperfilter, we obtain b∈Ki for all i=1,2. So b∈K1∩K2. Therefore K1∩K2 is a j-hyperfilter of S.
By Proposition 3.3, we obtain the following result.
Corollary 3.4. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2 and K1,K2 be two hyperfilters of S. K1∩K2 is a hyperfilter of S if K1∩K2≠∅.
Proposition 3.3 and Corollary 3.4 show that the intersection of finitely many j-hyperfilters(hyperfilters) of S is always a j-hyperfilter(hyperfilter) if their intersection is nonempty. In 2015, Tang et al.[32] showed that the union of two hyperfilters of an ordered semihypergroup H (for a special case n=2) is not necessarily a hyperfilter of H (see Example 3.5 in [32]). Using the idea of Lemma 3.6 in [32], we obtain the results as follows.
Proposition 3.5. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥3. For any 1<j<n, let K1,K2 be two j-hyperfilters of S. Then K1∪K2 is a j-hyperfilter of S if and only if K1⊆K2 or K2⊆K1.
Proof. Now, let j be a fixed positive integer with 1<j<n and n≥3. Let K1∪K2 be a j-hyperfilter of S. Assume that K1⊈K2 and K2⊈K1. There are a,b∈K1∪K2 such that a∈K1,a∉K2,b∉K1 and b∈K2. Since K1∪K2 is an n-ary subsemihypergroup, we have f(aj−1,bn−j+1)⊆K1∪K2. If f(aj−1,bn−j+1)∩K1≠∅ then, since K1 is a j-hyperfilter of S, we obtain b∈K1. It is impossible. So f(aj−1,bn−j+1)∩K1=∅. This implies that f(aj−1,bn−j+1)⊆K2. Since K2 is an n-ary subsemihypergroup, we obtain f(bj−1,f(aj−1,bn−j+1),bn−j)⊆K2. Then
Since K2 is a j-hyperfilter, we obtain a∈K2. It is impossible. Thus K1⊆K2 or K2⊆K1. Conversely, if K1⊆K2 or K2⊆K1 then K1∪K2 is a j-hyperfilter of S.
Corollary 3.6. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2 and K1,K2 be two hyperfilters of S. Then K1∪K2 is a hyperfilter of S if and only if K1⊆K2 or K2⊆K1.
Theorem 3.7. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2 and K∈P∗(S). For any 1≤j≤n, the following assertions are equivalent.
(i)K is a j-hyperfilter of S.
(ii)S∖K=∅ or S∖K is a completely prime j-hyperideal of S.
Proof. (i) ⟹ (ii) Let K be a j-hyperfilter of S. Suppose that S∖K≠∅. We show that S∖K is a completely prime j-hyperideal of S. First of all, we show that K is a j-hyperideal of S. Let a∈S∖K and bj−11,bnj+1∈S. If f(bj−11,a,bnj+1)∩K≠∅ then, since K is a j-hyperfilter, we get a∈K. It is impossible. So f(bj−11,a,bnj+1)∩K=∅. It implies that f(bj−11,a,bnj+1)⊆S∖K. Next, let x∈S and y∈S∖K such that x≤y. If x∉S∖K then x∈K. By Definition 3.1 (F2), we have y∈K. It is impossible. Hence x∈S∖K. Thus S∖K is a j-hyperideal of S. Next, we show that S∖K is completely prime. Let an1∈S such that f(an1)∩(S∖K)≠∅. Assume that ai∉S∖K for all i=1,...,n. Then ai∈K for all i=1,...,n. Since K is an n-ary subsemihypergroup, we obtain f(an1)⊆K. It implies that f(an1)∩(S∖K)=∅, which is impossible. Hence ai∈S∖K for some i=1,...,n. Thus S∖K is a completely prime j-hyperideal of S.
(ii) ⟹ (i) If S∖K=∅ then K=S is a j-hyperfilter of S. Now, suppose that S∖K is a completely prime j-hyperideal of S. We will show that K is a j-hyperfilter of S. First of all, let an1∈K. If f(an1)⊈K then f(an1)∩(S∖K)≠∅. Since S∖K is completely prime, we obtain ai∈S∖K for some i=1,...,n. It is impossible. Thus f(an1)⊆K. Next, let bn1∈S and f(bn1)∩K≠∅. If bj∉K then bj∈S∖K. Since S∖K is a j-hyperideal, we obtain f(bn1)⊆f(Sj−1,bj,Sn−j)⊆f(Sj−1,(S∖K),Sn−j)⊆S∖K. This is impossible. So bj∈K. Finally, let x∈K and y∈S such that x≤y. If y∉K then y∈S∖K. Since S∖K is a j-hyperideal, by Definition 2.1 (I2), we get x∈S∖K. It is impossible. So y∈K. Therefore K is a j-hyperfilter of S.
Using the similar proof of the previous theorem, we obtain the result as follows.
Corollary 3.8. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2 and K∈P∗(S). Then the following assertions are equivalent.
(i)K is a hyperfilter of S.
(ii)S∖K=∅ or S∖K is a completely prime hyperideal of S.
Example 3.9. From the ordered n-ary semihypergroup (S,f,≤) given in Example 3.2, we know that the set {w,x} is a proper 1-hyperfilter of S. By Theorem 3.7, we have {y,z}=S∖{w,x} is a completely prime 1-hyperideal of S. In fact, one can verify that a proper completely prime 1-hyperideal of S is {y,z} since f(xn1)∩{y,z}=∅ for all xn1∈S∖{y,z}.
Lemma 3.10. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2 and a,b∈S. For any 1≤j≤n, the following assertions hold:
(i) If b∈Nj(a) then Nj(b)⊆Nj(a).
(ii) If a≤b then Nj(b)⊆Nj(a).
(iii) If a≤b then Nj(a)∖Nj(b) is a completely prime j-hyperideal of Nj(a) where Nj(a)∖Nj(b)≠∅.
Proof. (i) Let b∈Nj(a). Since Nj(b) is the smallest j-hyperfilter of S containing b, we have Nj(b)⊆Nj(a).
(ii) Let a≤b. Since Nj(a) is a j-hyperfilter of S and a∈Nj(a), by Definition 3.1 (F2), we obtain b∈Nj(a). By (i), we have Nj(b)⊆Nj(a).
(iii) Let a≤b. Then Nj(b)⊆Nj(a). By Theorem 3.7, we have Nj(a)∖Nj(b)=∅ or Nj(a)∖Nj(b) is a completely prime j-hyperideal of Nj(a). Thus Nj(a)∖Nj(b) is a completely prime j-hyperideal of Nj(a) where Nj(a)∖Nj(b)≠∅.
Remark 3.11. Lemma 3.10 is still true if the principal j-hyperfilters Nj(a) and Nj(b) are replaced by the principal hyperfilters N(a) and N(b), respectively. Moreover, the results on this section also hold on n-ary semihypergroups (S,f).
4.
Semilattice strongly regular relations on n-ary semihypergroups
In this section, we introduce the concept of semilattice (strongly) regular relations on n-ary semihypergroups and investigate their related properties.
Let (S,f) be an n-ary semihypergroup with n≥2 and ρ be a relation on S. For any two elements A,B∈P∗(S), we write
AˉρB if and only if for any a∈A there exists b∈B such that aρb and for all b′∈B there exists a′∈A such that a′ρb′,
AˉˉρB if and only if aρb for all a∈A and b∈B, see [10].
For any 1≤j≤n, an equivalence relation ρ is called j-regular relation (strongly j-regular relation) if, for every a,b,xn1∈S,
Here, ρ is said to be a regular relation (strongly regular relation) if it is a j-regular relation (strongly j-regular relation) for all 1≤j≤n.
Lemma 4.1. Let (S,f) be an n-ary semihypergroup with n≥2. For any An1,Bn1∈P∗(S), the following statements hold:
(i) If ρ is regular and AkˉρBk, for all k=1,...,n, then f(An1)ˉρf(An1).
(ii) If ρ is strongly regular and AkˉˉρBk, for all k=1,...,n, then f(An1)ˉˉρf(An1).
Proof. The proof is straightforward.
Definition 4.2. Let (S,f) be an n-ary semihypergroup with n≥2. A regular relation (strongly regular relation) ρ on S is said to be a semilattice regular relation (semilattice strongly regular relation) if
for all x,xn1∈S and for all α∈Sn where Sn is the set of all permutations on {1,2,...,n}.
Note that any semilattice strongly regular relation, semilattice equivalence relation[29] and semilattice congruence[21] on semihypergroups (for case n=2) are the same.
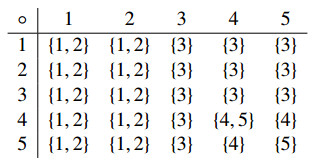
Example 4.3. Let S={1,2,3,4,5}. Define f:S×S×S→P∗(S) by f(x1,x2,x3)=(x1∘x2)∘x3, for all x1,x2,x3∈S, where ∘ is defined by the following table.
By applying Example 3.2 in [32], (S,f) is a ternary semihypergroup (an 3-ary semihypergroup). Let
It is easy to show that σ1,σ2 are equivalence relations on S. Furthermore, one can verify that σ2 is a semilattice strongly regular relation on S. On the other hand, σ1 is not a semilattice strongly regular relation on S because we have f(4,4,4)={4,5} but (4,5)∉σ1, so σ1 does not satisfy with the condition 4 ¯¯σ1f(4,4,4) in Definition 4.2.
For any K∈P∗(S), we write δK:={(a,b)∈S×S:a,b∈K or a,b∉K}. Clearly, δK is an equivalence relation on S.
Theorem 4.4. Let (S,f) be an n-ary semihypergroup with n≥2 and K be a completely prime hyperideal of S. Then δK is a semilattice strongly regular relation on S.
Proof. Let K be a completely prime hyperideal of S.
(1) We show that δK is a strongly regular relation. Firstly, let j be a fixed positive integer with 1≤j≤n. Let a,b,xj−11,xnj+1∈S such that aδKb. To show that f(xj−11,a,xnj+1)¯¯δKf(xj−11,b,xnj+1), let u∈f(xj−11,a,xnj+1) and v∈f(xj−11,b,xnj+1). Since aδKb, we have a,b∈K or a,b∉K.
Case 1.1: a,b∈K. Since K is a j-hyperideal, we get u∈f(xj−11,a,xnj+1)⊆K and v∈f(xj−11,b,xnj+1)⊆K. So uδKv.
Case 1.2: a,b∉K. Then we have 2 subcases to be considered as follows.
Case 1.2.1: There exists xi∈K for some i=1,...,j−1,j+1,...,n. Since K is an i-hyperideal, we obtain u∈f(xj−11,a,xnj+1)⊆K and v∈f(xj−11,b,xnj+1)⊆K. So uδKv.
Case 1.2.2: xi∉K for all i=1,...,j−1,j+1,...,n. Then f(xj−11,a,xnj+1)∩K=∅ and f(xj−11,b,xnj+1)∩K=∅. In fact, if f(xj−11,a,xnj+1)∩K≠∅ then, since K is completely prime, we obtain xi∈K for some i=1,...,n (we write xi=a if i=j), which is a contradiction. Similarly, if f(xj−11,b,xnj+1)∩K≠∅ then we also get a contradiction. Thus f(xj−11,a,xnj+1)∩K=∅ and f(xj−11,b,xnj+1)∩K=∅. Hence u∈f(xj−11,a,xnj+1)⊆S∖K and v∈f(xj−11,b,xnj+1)⊆S∖K. It follows that uδKv. From Case 1.1 and 1.2, we conclude that f(xj−11,a,xnj+1)¯¯δKf(xj−11,b,xnj+1) and so δK is a strongly j-regular relation. For arbitrary positive integer j, we obtain δK is a strongly regular relation.
(2) We show that δK is semilattice. Let a,an1∈S and α∈Sn. Firstly, we show that a¯¯δKf(an). Let u∈f(an). We consider two cases as follows.
Case 2.1: a∈K. Since K is a hyperideal of S, we have u∈f(an)⊆K. So aδKu.
Case 2.2: a∉K. Then f(an)∩K=∅. In fact, if f(an)∩K≠∅ then, since K is completely prime, we have a∈K. It is impossible. So f(an)∩K=∅. It follows u∉K. So aδKu. From Cases 2.1 and 2.2, we conclude that a¯¯δKf(an). Next, we show that f(an1)¯¯δKf(aα(n)α(1)). Let u∈f(an1) and v∈f(aα(n)α(1)). We consider two cases as follows.
Case 1: f(an1)∩K≠∅. Since K is completely prime, we obtain ai∈K for some i=1,...,n. Since α is bijective, there is i′∈{1,...,n} such that α(i′)=i. Since K is an i′-hyperideal and an i-hyperideal, we obtain f(aα(n)α(1))=f(aα(1),...,aα(i′),....,aα(n))⊆K and f(an1)=f(a1,...,ai,...,an)⊆K. Thus u,v∈K and it follows that uδKv.
Case 2: f(an1)∩K=∅. Then f(aα(n)α(1))∩K=∅. Indeed, if f(aα(n)α(1))∩K≠∅ then, since K is completely prime, we have aα(i′)∈K for some i′∈{1,...,n}. We set i=α(i′). Since K is an i-hyperideal, we obtain f(an1)=f(a1,...,ai,...,an)⊆K. It is impossible. Thus f(aα(n)α(1))∩K=∅. Hence u∈f(an1)⊆S∖K and v∈f(aα(n)α(1))⊆S∖K and it follows that uδKv. From Cases 1 and 2, we conclude that f(an1)¯¯δKf(aα(n)α(1)) and the proof is complete.
For any positive integer 1≤j≤n and n≥2, let Nj (N) denote the relation on an (ordered) n-ary semihypergroup S which is defined by
Clearly, Nj and N are equivalence relations on S. For any a∈S, we denote by (a)Nj the Nj-class containing a and the set S/Nj:={(a)Nj:a∈S}. For the relation N, we define analogously.
Theorem 4.5. Let (S,f) be an n-ary semihypergroup with n≥2. Then the following statements hold:
(i)N is a semilattice strongly regular relation.
(ii)N=⋂{δK:K∈CPI(S)},
where CPI(S) is the set of all completely prime hyperideals of S.
Proof. (i) First of all, we show that N is a strongly regular relation on S. Let a,b,xn1∈S such that aNb. Then N(a)=N(b). For any fixed positive integer j with 1≤j≤n, let u∈f(xj−11,a,xnj+1) and v∈f(xj−11,b,xnj+1). Since f(xj−11,a,xnj+1)∩N(u)≠∅ and N(u) is a hyperfilter, by Definition 3.1 (F1), we obtain a,xj−11,xnj+1∈N(u). By Lemma 3.10, we obtain N(a)⊆N(u). Since b∈N(b)=N(a), we get b∈N(u). Since b,xj−11,xnj+1∈N(u) and N(u) is an n-ary subsemihypergroup, we obtain v∈f(xj−11,b,xnj+1)⊆N(u). By Lemma 3.10, we have N(v)⊆N(u). Using the similar previous process, we also obtain that N(u)⊆N(v). So N(u)=N(v) and it follows that uNv. Hence f(xj−11,a,xnj+1)¯¯Nf(xj−11,b,xnj+1). So N is a strongly regular relation on S. Next, we show that N is a semilattice strongly regular relation on S. Let a,an1∈S and α∈Sn. To show that a¯¯Nf(an), let u∈f(an). Then f(an)∩N(u)≠∅. By Definition 3.1 (F1), we obtain a∈N(u). By Lemma 3.10, we get N(a)⊆N(u). Since N(a) is an n-ary subsemihypergroup and a∈N(a), we obtain u∈f(an)⊆N(a). By Lemma 3.10, we have N(u)⊆N(a). So N(a)=N(u) and it implies that a¯¯Nf(an). Finally, we show that f(an1)¯¯Nf(aα(n)α(1)). Let u∈f(an1) and v∈f(aα(n)α(1)). Since f(an1)∩N(u)≠∅, by Definition 3.1 (F1), we obtain an1∈N(u). It follows that v∈f(an1)⊆N(u) and so N(v)⊆N(u). Conversely, since f(aα(n)α(1))∩N(v)≠∅, by using the same process, we have N(u)⊆N(v). So N(u)=N(v) and it follows that uNv. Hence f(an1)¯¯Nf(aα(n)α(1)). Thus N is a semilattice strongly regular relation on S.
(ii) Firstly, we will show that N⊆⋂{δK:K∈CPI(S)}. Let (x,y)∈N. Then N(x)=N(y). Assume that (x,y)∉δK for some K∈CPI(S). Then there exist two cases:
Case 1.1: x∈K and y∉K. Then y∈S∖K⊆S. Since S∖(S∖K)=K is completely prime, by Corollary 3.8, we have S∖K is a hyperfilter of S. Since y∈S∖K, by Lemma 3.10, we obtain x∈N(x)=N(y)⊆S∖K. It is impossible.
Case 1.2: x∉K and y∈K. Using the similar proof as in Case 1.1, we also get a contradiction. From Cases 1.1 and 1.2, we conclude that (x,y)∈δK for all K∈CPI(S). Thus N⊆⋂{δK:K∈CPI(S)}. Conversely, let (x,y)∈δK for all K∈CPI(S). Assume that (x,y)∉N. Then there exist 2 cases, i.e. x∉N(y) or y∉N(x). Indeed, if x∈N(y) and y∈N(x) then, by Lemma 3.10, we get N(x)⊆N(y) and N(y)⊆N(x). Consequently, N(x)=N(y) and so (x,y)∈N. This is a contradiction. Thus x∉N(y) or y∉N(x).
Case 2.1: x∉N(y). Then x∈S∖N(y). Since N(y) is a hyperfilter and S∖N(y)≠∅, by Corollary 3.8, we have S∖N(y) is a completely prime hyperideal. Since x∈S∖N(y) and y∉S∖N(y), it follows that (x,y)∉δS∖N(y). This is a contradiction.
Case 2.2: y∉N(x). Using the similar proof as in Case 2.1, we get a contradiction. Hence (x,y)∈N. Therefore ⋂{δK:K∈CPI(S)}⊆N and the proof is complete.
As we have known from [21] that the relation N is the smallest semilattice strongly regular relation on semihypergroups. However, we illustrate by the following example that the similar result in n-ary semihypergroups, for n≥3, is not necessary true.
Example 4.6. Let S={1,−1,i,−i}. Then (S,⋅) is a commutative semigroup under the usual multiplication ⋅ over complex numbers. Define f:S×S×S→P∗(S) by f(x,y,z)={x⋅y⋅z}. Then (S,f) is a ternary semihypergroup. Clearly, CPI(S)={S}. In fact, suppose that A is an arbitrary hyperideal of S.
If 1∈A then S=f(S,1,1)⊆f(S,S,1)⊆A.
If −1∈A then S=f(S,−1,−1)⊆f(S,S,−1)⊆A.
If i∈A then S=f(S,−i,i)⊆f(S,S,i)⊆A.
If −i∈A then S=f(S,i,−i)⊆f(S,S,−i)⊆A.
Consequently, S=A. By Theorem 4.5(ii), we have
N=δS={(1,1),(1,−1),(1,i),(1,−i),(−1,1),(−1,−1),(−1,i),(−1,−i),
(i,1),(i,−1),(i,i),(i,−i),(−i,1),(−i,−1),(−i,i),(−i,−i)}.
Next, let
It is not difficult to show that ρ is a strongly regular relation on S. Furthermore, we have
Since (S,⋅) is commutative, we get f(x31)=f(xα(3)α(1)) and so f(x31) ˉˉρf(xα(3)α(1)) for all α∈S3. By Definition 4.2, we conclude that ρ is a semilattice strongly regular relation on S and ρ⊆N.
By the previous example, we observe that the relation N is not necessary the smallest semilattice strongly regular relation on n-ary semihypergroups, for n≥3, in general. To provide a sufficient condition that makes the above conclusion true, we need to introduce the following definition.
Definition 4.7. Let (S,f) be an n-ary semihypergroup with n≥3. A semilattice regular relation (semilattice strongly regular relation) ρ on S is called a ∗-semilattice regular relation (∗-semilattice strongly regular relation) if for every x,y∈S,
Example 4.8. Consider a ternary semihypergroup (S,f) given in Example 4.6. Obviously, −i ˉˉρ f(−i,−1,−1)={−i}. Since f(−i,−i,−1)={1} and (−i,1)∉ρ, we conclude that ρ is not a ∗-semilattice strongly regular relation on S.
However, the relation N is always a ∗-semilattice strongly regular relation on n-ary semihypergroups where n≥3.
Proposition 4.9. Let (S,f) be an n-ary semihypergroup with n≥3. Then the following assertions hold:
(i) If K is a completely prime hyperideal of S, then δK is a ∗-semilattice strongly regular relation on S.
(ii) The relation N is a ∗-semilattice strongly regular relation on S.
Proof. From Theorems 4.4 and 4.5, we obtain that δK and N are semilattice strongly regular relations on S.
(i) Let x,y∈S be such that x¯¯δKf(x,yn−1). To show that x¯¯δKf(xn−1,y), let a∈f(xn−1,y). We consider two cases as follows:
Case 1: x∉K. Since x¯¯δKf(x,yn−1), by the definition of δK, we have f(x,yn−1)∩K=∅. It follows that f(x,yn−1)∩(S∖K)≠∅. Since K is a completely prime hyperideal of S, by Corollary 3.8, we have S∖K is a hyperfilter of S. By (F1) in Definition 3.1, we have x,y∈S∖K. Since S∖K is an n-ary subsemihypergroup of S, we obtain a∈f(xn−1,y)⊆S∖K. By the definition of δK, we have xδKa. Thus x¯¯δKf(xn−1,y).
Case 2: x∈K. Since K is a hyperideal of S, by (I1) in Definition 2.1, we obtain a∈f(xn−1,y)⊆K. Consequently, xδKa and so x¯¯δKf(xn−1,y). From Cases 1 and 2, we conclude that δK is a ∗-semilattice strongly regular relation on S.
(ii) Let x,y∈S with x¯¯Nf(x,yn−1). Then N(x)=N(b) for all b∈f(x,yn−1). To show that x¯¯Nf(xn−1,y), let c∈f(xn−1,y). Since b∈f(x,yn−1)∩N(x), by (F1) in Definition 3.1, we have x,y∈N(x). Since N(x) is an n-ary semihypergroup, we have c∈f(xn−1,y)⊆N(x). By Lemma 3.10, we get N(c)⊆N(x). Conversely, since f(xn−1,y)∩N(c)≠∅, by (F1) in Definition 3.1, we have x∈N(c). So N(x)⊆N(c). Consequently, N(x)=N(c) and it follows that xNc for all c∈f(xn−1,y). Therefore x¯¯Nf(xn−1,y) and the proof is complete.
Theorem 4.10. Let (S,f) be an n-ary semihypergroup with n≥3. Let ρ be a ∗-semilattice strongly regular relation on S. Then there exists a collection C of proper completely prime hyperideals of S such that
Proof. Let x∈S. Setting
Since ρ is a ∗-semilattice strongly regular relation, we obtain xˉˉρf(xn). So x∈Fx. Firstly, we show that Fx is a hyperfilter of S.
(1) We show that Fx is an n-ary subsemihypergroup of S. Let yn1∈Fx. Then f(yn1)⊆Fx. Indeed, let u∈f(yn1). We will show that u∈Fx, i.e., xˉˉρf(xn−1,u). Let v∈f(xn−1,u). Since yk∈Fx for all k=1,...,n, we have xˉˉρf(xn−1,yk) for all k=1,...,n. Since ρ is a ∗-semilattice strongly regular relation on S, by associativity and Lemma 4.1, we obtain
Hence xˉˉρf(xn−1,f(yn1)). Since v∈f(xn−1,u)⊆f(xn−1,f(yn1)), we have xρv. So xˉˉρf(xn−1,u) and it implies that u∈Fx. Thus f(yn1)⊆Fx.
(2) We show that Fx satisfies (F1) in Definition 3.1. Let yn1∈S such that f(yn1)∩Fx≠∅. Then there exists v∈f(yn1) and v∈Fx. Then xˉˉρf(xn−1,v). First of all, we show that xˉˉρf(xn−1,f(yn1)). Let a∈f(xn−1,f(yn1)). Then a∈f(xn−1,d) for some d∈f(yn1). Since f(yn1)ˉˉρf(yn1) and v,d∈f(yn1), we have vρd. Since ρ is a strongly regular relation, we obtain f(xn−1,v)ˉˉρf(xn−1,d). Since xˉˉρf(xn−1,v), we obtain xˉˉρf(xn−1,d). Since a∈f(xn−1,d), we have xρa. Thus xˉˉρf(xn−1,f(yn1)). Next, we show that yk∈Fx for all k=1,...,n. For any 1≤k≤n, we have
Since ρ is a strongly regular relation, we obtain
Since ρ is a ∗-semilattice strongly regular relation on S, we have xˉˉρf(xn−1,yk). So yk∈Fx for all k=1,2,...,n. This follows that Fx satisfies the condition (F1) in Definition 3.1. By (1) and (2), we conclude that Fx is a hyperfilter of S. By Corollary 3.8, we have S∖Fx=∅ or S∖Fx is a completely prime hyperideal of S. If S∖Fx=S then, since Fx⊆S, we have Fx=∅. It is impossible. Thus S∖Fx is a proper completely prime hyperideal of S. Define
Next, we show that ρ=⋂x∈SδS∖Fx. Let (a,b)∈ρ and x∈S. We consider the following two cases.
Case 1: a∉S∖Fx. Then a∈Fx. We obtain xˉˉρf(xn−1,a). Since (a,b)∈ρ, we obtain f(xn−1,a)ˉˉρf(xn−1,b). Then xˉˉρf(xn−1,b) and so b∈Fx. It follows that b∉S∖Fx. Thus (a,b)∈δS∖Fx.
Case 2: a∈S∖Fx. If b∉S∖Fx then, using the similar proof as in Case 1, we have a∉S∖Fx, which is a contradiction. So b∈S∖Fx. It follows that (a,b)∈δS∖Fx. Thus ρ⊆⋂x∈SδS∖Fx. Conversely, let (a,b)∈⋂x∈SδS∖Fx. Then (a,b)∈δS∖Fa. Since a∈Fa, we have a∉S∖Fa. Since (a,b)∈δS∖Fa, we have b∉S∖Fa. So b∈Fa. By the definition of Fa, we have aˉˉρf(an−1,b). On the other hand, by using the similar process, we have bˉˉρf(bn−1,a). Then
It implies that (a,b)∈ρ. Therefore ⋂x∈SδS∖Fx⊆ρ and the proof is complete.
Corollary 4.11. Let (S,f) be an n-ary semihypergroup with n≥3. Then the relation N is the least ∗-semilattice strongly regular relation on S.
Proof. Let ρ be a ∗-semilattice strongly regular relation on S. By Theorem 4.10, there exists a collection C of proper completely prime hyperideals of S such that ρ=⋂K∈CδK. By Theorem 4.5, we have N=⋂K∈CPI(S)δK. Since C⊆CPI(S), we obtain that
5.
Complete ∗-semilattice strongly regular relations
As we have known from [21] that the relation N is not the smallest semilattice congruence on ordered semihypergroups in general. The following example show that the result is also true in case of the ∗-semilattice strongly regular relation on ordered n-ary semihypergroups with n≥3.
Example 5.1. Let S={a,b,c,d}. Define f:S×S×S→P∗(S) by f(x1,x2,x3)=(x1∘x2)∘x3, for all x1,x2,x3∈S, where ∘ is defined by the following table.
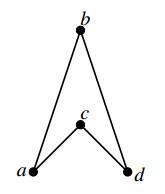
By applying Example 1 in [31], (S,f) is a ternary semihypergroup. Define a partial order ≤ on S by
Such relation can be presented by the following diagram.
Then (S,f,≤) is an ordered ternary semihypergroup. Moreover, we have N(b)={b} and N(a)=S=N(c)=N(d). It follows that
It is not difficult to show that
is a ∗-semilattice strongly regular relation on S and ρ⊆N.
Next, we introduce the concept of complete ∗-semilattice (strongly) regular relations on ordered n-ary semihypergroups, where n≥3, that generalizes Definition 4.1 in [21].
Definition 5.2. Let S be an ordered n-ary semihypergroup with n≥3. A ∗-semilattice regular relation (∗-semilattice strongly regular relation) ρ on S is said to be complete if for every x,y∈S,
Note that Theorem 4.4, Theorem 4.5 and Proposition 4.9 are also true for ordered n-ary semihypergroups where n≥3.
Proposition 5.3. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥3. Then the relation N is a complete ∗-semilattice strongly regular relation on S.
Proof. Firstly, let x,y∈S such that x≤y. We show that x¯¯Nf(xn−1,y). Let a∈f(xn−1,y). Since x≤y, by Lemma 3.10, we have y∈N(y)⊆N(x). Then x,y∈N(x). Since N(x) is an n-ary subsemihypergroup, we obtain a∈f(xn−1,y)⊆N(x). Hence N(a)⊆N(x). Conversely, since f(xn−1,y)∩N(a)≠∅, by (F1), we obtain x∈N(a). By Lemma 3.10, we get N(x)⊆N(a). So N(x)=N(a). It follows that xNa. Thus x¯¯Nf(xn−1,y).
Theorem 5.4. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥3. Let ρ be a complete ∗-semilattice strongly regular relation on S. Then there exists a collection C of proper completely prime hyperideals of S such that
Proof. Let x∈S. Define
From Theorem 4.10, it remains to show that the set Fx satisfies (F2) in Definition 3.1. Let y∈Fx and z∈S such that y≤z. Since y∈Fx, we have xˉˉρf(xn−1,y). Since y≤z and ρ is a complete ∗-semilattice strongly regular relation on S, we have yˉˉρf(yn−1,z). Since ρ is a ∗-semilattice strongly regular relation on S, we have yˉˉρf(yn). Next, we consider
Consequently, z∈Fx and the proof is complete.
Corollary 5.5. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥3. Then N is the smallest complete ∗-semilattice strongly regular relation on S.
Proof. The proof is similar to Corollary 4.11.
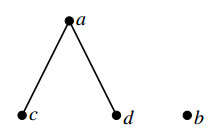
Example 5.6. Consider the ternary semihypergroup (S,f) given in Example 5.1. Define a partial order ≤ on S by
Such relation can be presented by the following diagram.
By applying Example 1 in [31], (S,f,≤) is an ordered ternary semihypergroup. There are 4 complete ∗-semilattice strongly regular relations as follows:
Furthermore, we have N(b)={b}, N(c)={c} and N(a)=N(d)=S. It follows that N:={(a,a),(a,d),(b,b),(c,c),(d,a),(d,d)}=σ1. Obviously, N is the smallest complete ∗-semilattice strongly regular relation on S.
6.
Decomposition of (completely) prime hyperideals of ordered n-ary semihypergroups
In this section, we show that every completely prime hyperideal on an ordered n-ary semihypergroups can be decomposable into its N-classes. But the result is not true in the case of prime hyperideals, see Example 6.6. This leads to answer the open problem given in [31]. However, we will provide a sufficient condition that makes the above conclusion true for case of prime hyperideals. Note that Theorems 4.4 and 4.5 are also true for every ordered n-ary semihypergroup with n≥2.
Theorem 6.1. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2. Let K be a completely prime hyperideal of S. Then
Proof. Firstly, we show that ⋃{(a)N:a∈K}⊆K. Let b∈(a)N for some a∈K. By Theorem 4.5, we have (a,b)∈N=⋂{δA:A∈CPI(S)}. So (a,b)∈δK. Since a∈K, we get b∈K. Thus ⋃{(a)N:a∈K}⊆K. As we have known that a∈(a)N for all a∈K, so K⊆⋃{(a)N:a∈K}. Therefore K=⋃{(a)N:a∈K}.
To solve the problem raised by Tang and Davvaz in [31], we firstly prove the following lemmas.
Lemma 6.2. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2. Let K be a nonempty subset of S satisfying the following property:
For any 1≤j≤n, if a nonempty subset S∖K is a prime j-hyperideal of S then K is a j-hyperfilter of S.
Proof. The proof is similar to the proof of the converse of Theorem 3.7 by applying the property (⊙).
Remark 6.3. For case n=2, we obtain that the notion of prime hyperideal on S satisfying the property (⊙) coincides with the notion of prime hyperideal on ordered semihypergroups introduced by Kehayopulu (see Definition 2.5 in [21]).
The following results, Lemma 6.4 and Theorem 6.5, generalize Proposition 2.5 and Theorem 2.10 in [21].
Lemma 6.4. Let (S,f,≤) be an ordered n-ary semihypergroup with n≥2. Then the following statements hold:
(i) For any K∈P∗(S) satisfying the property (⊙), K is a hyperfilter of S if and only if either S∖K=∅ or S∖K is a prime hyperideal of S.
(ii)N=⋂{δK:K∈PH(S)} where PH(S) is the set of all prime hyperideals of S satisfying the property (⊙).
Proof. As we have known that every completely prime hyperideal of S is always a prime hyperideal of S. By Corollary 3.8 and Lemma 6.2, the proof of (i) is complete. The proof of (ii) is similar to the proof of Theorem 4.5(ii) by applying (i).
Using the similar proof of Theorem 6.1, by using Lemma 6.4(ii), we obtain the result as follows.
Theorem 6.5. Let (S,f≤) be an ordered n-ary semihypergroup with n≥2. Let K be a prime hyperideal of S satisfying the property (⊙). Then K=⋃{(a)N:a∈K}.
The following example shows that a prime hyperideal of S that does not satisfy the property (⊙) cannot be decomposable into its N-classes.
Example 6.6. From the ordered n-ary semihypergroup (S,f,≤) given in Example 2.4, we obtain that the sets A2={y,z} and A3={w,x,z} are prime 2-hyperideals of S. Furthermore, A2,A3 are also prime hyperideals of S. Clearly, A3 satisfies the property (⊙) but A2 does not satisfy the property (⊙) since there exists w∈S such that f(wn)⊈A2 and f(wn)⊈S∖A2. On the other hand, we can verify that N(w)=N(x)=N(z)=S and N(y)={y}. Hence
Then (w)N={w,x,z}=(x)N=(z)N and (y)N={y}. Clearly,
and
Remark 6.7. If we set n=2 then the problem given in [31] is answered by Theorem 6.5 and Example 6.6.
7.
Conclusions
In this paper, we introduced the concept of j-hyperfilters of ordered n-ary semihypergroups, where a positive integer 1≤j≤n and n≥2, and discussed their related properties. Such notion can be considered as a generalization of left and right hyperfilters of ordered semihypergroups. The interesting properties of j-hyperfilters by means of completely prime j-hyperideals were established. Furthermore, we defined and investigated the semilattice strongly regular relation N on ordered n-ary semihypergroups by the hyperfilters. In particular, we illustrated by counterexample that the relation N is not necessary the least semilattice strongly regular relation on ordered n-ary semihypergroups where n≥3. Meanwhile, we introduced the concept of complete ∗-semilattice strongly regular relations on ordered n-ary semihypergroups, where n≥3, and proved that N is the smallest complete ∗-semilattice strongly regular relation. Finally, we provided some necessary conditions to show that every prime hyperideal can be decomposable into its N-classes. This result answers the related problem posed by Tang and Davvaz in [31].
Acknowledgments
The authors are highly grateful to the referees for their valuable comments and suggestions for improving the article. This research was supported by Chiang Mai University, Chiang Mai 50200, Thailand.
Conflict of interest
The authors declare no conflict of interest.









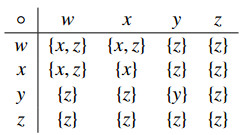
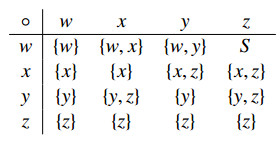
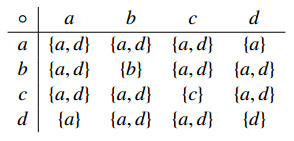




 DownLoad:
DownLoad: