Bipartite fixed-time output containment control of heterogeneous linear multi-agent systems

1.   Introduction

Cooperative control of multi-agent systems has aroused profound interest over the past couple of decades on account of its extensive applications in disparate fields, such as smart grids, transportation, sensor networks ^[1,2,3,4], etc. Consensus is a widespread study orientation of cooperative control, which has produced some classical literatures ^[5,6,7,8]. Thereinto, the previously mentioned pluri-plusieurs leaders control of MASs is diffusely applied during the practice, which can be regarded as the containment control problem. Containment control, as a normalized problem of distributed cooperative control, has developed into a consequential and vital area, in which the aim is to design an appropriate distributed director that the dynamic convex hull constituted by leaders are guaranteed to include all followers in MASs. So far, fruitful results have been achieved on this topic, see, e.g., ^{[9,10,11,12,13,14,15]}. In addition, this multi-agent systems is also divided into homogeneity and heterogeneity. In contrast to homogeneous multi-agent systems, there are heterogeneous multi-agent systems in which the dynamics of each agent is not identical. In reality, the situation is even more complex, and it is clear that typical examples of heterogeneous multi-agent systems are much more common than the overly simple homogeneous multi-intelligent systems. The study of cooperative control of heterogeneous multi-intelligent systems is therefore more realistic and challenging, and also has more promising applications.

With respect to the research of containment control (CC) problem, the rate of convergence is the key index to judge the quality of the designed CC protocols. It's worth noting that the forthcoming CC protocols only ensure asymptotic realization of containment control, which illustrates that containment control can not be completed in finite time. Nevertheless, it is often advisable to implement CC in a limited time frame in engineering applications. As a matter of fact, finite-time CC has many other advantages besides faster convergence rate, such as higher control precision and better anti-interference. Therefore, the finite-time CC problem has been investigated ^{[16,17,18,19,20]}. For instance, a finite-time adaptive containment control method for a nonlinear multi-agent system with actuator failures and mismatched disturbances was raised in ^[19], and it is proved that the errors of the control system are stable in finite time in the presence of actuator faults. In ^[20], an observer-based two-layer distributed containment control protocol was raised to overcome the related finite-time containment problem.

Notice that the setup time largely rests with the agents' the premier conditions in the finite-time protocols. It's hard to calculate settling time accurately since it's often difficult to obtain the exact information on the initial state of the agents, which restrict the use of the finite-time CC protocols in practical applications. As a result, a fixed-time control method can be applied, in which an upper limit on the settling time can be confirmed independently of initial conditions. In recent years, distributed fixed-time control for nonlinear networked systems is discussed in ^[21] by using event/self-triggered method over directed graphs, so that the estimated settling time can be determined independently of the initial states of networked agents. In ^[22], the fixed-time containment control for second-order nonlinear multi-agent systems (MASs) is studied and a novel non-singular terminal sliding mode control protocol is designed to guarantee FTCC with distributed nonlinear MASs.

Beware that the communication links in the literature above are all non-negative. That is to say, all the relationships between agents are collaborative. Nevertheless, signed networks are more common than traditional multi-agent systems networks. In other words, the simultaneity between collaboration and competition relationships is more logical and appropriate. This type of problem is named the bipartite containment control problem ^[23], where the interaction among agents can be effectively modeled by signed graph, and the antagonistic/cooperative interaction between agents can be represented by negative and positive arcs respectively. Lately, the bipartite CC problem has been discussed ^{[24,25,26,27,28]}. Particularly, in ^[24], the bipartite containment tracking problem of a class of signed graphs leader-following networks was studied, and it was proved that leader-following networks can converge to symmetric trajectories containing the same convex hull and the same modulus but different signs of each leading trajectory. And taking ^[27] as an example, based on the nonlinear decomposition method of input quantization, an event-triggered control scheme was developed by utilizing backstepping technology, which was based on a nonlinear decomposition approach of input quantization. Notwithstanding consequential achievement have been made in bipartite CC, and what is noteworthy is that little work has been done to deal with the finite/fixed-time bipartite containment control problems ^{[29,30,31,32]}. As far as we know, the system dynamics of the above problem are different from this paper, so there are problems that have not been solved.

Motivated by the aforesaid argumentation, the darrein target of this paper is to settle the problem of bipartite fixed-time output containment control for heterogeneous linear multi-agent systems with signed digraphs. Among others, the primary contributions of the article are given as follows.

(ⅰ) Inspired by ^[12] and ^[13], the text proposes a bipartite containment control protocol combined with an adaptive algorithm that estimates the system matrix of the leader and also the state of the leader. On the basis of the control protocol, the multiple agents in the system no longer depend on global information, which saves many measurement resources;

(ⅱ) The bipartite containment control studied in this paper is achieved with a fixed time premise. A large number of results have been produced on containment control of multi-agent systems in asymptotic time. In contrast, containment control under fixed-time algorithms has many advantages, such as high accuracy and robustness of control, in addition to the fast convergence. Part of the inspiration for this thought is from ^[17,20,23];

(ⅲ) Different from ^{[28,29,30,31,32]}. In this article, the object of study is linear time-invariant system. However, the problem of bipartite fixed-time output containment control on this base is comparatively few researched up till now.

The remainder of this article are the following: Section Ⅱ renders preliminaries and Section Ⅲ describes problem statement. The main results are shown in Section Ⅳ. The simulation results are shown in Section Ⅴ. At last, in Section Ⅵ, some conclusions are presented.

2.   Preliminaries

$\mathbb{R}$ stands for the set of real numbers. $\mathbb{R}^{N}$ is the set of real $N \times 1$ vectors, and we use $\mathbb{R}^{N \times M}$ to denote the set of real $N \times M$ matrices. In this paper, graph theory is utilized to signify the competitive-cooperative relationship between agents in MASs. A bunch of N+W agents as an illustration, their relationship can be represented by $\mathcal{G} = \left({\mathcal{V}, \mathcal{E}, \mathcal{A}} \right)$, a weighed digraph, which is composed of a node set $\mathcal{V} = \left\{ {{v_1}, {v_2}, ..., {v_n}} \right\}$, an adjacency matrix $\mathcal{A} = [{a_{ij}}] \in {\mathbb{R}^{(N+W) \times (N+W)}}$ and an edge set $\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}$, $\left({{v_j}, {v_i}} \right) \in \mathcal{E}$ denotes an edge representing agent $i$ can acquire information from agent $j$, wherein, agent $j$ and agent $i$ are adjacent. And the in-degree matrix is denoted by $\mathcal{D} = diag\left\{ {\sum\limits_{j = 1}^N {\left| {{a_{1j}}} \right|}, \sum\limits_{j = 1}^N {\left| {{a_{2j}}} \right|}, ..., \sum\limits_{j = 1}^N {\left| {{a_{Nj}}} \right|} } \right\}$. Thereby, It can be calculated that Laplacian matrix $\mathcal{L} = \mathcal{D}-\mathcal{A}$. In addition, there is a group $\mathcal{V}$ consist of two subgroups $\mathcal{V}_1$ and $\mathcal{V}_2$, and define it by equations that $\mathcal{V}_1 \cap \mathcal{V}_2 = \emptyset$ and $\mathcal{V}_1 \cup \mathcal{V}_2 = \mathcal{V}$, which means if ${v_j}$ and ${v_i}$ are existing the identical subgroup ${a_{ij}} > 0$; or else ${a_{ij}} < 0$. In particular, the collaboration and competition are severally indicated by ${a_{ij}} > 0$ and ${a_{ij}} < 0$. Furthermore, the signed digraph $\mathcal{G}$ can also be called structural balance diagram. Finally, ${\sigma _i} = 1$, if ${v_i} \in \mathcal{V}_1$, and ${\sigma _i} = - 1$, if ${v_i} \in \mathcal{V}_2$, respectively, which represents a symbolic parameter.

Lemma 1. ^[33] Let $q = {\left[{q_1^T, q_2^T, ..., q_N^T} \right]^T} \in {R^{{N_n}}}$, in which ${q_i} \in {R^n}$, $i = 1, 2, ..., N$, afterwards, the inequality below holds:

where $\alpha > 1$.

Lemma 2. ^[33] Let $q = {\left[{q_1^T, q_2^T, ..., q_N^T} \right]^T} \in {R^{{N_n}}}$, in which ${q_i} \in {R^n}$, $i = 1, 2, ..., N$, afterwards, the inequality below holds:

where $\beta \in \left({0, 1} \right)$.

Lemma 3. ^[21] There is a positive definite function continuously $V\left(q \right):{R^n} \to R_0^ +$, in which $\beta \in \left({0, 1} \right)$, $\alpha > 1$ and $a, b, c > 0$, we have

Afterwards, the settling time are as follows

Lemma 4. In this scenario, ${\mathcal{H}^*} = \mathcal{D}\mathcal{H}\mathcal{D}$ and $\mathcal{H}$ therein are positive definite, in which $\mathcal{H}$ is defined later in (9).

Lemma 5. ^[9] If and only if $\exists \mathcal{D} \in \mathcal{D}$, i.e., $\mathcal{D}\mathcal{A}\mathcal{D}$, is a non-negative matrix, the digraph $\mathcal{G}$ is structurally equilibrium. Furthermore, $\mathcal{D}$ can determine the bilaterality of the agents.

3.   Problem statement

In this paper, $\mathcal{F} = \{ {v_1}, {v_2}, ..., {v_N}\}$ can be considered as the followers set and the set of leaders is expressed by $\mathcal{R} = \{ {v_{N + 1}}, {v_{N + 2}}, ..., {v_{N + W}}\}$. On account of the graph theory, a heterogeneous linear multi-agent system is reckoned, then, the followers are expressed as hereunder mentioned:

where ${x_i} \in {\mathbb{R}^N}$ and ${y_i} \in {\mathbb{R}^Q}$ are the state and the output of the i-th follower, severally, ${u_i} \in {\mathbb{R}^P}$ is the input of the ith follower, and ${A_i}, {B_i}, {C_i}$ are the matrices with compatible dimensions. The leaders can be described by

where ${\omega_k} \in {\mathbb{R}^N}$ is the state of the k-th leader and ${y_k} \in {\mathbb{R}^Q}$ is the output of the k-th leader, separately.

Definition 1. In the case of $(1 - \lambda)x + \lambda y \in \mathcal{C}$, the set $\mathcal{C} \subseteq {\mathbb{R}^N}$ is convex for any $x, y \in \mathcal{C}$ and any $\lambda \in [0, 1]$. Let

be the leaders' outputs set and the inverted sign. $Co(Y_{\mathcal{L}})$ is the minimal convex set including the whole points in $Y_{\mathcal{L}}$. In other words, the convex hull of $Y_{\mathcal{L}}$ is the combination of all convex of points.

Definition 2. under the circumstance of the signed graph $\mathcal{G}$, the above-mentioned problem of the systems (5) and (6) can be settled by the following guidelines:

First of all, to deal with the problem of bipartite output containment control, the output containment control problem need be solved foremost. No matter what the starting statuses of multi-agent system are, the convex hull that the outputs of leaders contain will embrace some followers' outputs.

Accordingly, the leaders' inverse output trajectories will include the outputs of other followers.

Assumption 1. The eigenvalues of the matrix ${A_0}$ have zero real parts.

Assumption 2. ${B_i}$ are of full-row ranks, $i = 1, 2, ..., N$.

Assumption 3. For $i = 1, 2, ..., N$, There are solutions $\left({{X_i}, {U_i}} \right)$, $i = 1, 2, ..., N$, that satisfy the formulas below:

Assumption 4. The $\mathcal{G}$ is structurally equilibrium, there are at least one leader that has a directed spanning tree to it.

Ahead of researching more, the output containment error is caused by:

Turn the equation thereinbefore into matrix modality, hence let $e = col({e_1}, {e_2}, ..., {e_N})$, $y = col({y_1}, {y_2}, ..., {y_N})$, then (8) can be represented as

where ${\overline y _k} = {({\sigma _1}{\sigma _2}...{\sigma _N})^T} \otimes {y _k}$, ${\mathcal{A}_{0k}} = diag\left\{ {\left| {{a_{1k}}} \right|, \left| {{a_{2k}}} \right|, ..., \left| {{a_{Nk}}} \right|} \right\}$ and $\mathcal{H} = \sum\limits_{r = N + 1}^{N + W} {({1 / W})L + {\mathcal{A}_{0k}}}$. In accordance with the problem in Definition 2, satisfy $\mathop {\lim }\limits_{t \to \infty } {e_i} = 0$,

in which ${\zeta _{ik}} \in \mathbb{R}$ indicates the element of ${\mathcal{H}^{ - 1}}{\mathcal{A}_{0k}}{1_N}$. This manifests the bipartite output containment control problem can be settled by treating it as a adjustment problem of driving the $e \to 0$.

4.   Main results

In this section, we propose two main results of the article for the fixed-time bipartite containment control problem.

4.1.   Bipartite fixed-time observer

In order to realize the above fixed-time bipartite output containment control of heterogeneous MASs, we present a protocol as follow:

where $K_i^1, K_i^2, K_i^3 \in {R^{P \times N}}$ will be designed later in the Theorem 3. $P \in {R^{{n_0} \times {n_0}}} > 0$, ${d_1} > 0$, ${d_2} > 0$, $\alpha > 0$, $\beta > 0$, ${\mu _1} > 0$, ${\mu _2} > 0$, ${\mu _3} > 0$, $\tilde \alpha > 1$ and $\tilde \beta \in \left({0, 1} \right)$. ${\varsigma _i}$ indicates the metrical information gathered by the $i$-th agent alternating with its neighbors, which is defined as:

in which ${a_{ij}}$ and ${a_{ik}}$ are the the adjacency matrix A's elements, and it can take another form as follow:

Define the error variable $\bar f = f - {\left({\mathcal{H} \otimes {I_N}} \right)^{ - 1}}\sum\limits_{k = N + 1}^{N + W} {\left({{\mathcal{A}_{0k}} \otimes {I_n}} \right)\bar \omega }$. Then

Afterwards, we have the result as follow.

Theorem 1. Assume that Assumptions 1 and 4 are tenable for systems (6) and (11). Then, $\mathop {\lim }\limits_{t \to T} \bar f = 0$ holds if ${\mu _1} > {1 / {{\lambda _1}}}$, ${\mu _2} > 0$, ${\mu _3} > 0$, $\alpha > 1$, $\beta \in \left({0, 1} \right)$, $P$ satisfies

where $c > 0$, and ${\lambda _1} = {\lambda _{\min }}\left(\mathcal{H} \right)$. Besides, the setup time are as follow

where $\Gamma = \mathcal{H} \otimes P$, ${\Gamma ^2} = {\mathcal{H}^2} \otimes {P^2}$.

Proof. On the condition of Assumption 4, $H$ is positive definite and symmetrical. Next, there is an orthometric $U \in {R^{N \times N}}$, meeting $UH{U^T} = J = \text{diag}\left\{ {{\lambda _1}, {\lambda _2}, ..., {\lambda _N}} \right\}$.

Thinking about $V = {\bar f^T}\left({\mathcal{H} \otimes P} \right)\bar f$ as the preselected Lyapunov function for the system (14). Let $\tilde f = \left({U \otimes {I_{{n_0}}}} \right)\bar f$ and $\xi = \left({\mathcal{H} \otimes P} \right)\bar f$. Take the time derivative of $V$ with respect to (14) as follows

Due to ${\mu _1} > {1 / {{\lambda _1}}}$ and (15), one has

In line with Lemma 1 and Lemma 2, one has

Combining (18) and (19) with (17), it can be obtained

On account of $\beta \in \left({0, 1} \right)$ and $\alpha > 1$, it can be testified that $\left[{{{\left({1 + \beta } \right)} / 2}} \right] \in \left({0, 1} \right)$ and $\left[{{{\left({1 + \alpha } \right)} / 2}} \right] > 1$ establish. In light of Lemma 3, $\bar f = 0$ is fast stable globally in fixed-time. Hence, $\mathop {\lim }\limits_{t \to T} \bar f = 0$ holds, and $T$ satisfies the (16) inequality. The proof is done.

Afterwards, we will demonstrate that the control protocol designed on the base of the fixed-time observers is workable. The proof is similar to the demonstration of Theorem 3, so the procedure will be omitted.

4.2.   Adaptive bipartite fixed-time observer

In the previous section, we propose the fixed-time protocol to achieve the bipartite containment problem by a distributed bipartite compensator. Nonetheless, take note to the bipartite fixed-time observer, which is related to the leader's matrix ${A_0}$ and the overall agents topology. In fact, it's not practical in many aspects that every follower needs to get ${A_0}$. In another aspect, followers do not know the global information in effect, in particular with grand MASs scale.

Based on the above reasons, we devise an adaptive bipartite fixed-time protocol ulteriorly, satisfying $\mathop {\lim }\limits_{t \to {T_s}} \left({{A_{0i}} - {A_0}} \right) = 0$ and $\mathop {\lim }\limits_{t \to T} \bar f = 0$. Thereinto, the bipartite fixed-time observer can not merely complete the estimation of leader state and matrix ${A_0}$ simultaneously, but also avert relying on the global information.

The design form of the adaptive bipartite fixed-time protocol is written as:

where ${A_{0i}} \in {R^{{n_0} \times {n_0}}}$ is the estimation of ${A_0}$ in the protocol above, ${\vartheta _i} = \sum\limits_{j = 1}^N {\left| {{a_{ij}}} \right|\left({{A_{0i}} - {A_{0j}}} \right) + {a_{i0}}\left({{A_{0i}} - {A_0}} \right)}$, and ${c_i}$ is coupling gain. ${\kappa _1} > 0$, ${\kappa _2} > 0$, ${\mu _2} > 0$, ${\mu _3} > 0$, $\gamma > 0$, $\delta > 0$, $\alpha > 0$ and $\beta > 0$ are the parameters which will be confirmed soon. Similarly, $K_i^1, K_i^2\left(t \right), K_i^3 \in {R^{P \times N}}$ will be designed later in the Theorem 3.

Afterwards, we have the result as follow.

Theorem 2. Assume that Assumptions 1 and 4 are tenable for systems (6) and (21). Next, it gets: $i)$ $\mathop {\lim }\limits_{t \to {T_s}} \left({{A_{0i}} - {A_0}} \right) = 0$ holds if ${\kappa _1} > 0$, ${\kappa _2} > 0$, $\gamma > 1$ and $\delta \in \left({0, 1} \right)$; $ii)$ The setup times upper limit $T$ and ${T_s}$ are stationary, which have no connection with the initial conditions. Furthermore, each ${c_i}$ converges to a certain bounded value.

Proof. We prove the above separately.

$i)$ Provide a matrix error ${\bar A_{0i}} = {A_{0i}} - {A_0}$, and let ${\bar A_0} = {\left[{\bar A_{01}^T, \bar A_{02}^T, ..., \bar A_{0N}^T} \right]^T}$. The following form can be readily obtained:

in which ${\mathcal{H}^*}$ is positive and symmetric, as described in Lemma 5.

The operation ${\langle {{{\bar A}_0}} \rangle _j}$, $j = 1, 2, ..., {n_0}$, is defined to represent the $j$th column of ${\bar A_0}$. Next, it get

Let $V\left({{{\langle {{{\bar A}_0}} \rangle }_j}} \right) = \langle {{{\bar A}_0}} \rangle _j^T\left({{\mathcal{H}^ * } \otimes {I_{{n_0}}}} \right){\langle {{{\bar A}_0}} \rangle _j}$, and ${\xi _j} = \left({{\mathcal{H}^ * } \otimes {I_{{n_0}}}} \right){\langle {{{\bar A}_0}} \rangle _j}$. The time derivative of $V\left({{{\langle {{{\bar A}_0}} \rangle }_j}} \right)$ with respect to (23) can be expressed

where Lemmas 1 and 2 are utilized.

By the above, ${\langle {{{\bar A}_0}} \rangle _j} = 0$ is stable globally in fixed-time. The setup time

In addition, ${\bar A_0}$ is stable globally in fixed-time with the settling time ${T_s} < T_s^ * \buildrel \Delta \over = \max \left\{ {T_{s\left(1 \right)}^ *, T_{s\left(2 \right)}^ *, ..., T_{s\left({{n_0}} \right)}^ * } \right\}$. Hence, $\mathop {\lim }\limits_{t \to {T_s}} \left({{A_{0i}} - {A_0}} \right) = 0$ holds. $ii)$ Define the error $\bar f = f - {\left({\mathcal{H} \otimes {I_N}} \right)^{ - 1}}\sum\limits_{k = N + 1}^{N + W} {\left({{\mathcal{A}_{0k}} \otimes {I_n}} \right)\omega }$, and let $\bar f = {\left[{\bar f_1^T, \bar f_2^T, ..., \bar f_N^T} \right]^T}$. The augmented system can be obtained

where ${\tilde A_{0I}} = \text{blockdiag}\left({{{\bar A}_{01}}, {{\bar A}_{02}}, ..., {{\bar A}_{0N}}} \right)$. Let ${V_1} = {\bar f^T}\left({\mathcal{H} \otimes {I_{{n_0}}}} \right)\bar f$ and ${V_2} = \sum\limits_{i = 1}^N {{{\left({{c_i} - \theta } \right)}^2}}$, in which $\theta$ is a positive constant to be confirmed. Afterwards, for systems (21) and (26), $V = {V_1} + {V_2}$ can be regarded as an alternative Lyapunov function.

The time derivative of ${V_1}$ with respect to (26) are following when $t \in \left({0, {T_s}} \right)$

The time derivative of $V_2$ with respect to (21) can be indicated as

Let $\tilde f = \left({U \otimes {I_{{n_0}}}} \right)\bar f$ and $\varsigma = \left({\mathcal{H} \otimes {I_{{n_0}}}} \right)\bar f$. In accordance with Lemma 1 and Lemma 2, the following can be obtained:

There exists a $\theta > 0$ that $A_0^T + {A_0} - 2\theta {\lambda _i}{I_{{n_0}}}$ is Hurwitz. In light of the proof of i), it is understood that ${\tilde A_{0i}} = 0$ is fixed-time stable globally. Let ${\chi _1} = \left({\mathcal{H} \otimes {I_{{n_0}}}} \right){\tilde A_{0i}}$ and ${\chi _2} = \sum\limits_{k = N + 1}^{N + W} {\left({{\mathcal{A}_{0k}} \otimes {I_n}} \right){{\tilde A}_{0i}}}$. In finite time, both ${\chi _1}$ and ${\chi _2}$ converge to 0. After that, there are bounded constants ${c_0}$, ${c_1}$ and ${c_2}$, thus making the following fact true:

where ${c_0} \ge {\left({{1_N} \otimes {x_0}} \right)^T}\left({{1_N} \otimes {x_0}} \right)$. On account of the fact that $\frac{{{c_1} + {c_2}}}{{{\lambda _{\min }}\left(\mathcal{H} \right)}}$, $V$ and ${c_0}$ are bounded. Hence, $\bar f$ and ${c_i}$ are bounded. Therefore, $V\left({{T_s}} \right)$ is also bounded.

On the condition of $t \in \left[{{T_s}, \infty } \right]$, ${\tilde A_{0i}} = 0$. The time derivative of ${V_1}$ with respect to (26) can be equal to

The time derivative of ${V_2}$ along (21) is (28). We have

Distinctly, $\bar f$, ${c_i}$ and $V$ are bounded. There are $\theta > 0$ up to ${\Delta _c} = \max \left\{ {\theta - {c_i}, i = 1, 2, ..., N} \right\} > 0$. Next

Let ${\varpi _1} = {\left[{\frac{{{\mu _3}\left({1 - {\psi _1}} \right){\lambda _{\min }}\left(\mathcal{H} \right)}}{{{\Delta _c}{\lambda _{\max }}\left({{\mathcal{H}^2}} \right)}}} \right]^{\left({{2 / {1 - \beta }}} \right)}}{\left[{\frac{{{\lambda _{\min }}\left({{\mathcal{H}^2}} \right)}}{{{\lambda _{\max }}\left(\mathcal{H} \right)}}} \right]^{\left[{{{\left({1 + \beta } \right)} / {1 - \beta }}} \right]}}$, where ${\psi _1} \in \left({0, 1} \right)$. Define a bounded set ${\Xi _1} = \left\{ {\bar f\left({{T_s}} \right)\left| {\bar f{{\left({{T_s}} \right)}^T}\left({\mathcal{H} \otimes {I_{{n_0}}}} \right)\bar f\left({{T_s}} \right) \le {\varpi _1}} \right.} \right\}$.

If $\bar f\left({{T_s}} \right) \in {\Xi _1}$, then

Thus, $\bar f = 0$ is fixed-time stable globally. If $\bar f\left({{T_s}} \right) \notin {\Xi _1}$, then ${V_1}\left({{T_s}} \right) > {\varpi _1}$.There is a bounded $\tau > {T_s}$, so that for $t \ge \tau$, $\bar f\left(t \right) \in {\Xi _1}$. It is annotated by reducing it to fallacy. Assume the mentioned conclusion is invalid. So the following inequality is true for all $\tau$:

From (35), $V\left({{T_s}} \right)$ has no bound as $\tau \to \infty$, which contradicts the truth that $V\left({{T_s}} \right)$ is bounded. Hence, the result is correct. The time for $\bar f\left({{T_s}} \right)$ to enter the set ${\Xi _1}$ is calculated as

Let ${\varpi _2} = {\left[{\frac{{{\Delta _c}{\lambda _{\max }}\left({{\mathcal{H}^2}} \right)n_0^\alpha {N^{\left[{{{\left({\alpha {\rm{ - }}1} \right)} / 2}} \right]}}}}{{\left({{\mu _2}\left({1 - {\psi _2}} \right){\lambda _{\min }}\left(\mathcal{H} \right)} \right)}}} \right]^{\left({{2 / {\alpha - 1}}} \right)}}{\left[{\frac{{{\lambda _{\max }}\left(\mathcal{H} \right)}}{{{\lambda _{\min }}\left({{\mathcal{H}^2}} \right)}}} \right]^{\left[{{{\left({1 + \alpha } \right)} / {\left({\alpha - 1} \right)}}} \right]}}$, where ${\psi _2} \in \left({0, 1} \right)$. Define a bounded ${\Xi _2} = \left\{ {\bar f\left({{T_s}} \right)\left| {\bar f{{\left({{T_s}} \right)}^T}\left({\mathcal{H} \otimes {I_{{n_0}}}} \right)\bar f\left({{T_s}} \right) \ge {\varpi _2}} \right.} \right\}$, If $\bar f\left({{T_s}} \right) \in {\Xi _2}$, we have

It's known from the above proof that $\mathop {\lim }\limits_{t \to T} \left[{{f_i}- {{\left({\mathcal{H} \otimes {I_N}} \right)}^{ - 1}}\sum\limits_{k = N + 1}^{N + W} {\left({{\mathcal{A}_{0k}} \otimes {I_n}} \right){\omega _k}} } \right] = 0$ holds. It can be seen from (21) that ${c_i}$ is increasing monotonically. Combining the boundedness of ${c_i}$ and the global fixed-time stability of $\bar f$ in the above analysis, each coupling gain converges to a bounded value. The final demostration is done.

4.3.   Control protocol design

Then, we will show that control protocol designed according to adaptive fixed-time observers is feasible.

Theorem 3. For MASs (5) and (6), assume that Assumptions 1–4 hold and that an adaptive bipartite fixed-time observer is designed via Theorem 2. If $K_i^1$ satisfies $A_i+{B_i}{K_i^1}$ is Hurwitz, $K_i^2\left(t \right) = U_i\left(t \right)-{K_i^1}{X_i}\left(t \right)$, and $K_i^3$ satisfies ${B_i}{K_i^3} = {I_{n_i \times n_i}}$, the bipartite output containment problem can be solved by the control protocol (21).

Proof. Let $\bar{K}_i^2 (t) = K_i^2(t)-K_i^2$, $\bar{X}_i(t) = X_i(t)-X_i$, ${\bar {x}}_i = x_i - {\left({\mathcal{H} \otimes {I_N}} \right)^{ - 1}}\sum\limits_{k = N + 1}^{N + W} {\left({{\mathcal{A}_{0k}} \otimes {I_n}} \right){X_i}\bar{ \omega} }$, and $\hat{x}_i = x_i-{X_i}{f_i}$. Thus, we have

Due to the boundedness of $\bar K_i^2\left(t \right)$, $\bar X_i\left(t \right)$, and ${\bar f_i}$, one easily knows that $\bar x_i$ when $t \in \left({0, \max \left\{ {T, {T_{\max }}} \right\}} \right)$. According to the previous analysis, the first three variables are all 0 when $t \in \left({\max \left\{ {T, {T_{\max }}} \right\}, \infty } \right)$. Let ${A_{i\sigma }} = {A_i} + {B_i}K_i^1$. Then, we have

A candidate Lyapunov function ${V_{i\sigma }} = \bar x_i^T{\bar x_i}$ for the system (39) is considered. The time derivative of ${V_{i\sigma }}$ along (39) can be acquired

In accordance with Lemma 3, ${\bar x_i} = 0$ has global fast fixed time stability. It can be derived that $\bar x = {\left[{\bar x_1^T, \bar x_2^T, ..., \bar x_N^T} \right]^T} = 0$ is fast fixed-time stable globally. Thus, we have

The proof is done.

Corollary 1. For (5) and (6), assume that Assumptions 1-4 hold and that a bipartite fixed-time observer is designed via Theorem 1. If $K_i^1$ satisfies $A_i+{B_i}{K_i^1}$ is Hurwitz, $K_i^2 = U_i-{K_i^1}{X_i}$, and $K_i^3$ satisfies ${B_i}{K_i^3} = {I_{n_i \times n_i}}$, the bipartite output containment problem can be solved by the control protocol (11). The solution of the regulator (7) is $\left({{X_i}, {U_i}} \right)$, and the same control parameters as in Theorem 3.

5.   Numerical example

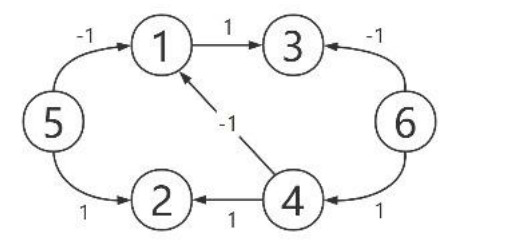
In this section, the validity of Theorem 2 is substantiated by two sets of numerical simulation. Consider the MASs in Figure 1, which includes four followers and two leaders. It is obvious that the digraph accords with Assumption 4 and is signed.

It's observed that 1, 2, 3, 4 represent followers and the others are leaders in Figure 1. In addition, it's revealed that the digraph $\mathcal{G}$ is structurally balanced and has two competing subgroup ${\mathcal{V}_1} = {1, 3}$ and ${\mathcal{V}_2} = {2, 4}$. Choose the relevant matrices as follows:

It can be testified that Assumptions 1–4 hold. In a general way, since the agents' initial parameters are selected at random, two sets of simulation diagrams are shown here to demonstrate generality.

According to Theorem 1, correlation parameters are selected as ${d_1} = {d_2} = 1$, ${\mu _1} = {\mu _2} = 1.5$, $\alpha = 1.2$, $\beta = 0.5$, $\tilde \alpha = 1.3$, $\tilde \beta = 0.3$. Besides, $K_i^2$ are confirmed by $U_i-{K_i^1}{X_i}$, and the solution of the regulator equations (7) is $(X_i, U_i)$. The evolutions in the agents' output $y_i$ over time are plotted in Figures 2 and 3. It is obvious to see that the two followers' output tracks (light blue and green lines) extend to the interior of the range invested by the leaders' output trajectories. Conversely, the outputs of the remaining two followers (purple and black lines) are opposite to the inverse tracks of the leaders' outputs. Thus, the adaptive protocol (21) supports the implementation of bipartite output containment control. In the end, the variations of adaptive coupling weights $c_i(t)$ assigned to each follower are shown in Figures 4 and 5. In addition, the bipartite containment output errors are represented in Figures 6 and 7, which can converge quickly to zero.

6.   Conclusions

In this paper, the discussion and design of bipartite fixed-time output containment control for a class of linear time-invariant system is investigated. By constructing a bipartite compensator distributively. The problem of bipartite output containment is treated as the escalation of adjustment problem of multiagent systems. Two protocols are proposed in order to realize bipartite fixed-time output containment control. Using the Lyapunov function theory and the descriptor systems stability method, some abundant criteria are deduced to guarantee adaptive bipartite fixed-time output containment of multi-agent systems. In the end, the feasibility of the anticipant theoretical results is verified by a set of simulation examples. In our prospective work, we are willing to study the bipartite predefined-time containment problem of more sophisticated MASs.

Acknowledgments

This work was partially supported by the National Natural Science Foundation of China under Grants 62271195, 61971181 and 62072164, and Outstanding Youth Science and Technology Innovation Team in Hubei Province under Grant T2022027 and B2022156.

Conflict of interest

The authors declare no conflict of interest.