The least squares Bisymmetric solution of quaternion matrix equation $AXB = C$

1.   Introduction

Throughout this paper, the set of positive integers, the real number field and quaternion skew-field are denoted by $\mathbb{N}$, $\mathbb{R}$ and $\mathbb{Q}$, respectively, the set of all real column vectors with order $t$ and the set of all real row vectors with order $t$ are denoted by $\mathbb{R}^{t}$ and $\mathbb{R}_t$, respectively, the set of all $m\times n$ real matrices and the set of all $m\times n$ quaternion matrices are denoted by $\mathbb{R}^{m\times n}$ and $\mathbb{Q}^{m\times n}$, respectively, the set of all $n\times n$ real symmetric matrices, the set of all $n\times n$ real Persymmetric matrices, the set of all $n\times n$ quaternion Hermitian matrices, the set of all $n\times n$ quaternion Persymmetric matrices, and the set of all $n\times n$ quaternion Bisymmetric matrices are denoted by $\mathbb{SR}^{n\times n}$, $\mathbb{PR}^{n\times n}$, $\mathbb{HQ}^{n\times n}$, $\mathbb{PQ}^{n\times n}$ and $\mathbb{BQ}^{n\times n}$, respectively, the conjugate of quaternion $a$ is denoted by $\bar{a}$, the $i-$th column of identity matrix $I_n$ is denoted by $\delta_n^i$, the exchange matrix with order $k$ is denoted by $V_k$, the transpose, the conjugate transpose, $M$-$P$ inverse of matrix $A$ are denoted by $A^T$, $A^H$ and $A^\dagger$, the Kronecker product of matrices is denoted by $\otimes$, the Frobenius norm of a matrix or Euclidean norm of a vector is denoted by $\left \|\cdot\right \|$.

Block matrix is a common method in matrix theory. By properly dividing the matrix into blocks, a high-order matrix can be transformed into some low-order matrices. At the same time, the structure of the original matrix become simple and clear, which can greatly simplify the operation steps or bring convenience to the theoretical derivation of the matrix. There are many problems can be solved or proved by block matrix. For example, when dealing with more complex constraint problems of matrix equation, it will be easier to discuss the submatrices. In this paper, we will use block matrices to solve quaternion matrix equation.

A quaternion $q \in \mathbb{Q}$ is expressed as $q = a + b{{\bf i}} + c{{\bf j}} + d{{\bf k}},$ where $a, b, c, d\in \mathbb{R},$ and three imaginary units ${{\bf i}}, {{\bf j}}, {{\bf k}}$ satisfy

Quaternion matrix equations and their least squares solutions are widely applied in many fields^[1,2,3,4,5]. So many scholars have studied various types solutions of quaternion matrix equations ^{[6,7,8,9,10,14,16,17,18,19,20,21,22,23,24,25]}. For example, Ivan I. Kyrchei got the minimum norm least squares solutions of quaternion matrix equations $AX = B$, $XA = B$ and $AXB = D$^[7]; Zeyad Al-Zhour get the general solutions of three important partitioned quaternions systems^[9]; Zhang get the j-self-conjugate least squares solution of quaternion matrix $X- A \hat{X}B = C$^[26]. But some matrices are difficult to be studied because of their complex structure, for example, Bisymmetric. Bisymmetric matrix is widely used in information theory, Markov process, physical engineering and other fields. But the process of studying it is very complicated due to its complex internal structures. So in this paper, we divide the quaternion Bisymmetric matrix into blocks and find out the relationship between the blocks. In addition, we apply it to solve the least squares problem of quaternion matrix equation

by the real representation^[26]. The specific problem is as follows.

Problem 1. Let $A, \ B, \ C\in \mathbb{Q}^{n\times n}$, and find out the set of least squares Bisymmetric solutions $S_{BQ}$, i.e.,

Find out the minimal form least squares solution $X_{BQ}\in S_{BQ}$, i.e.,

This paper is organized as follows. In Section 2, we recall some preliminary results. In Section 3, we find out the relationship between the Bisymmetric matrix, Hermitian and Persymmetric matrix, which will be used to solve Problem 1. In Section 4, we provide numerical algorithms for computing the minimal norm least squares Bisymmetric solutions of (1.1), and provide some experiments with different dimensions. Finally in Section 5, we make some concluding remarks.

2.   Preliminaries

Definition 2.1. ^[17] Let $A = (a_{ij})\in \mathbb{Q}^{n\times n}$, $A^\ast = (\bar{a}_{ji})\in \mathbb{Q}^{n\times n}$, $A^{(\ast)} = (\bar{a}_{n-j+1, n-i+1})\in \mathbb{Q}^{n\times n}$. Then $A^{(\ast)} = V_nA^\ast V_n$, in which $V_n = \left[\begin{array}{l} & & 1\\ & \ddots & \\ 1 & & \end{array} \right]$.

(1) $A\in \mathbb{Q}^{n\times n}$ is called Hermitan if $A = A^\ast.$

(2) $A\in\mathbb{Q}^{n\times n}$ is called Persymmetric if $A = A^{(\ast)}$.

(3) $A\in\mathbb{Q}^{n\times n}$ is called Bisymmetric if $a_{ij} = a_{n-i+1, n-j+1} = \bar{a}_{ji}$.

Definition 2.2. ^[26] For $A = A_1+A_2{{\bf i}}+A_3{{\bf j}}+A_4{{\bf k}}\in\mathbb{Q}^{m\times n}$, its real representation matrix $A^R$ is defined as below:

Now, we denote the $i$-$th$ row block and column block of $A^R$ as $A^R_{r_i}$, $A^R_{c_i}$, respectively.

The Frobenius norm of the quaternion matrix $A = A_1+A_2{{\bf i}}+A_3{{\bf j}}+A_4{{\bf k}}$ is defined as

and it is not difficult to verify $\|A\| = \frac{1}{2}\|A^R\| = \|A^R_{r_i}\| = \|A^R_{c_i}\|, \ \ i = 1, 2, 3, 4.$

The follows are some properties about $A^R_{r_i}$ and $A^R_{c_i}$ which can be used in this paper.

Lemma 2.1. ^[26] Suppose $A$, $B\in\mathbb{Q}^{m\times n}$, $C\in \mathbb{Q}^{n\times p}$, $l\in\mathbb{R}$. The following properties hold.

(1) $A = B\Leftrightarrow A^R = B^R\Leftrightarrow A^R_{r_i} = B^R_{r_i}\Leftrightarrow A^R_{c_i} = B^R_{c_i}, \ \ i = 1, 2, 3, 4.$

(2) $(A+B)_{r_i}^R = A_{r_i}^R+B_{r_i}^R, \ \ (A+B)^R_{c_i} = A_{c_i}^R+B_{c_i}^R, \ \ i = 1, 2, 3, 4.$

(3) $(lA)_{r_i}^R = lA^R_{r_i}, \ \ (lA)_{c_i}^R = lA^R_{c_i}, \ \ i = 1, 2, 3, 4.$

(4) $(AC)^R_{r_i} = A^R_{r_i}C^R, \ \ (AC)^R_{c_i} = A^RC^R_{c_i}, \ \ i = 1, 2, 3, 4.$

For the real matrix equation, the 'vec' which arranges each column of a matrix into a vector in order is an important tool, the following result gives the relationship of $vec(X^R)$ and $vec(X^R_{r_1})$.

Lemma 2.2. ^[26]Suppose $X\in \mathbb{Q}^{m\times n}.$ Then $vec(X^R) = Fvec(X^R_{r_1})$, where

and

3.   The solution of Problem 1

In this section, we will introduce the block matrices of Bisymmetric matrix, then we analyze the relationship between the internal elements of a Bisymmetric quaternion matrix, and solve Problem 1 according to this property and the real representation of quaternion matrix. Since the internal structures of Bisymmetric matrices are different in odd and even cases, we first consider the even case.

Theorem 3.1. Let $X\in \mathbb{BQ}^{2n\times 2n}$, and $X$ is divided into four parts with the same dimension

where $X_a$ and $X_d$ are two Hermitian matrices, $X_b$ $X_c$ are two Persymmetric matrices, satisfy

Proof. The proof of (3.1) and (3.2) are similar, so we only prove (3.1).

Let $X = \left[\begin{smallmatrix} x_a&x_b\\ x_c&x_d \end{smallmatrix}\right]\in\mathbb{Q}^{2n\times 2n},$ and $(x_{k}^{ij}) = x_k\in\mathbb{Q}^{n\times n}$, $k = a, \ b, \ c, \ d$, $''X^{ij}"$ and $''x_{k}^{ij}"$ are the element of $i$th row and $j$th column in $X$ and $x_k$, respectively, $1\leq i, j\leq n$, then

If $X$ is an Bisymmetry matrix, then

(3.1) holds.

Obviously, the study of Bisymmetry matrix is transformed into Hermitian matrix and Persynmetric matrix by Theorem 3.1. In order to simplify the operation, we extract independent elements in Hermitian matrix and Persynmetric matrix.

Definition 3.1. For $X\in \mathbb{R}^{n\times n}$, let

$\alpha_1 = (x_{11}, \cdots, x_{n1})$, $\alpha_2 = (x_{22}, \cdots, x_{n2})$, $\cdots$, $\alpha_{n-1} = (x_{(n-1)(n-1)}, x_{n(n-1)})$, $\alpha_{n} = x_{nn}$.

$\beta_1 = (x_{21}, \cdots, x_{n1})$, $\beta_2 = (x_{32}, \cdots, x_{n2})$, $\cdots$, $\beta_{n-2} = (x_{(n-1)(n-2)}, x_{n(n-2)})$, $\beta_{n-1} = (x_{n(n-1)})$.

$\alpha'_1 = (x_{1n}, \cdots, x_{nn})$, $\alpha'_2 = (x_{2(n-1)}, \cdots, x_{n(n-1)})$, $\cdots$, $\alpha_{n-1} = (x_{(n-1)2}, x_{n2})$, $\alpha'_{n} = x_{n1}$.

$\beta'_1 = (x_{2n}, \cdots, x_{nn})$, $\beta'_2 = (x_{3(n-1)}, \cdots, x_{n(n-1)})$, $\cdots$, $\beta'_{n-2} = (x_{(n-1)3}, x_{n3})$, $\beta'_{n-1} = (x_{n2})$.

and

The following theorem introduces the relationship of independent elements and 'vec' of Hermitian matrix and Persymmetric matrix, respectively.

Theorem 3.2. For $A\in \mathbb{SR}^{n\times n}$, $B\in \mathbb{PR}^{n\times n}$, $C$ and $D$ are constructed by letting the diagonal elements of $A$ and anti diagonal element of $B$ be 0, respectively, then

in which

Next, we give the relationship between 'vec' of a matrix and its four blocks.

Theorem 3.3. Let $X = \left(\begin{array}{cc} X_a&X_b\\ X_c&X_d \end{array}\right) \in \mathbb{Q}^{n\times n},$ $X_a\in \mathbb{Q}^{k\times k}$, $k\leq n$, then

in which $P' = diag(P_1, P_2),$ and

$P_1 = \left(\begin{smallmatrix} \delta_n^1 & \cdots & \delta_n^k & \cdots & 0 & \cdots & 0 & \delta_n^{k+1} & \cdots & \delta_n^n & \cdots & 0 & \cdots & 0\\ \vdots & & \vdots & & \vdots & & \vdots & \vdots & & \vdots & & \vdots & & \vdots\\ 0 & \cdots & 0 & \cdots & \delta_n^1 & \cdots & \delta_n^k & 0 & \cdots & 0 & \cdots & \delta_n^{k+1} & \cdots & \delta_n^n\\ \end{smallmatrix}\right)\in \mathbb{R}^{nk\times nk},$

$P_2 = \left(\begin{smallmatrix} \delta_n^1 & \cdots & \delta_n^k & \cdots & 0 & \cdots & 0 & \delta_n^{k+1} & \cdots & \delta_n^n & \cdots & 0 & \cdots & 0\\ \vdots & & \vdots & & \vdots & & \vdots & \vdots & & \vdots & & \vdots & & \vdots\\ 0 & \cdots & 0 & \cdots & \delta_n^1 & \cdots & \delta_n^k & 0 & \cdots & 0 & \cdots & \delta_n^{k+1} & \cdots & \delta_n^n\\ \end{smallmatrix}\right)\in \mathbb{R}^{n(n-k)\times n(n-k)}.$

Theorem 3.2 and Theorem 3.3 can be obtained by direct verification, so we omit the concrete proving process.

Theorem 3.4. Let $A, \ B, \ C\in\mathbb{Q}^{2n\times 2n}$, denote $\tilde{A} = (B^R\otimes A_{r1}^R)FP'KLW$, in which

$P = diag(P', P', P', P')$, $K = diag(K_1, \ K_1, \ K_1, \ K_1),$ $K_1 = diag(I_{n^2}, I_{n^2}, V^T\otimes V, V^T\otimes V)$, $L = diag(L_1, \ L_1, \ L_1, \ L_1)$,

$L_1 = \left(\begin{smallmatrix} I_{n^2} & 0\\ 0 &I_{n^2}\\ 0 &I_{n^2}\\ I_{n^2} & 0 \end{smallmatrix} \right)$, $W = diag(W_1, W_2, W_3, W_4, W_3, W_4, W_3, W_4)$, we can obtain

And then, the minimal norm least squares Bisymmetric solution $X_{BQ}$ of $(1.1)$ satisfies

Proof. By Lemma 2.1, we get

Let $X^R_{r1} = \left(\begin{matrix} X_1&X_2&X_3&X_4 \end{matrix}\right)$, and $X_i = \left(\begin{array}{cc} X_{ia}&X_{ib}\\ X_{ic}&X_{id} \end{array}\right)$.

The next work is removing the repeated elements in $vec (X)$.

Thus

if and only if

For the real matrix equation

According to the classical matrix theory, its least squares solutions can be represented as

Corollary 3.5. Let $A, \ B, \ C\in \mathbb{Q}^{n\times n}$, $(1.1)$ is compatible over $\mathbb{BQ}^{n\times n}$ if and only if

Moreover, if $(3.5)$ holds, the solution set of $(1.1)$ over $\mathbb{BQ}^{n\times n}$ is

in which $\tilde{A}$ and $ved(X)$ are described in Theorem 3.4.

Proof. (1.1) has a solution $X$ if and only if

By Theorem 3.4 and the properties of the $M$-$P$ inverse, we get

Therefore for $X_{BQ}\in S_{BQ}$, we obtain

Thus (1.1) is compatible over $\mathbb{BQ}^{n\times n}$ if and only if

Moreover, according to the classical matrix theory, the solution $X_{BQ}$ satisfies

So the formula (3.9) holds.

Next, we discuss the case of odd Bisymmetric dimension.

By studying the odd dimensional Bisymmetric matrix, we find that for any $X\in \mathbb{BQ}^{(2n-1)\times (2n-1)}$, after dividing $X$ into four blocks, $X_1\in\mathbb{Q}^{n\times n}$, $X_2\in\mathbb{Q}^{n\times (n-1)}$, $X_3\in\mathbb{Q}^{(n-1)\times n}$, $X_4\in\mathbb{Q}^{(n-1)\times (n-1)}$. Since $X_i(i = 1, 2, 3, 4)$ do not have the same order. So we add the new $n-th$ row between the original $n-th$ row and the original $(n+1)-th$ row, and add the new $n-th$ column between the original $n-th$ column and the original $(n+1)-th$ column, then we can get the new matrix $X'\in \mathbb{BQ}^{2n\times 2n}$.

We can use Theorem 3.4 to solve the problem. Finally, we delete the added elements.

Define some matrices: $(i)\ \ Z_1 = [0, I_{(n-1)}]\in\mathbb{R}^{(n-1)\times n}$; $(ii)\ \ Z_2\in \mathbb{R}^{n\times n}$ is $n\times n$ zeros matrix; $(iii)\ \ Z_3\in \mathbb{R}^{(n-1)\times n}$ is $(n-1)\times n$ zeros matrix.

Theorem 3.6. Let $X\in \mathbb{BQ}^{(2n-1)\times (2n-1)}$, then

where

The next work is to deal with independent elements.

In the following theorem, we associate the vec of $X\in\mathbb{BQ}^{(2n-1)\times ((2n-1))}$ with the vec of a newly constructed matrix $X'\in\mathbb{BQ}^{2n\times 2n}$.

Theorem 3.7. Let $X\in \mathbb{BQ}^{(2n-1)\times (2n-1)}$, we can obtain

in which $E = \left(\begin{smallmatrix} E_1 & & & \\ &E_1 & & \\ & &E_1 & \\ & & &E_1\\ \end{smallmatrix}\right)$,

Proof.

Theorem 3.8. Let $A, \ B, \ C\in \mathbb{BQ}^{(2n-1)\times (2n-1)}$, denote $\tilde{\tilde{A}} = (B^R\otimes A^R_{r1})FPEKLWG$, in which $G = \left(\begin{smallmatrix} G_1 & & & \\ &G_2 & & \\ & &G_2 & \\ & & &G_2 \end{smallmatrix}\right), G_1 = \left(\begin{smallmatrix} I_{n(n+1)/2} & \\ G_3 & \\ &I_{n(n-1)/2} \end{smallmatrix}\right)$, $G_2 = \left(\begin{smallmatrix} I_{n(n-1)/2} & \\ G_4 & \\ &I_{(n-1)(n-2)/2} \end{smallmatrix}\right), G_3 = \left(\begin{smallmatrix} \left(\delta_{\frac{n(n+1)}{2}}^{\frac{n(n+1)}{2}}\right)^T\\ \vdots\\ \left(\delta_{\frac{n(n+1)}{2}}^{\frac{(n+i)(n+1-i)}{2}}\right)^T\\ \vdots\\ \left(\delta_{\frac{n(n+1)}{2}}^n\right)^T\end{smallmatrix} \right), G_4 = G_3(n-1),$ the role of $G$ is to delete added elements. We can obtain

And then, the minimal norm least squares Bisymmetric solution $X_{BQ}$ of $(1.1)$ satisfies

Corollary 3.9. Let $A, \ B, \ C\in \mathbb{Q}^{(2n-1)\times (2n-1)}$, $(1.1)$ is compatible over $\mathbb{BQ}^{(2n-1)\times (2n-1)}$, if and only if

Moreover, if $(3.8)$ holds, the solution set of $(1.1)$ over $\mathbb{BQ}^{(2n-1)\times (2n-1)}$ is

in which $\tilde{\tilde{A}}$ and $ved(X)$ are described in Theorem 3.8.

4.   Algorithm and numerical experiments

In this section, we propose the corresponding algorithms based on the discussion in Section 3.

Algorithm 4.1. $(For\ Problem\ 1)$

(1) Input $A, \ B, \ C\in \mathbb{Q}^{n\times n}$, output\ $A^R_{r1}, \ B^R, \ C^R_{r1}.$

(2) Input $F, \ P, \ E, \ K, \ L, \ W, \ G$, output the matrix $\tilde{A}$ or $\tilde{\tilde{A}}$.

(3) Output the minimal norm least squares solution $X_{BQ}$ according to $(3.4)$ or $(3.7)$.

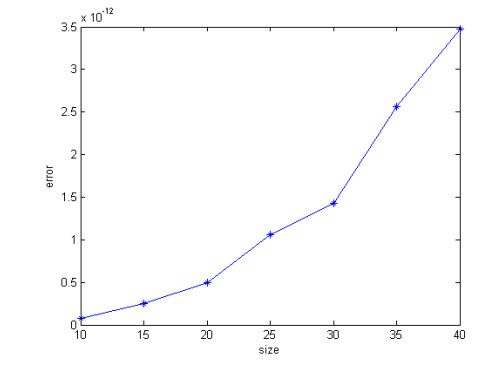
Example. The following tables are the test of different dimensions of the minimal norm least squares solution of Problems 1 according to Algorithm 4.1. The specific steps are as follows: first, generating the appropriate $A$, $B$ and $X$ of the corresponding structure randomly in MATLAB, and calculate $C = AXB$, then use the method in this paper to calculate the numerical solution, and then compute the error between the real solution and the numerical solution. As shown in Figure 1.The below figure shows the effectiveness of the method in Section 3.

5.   Conclusions

In this paper, we use internal relations between block Bisymmetric matrices, the real representation of quaternion matrix and the properties of $M$-$P$ inverse to study the least squares Bisymmetric solution of $AXB = C$. We obtain the least squares Bisymmetric solution of this quaternion matrix equation and its compatable conditions. This method is effective and it is more convenient to analyze the problems of solution with special structures of quaternion matrix equation.

Acknowledgments

This work is supported by the Natural Science Foundation of Shandong under grant ZR2020MA053.

Conflict of interest

The authors declare that there is no conflict of interest.