Three special kinds of least squares solutions for the quaternion generalized Sylvester matrix equation

1.   Introduction

In this paper, we adopt the following notations. $\mathbb{R}$ represents the real number field; $\mathbb{R}^n$ stands for the set of all real column vectors with order $n$; $\mathbb{R}^{m\times n}$ stands for the set of all $m\times n$ real matrices. $\mathbb{C}$ represents the complex number field; $\mathbb{C}^n$ stands for the set of all complex column vectors with order $n$; $\mathbb{C}^{m\times n}$ stands for the set of all $m\times n$ complex matrices. The sets $\mathbb{U}_n, \mathbb{U}_{-n}, \mathbb{V}_n, \mathbb{W}_n$ represent the set of all $n\times n$ tridiagonal symmetric matrices, tridiagonal skew-symmetric matrices, Brownian matrices, Generalized Rotation matrices, respectively. $\mathbb{Q}$ stands for the quaternion skew-field; $\mathbb{Q}^n$ stands for the set of all quaternion column vectors with order $n$; $\mathbb{Q}^{m\times n}$ represents the set of all $m\times n$ quaternion matrices; $\mathbb{HTQ}^{n\times n}$, $\mathbb{AHTQ}^{n\times n}$, $\mathbb{BQ}^{n\times n}$, $\mathbb{MQ}^{n\times n}$ represent the set of all $n\times n$ quaternion tridiagonal Hermitian matrices, quaternion tridiagonal anti-Hermitian matrices, quaternion Brownian matrices, quaternion Generalized Rotation matrices, respectively. $I_n$ represents the unit matrix with order $n$. For matrix $A$, $A^T, A^H, A^\dagger$ stand for the transpose, the conjugate transpose, Moore-Penrose inverse of matrix $A$, respectively. $\otimes$ represents the Kronecker product of matrices. $\left \|\cdot\right \|$ represents the Frobenius norm of a matrix or Euclidean norm of a vector. For $C = (c_1, c_2, \ldots, c_n)\in \mathbb{R}^{m\times n}$, $vec(C)$ means the vector operator, i.e., $vec(C) = (c_1^T, c_2^T, \ldots, c_k^T)^T$.

Matrix equations can be encountered in many areas, such as system theory, control theory, stability analysis, some fields of pure and applied mathematics and so on ^[1,2,3]. With the rapid development of these fields, more and more scholars are interested in matrix equations and have obtained many valuable results ^[4,5,6]. Now, we turn our attention to quaternion matrix equation. Quaternion matrix equations and their least squares solutions are widely applied in many fields, such as computer science, quantum mechanics, control theory, field theory and so on ^[7,8,9]. Therefore, many people are engaged in studying theoretical properties and numerical computations of quaternion matrix equations. By means of complex representation, Jiang et al. studied algebraic algorithm for quaternion least squares problem ^[10] and quaternion eigenvalue problem ^[11]; Yuan et al. studied the quaternion least squares problems for the quaternion matrix equations $AXB+CXD = E$ ^[12], $X-A\hat{X}B = C$ ^[13]. By applying the real representation of quaternion matrices, Wang et al. proposed an iterative method for solving the quaternion least squares problem ^[14].

Consider the generalized Sylvester matrix equation

If $B$ and $C$ are identity matrices, then the matrix Eq (1.1) reduces to the well-known Sylvester matrix Eq ^[15]. If $C$ and $D$ are identity matrices, then the matrix Eq (1.1) reduces to the well-known Stein matrix equation. It has extensive application value in robust control, feedback control, pole assignment design, neural network and so on ^[16,17,18]. There are many important results about their solutions, for example, ^[19] and ^[20] considered the solvability condition for the complex and real matrix Eq (1.1), respectively. For the quaternion matrix Eq (1.1), ^[21] derived necessary and sufficient conditions for the existence of a solution or a unique solution using the method of complex representation of quaternion matrices; ^[12,22] studied $\eta$-Hermitian and $\eta$-anti-Hermitian solutions to the quaternion matrix equations $AXB+CXD = E$, $AXB+CYD = E$, respectively; ^[23] obtained the expression of solutions of a system of quaternion matrix equations including $\eta$-Hermicity. Also, it is worth noting that a number of important results on Sylvester operators have been obtained in recent years. For instance, ^[24] studied some features of slice semi-regular functions $\mathcal{S\xi M}(\Omega)$ on a circular domain $\Omega$ and verified the equivalence of slice semi-regular functions via Sylvester operators; ^[25] applied the existing results to establish some outcomes of the study of the behaviour of a class of linear operators, which include the Sylvester ones, acting on slice semi-regular functions. The name of Sylvester operator is due to the fact that, when dealing with matrices, equation $S_{f, g}(\chi) = b$ is usually called Sylvester equation. In the most common use, Sylvester equations are special matrices equations, introduced by Sylvester himself ^[26], which are used in several subjects, including similarity, commutativity, control theory and differential equation ^[27]. In the quaternionic setting, such equations were studied with different purposes. In this paper, we consider the least squares problem with different constrains for quaternion matrix Eq (1.1) based on the real representation of quaternion matrices together with the $\mathcal{H}$-representation method, which is able to transform a matrix-valued equation into a standard vector-valued equation with independent coordinates. The related problems are described as follows.

Problem 1. Let $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$, and

Find out $(X_H, Y_A)\in \mathbb{T_L}$ such that

The solution $(X_H, Y_A)$ in Problem 1 is called the minimal norm least squares tridiagonal mixed solution.

Problem 2. Let $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$, and

Find out $(X_B, Y_B)\in \mathbb{B_L}$ such that

The solution $(X_B, Y_B)$ in Problem 2 is called the minimal norm least squares Brownian solution.

Problem 3. Let $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$, and

Find out $(X_M, Y_M)\in \mathbb{M_L}$ such that

The solution $(X_M, Y_M)$ in Problem 3 is called the minimal norm least squares Rotation solution.

The remaining content of this paper is organized as follows. In Section 2, we study and recall some preliminary results with regard to the real representation of a quaternion matrix, and then introduce some matrix sets with special structures. In Section 3, we give the concept of $\mathcal{H}$-representation and subsequently study its properties. In Section 4, on the basis of the real representation matrix of a quaternion matrix and $\mathcal{H}$-representation of matrices with special structures, operational properties, the properties of Frobenius norm and Moore-Penrose generalized inverse, we can convert Problems 1–3 into the corresponding problems of the real matrix equation over free variables, and then the unique solution $(X, Y)$ and expressions for special solution are established. In addition, the necessary and sufficient conditions for the quaternion matrix equation to have solution with special structure are included as corollaries. In Section 5, we provide numerical algorithms for solving Problems 1–3 by the results obtained in Section 4, and afterwards we present a numerical example to verify the feasibility of our proposed method. Finally, in Section 6, we put some conclusions.

2.   Basic definitions

We start by recalling the usual Kronecker product.

Definition 2.1. For any two matrices $A = (a_{ij})\in \mathbb{R}^{m\times n}, B\in \mathbb{R}^{p\times q}$, the Kronecker product of $A$ and $B$ is defined as

We now turn to recall the standard representation of a quaternion.

Definition 2.2. A quaternion $q \in \mathbb{Q}$ is represented as

where $q_1, q_2, q_3, q_4 \in \mathbb{R},$ and three imaginary units ${{{\rm{\bf i}}}}, {{{\rm{\bf j}}}}, {{{\rm{\bf k}}}}$ satisfy

Definition 2.3. A quaternion matrix $A\in \mathbb{Q}^{m\times p}$ is represented as

where $A_1, A_2, A_3, A_4 \in \mathbb{R}^{m\times p}$. The conjugate matrix of $A$ is defined as

We recall a standard norm in this setting.

Definition 2.4. ^[28] The Frobenius norm of $A = A_1 + A_2{{{\rm{\bf i}}}} + A_3{{{\rm{\bf j}}}} + A_4{{{\rm{\bf k}}}}$ is defined as

Definition 2.5. ^[28] For $A = A_1 + A_2{{{\rm{\bf i}}}} + A_3{{{\rm{\bf j}}}} + A_4{{{\rm{\bf k}}}}\in \mathbb{Q}^{m\times p}$, its real representation matrix $\overrightarrow{A}$ is defined as follows:

According to the matrix blocks of the real representation matrix $\overrightarrow{A}$, if we know a column block of $\overrightarrow{A}$, we know $\overrightarrow{A}$. For the sake of convenience, we use $\overrightarrow{A}_c$ to represent the first column block of $\overrightarrow{A}$, i.e.,

Next, we investigate some properties of $\overrightarrow{A}_c$, which will be used in the sequel.

Lemma 2.1. ^[28] Suppose $A, B\in \mathbb{Q}^{m\times n}, C\in \mathbb{Q}^{n\times p}, t\in \mathbb{R}$, then we have

Proof. We only provide detailed proof of $\overrightarrow{AC} = \overrightarrow{A}\overrightarrow{C}, \overrightarrow{AC}_c = \overrightarrow{A}\overrightarrow{C}_c$, and the rest are similarly verifiable. Suppose $A = A_1+A_2{{{\rm{\bf i}}}}+A_3{{{\rm{\bf j}}}}+A_4{{{\rm{\bf k}}}}\in \mathbb{Q}^{m\times n}$, $C = C_1+C_2{{{\rm{\bf i}}}}+C_3{{{\rm{\bf j}}}}+C_4{{{\rm{\bf k}}}}\in \mathbb{Q}^{n\times p}$, then

According to the Definition 2.5, we have

and

We now recall a couple of algebraic results about the structure of quaternion matrices and their real representation.

Lemma 2.2. ^[14] Suppose $X\in \mathbb{Q}^{p\times p}$, then $vec(\overrightarrow{X}) = Jvec(\overrightarrow{X}_c)$, where

and

Lemma 2.3. ^[14] Suppose $X = X_1+X_2{{{\rm{\bf i}}}}+X_3{{{\rm{\bf j}}}}+X_4{{{\rm{\bf k}}}}\in \mathbb{Q}^{p\times p}$, then

where

Remark 2.1. Either the $J$ in Lemma 2.2 or the $K$ in Lemma 2.3 is just a bridge connecting the left and right sides of its equation. By the structure of real representation of quaternion matrix and its first column block, we only need to figure out the relationship between the left and right sides of its equation to express $J$ or $K$.

We will now present four special matrix sets. We refer to ^[29] for all the concepts involved in this paper.

Definition 2.6. A tridiagonal symmetric matrix $P\in \mathbb{U}_n$ is an $n\times n$ matrix with the following form

Definition 2.7. A tridiagonal skew-symmetric matrix $P\in \mathbb{U}_{-n}$ is an $n\times n$ matrix with the following form

Definition 2.8. A matrix $P\in \mathbb{V}_n$ is called the Brownian matrix, if

Specifically, the form is as follows:

Definition 2.9. A Generalized Rotation matrix $P\in \mathbb{W}_n$ is an $n\times n$ matrix with the following form

3.   $\mathcal{H}$-Representation and its properties

In this section, we will briefly introduce the notion of $\mathcal{H}$-representation and the related properties. Besides, we will also analyze the structure of four special matrix sets mentioned above by means of $\mathcal{H}$-representation and present their $\mathcal{H}$-representation matrices.

Definition 3.1. ^[30] Consider a p-dimensional complex matrix subspace $\mathbb{X}\subset\mathbb{C}^{n\times n}$ over the field $\mathbb{C}$. Assume that $e_1, e_2, \ldots, e_p$ form a basis of $\mathbb{X}$, and define $H = [vec(e_1)\ vec(e_2)\ \ldots\ vec(e_p)].$ If for each $X\in \mathbb{X}$, we express $\psi(X) = vec(X)$ in the form of

with a $p\times 1$ vector $\widetilde{X}$, then $H\widetilde{X}$ is called an $\mathcal{H}$-representation of $\psi(X)$, and $H$ is called an $\mathcal{H}$-representation matrix of $\psi(X)$.

Remark 3.1. 1) The $\mathcal{H}$-representation of $\psi(X)$ for $X\in \mathbb{X}$ is not unique because of the fact that the matrix $H$ may be different owing to the basis choices of $\mathbb{X}$. Apparently, when the basis of $\mathbb{X}$ is fixed, the $\mathcal{H}$-representation matrix $H$, as well as $\widetilde{X}$, is uniquely determined; 2) $\psi$ is used here only as a function name for the convenience of defining its inverse in the sequel.

In what follows, based on the special matrix sets defined in Section 2, we present some simple examples to elucidate Definition 3.1.

Example 3.1. Let $\mathbb{X} = \mathbb{U}_3, X = (x_{ij})_{3\times 3}$, then $dim(\mathbb{X}) = 5$. If we select the following basis of $\mathbb{X}$

It is then easy to compute

Example 3.2. Let $\mathbb{X} = \mathbb{V}_3$, then $dim(\mathbb{X}) = 7$. If we select the following basis of $\mathbb{X}$

Then it is easy to compute

Example 3.3. Let $\mathbb{X} = \mathbb{W}_3$, then $dim(\mathbb{X}) = 3$. If we select the following basis of $\mathbb{X}$

Then we can obtian

In this paper, we are interested in the $\mathcal{H}$-representation for $\mathbb{X} = \mathbb{U}_n/\mathbb{U}_{-n}/\mathbb{V}_n/\mathbb{W}_n$. For $\mathbb{X} = \mathbb{U}_n$, we select a standard basis throughout this paper as

where $E_{ij} = (e_{lk})_{n\times n}$ with $e_{ij} = e_{ji} = 1$ and the other entries are zeros. Clearly, for the above given bases, if $\mathbb{X} = \mathbb{U}_n$, then for any $X_n = (x_{ij})_{n\times n}\in \mathbb{X}$, we have

For $\mathbb{X} = \mathbb{U}_{-n}$, we select a standard basis throughout this paper as

where $E_{ij}' = (e_{lk}')_{n\times n}$ with $e_{ij}' = -1, e_{ji}' = 1$ and the other entries are all zeros. For the above given bases, if $\mathbb{X} = \mathbb{U}_{-n}$, then for any $X_{-n} = (x_{ij}')_{n\times n}\in \mathbb{X}$, we have

For the convenience of description, the following $\mathbb{Z}$ and $\mathbb{W}$ both represent $\mathbb{X}$.

Similarly, for $\mathbb{Z} = \mathbb{V}_n$, we select a standard basis as

where $F_{ii} = (f_{lk})_{n\times n}$ with $f_{ii} = 1$, and $F_{ij}, F_{ji}$ are $n\times n$ matrices with $f_{ij} = 1$, $f_{ji} = 1$ for $\forall j > i$, respectively, and the other entries are zeros. Based on above bases, for any $Z_n = (z_{ij})_{n\times n}\in \mathbb{Z}$, we have

Likewise, for $\mathbb{W} = \mathbb{W}_n$, we select a standard basis as

with $D_{11} = I_n$ and $D_{i1} = \left[\begin{array}{cc} &I_{i-1}\\ \alpha I_{n-i+1} \end{array}\right], \ 2\leq i\leq n$.

Based on above bases, if $\mathbb{W} = \mathbb{W}_n$, then for any $W_n = (w_{ij})_{n\times n}\in \mathbb{W}$, we have

As soon as a standard basis is given, $\tilde{X}_n, \tilde{X}_{-n}, \tilde{Z}_n$, and $\tilde{W}_n$ are uniquely determined by $X_n, X_{-n}, Z_n$ and $W_n$, respectively. Thus, we can state the following definition:

Definition 3.2. We define $\sigma_1: X_n = (x_{ij})_{n\times n}\in \mathbb{U}_n\mapsto \tilde{X}_n$, where $\tilde{X}_n$ is defined in $(3.1)$, $\sigma_2: X_{-n} = (x_{ij}')_{n\times n}\in \mathbb{U}_{-n}\mapsto \tilde{X}_{-n}$, where $\tilde{X}_{-n}$ is defined in $(3.2)$, $\tau: Z_n = (z_{ij})_{n\times n}\in \mathbb{V}_n\mapsto \tilde{Z}_n$, where $\tilde{Z}_n$ is defined in $(3.3)$, and $\phi: W_n = (w_{ij})_{n\times n}\in \mathbb{W}_n\mapsto \tilde{W}_n$, where $\tilde{W}_n$ is defined in $(3.4)$.

Remark 3.2. $\psi, \sigma_1, \sigma_2, \tau$ and $\phi$ are obviously invertible in the sense that for any $(\nu, \nu_1, \nu_2, \nu_3, \nu_4)\in \mathbb{C}^{n^2}\times \mathbb{C}^{2n-1}\times \mathbb{C}^{n-1}\times \mathbb{C}^{3n-2}\times \mathbb{C}^n$, we have $(\psi^{-1}(\nu), \sigma_1^{-1}(\nu_1), \sigma_2^{-1}(\nu_2), \tau^{-1}(\nu_3), \phi^{-1}(\nu_4))\in \mathbb{C}^{n\times n}\times \mathbb{U}_n\times \mathbb{U}_{-n}\times \mathbb{V}_n\times \mathbb{W}_n$. It should be noted that $\psi, \sigma_1, \sigma_2, \tau$ and $\phi$ are defined on different domains.

Note that $\psi(X_n)$ is a column vector formed by all elements of $X_{n}$, while $\sigma_1(X_n)$, $\sigma_2(X_{-n})$, $\tau(Z_n)$, $\phi(W_n)$ are column vectors formed by different nonzero elements of $X_n$, $X_{-n}$, $Z_n$, $W_n$, respectively. For clarity, we denote the $H$-matrix in $\mathcal{H}$-representation corresponding to $\mathbb{X} = \mathbb{U}_n$ by $H_n^1$, the $H$-matrix in $\mathcal{H}$-representation corresponding to $\mathbb{X} = \mathbb{U}_{-n}$ by $H_{-n}^1$, the $H$-matrix in $\mathcal{H}$-representation corresponding to $\mathbb{X} = \mathbb{V}_n$ by $H_n^2$, the $H$-matrix in $\mathcal{H}$-representation corresponding to $\mathbb{X} = \mathbb{W}_n$ by $H_n^3$.

The following corollary is obvious from Definitions 3.1 and 3.2.

Corollary 3.1. For a $n^2\times 1$ vector $\mu_1$, if $\psi^{-1}(\mu_1)\in \mathbb{U}_n$, then there exists a $(2n-1)\times 1$ vector $\nu_1$, such that $\mu_1 = H_n^1\nu_1$. For a $n^2\times 1$ vector $\mu_2$, if $\psi^{-1}(\mu_2)\in \mathbb{U}_{-n}$, then there exists a $(n-1)\times 1$ vector $\nu_2$, such that $\mu_2 = H_{-n}^1\nu_2$. For a $n^2\times 1$ vector $\mu_3$, if $\psi^{-1}(\mu_3)\in \mathbb{V}_n$, then there exists a $(3n-2)\times 1$ vector $\nu_3$, such that $\mu_3 = H_n^2\nu_3$. For a $n^2\times 1$ vector $\mu_4$, if $\psi^{-1}(\mu_4)\in \mathbb{W}_n$, then there exists a $n\times 1$ vector $\nu_4$, such that $\mu_4 = H_n^3\nu_4$.

4.   The solutions for Problems 1–3

In this section, we solve Problems 1–3 via the real representation of quaternion matrices and $\mathcal{H}$-representation. We first convert above least squares problems into corresponding problems of real matrix equation by using the real representation, then in order to reduce the size of original problems, we remove the redundancy and extract effective elements through $\mathcal{H}$-representation. Finally, we obtain the solutions of Problems 1–3.

Lemma 4.1. ^[31] The least squares solutions of the linear system of equations $Ax = b$, with $A\in \mathbb{R}^{m\times n}$ and $b\in \mathbb{R}^m$ can be represented as

where, $y\in \mathbb{R}^n$ is an arbitrary vector. The minimal norm least squares solution of the linear system of equations $Ax = b$ is $A^{\dagger}b$.

Lemma 4.2. ^[31] The linear system of equations $Ax = b$, with $A\in \mathbb{R}^{m\times n}$ and $b\in \mathbb{R}^m$ has a solution $x\in \mathbb{R}^n$ if and only if

When $Ax = b$ is compatible, the general solution can be represented as

where, $y\in \mathbb{R}^n$ is an arbitrary vector. $Ax = b$ has a unique solution if and only if

In this case, the unique solution is $x = A^{\dagger}b.$

Theorem 4.3. Suppose $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$ be given. Hence the set $\mathbb{T_L}$ of Problem 1 can be expressed as

And then, the minimal norm least squares solution $(X_H, Y_A)$ of Problem 1 satisfies

Proof. For $X = X_1+X_2{{{\rm{\bf i}}}}+X_3{{{\rm{\bf j}}}}+X_4{{{\rm{\bf k}}}}\in \mathbb{HTQ}^{p\times p}, Y = Y_1+Y_2{{{\rm{\bf i}}}}+Y_3{{{\rm{\bf j}}}}+Y_4{{{\rm{\bf k}}}}\in \mathbb{AHTQ}^{q\times q}$, according to Lemmas 2.1–2.3, we have

where $J', K'$ have the same structure with the $J, K$, respectively. Since $X_1\in \mathbb{U}_p, X_t\in \mathbb{U}_{-p}$, $Y_1\in \mathbb{U}_{-q}, Y_t\in \mathbb{U}_q(t = 2, 3, 4)$, in light of Corollary 3.1, we can derive

For the convenience of what follows, let us denote

Then we can obtain

Thus $\left\|AXB+CYD-E\right\|$ assume its minimum value

if and only if $\left\|G_1\left(\begin{matrix}\check{X}\\\check{Y}\end{matrix}\right)-vec(\overrightarrow{E}_c)\right\|$ does.

For the real matrix equation

by Lemma 4.1, its least squares solution can be represented as

Moreover, (4.1) is derived by multiplying both sides of (4.4) by the matrix $H_1$. Meanwhile, (4.2) can be derived.

By virtue of Theorem 4.3, we can give the necessary and sufficient condition in order to prove the existence of tridiagonal mixed solution for the quaternion matrix equation $AXB+CYD = E$, and the expression for the tridiagonal mixed solution when (1.1) is compatible.

Corollary 4.4. Let $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$ be given, and $G_1$ be defined as in $(4.3)$.Then $(1.1)$ has a solution $X\in \mathbb{HTQ}^{p\times p}, Y\in \mathbb{AHTQ}^{q\times q}$, if and only if

If $(4.5)$ holds, the solutions set of $(1.1)$ can be represented as

Moreover, $(1.1)$ has unique tridiagonal mixed solution $(X_H', Y_A')$, if and only if

and the unique tridiagonal mixed solution $(X_H', Y_A')$ satisfies

Proof. According to the proof of Theorem 4.3, Lemma 4.2 and the definition of Moore-Penrose generalized inverse, we have

thus (1.1) has tridiagonal mixed solution $(X, Y)$ if and only if

So we get the formula in $(4.5)$. Under the condition that $(4.5)$ is established, the solution $(X, Y)$ of $(1.1)$ satisfies

Moreover, the solution $(X, Y)$ of (1.1) satisfies

Similarly, we can deduce (4.6) by multiplying both sides of the above equation by the matrix $H_1$. At the same time, the unique tridiagonal mixed solution (4.7) can also be obtained.

In what follows, we concentrate on Problems 2 and 3. By Theorem 3.1, for $(X, Y)$ with special structure, we can give its $\mathcal{H}$-representation matrix, which will help us extract effective elements and reduce the complexity of operations. Based on the above ideas, the following conclusions can be easily obtained.

Theorem 4.5. Suppose $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$. Hence the set $\mathbb{B_L}$ of Problem 2 can be represented as

and then, the minimal norm least squares solution $(X_B, Y_B)$ of Problem 2 satisfies

where

Corollary 4.6. Let $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$ be given. $G_2$ is defined in Theorem 4.5. Then $(1.1)$ has a solution $X\in \mathbb{BQ}^{p\times p}, Y\in \mathbb{BQ}^{q\times q}$, if and only if

If $(4.10)$ holds, the Brownian solutions set of $(1.1)$ can be represented as

furthermore, $(1.1)$ has unique Brownian solution $(X_B', Y_B')$, if and only if

and the unique Brownian solution $(X_B', Y_B')$ satisfies

Remark 4.1. When $X\in \mathbb{BQ}^{p\times p}$, $Y\in \mathbb{BQ}^{q\times q}$, according to Theorem 4.5, we can give $H_2$, $G_2$, then Corollary 4.6 can be obtained by a proof method similar to Corollary 4.4.

Similar to Theorem 4.5, when $X\in \mathbb{MQ}^{p\times p}$, $Y\in \mathbb{MQ}^{q\times q}$, we can give $H_3$, $G_3$ for studying Problem 3.

Theorem 4.7. Suppose $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$. Hence the set $\mathbb{M_L}$ of Problem 3 can be expressed as

and then, the minimal norm least squares solution $(X_M, Y_M)$ of Problem 3 satisfies

where

Corollary 4.8. Let $A\in \mathbb{Q}^{m\times p}, B\in \mathbb{Q}^{p\times n}, C\in \mathbb{Q}^{m\times q}, D\in \mathbb{Q}^{q\times n}, E\in \mathbb{Q}^{m\times n}$ be given. $G_3$ is defined in Theorem 4.7. Then $(1.1)$ has a solution $X\in \mathbb{MQ}^{p\times p}, Y\in \mathbb{MQ}^{q\times q}$, if and only if

If $(4.14)$ holds, the Rotation solutions set of $(1.1)$ can be expressed as

in addition, $(1.1)$ has unique Rotation solution $(X_M', Y_M')$, if and only if

and the unique Rotation solution $(X_M', Y_M')$ satisfies

5.   Algorithms and numerical experiments

In this section, on the basis of the discussions in Section 4, we propose the algorithms of solving Problems 1–3, and then give a numerical example to prove the feasibility of the proposed algorithms.

Algorithm 5.1. (Problem 1)

(1) Input $A, B, C, D, E\in\mathbb{Q}^{n\times n}$, output $\overrightarrow{B}_c^T, \overrightarrow{D}_c^T, \overrightarrow{A}, \overrightarrow{C}, vec(\overrightarrow{E}_c)$,

(2) Input $J, K, H_n^1, H_{-n}^1$, output $H_1, G_1$,

(3) According to $(4.2)$, calculate the minimal norm least squares solution $(X_H, Y_A)$ of Problem 1.

Algorithm 5.2. (Problem 2)

(1) Input $A, B, C, D, E\in\mathbb{Q}^{n\times n}$, output $\overrightarrow{B}_c^T, \overrightarrow{D}_c^T, \overrightarrow{A}, \overrightarrow{C}, vec(\overrightarrow{E}_c)$,

(2) Input $J, K, H_n^2$, output $H_2, G_2$,

(3) According to $(4.9)$, calculate the minimal norm least squares solution $(X_B, Y_B)$ of Problem 2.

Algorithm 5.3. (Problem 3)

(1) Input $A, B, C, D, E\in\mathbb{Q}^{n\times n}$, output $\overrightarrow{B}_c^T, \overrightarrow{D}_c^T, \overrightarrow{A}, \overrightarrow{C}, vec(\overrightarrow{E}_c)$,

(2) Input $J, K, H_n^3$, output $H_3, G_3$,

(3) According to $(4.13)$, calculate the minimal norm least squares solution $(X_M, Y_M)$ of Problem 3.

Example 5.1. Consider the quaternion matrix equation $AXB+CYD = E$, where

Denote $X^s = X^s_1+X^s_2{{{\rm{\bf i}}}}+X^s_3{{{\rm{\bf j}}}}+X^s_4{{{\rm{\bf k}}}}, Y^s = Y^s_1+Y^s_2{{{\rm{\bf i}}}}+Y^s_3{{{\rm{\bf j}}}}+Y^s_4{{{\rm{\bf k}}}}$.

(i) For $s = 1$. Then

Let $AX^1B+CY^1D = E$.

(ii) For $s = 2$. Then

Let $AX^2B+CY^2D = E$.

(iii) For $s = 3$. Then

Let $AX^3B+CY^3D = E$.

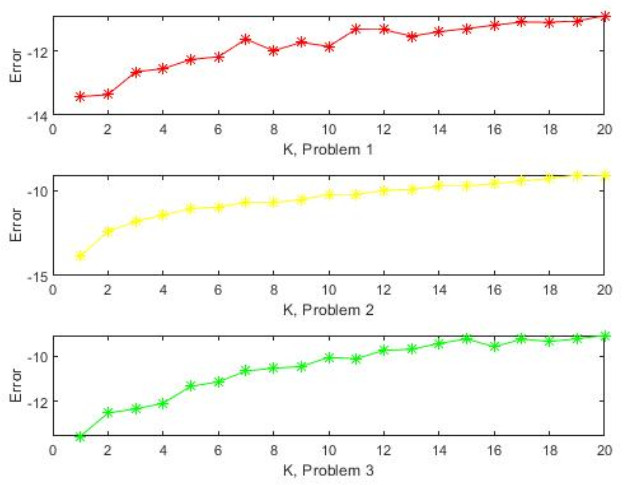
In all cases, the quaternion matrix Eq $(1.1)$ have the unique solutions $(X_H, Y_A)$, $(X_B, Y_B)$, $(X_M, Y_M)$, respectively. Of course, for $s\in \{1, 2, 3\}$, $(X^s, Y^s)$ is also the minimal norm least squares solution of the quaternion matrix Eq $(1.1)$ over $X\in \mathbb{HTQ}^{p\times p}/\mathbb{BQ}^{p\times p}/\mathbb{MQ}^{p\times p}$ and $Y\in \mathbb{AHTQ}^{q\times q}/ \mathbb{BQ}^{q\times q}/\mathbb{MQ}^{q\times q}$. By Algorithms 5.1–5.3, for $s\in \{1, 2, 3\}$, we compute $(X^{s'}, Y^{s'})$. Let $m = p = n = q = 2K$ and the error $\varepsilon = log_{10}(\left\|(X^{s'}, Y^{s'})-(X^s, Y^s)\right\|)$. The relation between $K$ and the error $\varepsilon$ is shown in Figure 1.

According to Figure 1, we obtain that the errors $\varepsilon$ are all no more than -9 for $s\in \{1, 2, 3\}$, which confirms the difference between the numerical solution and the exact solution is tiny. In other words, these three figures of Figure 1 are very similar, which is consistent with the actual situation. Therefore, our proposed algorithms are very feasible.

6.   Conclusions

In this paper, by combining the real representation of quaternion matrices with $\mathcal{H}$-representation, we convert the least squares problem of the quaternion matrix Eq (1.1) into a corresponding problem of the real matrix equation over free variables. Then we derive the expression of the minimal norm least squares solution for the quaternion matrix Eq (1.1) over different constrained matrices as in Problems 1–3. Our resulting expressions are expressed only by real matrices, and the algorithms only involve real operations. The final example shows that our proposed method is feasible and convenient to analyze such a matrix problem with special structures.

Acknowledgments

This work was supported by National Natural Science Foundation of China under grant 62176112; the Natural Science Foundation of Shandong under grant ZR2020MA053.

Conflict of interest

The authors declare that they have no competing interests.