The stability of bifurcating solutions for a prey-predator model with population flux by attractive transition

1.   Introduction

In this paper, we investigate the following Lotka-Volterra prey-predator model with population flux by attractive transition.

Where $u$ and $v$ are the population densities of the prey and predator. $d_{1}$ and $d_{2}$ are the random diffusion coefficients. $m_{1}$ represents the growth rate of the prey population. $d_{1}, \; d_{2}$ and $m_{1}$ are positive constants and $m_{2}$ is a real constant which can be negative. $m_{2}$ represents the mortality rate while it is negative and it represents the increasing rate of the predator population while it is positive. $b$ and $c$ are positive constants which describe the rate of increase of the predator and the rate of decrease of the prey due to the predation respectively. $J: = -\alpha u^{2}\nabla(\frac{v}{u}) = \alpha(-u\nabla v+v\nabla u)$ represents the population flux of the predator based on a biodiffusion in order that the transition probability of each individual of the predator depends on conditions at the point of arrival (see ^[2]). The nonnegative constant $\alpha$ is a magnitude of such a population flux by attractive transition.

If $\alpha = 0$ holds, then system (1.1) is reduced to the classical Lotka-Volterra prey-predator model. Some prey-predator models with the linear diffusion terms have been extensively studied by many mathematicians, see ^[3,4,5,6,7]. Kadota and Kuto ^[8] investigated a prey-predator system with cross diffusion of quasilinear fractional type. They discussed the local and global bifurcation solutions and obtained a sufficient condition for the existence of positive steady state solutions. Xu and Guo ^[10] considered the same model as in ^[8]. They studied the bifurcation steady states which bifurcated from the semitrivial solution with different bifurcating parameter and they obtained the stability of the local bifurcating solutions. Kuto ^[11] investigated a Lotka-Volterra prey-predator system with cross-diffusion in a spatially heterogeneous environment. Kuto obtained the global bifurcation branch of positive stationary solutions and the bifurcation branch could form a bounded fish-hook curve. Djilali ^[12] studied the influence of the nonlocal interspecific competition of the prey population on the dynamics of the diffusive predator-prey model with prey social behavior (i.e. herd behavior). It was proved that the turning patterns occur in the presence of the nonlocal competition and can not be found in the original system. Djilali ^[13] investigated a predator-prey model with social behavior (i.e. herd behavior). The existence of Hopf bifurcation and Turing driven instability were proved. By calculating the normal form, on the center of the manifold associated to the Hopf bifurcation points, the stability of periodic solution was proved. Djilali and Bentout ^[14] studied the same model as in ^[13]. They proved the non-existence of a non-constant steady state solution for some values of the diffusion coefficients. They also proved the existence of the non-constant steady state solution under a suitable condision on the diffusion coefficients by applying the Leray-Schauder degree theory.

In the following, we list the local bifurcation results and some preliminary results obtained in ^[1], which will be used in this paper. The corresponding steady state problem of (1.1) is as follows

It is easy to see that the second equation of (1.2) can be written as

Substituting the first equation of (1.2) into (1.3), we get

Together with (1.3) and (1.4), system (1.2) can be written as

For any fixed $m_{1} > d_{1}\lambda_{1}$(which $\lambda_{1}$ represents the least eigenvalue of $-\Delta$ with the homogeneous Dirichlet boundary condition on $\partial\Omega$), system (1.5) has a couple of sets of semitrivial solutions with parameter $m_{2}$ which can be denoted as follows

For the following equation

Assume $q(x)\in C(\overline{\Omega})$ holds, let $\lambda_{1}(q)$ be the least eigenvalue of (1.6), then $q\rightarrow \lambda_{1}(q):C(\overline{\Omega})\rightarrow {\bf{R}}$ is increasing, i.e. if $q_{1}(x)\leq q_{2}(x)$ and $q_{1}(x)\not\equiv q_{2}(x)$ in $\Omega$, then $\lambda_{1}(q_{1}) < \lambda_{1}(q_{2})$.

Define an operator $F:X \times {\bf{R}}\rightarrow Y$ by

Then solving system (1.2) is equivalent to solving the equation $F(u, v, m_{2}) = 0$.

It is easy to compute that

According to the result obtained in ^[1], we have

where $\psi^{*}$ satisfies the following equation

with $\|\psi^{*}\|_{\infty} = 1$, $m_{2} = f(m_{1}), \lim\limits_{m_{1}\rightarrow d_{1}\lambda_{1}}f(m_{1}) = d_{2}\lambda_{1}, \lim\limits_{m_{1}\rightarrow \infty}f(m_{1}) = -\infty$ and

In the following, we restate the existence of bifurcating solutions which bifurcate from $(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$ obtained in ^[1].

Lemma 1.1 (Proposition 4.4 in ^[1]) Let $m_{1}\in(d_{1}\lambda_{1}, \infty)$ be given arbitrarily. Positive solutions of (1.2) bifurcate from $\Gamma_{u}$ as $m_{2} = f(m_{1})$. There exists a neighborhood $\mathcal{N}_{1}$ of $(u, v, m_{2}) = (\theta_{d_{1}, m_{1}}, 0, f(m_{1}))\in X\times {\bf{R}}$ such that $F^{-1}(0)\cap\mathcal{N}_{1}$ consists of the union of $\Gamma_{u}\cap\mathcal{N}_{1}$ and the local curve

with some $\delta > 0$. Here $(\widetilde{u}, \widetilde{v}, \mu)(s)\in X\times{\bf{R}}$ is continuous differentiable for $s\in(-\delta, \delta)$ satisfying $\int_{\Omega}\psi^{*}\widetilde{v}(s) = 0$ for all $s\in(-\delta, \delta)$ and $(\widetilde{u}, \widetilde{v}, \mu)(0) = (0, 0, 0)$ and

All positive solutions contained in $F^{-1}(0)\cap\mathcal{N}_{1}$ can be expressed as

In the following, we rewrite the existence of bifurcating solutions which bifurcate from $(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$ obtained in ^[1], first we give some preliminary results which has been obtained in ^[1].

Let $V = v-\theta_{d_{2}, m_{2}}, \widetilde{F}(u, V, m_{2}): = F(u, V+\theta_{d_{2}, m_{2}}, m_{2})$, where $F$ is defined by (1.7). Thus we have

where

$Ker(\widetilde{F}_{(u, V)}(0, 0, m_{2})) = span\{\overline{\phi}, \overline{\psi}\}$, where $\overline{\phi}$ satisfies

with $m_{1} = d_{1}\lambda_{1}(\frac{c\theta_{d_{2}, m_{2}}}{d_{1}})( = :g^{-1}(m_{2})), \; \|\overline{\phi}\|_{\infty} = 1$, where $g^{-1}(m_{2})$ is continuously differentiable and monotone increasing for $m_{2} > d_{2}\lambda_{1}$ such that

For convenience, we denote the inverse function of $m_{1} = g^{-1}(m_{2})$ by $m_{2} = g(m_{1})$.

Now we restate the existence of bifurcating solutions which bifurcate from

$(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$ obtained in ^[1].

Lemma 1.2 (Proposition 4.6 in ^[1]) Let $m_{1}\in(d_{1}\lambda_{1}, \infty)$ be given arbitrarily. Positive solutions of (1.2) bifurcate from $\Gamma_{v}$ as $m_{2} = g(m_{1})$. There exists a neighborhood $\mathcal{N}_{2}$ of $(u, v, m_{2}) = (0, \theta_{d_{2}, g(m_{1})}, g(m_{1})))\in X\times {\bf{R}}$ such that $F^{-1}(0)\cap\mathcal{N}_{2}$ consists of the union of $\Gamma_{v}\cap\mathcal{N}_{2}$ and the local curve

with some $\delta > 0$. Here $(\widetilde{u}, \widetilde{v}, \mu)(s)\in X\times{\bf{R}}$ is continuous differentiable for $s\in(-\delta, \delta)$ satisfying $\int_{\Omega}\overline{\phi}\widetilde{u}(s) = 0$ for all $s\in(-\delta, \delta)$ and $(\widetilde{u}, \widetilde{v}, \mu)(0) = (0, 0, 0)$ and

All positive solutions contained in $F^{-1}(0)\cap\mathcal{N}_{2}$ can be expressed as

Oeda and Kuto ^[1] gives the asymptotic behavior of positive solutions of (1.2) as $\alpha\rightarrow \infty$ which can be written as follows.

Lemma 1.3 (Theorem 2.2 in ^[1]) Suppose that $(m_{1}, m_{2}, d_{1}, d_{2}, b, c)$ satisfies

Let $\{(u_{n}, v_{n})\}$ be any sequence of positive solutions to (1.2) with $\alpha = \alpha_{n}\rightarrow \infty$. Then the following alternative holds true.

(i) If $\{(\alpha_{n}\|u_{n}\|_{\infty})\}$ is unbounded, then

and

passing to a subsequence, where $s\in(0, 1)$ is defined by

(ii) If $\{(\alpha_{n}\|u_{n}\|_{\infty})\}$ is bounded, then there exists $(w, v)\in C^{2}(\overline{\Omega})\times C^{2}(\overline{\Omega})$ such that

passing to a subsequence, and moreover, $(w, v)$ is a positive solution to

According to the first type (ⅰ), the coexistence steady state $(u, v)$ of prey and predator can be approximated by a coexistence steady state of the competition model with equal conditions. In the second type (ⅱ), the component of prey shrinks with order $O(\frac{1}{\alpha})$ when $\alpha$ is sufficiently large. The bifurcation structure of positive solutions of (1.22) will be discussed in a forthcoming paper ^[9].

In this paper, we study the stability of bifurcating solutions obtained in ^[1]. Applying spectral analysis and the principle of exchange of stability, we obtain that the bifurcating solutions are stable/unstable under some certain conditions. The plan of this paper is as follows. In section 2, we prove that the bifurcating solutions near $(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$ are locally asymptotically stable/unstable under some certain conditions. In section 3, we prove that the bifurcating steady states near $(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$ are locally asymptotically stable/unstable under some certain conditions. A conclusion section ends the paper.

2.   The stability of bifurcating steady states near ($0, \theta_{d_{2}, g(m_{1})}, g(m_{1})$)

We consider the stability of bifurcating solutions near ($0, \theta_{d_{2}, g(m_{1})}, g(m_{1})$) of the following system.

Denote

Linearizing (2.1) at $(u(s), v(s))$ defined by (1.19) and investigating the following eigenvalue problem, by (2.2), we have

According to (1.7), (2.3) can be rewritten as follows

where $h_{21}(x)$ is defined by (1.15).

It is easy to see that

where $\overline{\phi}$ and $\overline{\psi}$ are defined by (1.16) and (1.18).

According to Shi ^[16] (Theorem 2.1 and (4.5)), we can define the functional

Theorem 2.1. For any fixed $m_{1}\in(d_{1}\lambda_{1}, \infty)$, the bifurcating steady state $(u(s), v(s))$ defined by (1.19) of system (1.2) is locally asymptotically stable when $\mu^{'}(0) < 0$ defined by (1.20); the bifurcating steady state $(u(s), v(s))$ defined by (1.19) of system (1.2) is locally asymptotically unstable when $\mu^{'}(0) > 0$ defined by (1.20).

Proof. First we show that 0 is the first eigenvalue of $F_{(u, v)}(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$.

From the above, we get that 0 is the eigenvalue of $F_{(u, v)}(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$. Therefore we will show that 0 is the first eigenvalue of $F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$. Otherwise, there exists a positive eigenvalue $\widetilde{\lambda}_{1}$ of $F_{(u, v)}(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$ with the corresponding eigenfunction $\left(\begin{array}{c} u_{1} \\v_{1} \\ \end{array} \right)\in X$ such that

that is

where $\widetilde{f}$ and $\widetilde{g}$ are defined by (2.2)

Assume $u_{1} = 0$ and $v_{1}\neq 0$ hold, from the second equation of (2.9), we obtain

Because of $\widetilde{\lambda}_{1}d_{2} > 0$ and in ^{[BK, 17]} (Lemma 2.1), it was proved that all the eigenvalues of the operator $(-d_{2}\Delta+2\theta_{d_{2}, g(m_{1})}-g(m_{1}))$ are strictly positive, which is in contradiction with (2.10), therefore we have $u_{1}\neq0$.

By virtue of (1.16) and the scalar elliptic equation theorem, 0 is the first eigenvalue of the first equation of (2.9), which contradicts $\widetilde{\lambda}_{1}$. Therefore we obtain that 0 is the first eigenvalue of $F_{(u, v)}(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$ and the other eigenvalues are negative.

For small $0 < s < \delta$, by Proposition I.7.2 in ^[15], there exist perturbed eigenvalue $\lambda(s)$ and continuous differential functions $\varphi_{1}(s), \varphi_{2}(s) \in X\cap Range(F_{u, v}(0, \theta_{d_{2}, g(m_{1})}, g(m_{1})))$ satisfying

with $\lambda(0) = \varphi_{1}(0) = \varphi_{2}(0) = 0.$

Similarly, there exist perturbed eigenvalue $\lambda(m_{2})$ and continuous differential functions $\varphi_{1}(m_{2}), \varphi_{2}(m_{2}) \in X\cap Range(F_{(u, v)}(0, \theta_{d_{2}, g(m_{1})}, g(m_{1})))$ satisfying

with $\lambda(m_{2}) = \varphi_{1}(m_{2}) = \varphi_{2}(m_{2}) = 0$.

Differentiating (2.12) with respect to $m_{2}$ at $m_{2} = g(m_{1})$ and together with $\lambda(m_{2}) = \varphi_{1}(m_{2}) = \varphi_{2}(m_{2}) = 0$, we obtain

where $\lambda^{'}(g(m_{1})) = \frac{d}{dm_{2}}\lambda(m_{2})|_{m_{2} = g(m_{1})}$.

According to (2.7) and (2.13), we have

In virtue of (2.5), we have

According to (2.7), (2.14) and (2.15), we get

Applying the formula I.7.40 in ^[15], we have

where $\dot{\lambda}(s) = \frac{d}{ds}\lambda(s)$.

Using Lemma 1.2 and (2.17), we have

where $\mu^{'}(0)$ is defined by (1.20).

By (2.18), when $\mu^{'}(0) < 0$ holds, then $\lambda(s) < 0$ for small $s > 0$, the bifurcating solution $(u(s), v(s))$ defined by (1.19) of system (1.2) is locally asymptotically stable.When $\mu^{'}(0) > 0$ holds, then $\lambda(s) > 0$ for small $s > 0$, the bifurcating solution $(u(s), v(s))$ defined by (1.19) of system (1.2) is locally asymptotically unstable.

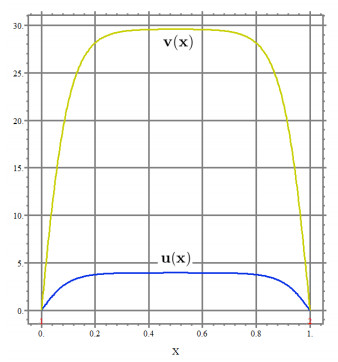
For system (2.1), let $\alpha = 100, \; b = 2, c = 10, \; m_{1} = 300, \; m_{2} = 20, \; \Omega = (0, 1), \; t = 1000$ and $(u_{0}, v_{0}) = (0.01sin^{2}(\pi x), 0.01sin(\pi x))$ hold, which guarantee $\mu^{'}(0) < 0$. We give the following simulation results which verify the stability of locally bifurcating steady states near $(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$, see Figure 1.

3.   The stability of bifurcating steady states near ($\theta_{d_{1}, m_{1}}, 0, f(m_{1})$)

In this section, we use the similar method in section 2 in order to investigate the stability of positive solutions bifurcating from $(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$.

We linearize (1.2) at $(u(s), v(s))$ defined by (1.12) and study the following eigenvalue problem

where $\widetilde{f}$ and $\widetilde{g}$ are defined by (2.2).

By (1.7), (3.1) can be rewritten by

where $\widetilde{g}$ is defined by (2.2).

Obviously, we have

where $\phi^{*}$ and $\psi^{*}$ are defined by (1.10) and (1.11).

According to Shi ^[16] (Theorem 2.1 and (4.5)), we can define the functional

Theorem 3.2. The bifurcating solution $(u(s), v(s))$ defined by (1.12) of system (1.2) is locally asymptotically stable when $\mu^{'}(0) > 0$ holds defined by (1.13); the bifurcating steady state $(u(s), v(s))$ defined by (1.12) of system (1.2) is locally asymptotically unstable when $\mu^{'}(0) < 0$ holds defined by (1.13).

Proof. We first prove that 0 is the first eigenvalue of $F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$.

From the above, we obtain that 0 is the eigenvalue of $F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$. Then we will prove that 0 is the first eigenvalue of $F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$. Otherwise, there exists a positive eigenvalue $\sigma_{1}$ of $F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$ with the corresponding eigenfunction $\left(\begin{array}{c}\widetilde{u}_{1} \\ \widetilde{v}_{1} \\ \end{array} \right)\in X$ such that

that is

where $\widetilde{g}$ is defined by (2.2).

If $\widetilde{v}_{1} = 0$ and $\widetilde{u}_{1}\neq 0$ hold, the first equation of (3.7) implies

In ^[17] (Lemma 2.1), it was proved that all the eigenvalues of the operator $(-d_{1}\Delta+2\theta_{d_{1}, m_{1}}-m_{1})$ are strictly positive, which is in contradiction with (3.8), then $\widetilde{v}_{1}\neq 0.$

According to (1.10) and the scalar elliptic equation theorem, 0 is the first eigenvalue of the second equation of (3.7), which contradicts $\sigma_{1}$. Then we have proved that 0 is the first eigenvalue of $F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1}))$ and the other eigenvalues are negative.

For small $0 < s < \delta$, by Proposition I.7.2 in ^[15], there exist perturbed eigenvalue $\sigma(s)$ and continuous differential functions $\omega_{1}(s), \omega_{2}(s) \in X\cap Range(F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1})))$ satisfying

with $\sigma(0) = \omega_{1}(0) = \omega_{2}(0) = 0.$

Similarly, there exist perturbed eigenvalue $\sigma(m_{2})$ and continuous differential functions $\omega_{1}(m_{2}), \omega_{2}(m_{2}) \in X\cap Range (F_{(u, v)}(\theta_{d_{1}, m_{1}}, 0, f(m_{1})))$ satisfying

with $\sigma(m_{2}) = \omega_{1}(m_{2}) = \omega_{2}(m_{2}) = 0$.

Differentiating (3.10) with respect to $m_{2}$ at $m_{2} = f(m_{1})$ and together with $\sigma(m_{2}) = \omega_{1}(m_{2}) = \omega_{2}(m_{2}) = 0$, we have

where $\sigma^{'}(f(m_{1})) = \frac{d}{dm_{2}}\sigma(m_{2})|_{m_{2} = f(m_{1})}$.

Together with (3.5) and (3.11), we obtain

According to (1.8), we have

Using (3.5), (3.12) and (3.13), we obtain

It follows from the formula I.7.40 in ^[15] that

where $\dot{\sigma}(s) = \frac{d}{ds}\sigma(s)$.

Together with Lemma 1.1 and (2.16), we obtain

where $\mu^{'}(0)$ is defined by (1.13). According to (3.16), when $\mu^{'}(0) > 0$ holds, then $\lambda(s) < 0$ for small $s > 0$, the bifurcating solution $(u(s), v(s))$ defined by (1.12) of system (1.2) is locally asymptotically stable. When $\mu^{'}(0) < 0$ holds, then $\lambda(s) > 0$ for small $s > 0$, the bifurcating solution $(u(s), v(s))$ defined by (1.12) of system (1.2) is locally asymptotically unstable.

4.   Conclusions

In this paper, we have investigated the local stability of bifurcation steady states obtained in ^[1] for a prey-predator model with population flux by attractive transition. By applying spectral analysis and the principle of exchange of stability, we show the stability/unstability of the bifurcating solutions under some certain conditions. We give numerical simulation result (which satisfies $\mu^{'}(0) < 0$) in order to verify the local stability of bifurcation solutions near the bifurcating point $(0, \theta_{d_{2}, g(m_{1})}, g(m_{1}))$.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No.11871048), Premium Funding Project for Academic Human Resources Development in Beijing Union University (BPHR2019CZ07, BPHR2020EZ01) and Scientific Research Program of Beijing Municipal Education Commission (KM202011417010).

Conflict of interest

The authors declare no conflicts of interest.