Weighted pseudo almost periodicity on neutral type CNNs involving multi-proportional delays and D operator

1.   Introduction

In many areas of the objective world, such as target tracking, machine learning system identification, associative memories, pattern recognition, solving optimization problems, image processing, signal processing, and so on ^[1,2,3,4,5], a lot of practical problems can be described by delay differential equations (DDEs). Therefore, the research of delay differential equations has been the subject of significant attention ^[6,7]. As we all know, time delays are inevitable in population dynamics models. For example, the maturation period should be considered in the study of simulated biological species ^[8,9], incubation periods should be considered in epidemiology area ^[7], and the synaptic transmission time among neurons should be considered in neuroscience field ^[10]. In particular, the dynamic behavior of most cellular neural network models is significantly affected by time delay, so the investigation on delayed cellular neural networks has been the world-wide focus.

It should be mentioned that proportional delay is one of important time-varying delays, which is unbounded and monotonically increasing, and is more predictable and controllable than constant delay and bounded time-varying delay. Over past decade, by introducing proportional time delay, investigations of the following neutral type proportional delayed cellular neural networks (CNNs) with D operators:

with initial value conditions:

have attracted great attention of some researchers. The main reason is that its successful applications in variety of areas such as optimization, associative memories, signal processing, automatic control engineering and so on (see ^{[11,12,13,14,15]} and the references therein). Here $n$ is the number of units in a neural network, $(x_{1}(t), x_{2}(t), \cdots, x_{n}(t))^T$ corresponds to the state vector, the decay rate at time $t$ is designated by $a_{i}(t)$, coefficients $p_{i}(t)$, $e_{ij}(t)$ and $b_{ij}(t)$ are the connection weights at the time $t$, $f_{j}$ and $g_{j}$ are the activation functions of signal transmission, $r_{i}(t)\geq 0$ denotes the transmission delay, $r_{i}$ and $q _{ij}$ are proportional delay factors and satisfy $0 < r_{i}, \ q _{ij} < 1$, $I_{i}(t)$ is outside input.

As pointed out by the authors of reference ^[16], the weighted pseudo almost periodic function consists of an almost periodic process plus a weighted ergodic component. It is well known that the weighted pseudo-almost periodic phenomenon is more common in the environment than the periodic, almost periodic and pseudo-almost periodic phenomenon, so the dynamic analysis of the weighted pseudo-almost periodic is more realistic ^{[17,18,19,20]}. Furthermore, when $p_{i}(t)\equiv 0$, the existence and exponential stability of weighted pseudo almost periodic solutions (WPAPS) of proportional delayed cellular neural networks (CNNs)

have been established in ^[22] under the following conditions

{Here, for $i\in N$, $\tilde{a}_{i} \in C(\mathbb{R}, \ (0, \ +\infty))$ is a bounded function, and $K_{i} > 0$ is a constant with

In addition, $f_{j}$ and $g_{j}$ are the activation functions with Lipschitz constants $L^{f}_{j}$ and $L^{g}_{j}$ obeying

} It should be mentioned that the authors in ^[22] use (1.4) to show that there exists a constant $\lambda \in (0, \min\limits_{i\in N}\tilde{a}_{i} ^{-})$ such that

With the aid of the fact that $\lim\limits_{t\rightarrow +\infty}e^{ \lambda (1-q_{ij}) t} = +\infty$, it is easy to see that (1.4) can not lead to (1.5). Meanwhile, Examples 4.1 and 4.2 in ^[22] also have the same error, where

and

can not also meet (1.5). For detail, the biological explanations on equations (1.4) and (1.5) can be found in ^[22]. Now, in order to improve ^[22], we will further study the existence and exponential stability of weighted pseudo almost periodic solutions for (1.1) which includes (1.3) as a special case. Moreover, this class of models has not been touched in the existing literature.

On account of the above considerations, in this article, we are to handle the existence and generalized exponential stability of weighted pseudo almost periodic solutions for system (1.1). Readers can find the following Remark 2.1 for extensive information. In a nutshell, the contributions of this paper can be summarized as follows. 1) A class of weighted pseudo almost periodic cellular neural network model with neutral proportional delay is proposed; 2) Our findings not only correct the errors in ^[22], but also improve and complement the existing conclusions in the recent publications ^[22,23]; 3) Numerical simulations including comparison analyses are presented to verify the obtained theoretical results.

The remainder of the paper is organized as follows. We present the basic notations and assumptions in Section 2. The existence and exponential stability of weighted pseudo almost periodic solutions for the addressed neural networks models are proposed in Section 3. The validity of the proposed method is demonstrated in Section 4, and conclusions are drawn in Section 5.

2.   Notations and assumptions

Notations. $\mathbb{R}$ and $\mathbb{R}^n$ denote the set of real numbers and the $n$-dimensional real spaces. For any $x = \{x_{ij}\}\in\mathbb{R}^{mn}$, let $|x|$ denote the absolute value vector given by $|x| = \{|x_{ij}|\}$, and define $\|x\| = \max\limits_{ij\in J}|x_{ij}(t)|$. Given a bounded continuous function $h$ defined on $\mathbb{R}$, let $h^{+} = \sup\limits_{t\in \mathbb{R}}|h(t)|, \ h^{-} = \inf\limits_{t\in \mathbb{R}}|h(t)|$. We define $\mathbb{U}$ be the collection of functions (weights) $\mu : \mathbb{R}\rightarrow (0, +\infty)$ satisfying

and

Let $BC(\mathbb{R}, \mathbb{R}^{n})$ denote the collection of bounded and continuous functions from $\mathbb{R}$ to $\mathbb{R}^{n}$. Then $(BC(\mathbb{R}, \mathbb{R}^{n}), \|\cdot\|_{\infty})$ is a Banach space, where $\|f\|_{\infty} : = \sup\limits_{ t\in \mathbb{R}} \|f (t)\|$. Also, this set of the almost periodic functions from $\mathbb{R}$ to $\mathbb{R}^{n}$ will be designated by $AP(\mathbb{R}, \mathbb{R}^{n})$. Furthermore, the class of functions $PAP_{0}^{\mu}(\mathbb{R}, \mathbb{R}^{n})$ be defined as

A function $f\in{BC(\mathbb{R}, \mathbb{R}^{n})}$ is said to be weighted pseudo almost periodic if there exist $h\in{AP(\mathbb{R}, \mathbb{R}^{n})}$ and $\varphi\in{PAP_{0}^{\mu}(\mathbb{R}, \mathbb{R}^{n})}$ satisfying

where $h$ and $\varphi$ are called the almost periodic component and the weighted ergodic perturbation of weighted pseudo almost periodic function $f$, respectively. We designate the collection of such functions by $PAP^{\mu}(\mathbb{R}, \mathbb{R}^{n}).$ In addition, fixed $\mu\in \mathbb{U}^{+}_{\infty}$, $(PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n}), \|.\|_{\infty})$ is a Banach space and $AP (\mathbb{R}, \mathbb{R}^{n})$ is a proper subspace of $PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$. For more details about the above definitions can be available from ^[17,18] and the references cited therein.

In what follows, for $i, j\in N,$ we shall always assume that $\ e_{ij }, b_{ij}, p_i, I_{i} \in PAP^{\mu}(\mathbb{R}, \mathbb{R})$, and

For $i, j \in N$, we also make the following technical assumptions:

$(H_1)$ there are a positive function $\tilde{a}_{i} \in BC(\mathbb{R}, \mathbb{R})$ and a constant $K_{i} > 0$ satisfying

$(H_2)$ there exist nonnegative constants $L^{f}_{j}$ and $L^{g}_{j}$ such that

$(H_3)$ $\mu \in \mathbb{U}^{+}_{\infty}$, we can find constants $\xi_{i} > 0$ and $\Lambda_{i} > 0$ such that

and

Remark 2.1. From $(H_1)$ and $(H_2)$, one can use an argument similar to that applied in Lemma 2.1 of ^[24] to demonstrate that every solution of initial value problem (1.1) and (1.2) is unique and exists on $[t_{0}, \ +\infty).$

3.   Results

In this section, we will establish some results about the global generalized exponential stability of the weighted pseudo almost periodic solutions of (1.1). To do this end, we first show the following Lemma.

Lemma 3.1. (see[^[22], Lemma 2.1]). Assume that $f\in PAP^{ \mu}(\mathbb{R}, \mathbb{R})$ and $\beta \in \mathbb{R}\setminus \{0\}$. Then, $f(\beta t)\in PAP^{\mu}(\mathbb{R}, \mathbb{R}).$

Using a similar way to that in lemma 2.3 of ^[22], we can show the following lemma:

Lemma 3.2. Assume that $(H_{1})$ and $(H_{2})$ hold. Then, the nonlinear operator $G$:

maps $PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$ into itself.

Theorem 3.1. Suppose that $(H_{1})$, $(H_{2})$ and $(H_{3})$ are satisfied. Then, system (1.1) has exactly one WPAPS $x^{*}(t)\in PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$, which is globally generalized exponentially stable, that is, for every solution $x(t)$ agreeing with $(1.1)-(1.2)$, there exists a constant $\sigma\in (0, \min\limits_{i\in N}\tilde{a}_{i}^{-})$ such that

Proof. With the help of $(H_{3})$, it is easy to see that there are constants $\sigma, \lambda \in (0, \ \min\limits_{i\in N}\tilde{a}_{i} ^{-})$ such that

and

which, along with the inequalities

yield

Consequently, applying a transformation:

leads to

Now, define a mapping $P: PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})\rightarrow PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$ by setting

it follows from Lemma 3.1 and Lemma 3.2 that $P\varphi \in PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$.

Moreover, by means of $(H_{1})$, $(H_{2})$ and $(H_{3})$, for $\varphi, \psi \in PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$, we have

which and the fact that $0 < \max\limits_{ i \in N}\{ p_i^++\Lambda_i\} < 1$ suggest that the contraction mapping $P$ possesses a unique fixed point

Thus, (1.5) and (3.5) entail that $x^{* } = \{x_{i}^{* }(t)\} = \{\xi_{i}y_{i}^{*}(t)\}\in PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$ is a weighted pseudo almost periodic solution of (1.1).

Finally, we demonstrate that $x^{* }$ is exponentially stable.

Designate $x(t) = \{x_{i}(t)\}$ be an arbitrary solution of (1.1) with initial value $\varphi(t) = \{\varphi_{i}(t)\}$ satisfying $(1.2).$

Label

Then

Without loss of generality, let

and $M$ be a constant such that

Consequently, for any $\varepsilon > 0$, it is obvious that

Now, we validate that

Otherwise, there must exist $i \in N$ and $\theta > t_{0}$ such that

Furthermore, from (3.6), we obtain

$\mbox{for all}\ \ \nu\in [\rho_jt_0, \ t], \ t \in[t_0, \ \theta), \ j\in J,$ which entails that

$\mbox{for all} \ t \in[\rho_it_0, \ \theta), \ j\in N.$

Note that

Multiplying both sides of (3.15) by $e ^{\int_{t_{0}}^{s}a_{i}(u)du}$, and integrating it on $[t_{0}, t]$, we get

Thus, with the help of (3.3), (3.9), (3.12) and (3.14), we have

This is a clear contradiction of (3.12). Hence, (3.11) holds. When $\varepsilon\longrightarrow 0^{+}$, we obtained

Then, using a similar derivation in the proof of (3.13) and (3.14), with the help of (3.17), we can know that

and

The proof of the Theorem 3.1 is now finished.

Theorem 3.2. Let $\mu\in \mathbb{U}^{+}_{\infty}$. Assume that $(H_{1})$ and $(H_{2})$ hold, and there exist constants $\gamma_{i}, \xi_{i} > 0$ such that

holds. Then, system (1.3) has a unique WPAPS $x^{*}(t)\in PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{n})$, and there is a constant $\sigma\in (0, \min\limits_{i\in N}\tilde{a}_{i}^{-})$ such that

here $i \in N,$ $x(t)$ is an arbitrary solution of system (1.3) with initial conditions:

Proof. From $(3.18)$ we can pick a positive constant $\Lambda_{i}^{*}$ such that

According to fact that (1.3) is a special case of (1.1) with $p_{i} ^{+} = 0 \ (i\in N)$, the proof proceeds in the same way as in Theorem 3.1.

Remark 3.1. Obviously, it is easy to see that all results in ^[22] are the special case of Theorem 2.2 in this manuscript. In particular, the wrong in (1.5) has been successfully corrected. This indicates that our results supplement and improve the previous references ^[22,23]

4.   A numerical example

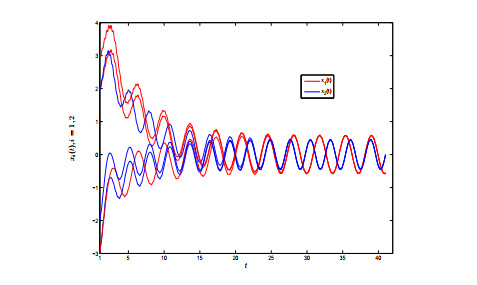
In order to reveal the correctness and feasibility of the obtained results, an example with the simulation is introduced in this section.

Example 4.1. Consider the following CNNs with D operator and multi-proportional delays:

Clearly,

Then, we can take

such that CNNs (1.1) with (4.1) satisfies all the conditions $(H_1)-(H_3)$. By Theorem 2.1, we can conclude that CNNs (4.1) has a unique weighted pseudo almost periodic solution $x^{*}(t)\in PAP^{ \mu}(\mathbb{R}, \mathbb{R}^{2})$, and every solutions of (4.1) is exponentially convergent to $x^{*}(t)$ as $t\rightarrow+\infty$. Here, the exponential convergence rate $\sigma\approx 0.01$. Simulations in Figure 1 reflect that the theoretical convergence is in sympathy with the numerically observed behaviors.

As far as we know, the weighted pseudo almost periodic dynamics of cellular neural networks with D operator and multi-proportional delays has never been studied in the previous literature ^{[29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]}. It is easy to see that all results in ^{[16,17,18,19,20,21,22,23,24,25,26,27,28]} cannot be directly applied to show the case that all solutions of (4.1) converge globally to the weighted pseudo almost periodic solution. In particular, all parameters in system (4.1) are chosen by applying Matlab software. It should be mentioned that the nonlinear activation function $f_{i}(x) = \frac{1}{20} \arctan x$ has been usually used as the sigmoid functions to agree with the experimental data of signal transmission in the real cellular networks networks.

5.   Conclusions

In this paper, we investigate the global dynamic behaviors on a class of neutral type CNNs with D operator and multi-proportional delays. Some new criteria have been gained to guarantee that the existence and exponential stability of weighted pseudo almost periodic solutions for the addressed system by combining the fixed point theorem and some differential inequality techniques. The obtained results are new and complement some corresponding ones of the existing literature. It should be mentioned that the technical assumptions can be easily checked by simple algebra methods and convenient for application in practice. In addition, this method affords a possible approach to study the weighted pseudo dynamics of other cellular neural networks with D operator and delays. In the future, we will make this further research.

Acknowledgments

The author would like to express his sincere appreciation to the editor and reviewers for their helpful comments in improving the presentation and quality of the paper. This work was supported by the Postgraduate Scientific Research Innovation Project of Hunan Province (No. CX20200892) and "Double first class" construction project of CSUST in 2020 ESI construction discipline, Grant No. 23/03.

Conflict of interest

We confirm that we have no conflict of interest.