An application of improved Bernoulli sub-equation function method to the nonlinear conformable time-fractional SRLW equation

1.   Introduction

The investigation of exact travelling wave solutions of nonlinear partial differential equations (NLPDEs) is important to understand the nonlinear physical process that appears in many areas of scientific fields such as nonlinear optics ^[1,2], plasma physics ^[3,4], biophysics ^[5] and discrete electrical transmission lines ^[6,7,8].

To find the exact solutions of these equations, many powerful methods have been applied in the literature by mathematicians and physicists. Some of these effective methods are extended tanh method ^[9,10], first integral method ^[11,12], sine-cosine method ^[13], dynamical system method ^[14], modified simple equation method ^[15,16], tanh method ^[17], generalized tanh function method ^[18], improved F expansion method with Riccati equation ^[19,20], modified exp$(\Omega(\xi))$-expansion function method ^[21,22], Kudryashov method ^[46] and improved Bernoulli sub-equation function method ^[23,24].

In recent years, the fractional differential equations have become a useful tool for describing nonlinear phenomena of science and engineering models. Many of techniques which applied to the nonlinear partial differential equations have been adapted for fractional nonlinear partial differential equations to find exact solutions. For example the functional variable method ^[25], the first integral method ^[26], the exp-function method ^[27], Kudryashov method ^[46], modified extended tanh method ^[47], fractional Riccati expansion method ^[28], modified extended tanh method ^[29,30] and many others.

In ^[31] a new simple well behaved definition of the fractional derivative called conformable fractional derivative is introduced. The conformable fractional derivative is theoretically easier than fractional derivative to handle. Also the conformable fractional derivative obeys some conventional properties that can't be satisfied by the existing fractional derivatives, for instance; the chain rule ^[32]. The conformable fractional derivative has the weakness that the fractional derivative of any differentiable function at the point zero is equal to zero. So that in ^[32,33], it is proposed a suitable fractional derivative that allows us to escape the lack of the conformable fractional derivative. During the last few years, many of techniques applied to find exact solutions for conformable fractional nonlinear partial differential equations ^{[34,35,36,37,38,39,40,41,42,43,44,45,46,47]}.

In this paper, we obtain the exact solutions of conformable time fractional Symmetric Regularized Long Wave (SRLW) equation by using IBSEFM. We consider

where $u = u(x, t), p, q$ and $r$ real parameters, $D_{tt}^{2\alpha }$ is the fractional differential operator of order $2\alpha$ in conformable sense. This equation is an interesting model to describe ion-acoustic and space charge waves with weak non linearity ^[47]. Before beginning to the solution procedure, we should give some significant properties of conformable fractional derivative. We explain the solution procedure in the third section and in the fourth section we give the implementation of the proposed procedure to conformable time fractional SRLW equation.

2.   Conformable fractional derivative

In this section, we give some basic definitions and theorems of the conformable fractional derivative.

The conformable derivative of order $\alpha$ with respect to the independent variable $t$ is defined as ^[31]

for a function $y = y(t):\left[ 0, \infty \right) \rightarrow \mathbb{R}.$

Theorem 2.1. Assume that the order of the derivative $\alpha \in \left(0, 1 \right]$ and suppose that $u = u(t)$ and $v = v(t)$ are $\alpha -$ differentiable for all positive $t.$ Then,

1. $D_{t}^{a}(c_{1}u+c_{2}v) = c_{1}D_{t}^{a}(u)+c_{2}D_{t}^{a}(v),$ for $\forall c_{1}, c_{2} \in \mathbb{R}.$

2.$D_{t}^{a}(t^{k}) = kt^{k-a}, \forall k\in \mathbb{R}.$

3.$D_{t}^{a}(\lambda) = 0,$ for all constant function $u(t) = \lambda.$

4. $D_{t}^{a}\left(uv\right) = uD_{t}^{a}(v)+vD_{t}^{a}(u).$

5.$D_{t}^{a}\left(\frac{u}{v}\right) = \frac{vD_{t}^{a}(u)-uD_{t}^{a}(v)}{ v^{2}}.$

6.$D_{t}^{a}\left(u\right) (t) = t^{1-\alpha }\frac{du}{dt}.$

Conformable fractional differential operator satisfies some critical fundamental properties like the chain rule, Taylor series expansion and Laplace transform.

Theorem 2.2. Let $u = u(t)$ be an $\alpha-$ conformable differentiable function and assume that $v$ is differentiable and defined in the range of $u.$ Then,

The proofs of these theorems are given in ^[32] and in ^[35] respectively.

3.   Basic properties of the improved Bernoulli sub-equation function method (IBSEFM)

In this section let us give the fundamental properties of the IBSEFM. We present the four main steps of the IBSEFM below the following:

Step 1: Let us consider the following conformable time-fractional PDE of the form

The goal is converting (3.1) with a suitable fractional transformation into the nonlinear ordinary differential equation. The wave transformation as;

where $v$ is a constant to be determined later. Using chain rule and substituting (3.2) in (3.1), we obtain the following nonlinear ordinary differential equation;

Step 2: We hypothesize that the solution of (3.3) may be presented below;

where $a_{0}, a_{1}, ..., a_{n}$ and $b_{0}, b_{1}, ..., b_{m}$ are coefficients which will be determined later. $m \neq 0, n \neq 0$ are arbitrary constants that chosen according to the balance principle and considering the form of Bernoulli differential equation below the following;

where $F(\eta)$ is polynomial. Substituting (3.4) and (3.5) in (3.3), it yields us an equation of polynomial $\Omega (F)$ of $F$ as following:

According to the balance principle that is the highest order derivative term and nonlinear term in (3.3), we can determine the relationship between $n, m$ and $M.$

Step 3: The coefficients of $\Omega (F(\eta))$ all be zero will give us an algebric system of equations;

Solving this system, we can specify the values of $a_{0}, a_{1}, ..., a_{n}$ and $b_{0}, b_{1}, ..., b_{m}.$

Step 4: When we solve differential equation (3.5), we obtain the following two situations according to $\sigma$ and $d$;

Using a complete discrimination system for polynomial of $F(\eta)$, we obtain the analytical solutions of (3.3) with the help of software programme and classify the exact solutions of (3.3). For a better interpretations of obtained results, we can plot two and three dimensional figures of analytical solutions by considering suitable values of parameters.

4.   Application of the IBSEFM method

In this section, the application of the IBSEFM to the conformable time-fractional SRLW equation is presented. Consider the following wave transform

where $a$ is the wave height and $v$ is the wave velocity.

Substituting (4.1) into (1.1) and integrating once respect to $\xi,$ we get nonlinear ordinary differential equation;

where $C$ is constant of integration and assume that $C = 0$ to reduce the complexity of the solutions. When we reconsider (4.2) for balance principle, considering between $U^{2}$ and $U^{\prime \prime }$, we obtain the following relationship:

This relationship of $m, n$ and $M$ gives us different versions of the solutions to (4.2) and we can obtain some analytical solutions as follows:

If we take $M = 3, n = 5, m = 1$ for (3.4) and (3.5), then we can write the following equations;

and

where $F^{\prime } = \sigma F+dF^{3}, a_{2}\neq 0, b_{1}\neq 0, \sigma \neq 0, d\neq 0.$ When we use (4.3)-(4.5) in (4.2), we obtain a system of algebraic equations from coefficients of polynomial of $F.$ By solving the algebraic system of equations with the help of mathematics software programme, it yields us the following coefficients:

Case 1:

Substituting these coefficients along with (3.6) in (4.3) we obtain the following solution of the conformable time fractional SRLW equation;

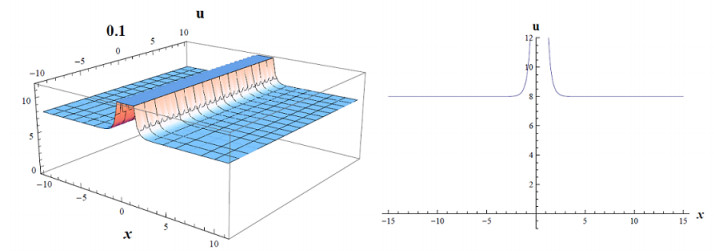
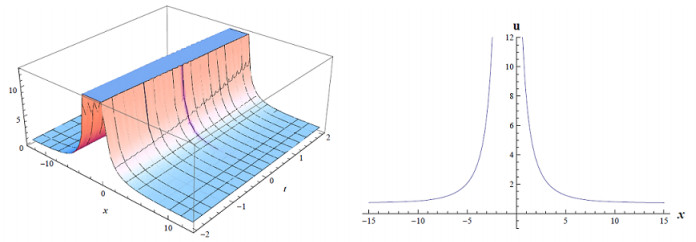
where $d, \sigma, a, r, E, q, d, \alpha$ are constants and not zero (Figure 1).

Case 2:

Substituting these coefficients along with (3.6) in (4.3) we obtain following solution of the conformable time fractional SRLW equation;

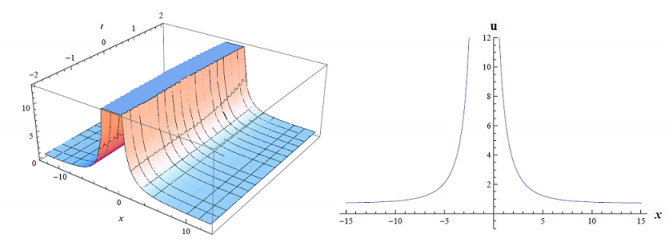
where $a, p, E, q, d, v, r, \alpha$ are constants and not zero (Figure 2).

Case 3:

Substituting these coefficients along with (3.6) in (4.3) we obtain following solution of the conformable time fractional SRLW equation;

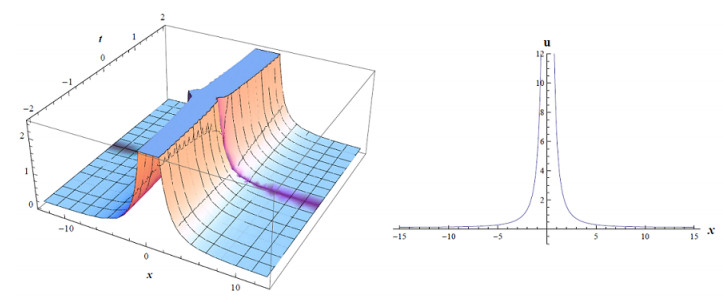
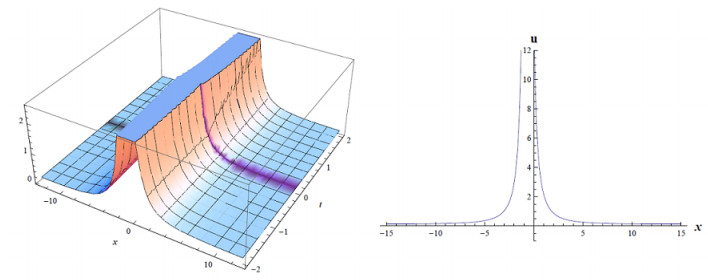
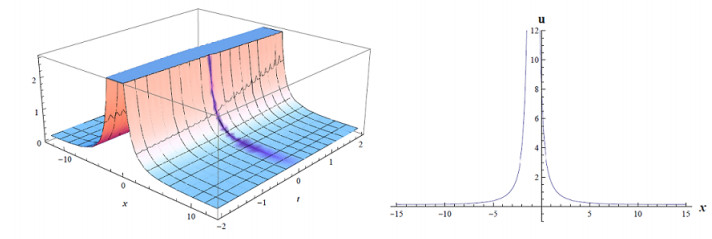
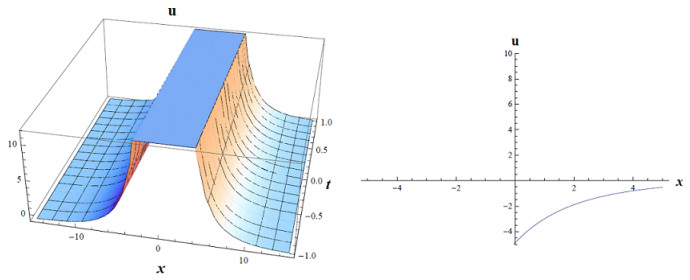
where $a, E, d, b_{0}, a_{4}, v, \sigma, \alpha$ are constants and not zero (Figures 3–7).

5.   Conclusion and Discussion

In this article, we have successfully applied the IBSEFM to the nonlinear conformable time-fractional SRLW equation to investigate some new exact solutions. It has been observed that all analytical solutions examined in this paper verify the nonlinear ordinary differential equation (4.2) which is obtained from nonlinear comformable time-fractional SRLW equation under the terms of wave transformation. All necessary computational calculations and graphs have been acquired by using software mathematics programme. According to the figures, one can see that the formats of travelling wave solutions in two and three dimensional surfaces are similar to the physical meaning of results. If we take more values of coefficients, we can obtain more travelling wave solutions for this model. This method is very reliable, efficient and submits new travelling wave solutions. Therefore, the IBSEFM can be applied to the other nonlinear fractional differential models.

Conflict of interest

All authors declare no conflicts of interest in this paper.