1. Introduction

Turbulence is a most prominent and ubiquitous phenomenon of fluid motion. Obstacles in understanding its nature arise from its extreme complexity, which, thanks to development in simulation method, has been overcome gradually to yield rich visual as well as numerical outcomes.

Along with experiments in laboratory and numerical simulations on computer, we need constructing a model that accounts for complex phenomena from a view point of universal concepts abstracted from observational data. Specifically, Richardson-Kolmogorov scaling and eddy viscosity have been established as the most fundamental notions, on which so-called eddy viscosity models (EVMs) are based. EVM is a truncated set of originally infinite number of equations for moments of velocity field derived from the Navier-Stokes equation. EVMs are phenomenology because of the truncation that requires physically plausible but more or less arbitrary assumptions. For a comprehensive review of turbulence in incompressible fluid, see, e.g., ^[1].

In the dynamical effective viscosity model (DEVM) proposed by Takahashi ^[2], the equations of mean turbulent flow are derived by the variational principle on a pseudo-action that does not involve the non-holonomic condition ^[3]. DEVM is constructed in terms of a general complex two by two matrix field and its Hermitian conjugate so as to fulfill invariance under Galilei transformation and rotation. The independent four variables are interpreted as a complex mean velocity and a complex effective viscosity, which are to be finally set real. When applied to channel and pipe flows, the equations in the simplest model, i.e., the minimal DEVM, reproduce the flow profiles fairly well, which suggests that the symmetry structure of the model must be most important. In addition, this success may be attributed to action-reaction correlations among elements of turbulence incorporated automatically into the model through the variational principle that renders the model free from the so-called closure problem.

One important objective of research of turbulence is to understand the spatial variation of Reynolds stress. The DEVM involves a scalar and a vector, but not a tensor and therefore says nothing about the Reynolds stress. In this paper, we extend the minimal DEVM so as to incorporate a tensor in invariant ways and explore if the tensor bears the property of the Reynolds stress in incompressible turbulent flow.

In Section 2, we elaborate how the minimal DEVM is extended to include a tensor. In Sec. 3, the model constructed in Sec. 2 is applied to turbulence in channel flow. Sec. 4 is devoted to a concluding remark.

---

2. Incorporating tensor in the minimal DEVM

We first give a review of the minimal DEVM. We introduce a traceless scalar matrix $\Phi$ by

$\Phi = {\mathit{\boldsymbol{u}}} \cdot {\mathit{\boldsymbol{\sigma }}},$

(2.1)

where ${\sigma _i}$, $i = x, \, y, \, z,$ are Pauli's spin matrices and ${\mathit{\boldsymbol{u}}}$ is a complex velocity field. Next, we define a following quantity

$\begin{array}{l} {A_{{\rm{NS}}}} = \int {{L_{{\rm{NS}}}}dt} \equiv \int {{{\cal L}_{{\rm{NS}}}}d\mathit{\boldsymbol{r}}} dt, \\ {{\cal L}_{{\rm{NS}}}} = \frac{{\rm{i}}}{2}{\rm{Tr}}\left( {{\Phi ^† }\Phi + \frac{1}{4}{\Phi ^† }\mathit{\boldsymbol{\sigma }}{\Phi ^† }.\mathit{\boldsymbol{\nabla}} \Phi - \frac{1}{4}\mathit{\boldsymbol{\nabla}} {\Phi ^† }.\Phi \mathit{\boldsymbol{\sigma }}\Phi + \frac{\nu }{2}{{\left( {\mathit{\boldsymbol{\nabla}} {\Phi ^† }} \right)}^2} - \frac{\nu }{2}{{\left( {\mathit{\boldsymbol{\nabla}} \Phi } \right)}^2}{\Phi ^† }{\bf{F}} + {{\bf{F}}^† }\Phi } \right). \end{array}$

(2.2)

Here, the dot stands for a partial derivative in time. $\nu$ is the kinematic viscosity. F is the force given by

${\bf{F}} \equiv {\mathit{\boldsymbol{\tilde f}}} \cdot {\mathit{\boldsymbol{\sigma }}} = \left( { - \frac{{\nabla p}}{\rho } + {{\mathit{\boldsymbol{f}}}_{{\text{ext}}}}} \right) \cdot {\mathit{\boldsymbol{\sigma }}}$

(2.3)

with $p$, $\rho$ and ${{\mathit{\boldsymbol{f}}}_{{\rm{ext}}}}$ being the pressure, density and external body force that acts on a unit mass. The Navier-Stokes equation is derived by the variation of ${A_{{\rm{NS}}}}$. We call the quantity like ${A_{{\rm{NS}}}}$ the pseudo-action (PA) because, although the correct equation of motion is derived by the variational principle, PA does not have a canonical structure of the kinetic energy subtracted by the potential energy and therefore its Legendre transformation does not give the system's energy.

The first three terms in ${\mathcal{L}_{{\rm{NS}}}}$ yield the Lagrange derivative terms. One can construct the minimal DEVM by extending $\Phi$ by giving it the center of $GL(2, \, C)$ as

$\Phi = \varphi + {\mathit{\boldsymbol{u}}} \cdot {\mathit{\boldsymbol{\sigma }}}$

(2.4)

where $\varphi$ is a complex scalar and by introducing into ${A_{{\rm{NS}}}}$ a minimal number of other terms invariant under $SU(2)\sim O(3)$ transformations. Taking variations, we have

${{\dot u}_{R, i}} + {{\mathit{\boldsymbol{u}}}_R} \cdot \mathit{\boldsymbol{\nabla}} {u_{R, i}} + {\varphi _R}{\partial _i}{\varphi _R} = \nu {\mathit{\boldsymbol{\nabla}} ^2}{u_{R, i}} + {f_{R, i}} - {{\mathit{\boldsymbol{u}}}_I} \cdot {\partial _i}{{\mathit{\boldsymbol{u}}}_I} + {u_{I, i}}\mathit{\boldsymbol{\nabla}} \cdot {{\mathit{\boldsymbol{u}}}_I}, \\ {{\dot \varphi }_R} + \mathit{\boldsymbol{\nabla}} ({\varphi _R}{{\mathit{\boldsymbol{u}}}_R}) = \nu {\mathit{\boldsymbol{\nabla}} ^2}{\varphi _R}, \\ {{\dot u}_{I, i}} + {{\mathit{\boldsymbol{u}}}_R} \cdot \mathit{\boldsymbol{\nabla}} {u_{I, i}}\, + {\varphi _R}{\partial _i}{\varphi _I} = - \nu {\mathit{\boldsymbol{\nabla}} ^2}{u_{I, i}} + {f_{I, i}} + {{\mathit{\boldsymbol{u}}}_I} \cdot {\partial _i}{{\mathit{\boldsymbol{u}}}_R} - {u_{I, i}}\mathit{\boldsymbol{\nabla}} \cdot {{\mathit{\boldsymbol{u}}}_R}, \\ {{\dot \varphi }_I} + {{\mathit{\boldsymbol{u}}}_R} \cdot \mathit{\boldsymbol{\nabla}} {\varphi _I} + {\varphi _R}\mathit{\boldsymbol{\nabla}} \cdot {{\mathit{\boldsymbol{u}}}_I} = - \nu {\mathit{\boldsymbol{\nabla}} ^2}{\varphi _I}, \\ $

(2.5)

where suffixes $R$ and $I$ denote real and imaginary part, respectively. We obtain the equations of motion for the minimal DEVM by setting $\varphi$ and ${\mathit{\boldsymbol{u}}}$ real, or $\Phi$ be Hermitian. Higher order interactions among ${\mathit{\boldsymbol{u}}}$ and $\varphi$ are introduced by incorporating higher order terms in ${\mathit{\boldsymbol{u}}}$ and $\varphi$. After such an extension, $\varphi$ comes to play the role of the effective or eddy viscosity ^[2].

We now incorporate a tensor into the model. Let ${R_{ij}}$, $i, j = 1\sim 3$, be the $(i, \, j)$ component of a tensor $R$, which is assumed to be invariant under the translation and Galilei transformation. At the beginning of constructing a model of turbulence, as in the minimal DEVM, a traceless complex vector matrix, which is an element of GL(2, C), is considered

${{\rm{R}}_i} = {R_{ij}}{\sigma _j}.$

(2.6)

(${{\rm{\tilde R}}_i} \equiv {\sigma _j}{R_{ji}}$ will do, too.) Repetition of indices implies summation. In (2.6), for simplicity, we omit the center of the group and express the PA mainly in terms of ${R_{ij}}$. We envisage that ${R_{ij}}$, like $\varphi$, is some physical entity which is conveyed by the flow and dissipates by the frictional force. This means that time derivative in the equation of motion is always accompanied with advection term. The relation between ${R_{ij}}$ and the observed Reynolds stress will be clarified after solving the equations of motion.

To begin with, we notice that the Lagrange derivative ${\dot R_{ij}} + {\mathit{\boldsymbol{u}}} \cdot \mathit{\boldsymbol{\nabla}} {R_{ij}}$ of ${R_{ij}}$ is derived by variation of $R_{ij}^*$ in

$R_{ij}^*{\dot R_{ij}} + \frac{1}{4}R_{ij}^*({\mathit{\boldsymbol{u}}} + {{\mathit{\boldsymbol{u}}}^*}) \cdot \mathit{\boldsymbol{\nabla}} {R_{ij}} - \frac{1}{4}\mathit{\boldsymbol{\nabla}} R_{ij}^* \cdot ({\mathit{\boldsymbol{u}}} + {{\mathit{\boldsymbol{u}}}^*}){R_{ij}}$

(2.7)

and subsequently by setting all quantities real. Thus, we are lead to consider the following SU(2) invariant PA

$\begin{array}{l} {A_{{\rm{R, Ld}}}} = i\int {\left( {R_{ij}^*{{\dot R}_{ij}} + \frac{1}{4}R_{ij}^*\left( {\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{u}}^*}} \right) \cdot \mathit{\boldsymbol{\nabla}} {R_{ij}} - \frac{1}{4}\mathit{\boldsymbol{\nabla}} R_{ij}^* \cdot \left( {\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{u}}^*}} \right){R_{ij}}} \right)} d\tau \\ \;\;\;\;\;\;\; = i\int {{\rm{Tr}}\left( {\frac{1}{2}{{\rm{R}}_i}^† {{{\rm{\dot R}}}_i} + \frac{1}{8}{\rm{R}}_i^† \left\{ {\mathit{\boldsymbol{\sigma }}, \Phi \mathit{\boldsymbol{ + }}{\Phi ^† }} \right\} \cdot \mathit{\boldsymbol{\nabla}} {{\rm{R}}_i} - \frac{1}{8}\mathit{\boldsymbol{\nabla}} {\rm{R}}_i^† \cdot \left\{ {\mathit{\boldsymbol{\sigma }}, \Phi \mathit{\boldsymbol{ + }}{\Phi ^† }} \right\}{{\rm{R}}_i}} \right)} d\tau \end{array}$

(2.8)

where $\Phi$ and ${{\rm{R}}_i}$ are traceless and $d\tau \equiv d{\mathit{\boldsymbol{r}}}dt$. Variation of ${A_{{\rm{R, }}\, {\rm{Ld}}}}$ in $R_{ij}^*$ gives

${\dot R_{ij}} + {{\mathit{\boldsymbol{u}}}_R} \cdot \mathit{\boldsymbol{\nabla}} {R_{ij}} + \frac{1}{2}{R_{ij}}\mathit{\boldsymbol{\nabla}} \cdot {{\mathit{\boldsymbol{u}}}_R}.$

(2.9)

These terms altogether indeed coincide with the Lagrange derivative of ${R_{ij}}$ for incompressible fluid that fulfils $\mathit{\boldsymbol{\nabla}} \cdot {{\mathit{\boldsymbol{u}}}_R} = 0$. The last term in (2.9) that gives rise to an effect in compressible flow is the necessary outcome in our formulation.

We know that the minimal DEVM without tensor, when applied to turbulent channel and pipe flows, reproduces the profiles of the mean velocity quite well. We do not wish to spoil this favorable feature of the model by incorporating the tensor. The above ${A_{{\rm{R, }}\, {\rm{Ld}}}}$ in fact does not affect the equation of motion for ${\mathit{\boldsymbol{u}}}$. It is because only the real part of ${\mathit{\boldsymbol{u}}}$ appears in ${A_{{\rm{R, }}\, {\rm{Ld}}}}$ so that the net effect of variation of ${{\mathit{\boldsymbol{u}}}^*}$ in ${A_{{\rm{R, }}\, {\rm{Ld}}}}$ vanishes, i.e., $({\rm{i}}/4)(R_{ij}^*\mathit{\boldsymbol{\nabla}} {R_{ij}} - \mathit{\boldsymbol{\nabla}} R_{ij}^*{R_{ij}}) = 0$ for $\operatorname{Im} {R_{ij}} = 0$. This property of ${A_{{\rm{R, }}\, {\rm{Ld}}}}$ can be shared by any other PAs involving ${R_{ij}}$ if the real part of ${\mathit{\boldsymbol{u}}}$ solely appear in them. In the followings, we will construct invariant PAs involving tensor by employing the real part of ${\mathit{\boldsymbol{u}}}$ only. Henceforth the symbol ${\mathit{\boldsymbol{u}}}$ stands for real velocity.

If ${R_{ij}}$ is to somehow express the Reynolds stress, $\overline {\delta {u_i}\delta {u_j}}$, the Reynolds stress equation tells us that the mean velocity and ${R_{ij}}$ interact via. ${\partial _k}{u_j}{R_{ik}} + {\partial _k}{u_i}{R_{kj}}$ that originates from the advection term in the Navier-Stokes equation. See, e.g., ^[1,4]. The PA that yields such terms will be given by

${A_{{\rm{R, adv}}}} = \frac{{\rm{i}}}{2}\int {(R_{ij}^* - {R_{ij}})\left( {{\partial _k}{u_j}({R_{ik}} + R_{ik}^*) + {\partial _k}{u_i}({R_{kj}} + R_{kj}^*)} \right)d\tau } .$

(2.10)

In terms of the Hermitian matrix field $\underline \Phi \equiv (\Phi + {\Phi ^† })/2 = \operatorname{Re} \varphi + {\mathit{\boldsymbol{u}}} \cdot {\mathit{\boldsymbol{\sigma }}}$, the above ${A_{{\rm{R, adv}}}}$ can be rewritten as

${A_{{\rm{R, adv}}}} = \frac{{\rm{i}}}{4}{\rm{Tr}}\int {\left( {R_{ij}^*\left( {{\sigma _j}{\partial _k}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } ({R_{ik}} + R_{ik}^*) + {\sigma _i}{\partial _k}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } ({R_{kj}} + R_{kj}^*)} \right) - h.c.} \right)d\tau } .$

(2.11)

Expressions in terms of the matrices ${{\rm{R}}_i}$ are also possible. They will be useful when we intend to extend the model so as to include the center of the group. In this paper, for simplicity, we restrict ourselves to the traceless ${{\rm{R}}_i}$.

Let us construct remaining interaction terms in PA that meet the invariance requirements. The diffusion of ${{\rm{R}}_i}$ is given by

${A_{{\rm{R, dif}}}} = \frac{{\rm{i}}}{4}\int {\left( {{\rm{Tr}}(\eta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } + \lambda )({{({\partial _k}R_{ij}^*)}^2} - {{({\partial _k}{R_{ij}})}^2})} \right)} d\tau .$

(2.12)

We list other possible lower order invariant interactions below. (Note the identities ${\rm{Tr(}}{\sigma _i}{{\rm{R}}_i}) = 2{R_{kk}}$, ${\rm{Tr(}}{{\rm{R}}_k}{{\rm{R}}_k}) = 2{R_{kl}}{R_{kl}}$ etc.)

$A_{\rm{R}}^{(1)} = \frac{{\rm{i}}}{2}\int {\left( {{g_0}{{(R_{kk}^*)}^2} + {g_1}{{(R_{ij}^*)}^2} - c.c.} \right)} d\tau\\A_{\rm{R}}^{(2)} = {\rm{i}}\int {\left( {{g_2}{\rm{Tr}}(F{\partial _i}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } {\sigma _j})R_{ij}^* - c.c.} \right)} d\tau = {\rm{i}}\int {\left( {{g_2}{{\tilde f}_j}{\partial _i}\operatorname{Re} \varphi R_{ij}^* - c.c.} \right)d\tau } \\A_{\rm{R}}^{(3)} = \frac{{\rm{i}}}{4}\int {\left( {({g_3}{\rm{Tr}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } + 2{{g'}_3}){\rm{Tr}}({\partial _i}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } {\sigma _j})R_{ij}^* - c.c.} \right)} d\tau = {\rm{i}}\int {\left( {({g_3}\operatorname{Re} \varphi + {{g'}_3}){\partial _i}{u_j}R_{ij}^* - c.c.} \right)d\tau }\\A_{\rm{R}}^{(4)} = {\rm{i}}\int {\left( {{\rm M}(\mathit{\boldsymbol{\nabla}} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } )R_{kk}^* - c.c} \right)d\tau } = {\rm{i}}\int {\left( {({g_4}({{(\mathit{\boldsymbol{\nabla}} \operatorname{Re} \varphi )}^2} + {{(\mathit{\boldsymbol{\nabla}} {\mathit{\boldsymbol{u}}})}^2}) + {{g'}_4}{{(\mathit{\boldsymbol{\nabla}} \operatorname{Re} \varphi )}^2})R_{kk}^* - c.c} \right)d\tau }\\A_{\rm{R}}^{(5)} = \frac{{\rm{i}}}{2}\int {{g_5}{\rm{Tr}}\left( {{\partial _i}\underline \Phi {\partial _j}\underline \Phi R_{ij}^* - c.c} \right)d\tau } = {\rm{i}}\int {{g_5}\left( {({\partial _i}\operatorname{Re} \varphi {\partial _j}\operatorname{Re} \varphi + {\partial _i}{\mathit{\boldsymbol{u}}} \cdot {\partial _j}{\mathit{\boldsymbol{u}}})R_{ij}^* - c.c} \right)d\tau }$

(2.13)

Note that, instead of employing the matrix $\underline \Phi = \Phi$, we can express the pseudo-action in terms of $\phi$ and ${\partial _i}{\mathit{\boldsymbol{u}}}$ by using $2\operatorname{Re} \phi = {\rm{Tr}}\Phi$ and $2{\partial _i}{\mathit{\boldsymbol{u}}} = {\partial _i}{\rm{Tr(}}\Phi {\mathit{\boldsymbol{\sigma }}})$.

$A_{\rm{R}}^{(1)}$ represents the inertia of the R-field. $A_{\rm{R}}^{(2)}$ describes generation or destruction of the R-field by the force or pressure gradient and the effective viscosity. Other interactions between $\Phi$ and R are given in $A_{\rm{R}}^{(3)}$ ~ $A_{\rm{R}}^{(5)}$, which involve up to the third order interactions. $M$ in $A_{\rm{R}}^{(4)}$ is a polynomial of $\mathit{\boldsymbol{\nabla}} \underline \Phi$ and acts isotropically to R. Here, we have adopted the simplest one

$M(\mathit{\boldsymbol{\nabla}} \Phi ) = \frac{{{g_4}}}{2}{\rm{Tr}}{(\mathit{\boldsymbol{\nabla}} \Phi )^2} = {g_4}\left( {{{(\mathit{\boldsymbol{\nabla}} \operatorname{Re} \phi )}^2} + {{(\mathit{\boldsymbol{\nabla}} {\mathit{\boldsymbol{u}}})}^2}} \right).$

(2.14)

The rotational asymmetry that possibly emerge from $A_{\rm{R}}^{(5)}$ implies a dependence of interaction on the direction relative to the mean flow and will give rise to the effect of boundary.

We sum up ${A_{{\rm{R, }}\, {\rm{Ld}}}}$, ${A_{{\rm{R, }}\, {\rm{dif}}}}$, $A_{\rm{R}}^{(1)}\sim A_{\rm{R}}^{(5)}$ to obtain the total PA, ${A_{\rm{R}}}$. Taking variations of $R_{ij}^*$ followed by letting all physical quantities be real leads to the equations for ${R_{ij}}$:

${{\dot R}_{ij}} + {\mathit{\boldsymbol{u}}} \cdot \mathit{\boldsymbol{\nabla}} {R_{ij}} = - {\partial _k}{u_j}{R_{ik}} - {\partial _k}{u_i}{R_{kj}} + \mathit{\boldsymbol{\nabla}} \left( {(\eta \varphi + \lambda )\mathit{\boldsymbol{\nabla}} {R_{ij}}} \right) - {g_0}{\delta _{ij}}{R_{kk}} - {g_1}{R_{ij}} - {g_2}{{\tilde f}_j}{\partial _i}\varphi \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, - ({g_3}\varphi + {{g'}_3}){\partial _i}{u_j} - {\delta _{ij}}M(\mathit{\boldsymbol{\nabla}} \Phi ) - {g_5}({\partial _i}\varphi {\partial _j}\varphi + {\partial _i}{\mathit{\boldsymbol{u}}} \cdot {\partial _j}{\mathit{\boldsymbol{u}}}). \\ $

(2.15)

The above 'R-equation' is not symmetric in $i$ and j. The symmetric and anti-symmetric components ${S_{ij}} \equiv ({R_{ij}} + {R_{ji}})/2$ and ${A_{ij}} \equiv ({R_{ij}} - {R_{ji}})/2$ obey the equations

${{\dot S}_{ij}} + {\mathit{\boldsymbol{u}}} \cdot \mathit{\boldsymbol{\nabla}} {S_{ij}} = - {\partial _k}{u_j}{S_{ik}} - {\partial _k}{u_i}{S_{jk}} + \mathit{\boldsymbol{\nabla}} \cdot \left( {(\eta \varphi + \lambda )\mathit{\boldsymbol{\nabla}} {S_{ij}}} \right) - {g_0}{\delta _{ij}}{S_{kk}} - {g_1}{S_{ij}} \\ \, \, \, \, \, \, \, \, \, \, - \frac{{{g_2}}}{2}({{\tilde f}_i}{\partial _j}\varphi + {{\tilde f}_j}{\partial _i}\varphi ) - \frac{1}{2}({g_3}\varphi + {{g'}_3})({\partial _i}{u_j} + {\partial _j}{u_i}) - {\delta _{ij}}M(\mathit{\boldsymbol{\nabla}} \Phi ) - {g_5}({\partial _i}\varphi {\partial _j}\varphi + {\partial _i}{\mathit{\boldsymbol{u}}} \cdot {\partial _j}{\mathit{\boldsymbol{u}}}), \\ $

(2.16a)

${{\dot A}_{ij}} + {\mathit{\boldsymbol{u}}} \cdot \mathit{\boldsymbol{\nabla}} {A_{ij}} = - {\partial _k}{u_j}{A_{ik}} + {\partial _k}{u_i}{A_{jk}} + \mathit{\boldsymbol{\nabla}} \left( {(\eta \varphi + \lambda )\mathit{\boldsymbol{\nabla}} {A_{ij}}} \right) - {g_1}{A_{ij}} \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, + \frac{{{g_2}}}{2}({{\tilde f}_i}{\partial _j}\varphi - {{\tilde f}_j}{\partial _i}\varphi ) - \frac{1}{2}({g_3}\varphi + {{g'}_3})({\partial _i}{u_j} - {\partial _j}{u_i}). \\ $

(2.16b)

Assuming a steady turbulence with sufficiently weak fields, from (2.16a), we have

${S_{ij}} \approx - \frac{1}{{2{g_1}}}({g_3}\varphi + {g{'}_3})({\partial _i}{u_j} + {\partial _j}{u_i}) - \frac{{{g_0}}}{{{g_1}}}{S_{kk}}{\delta _{ij}} - \frac{{{g_2}}}{{2{g_1}}}({\tilde f_i}{\partial _j}\varphi + {\tilde f_j}{\partial _i}\varphi ).$

(2.17)

This relation is compared with the Boussinesq hypothesis employed in some eddy viscosity models,

$- {\tau _{ij}} = {\nu _t}\left( {{\partial _i}{u_j} + {\partial _j}{u_i}} \right) - \frac{1}{3}{\tau _{kk}}{\delta _{ij}},$

(2.18)

where ${\tau _{ij}} = \overline {\delta {u_i}\delta {u_j}}$ is the Reynolds stress, ${\nu _t}$ the eddy viscosity and ${\tau _{kk}}/2$ the average turbulent kinetic energy. For locally homogeneous turbulent flow with zero average velocity gradient, (2.18) leads to ${\tau _{xx}} = {\tau _{yy}} = {\tau _{zz}}$, which is in contradiction to experiments (see, e.g., sec.4.1.4 in ^[1]). By contrast, (2.17) predicts the diagonal component ${S_{ii}}$ along the direction of the average flow to differ from the orthogonal components if ${\partial _i}\varphi$ is non-vanishing. However, we have to remember that (2.17) hold only approximately and the full equation (2.16a) has to generally be solved.

We obtain the equation for the would-be turbulent kinetic energy $K \equiv \sum\nolimits_i {{S_{ii}}} /2$ by setting $i = j$ and summing over the indices in the equations for ${S_{ij}}$. Having the homogeneous turbulence in mind, let us further assume that ${S_{ij}}$ are spatially constant and the mean velocity and the viscosity field take the forms ${u_i} = {w_{ij}}{r_j}$ and $\varphi = {s_i}{r_i}$. We then have

$\dot K = - {S_{ij}}{w_{ij}} - (3{g_0} + {g_1})K - \frac{{{g_2}}}{2}{\mathit{\boldsymbol{\tilde f}}} \cdot {\mathit{\boldsymbol{s}}} - \frac{3}{2}M(\mathit{\boldsymbol{\nabla}} \Phi ) - \frac{{{g_5}}}{2}\left( {{{\mathit{\boldsymbol{s}}}^2} + w_{ij}^2} \right).$

(2.19)

The corresponding equation for the turbulent kinetic energy derived from the Reynolds equation is

${\dot K^{({\rm{R}})}} = - \overline {\delta {u_i}\delta {u_j}} {w_{ij}} - \nu \overline {{{\left( {\mathit{\boldsymbol{\nabla}} \delta {\mathit{\boldsymbol{u}}}} \right)}^2}} + \overline {\delta {\mathit{\boldsymbol{f}}} \cdot \delta {\mathit{\boldsymbol{u}}}} ,$

(2.20)

where the superscript $({\rm{R}})$ and the symbol $\delta$ stand for the Reynolds equation and the fluctuation, respectively. Comparing these equations, we expect that the first term in $K$-equation will represent the production of the turbulent kinetic energy due to shear flow. The dissipative term in ${K^{({\rm{R}})}}$-equation is intensively represented by the second term in $K$-equation provided that $3{g_0} + {g_1} > 0$. The remaining terms in the $K$-equation are new ones peculiar to our modeling.

The substantial difference between our R-equation and the Reynolds equations lies in that the latter do not close because of the third moments, while the former does in the sense of the fulfillment of the variational principle. If the success of the minimal DEVM is due to the closure nature of its dynamical system, we may hope the R-equation to work as well.

---

3. Channel turbulent flow

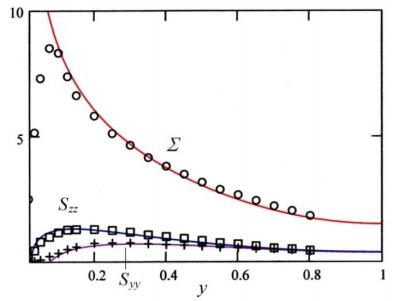
In this section, we apply the S-equations (2.16a) in the previous section to a channel turbulent flow. We are interested in the relation between calculated ${S_{ij}}$ and the observed Reynolds stress $\overline {\delta {u_i}\delta {u_j}}$. The experiment of the diagonal Reynolds stress for channel flow has been known as is given in, e.g., ^[5]. Many works on the direct numerical simulation (See, e.g., ^[6,7,8]) have reported results consistent with the experiment. The check of the consistency is important because experiments on turbulence in laboratory sometimes exhibit discrepancy ^[6]. In the followings, we refer to the results on the Reynolds stress reported in ^[5] for diagonal components and in ^[9] for an off-diagonal component. They are shown in Figure 1.

For a channel flow ${\mathit{\boldsymbol{\bar u}}} = ({u_x}, \, 0, \, 0)$ with a unit half channel width, we choose the y-axis to be perpendicular to the walls so that it is sufficient to consider $0 \leqslant y \leqslant 1$ because of the symmetry. One of the walls is at $y = 0$. Taking the symmetry of the Reynolds stress into account, we set

${S_{xz}} = {S_{zx}} = {S_{yz}} = {S_{zy}} = 0.$

(3.1)

Assuming that ${S_{ij}}$ has $y$-dependences only, the remaining quantities in (2.16) obey the equations (the prime stands for derivative in $y$)

${\left( {(\eta \varphi + \lambda ){{S'}_{xx}}} \right)^\prime } - 2{u{'}_x}{S_{xy}} - {g_0}\mathit{\Sigma } - {g_1}{S_{xx}} - M(\mathit{\boldsymbol{\nabla}} \Phi ) = 0,$

(3.2a)

${\left( {(\eta \varphi + \lambda ){{S'}_{yy}}} \right)^\prime } - {g_0}\mathit{\Sigma } - {g_1}{S_{yy}} - M(\mathit{\boldsymbol{\nabla}} \Phi ) - {g_5}({\varphi '^2} + u{'}_x^2) = 0,$

(3.2b)

${\left( {(\eta \varphi + \lambda ){{S'}_{zz}}} \right)^\prime } - {g_0}\mathit{\Sigma } - {g_1}{S_{zz}} - M(\mathit{\boldsymbol{\nabla}} \Phi ) = 0,$

(3.2c)

${\left( {(\eta \varphi + \lambda ){{S'}_{xy}}} \right)^\prime } - {u{'}_x}{S_{yy}} - {g_1}{S_{xy}} - \frac{{{g_2}}}{2}{\tilde f_x}\varphi ' - \frac{1}{2}({g_3}\varphi + {g{'}_3}){u{'}_x} = 0,$

(3.2d)

${\left( {(\eta \varphi + \lambda ){{A'}_{xy}}} \right)^\prime } - {g_1}{A_{xy}} + \frac{{{g_2}}}{2}{\tilde f_x}\varphi ' + \frac{{{g_3}}}{2}\varphi {u{'}_x} = 0.$

(3.2e)

Here, ${S_{xx}} + {S_{yy}} + {S_{zz}} \equiv \mathit{\Sigma }$. Summing (3.2a) ~ (3.2c) yields the equation for $\mathit{\Sigma }$

${\left( {(\eta \varphi + \lambda )\mathit{\Sigma } '} \right)^\prime } - 2{u{'}_x}{S_{xy}} - (3{g_0} + {g_1})\mathit{\Sigma } - 3M(\mathit{\boldsymbol{\nabla}} \Phi ) - {g_5}({\varphi '^2} + u{'}_x^2) = 0$

(3.3)

We would like to find out whether there exist values of parameters with which these equations reproduce the experimental results for the Reynolds stress ^[5,6,7,8]. Unfortunately, these equations have too many parameters to handle directly. In order to minimize the unruly effects from varying these model parameters, we consider only the equations for ${S_{yy}}$, ${S_{zz}}$, ${S_{xy}}$ and $\mathit{\Sigma }$.

In the previous work ^[2], a dimensionless field — viscosity function — was introduced by $\varphi /{\xi _0} \to \varphi$ with a parameter ${\xi _0}$ that has the dimension of velocity. ${\xi _0}$ is the position where the potential of original dimensionful $\varphi$ takes the local minimum, thereby restricting the range of the dimensionless $\varphi$ as $\varphi < 1$. For convenience, we also rescale the mean velocity field as

${u_x} \to {\xi _0}{u_x}$

and divide the equations by $\eta {\xi _0}$ to express the equations (3.3), (3.2b) and (3.2d) as

${((\varphi + \bar \lambda )\mathit{\Sigma } ')^\prime } - \frac{2}{\eta }{{u'}_x}{S_{xy}} - (3{{\bar g}_0} + {{\bar g}_1})\mathit{\Sigma } - 3{{\bar g}_4}({{\varphi '}^2} + u{'}_x^2) - {{\bar g}_5}({{\varphi '}^2} + u{'}_x^2) = 0, \\ {((\varphi + \bar \lambda ){{S'}_{yy}})^\prime } - {{\bar g}_0}\mathit{\Sigma } - {{\bar g}_1}{S_{yy}} - {{\bar g}_4}({{\varphi '}^2} + u{'}_x^2) - {{\bar g}_5}({{\varphi '}^2} + u{'}_x^2) = 0, \\ {((\varphi + \bar \lambda ){{S'}_{xy}})^\prime } - \frac{1}{\eta }{{u'}_x}{S_{yy}} - {{\bar g}_1}{S_{xy}} - \frac{{{{\bar g}_2}}}{2}{{\tilde f}_x}\varphi ' - \frac{1}{2}({{\bar g}_3}\varphi + {{\bar g'}_3}){{u'}_x} = 0, \\ $

(3.4)

where new constants were introduced by

$\bar \lambda = \lambda /(\eta {\xi _0}), \, \, \, {\bar g_{0, 1}} = {g_{0, 1}}/(\eta {\xi _0}), \, \, \, {\bar g_2} = {g_2}/\eta , \, \, {\bar g_3} = {g_3}{\xi _0}/\eta , \, \, \, \, {\bar g{'}_3} = {g{'}_3}/\eta , \, \, {\bar g_{4, 5}} = {g_{4, 5}}{\xi _0}/\eta .$

Note that the equations for $\mathit{\Sigma }$, ${S_{yy}}$ and ${S_{xy}}$ are closed.

${u_x}(y)$ has been known from experiments ^[5,10] or by direct numerical calculation ^[6,7,8]. Its approximate functional form is given in Appendix. $\varphi (y)$ in minimal DEVM has been numerically calculated by Takahashi ^[2], according to which, $\varphi (y)$ approximately linearly increases near the wall and gradually approaches a constant value. For the present calculation for flows with the Reynolds number of a few thousands, we adopt an approximation

$\varphi (y) \approx 0.6\sin ({\rm{\pi }}y/2)$

(3.5)

for the sake of simplicity in numerical calculations. The $\mathit{\Sigma }$ obtained by solving (3.4) is employed in solving (3.2c) for ${S_{zz}}$. The results are shown in Fig.1 together with the experimental data. The model parameters are found by trial and error. The "boundary" condition is given at $y = 1$, i.e., at the center of the channel. The calculation shows fairly good agreements with experiments in the region $y > 0.3$ for the choice of the model parameters given in the caption. Other set of values may be also possible.

Marked deficits in $\mathit{\Sigma }$ and ${S_{yy}}$ from the experimentally known Reynolds stress are observed in $y < 0.3$. This indicates that our model lacks some terms that should be effective near the wall. From Fig.1, it is anticipated that addition of interactions of ${S_{xx}}$ and ${S_{yy}}$ with $\mathit{\boldsymbol{\nabla}} \underline \Phi$ will remedy the disagreement for $\mathit{\boldsymbol{\nabla}} \underline \Phi$ has relatively large values in the vicinity of the wall. The simplest candidates may consist of terms ${\rm{i}}F(\mathit{\boldsymbol{\nabla}} \underline \Phi )R_{ij}^*{\partial _k}{u_i}{\partial _k}{u_j}$, ${\rm{i}}G(\mathit{\boldsymbol{\nabla}} \underline \Phi )R_{ij}^*{\partial _i}\phi {\partial _j}\phi$, ${\rm{i}}H(\mathit{\boldsymbol{\nabla}} \underline \Phi )R_{ij}^*{\partial _i}{u_k}{\partial _j}{u_k}$ and their complex conjugates. For the sake of simplicity, we try the first two terms with

$F = {g_6}{(\mathit{\boldsymbol{\nabla}} \varphi )^2}, \, \, \, \, \, G = {g_7}{(\mathit{\boldsymbol{\nabla}} \varphi )^2},$

(3.6)

which respectively give new contribution to the equation for ${S_{xx}}$ and ${S_{yy}}$ near $y = 0$. Accordingly, the equations for $\mathit{\Sigma }$ and ${S_{yy}}$ are altered as

${((\varphi + \bar \lambda )\mathit{\Sigma } ')^\prime } - \frac{2}{\eta }{{u'}_x}{S_{xy}} - (3{{\bar g}_0} + {{\bar g}_1})\mathit{\Sigma } - 3{{\bar g}_4}({{\varphi '}^2} + u{'}_x^2) - {{\bar g}_5}({{\varphi '}^2} + u{'}_x^2) - {{\bar g}_6}{{\varphi '}^2}u{'}_x^2 - {{\bar g}_7}{{\varphi '}^4} = 0, \\ {((\varphi + \bar \lambda ){{S'}_{yy}})^\prime } - {{\bar g}_0}\mathit{\Sigma } - {{\bar g}_1}{S_{yy}} - {{\bar g}_4}({{\varphi '}^2} + u{'}_x^2) - {{\bar g}_5}({{\varphi '}^2} + u{'}_x^2) - {{\bar g}_7}{{\varphi '}^4} = 0, \\ $

(3.7)

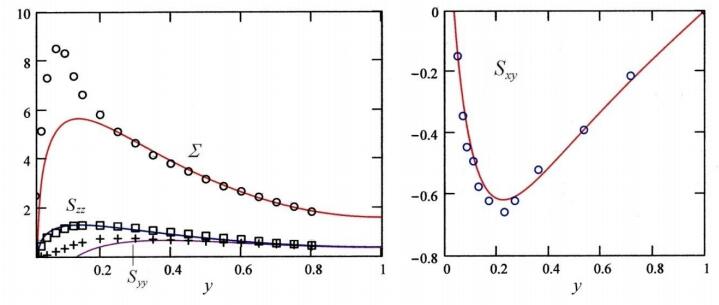
where ${\bar g_{6, 7}} = {g_{6, 7}}\xi _0^3/\eta$. These equations together with the one for ${S_{xy}}$ are solved with the result depicted in Figure 2. As was expected, the region of $y$ with better fitting to data has been extended toward the wall. ${S_{zz}}$ and ${S_{xy}}$ are not visibly changed by the above modification of the equations.

We notice that the components of the symmetric tensor agree semi-quantitatively with the experimental results for the Reynolds stress in the central and upper half of the logarithmic region.

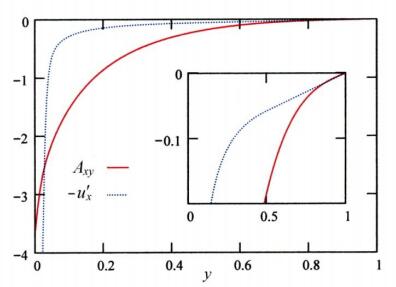
Finally, in Figure 3, we show the result for the antisymmetric component ${A_{xy}}$ which is obtained by solving the $A$-equation (3.2e) with a boundary condition ${A_{xy}} = 0, \, \, {A{'}_{xy}} = {u{'}_x}$ at $y = 1$. Although $A$ is antisymmetric, it substantially differs from the vorticity. The physical meaning of $A$ is unclear.

---

4. Concluding remarks

We constructed a conventional model that incorporates a tensor into the minimal DEVM in an invariant way and explored if the symmetric part of the tensor shows some correspondence to the Reynolds stress observed in channel turbulent flow. The new tensor terms were added to the minimal DEVM so as not to affect the mean velocity which had already been well reproduced within the minimal DEVM ^[2]. We found that a correspondence to the Reynolds stress in fact exists off the wall and is improved further by adding higher order interaction terms. A new form of the Boussinesq hypothesis adapted to the model was also found. The preliminary result reported in this paper suggests that tensor model seems promising in describing the Reynolds stress.

A relative improvement of the model was achieved by incorporating higher order terms which are not small as compared with the lower order terms. Indeed, our fitting gives

$\max (|{\bar g_6}|, \, |{\bar g_7}|)/\max (|{\bar g_0}|, \, |{\bar g_1}|, \, |{\bar g_2}{\tilde f_x}|, \, {\bar g_3}|, \, |{\bar g{'}_3}|, \, |{\bar g_4}|, \, |{\bar g_5}|) = 0.75.$

Higher order terms may not be safely neglected.

The DEVM gives the action-reaction relations among the elements of fluid through the variational principle as was manifested in ^[2]. Taking advantage of this property of the DEVM, we also want to know what the reaction of the Reynolds stress to the mean flow is. It is desirable to find a more sophisticated method for constructing a model.

From an aesthetic point of view, it is preferable to treat tensor and vector equally. For this purpose, it may be worthwhile to consider integrating the components of the tensor as a vector matrix by

${{\rm{R}}_i} = {R_{ij}}{\sigma _j}~ {\rm or}~{{\rm{\tilde R}}_i} = {\sigma _j}{R_{ji}}$

and explicitly express the pseudo-action in an SU(2) invariant way. In order to close multiplications in GL(2, C), we add the center as

${{\rm{R}}_i} = {v_i} + {R_{ij}}{\sigma _j}~ {\rm or}~{{\rm{\tilde R}}_i} = {v_i} + {\sigma _j}{R_{ji}}$

Here, ${\mathit{\boldsymbol{v}}}$ can be a vector or an axial-vector. Such an extension of ${{\rm{R}}_i}$ is analogous to the one in the minimal DEVM, wherein the effective viscosity was introduced by requiring the scalar matrices $\Phi$ and ${\Phi ^† }$ to form a set closed under multiplication. It is interesting to note that, if we require these matrices to have a definite parity, ${\mathit{\boldsymbol{v}}}$ will be an axial-vector. One candidate is the vorticity. The role of the antisymmetric components of the tensor $R$, if any, will be reexamined in such a model that embodies the aim of the original DEVM. Further study along this line will be intriguing.

---

Appendix. An empirical formula for the mean velocity of turbulent channel flow

The interval of the dimensionless coordinate $\zeta$ is divided into three regions.

ⅰ) Viscous sublayer + buffer region $\zeta \leqslant {\zeta _1}$:

$u(\zeta ) = A\sin (\zeta /A).$

ⅱ) Buffer region + logarithmic region ${\zeta _1} \leqslant \zeta \leqslant {\zeta _2}$:

$u(\zeta ) = (2.4\ln \zeta + 5.5)[1 - B\exp ( - C(\zeta - {\zeta _1}))].$

ⅲ) Central region ${\zeta _2} \leqslant \zeta \leqslant {\zeta _{\max }}$:

$u(\zeta ) = D - E{({\zeta _{\max }} - \zeta )^2}.$

Imposing a condition that $u(\zeta )$ belongs to the ${C^1}$ class yields following relations among constants

$B(A) = 1 - A\sin ({\zeta _1}/A)/Fl({\zeta _1}),$

$C(A) = \frac{{\cos ({\zeta _1}/A) - (2.4/{\zeta _1})(1 - B(A))}}{{B(A)Fl({\zeta _1})}},$

$D(A) = Fl({\zeta _2})\left( {1 - B(A)\exp [ - C(A)({\zeta _2} - {\zeta _1})]} \right) + E(A){({\zeta _{\max }} - {\zeta _2})^2},$

$E(A) = \frac{1}{{2({\zeta _{\max }} - {\zeta _2})}}\left[ {\frac{{2.4}}{{{\zeta _2}}} + B(A)\left( {Fl({\zeta _2})C(A) - \frac{{2.4}}{{{\zeta _2}}}\exp [ - C(A)({\zeta _2} - {\zeta _1})]} \right)} \right],$

where

$Fl(\zeta ) = 2.4\ln \zeta + 5.5\, .$

In the text, following values are employed

${\zeta _1} = 10, \, \, \, {\zeta _2} = {\zeta _{\max }}/2, \, \, \, {\zeta _{\max }} = 450, \, \, \, A = 15\, .$

---

Conflict of interest

The authors declare no conflict of interest.

---