Enhancing the characteristics of MHD squeezed Maxwell nanofluids via viscous dissipation impact

1.   Introduction

Unlike Newtonian fluids which maintain a constant viscosity, non-Newtonian fluids are characterized by their viscosity being dependent on the amount of shear rate or stress applied to them. The Maxwell fluid is a typical illustration of a non-Newtonian fluid, and it is frequently utilized to simulate the rheological properties of intricate fluids, including polymers, suspensions, and emulsions ^[1]. According to this model, the non-Newtonian fluid consists of both an elastic and a viscous component, with the time-varying shear stress arising from the relaxation of the elastic component. The scientific community has taken a keen interest in the behavior of non-Newtonian fluids, as it has been observed across a broad range of applications, including biological fluids and industrial processes. Through the use of experimental and computational techniques, numerous investigations have explored the flow characteristics of Maxwell fluids under various conditions, such as shear flow, extensional flow, and oscillatory flow. The outcomes of these studies have furnished significant insights into the underlying physical mechanisms that regulate the behavior of these fluids. Furthermore, they have played a pivotal role in the advancement of new models and simulation methodologies for anticipating and comprehending the behavior of non-Newtonian fluids, including the Maxwell fluid ^[2,3]. The significance of non-Newtonian Maxwell fluid has resulted in extensive discussions by numerous authors. Several references [4,5,6,7] have included discussions on various manufacturing applications of this type of fluid.

Nanofluid flow refers to the movement of a fluid that contains suspended nanoparticles, which is induced by an external force or pressure gradient. The properties of the fluid, such as viscosity and thermal conductivity, can be significantly modified by the presence of nanoparticles, leading to complex behavior. This has important implications for various engineering applications, including cooling systems and heat transfer in electronic devices. Researchers are actively studying nanofluid flow to gain a better understanding and control of its behavior for practical purposes. The significant importance of nanofluid research has led numerous researchers to focus their efforts on this area. Shen et al. ^[8] conducted an extensive study on non-Newtonian Sisko nanofluid flow influenced by fractional Cattaneo heat flux, while Zhang et al. ^[9] explored Maxwell nanofluid flow through a porous medium. Recently, Ayub et al. ^[10] investigated radiative cross nanofluid flow, and another study by Ayub et al. ^[11] and colleagues examined time-dependent cross nanofluid flow with melting heat transport. In addition, Shen et al. ^[12] conducted an important investigation on nanofluid flow with fractional derivatives, while Chen et al. ^[13] thoroughly researched the entropy generation of Darcy-Forchheimer nanofluid flow.

Maxwell nanofluid is produced by introducing electrically conductive particles into a base fluid, resulting in a type of nanofluid. The size of the particles dispersed in Maxwell nanofluids typically falls within the nanometer range and they are commonly made of metals such as copper or silver. The introduction of these particles into the base fluid can modify the thermal and electrical characteristics of the fluid, thus making Maxwell nanofluids a potential solution for various applications, such as electronic cooling and heat transfer. The distinct attributes exhibited by Maxwell nanofluids have sparked substantial attention in recent times, resulting in an expanding research field dedicated to comprehending and refining their performance. The importance of Maxwell nanofluid flow has prompted many authors to investigate its behavior, including the impact of various physical phenomena and mass transfer, as evidenced by references [14,15,16,17].

In recent years, squeezed nanofluid has emerged as a novel type of nanofluid, garnering significant interest. It is produced by compressing a base fluid that contains suspended nanoparticles, resulting in a reduction in particle size and an increase in concentration. This compression process can impart distinct attributes to the squeezed nanofluid, such as improved heat transfer performance and enhanced thermal conductivity ^[18]. Squeezed nanofluid has the potential to enhance the efficacy of heat transfer systems, which is one of its main advantages. By increasing the concentration of nanoparticles within the fluid, squeezed nanofluid can improve thermal conductivity, enabling more efficient heat transfer. This feature can prove especially advantageous in domains like electronic cooling, where efficient heat dissipation is vital to ensure optimal system performance. Multiple investigations have been conducted to examine the flow and thermal characteristics of squeezed nanofluids across various shapes and structures ^[19,20,21]. The findings of these research studies provide crucial insights into the behavior of squeezed nanofluid flow, which can be pivotal in the design optimization and performance enhancement of devices that employ this flow.

The authors have been inspired by the referenced literature review and the benefits of squeezed flow in several scientific and engineering disciplines, including biomedicine and biology. With this in mind, they have undertaken an investigation of the dynamics of unsteady flow and heat mass transfer of Maxwell nanofluid in a squeezed flow setup over a sensor surface. The study considers the impact of magnetic fields, variable thermal conductivity, variable viscosity, and viscous dissipation.

The literature's findings regarding the multiple potential applications of viscous dissipation in non-Newtonian nanofluids have inspired the authors to explore the benefits of squeezed flow across various scientific and engineering domains, such as biomedicine and biology. One such application is the optimization and design of advanced heat transfer systems in various industrial sectors like microelectronics, energy conversion, and biomedical engineering. The incorporation of non-Newtonian nanofluids with improved heat transfer properties can significantly enhance the performance of these systems, leading to increased efficiency and reduced expenses. Due to this importance, this paper's novelty lies in considering Maxwell squeezed nanofluid flow over a sensor surface while taking into account both the effects of viscous dissipation and an external magnetic field, which highlights its significance.

2.   Description of physical model

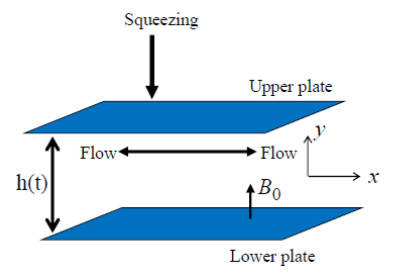
This model considers the unsteady flow of squeezed non-Newtonian Maxwell nanofluid with a constant density over a sensor surface under the influence of a variable viscosity and variable thermal conductivity. Let $u(x, y)$ and $v(x, y)$ denote the velocity components in the $x$ and $y$ directions, respectively (as shown in Figure 1).

Figure 1.  Physical model of the problem.

DownLoad: Full-Size Img PowerPoint

The continuity equation, momentum equation, energy equation, and constitutive equation are included in the model. The magnetic field affects the momentum equation, while the dissipation phenomenon influences the energy equation. Thus, we will consider the flow of a Maxwell nanofluid that is squeezed between two parallel plates with a variable height of $h(t)$. The height $h(t)$ between the two surfaces in the current investigation is determined by the following relation ^[21]: $h(t) = h_{0}/(S+\beta t)^{\frac{1}{\beta}}$, where $h_{0}$ is a constant. Between two parallel plates lies a micro cantilever sensor with a length of $L$. Assumptions are made that the squeezing of the free stream takes place from the tip to the surface and that the lower plate remains fixed while the upper plate undergoes squeezing. The fluid's behavior near the sensor surface is crucial in a squeezing fluid, as the pressure distribution on the surface is affected by the squeezing motion. The study assumes that the nanofluid flow follows the no-slip condition and there are no chemical reactions occurring during the flow. The base flow is assumed to be incompressible, and the nanoparticles are assumed to be in thermal equilibrium with the base flow. Furthermore, any radiative heat transfer effects can be ignored in this study. The flow is propelled by the external free stream velocity $U$, while a magnetic field with a strength of $B_{0}$ is applied in the $y$- direction and perpendicular to the channel. Below are the equations that model this problem, which are nonlinear differential equations divided into continuity, momentum, energy, and concentration equations ^[22,23]:

In this context, the nanofluid density is symbolized by $\rho_{\infty}$, and the Maxwell coefficient is given by $\delta$. The dynamic viscosity of the nanofluid, represented as $\mu(T)$, depends on the temperature $T$. Furthermore, the pressure is indicated by $p$, while the thermal conductivity is expressed by $\kappa$. Moreover, $\tau$ is the ratio of the heat capacity of the micro-particles to the heat capacity of the surrounding fluid. Similarly, the Brownian diffusion coefficient is represented by $D_B$, while the concentration of nanoparticles is denoted by $C$. In addition, the thermophoretic phenomenon is defined by a diffusion coefficient that is specific to thermophoresis, which is denoted by $D_T$. As a result, the boundary conditions that correspond to the problem's geometry are given below ^[23]:

here, the character $\nu_{\infty}$ denotes the ambient kinematic viscosity, which is calculated as the ratio of the ambient dynamic viscosity $\mu_{\infty}$ to the ambient density $\rho_{\infty}$. Additionally, $q_{1}$ denotes the wall heat flux, while $q_{2}$ represents the wall mass flux. Furthermore, $v_{0}(t)$ refers to the permeable velocity, which can be taken to be constant and denoted by $v_{i}$. In science, it is a widespread practice to simplify a system of partial differential equations using similarity transformations. This involves introducing new variables that are related to the original variables through a scaling factor. Therefore, the following transformations are commonly used ^[23]:

Here, $\phi$ is a stream function, which physically means that at each point in space, the stream function is a scalar field whose gradient is perpendicular to the fluid flow, which makes it a valuable tool for describing two-dimensional, incompressible flows. By satisfying the continuity equation for an incompressible flow, the stream function ensures that mass is conserved throughout the fluid domain, making it a useful tool for analyzing fluid motion. $\eta$ is a similarity variable which is a non-dimensional parameter that is created by dividing a physical quantity by a characteristic scale that is associated with the system. The use of this variable simplifies the analysis of physical problems by decreasing the number of variables that require consideration. The non-dimensional fluid temperature is represented by $\theta$, while the non-dimensional stream function is denoted by $f$. The squeezed flow index is represented by the symbol $\beta$, while the dimensionless constant is denoted by $S$. Under specific circumstances, it may be advantageous to represent a physical problem using a set of ordinary differential equations instead of partial differential equations. Moreover, our approach assumes that the thermal conductivity $\kappa$ and viscosity $\mu$ of the nanofluid are functions of the dimensionless temperature $\theta$, as described by the relationships presented in ^[24,25]. Therefore, the thermal conductivity $\kappa$ is given by $\kappa_{\infty}$ times $(1+\varepsilon\theta)$ or $\kappa = \kappa_{\infty}(1+\varepsilon\theta)$, while the nanofluid viscosity $\mu$ can be expressed as $\mu_{\infty}$ times the exponential of $-\alpha\theta$ or $\mu = \mu_{\infty}e^{-\alpha\theta}$. Now, by utilizing Eqs (2.8) and (2.9) and ensuring the continuity equation Eq (2.1) are satisfied, the resulting equations can be written in the following form:

Additionally, the relevant boundary conditions can be formulated in the following manner:

Moreover, it is evident that the system mentioned earlier is primarily controlled by the factors enumerated below.

The Maxwell parameter $\lambda$, the surface permeable velocity parameter $f_{0}$, the magnetic parameter $M$, the Eckert number $Ec$ and the Prandtl number $Pr$ represent these factors, respectively. Additionally, the remaining governing parameters can be formulated as follows:

The thermophoresis parameter, the Lewis number and the Brownian motion parameter are designated as these parameters, respectively. Moreover, there exist specific physical quantities that can mathematically portray the behavior of flow, heat transfer, and mass transfer in a fascinating way. These quantities are referred to as the local skin-friction coefficient $Cf_{x}$, the local Nusselt number $Nu_{x}$, and the local Sherwood number $Sh_{x}$. They are defined in the following manner:

where $Re_{x} = \frac{a x^{2}}{\nu_{\infty}}$ is the local Reynolds number.

3.   Confirming the validity of the code

Once the mathematical model for the squeezed Maxwell nanofluid flow, accounting for the effects of viscous dissipation, has been established, the subsequent stage is to create a computational algorithm to solve the equations. Verifying the accuracy of the code is of utmost importance prior to conducting any simulations. This section seeks to describe the validation procedure and compare the obtained results with existing literature findings. In order to establish the precision and dependability of the present numerical approach, it is validated through a comparison of its solutions with previously published findings from research conducted by Shankar et al. ^[26]. The authors have provided Table 1 to illustrate the procedure for validation. The comparison was carried out for varying values of the squeezed flow index parameter $\beta$ and Prandtl number $Pr$, with the condition $\theta^{\prime}(0) = -1$ being used instead of $\theta(0) = 1$. Nevertheless, the credibility of the present numerical results is confirmed by the following table, which attests to their dependability and accuracy.

Table 1.  Values of $\theta(0)$ for various values of $\beta$ and $Pr$ with the results of Shankar et al. ^[26] when $\lambda = \alpha = M = f_{0} = \Omega_{1} = \Omega_{2} = \varepsilon = Ec = 0$.

$\beta$	$Pr$	Shankar et al. [26]	Present work
1.0		0.381823375689146	0.38182337567098521
1.5	6.7	0.330840498714310	0.33084049872154031
2.0		0.295440261684154	0.29544026198541020
	2.0	0.654123423120187	0.65412342311200541
1.0	5.0	0.435614607270683	0.43561460726985210
	6.7	0.381823375689146	0.38182337569850251

---

 | Show Table

DownLoad: CSV

4.   Graphical and tabular findings with discussion

The primary motivation of this section is to examine how different relevant factors affect the distributions of velocity $f'(\eta)$, temperature $\theta(\eta)$, and concentration $\phi(\eta)$. Figure 2 demonstrates how the characteristics of the magnetic parameter $M$ affect the fields of velocity, temperature, and concentration. Elevated magnetic parameter values result in increased nanofluid velocities while simultaneously causing a decrease in the corresponding temperature and concentration. Physically, the magnetic parameter affects the squeezed nanofluid by inducing a magnetic field that produces a Lorentz force, which propels the fluid's movement. This movement causes a rise in the velocity of the nanofluid. Nevertheless, the magnetic field also has a cooling influence on the fluid, leading to a reduction in temperature. Furthermore, due to the movement of the nanofluid, it tends to accumulate near the surface walls, leading to a slightly decrease in the overall concentration of the fluid.

Figure 2.  (a) $f'(\eta)$ and $\theta(\eta)$ for various $M$, (b) $\phi(\eta)$ for various $M$.

DownLoad: Full-Size Img PowerPoint

Figure 3 demonstrates the behavior of the velocity $f'(\eta)$, concentration $\phi(\eta)$, and temperature $\theta(\eta)$ plots with respect to changes in the similarity variable, as the squeezed flow index parameter $\beta$ is varied. An increase in the squeezed flow index parameter results in a reduction in the concentration, temperature, and velocity of the squeezed Maxwell nanofluid. The reduction in velocity profile is due to the fact that the upper plate moves closer to the lower stretching plate, resulting in an increase in the force acting on the fluid, which leads to greater deformation of the fluid. Physically, as the nanofluid moves through a narrow gap between two plates, its velocity reduces due to the principle of mass conservation. This is because the same amount of fluid has to pass through a smaller area, leading to a decrease in its velocity. Along with this, the fluid's temperature also decreases since the reduction in velocity converts some of the kinetic energy into heat and potential energy, causing the fluid to cool down.

Figure 3.  (a) $f'(\eta)$ and $\theta(\eta)$ for various $\beta$, (b) $\phi(\eta)$ for various $\beta$.

DownLoad: Full-Size Img PowerPoint

The variations in the surface permeable velocity parameter $f_{0}$ and their impact on the temperature distribution $\theta(\eta)$, nanoparticle concentration $\phi(\eta)$, and nanofluid velocity $f'(\eta)$ are depicted in Figure 4. The findings indicate that an escalation in the surface permeable velocity parameter results in a reduction of the temperature and concentration of the compressed nanofluid, as well as an elevation in the velocity profile in the boundary layer area. In terms of physics, enhancing the surface permeable velocity parameter results in stronger adhesion of the fluid to the sensor surface. This reduces the likelihood of boundary layer formation, resulting in improved fluid velocity profile and more accurate measurement. This stronger adhesion is due to the fluid's increased ability to penetrate and interact with the surface, resulting in stronger intermolecular interaction and better adherence.

Figure 4.  (a) $f'(\eta)$ and $\theta(\eta)$ for various $f_{0}$, (b) $\phi(\eta)$ for various $f_{0}$.

DownLoad: Full-Size Img PowerPoint

Following that, Figure 5 illustrates how the viscosity parameter $\alpha$ varies with changes in nanoparticle concentration, temperature, and velocity distributions. When the viscosity parameter has a high value, the velocity profile experiences an increase across the entire boundary layer region, while the nanoparticle concentration and corresponding temperature exhibit an opposite trend with respect to the same parameter. Physically, the viscosity parameter is a measure of how much the solid nanoparticles interact with the fluid in a nanofluid. When this parameter is increased, it means that there is a stronger interaction between the fluid and the nanoparticles. This results in an increase in the velocity profile of the squeezed nanofluid flow, as the interaction between the fluid and nanoparticles becomes more intense.

Figure 5.  (a) $f'(\eta)$ and $\theta(\eta)$ for various $\alpha$, (b) $\phi(\eta)$ for various $\alpha$.

DownLoad: Full-Size Img PowerPoint

The behavior of the Eckert number $Ec$ on the concentration $\phi(\eta)$ and temperature $\theta(\eta)$ fields is illustrated in Figure 6. The decay of the concentration profile is examined to occur at increased values of the Eckert number, while the temperature of the nanofluid is boosted by the same parameter owing to the elevated thermal conductivity of the nanofluid. A lower Eckert number results in a reduction in the convective heat transfer coefficient, which leads to an increase in the temperature distribution of the squeezed nanofluid flow. This physical phenomenon happens due to the lower kinetic energy of the fluid at lower Eckert numbers, which in turn reduces the rate of heat transfer from the fluid to the nanoparticles. Physically, when the Eckert number increases in a Maxwell squeezed nanofluid flowing over a sensor surface, it causes the fluid to have more kinetic energy. This extra energy creates more turbulence and mixing, which improves the dispersion of nanoparticles and makes the temperature distribution over the sensor surface more uniform. Additionally, the higher kinetic energy increases the heat transfer rate, further improving the temperature distribution. Overall, increasing the Eckert number enhances heat transfer efficiency and produces a more even temperature distribution over the nanofluid's sensor surface.

Figure 6.  (a) $\theta(\eta)$ for various $Ec$, (b) $\phi(\eta)$ for various $Ec$.

DownLoad: Full-Size Img PowerPoint

The impact of the thermal conductivity parameter $\varepsilon$ on both the concentration distribution $\phi(\eta)$ and temperature $\theta(\eta)$ characteristics of the Maxwell nanofluid are illustrated in Figure 7. When the thermal conductivity parameter is increased, the temperature field grows, while the concentration of nanoparticles in the squeezed nanofluid flow slightly decreases. Physically, the thermal conductivity of a material refers to its ability to conduct heat, and a higher value indicates better heat transfer. When a fluid flows over a surface, a higher thermal conductivity results in better heat transfer from the surface to the fluid, leading to a more even temperature distribution over the surface. This means that a higher thermal conductivity allows for more efficient heat transfer and a more uniform temperature distribution over the surface. Consequently, the temperature field of the squeezed nanofluid flow is enhanced.

Figure 7.  (a) $\theta(\eta)$ for various $\varepsilon$, (b) $\phi(\eta)$ for various $\varepsilon$.

DownLoad: Full-Size Img PowerPoint

Figure 8 reveals the features of the thermophoresis parameter $\Omega_{1}$ on the concentration $\phi(\eta)$ and temperature $\theta(\eta)$ distributions. Higher values of the thermophoresis parameter result in an increase in both concentration and temperature distributions. The thermophoresis parameter characterizes the movement of nanoparticles in response to the temperature gradient in a squeezed nanofluid flow. When the thermophoresis parameter increases, nanoparticles tend to migrate towards the hotter regions of the flow due to their higher mobility, resulting in an increase in their concentration in those regions. Further, the current study has verified the findings of previous research conducted by Muhammad et al. ^[27] regarding the effect of the thermophoresis parameter on temperature distribution.

Figure 8.  (a) $\theta(\eta)$ for various $\Omega_{1}$, (b) $\phi(\eta)$ for various $\Omega_{1}$.

DownLoad: Full-Size Img PowerPoint

As the Brownian motion factor $\Omega_{2}$ increases, Figure 9 illustrates the smooth plotting of unique profiles for $\phi(\eta)$ and $\theta(\eta)$. The Brownian motion factor represents the degree of random motion exhibited by particles suspended in a fluid due to their collisions with the fluid molecules. It is calculated based on the ratio of the thermal energy of the fluid to the binding energy of the particle and is influenced by various factors such as the particle size, fluid viscosity, and temperature. When the Brownian motion factor is increased, it results in improvements in both the temperature distribution $\theta(\eta)$ and the thermal boundary layer thickness. Additionally, as the cumulative Brownian motion factor increases, the concentration profiles $\phi(\eta)$ demonstrate a decreasing trend throughout the boundary layer. Physically, an increase in the Brownian motion parameter causes nanoparticles to collide randomly, making it difficult for them to adhere to a surface. As a result, the concentration of the nanofluid over the sensor surface decreases due to the increased likelihood of the fluid flow carrying away the nanoparticles. Additionally, the increased Brownian motion can cause the nanoparticles to clump together, further reducing the concentration of the nanofluid on the surface.

Figure 9.  (a) $\theta(\eta)$ for various $\Omega_{2}$, (b) $\phi(\eta)$ for various $\Omega_{2}$.

DownLoad: Full-Size Img PowerPoint

It has become essential to calculate the local Nusselt number $Nu_{x}Re_{x}^{\frac{-1}{2}}$, the local skin friction coefficient $Cf_{x}Re_{x}^{\frac{1}{2}}$, and the local Sherwood number $Sh_{x}Re_{x}^{\frac{-1}{2}}$, as they play a crucial role in analyzing and predicting the mechanism of heat transfer and fluid flow properties in various engineering and practical applications. It is evident from Table 2 that the Sherwood number experiences a notable increase when the squeezed flow index parameter, surface permeable velocity parameter, viscosity parameter, Eckert number, and thermophoresis parameter are high. Furthermore, the skin-friction coefficient is heightened when the magnetic parameter, surface permeable velocity parameter, and viscosity parameter are increased, while it decreases with an increase in the squeezed flow index parameter, thermophoresis parameter, Eckert number, Brownian motion factor, and thermal conductivity parameter. Moreover, the local Nusselt number demonstrates an increase when the magnetic parameter, squeezed flow index parameter, surface permeable velocity parameter, and viscosity parameter are higher. Conversely, the opposite trend is observed for the Brownian motion factor, thermophoresis parameter, and thermal conductivity parameter.

Table 2.  Values of $Cf_{x}Re_{x}^{\frac{1}{2}}$, $Nu_{x}Re_{x}^{\frac{-1}{2}}$ and $Sh_{x}Re_{x}^{\frac{-1}{2}}$ for different values of $M, \beta, f_{0}, \alpha,$ $Ec, \varepsilon, \Omega_{1}$ and $\Omega_{2}$ with $\lambda = 0.1, Pr = 1.0$ and $Le = 1.0$.

$M$	$\beta$	$f_{0}$	$\alpha$	$Ec$	$\varepsilon$	$\Omega_{1}$	$\Omega_{2}$	$Cf_{x}Re_{x}^{\frac{1}{2}}$	$Nu_{x}Re_{x}^{\frac{-1}{2}}$	$Sh_{x}Re_{x}^{\frac{-1}{2}}$
0.0	0.2	-0.1	0.2	0.1	0.2	0.2	0.8	1.60681	0.555231	0.953794
1.0	0.2	-0.1	0.2	0.1	0.2	0.2	0.8	2.04882	0.567370	0.989996
2.0	0.2	-0.1	0.2	0.1	0.2	0.2	0.8	2.41017	0.574084	1.015211
0.5	0.1	-0.1	0.2	0.1	0.2	0.2	0.8	1.86062	0.539387	0.942278
0.5	0.5	-0.1	0.2	0.1	0.2	0.2	0.8	1.77448	0.627278	1.062850
0.5	1.0	-0.1	0.2	0.1	0.2	0.2	0.8	1.64924	0.726166	1.198831
0.5	0.2	-0.25	0.2	0.1	0.2	0.2	0.8	2.00011	0.609939	1.064171
0.5	0.2	-0.5	0.2	0.1	0.2	0.2	0.8	2.29167	0.694423	1.223310
0.5	0.2	-1.0	0.2	0.1	0.2	0.2	0.8	3.00855	0.880711	1.571051
0.5	0.2	-0.1	0.0	0.1	0.2	0.2	0.8	1.71891	0.678709	1.203792
0.5	0.2	-0.1	0.5	0.1	0.2	0.2	0.8	3.57039	0.718533	1.254370
0.5	0.2	-0.1	1.0	0.1	0.2	0.2	0.8	7.74593	0.759392	1.303873
0.5	0.2	-0.1	0.2	0.0	0.2	0.2	0.8	1.85851	0.608174	0.963431
0.5	0.2	-0.1	0.2	1.0	0.2	0.2	0.8	1.68490	0.150477	1.065832
0.5	0.2	-0.1	0.2	1.5	0.2	0.2	0.8	1.60477	0.015932	1.116160
0.5	0.2	-0.1	0.2	0.2	0.0	0.2	0.8	1.83422	0.543631	0.980312
0.5	0.2	-0.1	0.2	0.2	0.5	0.2	0.8	1.80821	0.484172	0.987527
0.5	0.2	-0.1	0.2	0.2	1.0	0.2	0.8	1.79093	0.444591	0.991261
0.5	0.2	-0.1	0.2	0.2	0.2	0.0	0.8	1.83528	0.547993	0.993013
0.5	0.2	-0.1	0.2	0.2	0.2	0.5	0.8	1.80463	0.473064	0.989301
0.5	0.2	-0.1	0.2	0.2	0.2	0.8	0.8	1.78897	0.434671	1.012320
0.5	0.2	-0.1	0.2	0.2	0.2	0.2	0.5	1.85265	0.591249	0.954547
0.5	0.2	-0.1	0.2	0.2	0.2	0.2	0.8	1.82228	0.516321	0.983858
0.5	0.2	-0.1	0.2	0.2	0.2	0.2	1.5	1.76475	0.372196	1.002912

---

 | Show Table

DownLoad: CSV

5.   Conclusions

The novel aspect of this paper is that it examines the flow of the Maxwell squeezed nanofluid over a sensor surface, taking into account the impacts of both an external magnetic field and viscous dissipation. Based on this discussion, several conclusions can be drawn. The presence of the magnetic field affects the momentum equation, while the dissipation phenomenon affects the temperature field. By applying suitable similarity transformations, the governing set of nonlinear partial differential equations that characterize the problem are converted into a system of nonlinear ordinary differential equations. Subsequently, the technique of numerical shooting is employed to solve the transformed equations. MATHEMATICA software is used to graphically and tabularly analyze the flow behavior of velocity, concentration, skin friction, temperature, and heat mass transfer rate. Below are the key findings of the model:

$1)$ For dominant magnetic parameter, surface permeable velocity parameter, and variable viscosity parameter values, there is an increase in the velocity field.

$2)$ The thermophoresis parameter shows an increase in the concentration field, while the squeezed flow index parameter and the Eckert number exhibit the opposite trend.

$3)$ The magnetic parameter, viscosity parameter, and squeezed flow index parameter are all positively related to the local Nusselt number, resulting in an increasing function.

$4)$ The skin friction coefficient exhibits similar behavior with respect to the magnetic number, surface permeable velocity parameter, and viscosity parameter.

$5)$ The Brownian motion factor has opposite effects on the concentration and temperature of the squeezed nanofluid flow.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We would like to extend our sincere gratitude and appreciation to the anonymous reviewers for dedicating their time and effort in conducting a comprehensive review of our paper. Their valuable comments and constructive feedback have undoubtedly played a pivotal role in enhancing the quality of our work.

Conflict of interest

The authors declare that they have no competing interests.