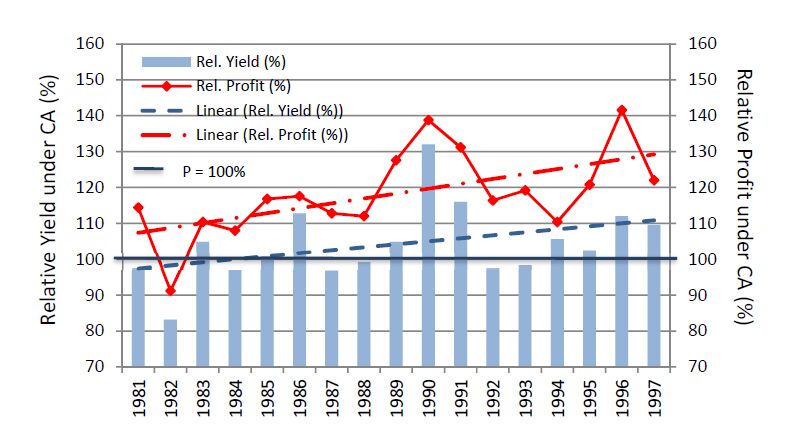
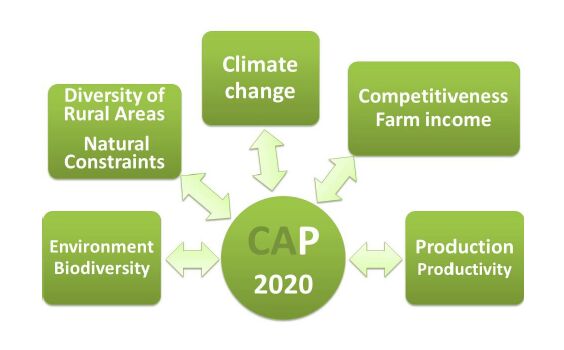
Conservation Agriculture and its contribution to the achievement of agri-environmental and economic challenges in Europe

Emilio J. González-Sánchez; Amir Kassam; Gottlieb Basch; Bernhard Streit; Antonio Holgado-Cabrera; Paula Triviño-Tarradas; Emilio J. González-Sánchez; Amir Kassam; Gottlieb Basch; Bernhard Streit; Antonio Holgado-Cabrera; Paula Triviño-Tarradas

doi:10.3934/agrfood.2016.4.387

AIMS Agriculture and Food

2016, Volume 1, Issue 4: 387-408. doi: 10.3934/agrfood.2016.4.387

Previous Article Next Article

Review Special Issues

Conservation Agriculture and its contribution to the achievement of agri-environmental and economic challenges in Europe

Emilio J. González-Sánchez ^{1,2,3
,
,},
Amir Kassam ^2,4,
Gottlieb Basch ^2,5,
Bernhard Streit ⁶,
Antonio Holgado-Cabrera ²,
Paula Triviño-Tarradas ^1,2

1.
ETSIAM, Universidad de Córdoba, Spain
2.
European Conservation Agriculture Federation (ECAF), Belgium
3.
Asociación Española Agricultura de Conservación. Suelos Vivos (AEAC.SV), Spain
4.
Reading University, UK
5.
Institute of Mediterranean Agricultural and Environmental Sciences (ICAAM), University of Evora, Portugal
6.
Bern University of Applied Sciences, School of Agricultural, Forest and Food Sciences, Switzerland

Received: 07 July 2016 Accepted: 08 October 2016 Published: 17 October 2016

Conservation Agriculture is an ecosystem approach to farming capable of providing solutions for numerous of the agri-environmental concerns in Europe. Certainly, most of the challenges addressed in the Common Agriculture Policy (CAP) could be tackled through Conservation Agriculture (CA). Not only the agri-environmental ones, but also those concerning farmer and rural communities’ prosperity. The optimisation of inputs and similar yields than conventional tillage, make Conservation Agriculture a profitable system compared to the tillage based agriculture. Whereas this sustainable agricultural system was conceived for protecting agrarian soils from its degradation, the numerous collateral benefits that emanate from soil conservation, i.e., climate change mitigation and adaptation, have raised Conservation Agriculture as one of the global emerging agrosciences, being adopted by an increasing number of farmers worldwide, including Europe.

Keywords:

Citation: Emilio J. González-Sánchez, Amir Kassam, Gottlieb Basch, Bernhard Streit, Antonio Holgado-Cabrera, Paula Triviño-Tarradas. Conservation Agriculture and its contribution to the achievement of agri-environmental and economic challenges in Europe[J]. AIMS Agriculture and Food, 2016, 1(4): 387-408. doi: 10.3934/agrfood.2016.4.387

Related Papers:

[1]	Muhammad Asim, Ghada AlNemer . Boundedness on variable exponent Morrey-Herz space for fractional multilinear Hardy operators. AIMS Mathematics, 2025, 10(1): 117-136. doi: 10.3934/math.2025007
[2]	Jie Sun, Jiamei Chen . Weighted estimates for commutators associated to singular integral operator satisfying a variant of Hörmander's condition. AIMS Mathematics, 2023, 8(11): 25714-25728. doi: 10.3934/math.20231311
[3]	Kieu Huu Dung, Do Lu Cong Minh, Pham Thi Kim Thuy . Commutators of Hardy-Cesàro operators on Morrey-Herz spaces with variable exponents. AIMS Mathematics, 2022, 7(10): 19147-19166. doi: 10.3934/math.20221051
[4]	Yueping Zhu, Yan Tang, Lixin Jiang . Boundedness of multilinear Calderón-Zygmund singular operators on weighted Lebesgue spaces and Morrey-Herz spaces with variable exponents. AIMS Mathematics, 2021, 6(10): 11246-11262. doi: 10.3934/math.2021652
[5]	Wanjing Zhang, Suixin He, Jing Zhang . Boundedness of sublinear operators on weighted grand Herz-Morrey spaces. AIMS Mathematics, 2023, 8(8): 17381-17401. doi: 10.3934/math.2023888
[6]	Babar Sultan, Mehvish Sultan, Qian-Qian Zhang, Nabil Mlaiki . Boundedness of Hardy operators on grand variable weighted Herz spaces. AIMS Mathematics, 2023, 8(10): 24515-24527. doi: 10.3934/math.20231250
[7]	Javeria Younas, Amjad Hussain, Hadil Alhazmi, A. F. Aljohani, Ilyas Khan . BMO estimates for commutators of the rough fractional Hausdorff operator on grand-variable-Herz-Morrey spaces. AIMS Mathematics, 2024, 9(9): 23434-23448. doi: 10.3934/math.20241139
[8]	Ming Liu, Bin Zhang, Xiaobin Yao . Weighted variable Morrey-Herz space estimates for $m$ th order commutators of $n-$ dimensional fractional Hardy operators. AIMS Mathematics, 2023, 8(9): 20063-20079. doi: 10.3934/math.20231022
[9]	Shuhui Yang, Yan Lin . Multilinear strongly singular integral operators with generalized kernels and applications. AIMS Mathematics, 2021, 6(12): 13533-13551. doi: 10.3934/math.2021786
[10]	Naqash Sarfraz, Muhammad Aslam . Some weighted estimates for the commutators of $p$ -adic Hardy operator on two weighted $p$ -adic Herz-type spaces. AIMS Mathematics, 2021, 6(9): 9633-9646. doi: 10.3934/math.2021561

Abstract

1. Introduction and notations

Let $T$ be the Calderón-Zygmund singular integral operator and $b$ be a locally integrable function on $R^n$ . The commutator generated by $b$ and $T$ is defined by $[b, T]f = bT(f)-T(bf)$ . The investigation of the commutator begins with Coifman-Rochberg-Weiss pioneering study and classical result (see ^[6]). The classical result of Coifman, Rochberg and Weiss (see ^[6]) states that the commutator $[b, T]f = T(bf)-bTf$ is bounded on $L^p(R^n)$ for $1 < p < \infty$ if and only if $b\in BMO(R^n)$ . The major reason for considering the problem of commutators is that the boundedness of commutator can produces some characterizations of function spaces (see ^[1,6]). Chanillo (see ^[1]) proves a similar result when $T$ is replaced by the fractional integral operator. In ^[11], the boundedness properties of the commutators for the extreme values of $p$ are obtained. In recent years, the theory of Herz space and Herz type Hardy space, as a local version of Lebesgue space and Hardy space, have been developed (see ^[8,9,12,13]). The main purpose of this paper is to establish the endpoint continuity properties of some multilinear operators related to certain non-convolution type fractional singular integral operators on Herz and Herz type Hardy spaces.

First, let us introduce some notations (see ^{[8,9,10,12,13,15]}). Throughout this paper, $Q$ will denote a cube of $R^n$ with sides parallel to the axes. For a cube $Q$ and a locally integrable function $f$ , let $f_Q = |Q|^{-1}\int_Qf(x)dx$ and $f^{\#}(x) = \sup\limits_{Q\ni x}|Q|^{-1}\int_Q|f(y)-f_Q|dy$ . Moreover, $f$ is said to belong to $BMO(R^n)$ if $f^{\#} \in L^\infty$ and define $||f||_{BMO} = ||f^{\#}||_{L^\infty}$ ; We also define the central $BMO$ space by $CMO(R^n)$ , which is the space of those functions $f\in L_{loc}(R^n)$ such that

$||f||_{CMO} = \sup\limits_{r > 1}|Q(0, r)|^{-1}\int_Q|f(y)-f_Q|dy < \infty.$

It is well-known that (see ^[9,10])

$||f||_{CMO}\approx\sup\limits_{r > 1}\inf\limits_{c\in C}|Q(0, r)|^{-1}\int_Q|f(x)-c|dx.$

For $k\in Z$ , define $B_k = \{x\in R^n: |x|\le 2^k\}$ and $C_k = B_k\setminus B_{k-1}$ . Denote by $\chi_k$ the characteristic function of $C_k$ and $\tilde\chi_k$ the characteristic function of $C_k$ for $k\ge1$ and $\tilde\chi_0$ the characteristic function of $B_0$ .

Definition 1. Let $0 < p < \infty$ and $\alpha\in R$ .

(1) The homogeneous Herz space $\dot K_p^\alpha(R^n)$ is defined by

$\dot K_p^\alpha(R^n) = \{f\in L_{loc}^p (R^n \setminus \{0\}): ||f||_{\dot K_p^\alpha} < \infty\},$

where

$||f||_{\dot K_p^\alpha} = \sum\limits_{k = -\infty}^\infty 2^{k\alpha}||f\chi_k||_{L^p};$

(2) The nonhomogeneous Herz space $K_p^\alpha(R^n)$ is defined by

$K_p^\alpha(R^n) = \{f\in L_{loc}^p (R^n): ||f||_{K_p^\alpha} < \infty\},$

where

$||f||_{K_p^\alpha} = \sum\limits_{k = 0}^\infty 2^{k\alpha}||f\tilde\chi_k||_{L^p}.$

If $\alpha = n(1-1/p)$ , we denote that $\dot K_p^\alpha(R^n) = \dot K_p(R^n)$ , $K_p^\alpha(R^n) = K_p(R^n)$ .

Definition 2. Let $0 < \delta < n$ and $1 < p < n/\delta$ . We shall call $B_p^{\delta}(R^n)$ the space of those functions $f$ on $R^n$ such that

$||f||_{B_p^{\delta}} = \sup\limits_{d > 1}d^{-n(1/p-\delta/n)}||f\chi_{Q(0, d)}||_{L^p} < \infty.$

Definition 3. Let $1 < p < \infty$ .

(1) The homogeneous Herz type Hardy space $H \dot K_p(R^n)$ is defined by

$H \dot K_p(R^n) = \{f\in S'(R^n): G(f)\in \dot K_p(R^n)\},$

where

$||f||_{H\dot K_p} = ||G(f)||_{\dot K_p}.$

(2) The nonhomogeneous Herz type Hardy space $HK_p(R^n)$ is defined by

$HK_p(R^n) = \{f\in S'(R^n): G(f)\in K_p(R^n)\},$

where

$||f||_{HK_p} = ||G(f)||_{K_p}.$

where $G(f)$ is the grand maximal function of $f$ .

The Herz type Hardy spaces have the atomic decomposition characterization.

Definition 4. Let $1 < p < \infty$ . A function $a(x)$ on $R^n$ is called a central $(n(1-1/p), p)$ -atom (or a central $(n(1-1/p), p)$ -atom of restrict type), if

1) Supp $a\subset B(0, d)$ for some $d > 0$ (or for some $d\ge 1$ ),

2) $||a||_{L^p}\le |B(0, d)|^{1/p-1}$ ,

3) $\int a(x)dx = 0$ .

Lemma 1. (see ^[9,13]) Let $1 < p < \infty$ . A temperate distribution $f$ belongs to $H\dot K_p(R^n)$ (or $HK_p(R^n)$ ) if and only if there exist central $(n(1-1/p), p)$ -atoms(or central $(n(1-1/p), p)$ -atoms of restrict type) $a_j$ supported on $B_j = B(0, 2^j)$ and constants $\lambda_j$ , $\sum_j|\lambda_j| < \infty$ such that $f = \sum_{j = -\infty}^\infty \lambda_ja_j$ (or $f = \sum_{j = 0}^\infty \lambda_j a_j$ )in the $S'(R^n)$ sense, and

$||f||_{H\dot K_p}(\ or \ ||f||_{HK_p})\approx\sum\limits_j|\lambda_j|.$

2. Theorems

In this paper, we will consider a class of multilinear operators related to some non-convolution type singular integral operators, whose definition are following.

Let $m$ be a positive integer and $A$ be a function on $R^n$ . We denote that

$R_{m+1}(A;x, y) = A(x)-\sum\limits_{|\beta|\le m}\frac{1}{\beta!}D^\beta A(y)(x-y)^\beta$

and

$Q_{m+1}(A;x, y) = R_m(A;x, y)-\sum\limits_{|\beta| = m}\frac{1}{\beta!}D^\beta A(x)(x-y)^\beta.$

Definition 5. Fixed $\varepsilon > 0$ and $0 < \delta < n$ . Let $T_\delta : S\to S'$ be a linear operator. $T_\delta$ is called a fractional singular integral operator if there exists a locally integrable function $K(x, y)$ on $R^n \times R^n$ such that

$T_\delta(f)(x) = \int_{R^n} K(x, y)f(y)dy$

for every bounded and compactly supported function $f$ , where $K$ satisfies:

$|K(x, y)|\le C|x-y|^{-n+\delta}$

and

$|K(y, x)-K(z, x)|+|K(x, y)-K(x, z)|\le C|y-z|^\varepsilon|x-z|^{-n-\varepsilon+\delta}$

if $2|y-z|\le |x-z|$ . The multilinear operator related to the fractional singular integral operator $T_\delta$ is defined by

$T_\delta^A(f)(x) = \int_{R^n}\frac{R_{m+1}(A;x, y)}{|x-y|^m}K(x, y)f(y)dy;$

We also consider the variant of $T_\delta^A$ , which is defined by

$\tilde T_\delta^A(f)(x) = \int_{R^n}\frac{Q_{m+1}(A;x, y)}{|x-y|^m}K(x, y)f(y)dy.$

Note that when $m = 0$ , $T_\delta^A$ is just the commutators of $T_\delta$ and $A$ (see ^[1,6,11,14]). It is well known that multilinear operator, as a non-trivial extension of commutator, is of great interest in harmonic analysis and has been widely studied by many authors (see ^[3,4,5]). In ^[7], the weighted $L^p$ ( $p > 1$ )-boundedness of the multilinear operator related to some singular integral operator are obtained. In ^[2], the weak ( $H^1$ , $L^1$ )-boundedness of the multilinear operator related to some singular integral operator are obtained. In this paper, we will study the endpoint continuity properties of the multilinear operators $T_\delta^A$ and $\tilde T_\delta^A$ on Herz and Herz type Hardy spaces.

Now we state our results as following.

Theorem 1. Let $0 < \delta < n$ , $1 < p < n/\delta$ and $D^\beta A\in BMO(R^n)$ for all $\beta$ with $|\beta| = m$ . Suppose that $T_\delta^A$ is the same as in Definition 5 such that $T_\delta$ is bounded from $L^p(R^n)$ to $L^q(R^n)$ for any $p, q\in (1, +\infty]$ with $1/q = 1/p-\delta/n$ . Then $T_\delta^A$ is bounded from $B_p^{\delta}(R^n)$ to $CMO(R^n)$ .

Theorem 2. Let $0 < \delta < n$ , $1 < p < n/\delta$ , $1/q = 1/p-\delta/n$ and $D^\beta A\in BMO(R^n)$ for all $\beta$ with $|\beta| = m$ . Suppose that $\tilde T_\delta^A$ is the same as in Definition 5 such that $\tilde T_\delta^A$ is bounded from $L^p(R^n)$ to $L^q(R^n)$ for any $p, q\in (1, +\infty)$ with $1/q = 1/p-\delta/n$ . Then $\tilde T_\delta^A$ is bounded from $H\dot K_p(R^n)$ to $\dot K_q^\alpha(R^n)$ with $\alpha = n(1-1/p)$ .

Theorem 3. Let $0 < \delta < n$ , $1 < p < n/\delta$ and $D^\beta A\in BMO(R^n)$ for all $\beta$ with $|\beta| = m$ . Suppose that $\tilde T_\delta^A$ is the same as in Definition 5 such that $\tilde T_\delta^A$ is bounded from $L^p(R^n)$ to $L^q(R^n)$ for any $p, q\in (1, +\infty)$ with $1/q = 1/p-\delta/n$ . Then the following two statements are equivalent:

(ⅰ) $\tilde T_\delta^A$ is bounded from $B_p^{\delta}(R^n)$ to $CMO(R^n)$ ;

(ⅱ) for any cube $Q$ and $z\in 3Q\setminus 2Q$ , there is

$\frac{1}{|Q|}\int_Q\left|\sum\limits_{|\beta| = m}\frac{1}{\beta!}|D^\beta A(x)-(D^\beta A)_Q| \int_{(4Q)^c}K_{\beta}(z, y)f(y)dy\right|dx\le C||f||_{B_p^{\delta}},$

where $K_{\beta}(z, y) = \frac{(z-y)^\beta}{|z-y|^m}K(z, y)$ for $|\beta| = m$ .

Remark. Theorem 2 is also hold for nonhomogeneous Herz and Herz type Hardy space.

3. Proofs of theorems

To prove the theorem, we need the following lemma.

Lemma 2. (see ^[5]) Let $A$ be a function on $R^n$ and $D^\beta A\in L^q(R^n)$ for $|\beta| = m$ and some $q > n$ . Then

$|R_m(A;x, y)|\le C|x-y|^m\sum\limits_{|\beta| = m}\left(\frac{1}{|\tilde Q(x, y)|}\int_{\tilde Q(x, y)}|D^\beta A(z)|^q dz\right)^{1/q},$

where $\tilde Q(x, y)$ is the cube centered at $x$ and having side length $5\sqrt{n}|x-y|$ .

Proof of Theorem 1. It suffices to prove that there exists a constant $C_Q$ such that

$\frac{1}{|Q|}\int_Q|T_\delta^A(f)(x)-C_Q|dx \le C||f||_{B_p^{\delta}}$

holds for any cube $Q = Q(0, d)$ with $d > 1$ . Fix a cube $Q = Q(0, d)$ with $d > 1$ . Let $\tilde Q = 5\sqrt{n}Q$ and $\tilde A(x) = A(x)-\sum\limits_{|\beta| = m}\frac{1}{\beta!}(D^\beta A)_{\tilde Q}x^\beta$ , then $R_{m+1}(A; x, y) = R_{m+1}(\tilde A; x, y)$ and $D^\beta\tilde A = D^\beta A-(D^\beta A)_{\tilde Q}$ for all $\beta$ with $|\beta| = m$ . We write, for $f_1 = f\chi_{\tilde Q}$ and $f_2 = f\chi_{R^n\setminus\tilde Q}$ ,

$\begin{eqnarray*} T_\delta^A(f)(x)& = &\int_{R^n}\frac{R_{m+1}(\tilde A; x, y)}{|x-y|^m}K(x, y)f(y)dy = \int_{R^n}\frac{R_m(\tilde A; x, y)}{|x-y|^m}K(x, y)f_1(y)dy \\ &\;& -\sum\limits_{|\beta| = m}\frac{1}{\beta!}\int_{R^n}\frac{K(x, y)(x-y)^\beta}{|x-y|^m}D^\beta\tilde A(y)f_1(y)dy +\int_{R^n}\frac{R_{m+1}(\tilde A; x, y)}{|x-y|^m}K(x, y)f_2(y)dy, \end{eqnarray*}$

then

$\begin{eqnarray*} &\;& \frac{1}{|Q|}\int_Q\left|T_\delta^A(f)(x)-T_\delta^{\tilde A}(f_2)(0)\right|dx \le\frac{1}{|Q|}\int_Q\left|T_\delta\left(\frac{R_m(\tilde A;x, \cdot)}{|x-\cdot|^m}f_1\right)(x)\right|dx \\ &\;& +\sum\limits_{|\beta| = m}\frac{1}{\beta!}\frac{1}{|Q|}\int_Q\left|T_\delta\left(\frac{(x-\cdot)^\beta} {|x-\cdot|^m}D^\beta\tilde A f_1\right)(x)\right|dx+\left|T_\delta^{\tilde A}(f_2)(x)-T_\delta^{\tilde A}(f_2)(0)\right|dx \\ &: = & I+II+III. \end{eqnarray*}$

For $I$ , note that for $x\in Q$ and $y\in \tilde Q$ , using Lemma 2, we get

$R_m(\tilde A; x, y)\le C|x-y|^m\sum\limits_{|\beta| = m}||D^\beta A||_{BMO},$

thus, by the $L^p(R^n)$ to $L^q(R^n)$ -boundedness of $T_\delta^A$ for $1 < p, q < \infty$ with $1/q = 1/p-\delta/n$ , we get

$\begin{eqnarray*} I &\le& \frac{C}{|Q|}\int_Q \left|T_\delta\left(\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}f_1\right)(x)\right|dx \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\left(\frac{1}{|Q|}\int_Q|T_\delta(f_1)(x)|^qdx\right)^{1/q} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}|Q|^{-1/q}||f_1||_{L^p} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}r^{-n(1/p-\delta/n)}||f\chi_{\tilde Q}||_{L^p} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}||f||_{B_p^{\delta}}. \end{eqnarray*}$

For $II$ , taking $1 < s < p$ such that $1/r = 1/s-\delta/n$ , by the $(L^s, L^r)$ -boundedness of $T_\delta$ and Holder's inequality, we gain

$\begin{eqnarray*} II &\le& \frac{C}{|Q|}\int_Q \left|T_\delta\left(\sum\limits_{|\beta| = m}(D^\beta A-(D^\beta A)_{\tilde Q})f_1\right)(x)\right|dx \\ &\le& C\sum\limits_{|\beta| = m}\left(\frac{1}{|Q|}\int_Q\left|T_\delta\left((D^\beta A-(D^\beta A)_{\tilde Q}\right)f_1)(x)\right|^rdx\right)^{1/r} \\ &\le& C|Q|^{-1/r}\sum\limits_{|\beta| = m}||(D^\beta A-(D^\beta A)_{\tilde Q})f_1||_{L^s} \\ &\le& C|Q|^{-1/r}||f_1||_{L^p}\sum\limits_{|\beta| = m}\left(\frac{1}{|Q|}\int_{\tilde Q} |D^\beta A(y)-(D^\beta A)_{\tilde Q}|^{ps/(p-s)}dy\right)^{(p-s)/(ps)}|Q|^{(p-s)/(ps)} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}r^{-n/q}||f\chi_{\tilde Q}||_{L^p} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}||f||_{B_p^{\delta}}. \end{eqnarray*}$

To estimate $III$ , we write

$\begin{eqnarray*} T_\delta^{\tilde A}(f_2)(x)-T_\delta^{\tilde A}(f_2)(0)& = &\int_{R^n}\left[\frac{K(x, y)}{|x-y|^m}-\frac{K(0, y)}{|y|^m}\right]R_m(\tilde A;x, y)f_2(y)dy \\ &\;& +\int_{R^n}\frac{K(0, y)f_2(y)}{|y|^m}[R_m(\tilde A; x, y)-R_m(\tilde A; 0, y)]dy \\ &\;& -\sum\limits_{|\beta| = m}\frac{1}{\beta!}\int_{R^n}\left(\frac{K(x, y)(x-y)^\beta}{|x-y|^m}-\frac{K(0, y)(-y)^\beta}{|y|^m}\right)D^\beta\tilde A(y)f_2(y)dy \\ &: = & III_1+III_2+III_3. \end{eqnarray*}$

By Lemma 2 and the following inequality (see ^[15])

$|b_{Q_1}-b_{Q_2}|\le C\log(|Q_2|/|Q_1|)||b||_{BMO} \ for \ Q_1 \subset Q_2,$

we know that, for $x\in Q$ and $y\in 2^{k+1}\tilde Q\setminus 2^k\tilde Q$ ,

$\begin{eqnarray*} |R_m(\tilde A;x, y)|&\le& C|x-y|^m\sum\limits_{|\beta| = m}(||D^\beta A||_{BMO}+|(D^\beta A)_{\tilde Q(x, y)}-(D^\beta A)_{\tilde Q}|) \\ &\le& C k|x-y|^m\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}. \end{eqnarray*}$

Note that $|x-y|\sim |y|$ for $x\in Q$ and $y\in R^n\setminus\tilde Q$ , we obtain, by the condition of $K$ ,

$\begin{eqnarray*} |III_1|&\le& C\int_{R^n}\left(\frac{|x|}{|y|^{m+n+1-\delta}}+\frac{|x|^\varepsilon} {|y|^{m+n+\varepsilon-\delta}}\right)|R_m(\tilde A; x, y)||f_2(y)|dy \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{k = 0}^\infty\int_{2^{k+1}\tilde Q\setminus2^k\tilde Q}k\left(\frac{|x|} {|y|^{n+1-\delta}}+\frac{|x|^\varepsilon}{|y|^{n+\varepsilon-\delta}}\right)|f(y)|dy \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{k = 1}^\infty k(2^{-k}+2^{-\varepsilon k})(2^k r)^{-n(1/p-\delta/n)}||f\chi_{2^k\tilde Q}||_{L^p} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{k = 1}^\infty k(2^{-k}+2^{-\varepsilon k})||f||_{B_p^{\delta}} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}||f||_{B_p^{\delta}}. \end{eqnarray*}$

For $III_2$ , by the formula (see ^[5]):

$R_m(\tilde A; x, y)-R_m(\tilde A; x_0, y) = \sum\limits_{|\gamma| < m}\frac{1}{\gamma!}R_{m-|\gamma|}(D^\gamma\tilde A; x, x_0)(x-y)^\gamma$

and Lemma 2, we have

$|R_m(\tilde A; x, y)-R_m(\tilde A; x_0, y)|\le C\sum\limits_{|\gamma| < m}\sum\limits_{|\beta| = m}|x-x_0|^{m-|\gamma|}|x-y|^{|\gamma|}||D^\beta A||_{BMO},$

thus, similar to the estimates of $III_1$ , we get

$|III_2| \le C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{k = 0}^\infty\int_{2^{k+1}\tilde Q\setminus2^k\tilde Q} \frac{|x|}{|y|^{n+1-\delta}}|f(y)|dy \le C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}||f||_{B_p^{\delta}}.$

For $III_3$ , by Holder's inequality, similar to the estimates of $III_1$ , we get

$\begin{eqnarray*} |III_3|&\le&C\sum\limits_{|\beta| = m}\sum\limits_{k = 0}^\infty\int_{2^{k+1}\tilde Q\setminus2^k\tilde Q}\left(\frac{|x|} {|y|^{n+1-\delta}}+\frac{|x|^\varepsilon}{|y|^{n+\varepsilon-\delta}}\right)|D^\beta \tilde A(y)||f(y)|dy \\ &\le& C\sum\limits_{|\beta| = m}\sum\limits_{k = 1}^\infty (2^{-k}+2^{-\varepsilon k})(2^k r)^{-n(1/p-\delta/n)} \left(|2^k\tilde Q|^{-1}\int_{2^k\tilde Q}|D^\beta A(y)-(D^\beta A)_{\tilde Q}|^{p'}dy\right)^{1/p'}||f\chi_{2^k\tilde Q}||_{L^p} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{k = 1}^\infty (2^{-k}+2^{-\varepsilon k})(2^k r)^{-n(1/p-\delta/n)} ||f\chi_{2^k\tilde Q}||_{L^p} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}||f||_{B_p^{\delta}}. \end{eqnarray*}$

Thus

$III\le C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}||f||_{B_p^{\delta}},$

which together with the estimates for $I$ and $II$ yields the desired result. This finishes the proof of Theorem 1.

Proof of Theorem 2. Let $f\in H\dot K_p(R^n)$ , by Lemma 1, $f = \sum_{j = -\infty}^\infty\lambda_ja_j$ , where $a_j's$ are the central $(n(1-1/p), p)$ -atom with supp $a_j \subset B_j = B(0, 2^j)$ and $||f||_{H\dot K_p}\approx\sum_j|\lambda_j|$ . We write

$\begin{eqnarray*} ||\tilde T_\delta^A(f)||_{\dot K_q^\alpha}& = &\sum\limits_{k = -\infty}^\infty 2^{kn(1-1/p)}||\chi_k\tilde T_\delta^A(f)||_{L^q} \\ &\le&\sum\limits_{k = -\infty}^\infty 2^{kn(1-1/p)}\sum\limits_{j = -\infty}^{k-1}|\lambda_j|||\chi_k\tilde T_\delta^A(a_j)||_{L^q} +\sum\limits_{k = -\infty}^\infty 2^{kn(1-1/p)}\sum\limits_{j = k}^\infty|\lambda_j|||\chi_k\tilde T_\delta^A(a_j)||_{L^q} \\ & = & J+JJ. \end{eqnarray*}$

For $JJ$ , by the $(L^p, L^q)$ -boundedness of $\tilde T_\delta^A$ for $1/q = 1/p-\delta/n$ , we get

$\begin{eqnarray*} JJ &\le& C\sum\limits_{k = -\infty}^\infty 2^{kn(1-1/p)}\sum\limits_{j = k}^\infty|\lambda_j|||a_j||_{L^p}\le C\sum\limits_{k = -\infty}^\infty 2^{kn(1-1/p)}\sum\limits_{j = k}^\infty|\lambda_j|2^{jn(1/p-1)} \\ &\le& C\sum\limits_{j = -\infty}^\infty|\lambda_j|\sum\limits_{k = -\infty}^j2^{(k-j)n(1-1/p)}\le C\sum\limits_{j = -\infty}^\infty|\lambda_j|\le C||f||_{H\dot K_p}. \end{eqnarray*}$

To obtain the estimate of $J$ , we denote that $\tilde A(x) = A(x)-\sum_{|\beta| = m}\frac{1}{\beta!}(D^\beta A)_{2B_j}x^\beta$ . Then $Q_m(A; x, y) = Q_m(\tilde A; x, y)$ and $Q_{m+1}(A; x, y) = R_m(A; x, y)-\sum_{|\beta| = m}\frac{1}{\beta!} (x-y)^\beta D^\beta A(x)$ . We write, by the vanishing moment of $a$ and for $x \in C_k$ with $k\ge j+1$ ,

$\begin{eqnarray*} \tilde T_\delta^A(a_j)(x)& = & \int_{R^n}\frac{K(x, y)R_m(A;x, y)}{|x-y|^m}a_j(y)dy-\sum\limits_{|\beta| = m}\frac{1}{\beta!} \int_{R^n}\frac{K(x, y)D^\beta\tilde A(x)(x-y)^\beta}{|x-y|^m}a_j(y)dy \\ & = & \int_{R^n}\left[\frac{K(x, y)}{|x-y|^m}-\frac{K(x, 0)}{|x|^m}\right]R_m(\tilde A;x, y)a_j(y)dy \\ &\;& +\int_{R^n}\frac{K(x, 0)}{|x|^m}[R_m(\tilde A;x, y)-R_m(\tilde A; x, 0)]a_j(y)dy \\ &\;& -\sum\limits_{|\beta| = m}\frac{1}{\beta!}\int_{R^n}\left[\frac{K(x, y)(x-y)^\beta}{|x-y|^m}-\frac{K(x, 0)x^\beta}{|x|^m}\right] D^\beta\tilde A(x)a_j(y)dy. \end{eqnarray*}$

Similar to the proof of Theorem 1, we obtain

$\begin{eqnarray*} |\tilde T_\delta^A(a_j)(x)|&\le& C\int_{R^n}\left[\frac{|y|}{|x|^{m+n+1-\delta}}+\frac{|y|^\varepsilon}{|x|^{m+n+\varepsilon-\delta}}\right] |R_m(\tilde A; x, y)||a_j(y)|dy \\ &\;& +C\sum\limits_{|\beta| = m}\int_{R^n}\left[\frac{|y|}{|x|^{n+1-\delta}}+\frac{|y|^\varepsilon}{|x|^{n+\varepsilon-\delta}}\right]|D^\beta\tilde A(x)||a_j(y)|dy \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\left[\frac{2^j}{2^{k(n+1-\delta)}}+\frac{2^{j\varepsilon}} {2^{k(n+\varepsilon-\delta)}}\right]+C\sum\limits_{|\beta| = m}\left[\frac{2^j}{2^{k(n+1-\delta)}}+\frac{2^{j\varepsilon}} {2^{k(n+\varepsilon-\delta)}}\right]|D^\beta\tilde A(x)|, \end{eqnarray*}$

thus

$\begin{eqnarray*} J&\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{k = -\infty}^\infty 2^{kn(1-1/p)}\sum\limits_{j = -\infty}^{k-1}|\lambda_j| \left[\frac{2^j}{2^{k(n+1-\delta)}}+\frac{2^{j\varepsilon}}{2^{k(n+\varepsilon-\delta)}}\right]2^{kn/q} \\ &\;&+C\sum\limits_{|\beta| = m}\sum\limits_{k = -\infty}^\infty 2^{kn(1-1/p)}\sum\limits_{j = -\infty}^{k-1}|\lambda_j|\left[\frac{2^j}{2^{k(n+1-\delta)}} +\frac{2^{j\varepsilon}}{2^{k(n+\varepsilon-\delta)}}\right]\left(\int_{B_k}|D^\beta\tilde A(x)|^q dx \right)^{1/q} \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{k = -\infty}^\infty 2^{kn(1-\delta/n)}\sum\limits_{j = -\infty}^{k-1}|\lambda_j| \left[\frac{2^j}{2^{k(n+1-\delta)}}+\frac{2^{j\varepsilon}}{2^{k(n+\varepsilon-\delta)}}\right] \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{j = -\infty}^\infty|\lambda_j|\sum\limits_{k = j+1}^\infty[2^{j-k}+ 2^{(j-k)\varepsilon}] \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}\sum\limits_{j = -\infty}^\infty|\lambda_j| \\ &\le& C\sum\limits_{|\beta| = m}||D^\beta A||_{BMO}||f||_{H\dot K_p}. \end{eqnarray*}$

This completes the proof of Theorem 2.

Proof of Theorem 3. For any cube $Q = Q(0, r)$ with $r > 1$ , let $f \in B_p^{\delta}$ and $\tilde A(x) = A(x) -\sum\limits_{|\beta| = m}\frac{1}{\beta!}(D^\beta A)_{\tilde Q}x^\beta$ . We write, for $f = f\chi_{4Q}+f\chi_{(4Q)^c} = f_1+f_2$ and $z\in 3Q\setminus2Q$ ,

$\begin{eqnarray*} \tilde T_\delta^A(f)(x)& = &\tilde T_\delta^A(f_1)(x)+\int_{R^n}\frac{R_m(\tilde A; x, y)}{|x-y|^m}K(x, y)f_2(y)dy \\ &\;& -\sum\limits_{|\beta| = m}\frac{1}{\beta!}(D^\beta A(x)-(D^\beta A)_Q)(T_{\delta, \beta}(f_2)(x)-T_{\delta, \beta}(f_2)(z)) \\ &\;& -\sum\limits_{|\beta| = m}\frac{1}{\beta!}(D^\beta A(x)-(D^\beta A)_Q)T_{\delta, \beta}(f_2)(z) \\ & = & I_1(x)+I_2(x)+I_3(x, z)+I_4(x, z), \end{eqnarray*}$

where $T_{\delta, \beta}$ is the singular integral operator with the kernel $\frac{(x-y)^\beta}{|x-y|^m}K(x, y)$ for $|\beta| = m$ . Note that $(I_4(\cdot, z))_Q = 0$ , we have

$\tilde T_\delta^A(f)(x)-(\tilde T_\delta^A(f))_Q = I_1(x)-(I_1(\cdot))_Q+I_2(x)-I_2(z)-[I_2(\cdot)-I_2(z)]_Q-I_3(x, z)+(I_3(x, z))_Q-I_4(x, z).$

By the $(L^p, L^q)$ -bounded of $\tilde T_\delta^A$ , we get

$\frac{1}{|Q|}\int_Q |I_1(x)|dx \le \left(\frac{1}{|Q|}\int_Q|\tilde T_\delta^A(f_1)(x)|^qdx\right)^{1/q} \le C|Q|^{-1/q}||f_1||_{L^p}\le C||f||_{B_p^{\delta}}.$

Similar to the proof of Theorem 1, we obtain

$|I_2(x)-I_2(z)|\le C||f||_{B_p^{\delta}}$

and

$\frac{1}{|Q|}\int_Q |I_3(x, z)|dx \le C||f||_{B_p^{\delta}}.$

Then integrating in $x$ on $Q$ and using the above estimates, we obtain the equivalence of the estimate

$\frac{1}{|Q|}\int_Q |\tilde T_\delta^A(f)(x)-(\tilde T_\delta^A(f))_Q|dx \le C||f||_{B_p^{\delta}}$

and the estimate

$\frac{1}{|Q|}\int_Q |I_4(x, z)|dx \le C||f||_{B_p^{\delta}}.$

This completes the proof of Theorem 3.

4. Applications

In this section we shall apply the theorems of the paper to some particular operators such as the Calderón-Zygmund singular integral operator and fractional integral operator.

Application 1. Calderón-Zygmund singular integral operator.

Let $T$ be the Calderón-Zygmund operator defined by (see ^[10,11,15])

$T(f)(x) = \int_{R^n} K(x, y)f(y)dy,$

the multilinear operator related to $T$ is defined by

$T^A(f)(x) = \int_{R^n}\frac{R_{m+1}(A; x, y)}{|x-y|^m}K(x, y)f(y)dy.$

Then it is easily to see that $T$ satisfies the conditions in Theorems 1–3, thus the conclusions of Theorems 1–3 hold for $T^A$ .

Application 2. Fractional integral operator with rough kernel.

For $0 < \delta < n$ , let $T_\delta$ be the fractional integral operator with rough kernel defined by (see ^[2,7])

$T_\delta f(x) = \int_{R^n}\frac{\Omega(x-y)}{|x-y|^{n-\delta}}f(y)dy,$

the multilinear operator related to $T_\delta$ is defined by

$T_\delta^A f(x) = \int_{R^n}\frac{R_{m+1}(A;x, y)}{|x-y|^{m+n-\delta}}\Omega(x-y)f(y)dy,$

where $\Omega$ is homogeneous of degree zero on $R^n$ , $\int_{S^{n-1}}\Omega(x')d\sigma(x') = 0$ and $\Omega\in Lip_\varepsilon(S^{n-1})$ for some $0 < \varepsilon\le 1$ , that is there exists a constant $M > 0$ such that for any $x, y\in S^{n-1}$ , $|\Omega(x)-\Omega(y)|\le M|x-y|^\varepsilon$ . Then $T_\delta$ satisfies the conditions in Theorem 1. In fact, for $supp f \subset (2Q)^c$ and $x\in Q = Q(x_0, d)$ , by the condition of $\Omega$ , we have (see ^[16])

$\left|\frac{\Omega(x-y)}{|x-y|^{n-\delta}}-\frac{\Omega(x_0-y)}{|x_0-y|^{n-\delta}}\right| \le C\left(\frac{|x-x_0|^\varepsilon}{|x_0-y|^{n+\varepsilon-\delta}}+\frac{|x-x_0|}{|x_0-y|^{n+1-\delta}}\right),$

thus, the conclusions of Theorems 1–3 hold for $T_\delta^A$ .

Acknowledgements

The author would like to express his deep gratitude to the referee for his/her valuable comments and suggestions. This research was supported by the National Natural Science Foundation of China (Grant No. 11901126), the Scientific Research Funds of Hunan Provincial Education Department. (Grant No. 19B509).

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	FAO, Sustainable Crop Production Intensification. 2015. Available from: http://www.fao.org/agriculture/crops/thematic-sitemap/theme/spi/en/.
[2]	Baig MN, Gamache PM (2009) The Economic, Agronomic and Environmental Impact of No-Till on the Canadian Prairies. Alberta Reduced Tillage Linkages, Canada.
[3]	Kassam A, Friedrich T, Derpsch R (2010) Conservation Agriculture in the 21st Century: A Paradigm of Sustainable Agriculture. Proceedings of the European Congress on Conservation Agriculture: Towards Agro-Environmental Climate and Energetic Sustainability. Madrid, 19-68.
[4]	Strelecek F, Lososova J, Zdenek R (2008) Economic results of agricultural holdings in less favoured areas. Agric Econ 44: 510-520.
[5]	European Commission, Commission Communication on the CAP towards 2020. 2010. Available from: http://ec.europa.eu/agriculture/cap-post-2013/communication/index_en.htm.
[6]	Fernández-Ugalde O, Virto I, Bescansa P, et al. (2009) No-tillage improvement of soil physical quality in calcareous, degradation-prone, semiarid soils. Soil Till Res 106: 29-35. doi: 10.1016/j.still.2009.09.012
[7]	Soane BD, Ball BC, Arvidsson J, et al. (2012) No-till in northern, western and south-western Europe: A review of problems and opportunities for crop production and the environment. Soil Till Res 118: 66-87. doi: 10.1016/j.still.2011.10.015
[8]	González-Sánchez EJ, Ordoñez-Fernández R, Carbonell-Bojollo R, et al. (2012) Meta-analysis on atmospheric carbon capture in Spain through the use of conservation agriculture. Soil Till Res 122: 52-60. doi: 10.1016/j.still.2012.03.001
[9]	Holland JM (2004) The environmental consequences of adopting conservation tillage in Europe: reviewing the evidence. Agric Ecosyst Environ 103: 1-25. doi: 10.1016/j.agee.2003.12.018
[10]	Ball BC, Tebrugge F, Sartori L, et al. (1998) Influence of no tillage on physical, chemical and biological soil properties. In: Tebrugge, F., Bohrnsen, A. (Eds.), Experience with the Applicability of No-tillage Crop Production in the West-European Countries. Final Report, Fachverlag Kohler, 35396 Giessen, Germany, 7-27.
[11]	Brautigam V, Tebrugge F (1997) Influence of long-termed no-tillage on soil borne plant pathogens and on weeds. In: Tebrugge, F., Bohrnsen, A. (Eds.), Experiences with the Applicability of No-tillage Crop Production in the West-European Countries. Proc. EC-Workshop III, Wissenschaftlicher Fachverlag, Giessen, Germany, 17-29.
[12]	Crabtree B (2010) Weed control is superior with no-till. In: Crabtree, B. (ed.) Search for Sustainability with No-Till Bill in Dryland Agriculture. Beckenham, W.A.: Crabtree Agricultural Consulting, 27-36.
[13]	Barros JFC, Basch G, Carvalho M (2008) Effect of reduced doses of a postemergence graminicide to control Avena sterilis L. and Lolium rigidum G. in no-till wheat under Mediterranean environment. Crop Prot 27: 1031-1037.
[14]	Conover RR, Dinsmore SJ, Burger LW (2011) Effects of conservation practices on bird nest density and survival in intensive agriculture. Agric Ecosyst Environ 141: 126-132. doi: 10.1016/j.agee.2011.02.022
[15]	Silva-Andrade HL, de Andrade LP, Muñiz LS, et al. (2016) Do Farmers Using Conventional and Non-Conventional Systems of Agriculture Have Different Perceptions of the Diversity of Wild Birds? Implications for Conservation. PLoS One 11: e0156307.
[16]	FAO, Conservation Agriculture Adoption Worldwide. 2016. Available from: http://www.fao.org/ag/ca/6c.html.
[17]	Christoffoleti PJ, Galli AJB, Carvalho JP, et al. (2008) Glyphosate sustainability in South American cropping systems. Pest Manag Sci 64: 422-427. doi: 10.1002/ps.1560
[18]	Gonzalez-Sánchez EJ, Veroz-Gonzalez O, Blanco-Roldan GL (2015) A renewed view of conservation agriculture and its evolution over the last decade in Spain. Soil Till Res 146: 204-212.
[19]	European Commission, Addressing soil quality issues in the EU. 2006. Available from: http://ec.europa.eu/environment/soil/process_en.htm
[20]	Hanspach J, Hartel T, Milcu AI, et al. (2014) A holistic approach to studying social-ecological systems and its application to southern Transylvania. Ecol Soc 19: 32.
[21]	ECAF (1999) Conservation Agriculture in Europe: Environmental, Economic and EU Policy Perspectives. European Conservation Agriculture Federation, Brussels, Belgium.
[22]	González-Sánchez EJ, Ordoñez-Fernández R, Carbonell-Bojollo R, et al. (2012) Meta-analysis on atmospheric carbon capture in Spain through the use of conservation agriculture. Soil Tillage 122: 52-60. doi: 10.1016/j.still.2012.03.001
[23]	Gao Y, Dang XH, Yu Y, et al. (2016) Effects of Tillage Methods on Soil Carbon and Wind Erosion. Land Degrad Dev 27: 583-591. doi: 10.1002/ldr.2404
[24]	Chaplota V, Mchunub CN, Mansonc A, et al. (2012) Water erosion-induced CO2 emissions from tilled and no-tilled soils and Sediments. Agric Ecosyst Environ 159: 62-69.
[25]	Montgomery D (2007) Dirt: The erosion of civilizations. University of California Press, Berkeley.
[26]	Kassam A (2009) Sustainability of farming in Europe: is there a Role for conservation agriculture? J Farm Manag 13: 717-728.
[27]	Millennium Ecosystem Assessment (2005) Ecosystems and Human Well-Being: Synthesis. Millennium Ecosystem Assessment. Island Press, Washington, DC.
[28]	Marja R, Herzon I, Viik E, et al. (2014) Environmentally friendly management as an intermediate strategy between organic and conventional agriculture to support biodiversity. Biol Conserv 178: 146-154. doi: 10.1016/j.biocon.2014.08.005
[29]	Plaza-Bonilla D, Arrue JL, Cantero-Martinez C, et al. (2015) Carbon management in dryland agricultural systems. A review. Agron Sustain Dev 35: 1319-1334.
[30]	Lindwall CW, Sonntag B (2010) Landscape Transformed: The History of Conservation Tillage and Direct Seeding. Knowledge Impact in Society. University of Saskatchewan, Saskatoon.
[31]	FAO (2011) Save and Grow: A new paradigm of agriculture. FAO, Rome, Italy.
[32]	González-Sánchez E, Pérez García JJ, Gómez Ariza M (2010) Sistemas agrarios sostenibles económicamente: el caso de la siembra directa. Vida Rural 312: 24-27.
[33]	Reicosky D, Archer DW (2007) Moldboard plow tillage and short-term carbon dioxide release. Soil Till Res 94: 109-121. doi: 10.1016/j.still.2006.07.004
[34]	Reicosky D (2001) Conservation Agriculture: Global environmental benefits of soil carbon management. In: García-Torres L, Benítes J, Martínez-Vilela A., (eds.) Conservation Agriculture - A Worldwide Challenge. 3-12.
[35]	Carbonell-Bojollo R, González-Sánchez EJ, Veroz-González O, et al. (2011) Soil management systems and short term CO2 emissions in a clayey soil in southern Spain. Sci Total Environ 409: 2929-2935. doi: 10.1016/j.scitotenv.2011.04.003
[36]	Marquez-García F, Gonzalez-Sánchez EJ, Castro-García S, et al. (2013) Improvement of soil carbon sink by cover crops in olive orchards under semiarid conditions. Influence of the type of soil and weed. Span J Agric Res 11: 335-346.
[37]	Kassam A, Friedrich T, Derpsch R, et al. (2012) Conservation agriculture in the dry Mediterranean climate. Field Crops Res 132: 7-17. doi: 10.1016/j.fcr.2012.02.023
[38]	Carbonell-Bojollo R, González-Sánchez EJ, Ruibérriz De Torres MR (2015) Soil organic carbon fractions under conventional and no-till management in a long-term study in southern Spain. Soil Res 53: 113-124.
[39]	Smith P, Powlson DS, Glendining MJ, et al. (1998) Preliminary estimates of the potential for carbon mitigation in European soils through no-till farming. Glob Chang Biol 4: 679-685. doi: 10.1046/j.1365-2486.1998.00185.x
[40]	McConkey B, Chang Liang B, Padbury G, et al. (2000) Carbon sequestration and direct seeding. In Proceeding: direct seeding “Sustainable Farming in the new Millennium” 12th Annual Meeting, Conference and Trade Show of the Saskatchewan Soil Conservation Association, February 9 and 10, 2000.
[41]	Eurostat, 2010. Available from: http://ec.europa.eu/eurostat.
[42]	Lal R, Kimbel JM, Follet RF, et al. (1988) The potential of US Cropland to sequester carbon and mitigate the greenhouse effect. Ann Arbor Press, MI.
[43]	European Commission, Legal proposals for the CAP after 2013. 2011. Available from: http://ec.europa.eu/agriculture/cap-post-2013/legal-proposals/index_en.htm.
[44]	Hobbs PR (2007) Conservation agriculture: what is it and why is it important for future sustainable food production? J Agric Sci 145: 127-137. doi: 10.1017/S0021859607006892
[45]	Friedrich T, Kassam A, Corsi S (2014) Conservation Agriculture: Global Prospects and Challenges. Conservation Agriculture in Europe. CABI.
[46]	Lafond GP, Walley F, Schoenau J (2008) Long-term vs. short-term conservation tillage. In: Proceedings of the 20th Annual meeting and Conference of the Saskatchewan Soil Conservation Association, 28-43. 12-13 February. Regina, Saskatchewan.
[47]	Carvalho M, Basch G, Barros J, et al. (2010) Strategies to improve soil organic matter under Mediterranean conditions and its consequences on the wheat response to nitrogen fertilization. Proceedings of the European Congress on Conservation Agriculture: Towards Agro-Environmental Climate and Energetic Sustainability. Madrid, 303-308.
[48]	Friedrich T (2005) Does no-till farming require more herbicides? Outlooks Pest Manag 16: 188-191. doi: 10.1564/16aug12
[49]	Friedrich T, Kassam A (2012) No-till farming and the environment: do no-till systems require more chemicals? Outlooks Pest Manag 23: 153-157. doi: 10.1564/23aug02
[50]	Tebrügge F, Böhrnsen A (1997) Crop yields and economic aspects of no-tillage compared to plough tillage: Results of long-term soil tillage field experiments in Germany. In: Tebrügge, F., Böhrnsen, A. (Eds.), Experience with the Applicability of No-tillage Crop Production in the West-European Countries. Proceedings of the EC Workshop-IV., Wissenschaftlicher Fachverlag, 35428 Langgöns, Germany, 25-43.
[51]	Plan de Desarrollo Rural de Andalucía, 2007-2013 (Medidas 214/12 and 214/14). Available from: http://www.juntadeandalucia.es/agriculturaypesca/portal/export/sites/default/comun/galerias/galeriaDescargas/cap/la-consejeria/planes-y-politicas/programa-desarrollo-rural-de-la-agricultura/PDR_v.3_APROBADO_xPDRAndalucia_080220_3x.pdf
[52]	Bayerisches Kulturlandschaftsprogramm (KULAP), 2012. Available from: http://www.stmelf.bayern.de/mam/cms01/agrarpolitik/dateien/p2_kulap_massnahmenuebersicht.pdf.
[53]	Piano di Sviluppo Rurale Regione Veneto Misura 214/i, 2012. Available from: https://www.regione.veneto.it/static/www/agricoltura-e-foreste/214i_14052012.pdf.
[54]	Kanton Bern - Kantonales Förderprogramm Boden, 2009-2015. Available from: http://www.vol.be.ch/vol/de/index/landwirtschaft/landwirtschaft/bodenschutz/foerderprogramm_bodenkantonbern.html.
[55]	Van Orshoven J, Terres JM, Eliasson Å, Common bio-physical criteria to define natural constraints for agriculture in Europe. European Commission, 2008. Available from: http://agrienv.jrc.ec.europa.eu/Common%20Criteria%20Fact%20sheets.pdf.
[56]	Peterson GA, Westfall DG (2004) Managing precipitation use in sustainable dryland agroecosystems. Ann Appl Biol 144: 127-138.
[57]	Cantero-Martinez C, Gabina D, Arrue JL (2007) Evaluation of conservation agriculture technology in Mediterranean agriculture systems. In: Stewart, B., Fares Asfary, A. Belloum, A., Steiner, K. and Friedrich, T (Eds.), The Proceedings of the International Workshop on Conservation Agriculture for Sustainable Land Management to Improve the Livelihood of People in Dry Areas. 7-9 May 2007, ACSAD and GTZ, Damascus, Syria, 157-164.
[58]	Bot A, Benites J (2005) The importance of soil organic matter, key to drought-resistant soil and sustained food production; FAO Soils Bulletin 80, FAO, Rome.
[59]	Van-Camp L, Bujarrabal B, Gentile AR, et al., Organic Matter. European Commission, 2004. Available from: http://eusoils.jrc.ec.europa.eu/ESDB_Archive/Policies/STSWeb/vol3.pdf.
[60]	Rodriguez-Martín JA, Rodríguez Martín J, Álvaro-Fuentes J, et al. (2016) Assessment of the soil organic carbon stock in Spain. Geoderma 264: 117-125. doi: 10.1016/j.geoderma.2015.10.010
[61]	Tullberg J (2010) Tillage, traffic and sustainability-A challenge for ISTRO. Soil Till Res 111: 26-32. doi: 10.1016/j.still.2010.08.008
[62]	Antille DL, Chamen WCT, Tullberg JN, et al. (2015) The potential of controlled traffic farming to mitigate greenhouse gas emissions and enhance carbon sequestration in arable land: a critical review. Trans ASABE 58: 707-731.
[63]	Sitholea NJ, Magwazaa LS, Mafongoya PL (2016) Conservation agriculture and its impact on soil quality and maize yield: A South African perspective. Soil Till Res 162: 55-67. doi: 10.1016/j.still.2016.04.014
[64]	Thierfelder C, Rusinamhodzi L, Ngwira AR, et al. (2015) Conservation agriculture in Southern Africa: Advances in knowledge. Renew Agric Food Syst 30: 328-348. doi: 10.1017/S1742170513000550
[65]	McIntyre BD, Herren HR, Wakhungu J (2008) Agriculture at a Crossroads: Synthesis. Report of the International Assessment of Agricultural Knowledge, Science and Technology for Development (IAASTD) Island Press, Washington, DC.
[66]	Foresight (2011) The Future of Food and Farming. The Government Office for Science, London.

Reader Comments

Your name:*

Email:*
© 2016 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)