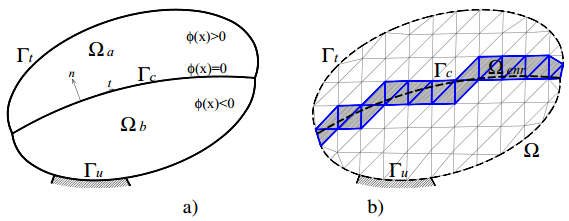
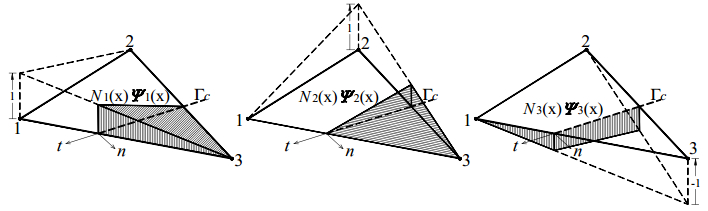
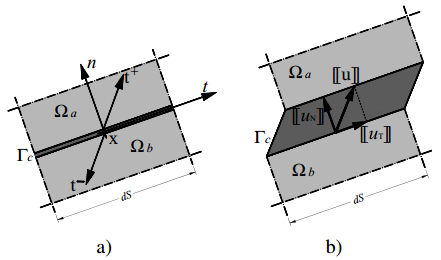
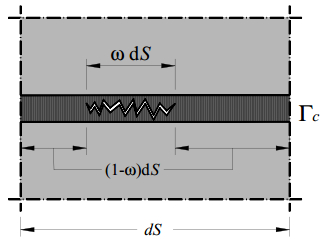
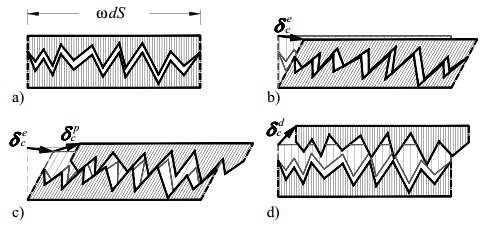
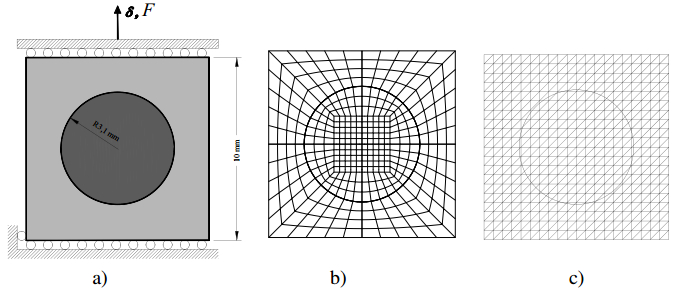
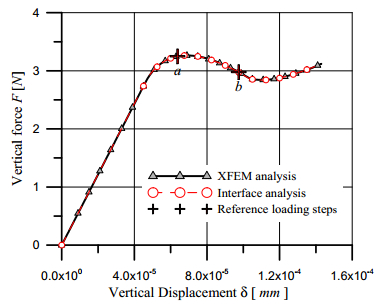
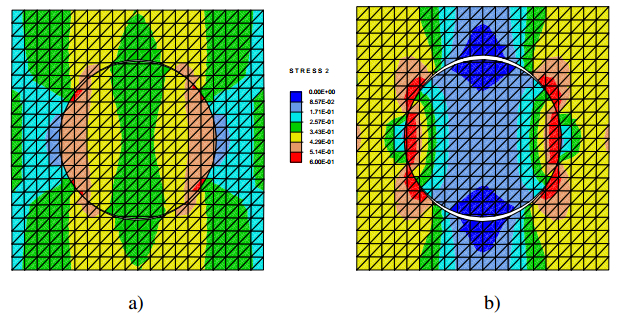
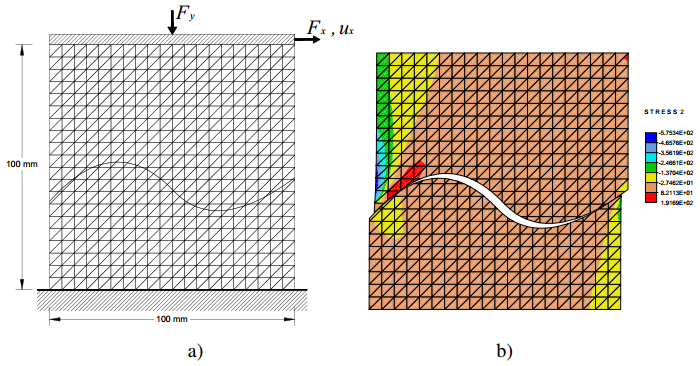
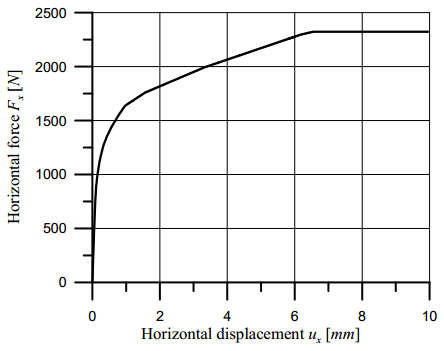
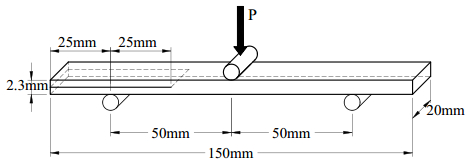
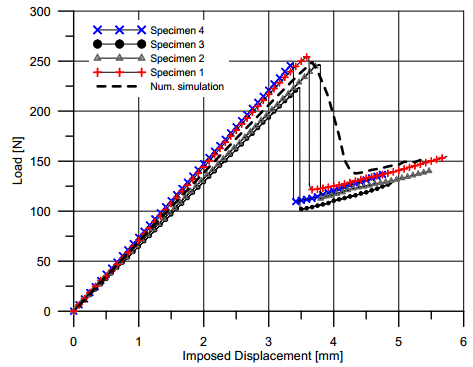
In the present paper, the complex mechanical behaviour of the surfaces joining two different bodies is analysed by a cohesive-frictional interface constitutive model. The kinematical behaviour is characterized by the presence of discontinuous displacement fields, that take place at the internal connecting surfaces, both in the fully cohesive phase and in the delamination one. Generally, in order to catch discontinuous displacement fields, internal connecting surfaces (adhesive layers) are modelled by means of interface elements, which connect, node by node, the meshes of the joined bodies, requiring the mesh to be conforming to the geometry of the single bodies and to the relevant connecting surface. In the present paper, the Extended Finite Element Method (XFEM) is employed to model, both from the geometrical and from the kinematical point of view, the whole domain, including the connected bodies and the joining surface. The joining surface is not discretized by specific finite elements, but it is defined as an internal discontinuity surface, whose spatial position inside the mesh is analytically defined. The proposed approach is developed for two-dimensional composite domains, formed by two or more material portions joined together by means of a zero thickness adhesive layer. The numerical results obtained with the proposed approach are compared with the results of the classical interface finite element approach. Some examples of delamination and frictional contact are proposed with linear, circular and curvilinear adhesive layer.
1.
Introduction
The fluoride content of surface water is important for two very different reasons, i.e. human health and mineral prospecting. The usual level is normally far below the assumed harmful value of 1.5 ppm F [1,2,3,4,5] and essentially depends on leaching from rocks and soils involved in the water flow. It is affected by the occurrence and distribution of fluorite-bearing mineral deposits [6] and/or by the direct or indirect influence of some types of volcanic activity and their products, thermal springs included [7,8,9,10].
F-bearing minerals occur as major components or common accessories in several types of ore associations. Fluorite is the most abundant and frequent mineral, but other important F-bearing compounds are well represented: among them fluorapatite, monazite, bastnaesite, topaz etc. Related ore deposits may be emplaced in various environments, and F-bearing minerals are known in hydrothermal deposits, carbonatite complexes, and kimberlites (fluorophlogopite: [11]). However, the most important type of fluorine-bearing mineralization is produced by the activity of hydrothermal systems controlling the fluid flow in the earth's crust. These systems are responsible for complex processes involving the leaching, transport, and deposition of substances that derive either from fluid-rock interaction or from the direct supply of magmatic sources. Hydrothermal fluids mostly involve exogenetic waters, and give rise to typical processes of the "intermediate environment" [12]. Whatever the water's origin, the importance of the involved volatiles is to be highlighted. Among them, fluorine shows a constant trend of occurrence constrained by the existence of regionally developed, deep-seated tectonic structures, commonly associated with mafic-felsic bimodal volcanism.
Van Alstine (1976) [13] pointed out the close association of major fluorspar districts with continental rifts and lineaments all over the world. According to the data from several studies, it is interesting to note that this structural control seems to extend well beyond the mineralization processes.
From a geochemistry point of view, the average natural concentration of F in the Earth's crust is around 600 mg kg−1 [14]); while the natural background in air is 0.5 ng m−3 [15], due to the high electronegativity of fluoride and its tendency to form nonvolatile and relatively insoluble compounds [16]. Since the mobility of fluoride is strongly controlled by temperature and salinity, which in turn influence the equilibrium constant of fluorite (CaF2), the amount of soluble fluoride is considered directly linked to the amount of Ca2+. Because of this link, between F and Ca, some authors have suggested that the scarcity of Ca in solution (i.e. its precipitation) might explain the presence of high fluoride in ground and surface waters [10]. This depletion of Ca from solution has also been linked to conditions of cation exchange between calcium and sodium (Na+) in clay minerals [10]. As reported by Vithanage and Bhattacharya (2015) [17] review, fluoride-rich groundwaters are positively correlated to HCO3− and Na+ levels; they have a strong influence on fluoride dissolution and, in addition, they are generally linked to high pH and therefore high OH− levels. Fluorine (F−) and OH− ions are notably exchangeable in minerals due to similar ionic radius and charge [18].
In the following sections, we discuss on the occurrence of fluoride in the natural environment and its importance in the understanding of East African Rift and Sardinian Ore Deposits.
Additionally, we briefly analyse the role of natural occurring fluoride and its impact on the human health of exposed population, and highlight limits of the most established defluoridation techniques as well as highlight the potentiality of new techniques.
2.
Rifts and fluorite mineralization
Rifts are here considered as expressions of regionally important fracture systems, which develop to noticeable depths, thus reaching either crustal melting levels or the apical boundaries of possible existing magmatic chambers or their neighbourhoods. Intracontinental hotspots are identified as the origin of rifting by Sawkins (1976) [19], who ascribes the heat source for the generation of Pb-Zn-F-Ba-enriched peralkaline rocks to their activity. According to Sawkins, these hotspots would thus also be responsible for the ore-forming processes that lead to Mississippi-Valley type deposits. However, according to Bailey (1978) [20] rifting develops from the re-activation of earlier zones of weakness in continental plates, and leads to the channelling of volatile release from the deeper mantle. Mantle metasomatism, thermal decomposition of some of the volatile-bearing minerals, and melting should be all effects of the rifting evolution, so that the escape of gases (especially carbon and halogen compounds) must be considered the result of mantle degassing supplemented by the supply of the above volatiles from the thermal decomposition of F-bearing silicates.
In any case, rift fracture systems are recognised as the easiest way of upward migration of magmatic fluids, which are ultimately part of the residual melt that is often particularly enriched in fluorine. Mixing with downward moving meteoric waters gives rise to very active hydrothermal solutions, and fluorspar deposits frequently originate in suitable equilibrium conditions. The genetic temperature interval of fluorite is wide: it may participate in paragenetic sequences belonging to pneumatolytic up to epithermal conditions. In conclusion, fluorspar deposits are the best source of fluorine leaching by surface waters, and the measured values of waters in mineralized districts are clearly expected to be often highly anomalous, in comparison with the regional average.
2.1. The Sardinian and East African cases
2.1.1. The Sardinian case
The scientific literature reports many good examples of fluorspar mineral deposits, or fluorspar-bearing mineral deposits whose occurrence can be at once recognized as genetically and structurally controlled by rift fracture systems, or by rift-related fracture lineaments of regional importance. Among them it is worth mentioning Broken Hill [21], the Illinois-Kentucky fluorspar deposits [22], the Pb-Zn-fluorite-barite deposits of the Benue Trough [23], and the Kerio Valley fluorite deposits of the East African Rift Valley System [24].
A very good model of fluorine behaviour is traceable in the geological history of Sardinia. Located in the center of the Mediterranean sea, Sardinia can be considered a faithful record of the events that characterised the geological history of the European lithosphere since the late Precambrian [25,26,27]. The structural fabric reflects Caledonian, Hercynian and Alpine orogeneses, which were accompanied by important magmatic events.
A summary of Sardinian geologic history starts with a first document of Precambrian age, i.e. the terrigenous metasediments of the "Bithia Formation" [28], followed by the Cambrian-Lower Ordovician sequence, evolving from a lagoonal to a neritic environment through an epicontinental platform phase. The lithotypes of the latter sequence start from terrigenous metasediments with intercalations of oolitic limestones (Nebida Formation), followed by the so called "Metalliferous" carbonatic member (Gonnesa Formation), with dolostones, limestones and nodular limestones, rich in stratabound Pb-Zn and Ba deposits. Terrigenous metasediments of Tremadocian age (Cabitza Formation) conclude the sequence, which is well represented in SW Sardinia, while in the SE and in the central part of the island, coeval siliciclastic sequences occur [25].
The Caledonian orogenesis gave rise to a compressional event ("Sardic Phase") that is evident in SW Sardinia, and to an uplift accompanied by magmatic activity with basaltic-andesitic to rhyolitic-rhyodacitic volcanism in the south-eastern part of the island. Such an evolution is marked by a general unconformity between the Cambrian-Lower Ordovician complexes and the overlying sequences, which start with terrigenous continental to littoral metasediments locally associated with alkalibasaltic metavolcanics. The sequences evolve upwards to neritic argillitic and carbonatic deposits ("Ashgillian limestones"), and are followed by typical Silurian black shales and cherts that bear the imprint of the influence of syn-rift to post-rift evolution [29]. The Silurian formations grade into Lower and Middle Devonian pelagic marly shales and nodular limestones, until the last sequence of pelagic limestones (SE Sardinia) or terrigenous metasediments (NW Sardinia) is reached [25].
The Sardinian crystalline basement belongs to the South European Hercynian chain, and bears clear effects of its complex regional metamorphism. This metamorphism developed through different phases, and was accompanied by intense magmatic activity with the emplacement of the Sardinian-Corsican batholith. According to Carmignani et al. (1994) [25] the Sardinian structural fabric is characterised by a gradual sequence of metamorphic zones, from the northern high-grade complex to the southern low-grade complex, through an intermediate nappe zone. Metamorphic core complexes may crop out, associated with post-collisional extensional structures.
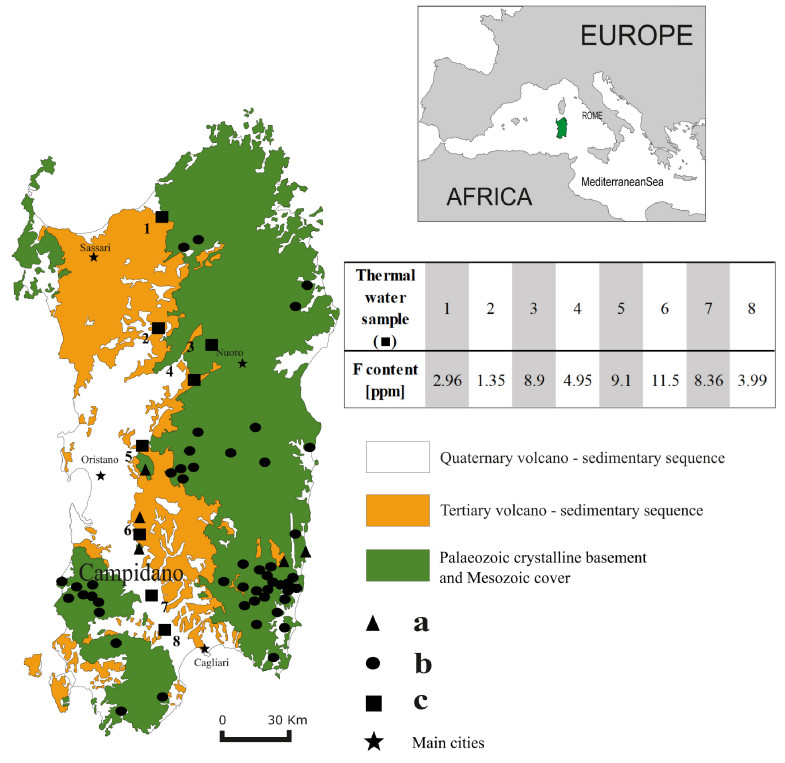
The Hercynian magmatism was characterised by the emplacement of a major high-K calc-alkaline association, and was followed by post-granitic Permo-Triassic acidic to basic dike injections. After the post-Hercynian exhumation, Sardinia was periodically and partially affected by marine invasions, and also during the Cainozoic it was repeatedly subjected to marine sedimentation, interrupted by long emersion periods. During these periods several intense volcanic cycles developed, giving rise to sequences of variable composition, from the early andesite lavas and tuffs to the late basaltic flows. Tertiary repercussions of Alpine tectonic activity were especially characterised by the Sardinian Rift [26], which is concretely influenced by the contemporaneous formation of a complex European rift system. The N-S trending Sardinian rift is considered an aborted arm of this system, and cuts through the island, displacing both the crystalline basement and the volcano-sedimentary cover. During its evolution, the Sardinian rift was filled with thick sedimentary sequences and with the products of important calc-alkaline volcanic phases. The last tectonic movements, accompanied by some volcanic activity, reactivated the Alpine systems, and were also responsible for the Pliocene-Quaternary "Graben of Campidano", a NW-SE trough superimposed on the southern part of the Oligocene-Miocene rift structure (Figure 1).
During such a long history, Sardinia developed an important metallogenic province, where several types of ore deposits occur. Pb-Zn-(Ag) ores associated with minor or major quartz, fluorite, barite, and calcite in discordant veins hosted in various Palaeozoic country rocks are very frequent, and Pb-Zn-(Ag) in massive or disseminated orebodies, and barite in stratabound or massive karst-filling orebodies, are typical in the Cambrian "Metalliferous" limestones. Many other types of Palaeozoic mineralization are reported: copper and mixed sulphides in concordant stratabound lenses, W-Mo-Sn ores in pneumatolytic setting, stibnite and scheelite in shear zones. Last but not least, epithermal gold deposits of economic importance are hosted in volcanics of the Sardinian Tertiary rift and in metamorphic-dominated areas [30,31].
Fluorite occurrences are widespread in Sardinia, but fluorine activity did not affect any Cambrian environment. In other words, nowhere do Cambrian outcrops show traces of fluorine activity, and fluorite mineralization is totally absent, even in presence of the frequent and often large Pb-Zn- and Ba-bearing orebodies. F-bearing mineral associations are mainly hosted by Ordovician-Silurian metasediments and metavolcanics or by Hercynian magmatic products, in discordant veins or concordant or stratabound orebodies, or skarn lenses, that are particularly clustered in the neighbourhood of the predominant Cambrian complex of SW Sardinia. The first appearance of fluorine in the stratigraphic Palaeozoic sequence of Sardinia is chronologically confined to the events following the Caledonian tectonic activity. Actually, widespread fluorite-barite infillings occur in paleokarst systems, that developed close to the erosion paleosurface, just below the Ordovician unconformity, in the Cambrian "Metalliferous" limestones.
The sudden appearance of fluorite in the Ordovician series was formerly explained [32] according to a possible leaching and mobilisation of F-bearing protores from the post-Cambrian sequences, followed by deposition in available open spaces (karst systems possibly related to the pre-Ordovician paleosurface and/or fracture infillings into post-Cambrian competent rocks). We now propose to consider the assumption of Vai (1991) [29] concerning a major oblique rifting cycle developing from the late Cambrian to the early Ordovician in the circum-Mediterranean area, corresponding to the "Sardic Phase" of the Caledonian orogenic cycle. The bimodal volcanic activity referred to as belonging to this age in the Palaeozoic Sardinian sequence is in good agreement with such an assumption. In this framework the conclusions of Worl et al. (1973) [33] and Van Alstine [13] about the link of fluorite hydrothermal deposits with major regional displacements and rift systems appear to be of the greatest importance. Actually, such an interpretation well explains the sudden appearance of the substantial fluorine contribution to the Ordovician geochemical landscape of Sardinia. Therefore the rifting processes assumed by Vai (1991) [29] can be considered the most reasonable and reliable means of supply of volatiles to the existing hydrothermal systems, as already discussed and proposed by Bailey (1978) [20]. Such an "early fluorine" can be considered responsible for syngenetic protores in Silurian-Devonian volcano-sedimentary sequences, remobilized and concentrated in both concordant and discordant stratabound orebodies during the Hercynian magmatic activity. Accordingly, "early fluorine" could have been available and active long enough to join the onset of the Hercynian magmatic cycle.
Thus, fluorine plays a substantial role during the Hercynian magmatism, and becomes even more important in the late orogenetic phase, while fluorite occurrences especially characterize the last pluton emplacement (postkinematic leucogranites) in the Sardinian-Corsican batholith. Fluorite is a common accessory mineral in the leucogranites, reaching at times high concentrations. However, its abundance in association with leucogranites cannot be referred to as effect of the sole remobilization of "early fluorine". Again, we encounter the structural conditions already described as typical of regions rich of fluorite deposits. Actually, the end of the Hercynian cycle is characterized by a post-collisional evolution with important extensional effects [25], that produced collapse of the collisional structures, and the exhumation of metamorphic core complexes. Shear zones, crustal fracturing, and development of a Permian rift [34] accompanied by the important Permian magmatism give rise to the establishment of structural support and new favourable conditions for the reappearance of fluorine. Moreover, very frequently fluorite mineralization occurs in composite association with basaltic dikes in fractures where fluorite is clearly deposited last. The dikes appear to belong to a late-Permian magmatism, and are entirely attributed to mantle sources [35]. Therefore we may assume that mantle degassing follows the same ways for the release of volatiles. Both the common occurrence and the field relations suggest the existence of a chronologic and perhaps genetic link between emplacement of basaltic dikes and invasion of F-bearing hydrothermal fluids strictly confined to the same fractures. Sometimes basaltic dikes are cut and displaced by fluorite mineralised fractures, suggesting prolonged hydrothermal activity, long after the last emplacement of late- to post-Hercynian magmatic products.
The Palaeozoic history of Sardinian fluorine can therefore be summarised according to two main phases. First, the early, widespread appearance of the element in the geochemical landscape, in connection with the establishment of an Ordovician rifting cycle in the circum-Mediterranean area, which accounts for the syngenetic protores. The second phase was particularly important and was given by the remobilization and concentration of the "early fluorine" in both concordant and discordant stratabound fluorspar and fluorite-bearing deposits, accompanied by supply of new fluorine through post-collisional Hercynian extensional structures (rifts and shears), in association with both post-kinematic leucogranites and basaltic dikes of deep-seated origin.
The dramatic Cainozoic evolution of Sardinian geological history, characterised by various marine invasions and regressions and repeated phases of volcanic activity, is basically controlled by the rotation of the Corsica-Sardinia microplate, and again, by the development of a new rift: the Oligo-Miocene Sardinian rift [26]. This important structure is displayed all along the western part of the island, and its fault systems ranging N-S to NW-SE extend within the basement and give rise to the uplift of metamorphic core complexes.
Many fractures, belonging to the Tertiary rift and displacing both the crystalline basement and the post-Palaeozoic (mostly Tertiary) cover, have more recently been discovered to contain fluorite concentrations [36]. Consequently, we could postdate some of the deposits so far considered genetically connected with the hydrothermal activity of the last Hercynian magmatic cycle, since their link with Tertiary metallogenic events is not to be ruled out.
Many thermal springs are at present known in Sardinia. The study of their composition [7] shows that the fluoride content of waters from springs directly or indirectly related to the fracture systems of the Tertiary rift is remarkably high (Figure 1). It seems reasonable to accept a still ongoing hydrothermal process, a sort of continuation of the process responsible for the Tertiary fluorite deposition. These waters appear to be in equilibrium with fluorite, whereas waters belonging to other Sardinian thermal springs not related with the Tertiary rift structures are largely undersaturated with respect to this mineral [7].
2.1.2. The East African cases
A peculiar situation is observed in the East African Rift (EAR), where the surface waters normally have very high fluorine concentrations (tens of ppm are very frequent: [9,37,38], and in some cases are true brines (1627 ppm F in lake waters [33]). According to Calderoni et al. (1993) [8], even if in a number of springwaters the product of F− and Ca2+ activities exceeds the solubility product of fluorite, precipitation of CaF2 is not observed in the Ethiopian Rift Valley. Actually, the EAR is a continental rather than a regional structure, and today we know at least three fluorite occurrences directly or indirectly related to its fracture systems (Figure 2): the Kerio Valley deposits, the Lake Kivu sediments, and the Negash barite-fluorite veins.
The Kerio Valley deposits [24] are the fluorite production centers in Kenya. They occur as concordant lenses hosted by metamorphic rocks of the Basement System of the Mozambique Belt, faulted and displaced according to the structures of the Rift Valley before the mineralization processes.
In particular levels of the Lake Kivu sediments [39], fluorine occurring as CaF2 has been measured in the 0.1–0.6% range. Its origin is referred to as discharge into Lake Kivu from hydrothermal solutions related to volcanic activity, in turn connected to the EAR fractures.
The Negash barite-fluorite veins [40,41] were discovered in Tigray, north of Mekele, and belong to a district occurring at the western limit of the EAR, Tigray section. The mineralization is characterised by barite in stock-works and veins, with hematite. Fluorite appears in massive textures associated with barite in some veins.
Therefore, if we bear in mind the widespread abundance of fluorine in the EAR surface waters, including witnesses of its discharge as fluorite in the deposits, together with the usual, described association of fluorspar districts with continental rifts and lineaments [13], it seems very reasonable to ascribe the supply of F in the EAR to hydrothermal fluids migrating along the fracture systems of this continental structure. Very probably these fluids initially derive from mantle degassing, and are subsequently enriched by volatiles from the thermal decomposition of volatile-bearing minerals [20], and by leaching and extraction from the country rocks. According to Yirgu et al. (1999) [9], the supply of F in the EAR waters is ascribable mostly to the leaching of the widespread pumices, which appear to have lost a large fraction of their fluorine content during their interaction with water, whereas acid lavas and ignimbrites do not show any significant loss. Actually, this assumption looks to be only acceptable for some parts or sections of the EAR. Considering the above mentioned similar structures and their relations with the abundance of fluorine in the surface waters, it seems very reasonable to credit the contribution of deep-seated sources of fluorine that use the rift fracture systems all along the EAR as the most suitable pathways.
3.
Fluorine and human health
The role of fluorine on human health has been addressed since the nineteenth century, from early understanding of its interaction with bones and teeth, to the recognition of its association with dental caries, fluorosis [10] and chronic kidney disease [42,43,44]; up to the recent investigations on the study of its synergistic and antagonistic effects with other chemical compounds [45].
Contrary to other substances, fluoride has no colour and no smell, it doesn't alter taste and therefore is a silent and subtle element that acts both as a boon and bane for the human health. Nowadays, millions people worldwide consume waters with concentrations higher than the WHO-recommended threshold of 1.5 mg L−1 [46]. Which, considering that the current WHO guidelines on drinking water quality have been evaluated to account for a specific target, a precise daily water consumption and standardized conditions, it's only accountable in supporting the risk evaluation of the individual chemical element.
Since its natural presence at high levels can be found both in water and food, its removal isn't always a viable option for the local communities, especially in the rural areas of least developed countries. Because of these factors, numerous countries have no option but to adopt higher limits, accepting a higher health risk for the population. Unfortunately, this problem is emphasized in non-urban communities (especially in those without public water supply), where without the state intervention or monitoring one cannot easily evaluate the fluoride content of their wells or springs.
Fluoride is mainly absorbed through:
● Oral uptake: the main absorption is carried in the gastrointestinal tract, with little amounts absorbed in the oral cavity through saliva, except from extended contact time in topical application of F-rich products [47]. The major portion of the fluoride is absorbed in the stomach and small intestine, provoking a rapid increase in the blood levels of fluoride in 20–60 minutes [48] with a following quick decrease in the following hours [49] depending on the dose, the fluoride clearance from plasma by kidney and the accretion/dissolution by skeleton. Additionally, in the presence of low pH in the stomach, the absorption rate is increased due to the reaction and formation of hydrogen fluoride [50], which is characterised by a greater permeability coefficient than the ionic form in different soft tissues [51]. In the little intestine, contrary to the stomach, fluoride is mostly absorbed as fluorine ions (F−), instead of hydrofluoric acid, with no dependence on pH [52].
● Inhalation: high air levels of fluoride are mainly the result of industrial emissions and volcanic emissions, however these sources shouldn't be underestimated since both fluorine and HF (hydrofluoric acid) are completely absorbed through the upper respiratory tract. The fluoride is than distributed in the body, being mostly retained by the skeleton. The effects of fluorine and hydrogen fluoride exposure are acute, varying from mild eye and skin irritation to pulmonary haemorrhage and bronchial ulceration at high doses.
While almost 50% of the fluoride intake is excreted through the renal activity, 99% of the retained fluoride in the body is fixed in calcified tissues, mainly in the bones and teeth, through a substitution of OH− by F− groups in the hydroxyapatite [Ca10(PO4)6(OH)2] structure, with the formation of fluorapatite crystals [Ca10(PO4)6F2]. The accumulation of fluoride in the skeleton and teeth is reversible, as fluoride is regularly released in the blood plasma and distributed in the different tissues and fluids.
Normally, a typical fluoride intake doesn't lead to high fluoride accumulation since the combined effect of urinary excretion and bone uptake allows to keep a correct homeostasis: the urinary excretion is reduced during the skeletal development and vice versa. However, in the presence of high doses and long exposures to fluoride, the deposition process of fluorapatite is uninterrupted, leading to the hardening and density increase of the bones (i.e. osteosclerosis); the result is an abnormal growth and deformation that, in the most severe cases, obstructs the blood and nervous vessels [53]. This condition, called skeletal fluorosis, is considered to arise with the consumption of more than 4 mg d−1, with an increase in the severity of the condition proportional to the increased dose of fluoride.
The amount of fluoride retained by the skeleton has shown to decreases with age, contrary to the amount excreted through urine which increases; because of this, 86.8% of fluoride is retained by infants, twice as the amount retained by adults [50]. These rates however, when exposed to high intakes > 4 mg d−1, have highlighted that only 50% is retained by the skeleton, resulting in an increased excretion through urine, i.e. kidney activity. In the presence of a high-calcium diet, the excreted fluoride in faeces has been recorded in higher levels than the intake, suggesting a more complex system of fluoride binding and migration in the intestinal tract [50].
Even though fluoride isn't considered an essential element, its supplement has undoubtedly proved its positive effects on the prevention of dental decay [54], when consumed under specific thresholds and controlled consumptions, which lead to the development of numerous community-fluoridation programs for the fluoridation of public waters since the early 1900s. The effects of its consumption in concentrations around 1.0 mg L−1 in drinking water, has long been observed as beneficial in preventing tooth decay over large communities [55,56,57]. From the observations on communities affected by endemic mottled teeth, these early studies understood the relationship between F-rich waters (e.g. warm springs, deep basement aquifers) and low dental caries rate, considering its effect as both post-eruptive and pre-eruptive (i.e. after and before eruption of the deciduous tooth, as a result of systemic fluoride exposure) but also acknowledging the presence of a "threshold dose" in the onset of dental fluorosis. Following this pre-eruptive consideration and the related studies on the improvement of the enamel by fluoride fixing in the crystalline structure, fluoride supplements have started to being advised to pregnant women as a solution to reduce the frequency of the child's caries and as a solution to improve the overall "quality" of the deciduous teeth produced [58,59]. Regarding the supplement of fluoride during pregnancy and the role of pre-eruptive fluoride supplement, the placental transfer of fluoride from mother to fetus is a hot topic which still discussed [60,61]. While the positive effects of fluoride supplement were being investigated, the presence of health problems linked to f-rich waters had started to arise in numerous countries [62,63], prompting an urgent intervention and regulation in the public use.
4.
Potentialities and limitations of the currently available defluoridation techniques
Issues related to water supply have nowadays become among the most attractive topics [64]. Considering this, it would be of utmost importance to identify a method of purification of F− rich water that allows making it safe for human use, especially in those countries where water is scarce, but there is availability of fluorine-contaminated water resources. However, most technical and economical issues related to this remain unsolved. The apparatus should respect different criteria of feasibility to be useful for this purpose [65,66]: 1) the system should be environmentally friendly avoiding the use of chemicals or other substances that can be dangerous for the ecosystem; 2) the technology should be feasible to build up and implemented considered also the area where should operate; 3) the system should have high efficiency (80–100%); 4) the device should be low cost, affordable, reliable, easy to operate and, hence, accessible to rural communities; 5) the device has to allow up-scaling from household to community level.
A common technology for fluoride removal is precipitation/coagulation, which consists of using chemical agents, coagulants, and flocculants to wastewater to form fluoride precipitation or flocculation precipitation and then achieve the purpose of removing fluoride in water through solid-liquid separation [67,68]. Coagulants improve the rate of solid-liquid separation in an aqueous medium, improving the solid capacity of settling and making easier the filtration by forming larger aggregations. This method shows low efficiency, and it is not feasible when the concentration of fluoride in the water is less than 20–30 mg/L [69]. Moreover, it presents the problem of the collection of precipitate and the presence of leaching substances (like aluminum and chloride) in the treated water [70,71].
Adsorption is another technique often used in defluoridation. It is a surface process that leads molecules to transfer from a fluid bulk to a solid surface (called adsorbent). This can occur because of physical forces or by chemical bonds through which the adsorbent is able to retain the pollutant. Usually it is reversible (the reverse process is called desorption), then it is responsible not only for a subtraction of substances, but also for their possible release. In the literature, several examples of adsorbents, tested for water defluoridation, can be found: graphene and carbon-based materials [72,73], modified alumina [74,75,76], porous MgO nanostructures [77], zeolites [78,79,80], and even bio-based materials [81,82]. Furthermore, combined methods like the combination of adsorption methods and physical fluoride removal strategies based on static electric fields were also investigated [83,84]. The ideal adsorbent would be an efficient, low-cost, and easily accessible material. Regarding the efficiency, for this process, it can vary from 50 to 90%, depending on the material. The limitations of this method are linked to the pH of the water, that must be optimized, and to the selectivity of the adsorbent, because often other ions like sulphate, phosphate, and bicarbonate, can compete [17]. Finally, the adsorbent material needs to be regenerated and sometimes this procedure is not easy and requires specific skills and materials and, in any case, it limits the cycle of use [85].
Another important method is the separation through membrane processes, like nanofiltration [86], reverse osmosis [87], electrodialysis [88], or the use of selective membranes [89]. These methods guarantee high removal efficiency (95%), with the advantage that colour and taste of the treated water are not affected by the treatment. However, the membranes are often subject to fouling problems, therefore they require maintenance by specialized personnel and the materials could be expensive or difficult to find on-site [90]. Electrodialysis is a membrane process utilizing charge-selective membranes and it is pressure-based. The most common configuration of electrodialysis utilizes a technique of periodically changing the polarity of the system electrodes returning in a reversed flow through the system, yielding some back-flushing of the membrane surface. This is known as electrodialysis reversal. Compared to the other membrane separation processes, it could have higher efficiencies, but it requires to have access to electricity, and the operation costs are higher.
5.
Conclusions
The starting point of our study is given by the weight value of the environment influence on the health of the resident human population [91,92,93,94].
The relations between environment and human health are strictly connected with the achieved equilibria of the elements playing a role in a region, residence site of a given population [95,96,97,98].
The existing anomalies in the distribution of some elements may be responsible of often strongly negative fall-outs, because of the overtaking of the internationally accepted concentration limits [99,100,101].
The example we discuss about in our study deals with Fluorine, its distribution in the surface waters, its origin, and its direct or indirect weight on the human health, and finally, on the techniques available today for the depletion of fluorine in water for human consumption, bearing in mind, however, the areas of the world where this problem is important and which are normally in rural areas of developing countries. F has been selected because its influence on the fluorosis distribution is already known, and because (as fluorite) it is the subject of our studies since long ago, being a very frequent component of the Sardinian ore deposits paragenesis.
Rift fracture systems are thus recognised as being the easiest way of upward migration of magmatic fluids, which are ultimately part of the residual melt that is often particularly enriched in fluorine.
Mixing with downward moving meteoric waters gives rise to very active hydrothermal solutions, so that fluorspar deposits frequently originate in suitable equilibrium conditions. The genetic temperature of fluorite is wide: it may participate in paragenetic sequences belonging to pneumatolytic up to epithermal conditions.
The proposed link between fluorite districts and continental rifts and lineaments [13] is continuously supported by the results of further studies. The emplacement of fluorspar deposits appears to be a major consequence of very intense activity of F-bearing hydrothermal fluids along the important fault systems typical of rift structures or lineaments and displacements of regional to continental importance. The given examples of Sardinia and EAR show that the origin and consequent behaviour of fluorine is strictly controlled by the rift fracture systems. In this framework, the availability of fluorine for surface waters depends on two possible types of sources: a direct supply and an indirect supply. Directly from spring waters and ground waters fed by hydrothermal systems related to present rifting, and indirectly from the leaching of products of rift-related activities, such as fluorite-bearing deposits, sedimentary or meta-sedimentary rift-related sequences (Lake Kivu type), and volcanic or metavolcanic complexes emplaced along rift structures. The whole geological history of a given area must be taken into account in interpreting its present fluorine geochemistry, in order to detect possible past influences of rift structures on the evolution of its fabric. Fluorspar deposits must be considered only a possible end effect of hydrothermal systems that always form along rift fracture systems and lineaments, and involve huge volumes of F-rich solutions. In any case, these solutions are directly or indirectly responsible for the origin and geochemical balance of fluorine in the surface waters. On the other hand, the distribution of the elements on the surface is controlled by a number of processes, which are partly related to the human activity itself, and partly to natural phenomena of regional to planetary importance.
In conclusion, fluorite deposits are the best source of fluorine leaching by surface waters, and the measured values of waters in mineralised districts must be expected to be often highly anomalous, in comparison to the regional background. On this basis, we rely that this study will allow to identify areas particularly favorable to the onset of certain pathologies linked to high levels of geogenic fluorine, in order to prevent them, also through new impoverishment techniques that can be concretely adopted, even in particularly difficult suitable areas.
Acknowledgments
We wish to thank Prof. Roberto Valera for advice and continuous support in the original research.
This work was supported by grants from Fondazione di Sardegna (GETHERE, F71/17000190002) and Fondo FIR 2020 (1044/2009), Università degli Studi di Cagliari, to P.V.
Conflict of interest
The authors declare to have no potential conflicts of interest.









 DownLoad:
DownLoad: