Cities as innovation poles in the digital transition. The Italian case

1.   Introduction

In 1973, the classic Black-Scholes (BS) model ^[1] provided an effective method for pricing financial derivatives and greatly simplifying the pricing process. Since then, many scholars have conducted research and promoted the model ^[2,3]. Asian options, a special type of financial derivative, are appealing due to their unique valuation method, which relies on the mean value of the underlying asset over a set contract period.

However, the BS model may not align with actual financial markets and could fail to provide accurate pricing for complex financial derivatives. In 1968, Mandelbrot and Van Ness ^[4] proposed a stochastic process: fractional Brownian motion (fBm). If the Hurst parameter $H \ne \frac{1}{2}$, the fractional Brownian motion is not a semi-martingale, which implies that there must be arbitrage opportunities ^[5,6]. Bojdecki et al. ^[7] advanced that sub-fractional Brownian motion (sfBm), which not only possesses similar properties to fractional Brownian motion but also features non-stationary increments with weaker correlations on non-overlapping intervals and a faster decay of covariance, aligns better with financial market dynamics. Based on this, Tubor ^[8] investigated new properties of sfBm. Xu and Li ^[9] tackled the valuation conundrum linked to compound options. For further applications of sfBm in financial models, please refer to ^[10,11,12]. Despite these advancements, the use of sfBm as a stochastic driver may still result in arbitrage opportunities akin to those associated with fBm. Zhang and Xiao ^[13] showed that the Black-Scholes model driven by fractional Gaussian processes allows for arbitrage opportunities. Since sub-fractional Brownian motion is a more general Gaussian process and is also not a semi-martingale, the application of this model to financial markets necessitates the study of arbitrage possibilities. EI-Nouty and Zili ^[14] proposed the concept of mixed sub-fractional Brownian motion (msfBm), which lies between Brownian motion and sfBm. The mixed sub-fractional Brownian motion incorporates the semi-martingale condition when $H \in \left({\frac{3}{4}, 1} \right)$, making this stochastic process more suitable for inclusion in option pricing models ^[15]. Furthermore, constructing an appropriate portfolio can enable models with the Hurst parameter $H \in \left({0, 1} \right)$ to avoid arbitrage in financial markets ^[16]. For example, Guo et al. ^[17] combined the fractal option pricing model with a new intelligent algorithm to predict the implied volatility in financial assets. Cai et al. ^[18] found the LSE of the drift parameter of mixed sub-fractional O-U process.

The aforementioned studies collectively presupposed fixed short-term interest rates, which do not reflect the dynamic nature of real interest rates that exhibit mean reversion. The Vasicek model ^[19], a fundamental interest rate model in finance, describes the evolution of interest rates and has become a cornerstone in the analysis and management of interest rate risks. It provides a theoretical framework that aids in making informed financial decisions and developing sophisticated risk management strategies. Ewald et al. ^[20] priced options for Asian commodity futures contracts by incorporating stochastic convenience yields, stochastic interest rates, and commodity spot prices, and considered the scenario with jumps. More related studies can be found in ^{[21,22,23,24,25]} to further understand the importance of stochastic interest rate models in option pricing. Building on these studies, in this paper, a model for pricing geometric average Asian options is formulated under the msfBm regime, while the short rate follows the Vasicek process.

Then, in Section 2, we state the necessary foundational knowledge. In Section 3, we provide the formula for a zero-coupon bond under the msfBm, based on certain assumptions. In Section 4, we give the solution for valuing geometric average Asian options with fixed strike price. In Section 5, we present relevant numerical calculations and an empirical study to further explore the effects of varying parameters on the model.

2.   Preliminaries

The Vasicek model is recognized as a significant model for the short rate that can be combined with other pricing models. The incorporation of mixed sub-fractional Brownian motion can offer more comprehensive risk management solutions. Now, we introduce the relevant knowledge of msfBm, which is covered in ^[7,14,26].

Definition 2.1. The Gaussian process ${\xi _H} = \{ {\xi _H}\left(t \right), t \geqslant 0\}$ defined on a probability space $\left({{{\Omega }}, \mathcal{F}, P} \right)$ that satisfies the following conditions

(1) ${\xi _H}\left(0 \right) = 0,$

(2) $E\left({{\xi _H}\left(t \right) \cdot {\xi _H}\left(s \right)} \right) = {s^{2H}} + {t^{2H}} - \frac{1}{2}\left[{{{\left({s + t} \right)}^{2H}} + {{\left| {t - s} \right|}^{2H}}} \right],$

is called a sub-fractional Brownian motion, where $H$ is the Hurst parameter with a value range of $\left({0, 1} \right)$, and ${B_H}(t)$ is a standard Brownian motion when $H = \frac{1}{2}$.

Definition 2.2. Let $\left({{{\Omega }}, \mathcal{F}, P} \right)$ be a probability space. The mixed sub-fractional Brownian motion ${M^{\beta, \gamma, H}} = \left\{ {M_t^{\beta, \gamma, H}, t \geqslant 0} \right\}$is a stochastic process with $H \in \left({0, 1} \right)$, defined by

where $B\left(t \right)$ is a Brownian motion and ${\xi _H}\left(t \right)$ is a sub-fractional Brownian motion. We have

where $M_t^{\beta, \gamma, H}$is a sfBm when $\beta = 0$ and $\gamma = 1$, $M_t^{\beta, \gamma, H}$ is a standard Brownian motion when $\beta = 1$ and $\gamma = 0$ or when $\beta = 0$, $\gamma = 1$ and $H = \frac{1}{2}$.

Definition 2.3. Asian options are divided into geometric average Asian options and arithmetic average Asian options. Taking fixed strike Asian call options as an example, the payoff is ${\left({{J_T} - K} \right)^ + }$, where $K$ is the strike price, $T$ is the expiration date, and ${J_t}$ is the average price of the underlying asset over the predetermined interval. In continuous time, the arithmetic average is represented by

the geometric average is represented by

Then, we present some basic assumptions of this paper.

(ⅰ) Short selling is allowed without penalty; there are no taxes and friction; stocks do not pay dividends; investors borrow and lend at the risk-free rate.

(ⅱ) The stock price $S\left(t \right)$ satisfies the mixed sub-fractional Brownian motion of risk neutrality, given by

where $r\left(t \right)$ is a short rate and satisfies the following msfBm-Vasicek model

where ${\sigma _{{S_1}}}$, ${\sigma _{{S_2}}}$, ${\sigma _{{r_1}}}$, and ${\sigma _{{r_2}}}$ are constants, ${B^S}\left(t \right)$, $\xi _H^S\left(t \right)$, ${B^r}\left(t \right)$, and $\xi _H^r\left(t \right)$ are independent of each other.

3.   Pricing formula for zero-coupon bond

A zero-coupon bond is issued at a price below its face value and does not pay any interest during the period. Upon maturity at time $T$, investors are entitled to receive a cash return equivalent to $\$$1. The price of such a bond is influenced by the passage of time and the variability in interest rates. We denote the price of a zero-coupon bond at time $t$, maturing at time $T$, as $P\left({r, t; T} \right)$.

Theorem 3.1. In the mixed sub-fractional Vasicek process, the price of a zero-coupon bond with maturity $T$ at time $t \in \left[{0, T} \right]$ is given by

where

Proof. By using the risk hedging formula and Itô formula ^[19], select two zero-coupon bonds with different maturities, denoted as ${P_1} = {P_1}\left({r, t; {T_1}} \right)$ and ${P_2} = {P_2}\left({r, t; {T_2}} \right)$, to hedge the risks. Now consider a portfolio $\Pi$ consisting of one unit of ${P_1}$ and $\Delta$ units of ${P_2}$, we can obtain

The change in the portfolio over the time interval $\left({t, t + {\text{d}}t} \right)$ is given by

where ${\left({{\text{d}}r} \right)^2} = \left({\sigma _{{r_1}}^2 + 2H{t^{2H - 1}}\left({2 - {2^{2H - 1}}} \right)\sigma _{{r_2}}^2} \right){\text{d}}t + o\left({{\text{d}}t} \right).$

Let $\Delta = \frac{{\partial {P_1}/\partial r}}{{\partial {P_2}/\partial r}}$, Eq (3.2) becomes

Furthermore, since the investment portfolio is risk-free, that is, $E\left({{\text{d}}\Pi } \right) = r\left(t \right)\Pi {\text{d}}t$, we have

Then, we can obtain

Thus, the zero-coupon bond $P\left({r, t; T} \right)$ satisfies the following partial differential equation given by

Given that $A\left({T, T} \right) = 0$ and $B\left({T, T} \right) = 0$, it is not difficult to find a solution for the price of a zero-coupon bond at time $t$ of the following form

Substituting Eq (3.6) into Eq (3.5), we can derive

After simplification, we have

Then, we can obtain

Proof is completed.

4.   Valuation equation for geometric average Asian options

In this section, examine a mixed sub-fractional version of the BS model, i.e., a simple financial market consisting of zero-coupon bonds, underlying assets, and options on underlying assets.

Theorem 4.1. The value of geometric average Asian call options with fixed strike price is denoted as $V = V\left({S, J, r, t} \right)$. Based on assumptions (2.1) and (2.2), the partial differential equation and boundary conditions are given by

Proof. Considering that the portfolio $\Pi$ consists of one unit option $V\left({S, J, r, t} \right)$, ${\Delta _{1t}}$ units of underlying assets and ${\Delta _{2t}}$ units of zero-coupon bonds $P\left({r, t; T} \right)$, the value of the portfolio at time $t$ is given by

Choosing the appropriate ${\Delta _{1t}}$ and ${\Delta _{2t}}$ makes the portfolio risk-free in $\left({t, t + {\text{d}}t} \right)$, we can obtain

Let ${\Delta _{1t}} = \frac{{\partial V}}{{\partial S}}$ and ${\Delta _{2t}} = \frac{{\partial V/\partial r}}{{\partial P/\partial r}}$, using the principle of no arbitrage, we have

we can calculate that

Proof is completed.

Theorem 4.2. Assuming that the stock price satisfies Eq (2.1), and the interest rate satisfies Eq (2.2), the price of the geometric average Asian call option at time $t \in \left[{0, T} \right]$ with strike price $K$ and maturity date $T$ is given by

where

Proof. To simplify the variable-coefficient equation with three variables down to one with two variables, we perform a variable substitution. Thus, let

Sometimes, we denote $P\left({r, t; T} \right)$ as $P$ to simplify notation. Then, through calculation, we have

Substituting Eq (4.5) into Eq (4.1) and organizing it, we can obtain

By integrating Eqs (4.4) and (3.5), we can derive

where

By substituting the deformation of Eq (4.4) into Eq (4.6), the equation can be transformed into

where ${\beta _2}\left(t \right) = - A\left({t, T} \right) - rB\left({t, T} \right).$

To simplify Eq (4.7), we can make the following variable substitution

It can be determined that

Substituting the above results into Eq (4.7), we find that

where ${\beta _3}\left(t \right) = {\left({\frac{{T - t}}{T}} \right)^2}\beta _1^2\left(t \right)$ and ${\beta _4}\left(t \right) = \frac{1}{T}{\beta _2}\left(t \right) - \frac{{T - t}}{T}\beta _1^2\left(t \right)$.

The last time using variable substitution to simplify Eq (4.10) into a heat conduction equation, let

It can be deduced that

Then, Eq (4.10) can be converted to

According to the heat conduction theory, the solution of this equation can be expressed as

where

Substituting Eq (4.8) into Eq (4.14), we can obtain

where

Combining Eqs (4.4) and (4.15), it follows that

where

Proof is completed.

Theorem 4.3. The call-put parity relationship for geometric average Asian options with fixed strike price is given by

where $p\left({S, J, r, t} \right)$ is the price of geometric average Asian put options and

Proof. Let

According to Theorem 4.1, $W\left({S, J, r, t} \right)$ satisfies the following definite solution problem

Making the following variable substitutions

Substituting Eq (4.17) into Eq (4.16), we have

where

Let

By inserting Eq (4.19) into Eq (4.18), this yields

where

By letting

then, we can obtain

and

To solve Eq (4.22), we select appropriate $a\left(t \right)$ and $b\left(t \right)$ so that

Thus, we can derive

where

Substituting Eqs (4.21) and (4.23) into Eq (4.17), we have

Proof is completed.

Corollary 4.1. Let the price of the arithmetic average Asian call options with fixed strike price be denoted as $\hat V\left({S, J, r, t} \right)$, and let the price of the put options be $\hat p\left({S, J, r, t} \right)$. The put-call parity formula for arithmetic average Asian options is

where

Proof. Denoting

According to Theorem 4.1 and Theorem 4.3, we can similarly derive

By employing a change of variables, we define

Substituting Eq (4.25) into Eq (4.24), we can obtain

where

Let

By substituting Eq (4.27) into Eq (4.26), we can deduce

Let

then, we have

and

By combining Eqs (4.28) and (4.30), we can compare the coefficients to obtain

Solving the aforementioned system of equations yields

Finally, we can derive

5.   Numerical analysis

In this section, we provide specific values for each parameter to conduct the following numerical calculations.

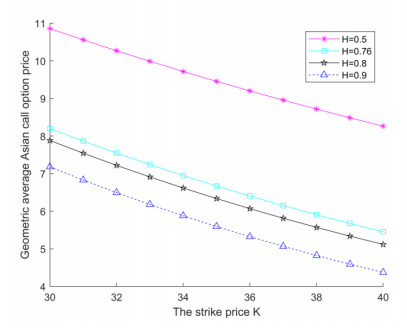
From Figure 1, it can be observed that when $H = 0.5$, the msfBm simplifies to a geometric Brownian motion. At this point, the price of geometric average Asian call options peaks, whereas it reaches its minimum at $H = 0.9$. An increment in the Hurst index is indicative of the manifestation of long-range correlations in the asset price, suggesting a persistent price trend. In specific situations, the expected small fluctuations in the asset price in the market will lead to a decrease in the option value. Figure 2 indicates that as the short rate rises, the price of the options gradually increases. This is because an increase in the interest rate could potentially raise the payoff of the options at maturity, thereby enhancing the holding value of the options. Figure 3 shows that the valuation of the options is positively influenced by a rise in the initial stock price. From Figure 4, the price of the options increases with the extension of the expiration date. As the remaining time for the option contract increases, it gives the holders more time to wait for a potential rise in the stock price. Therefore, the possibility of the investors making a profit is greater, and the price of the options will also increase accordingly. Conversely, it diminishes with an upsurge in the strike price. As the strike price increases, buyers have to pay a higher price to exercise the options, which compresses the profit margin and thus reduces the value of the options. Figure 5 illustrates that the pricing of options under the current model closely mirrors that of the sub-fractional Vasicek model. Notably, the pricing discrepancy for options between our model and Vasicek model widens initially and then narrows, and the pricing gap between our model and BS model exhibits a consistent upward trend.

According to Tables 1 and 2, it can be observed that the lowest pricing for geometric average Asian call options is associated with the BS model. In the case of a brief expiration period, the price of the options under the sfBm-Vasicek model marginally surpasses that of our model, especially with an increasing stock price, and there is minimal variation between the two models. For longer expiration dates, the option price under our model exceeds that under the sfBm-Vasicek model, with the price difference becoming more pronounced. Moreover, the price of options under our model and the Vasicek model are getting closer. Overall, our model demonstrates a degree of rationality and is deemed suitable for developing option pricing models in financial markets.

We select copper options for three-month futures as the sample, with a cutoff time of October 2006, and the data are sourced from the London Metal Exchange. Since all trading products on the LME are priced in US dollars, we adopt the interest rate of one-year US Treasury bonds.

We calculate the value of $H$ using the R/S method. Define a return sequence $\left\{ {{R_t}, {R_t} = \frac{{\ln {P_{t + 1}}}}{{\ln {P_t}}}} \right\}$ of length $N$ and divide it into $A$ consecutive sub-intervals of length $n$. Label each sub-interval as ${I_a}, a = 1, \cdots, A.$ Thus, each point in ${I_a}$ can be represented as

For each sub-interval ${I_a}$ of length $n$, calculate its mean as

The cumulative mean deviation ${X_{k, a}}$ for a single sub-interval is calculated as

The sum of the cumulative mean deviation sequence $\left\{ {{X_{1, a}}, {X_{2, a}}, \cdots {X_{n, a}}} \right\}$ for a single sub-interval is zero. The range of an individual sub-interval is defined as

Subsequently, the standard deviation ${S_{{I_a}}}$ for each sub-interval is given by

Therefore, for the partition length $n$, we can compute the average rescaled range for $A$ sub-intervals as

Repeat the above calculation process for different partition lengths (i.e., different time scales) n to obtain multiple average rescaled range values. There is a linear relationship between $\log \left({\frac{R}{S}} \right)$ and $\log \left(n \right)$ ^[27]

Finally, a double logarithmic regression is performed on $n$ and R/S, and the slope is the parameter of long-range correlations, that is, the Hurst index. Therefore, we can obtain $H = 0.6$.

From Table 3, it is evident that the RMSE of our model is the smallest, indicating that the option price derived from our model is the closest to the market price. Furthermore, the price from our model is also quite close to that of the sfBm-Vasicek model. This suggests that it is essential to include factors such as the long-range correlations of the underlying asset and stochastic interest rate in the option pricing model, as they significantly influence the option price.

6.   Conclusions

Geometric average Asian options are important exotic options. The mixed sub-fractional Brownian motion, chosen as a stochastic process, is capable of more accurately depicting the characteristics of long-range correlations. Since the Vasicek model is a very classical model, it is combined with the msfBm to simultaneously address the pricing issue. By using partial differential equations and multiple variable substitution methods, the valuation equations for the model are deduced. Finally, numerical computations are utilized to assess the effects of diverse parameters. The efficacy of our model is demonstrated through a comparative analysis of the pricing discrepancies for options between different models, which provides a reference for option pricing theory and practice.

Author contributions

Xinyi Wang: Conceptualization, Methodology, Writing—original draft, Writing—review & editing, Funding acquisition; Chunyu Wang: Writing—review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work was supported by the General Project of Philosophy and Social Science Research in Colleges and Universities of Jiangsu Province (2023SJYB1714).

Conflict of interest

The authors declare no conflicts of interest.