Transferring monolingual model to low-resource language: the case of Tigrinya

1.   Introduction

In much of the literature, time fractional models are defined using the Caputo definition ^{[32,33,34,35,36]}, in which time fractional models are models described by fractional differential equations or pseudo state space descriptions. The Caputo definition is widely acclaimed because it makes it possible to define initial conditions that relate to the integer derivatives of the derived functions in the models considered. However, this paper shows that this definition does not take initial conditions properly into account if used to define a time fractional model.

The problem was analysed for the first time by Lorenzo and Hartley ^[1,2]. To take the past of the model into account in a convenient way in a finite interval, they introduced an initialization function. The idea of replacing the commonly used initial values by an initial function was further developed in ^[3]. In ^[4], the need to consider the "prehistories" before the initial instant of the derivate functions was shown, making it possible to address the initialisation of fractional visco-elastic equations to reach a unique solution. In ^[5,6], a counter example was used to demonstrate that initial conditions cannot be correctly taken into account in a dynamical model whether by Caputo or Riemann-Liouville definitions. This led to the conclusion in ^[7] that fractional derivative and time fractional model initializations are two distinct problems. Still using an initial time shifting method, counter examples were proposed in ^[8] to show similar initialisation problems with the Caputo definition for partial differential equations. A time shifting technique was also recently used in ^[9] to analyse a groundwater flow model with time Caputo or Riemann-Liouville fractional partial derivatives. The non-objectivity of these models was demonstrated in this paper. The authors in ^[9] did not address the problem of initialization, but this objectivity can be restored by also introducing an initialization function (instead of initial conditions).

As previously mentioned, several studies and several solutions have already been published on initialisation of fractional models, but many papers in which the initial conditions are taken into account incorrectly are also still published. Thus the novelties and the contributions of the paper are new demonstrations and new simulations that highlight how initialisations must be done with a time fractional model. Thus, in this paper, two examples are used to show that the Caputo definition does not enable initial conditions to be correctly handled when this definition is used to define a time fractional model. In the first example, the response of a simple model, assumed to be at rest, is calculated analytically on a given time interval. Then inside this interval, a second response is computed by considering initial conditions resulting from the first simulation, and ignoring the model past before the considered initial time. This is the initialisation currently found in the literature and this example shows that it is unable to ensure the correct model trajectories. In the second example, two different histories are generated that produce the same initial conditions for the model. This example shows that in spite of equal initial conditions, the model response is different, thus showing that all the model past must be taken into account to define its future. A similar analysis is also carried out with the Riemann-Liouville and the Grünwald-Letnikov's definitions, suggesting that other definitions should also be problematic. Note that all the analyzes carried out and conclusions obtained in this paper relate to models involving only time fractional derivatives and not space fractional derivatives as in ^[29,30,31].

2.   Problem analysis with Caputo's definition

The fractional integral of order $\nu$, $0 < \nu < 1$, of a function $y\left(t\right)$ is defined by ^[10]:

$\varGamma \left(.\right)$ being Euler's gamma function. From this definition, the Caputo derivative definition of order $\nu$, $0 < \nu < 1$, of a function $y\left(t\right)$ is defined by ^[11]:

Laplace transform applied to relation (2) reveals how initial conditions are associated to this definition:

To demonstrate that Caputo definition is not able to take initial conditions correctly into account when used to define a time fractional model (a fractional differential equation or a pseudo state space description), the following model is considered

In relation (4), ${\boldsymbol{D}}^{\boldsymbol{\nu }}$ denotes the Caputo definition in this section but denotes the Riemann-Liouville or Grünwald-Letnikov definitions in the next section. Then, the following algorithm is used to study model (4).

Algorithm 1

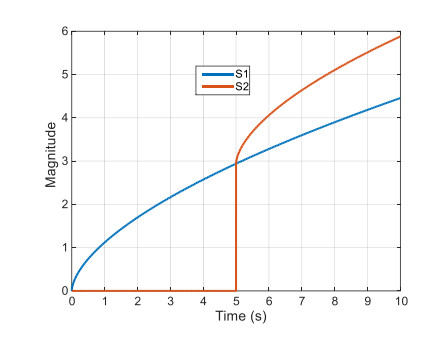
1-Simulation on the time interval $\left[0, {\rm{t}}_{1}\right]$ of the time fractional model (for instance model (4)) with null initial conditions (for $\rm{t}\in \left]-\rm{\infty }, 0\right]$). Let ${\rm{S}}_{1}$ denote this simulation.

2-Record the model output $\rm{y}\left(\rm{t}\right)$ and the integer derivatives of $\rm{y}\left(\rm{t}\right)$ (denoted $\rm{y}\rm{\text{'}}\left(\rm{t}\right)$, $\rm{y}\rm{\text{'}}\rm{\text{'}}\left(\rm{t}\right)$, ….) at time ${\rm{t}}_{0}$ such that $0 < {\rm{t}}_{0} < {\rm{t}}_{1}$.

3-Simulate the model again on $\left[{\rm{t}}_{0}, {\rm{t}}_{1}\right]$, using $\rm{y}\left({\rm{t}}_{0}\right)$, $\rm{y}\rm{\text{'}}\left({\rm{t}}_{0}\right)$, $\rm{y}\rm{\text{'}}\rm{\text{'}}\left({\rm{t}}_{0}\right)$ … as initial conditions. Let ${\rm{S}}_{2}$ denote this simulation.

4-Compare ${\rm{S}}_{1}$ and ${\rm{S}}_{2}$ on $\left[{\rm{t}}_{0}, {\rm{t}}_{1}\right]$ and notice if they are different.

Algorithm 1 is now applied to model (4) with $a = 0$. The model is assumed to be at rest before $t = 0$, and the input $u\left(t\right)$ is assumed to be a Heaviside function $H\left(t\right)$. In such conditions, relation (4) is equivalent to ^[11]

As a consequence, the simulation defined in Algorithm 1 provides the following solutions:

Figure 1 proposes a comparison of ${S}_{1}$ and ${S}_{2}$ and reveals a difference, thus demonstrating that the Caputo definition does not correctly take initial conditions into account.

Another way to illustrate this result is to consider two different input signals ${u}_{1}\left(t\right)$ and ${u}_{2}\left(t\right)$ that create two different histories with:

The model is assumed to be at rest on $t\in \left]-\infty, {t}_{i}\right]$. A constraint is also imposed on these signals so that at $t = 0$, the two resulting model outputs coincide:

The output ${y}_{i}\left(t\right)$ is thus defined by:

where ${E}_{\alpha, \beta }^{\gamma }\left(z\right)$ is the Mittag-Leffler function defined by ^[12]:

Condition (9) thus leads to

thus leading to the condition:

With $\nu = 0.4$, $a = 1$, ${t}_{1} = -8s$, ${t}_{2} = -2s$, ${A}_{2} = 5$ and thus ${A}_{1}\approx 4.17$, Figure 2 shows the signal inputs ${u}_{1}\left(t\right)$ and ${u}_{2}\left(t\right)$ used for the analysis and proposes a comparison of the resulting outputs. This figure shows that the two responses have the same values at $t = 0$, but that the evolutions for $t>0$ are not the same. The information at $t = 0$ is thus not enough to predict the future of the model. All the past must be taken into account to predict the future of the model, which confirms that initialization as defined by the Caputo definition is not acceptable if used to define a time fractional model such as (4).

3.   Analysis with other definitions

The previous section showed that the Caputo definition should no longer be used to define time fractional models such as (4). What about other definitions?

3.1.   The Riemann-Liouville definition

The Riemann-Liouville derivative of order $\nu$, $0 < \nu < 1$, of a function $y\left(t\right)$ is defined by ^[11]:

Laplace transform applied to relation (14) reveals how initial conditions are associated to this definition:

As a consequence, in ^[11,13], the initialisation of relation (4) is defined by

and thus the initialisation problem of relation (4) is equivalent to the integral equation

Algorithm 1 is applied again to model (4) with $a = 0$. The model is assumed to be at rest before $t = 0$, and the input $u\left(t\right)$ is assumed to be a Heaviside function $H\left(t\right)$. Algorithm 1 provides the following solutions:

Relation (19) seems to say that any value of ${y}_{0}$ can be chosen, but whatever the value selected, for ${S}_{2}$ $y\left(t\right)$ tends toward infinity as $t$ tends toward ${t}_{0}$ if ${y}_{0}\ne 0$ whereas $y\left(t\right) = {{t}_{0}}^{\nu }/\rm{\Gamma }\left(\nu +1\right)$ for ${S}_{1}$. The two simulations thus give different results. This is illustrated by Figure 3 for various values of ${y}_{0}$.

3.2.   The Grünwald-Letnikov definition

The Grünwald-Letnikov derivative of order $\nu$, $0 < \nu < 1$, of a function $y\left(t\right)$ is defined by:

with $\left(\begin{array}{c}\nu \\ m\end{array}\right) = \frac{\rm{\Gamma }\left(\nu +1\right)}{m!\rm{\Gamma }\left(\nu -m+1\right)} = \frac{\nu \left(\nu -1\right)\left(\nu -2\right)\dots \left(\nu -m+1\right)}{m\left(m-1\right)\left(m-2\right)\dots \left(m-m+1\right)}$.

This definition is often used in the literature as it provides a simple numerical scheme for fractional derivative implementation. In some research ^[14,15,16], these numerical schemes are used to solve the initialisation problem:

In this case, it is not the Grünwald-Letnikov derivative definition which is questionable, but the idea that a time fractional model can be initialized solely with information on the initial moment. From relation (20), it is possible to observe that variable $m$ goes from 0 to infinity, and thus this definition is able to take into account the past of the derivative function, prior to ${t}_{0}$. In (21), the problem is the way the initial conditions are defined.

To illustrate this problem, Algorithm 1 is applied to model (4) with $a = 1$. The model is assumed to be at rest before $t = 0$, and the input $u\left(t\right)$ is assumed to be a Heaviside function $H\left(t\right)$. In such conditions, the simulation ${S}_{1}$ defined in Algorithm 1 provides the following solution:

Simulation ${S}_{2}$ is done using the Grünwald-Letnikov formula (20) and provides

This simulation is done under two conditions:

- ${S}_{21}:$ by taking into account all the past of the model (all the values of $y\left(t\right)$ on $t\in \left[0, {t}_{0}\right]$, provided by ${S}_{1}$)

- ${S}_{22}:$ by considering only an initial condition at ${t}_{0}$ (value of $y\left(t\right)$ at ${t}_{0}$ provided by ${S}_{1}$).

The comparison of the three simulations is done in Figure 4 and reveals that the Grünwald-Letnikov definition produces an exact solution provided that all the past of the model is taken into account.

Relation (23) is particularly interesting because it shows that a time fractional model (here a fractional integrator) is represented by an infinite difference equation, and therefore an initialization of all its terms is necessary for a prediction of the output $y\left(t\right).$

This remark could also apply to the Caputo and Riemann-Liouville definitions which would lead to their reformulations with integrals on the interval $\left]-\rm{\infty }, \rm{ }t\right]$ as suggested in ^[27],

4.   Need to take into account all of the model past

The need to take into account the all past of a time fractional model and not just the knowledge of its pseudo state at a single point in the past can be demonstrated quite simply on relation (4) (a particular case of fractional differential equation or of pseudo state space description). Contrary to what relation (4) might suggest, Figure 5 highlights that the implementation of fractional differential equations does not explicitly involve the fractional differentiation operator but the fractional order integration operator ${\boldsymbol{I}}^{\boldsymbol{\nu }}$. Thus in practice, it is not necessary to specify which particular definition is used for ${\boldsymbol{D}}^{\boldsymbol{\nu }}$ in equation (4). Moreover, even if the system is assumed to have zero initial conditions at $t = 0$, namely if the system is supposed at rest ($u\left(t\right) = y\left(t\right) = 0$, $\forall t < 0$), it is important to note that $y\left(t\right)$ cannot be considered as a state for the time fractional model and that all the past of $y\left(t\right)$ is required to compute the model evolution.

To better illustrate such a concept, a simple time fractional model is used: a fractional integrator supposed at rest at $t = 0$. The corresponding block diagram is shown in Figure 6.

For an integer integrator, $\nu = 1$, relation (4) is really a state space description. At ${t}_{1}>0$, state $y\left(t\right)$ can be computed if the input between 0 and ${t}_{1}$ is known:

Values of $y\left(t\right)$ at later times than ${t}_{1}$ are given by:

Thus, $y\left(t\right)$ can be computed if $\underline{x}\left(t\right)$ is known within ${t}_{1}$ and $t$. Integrator output at time ${t}_{1}$ thus summarizes the whole model past. $y\left(t\right)$ is really the state of the dynamic model, in agreement with the definition given in ^[26].

Let us apply the same reasoning to the fractional integrator case of order $\nu$. From the definition of fractional integration, value of $y\left(t\right)$ at ${t}_{1}>0$ can be computed if the input between $t = 0$ and ${t}_{1}$ is known:

Variable $y\left(t\right)$, $\forall t>{t}_{1}$, is thus given by:

Two notable differences can be highlighted with respect to the integer case. First, term $\alpha \left(t\right)$ in equation (27) is not a constant but depends on the considered time $t$. Moreover, even if ${y}_{1} = y\left({t}_{1}\right)$ is known, it is not enough to compute $\alpha \left(t\right)$. Output $y\left(t\right)$ of the fractional integrator is thus not a state. The same analysis can be held for the general case of a pseudo state description or a fractional differential equation.

Beyond discussions on the concept of state, computation of $\alpha \left(t\right)$ in relation (27) whatever time $t$, requires to know $y\left(t\right)$ $\forall t\in \left[0..{t}_{1}\right]$, thus all the model past. This clearly shows that knowledge of $y\left(t\right)$ at a unique point of the past is not enough.

5.   Conclusions

Fractional operators and the resulting time fractional models are known for their memory property. However, for the following two reasons, many studies proposed in the literature seem to ignore this property when the model initialization problem is considered:

-they use the Caputo definition that involves only integer derivatives of the derivate function at the initial time,

-they use other definitions but initialization is done by taking only an initial value for the initial time into consideration.

This kind of initialization means that the operator or model memory exists everywhere on the time axis, except at the initial time. This is not consistent. Memory is an intrinsic property that exists all the time and that is proved in this paper with very simple examples. If from a mathematical point of view, most of the fractional derivative definitions encountered in the literature ^[17] are not problematic, this paper shows that the Caputo and Riemann-Liouville definitions are not able to ensure a proper initialization when used in a model definition. The paper also shows that this problem is not encountered with the Grünwald-Letnikov definition, provided that all the past of the model (from $t\to -\infty$) is taken into account. And this is precisely one of the drawbacks of time fractional models that induces a physical inconsistency and many analysis problems ^[17].

What are the possible solutions? One solution can be to add an initialization function to the definition of the model. This is what was proposed by Lorenzo and Hartley ^[1,2]. Yet again however, it requires the knowledge of all the model past (from $t\to -\infty$). Another solution consists in introducing new kernels for the definition of fractional integration as in ^[19]. But the goal would not be to solve only a singularity problem as in ^[19], but to reach a finite memory length as was done for instance in ^[20]. Note that while it was claimed in ^[21] that this class of kernels was too restrictive, it is linked to the problem analyzed in this paper: the inability of the Caputo definition to take into account initial conditions properly if used to define a time fractional model ^[22]. The other solution is to introduce new solutions for fractional behavior modeling, without the drawbacks associated to time fractional models ^[18]:

-distributed time delay models ^[23];

-non-linear models ^[24];

-partial differential equation with spatially varying coefficients ^[25].

All the conclusions presented in this paper can they be extended to models involving space fractional derivatives as in ^[29,30,31]? As shown in ^[28], whatever the variable on which the derivative relates, a fractional model remains a doubly infinite dimensional model and as such requires an infinite amount of information for its initialization. The question remains open, however, the authors will seek to answer it in their future work.