Stability prediction of circular sliding failure soil slopes based on a genetic algorithm optimization of random forest algorithm

1.   Introduction

Landslide disasters are influenced by multiple factors, and their combination and interaction can be complex. Traditional technical methods for investigating landslides have low efficiency and poor precision. Additionally, the characteristics of landslide disasters, such as their hidden, sudden, and uncertain nature, make them difficult to predict and prevent. Therefore, it is crucial to develop more effective methods for disaster reduction and prevention. The machine learning method can extract hidden rules and features from large amounts of data, enabling accurate research and assessment of landslide stability.

Machine learning methods have advanced the development of geological disaster prevention and mitigation towards intelligence ^[1,2]. In the field of intelligent landslide disaster prevention and mitigation, common machine learning methods that consider both classification and regression functions include naive Bayes, logistic regression, and K-nearest decision tree. These models are intuitive and easy to implement. More complex and effective methods include support vector machines, random forests, and extreme gradient boosting. Many scholars have explored these methods.

With the rapid development of machine learning (ML) as a Data Science branch, and its spread over many engineering fields, many researchers have started looking into disciplinary or thematic applications of ML methods ^[3,4]. For instance, Hossein et al. investigated the applicability of machine learning based model combination in slope stability assessment ^[5,6]. They compared several algorithms by estimating the factor of safety (FOS) for slope stability evaluation and concluded that random forest (RF) outperforms other intelligent models; Kardani et al. used a hybrid stacking ensemble method with the artificial bee colony (ABC) algorithm to select the best combination of classifiers from a pool of 11 individual optimized machine learning (OML) algorithm classifiers and determine a suitable meta-classifier ^[7]. They found that the hybrid stacking ensemble method outperformed the basic ensemble method. Mahmoodzadeh et al. employed six machine learning techniques to forecast slope safety systems ^[8]. They found that Gaussian process regression was the most precise model for predicting slope stability among the various models tested. Ma and Mei introduced six typical deep learning models and reviewed the application of deep learning in geohazard analysis around six typical geological hazards such as landslides, and summarized common application examples ^[9]. Ahangari et al. investigated the performance of five machine learning models in predicting slope safety factor ^[10]. They estimated 70 slopes in the South Pars region (Southwest Iran) and found that the multilayer perceptron model had the highest rating. To quickly and accurately estimate the factor of safety. Habib et al. used advanced integrated machine learning techniques to calculate the factor of safety and comprehensively evaluated the performance of these integrated techniques in comparison with established methods such as finite element methods and empirical modeling, and identified their potential as robust and reliable alternatives in the field of slope stability assessment ^[11]. Bansal and Sarkar investigated the safety determination process under dry and saturated conditions using the limit equilibrium method and the commercial software Geo Studio ^[12]. They analyzed and compared the results using computational intelligence and machine learning methods. They identified the novel integrated method, R-Boost, to provide maximum accuracy; (Zhang et al.) clearly listed the advantages and disadvantages of the methods developed in these papers by reviewing papers published between 2002 and 2022 on the topic of applying ML to slopes ^[2], among others. Then, we focus on comparing three algorithmic models within the random forest model to determine the better prediction algorithm and parameter settings.

The random forest algorithm is a widely used and highly flexible method that is suitable for non-linear and high-dimensional data sets. However, parameter tuning is typically performed using either the grid search method or default values ^[2]. If the grid division is too small, it can result in long computation times and low efficiency. Conversely, if the grid division is too large, it can lead to the model falling into a local optimum, resulting in a poor model. Here, we present the GA-RF hybrid intelligent algorithm, which is based on the genetic algorithm and is used to optimize the random forest algorithm. The algorithm is then used to establish a slope stability prediction model. The GA-RF algorithm has a wider search space, which enables it to search for the optimal solution globally, and it has higher accuracy for the regression prediction of slope stability.

2.   A slope stability prediction model based GA-RF algorithm

2.1.   Basic principles of random forest model

The Random Forest algorithm is a machine learning method that comprises multiple decision trees ^[13]. Each decision tree is trained by randomly sampling samples and features from the training dataset. The random forest algorithm uses self-service resampling technology to generate a new set of training samples by randomly sampling n samples from the original training sample set N. This new set is then used to train the decision tree, which is then used to generate a random forest. The classification of new data is determined by a vote among the decision trees in the forest. The language has been made more objective, concise, and clear, with technical terms explained and passive tone employed. The sentence structure has been simplified and grammatical errors corrected. The content has not been changed beyond improving clarity and objectivity. Essentially, this is an enhancement of the decision tree algorithm that combines multiple decision trees. Each tree is established based on independently drawn samples.

2.1.1.   The decision tree algorithm

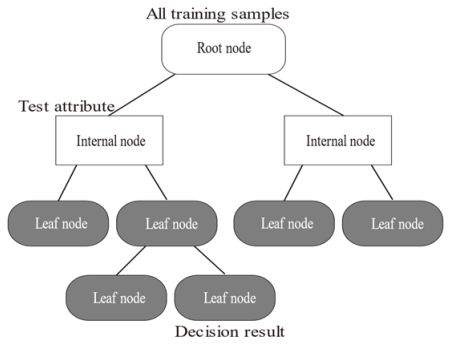
The decision tree model is a tree structure used for classification and regression. It consists of nodes and directed edges. Figure 1 shows a typical decision tree with a root node, internal nodes, and leaf nodes. The decision-making process for a decision tree should begin at the root node and compare the data to be measured with the feature nodes in the tree. The next comparison branch should be selected based on the comparison results until the leaf node is reached, which will provide the final decision result.

Figure 1.  Decision tree diagram.

DownLoad: Full-Size Img PowerPoint

Assuming that x and y are input and output variables respectively, and are continuous variables, assume that the training data set is as follows:

The feature vector is:

The n is the number of features, ${i}$ = 1, 2... N, N is the sample size.

Before partitioning, a feature subset is selected at random with equal probability from the feature vector. In each partition, all values of the features in the subset are traversed, and the optimal segmentation point is selected as the point with the smallest root mean square error. Write it as the $j$th feature variable in the training set and its value $s$, and define two regions:

And:

The optimal $j$ and $s$ are obtained by solving the following formula:

The optimal intersection point $(\mathrm{j}, \mathrm{s})$ can be found by solving the least squares error. This point is then used to minimize the sum of the squared errors of the two partitions. According to the theoretical proof, ${\mathrm{c}}_{1}$ and ${\mathrm{c}}_{2}$ represent the mean of the corresponding Y values in the two regions, respectively. The input space is divided into two regions based on the optimal segmentation points, and the partitioning process is repeated for each newly generated region until the stop condition is met. A regression tree, also known as a least squares regression tree, is constructed using this method.

After completing the division, the predicted values for the leaf nodes must be determined. If the output value on the leaf node is unique, it is taken as the predicted value. Otherwise, the predicted value for that leaf node is the average of all sample output values.

2.1.2.   Decision tree attribute partitioning

The selection of the partition attribute is a crucial step in constructing a decision tree. The goal is to have the samples belong to the same class as much as possible while the tree grows, resulting in reduced impurity of the nodes. To assess the impact of node partitioning, compare the impurity of the parent node before partitioning with that of the child node after partitioning. The evaluation of partitioning is based on the measurement of impurity reduction, as expressed in Eq (6).

The ${\Delta }_{I}$ indicates the degree to which the impurity is reduced. $I\left(parent\right)$ represents the amount of father node impurity; $k$ indicates the number of partition attribute values; $N\left(j\right)$ is the number of samples on the $j$th son node; $N$ represents the number of samples on the parent node; and $I\left(j\right)$ represents the impurity measure of the $j$th son node.

Given any node $t$, we need to define its measure of impurity, let $p\left(i\right)$ be the proportion of Class $i$ samples in node $t$, then the impurity measurement of node $t$ mainly includes the following three kinds.

1) Entropy: A measure that expresses the uncertainty of a random variable; the greater the entropy, the greater the uncertainty of the random variable.

2) Gini index: A measure of the purity of a node. It is used to assess the degree of mixing of samples in a node. The smaller the Gini index, the purer the samples in the node, i.e., the higher the percentage of samples belonging to the same category.

3) Misclassification rate: indicates the proportion of misclassified samples to the total number of samples in a classification problem.

2.1.3.   Bagging series algorithms

The Bagging Series Algorithms are an integrated learning approach designed to address data imbalances and enhance overall model performance by combining the prediction results of multiple base learners ^[14].

The Bagging algorithm involves obtaining the training set of the base learner through random sampling of the original samples. If there are M original samples, N sets of samples are taken. Each group of samples is obtained through random sampling with replacement, with a sample size of M. This results in N groups of sampling sets, which are trained independently to obtain N base learners. The Bagging algorithm is then used to combine these base learners into a strong learner. The probability of each sample in the original set not being selected is $(1-\frac{1}{M}{)}^{M}$. When M tends to converge to positive infinity, the$\underset{M\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}(1-\frac{1}{M}{)}^{M} = \frac{1}{e}$, approximately 36.8%. This indicates that about one-third of the samples in the original sample set are not included each time, effectively increasing the model's tolerance to noise. This method is suitable for poorly stabilized models or those prone to overfitting.

2.1.4.   Random forest algorithm modeling process

The random forest model is built as shown in Figure 2, which is a combination of Bagging integration algorithm and decision tree. The specific process is as follows:

1) The Bagging algorithm involves sampling the original sample from a set of M samples and then returning the completed samples to the sample set, where they may or may not be selected multiple times. This process generates N training sets;

2) Train with N training sets to generate N complete decision trees;

3) At each node of the decision tree, a subset of features is randomly selected from all available features. The data is then divided into two subsets by selecting the optimal splitting point based on the division criteria (e.g., entropy, Gini index, misclassification rate, etc.) described in Section 2.1.2 of this paper;

4) Finally, the generated multiple decision trees are composed into the final random forest. The decision tree categorizes the samples to be classified, records the number of votes for each category, and selects the category with the most votes as the final prediction result. For the regression problem, each decision tree predicts the samples to be predicted, and the final prediction result is obtained by calculating the average of the prediction results of all the decision trees.

Figure 2.  Schematic diagram of the random forest algorithm.

DownLoad: Full-Size Img PowerPoint

2.2.   Construction of slope stability prediction model based on GA-RF algorithm

We present the GA-RF algorithm, a hybrid intelligent algorithm that optimizes the genetic algorithm to the random forest algorithm. The algorithm exhibits lower variance, higher model stability, and a reduced propensity for overfitting at higher performance levels. Furthermore, the GA-RF algorithm enables the observation of feature importance, facilitating the visualization of the contribution of each parameter. The algorithm is used to establish a slope stability prediction model and intelligently evaluate the slope stability state. The establishment process involves four steps: feature variable selection and data set establishment, training set and test set division, data pre-processing, and model parameter optimization.

2.2.1.   Feature variable selection and data set establishment

Slope stability can be affected by a range of factors. Slope height ($H$), overall slope angle ($\beta$) and unit weight ($\gamma$) are the basic geometric design parameters of slopes, which determine the conditions of soil slope failure, and the slope stability decreases sharply with the increase of slope height; cohesion ($C$) and angle of internal friction ($\phi$) are the two key mechanical parameters related to the stability of slopes, particularly for the Mohr-Coulomb failure criterion; Pore water pressure has a more significant effect on the shear strength and stability of slope geotechnical bodies. Therefore, the slope stability analysis was conducted using six characteristic variables: slope soil weight ($\gamma$), slope height ($H$), pore pressure ($P$), cohesion ($C$), angle of internal friction ($\phi$), and slope inclination ($\beta$), were chosen as the characteristic variables for the slope stability analysis, and the slope factor of safety ($Fs$) was used as the quantitative index of the degree of slope stability.

We select 80 sets of sample data of circularly damaged slopes from Introduction to Intelligent Rock Mechanics written by Feng as the slope stability evaluation dataset ^[15]. The construction of random forests does not necessitate a vast number of samples; rather, it requires that the samples be representative. The 80 sets of samples are deemed to be sufficiently representative to meet this need. Each set of data samples contains two parts of eigenvectors as well as the corresponding safety coefficients. The text adheres to conventional structure, clear and objective language, formal register, precise word choice, and grammatical correctness. The content has not been changed beyond improving its adherence to the desired characteristics. The specific slope stability evaluation sample data set is shown in Table 1.

Table 1.  Data set of slope stability evaluation.

Nums.	($\gamma$)/ kN/m3	($C$)/kPa	($\phi$)/°	($\beta$)/°	($H$)/m	($P$)	$Fs$
1	12.00	0.00	30	35	8.00	0.32	0.86
2	23.47	0.00	32	37	214.00	0.32	1.08
3	16.00	70.00	20	40	115.00	0.32	1.11
4	20.41	24.91	13	22	10.67	0.35	1.40
5	19.63	11.97	20	22	12.19	0.41	1.35
6	21.82	8.62	32	28	12.80	0.49	1.03
7	20.41	33.52	11	16	45.72	0.20	1.28
8	118.84	15.32	30	25	10.67	0.38	1.63
9	18.84	0.00	20	20	7.62	0.45	1.05
10	25	120.00	45	53	120.00	0.32	1.30
11	25	55	36.00	45	239.00	0.25	1.71
12	25	63	32	44.50	239.00	0.25	1.49
13	25	63	32.00	46	300.00	0.25	1.45
14	25	48	40	45	330.00	0.25	1.62
15	31.3	68.60	37	47.50	262.50	0.25	1.20
16	31.3	68.60	37	47	270.00	0.25	1.20
17	31.3	58.80	35.5	47.50	438.50	0.25	1.20
18	31.30	58.80	35.5	47.5	502.70	0.25	1.20
19	31.30	68.00	37	47	360.50	0.25	1.20
20	31.30	68.00	37	8	305.50	0.25	1.20
21	18.68	26.34	15	35	8.23	0.32	1.11
22	16.50	11.49	0.00	30	3.66	0.32	1.00
23	118.84	14.36	25.00	20	30.50	0.32	1.88
24	18.84	57.46	20.00	20	30.50	0.32	2.05
25	28.44	29.42	35.00	35	100.00	0.32	1.78
26	28.44	39.23	38.00	35	100.00	0.32	1.99
27	20.60	16.28	26.5	30	40.00	0.32	1.25
28	14.80	0.00	17	20	50.00	0.32	1.13
29	14.00	11.97	26	30	88.00	0.32	1.02
30	21.43	0.00	20	20	61.00	0.50	1.03
31	19.06	11.71	28	35	21.00	0.11	1.09
32	18.84	14.36	25	20	30.50	0.45	1.11
33	21.51	6.94	30.00	31	76.81	0.38	1.01
34	14.00	11.97	26.00	30	88.00	0.45	0.63
35	18.00	24.00	30.15	45	20.00	0.12	1.12
36	23.00	0.00	20	20	100.00	0.30	1.20
37	22.40	100.00	45	45	15.00	0.25	1.80
38	22.40	10.00	35	45	10.00	0.40	0.90
39	20.00	20.00	36	45	50.00	0.50	0.83
40	20.00	0.00	36	45	50.00	0.25	0.79
41	20.00	0.00	36.00	45	50.00	0.50	0.67
42	22.00	0.00	40.00	33	8.00	0.35	1.45
43	24.00	0.00	40	33	8.00	0.30	1.58
44	20.00	0.00	24.5	20	8.00	0.35	1.37
45	18.00	5.00	30	20	8.00	0.30	2.05
46	27.00	40.00	35	43	420.00	0.25	1.15
47	27.00	50.00	40	42	407.00	0.25	1.44
48	27.00	35.00	35	42	359.00	0.25	1.27
49	27.00	37.50	35.00	37.8	320.00	0.25	1.24
50	27.00	32.00	33.00	42.6	301.00	0.25	1.16
51	27.00	32.00	33	42.4	289.00	0.25	1.30
52	27.30	14.00	31	41	110.00	0.25	1.25
53	27.30	31.50	29.7	41	135.00	0.32	1.25
54	27.30	16.80	28	50	90.50	0.32	1.25
55	27.30	26.00	31	50	92.00	0.32	1.25
56	27.30	10.00	39	41	511.00	0.32	1.43
57	27.30	10.00	39.00	40	470.00	0.32	1.42
58	25.00	46.00	35.00	47	443.00	0.32	1.28
59	25.00	46.00	35	44	435.00	0.32	1.37
60	25.00	46.00	35	46	432.00	0.32	1.23
61	26.00	150.00	45	30	200.00	0.32	1.20
62	18.50	25.00	0	30	6.00	0.32	1.09
63	18.50	12.00	0	30	6.00	0.32	0.78
64	22.40	10.00	35	30	10.00	0.32	2.00
65	21.40	10.00	30.34	30	20.00	0.32	1.70
66	22.00	20.00	36.00	45	50.00	0.32	1.02
67	22.00	0.00	36	45	50.00	0.32	0.89
68	12.00	0.00	30	45	4.00	0.32	1.46
69	12.00	0.00	30	45	8.00	0.32	0.80
70	12.00	0.00	30	45	4.00	0.32	1.44
71	31.30	68.00	37	49	200.50	0.32	1.20
72	20.00	20.00	36	45	50.00	0.32	0.96
73	27.00	40.00	35.00	47.1	292.00	0.32	1.15
74	25.00	46.00	35.00	50	284.00	0.32	1.34
75	31.30	68.00	37	46	366.00	0.32	1.20
76	25.00	46.00	36	44.5	299.00	0.32	1.55
77	27.30	10.00	39	40	480.00	0.32	1.45
78	25.00	46.00	35	46	393.00	0.32	1.31
79	25.00	48.00	40	49	330.00	0.32	1.49
80	31.30	68.60	37	47	305.00	0.32	1.20

---

 | Show Table

DownLoad: CSV

2.2.2.   Training set and test set partition

To ensure that the model fully utilizes samples during training, while effectively learning features and patterns from the dataset, while also considering the model's generalization ability. In this article, the k-fold cross validation method with k = 10 is employed for the processing of the dataset. K-fold crossover divides 70 random sets of data into the training set and the remaining 10 sets as the testing set. The training set is employed for the purpose of training the parameters and weights of the model, whereas the test set is utilized for the evaluation of the accuracy and generalization ability of the trained model.

2.2.3.   Data preprocessing

1) Missing value smoothing optimization

During data preprocessing, missing values may occur in the training set. In order to maintain the overall feature distribution of the dataset and to reduce interference with model training, it is necessary to employ smoothing optimization to address the issue of missing values. This is achieved by replacing the missing values with the average of the features in which they are located. This practice is widely used in practical applications to improve model stability and generalization.

2) Noise point removal

To prevent noise caused by sample data errors, this paper introduces the concept of Z-score, where the formula of Z-score is as follows:

In the previous article, X is the value of the data set, μ is the mean of the data set and Z is the standard deviation of the data set.

The absolute value of the Z-score allows the degree of difference between the data points and the mean to be determined. A Z-score close to 0 indicates that the data point is close to the mean, whereas a Z-score far from 0 indicates that the data point is very different from the mean. The entire training set was acquired through the Random Forest algorithm, and the Z-score was calculated by predicting the factor of safety for all the training sets by taking the value of the difference between the predicted and actual values. The Z-score enables the quantification of the prediction bias for each sample. During the debugging process, it was discovered that the empirically adopted 2 times standard deviation threshold was ineffective, and thus 1.5 times standard deviation was adopted as the threshold. Samples that exceed the specified threshold are identified as outliers and removed from the training set. The model is then optimized by removing these outliers and any other irrelevant data from the data set.

3) Data normalization processing

When analyzing the various influencing factors, it is important to note that the sub-indicators have different scales and types, making them incomparable. Therefore, it is necessary to normalize these sub-indicators to a certain dimensionless interval using a utility function before conducting a comprehensive evaluation.

To improve the performance and convergence speed of the machine learning algorithm, data normalization is necessary. This ensures that the influence of data features on the model is balanced, avoiding excessive influence of certain features due to different magnitudes. The following formula can be used:

In the previous article, ${x}^{\mathrm{*}}$ represents the processed slope data, The $i$ represents the $i$th data sample, $N$ represents the total number of samples, ${x}_{i}$ represents the original slope data at the $i$th point, and $\stackrel{-}{x}$ represents the mean of $N$ sample data.

2.2.4.   Model parameter optimization

The conventional method for parameter optimization is the grid search method, which calculates the objective function value of the parameter combination by traversing each grid point. However, this method is prone to falling into local optimal solutions and has high time complexity. The Random Forest algorithm is mainly affected by three parameters: Num Trees (number of decision trees), Min Leaf Size (minimum number of leaves), and Max Num Splits (maximum depth of tree). To enhance parameter optimization efficiency and accuracy, this paper employs a genetic algorithm for adaptive parameter optimization, specifically for the three parameters of the random forest algorithm. The RMSE serves as the applicable function of the genetic algorithm.

The process of GA-RF parameter optimization is shown in Figure 3. and the specific steps are respectively:

1) The settings for the three parameters of random forests are as follows: Num Trees (number of decision trees) should be set between 100 and 500, Min Leaf Size (minimum number of leaves) should be set between 1 and 50, and Max Num Splits (maximum depth of burial of trees) should be set between 10 and 200.

2) The genetic algorithm parameters were initialized according to an initialized cluster size of 5, an iteration number of 50, a crossover probability of 0.8 and a variance probability of 0.1, the initial population was selected and the random forest parameters were determined.

3) To create a random forest algorithm model, use genetic algorithms to predict the safety factor and continue iterating to optimize the parameters of the algorithm. This will make the calculated value, as per Eq (18), smaller. If the number of iterations is not met to update the parameters, continue iterating until the desired number of iterations is reached and the output parameters are complete.

Figure 3.  Flow chart of stochastic forest algorithm optimized based on genetic algorithm.

DownLoad: Full-Size Img PowerPoint

The parameters of the random forest algorithm determined by GA-RF parameter optimization are shown in Table 2, where all splits strategy is used for feature subset, that is, all features are used for each tree. The type of decision tree in random forest using Eq (10) Gini index as a partition quasi can reduce the impurity of the decision tree and thus improve the model performance.

Table 2.  Parameter setting table of random forest model.

Parameters	Meaning	Value
Num Trees	Number of decision trees	176
Min Leaf Size	Minimum leaf number	1
Max Num Splits	The maximum depth of the tree	87
Feature Subspace	The feature subset of the tree	all splits
Split Criterion	Types of decision trees in a random forest	Gdi

---

 | Show Table

DownLoad: CSV

3.   Model accuracy verification and analysis

Figure 4 illustrates the predicted versus true values for the training and test sets, respectively, as depicted in charts a and b. Plot c represents the average feature importance plot, while graph d depicts the variation of error with the number of decision trees.

Figure 4.  Result plots for random forest algorithm models containing k-fold cross-validation.

DownLoad: Full-Size Img PowerPoint

For the landslide prediction model, R², MAE, RMSE, MRE, and other indicators are commonly used to validate the prediction accuracy of the model.

R² indicates the proportion of the variance of the dependent variable that can be explained by the model, with the value ranging from 0 to 1, the closer it is to 1, the better the model fits, and its calculation formula is as follows:

MAE represents the absolute value of data deviation and is calculated as follows:

RMSE and MAE are basically of the same order of magnitude, but RMSE will be a bit larger than MAE, and RMSE penalizes data points with large prediction errors, which are calculated as follows:

MRE is used as a measure of the relative magnitude of forecast error and is calculated as follows:

The $N$ is the number of samples and ${y}_{i}$ is the true value of the$i$th sample; ${\widehat{y}}_{i}$ is the $i$th model prediction; and $\stackrel{-}{y}$ is the average of the real value labels. In Eqs (16) and (17), $u$ is the sum of squares of residuals and the $v$ is the total sum of squares.

In this paper, the accuracy of the three prediction models is compared and quantitatively evaluated using the four indicators of R², MAE, RMSE, and MRE in a comprehensive manner, and the accuracy statistics are shown in Figure 4.

Table 3.  Average of model accuracy metrics after adding k-fold cross-validation.

Training set data				Test set data
RMSE	R2	MAE	MBE	RMSE	R2	MAE	MBE
0.0823	0.8852	0.0570	-0.0009	0.1681	0.4042	0.1266	-0.0021

---

 | Show Table

DownLoad: CSV

In conclusion, the GA-RF model demonstrates satisfactory performance in terms of R², RMSE, MAE and MBE values, and is capable of making effective predictions. It can be reasonably inferred that the GA-RF model exhibits high prediction accuracy due to its aggregation of predictions from multiple trees through a voting process or weighted average calculation.

4.   Analysis of factors affecting model prediction accuracy

The prediction model for slope stability is affected by three primary parameters. Num Trees, Min Leaf Size, and Max Num Splits. To quantitatively analyze the impact of each parameter on the model accuracy, we conducted an influence factor analysis of the model prediction accuracy using the control variable method. We set Num Trees at [150,300,450], Min Leaf Size at [1,3,5,10,20], and Max Num Splits at [10,100]. The effect of these three parameters on the model accuracy was tested by adjusting the model code.

4.1.   Effect of Num Trees on model accuracy

Figure 5 displays the error curve with varying Num Trees of 150,300 and 450, respectively. The error curve shows that the error consistently decreases as the number of decision trees increases. Once the number of decision trees surpasses 200, the error stabilizes and fluctuates around 0.022. To balance model accuracy and computational efficiency, the optimal number of decision trees is set between 150 and 450, and is determined through debugging.

Figure 5.  The error curve with different Num Trees.

DownLoad: Full-Size Img PowerPoint

4.2.   Effect of Min Leaf Size on model accuracy

Figure 6 displays the predicted outcome of the training set with varying Min Leaf Size of 1, 3, 5, 10, and 20, respectively. Figure 7 clearly displays the predicted outcome of the test set with varying Min Leaf Size with 1, 3, 5, 10, and 20, respectively.

Figure 6.  The predicted outcome of the training set with different Min Leaf Size.

DownLoad: Full-Size Img PowerPoint

Figure 7.  The predicted outcome of the test set with different Min Leaf Size.

DownLoad: Full-Size Img PowerPoint

As the minimum number of leaves increases, the root-mean-square error also increases, resulting in more significant deviations from the actual values. When the minimum number of leaves exceeds 10, the prediction values deviate even further from the actual values. To achieve better simulation results, control the minimum number of leaves between 1 and 5 and select a superior minimum leaf tree compared to the prediction.

4.3.   Effect of max Num splits on model accuracy

Table 5 displays the impact of the varying Max Num Splits on the model accuracy with 10, 20, 30, 40, 60, 80, and 100, respectively. As the Max Num Splits increases, both the coefficient of determination R² and the mean absolute error MAE increase and stabilize, while the mean deviation MBE decreases and stabilizes. These findings demonstrate a clear relationship between burial depth and the accuracy of the results. Based on the analysis, it is recommended to set the maximum burial depth between 40 and 100.

Table 5.  Impact of various Max Num Splits on model accuracy.

Max Num Splits	Training set data			Test set data
	R2	MAE	MBE	R2	MAE	MBE
10	0.6892	0.1021	-0.0012	0.2679	0.1471	-0.0020
20	0.8390	0.0705	-0.0006	0.3672	0.1316	-0.0013
30	0.8841	0.0577	-0.0004	0.4092	0.1266	0.0011
40	0.8858	0.0565	-0.0010	0.3953	0.1278	-0.0032
60	0.8851	0.0570	-0.0009	0.4041	0.1266	-0.0021
80	0.8851	0.0570	-0.0009	0.4041	0.1266	-0.0021
100	0.8851	0.0570	-0.0009	0.4041	0.1266	-0.0021

---

 | Show Table

DownLoad: CSV

5.   Discussion

Machine learning algorithms are highly effective in overcoming the shortcomings of traditional geological investigation and planning means, which are often time-consuming and labor-intensive. Additionally, they can surpass the limitations of single traditional landslide prediction parameters and achieve higher prediction accuracy ^[16]. As a result, machine learning algorithms provide robust support for the rapid development of landslide disaster prediction and forecasting. We propose a highly effective high-dimensional stability prediction model based on the GA-RF algorithm. It is worth noting that this model is specifically designed for circular damage type slopes. However, future research can be conducted to explore its applicability to other damage types, such as linear, folded, wedge, and other slopes.

The accuracy of landslide prediction forecasting using machine learning algorithms is determined by various factors, such as the quality of basic data, the machine learning model, the selection and quantification of evaluation factors, and the cleaning of anomalous data ^[16]. Quality of basic data is the primary factor influencing the accuracy of landslide prediction and forecasting, as supported by both domestic and international research findings ^[17]. Quantity of data and algorithmic model follow in importance. Thus, prioritizing the quality of basic data is crucial. The 'air-sky-earth-internal' integrated multi-dimensional and multi-field three-dimensional observation technology has gained popularity for landslide disaster analysis. It is now more feasible and necessary than ever before to obtain high-quality basic data. A unified approach to data analysis is crucial for the construction of landslide intelligent prediction and forecasting models. Due to the heterogeneous nature of landslide monitoring data, which comes from multiple sources and is expressed in diverse forms, and the inconsistency of data scale, cross-scale, and multi-modality, it is imperative to employ assertive and decisive language to emphasize the importance of a unified approach.

Landslides are essentially a nonlinear dissipative dynamical system that develops and evolves under the control of geotechnical body conditions and under the influence of multiple triggering factors. Although machine learning algorithms are commonly used for landslide prediction and forecasting, it is important to note that they do not consider the physical and mechanical mechanisms of landslide evolution. Therefore, it can be challenging to provide a comprehensive explanation for the occurrence of landslides ^[18]. Landslides occur in varying geological conditions, but with our expertise, we can confidently state that the prediction model has significant uncertainties. However, we can assure you that the model's applicability and prediction accuracy can be improved.

Our proposed method for intelligent predictive forecasting of landslides based on machine learning combines the physical and mechanical mechanisms of landslide evolution. We use a deep fusion and unified expression method for multi-dimensional and multi-field three-dimensional observation data. The result is a highly reliable and applicable model.

6.   Conclusions

The purpose of the GA-RF slope stability prediction model with k-fold cross-validation developed in this paper is to create a stability prediction model based on a hybrid intelligent algorithm for high-dimensional feature variable data of slopes. This method combines the advantages of genetic algorithm optimization and random forest algorithms, and also has good generalization ability by fully utilizing the dataset. While the model's performance is not yet optimal, it can be expected to have broad optimization potential. It can be posited that this represents a beneficial attempt to predict landslide disasters. It is my hope that this article will serve as a catalyst for further discourse on this important topic.

This article establishes a GA-RF high-dimensional slope stability prediction model using k-fold cross validation, selecting soil gravity (γ), slope height (H), pore pressure value (P), cohesion (C), internal friction angle (φ), and slope inclination angle (°) as characteristic variables. A series of experiments were conducted on the model, and acceptable conclusions were obtained. However, it should be noted that there are still some limitations. The model has been tested and validated only for circular damage types of slopes. In order to achieve greater universality and robustness, further experimentation and validation are required with larger sample sizes and data from a wider range of slope types. Furthermore, there is potential for additional optimization of the model.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was financially supported by National Natural Science Foundation of China (Nos. 42162023 & 42162025); Key Research and Development Program of Jiangxi Province (No. 20203BBGL73220); Research Foundation of Education Bureau of Jiangxi Province, China (No. GJJ201904); Water Science and Technology Fund of Jiangxi Province in China (Nos. 202124ZDKT15 & 202223YBKT03); and Research Project on Teaching Reform in Higher Education Institutions in Jiangxi Province (No. JXJG-23-18-23).

Conflict of interest

The authors declare there is no conflict of interest.