1.
Introduction
The topic addressed in this paper is the computation of the Euclidean symmetries of a certain type of algebraic object, namely rational surfaces. Thus, in the rest of this paper, a "symmetry" will mean an isometry of the ambient space that leaves the embedded surface invariant; in particular, such a mapping also leaves invariant the Gauss and mean curvatures of the surface. Capturing the information on the Euclidean symmetries of an object is a natural step if one wants to understand its geometry, visualize it accurately, or store it efficiently. Although in applied mathematics the computation of symmetries has been addressed for decades, with a very wide variety of techniques often involving numerics and statistical methods, in the past fifteen years, there has been a growing interest in applying methods from symbolic computation to this problem. In this sense, in applied mathematics the object to be analyzed is usually a 2D or 3D image, and in practice often a 2D or 3D point cloud, and one seeks approximate symmetries, rather than exact ones. When the problem is seen from the point of view of symbolic computation, which is the perspective we use in this paper, one is attracted toward exact objects with more structure, and looks for their exact symmetries. Typically, the objects considered are (algebraic) varieties defined by polynomials with integer coefficients, either implicitly given, i.e., as zeros of a given set of polynomials, or defined by means of a parametrization with rational components, i.e., quotients of polynomials.
Although implicitly defined varieties have been addressed (see [1,2,3] for implicit planar curves, and [4,5,6] for implicit surfaces), the case that has attracted more attention has been that of rational curves and surfaces, probably because the rational representation is preferred in computer-aided geometric design, a field where the problem has some relevance. For rational parametric curves, the problem is quite well-understood, and in fact a more general question, namely identifying whether or not two rational curves are affinely or projectively equivalent, has been investigated in many papers. Although a complete list would be long, some notable contributions are [7], on symmetries of space curves, and [5,8], on projective equivalences of rational curves in any dimension; see the bibliographies of these papers for other references. Observe also that isometries and affine equivalences are special instances of projective equivalences.
However, for rational surfaces the problem is harder, both theoretically and computationally. Here we have two types of contributions, a first group providing more general algorithms, and a second group focused on special types of surfaces whose properties one can exploit. Among the first group, [9] considers involutions of parametric polynomial surfaces, [10] addresses affine and projective equivalences of rational surfaces without projective base points (although base points are not uncommon; note that rational curves do not have base points, which makes the problem easier for curves), and [11], which improves on the results of [10] and provides an algorithm for computing the projective equivalences between two rational surfaces without additional requirements. The algorithm in [11] is certainly very general, but still has some drawbacks: on one hand, the problem is reduced to five possible cases, but only two of them are solved in the paper; on the other hand, the algorithm is involved (check the partial implementation in [12]) and requires a strong background of algebraic geometry, so it is not so easily accessible for readers not familiar with such a topic. Let us also mention that in [10], the input is a polynomial or rational parametrization (in projective form) of a surface, with real coefficients; in [11], the input is a rational parametrization of a surface with coefficients over an algebraically closed field.
Among the second group of papers, namely papers related to rational surfaces with special properties, one has [13], for canal surfaces, [14], for translational and minimal surfaces, and [5,15], for ruled surfaces; in fact, [14,15] address the more general question of computing affine equivalences, and [5] studies projective equivalences.
In this paper, we present two contributions to the problem. The first one is a general algorithm which uses the two natural invariants for surfaces, namely Gauss curvature and mean curvature, therefore generalizing to surfaces the idea of [7] for space curves. The algorithm is very easy to implement, although it can be computationally costly. The reason is that the algorithm requires one to compute the resultant of two polynomials derived from the two curvatures; however, while the Gauss curvature of a rational surface is always rational, the mean curvature in general has a square root, so we need to use the square of the mean curvature instead, which increases the degree. If we work with a PN surface, namely a rational surface where the modulus of the normal vector is rational (see for instance [16]), we can skip that part and reduce the computational cost, so the algorithm works better; otherwise, we need very sparse parametrizations. As for a comparison with existing algorithms, compared to [10], projective base points are not a problem for our algorithm, although unlike ours, [10] also works in higher dimension. Compared to [11], our algorithm is much simpler. However, it is true that for non-sparse, non-PN surfaces, the computational cost can be high, so in the cases covered by [10,11] and without further advantages that make our algorithm competitive (e.g., the cases already mentioned or ruled surfaces, see the next paragraph), using [10,11] could be preferrable.
The second contribution is a specific algorithm for rational ruled surfaces. We prove that every symmetry of a rational ruled surface is a symmetry of the line of striction of the surface, which is a rational space curve. Thus, we reduce the problem to that of space curves, which can be efficiently solved. The resulting algorithm provides better timings than the general algorithm described in the previous paragraph and the algorithm in [15], as we will show with several examples. Compared to [5], it is worth noticing that the algorithm in [5] also reduces the problem to the case of curves. However, there are two main differences with our algorithm: (i) [5] uses rational curves in P5, so the dimension of the curves is higher; (ii) the algorithm in [5] requires one to solve a quadratic system of equations in 7 parameters, which may cause difficulties in some cases (see page 8 of [5]). It is true though that the algorithm in [5] can solve the more general problem of finding the projective equivalences between two ruled surfaces, while our algorithm only aims to compute the symmetries of a given surface.
The two algorithms presented in the paper have been implemented in Maple, and are available on the website of one of the authors [17]; a Zenodo version is also available [18].
The structure of the paper is the following. In Section 2, we provide the necessary background to develop our results. The general algorithm is presented in Section 3. The algorithm for ruled surfaces is given in Section 4, where we also analyze the special case of developable surfaces. Section 5 reports on the experimentation carried out on different types of surfaces, general and ruled, using the implementation carried out in Maple; here we also offer some comparative results with the algorithms in [10,11]. We close with our conclusion in Section 6.
2.
General background, notation, and hypotheses
Let x(t,s) be a rational parametrization of a surface S⊂R3. We say that x(t,s) is a proper parametrization of S if the parametrization x, seen as a rational mapping x:R2→R3, is birational onto its image, so that the inverse x−1 exists and is also rational. Thus, proper mappings are injective except perhaps at a subset of S of dimension at most 1. Checking whether or not a surface parametrization is proper, and reparametrizing it to be proper in the case when it is not, is not easy, but one can always heuristically check properness by taking a random point (t0,s0), and solving x(t,s)=x(t0,s0): if the only solution is t=t0,s=s0, then x(t,s) is proper with high probability.
The notion of properness also applies to rational parametrizations c(t) of a curve C⊂R3. In this case, however, checking properness and reparametrizing non-proper parametrizations is much easier: once all the components of c(t) have the same denominator, checking properness amounts to computing the gcd of the components of the numerators of c(t)−c(s). If the degree of this gcd is 1, then c(t) is proper; if it is not, one can compute a proper reparametrization using the information provided by this gcd. The interested reader can read further on this topic in [19].
A Euclidean symmetry (also called isometry) of R3 is a mapping f:R3→R3, f(x)=Ax+b, where A is an orthogonal 3×3 matrix, so ATA=I with I the identity matrix, and b∈R3; notice that det(A)=±1. We say that such a mapping f is a symmetry of a surface S (resp., a curve C) if f(S)=S (reap., f(C)=C). When we work with proper, rational parametrizations of curves or surfaces, one can reduce the computation of the symmetries of the curve or surface, if any, to the existence of birational parametrizations in the parameter space, R in the case of curves, and R2 in the case of surfaces, satisfying a certain condition; see the result that follows. For curves, we can go a bit further taking into account that the birational mappings of the real line (and in fact of the projective complex line) are the Möbius transformations, i.e., the mappings
More precisely, we have the following result; see for instance [7] for a proof.
Proposition 1. Let C⊂R3 be a rational curve defined by a rational, proper parametrization c(t), and let f:R3→R3 be a symmetry of C. Then there exists a Möbius transformation φ:R→R such that
i.e., making commutative the following diagram:
For properly parametrized surfaces, we also have a commutative diagram analogous to Eq (2.2), an observation used in papers like [9,10]. Indeed, if S⊂R3 is a rational surface defined by a rational, proper parametrization x(t,s), and f:R3→R3 is a symmetry of S, then there exists a birational mapping ψ:R2→R2 making commutative the diagram
i.e., such that
Remark 1. In fact, Proposition 1 holds whenever we have a birational transformation, not necessarily a Euclidean symmetry, f:Rn→Rn mapping two rational curves C1,C2 properly parametrized by x1,x2. Similarly, the diagram in Eq (2.3) works also when we have two surfaces S1,S2, properly parametrized, and a birational transformation mapping one of them onto the other. The hypothesis on the properness of the parametrizations is key in both cases.
Birational mappings of the (projective) plane are called Cremona transformations, and are known to be generated by linear projective mappings and quadratic transformations. However, while the birational mappings of the complex and real line are, exactly, the Möbius transformations, and therefore we have a closed form for them, no closed form is known for the Cremona transformations. This is the reason why in several papers related to the problem treated here, e.g., [9,10,15], one studies rational parametrizations with additional properties so that a general form for the Cremona transformations behind f can be guessed. In [9], under the considered hypotheses, the transformation is linear; in [10], it is linear projective and in [15], the first component of the transformation is a univariate Möbius mapping, while the second component is more complicated, but with a known general form. Notice that, in general, Möbius transformations or Cremona transformations do not preserve the metric.
2.1. Background on differential geometry
Let us briefly recall some notions from differential geometry that will be needed later; we refer to [20,21,22] for more information on this topic.
Let x(t,s) be a parametrization of a surface S⊂R3. We say that x(t,s) is regular at (t0,s0)∈R2 if the partial derivatives xt,xs are linearly independent at the point. At regular points P=x(t,s), the tangent plane to S is well-defined and corresponds to
where L(xt,xs) denotes the linear variety spanned by xt,xs. The normal direction to the tangent plane is therefore that of
Additionally, the unitary normal vector is defined as
Notice that if x(t,s) is rational, in general nx(t,s) is not rational, since a square root is expected in the denominator. Additionally, since nx(t,s) is unitary, one can also see nx as a mapping from the surface S onto the unit sphere S2, i.e., nx:S→S2; this mapping is called the Gauss map.
The first fundamental form and the second fundamental form are two symmetric quadratic forms defined at each tangent plane TP(S) of S, with P being regular. The first fundamental form captures the metric of the surface, and is defined by the matrix
The second fundamental form captures the local shape of the surface around the point, and is defined by the matrix
The Weingarten map Wx is the (linear) mapping Wx:TP(S)→TP(S) defined as Wx=−dnx, i.e., the differential of the Gauss map with a changed sign. The matrix defining Wx is
The determinant of Wx is the Gauss curvature of the surface, Kx, and the trace of Wx is the mean curvature, Hx. In terms of the entries of the matrices Ix and IIx (see for instance Section 3.4 of [23]),
Observe that if x(t,s) is rational, Kx is always a rational function. However, in general Hx is not rational because of the presence of a square root (due to the functions L,M, and N in the numerator of the formula for Hx), but H2x is certainly rational.
3.
A general algorithm
Let x(t,s) be a rational, proper parametrization of a surface S⊂R3. Our goal is to provide an algorithm for computing the symmetries f of S, if any. In order to compute the symmetries f, the idea, from the diagram in Eq (2.3), is to first find the Cremona transformations ψ satisfying f∘x=x∘ψ, and then compute the f themselves. Notice that if f(x)=Ax+b is a symmetry of S, Eq (2.4) yields Ax(t,s)+b=(x∘ψ)(t,s); if ψ is known, one can compute A,b by directly solving the linear system stemming from this equality, or by solving a linear system computed from Ax(t,s)+b=(x∘ψ)(t,s) after giving enough values of (ti,si).
In order to find ψ, we will use the Gauss curvature Kx and the mean curvature Hx of the parametrization. The first step is to find the relationships between: (ⅰ) Kx,Hx and Kf∘x,Hf∘x; (ⅱ) Kx,Hx and Kx∘ψ,Hx∘ψ. In turn, this requires one to see how nx,Ix and IIx are affected when moving from x to f∘x or x∘ψ. We start with f∘x.
Lemma 2. Let x(t,s) be a rational parametrization of a surface S, and let f(x)=Ax+b be a Euclidean symmetry.
1) If∘x=Ix.
2) nf∘x=det(A)Anx.
3) IIf∘x=det(A)IIx.
Proof. To see 1), let ˜x=f∘x, so ˜x(t,s)=Ax(t,s)+b. Then ˜xt=Axt and ˜xs=Axs. Since A is orthogonal, ˜xt⋅˜xt=xt⋅xt, ˜xt⋅˜xs=xt⋅xs, ˜xs⋅˜xs=xt⋅xt, and 1) follows. To see 2), we observe that
Since A is orthogonal, A−T=A, and therefore ˜xtטxs=det(A)A(xt×xs). Then 2) follows by using Eq (2.6), taking into account that since A is orthogonal, norms are preserved. Finally, for 3), we observe first that ˜xtt=Axtt, ˜xts=Axts and ˜xss=Axss; and then the result follows from the definition of the second fundamental form and statement 2), again taking into account that since A is orthogonal, dot products are preserved. □
Corollary 3. Let x(t,s) be a rational parametrization of a surface S, and let f(x)=Ax+b be a Euclidean symmetry. Then
Proof. The equality Wf∘x=det(A)Wx follows from Eq (2.9), taking into account the statements 1) and 3) of Lemma 2. The remaining equalities follow from the fact that Kf∘x and Hf∘x are the determinant and trace of the matrix Wf∘x. □
Now let us analyze the relationship between Kx,Hx and Kx∘ψ,Hx∘ψ. In order to do this, we need to recall first the relationship between the first and second fundamental forms of x and x∘ψ; this is essentially known, but we include it here for the convenience of the reader. Let us denote y:=x∘ψ, ψ(t,s)=(ψ1(t,s),ψ2(t,s)). Using the Chain Rule,
where yt,ys are evaluated at (t,s), and xt(ψ),xs(ψ) denote the evaluations of xt,xs at ψ(t,s). In matrix notation, we have
where J represents the Jacobian of ψ. Taking Eq (2.7) into account, we get that
where, again, the entries of the first fundamental form at the left-hand side must be evaluated at (t,s), while at the right-hand side, the entries of the form are evaluated at ψ(t,s). To relate ny and nx we also use Eq (3.2). Finally, to relate IIy and IIx we need to differentiate Eq (3.1) again, applying the Chain Rule; although the calculations are lengthy, we get the same result that we obtained for the first fundamental form. So we have the following lemma.
Lemma 4. Let x(t,s) be a rational parametrization of a surface S, let ψ be a planar rational mapping, and let J be the Jacobian of ψ.
1) Ix∘ψ=JT⋅Ix(ψ)⋅J.
2) nx∘ψ=det(J)|det(J)|nx(ψ).
3) IIx∘ψ=JT⋅IIx(ψ)⋅J.
Now we can prove what we need.
Corollary 5. Let x(t,s) be a rational parametrization of a surface S, let ψ be a planar birational mapping, and let J be the Jacobian of ψ. Then
and
Proof. From Eq (2.9) and statements 1) and 3) of Lemma 4,
and Eq (3.3) is proved. Since from Eq (3.3) the matrices Wx∘ψ, Wx(ψ) are similar, they have the same determinant and trace, and Eq (3.4) follows. □
Finally we reach the following result.
Proposition 6. Let x(t,s) be a proper parametrization of a surface S, and let f(x)=Ax+b be a Euclidean symmetry of S. Then there exists a birational planar mapping ψ satisfying that f∘x=x∘ψ, and
Proof. From the diagram in Eq (2.3), there exists a binational mapping ψ such that f∘x=x∘ψ. By Corollary 3, Kf∘x=Kx, and by Eq (3.4), Kx∘ψ=Kx(ψ). Since f∘x=x∘ψ, we get the result for Kx. For Hx, the idea is the same. □
Let us see how to derive an algorithm from Proposition 6 in order to compute the symmetries of S. First, we will use ˆHx=H2x, which is a rational function, instead of Hx. Writing
we observe that the above equalities are satisfied, under the hypotheses of Proposition 6, for u=ψ1(t,s), v=ψ2(t,s). Next Kx and ˆHx are rational functions, so after clearing denominators, the above equations lead to
where ξ1 and ξ2 are two polynomials in the variables t,s,u, and v, the first one coming from Kx, and the second one from ˆHx. By well-known properties of resultants, if t,s,u and v satisfy Eq (3.6) then t,s and u satisfy
and t,s and v satisfy
Now let
where ψi,n,ψi,d, for i=1,2, are polynomials, and gcd(ψi,n,ψi,d)=1 for i=1,2. Then we have the following result.
Theorem 7. Let x(t,s) be a proper parametrization of a surface S, and let f(x)=Ax+b be a Euclidean symmetry of S. Then there exists a binational planar mapping ψ=(ψ1,ψ2), with components as in Eq (3.9), such that ψ1,d(t,s)u−ψ1,n(t,s) is a factor of η1(t,s,u), and ψ2,d(t,s)v−ψ2,n(t,s) is a factor of η2(t,s,v).
Proof. From the diagram in Eq (2.3), there exists a birational mapping ψ such that f∘x=x∘ψ. Then for any (t,s), we have that (t,s,ψ1(t,s),ψ2(t,s)) satisfies Eq (3.6), and therefore (t,s,ψ1(t,s)) fulfills Eq (3.7), and (t,s,ψ2(t,s)) fulfills Eq (3.8). Hence, all the points of the surface (in the (t,s,u) space) defined by ψ1,d(t,s)u−ψ1,n(t,s)=0 are also points of the surface η1(t,s,u)=0. Furthermore, since gcd(ψ1,n,ψ1,d)=1 the polynomial ψ1,d(t,s)u−ψ1,n(t,s) is irreducible, so by Study's Lemma (see Section 6.13 of [24]), ψ1,d(t,s)u−ψ1,n(t,s) divides η1(t,s,u). For ψ2,d(t,s)v−ψ2,n(t,s), we argue in the same way.
Thus, if, say, η1(t,s,u) is not identically zero, we can look for the factors of η1 which are linear in u, which provides the functions ψ1(t,s), substitute u=ψ1(t,s) into ξ1(t,s,u,v), ξ2(t,s,u,v), and recover v from the linear factor in v of the gcd of the polynomials in t,s,v resulting from that substitution. We might also work with η2(t,s,v), but we do not need to compute both resultants. Notice that in this process it is not necessary to know a priori the form of ψ(t,s). Furthermore, once ψ is known, we can compute f from the equality f∘x=x∘ψ. This leads to an algorithm, Algorithm 1, for computing the symmetries of S. The algorithm works whenever both resultants η1,η2 are not identically zero, if η1,η2 are both identically zero then either ξ1,ξ2 share a factor, or some of them are identically zero. We can identify some cases where this can happen:
● Gauss curvature being constant: It is well-known that the only surfaces with nonzero constant Gauss curvature K are isometric to the sphere, if K>0, or to the pseudosphere, if K<0. However, the pseudosphere is a surface of revolution whose directrix is a trascendental curve, the tractix, so the pseudosphere is not algebraic. This implies that the only irreducible algebraic surface with constant nonzero Gaussian curvature is the sphere. However, there are algebraic, and in fact rational, surfaces with vanishing Gauss curvature; these surfaces are called developable surfaces, and will come up in the next section.
● Mean curvature being constant: These surfaces certainly exist, and among them we have the remarkable class of surfaces where H=0, called minimal surfaces. Symmetries of rational minimal surfaces are treated in [14].
● Certain functional relationships between the Gauss curvature and the mean curvature: An example is the case of linear Weingarten surfaces (see for instance [25]), which are surfaces where aH+bK=c, for constants a,b and c; this family includes as particular cases surfaces with constant Gauss or mean curvature.
In these cases the algorithm fails, and an alternative must be used; nevertheless, for developable surfaces we can use the ideas in the next section, and for minimal surfaces we can use [14].
Example 1. Consider the toy example of the ellipsoid parametrized by
In this case, Algorithm 4 provides 8 symmetries, including the trivial symmetry (the identity), corresponding to the Cremona transformations:
and
For instance, the symmetry corresponding to the first Cremona transformation, (tt2+s2,−st2+s2), is f(x)=Ax with
Notice in particular that the above Cremona transformation is not linear projective, i.e., its components are not quotients of linear polynomials in t,s.
4.
Symmetries of ruled surfaces
4.1. Background on ruled surfaces
We say that S⊂R3 is ruled if S is covered by lines, called the rulings of the surface. These surfaces are well-known in differential geometry; one can check classical texts like [20,21,22] for further reading on the topic, and also for several facts that we will be using in this subsection.
If S is rational, then we can always find [26], a rational parametrization of the form
where u(t),v(t) parametrize space rational curves. The curve defined by u(t) is called the directrix. We refer to Eq (4.1) as a standard parametrization of S, and we will assume the ruled surface S we work with to be parametrized in this way; notice that, regardless of potential reparametrizations of u(t),v(t), a standard parametrization of S is not necessarily unique, since different curves may serve as directrices of the surface.
A special type of ruled surface, called developable surfaces, is classical in differential geometry, and widely used in applications. Intuitively speaking, developable surfaces are the surfaces that can be "unfolded" onto the plane, so that we can find a dipheomorphic mapping ϕ:S→R2 preserving distances.
Developable surfaces can be characterized as the ruled surfaces with vanishing Gauss curvature. Also, if S is parametrized by Eq (4.1) then S is developable if and only if the mixed product [u′(t),v(t),v′(t)] is identically zero. This allows us to classify developable surfaces in three types:
(ⅰ) Cylindrical surfaces: Ruled surfaces where all the rulings are parallel to the same vector. Thus, they can be parametrized as
where v0 is a constant vector.
(ⅱ) Conical surfaces: These are ruled surfaces where all the rulings intersect at the same point, called the vertex of the surface. By applying, if necessary, a translation so that the vertex coincides with the origin, these surfaces can be parametrized as
(ⅲ) Tangential surfaces: Ruled surfaces consisting of the union of tangent lines to the directrix, which can be parametrized as
Cylindrical surfaces and conical surfaces can be recognized, for example, using the algorithm in [27]; furthermore, in those cases we can find the constant direction of the rulings, for cylindrical surfaces, and the vertex, for conical surfaces.
4.2. Computation of symmetries of ruled surfaces
In order to compute the symmetries of a ruled surface, we also need to recall the notion of a line of striction (see for instance Sections 3–5 of [20] for further information on this notion and its properties). Given a ruled surface S, parametrized as in Eq (4.1), the line of striction E is a parametric space curve c(t), contained in S, such that c′(t) is orthogonal to v′(t). The expression for the line of striction is
and can be proven to be independent of the directrix considered in Eq (4.1). In particular, if Eq (4.1) is rational then c(t) is also rational. This expression does not make sense for cylindrical surfaces; also, for conical surfaces, the line of striction degenerates into a point. Excluding cylindrical surfaces, we can always assume that S is parametrized as in Eq (4.1), where the directrix is the line of striction. One can check that for tangential developable surfaces, the directrix appearing in Eq (4.4) is already the line of striction.
The reason why the line of striction is useful in our context is that any symmetry of the surface is also a symmetry of the line of striction. In order to see this, let the directrix u(t) be the line of striction, and let f(x)=Ax+b be a symmetry of S. Then
also parametrizes S, and we can derive the following theorem.
Theorem 8. Let f(x)=Ax+b be a symmetry of a ruled surface S, and let E be the line of striction of S. Then f is also a symmetry of E.
Proof. Assume that the directrix u(t) is the line of striction E. Let us see that the parametrization ˜u(t) in Eq (4.6), which parametrizes the image of E under f, is also a parametrization of E. Indeed,
Since A is an orthogonal matrix, (Au′(t))⋅(Av′(t))=u′(t)⋅v′(t)=0. Thus, ˜u(t) satisfies the condition defining the line of striction, parametrized by u(t), so ˜u(t) also parametrizes E. Thus f(E)=E, and the result follows. □
The symmetries of the line of striction can be computed using known algorithms for space rational curves. Thus, whenever the line of striction has finitely many symmetries, we just need to test which ones are also symmetries of S. If the line of striction has infinitely many symmetries, i.e., if the line of striction is either a line or a circle, then we can use the algorithm in the previous section, or other algorithms known for ruled surfaces. Notice that cylindrical and conical surfaces are excluded in this approach.
4.3. Developable surfaces
Since developable surfaces have zero Gauss curvature, the general algorithm presented in Section 3 is not applicable to them. Also, for two of the subfamilies of developable surfaces, cylindrical and conical surfaces, using the line of striction is not an option, either.
For cylindrical surfaces, the symmetries of the surface follow from the symmetries of a normal section of the surface, i.e., the intersection of the surface with a plane Π normal to the direction v of the rulings. Because Eq (4.1) is linear in s, the intersection of S with a plane Π normal to the rulings is a rational planar curve, so its symmetries can be computed using known algorithms for rational curves. Notice also that cylindrical surfaces are invariant under translations by any vector parallel to v.
For conical surfaces, parametrized as in Eq (4.3), we just need to consider symmetries fixing the origin, i.e., symmetries f(x)=Ax, since in Eq (4.3) the origin is the vertex of the surface, which must be kept invariant under any symmetry. Then we can just apply the method in Section 4.1 of [15]. Notice that any symmetry of the curve defined by v(t) (see Eq (4.3)) will also be a symmetry of the surface, but the converse is false (e.g., a cone of revolution, with v(t) corresponding to an ellipse contained in the cone).
Finally, in the case of tangential developable surfaces, Theorem 8 works without any problem. However, we can go a bit further.
Proposition 9. Let S be a rational tangential developable surface. Then f:R3→R3 is a symmetry of S if and only if f is a symmetry of its line of striction.
Proof. The implication (⇒) is Theorem 8, so let us address (⇐). Thus, let f:R3→R3, f(x)=Ax+b be a symmetry of the line of striction of S, let u(t) be a rational parametrization of the line of striction, and let us assume without loss of generality that u(t) is proper. By Proposition 1, Au(t)+b=(u∘φ)(t), with φ(t) a Möbius transformation. Considering the parametrization of S provided by Eq (4.4),
Differentiating Au(t)+b=(u∘φ)(t) and using the Chain Rule, we deduce that Au′(t)=u′(φ(t))φ′(t). Substituting this into Eq (4.7), we obtain
The above equation can be written as
with ψ2(t,s)=sφ′(t). Eq (4.9) means, by the diagram in Eq (2.3), that f is a symmetry of S. □
Observe that, for tangential surfaces, the line of striction u(t) cannot be planar, since in that case the surface S is a plane, which is a trivial case. Thus, the number of symmetries of u(t) must be finite.
5.
Experimentation
In this section, we provide some experimentation on the algorithms given in the previous sections. We have implemented both algorithms in the CAS Maple [28], and tried several examples, using an Intel(R) Core(TM) i7 with a 3.6 GHz processor and 32 Gb RAM. All the examples and implementation can be found in the last author's personal website [17], and also in [18]. We start with the general algorithm described in Section 3, and then move to ruled surfaces and the algorithm given in Section 4.
5.1. General algorithm
In order to test the algorithm for the general case, we consider several surfaces of three different types: toric surfaces, PN surfaces, and conoids; in all these cases, the surfaces have projective base points, so the algorithm in [10] is not applicable. Additionally, we have also considered some examples from the papers [10,11]. As an overall comment, let us mention that most of the time is consumed by the computation of the resultant in Step 2 of Algorithm 1, which is the bottleneck of the algorithm.
Torics. A toric surface is a surface parametrized by x(t,s)=(tm1sn1,tm2sn2,tm3sn3), where mi,ni∈Z. In Table 1, we provide the computation time (t, in seconds) for detecting symmetries of toric surfaces with various degrees.
PN surfaces. A PN surface is a rational surface with a rational normal vector field. In the case of PN surfaces, we replace in our algorithm the equation ˆHx(t,s)=ˆHx(u,v) by Hx(t,s)=±Hx(u,v). This reduces the degree of the equations in the resultants. In order to generate non-trivial PN surfaces we use the strategy given in [16], where the authors provide a method using quaternions. First, we consider the cubic PN surface (see Figure 1b) given by the following rational parametrization.
This PN surface has one projective base point, [−3:1:0], and admits two symmetries corresponding to the Cremona transformations
with symmetries
The whole computation of this example took 0.203 second. Now, consider the cubic PN surface (see Figure 1a) given by the following rational parametrization.
This PN surface has two projective base points [i:1:0] and [−i:1:0]. The surface admits two symmetries corresponding to the Cremona transformations
with symmetries
The whole computation of this example took 0.125 second.
● Plücker's conoids. Plücker's conoid is a ruled surface defined by the following parametrization
In our tests, we used a generalization of Plücker's conoid, which is again a ruled surface, defined by
where n>0. Using the fact that
and exploiting the Chebychev polynomials of the second kind Uk, we get a rational parametrization of the generalized Plücker's conoid as
where k>0 (see Figure 2 for the plots of the surfaces for k∈{1,2,3,4}). In Table 2, we provide the computation times for detecting symmetries of the generalized Plücker's conoids with various degrees. Notice that any generalized Plücker's conoid has two projective base points, [1:0:0] and [0:1:0].
Some examples from [10,11].
We have tried examples of quadratically parametrizable surfaces considered in Section 5.1 of [10]. Following the notation in [10], they are denoted as Σ1,…,Σ9, where Σ1,…,Σ6 are base-point free (so the algorithm in [10] can be applied), and Σ7,Σ8,Σ9 are not (and the algorithm in [10] cannot be applied). We list the timings in Table 3. We can also find timings in [10], although in the case of [10], the algorithm finds projective mappings leaving the surface invariant, and not only isometries. For Σ1 and Σ2, the timings in [10] are much better. For Σ3 to Σ6, the timings for our algorithm and the one in [10] are comparable. Σ7,Σ8 and Σ9, however, cannot be solved by [10]. In all the cases, the parametrizations have small coefficients.
We have also tried some concrete examples of quadratically parametrized surfaces appearing in [10] (see Table 6 in [10]). We provide the timings in Table 4, where the first column reproduces the classification as spelt in [10].
As for a comparison with [11], in the GitHub implementation [12] of the algorithm in [11], one can find five examples, concerning the Roman surface (Example 1 in [12]), Veronese-Segre surfaces (Example 2), adjoints to double ruled quadrics (Example 4), the rational normal scroll (Example 5), and conic bundles (Example 6). Out of the five examples, our algorithm can find the 24 symmetries of the first one, the Roman surface
in 50.016 seconds. There are no timings in [11], so here we cannot compare. However, for the remaining four examples, the computations with our algorithm were too costly, meaning that the resultant in Step 2 of Algorithm 1 took too long to compute.
5.2. Ruled surfaces
Here we consider the method in Section 4, which requires us to determine first the line of striction of the surface. Then we apply the method in [7] to find the symmetries of the rational curve defined by the line of striction. In Table 5, we compare the timing (tr) of the algorithm for ruled surfaces in Section 4, the timing (te) of the algorithm given in [15], and the the timing (tg) for the general algorithm given in Section 3. One can see that the method in Section 4 beats the other methods in all cases.
Remark 2. The Plücker conoids analyzed in the previous subsection are also ruled surfaces, but their striction lines are straight lines, and therefore the ideas of Section 4 are not useful for that case.
Remark 3. In Table 5, we have not included the comparison with [5], where no timings are provided. But in any case, as we mentioned in the Introduction to this paper, the algorithm in [5] requires using rational curves in higher dimension (P5) plus a further step involving the solution of a polynomial quadratic system in a high number of variables, namely 7. Thus, one can expect that the timings of [5] are, in general, much higher than ours. Recall, though, that the algorithm in [5] is aimed to the more general problem of finding projective equivalences between ruled surfaces.
6.
Conclusions
While the problem of computing the symmetries of rational curves, and related questions, has received much attention in the literature, similar problems for rational surfaces still pose several challenges. In this paper, we have provided two algorithms related to this question. The first one is simple, very general, and, at least theoretically, can be applied to a wide variety of parametrizations. However, the computations can be hard, so in practice one requires some kind of advantage in the parametrizations: some cases where the algorithm works well, as we have shown in the experimentation section, are the cases of PN surfaces, toric surfaces, and Plücker conoids. The second algorithm we provide is specific for ruled surfaces, and proceeds by reducing the problem to the case of space curves (which we can solve efficiently) by using the line of striction of the surface. As is also shown in the experimentation section, this last algorithm beats other algorithms that have been considered for the same problem.
For the general algorithm, the bottleneck of the algorithm is the computation of the resultant of the polynomials derived from the curvatures of the surface. Using the curvatures of the surface is a quite natural idea, so a possibility for further research is to look for strategies to compute this resultant in a more efficient way. In any case, we do not claim that the first algorithm provided in this paper should always be used. Apparently, all the algorithms presented so far to solve the problem considered in this paper have some kind of limitation or drawback. We just intend to contribute to the problem with an algorithm that can be useful in some cases, and perhaps in cases where other algorithms may fail. As for the second algorithm, for ruled surfaces, we dare say that the algorithm is more efficient than the other algorithms presented to this day. Nevertheless, for this second algorithm, it can certainly happen that the line of striction is a line or a circle, in which case we would have infinitely many symmetries to test. In that situation, one should choose an alternative algorithm among the ones reviewed in this paper.
The ideas presented in this paper can be extended without any effort to compute isometries between rational surfaces, both in the cases of non-ruled and ruled surfaces. As for other generalizations, in order to detect, for instance, affine or projective equivalences between rational surfaces, we would need to replace the Gauss and mean curvature by affine or projective invariants. Finding invariants with the properties that we require, which include a "good" behavior with respect to reparametrizations, is not a trivial task (see [29] for a similar question for curves). So we leave this question here as an open problem.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
Juan Gerardo Alcázar and Carlos Hermoso are supported by the grant PID2020-113192GB-I00 (Mathematical Visualization: Foundations, Algorithms and Applications) from the Spanish MICINN. Juan G. Alcázar and Carlos Hermoso are also members of the Research Group ASYNACS (Ref. ccee2011/r34). Juan Gerardo Alcázar and Uğur Gözütok are supported by TUBITAK (The Scientific and Technological Research Council of Türkiye) in the scope of 2221-Fellowships for Visiting Scientists and Scientists on Sabbatical Leave. The authors would like to thank the reviewers of the paper for their comments, which allowed us to improve the paper.
Conflict of interest
The authors declare there is no conflict of interest.









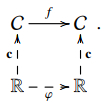
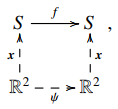
 DownLoad:
DownLoad: