Figure 1.
T2WI and T1WI MRI slices at the same location in a patient with PAS.
Citation: Saulo Orizaga, Ogochukwu Ifeacho, Sampson Owusu. On an efficient numerical procedure for the Functionalized Cahn-Hilliard equation[J]. AIMS Mathematics, 2024, 9(8): 20773-20792. doi: 10.3934/math.20241010
| [1] | Xiaoli Wang, Lizhen Wang . Traveling wave solutions of conformable time fractional Burgers type equations. AIMS Mathematics, 2021, 6(7): 7266-7284. doi: 10.3934/math.2021426 |
| [2] | Zui-Cha Deng, Fan-Li Liu, Liu Yang . Numerical simulations for initial value inversion problem in a two-dimensional degenerate parabolic equation. AIMS Mathematics, 2021, 6(4): 3080-3104. doi: 10.3934/math.2021187 |
| [3] | Mohammad Partohaghighi, Ali Akgül, Jihad Asad, Rania Wannan . Solving the time-fractional inverse Burger equation involving fractional Heydari-Hosseininia derivative. AIMS Mathematics, 2022, 7(9): 17403-17417. doi: 10.3934/math.2022959 |
| [4] | M. J. Huntul . Inverse source problems for multi-parameter space-time fractional differential equations with bi-fractional Laplacian operators. AIMS Mathematics, 2024, 9(11): 32734-32756. doi: 10.3934/math.20241566 |
| [5] | Humaira Yasmin, Aljawhara H. Almuqrin . Analytical study of time-fractional heat, diffusion, and Burger's equations using Aboodh residual power series and transform iterative methodologies. AIMS Mathematics, 2024, 9(6): 16721-16752. doi: 10.3934/math.2024811 |
| [6] | Jian-Gen Liu, Jian Zhang . A new approximate method to the time fractional damped Burger equation. AIMS Mathematics, 2023, 8(6): 13317-13324. doi: 10.3934/math.2023674 |
| [7] | Farman Ali Shah, Kamran, Zareen A Khan, Fatima Azmi, Nabil Mlaiki . A hybrid collocation method for the approximation of 2D time fractional diffusion-wave equation. AIMS Mathematics, 2024, 9(10): 27122-27149. doi: 10.3934/math.20241319 |
| [8] | Asif Khan, Tayyaba Akram, Arshad Khan, Shabir Ahmad, Kamsing Nonlaopon . Investigation of time fractional nonlinear KdV-Burgers equation under fractional operators with nonsingular kernels. AIMS Mathematics, 2023, 8(1): 1251-1268. doi: 10.3934/math.2023063 |
| [9] | Xiangtuan Xiong, Wanxia Shi, Xuemin Xue . Determination of three parameters in a time-space fractional diffusion equation. AIMS Mathematics, 2021, 6(6): 5909-5923. doi: 10.3934/math.2021350 |
| [10] | Shuang-Shuang Zhou, Saima Rashid, Asia Rauf, Khadija Tul Kubra, Abdullah M. Alsharif . Initial boundary value problems for a multi-term time fractional diffusion equation with generalized fractional derivatives in time. AIMS Mathematics, 2021, 6(11): 12114-12132. doi: 10.3934/math.2021703 |
Placenta accrete spectrum (PAS) disorder is defined as the abnormal invasion of trophoblast cells into the myometrium at different depths of infiltration. It occurs mainly in patients with placenta previa or previous cesarean section [1]. Common complications of PAS include catastrophic perinatal hemorrhage and injury of bladder, rectal and urethral [2]. There are many high-risk factors for PAS, including the history of cesarean section, placenta previa, multiple miscarriages and curettage, history of other uterine-related surgeries such as myomectomy, and advanced maternal age [3,4]. With the increase of various risk factors such as cesarean section and abortion, the incidence of PAS is also increasing year by year [5,6,7,8]. China is a country with a relatively high cesarean section rate [9]. With the implementation of the three-child policy, the number of late marriages and childbearing has increased. It can be speculated that the incidence of PAS in China will further rise. Therefore, the prenatal prediction of PAS is of important practical significance.
The traditional detection methods of PAS based on MRI generally include three consecutive steps: region of interest segmentation, image feature extraction and PAS detection [10]. A recent study showed that experienced radiologists performed significantly better than junior radiologists (90.9% of sensitivity and 75% of specificity for senior attending physicians, 81.8% of sensitivity and 61.8% of specificity for primary attending physicians) [11]. In order to reduce the reliance on the clinical experience of doctors and improve the diagnostic level of PAS, some scoring systems for the diagnosis of placental invasion have been proposed in recent years, which have not been widely tested [12]. Some scholars [13,14] used machine learning methods to detect PAS based on radiomics features and clinical factors (such as whether it was a scarred uterus, whether there was a history of cesarean section, and whether there was a history of miscarriage, etc.). There are also a few studies [15] using deep neural networks to learn powerful visual representations in MR images to predict PAS, but detection of PAS based on MRI is still a challenging task, there are several problems:
(1) Radiomics features are explicitly designed or handcrafted. Although the number of features can reach tens of thousands, these features are shallow and low-level image features. The heterogeneity within the placenta and the relationship between the placenta and adjacent tissues may not be fully characterized, thus limiting the predictive potential of the model.
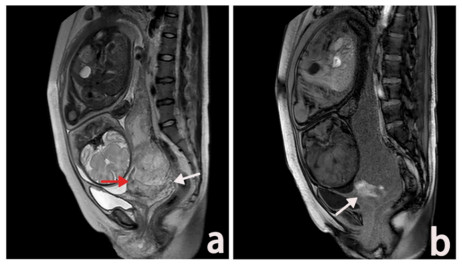
(2) In clinical practice, doctors usually diagnose PAS based on the placental signal reflected by T2WI MR images supplemented by the bleeding conditions reflected by T1WI MR images. Traditional MR image analysis methods are difficult to extract multiple sequences of MR image features at the same time and assign corresponding weights to predict PAS according to their significance. Figure 1 shows T2WI and T1WI MRI slices of a patient with PAS at the same location.
Among them, Figure 1(a) is a sagittal view of T2WI, which shows PAS in the posterior and lower part of placenta (white arrow), and a strip of low signal on T2WI (red arrow) is seen in the placenta; Figure 1(b) is a sagittal view of T1WI, and a mass of hyperintense hemorrhage is seen in the placenta (white arrow).
In order to solve the above problems, we proposed a dual-path neural network fused with a multi-head attention module, which includes a dual-path neural network and a multi-head attention module. Dual-path neural network can extract T2WI and T1WI MR image features. Specifically, the presence of low-intensity bands or small patches in the placenta on T2WI sequences may indicate PAS; Intraplacental hemorrhage is usually seen in the placenta of T1WI MR images with patchy slightly high signal intensity, which may also suggest PAS. The multi-head attention module assigns different weights to the features of different sequences through learning and fuses them to better measure the importance of different sequence features.
The main contributions of this paper are: (1) A dual-path neural network is designed to extract the features of T2WI and T1WI sequences of MR images; (2) A multi-head attention module is proposed to learn the weights of different features to generate final features with stronger discrimination. Experimental results on an independent validation dataset show that the detection accuracy achieved by our method is superior to the methods using only a single sequence of MR images. The comparative experimental results also show the effectiveness of the multi-head attention module proposed in this paper.
In this section, we discuss the work most related to our work: detection of PAS based on MRI. MRI is less affected by intestinal gas and bones, has high tissue resolution and can be imaged at any angle in multiple directions, so it is especially recommended for cases with unclear posterior placenta and ultrasound results and/or high clinical suspicion [16,17,18]. In practice, MR images can provide important information for doctors to predict and diagnose the type of PAS. Recently, there have been many studies with promising performance. These algorithms typically use hand-designed or measured features to detect PAS. For example, Zheng et al. [19] used the observed imaging features on MR images to diagnose PAS, such as whether it is placenta previa, whether the placenta is thickened, etc. However, manually designing and measuring features is time-consuming and labor-intensive. To overcome this difficulty, several radiomics or deep learning-based methods have been proposed to automatically extract MRI features. For example, Romeo et al. [13] used a machine learning algorithm to predict the types of PAS based on radiomics features. Li et al. [15] used an auto-encoding network to extract features of MR images to predict the types of PAS. However, most of the current studies are based on a single sequence of MRI for the detection of PAS. In clinical practice, doctors usually diagnose PAS based on the placental signal reflected by T2WI MR images supplemented by the bleeding conditions reflected by T1WI MR images. Therefore, we propose a dual-path neural network fused with a multi-head attention module to detect PAS. The model first uses a dual-path neural network to extract T2WI and T1WI MR image features separately, and then combines these features. The multi-head attention module learns multiple different attention weights to focus on different aspects of the placental image to generate discriminative final features.
This retrospective study was approved by the Ethics Committee of The Affiliated Hospital of Medical College of Ningbo University, and all patients' identities were de-identified to protect patient privacy. The MR images were collected from The Affiliated Hospital of Medical College of Ningbo University and Ningbo Women & Children's Hospital from January 2018 to May 2021.
All MRI examinations were performed by radiologists with more than 5-year of work experience using 1.5 Tesla units to perform 8 or 16-channel array sensitivity-coded abdominal coil scans. The imaging equipment of The Affliated Hospital of Medical College of Ningbo University is Ge signa twinspeed 1.5T superconducting dual gradient magnetic resonance scanner with 8-channel body phased array coil. The imaging equipment of Ningbo Women & Children's Hospital is Philips Achieva Noval Dual 1.5T superconducting dual gradient magnetic resonance scanner, using a 16-channel body phased array coil. In this study, we chose the supine sagittal image of the conventional T2WI and T1WI sequence (side-lying imaging is prone to curling artifacts due to the bulge of the abdomen) as the experimental sequence.
Inclusion criteria are as follows: (1) Patients who underwent T2WI and T1WI MRI after 30 weeks of gestation; (2) Those with clear placenta invasion or pathological records after cesarean section; (3) Image quality is good. The exclusion criteria are as follows: (1) Patients without T2WI or T1WI MRI data; (2) Patients with mismatched number of T2WI and T1WI MRI slices; (3) Patients without clinical or surgical pathological confirmation; (4) Patients with severe image artifact.
Based on the above criteria, we collected a total of 321 cases, including 142 normal cases and 179 cases of PAS (including accrete, increta and percreta). The degree of invasion in all patients was determined based on surgical findings, intraoperative diagnosis and pathological examinations. Table 1 is the distribution table of our dataset.
| Normal | Accrete | Increta | Percreta | |
| Jan., 2018~Dec., 2019 | 86 | 17 | 114 | 8 |
| Jan., 2020~May, 2021 | 56 | 14 | 22 | 4 |
| Total | 142 | 31 | 136 | 12 |
DownLoad:
CSV
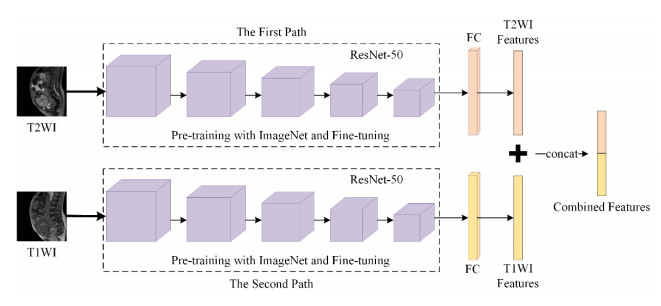
In order to extract the features of dual-sequence MR images, we designed a dual-path neural network to extract T2WI and T1WI MR image features. The dual-path neural network consists of two independent backbone networks, and finally combines the features extracted from the two backbone networks. Taking ResNet-50 as the backbone network as an example [20], the structure of the dual-path neural network is shown in Figure 2.
As shown in Figure 2, the dual-path neural network consists of two independent backbone networks. The backbone network ResNet-50 includes 5 convolution blocks. The last layer of each convolution block outputs a feature map of a specific scale as the input of next convolution block, and the size of the feature map output by the previous convolution block is 1/2 of the size of the feature map output by the next convolution block. The final output of each backbone network is a 128-dimensional feature vector, and the outputs of the two backbone networks are spliced as the extracted combined features.
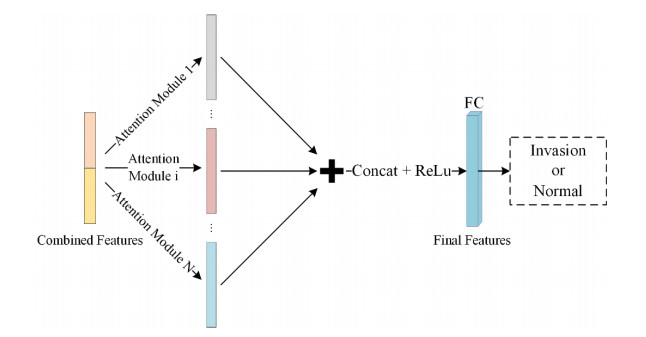
We obtained the combined features that fused the two sequences of MR images by the dual-path neural network. To assign different weights to different features and perform further fusion, we proposed a multi-head attention module. The output of the attention module usually focuses on a specific part of the image, such as: intraplacental heterogeneity information in T2WI MR images or hemorrhage information in T1WI MR images. A single attention unit can usually only reflect one aspect of an image. However, it may be more effective to have multiple attention units focus on different features in different sequences of images and to describe the images of the entire case together as the MRI data contains multiple sequences. Therefore, to be able to represent multiple aspects of an image, multiple attention units are needed to focus on different aspects of the image. Multiple attention units focus on the same input, but the parameters between multiple units are independent of each other.
Based on the above ideas, this paper proposed a multi-head attention module, which learns multiple sets of parameters to focus on different aspects of the final feature as shown in Figure 3.
Specifically, multiple sets of paired scalars are learned. The first scalar scales the global features linearly, and the second scalar acts as a bias to introduce nonlinear factors. The above process can be expressed as:
| Vi=ωi∗T+bi | (1) |
where ωi and bi represent the scalar parameter pair learned by the ith attention unit. After obtaining the feature Vi output by the attention unit, L2 regularization is performed on it, and the features obtained by all units are spliced together, and after nonlinear transformation, it is used as the output of the multi-head attention module. The process can be expressed as:
| V=Relu(V1⊕V2⊕⋯⊕VN) | (2) |
where V represents the final feature, ⊕ represents the splicing operation, and the nonlinear transformation uses the Relu activation function. In subsequent experimental sections, we will compare the detection accuracy of attention module networks with different head counts.
The dataset we collected included 142 normal cases and 179 cases of PAS (31 accrete, 136 increta and 12 percreta). The number of T2WI and T1WI sequence slices in each case is equal, including 24–48 slices. Both sequences scan the same part of the patient, so the slices of the two sequences can be in one-to-one correspondence. We excluded 5 slices from the head and tail of the two sequences in each case because there was no uterine area in these slices. To expand the dataset, we treat each T2WI image and its corresponding T1WI image as a slice group [21,22].
Background information occupies a large proportion in MR images and has a large impact on subsequent feature extraction and classification [23,24]. We crop the center region of the image, and the cropped size is 256 × 256. We randomly split the dataset into a training set and an independent validation set in a 4:1 ratio. Table 2 is the data set split table.
| Class | Train | Validation |
| Normal | 1886 | 472 |
| PAS | 2451 | 613 |
DownLoad:
CSV
All models are implemented in PyTorch. Batch normalization [25] is used for all models. All networks are trained using one RTX 2080Ti GPU with 50 training epochs for the dual-path neural network and the multi-head attention module. We used the Adam Optimizer with a small learning rate 10−4. In addition, the two backbone networks in the dual-path neural network are separately trained on T2WI and T1WI sequence image data respectively. Based on the trained model, the features are extracted and spliced to obtain the combined features which are used for the training of the multi-head attention module.
Evaluate the performance of classification methods using a confusion matrix. The true positive (TP), true negative (TN), false positive (FP) and false negative (FN) values are obtained from the confusion matrix to calculate four performance evaluation metrics as follows:
| Accuracy=TN+TPTN+TP+FN+FP | (3) |
| Precision=TPTP+FP | (4) |
| Recall=TPTP+FN | (5) |
| F1score=2×Precision×RecallPrecision+Recall | (6) |
Among them, accuracy represents the percentage of samples that exactly match the real situation; precision is the proportion of true positives in samples predicted as positive examples; Recall is the proportion of true positives in true positive examples; F1-score is the harmonic mean of precision and recall. In order to avoid dividing by 0 in the calculation process, when TP is 0, the F1 score is recorded as 0.
In order to prove that the features of dual-sequence MR images are effective for the detection of PAS, we use three machine learning methods to compare the detection accuracy of the three features on an independent validation set. The three machine learning methods are: decision tree (DT), random forest (RF), and support vector machine (SVM); the three features are: features extracted from T2WI MR images, features extracted from T1WI MR images, and combined features obtained by splicing the above two features. Table 3 shows the comparison results.
| Methods | Features | Accuracy | F1 score |
| Decision Tree | T2WI features | 0.857 | 0.870 |
| T1WI features | 0.681 | 0.715 | |
| Combined features | 0.854 | 0.868 | |
| Random Forest | T2WI features | 0.864 | 0.876 |
| T1WI features | 0.709 | 0.733 | |
| Combined features | 0.862 | 0.874 | |
| Support Vector Machine | T2WI features | 0.862 | 0.875 |
| T1WI features | 0.700 | 0.737 | |
| Combined features | 0.869 | 0.882 |
DownLoad:
CSV
It can be seen in Table 3 that the method using SVM achieves the highest accuracy and F1 score on combined features, which are 0.869 and 0.882 respectively, which are higher than the accuracy of the same method on T2WI features and T1WI features. Based on DT and RF, the accuracy and F1 score of T2WI features and combined features are almost equal, and the accuracy and F1 score of T1WI features are lower than those of the above two features. In summary, simply splicing the features of the two sequences can improve the detection accuracy of PAS, but the effect is not obvious. Based on the SVM method, we used T2WI features and combined features to draw receiver operating characteristic (ROC) curves and performed the significance test (DeLong's Test) of the area under the ROC curves (AUC). The experimental results are shown in Table 4.
| T2WI features ~ Combined features | |
| Difference between areas | 0.0236 |
| Standard Error | 0.00362 |
| 95% Confidence Interval | 0.0165 to 0.0307 |
| z statistic | 6.519 |
| Significance level | P < 0.0001 |
DownLoad:
CSV
As can be seen from Table 4, the P-value is less than 0.0001, which indicates that there is a significant difference between the AUCs of the two kinds of features. To further improve model performance, we design a multi-head attention module to pay attention to different features in different sequences of MR images. The multi-head attention module can assign their respective weights according to their importance to improve the detection accuracy.
In order to compare the detection accuracy of attention modules with different numbers of heads in the detection of PAS, we calculated the detection accuracy and F1 score of attention modules with different numbers of heads on the independent validation set. Table 5 shows the comparison results. The case where the number of attention heads is 0 means that the attention mechanism is not used. It only uses one Relu layer and fully connected layers (the output dimension of the fully connected layer is 2, which means normal or invasion respectively) to detect PAS.
| The number of heads | Accuracy | F1 score |
| 0 | 0.857 | 0.873 |
| 2 | 0.859 | 0.874 |
| 4 | 0.874 | 0.888 |
| 8 | 0.886 | 0.899 |
| 16 | 0.861 | 0.876 |
DownLoad:
CSV
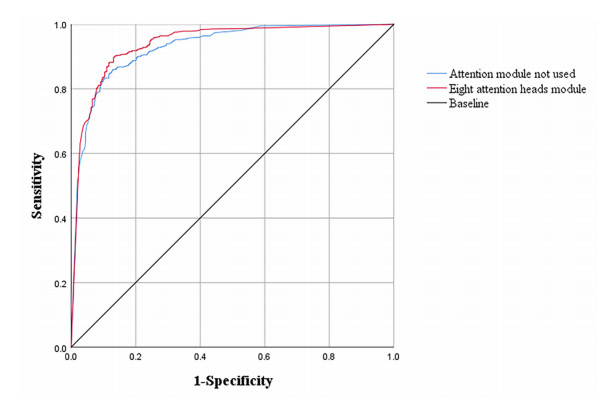
As can be seen from Table 5, the detection accuracy and F1 score of using the attention module are improved compared with those without the attention module. The highest accuracy and F1 score were achieved with 8 attention heads, 0.886 and 0.899 respectively. When the number of heads is less than 8, the fitting ability of the model is insufficient due to insufficient parameters. When the number of heads is greater than 8, because the model has too many parameters and the size of the training set is not large, the model is over-fitted, and the accuracy rate decreases to a certain extent. Therefore, an attention module with 8 heads is used in the experiment. To further compare the model performance with and without the attention module, we plot the ROC curves. Figure 4 shows the ROC curves with and without the 8-head attention module.
As shown in Figure 4, the performance of the model with the 8-head attention module is significantly higher than that of the model without the attention module. To compare the performance of the two models more intuitively, we calculated the AUC. The results are shown in Table 6.
| Methods | AUC |
| Attention module not used | 0.930 |
| Eight attention heads module | 0.940 |
DownLoad:
CSV
In order to objectively evaluate the performance of the model and eliminate the impact of data leakage on the experimental results, we select 40 samples that do not appear in the training set from the validation set to form a new test set (20 for normal, 20 for PAS), and verify the performance of the proposed model with 8-head attention module from the accuracy and F1 score. The experimental results show that the model can also achieve ideal results on the test set, reaching an accuracy of 0.825 and an F1 score of 0.837.
This paper proposed a method to detect PAS by extracting and fusing dual sequence placental MR image features using a dual-path neural network. The proposed model mainly includes a dual-path neural network and a multi-head attention module. The dual-path neural network is used to extract the features of the two sequences of MR images and perform feature fusion; the multi-head attention module learns the corresponding weights for different features in different sequences to generate more discriminative final features. Experimental results on an independent validation set demonstrate the effectiveness of each module in our method, with clear advantages over methods that only use a single sequence of MR images. This method may assist physicians in clinical diagnosis, help physicians make perinatal planning and improve maternal outcomes.
This work was supported by the Key Talents of Ningbo City Health Technology under Grant 2020SWSQNGG-06 and Zhejiang Province Medicine and Health Project under Grant 2022KY1149.
The authors declare that there are no conflicts of interest.
| [1] |
J. W. Cahn, J. E. Hilliard, Free energy of a nonuniform system. I. interfacial free energy, J. Chem. Phys., 28 (1958), 258–267. https://doi.org/10.1063/1.1744102 doi: 10.1063/1.1744102
|
| [2] |
S. M. Allen, J. W. Cahn, A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening, Acta Metall., 27 (1979), 1085–1095. https://doi.org/10.1016/0001-6160(79)90196-2 doi: 10.1016/0001-6160(79)90196-2
|
| [3] |
A. Miranville, The Cahn-Hilliard equation and some of its variants, AIMS Math., 2 (2017), 479–544. https://doi.org/10.3934/Math.2017.2.479 doi: 10.3934/Math.2017.2.479
|
| [4] |
S. M. Wise, J. S. Lowengrub, H. B. Frieboes, V. Cristini, Three-dimensional multispecies nonlinear tumor growth-i: Model and numerical method, J. Theor. Biol., 253 (2008), 524–543. https://doi.org/10.1016/j.jtbi.2008.03.027 doi: 10.1016/j.jtbi.2008.03.027
|
| [5] |
H. Garcke, K. F. Lam, V. Styles, Cahn-hilliard inpainting with the double obstacle potential, SIAM J. Imaging Sci., 11 (2018), 2064–2089. https://doi.org/10.1137/18M1165633 doi: 10.1137/18M1165633
|
| [6] |
A. L. Bertozzi, S. Esedoglu, A. Gillette, Inpainting of binary images using the cahn-hilliard equation, IEEE T. Image Proc., 16 (2007), 285–291. https://doi.org/10.1109/TIP.2006.887728 doi: 10.1109/TIP.2006.887728
|
| [7] |
L. Q. Chen, Phase-field models for microstructure evolution, Annu. Rev. Mater. Res., 32 (2002), 113–140. https://doi.org/10.1146/annurev.matsci.32.112001.132041 doi: 10.1146/annurev.matsci.32.112001.132041
|
| [8] | J. W. Barrett, J. F. Blowey, Finite element approximation of the Cahn-Hilliard equation with concentration dependent mobility, Math. Comp., 68 (1999), 487–517. |
| [9] |
K. Glasner, S. Orizaga, Improving the accuracy of convexity splitting methods for gradient flow equations, J. Comput. Phys., 315 (2016), 52–64. https://doi.org/10.1016/j.jcp.2016.03.042 doi: 10.1016/j.jcp.2016.03.042
|
| [10] |
H. Song, Energy SSP-IMEX Runge-Kutta methods for the Cahn-Hilliard equation, J. Comput. Appl. Math., 292 (2016), 576–590. https://doi.org/10.1016/j.cam.2015.07.030 doi: 10.1016/j.cam.2015.07.030
|
| [11] |
J. M. Church, Z. Guo, P. K. Jimack, A. Madzvamuse, K. Promislow, B. Wetton, et al., High accuracy benchmark problems for allen-cahn and cahn-hilliard dynamics, Commun. Comput. Phys., 26 (2019), 947–972. https://doi.org/10.4208/cicp.OA-2019-0006 doi: 10.4208/cicp.OA-2019-0006
|
| [12] |
J. Shen, J. Xu, J. Yang, The scalar auxiliary variable (SAV) approach for gradient flows, J. Comput. Phys., 353 (2018), 407–416. https://doi.org/10.1016/j.jcp.2017.10.021 doi: 10.1016/j.jcp.2017.10.021
|
| [13] |
S. Orizaga, K. Glasner, Instability and reorientation of block copolymer microstructure by imposed electric fields, Phys. Rev. E, 93 (2016), 052504. https://doi.org/10.1103/PhysRevE.93.052504 doi: 10.1103/PhysRevE.93.052504
|
| [14] |
K. R. Elder, M. Grant, Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals, Phys. Rev. E, 70 (2004), 051605. https://doi.org/10.1103/PhysRevE.70.051605 doi: 10.1103/PhysRevE.70.051605
|
| [15] |
H. Gomez, X. Nogueira, An unconditionally energy-stable method for the phase field crystal equation, Comput. Meth. Appl. Mech. Eng., 249-252 (2012), 52–61. https://doi.org/10.1016/j.cma.2012.03.002 doi: 10.1016/j.cma.2012.03.002
|
| [16] |
H. Gomez, M. Bures, A. Moure, A review on computational modelling of phasetransition problems, Philos. T. Royal Soc. A: Math. Phys. Eng. Sci., 377 (2019), 20180203. https://doi.org/10.1098/rsta.2018.0203 doi: 10.1098/rsta.2018.0203
|
| [17] |
G. Gompper, M. Schick, Correlation between structural and interfacial properties of amphiphilic systems, Phys. Rev. Lett., 65 (1990), 1116–1119. https://doi.org/10.1103/PhysRevLett.65.1116 doi: 10.1103/PhysRevLett.65.1116
|
| [18] |
W. Feng, Z. Guan, J. Lowengrub, C. Wang, S. M. Wise, Y. Chen, A uniquely solvable, energy stable numerical scheme for the functionalized cahn–hilliard equation and its convergence analysis, J. Sci. Comput., 76 (2018), 1938–1967. https://doi.org/10.1007/s10915-018-0690-1 doi: 10.1007/s10915-018-0690-1
|
| [19] |
C. Zhang, J. Ouyang, C. Wang, S. M. Wise, Numerical comparison of modified-energy stable SAV-type schemes and classical BDF methods on benchmark problems for the functionalized cahn-hilliard equation, J. Comput. Phys., 423 (2020), 109772. https://doi.org/10.1016/j.jcp.2020.109772 doi: 10.1016/j.jcp.2020.109772
|
| [20] |
A. L. Bertozzi, N. Ju, H. W. Lu, A biharmonic-modified forward time stepping method for fourth order nonlinear diffusion equations, Discrete Contin. Dyn. Syst., 29 (2011), 1367–1391. https://doi.org/10.3934/dcds.2011.29.1367 doi: 10.3934/dcds.2011.29.1367
|
| [21] |
D. J. Eyre, Unconditionally gradient stable time marching the Cahn-Hilliard equation, MRS Online Proceedings Library (OPL), 529 (1998), 39. https://doi.org/10.1557/PROC-529-39 doi: 10.1557/PROC-529-39
|
| [22] |
S. Dai, Q. Du, Computational studies of coarsening rates for the Cahn-Hilliard equation with phase-dependent diffusion mobility, J. Comput. Phys., 310 (2016), 85–108. https://doi.org/10.1016/j.jcp.2016.01.018 doi: 10.1016/j.jcp.2016.01.018
|
| [23] |
H. D. Ceniceros, C. J. Garcia-Cervera, A new approach for the numerical solution of diffusion equations with variable and degenerate mobility, J. Comput. Phys., 246 (2013), 1–10. https://doi.org/10.1016/j.jcp.2013.03.036 doi: 10.1016/j.jcp.2013.03.036
|
| [24] | L. N. Trefethen, Spectral Methods in MatLab, New York: SIAM, 2000. |
| [25] |
G. Sheng, T. Wang, Q. Du, K. G. Wang, Z. K. Liu, L. Q. Chen, Coarsening kinetics of a two phase mixture with highly disparate diffusion mobility, Commun. Comput. Phys., 8 (2010), 249–264. https://doi.org/10.4208/cicp.160709.041109a doi: 10.4208/cicp.160709.041109a
|
| [26] |
J. Zhu, L. Q. Chen, J. Shen, V. Tikare, Coarsening kinetics from a variablemobility cahn-hilliard equation: application of a semi-implicit fourier spectral method, Phys. Rev. E, 60 (1999), 3564. https://doi.org/10.1103/PhysRevE.60.3564 doi: 10.1103/PhysRevE.60.3564
|
| [27] |
D. Li, Z. Qiao, T. Tang, Characterizing the stabilization size for semi-implicit Fourier-spectral method to phase field equations, SIAM J. Numer. Anal., 54 (2016), 1653–1681. https://doi.org/10.1137/140993193 doi: 10.1137/140993193
|
| [28] |
D. Li, Z. Qiao, On second order semi-implicit fourier spectral methods for 2d Cahn-Hilliard equations, J. Sci. Comput., 70 (2017), 301–341. https://doi.org/10.1007/s10915-016-0251-4 doi: 10.1007/s10915-016-0251-4
|
| [29] |
Z. Xu, H. Zhang, Stabilized semi-implicit numerical schemes for the Cahn-Hilliard-like equation with variable interfacial parameter, J. Comput. Appl. Math., 346 (2019), 307–322. https://doi.org/10.1016/j.cam.2018.06.031 doi: 10.1016/j.cam.2018.06.031
|
| [30] |
L. Duchemin, J. Eggers, The explicit-implicit-null method: Removing the numerical instability of PDEs, J. Comput. Phys., 263 (2014), 37–52. https://doi.org/10.1016/j.jcp.2014.01.013 doi: 10.1016/j.jcp.2014.01.013
|
| [31] |
Y. Yan, W. Chen, C. Wang, S. M. Wise, A second-order energy stable BDF numerical scheme for the Cahn-Hilliard equation, Commun. Comput. Phys., 23 (2018), 572–602. https://doi.org/10.4208/cicp.OA-2016-0197 doi: 10.4208/cicp.OA-2016-0197
|
| [32] | C. Canuto, M. Y. Hussaini, A. Quarteroni, T. A. Zang, Spectral Methods: Fundamentals in Single Domains, Berlin: Springer Science Business Media, 2007. |
| [33] |
J. Shen, J. Xu, J. Yang, A new class of efficient and robust energy stable schemes for gradient flows, SIAM Rev., 61 (2019), 474–506. https://doi.org/10.1137/17M1150153 doi: 10.1137/17M1150153
|
| [34] |
A. Christlieb, J. Jones, K. Promislow, B. Wetton, M. Willoughby, High accuracy solutions to energy gradient flows from material science models, J. Comput. Phys., 257 (2014), 193–215. https://doi.org/10.1016/j.jcp.2013.09.049 doi: 10.1016/j.jcp.2013.09.049
|
| [35] |
A. Doelman, G. Hayrapetyan, K. Promislow, B. Wetton, Meander and pearling of single-curvature bilayer interfaces in the functionalized cahn-hilliard equation, SIAM J. Math. Anal., 46 (2014), 3640–3677. https://doi.org/10.1137/13092705X doi: 10.1137/13092705X
|
| [36] |
C. Zhang, J. Ouyang, Unconditionally energy stable second-order numerical schemes for the functionalized cahn–hilliard gradient flow equation based on the SAV approach, Comput. Math. Appl., 84 (2021), 16–38. https://doi.org/10.1016/j.camwa.2020.12.003 doi: 10.1016/j.camwa.2020.12.003
|
| [37] |
K. Promislow, Q. Wu, Existence of pearled patterns in the planar functionalized cahn-hilliard equation, J. Diff. Equ., 259 (2015), 3298–3343. https://doi.org/10.1016/j.jde.2015.04.022 doi: 10.1016/j.jde.2015.04.022
|
| [38] |
Z. Tan, L. Chen, J. Yang, Generalized allen-cahn-type phase-field crystal model with fcc ordering structure and its conservative high-order accurate algorithm, Comput. Phys. Commun., 286 (2023), 108656. https://doi.org/10.1016/j.cpc.2023.108656 doi: 10.1016/j.cpc.2023.108656
|
| [39] |
N. Gavish, J. Jones, Z. Xu, A. Christlieb, K. Promislow, Variational models of network formation and ion transport: Applications to perfluorosulfonate ionomer membranes, Polymers, 4 (2012), 630–655. https://doi.org/10.3390/polym4010630 doi: 10.3390/polym4010630
|
| [40] |
J. Burkardt, M. Gunzburger, W. Zhao, High-precision computation of the weak galerkin methods for the fourth-order problem, Numer. Algor., 84 (2020), 181–205. https://doi.org/10.1007/s11075-019-00751-5 doi: 10.1007/s11075-019-00751-5
|
| 1. | Jiawei Wang, Yanqin Liu, Limei Yan, Kunling Han, Libo Feng, Runfa Zhang, Fractional sub-equation neural networks (fSENNs) method for exact solutions of space–time fractional partial differential equations, 2025, 35, 1054-1500, 10.1063/5.0259937 |
Figures(16) / Tables(1)
Saulo Orizaga, Ogochukwu Ifeacho, Sampson Owusu. On an efficient numerical procedure for the Functionalized Cahn-Hilliard equation[J]. AIMS Mathematics, 2024, 9(8): 20773-20792. doi: 10.3934/math.20241010
| Normal | Accrete | Increta | Percreta | |
| Jan., 2018~Dec., 2019 | 86 | 17 | 114 | 8 |
| Jan., 2020~May, 2021 | 56 | 14 | 22 | 4 |
| Total | 142 | 31 | 136 | 12 |
DownLoad:
CSV
| Class | Train | Validation |
| Normal | 1886 | 472 |
| PAS | 2451 | 613 |
DownLoad:
CSV
| Methods | Features | Accuracy | F1 score |
| Decision Tree | T2WI features | 0.857 | 0.870 |
| T1WI features | 0.681 | 0.715 | |
| Combined features | 0.854 | 0.868 | |
| Random Forest | T2WI features | 0.864 | 0.876 |
| T1WI features | 0.709 | 0.733 | |
| Combined features | 0.862 | 0.874 | |
| Support Vector Machine | T2WI features | 0.862 | 0.875 |
| T1WI features | 0.700 | 0.737 | |
| Combined features | 0.869 | 0.882 |
DownLoad:
CSV
| T2WI features ~ Combined features | |
| Difference between areas | 0.0236 |
| Standard Error | 0.00362 |
| 95% Confidence Interval | 0.0165 to 0.0307 |
| z statistic | 6.519 |
| Significance level | P < 0.0001 |
DownLoad:
CSV
| The number of heads | Accuracy | F1 score |
| 0 | 0.857 | 0.873 |
| 2 | 0.859 | 0.874 |
| 4 | 0.874 | 0.888 |
| 8 | 0.886 | 0.899 |
| 16 | 0.861 | 0.876 |
DownLoad:
CSV
| Methods | AUC |
| Attention module not used | 0.930 |
| Eight attention heads module | 0.940 |
DownLoad:
CSV
| Normal | Accrete | Increta | Percreta | |
| Jan., 2018~Dec., 2019 | 86 | 17 | 114 | 8 |
| Jan., 2020~May, 2021 | 56 | 14 | 22 | 4 |
| Total | 142 | 31 | 136 | 12 |
| Class | Train | Validation |
| Normal | 1886 | 472 |
| PAS | 2451 | 613 |
| Methods | Features | Accuracy | F1 score |
| Decision Tree | T2WI features | 0.857 | 0.870 |
| T1WI features | 0.681 | 0.715 | |
| Combined features | 0.854 | 0.868 | |
| Random Forest | T2WI features | 0.864 | 0.876 |
| T1WI features | 0.709 | 0.733 | |
| Combined features | 0.862 | 0.874 | |
| Support Vector Machine | T2WI features | 0.862 | 0.875 |
| T1WI features | 0.700 | 0.737 | |
| Combined features | 0.869 | 0.882 |
| T2WI features ~ Combined features | |
| Difference between areas | 0.0236 |
| Standard Error | 0.00362 |
| 95% Confidence Interval | 0.0165 to 0.0307 |
| z statistic | 6.519 |
| Significance level | P < 0.0001 |
| The number of heads | Accuracy | F1 score |
| 0 | 0.857 | 0.873 |
| 2 | 0.859 | 0.874 |
| 4 | 0.874 | 0.888 |
| 8 | 0.886 | 0.899 |
| 16 | 0.861 | 0.876 |
| Methods | AUC |
| Attention module not used | 0.930 |
| Eight attention heads module | 0.940 |
