Mutation prediction in the SARS-CoV-2 genome using attention-based neural machine translation

1.   Introduction

COVID-19 is known as the biggest pandemic of the 21st century caused by SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2) which is responsible for more than 6.9 million deaths and more than 770 million infections worldwide since its onset ^[1]. The first-ever case was reported in November 2019 and, for almost three years, the world has suffered a lot because it is hard to contain the virus due to its frequently occurring mutations and complex mechanism of action.

Viruses are known as obligate intracellular parasites that neither belong to living nor non-living organisms due to their unique course of reproduction. They behave like living beings and reproduce only when they are inside their host but remain dormant otherwise like non-living beings. SARS-CoV-2 belongs to the category of ss(+)RNA (single-stranded) viruses having a size of 29.9 Kb ^[2], its genome contains 12 functional open reading frames (ORFs) constituting $\sim$30,000 nucleotide base pairs, 38% GC content with 11 protein-coding regions and 12 expressed proteins. It has four major structural proteins, i.e., spike (S), envelope (E), membrane (M), and nucleocapsid (N), appearing in an order of $5^{\prime}$ to $3^{\prime}$; considered as the foremost vaccine and drug targets. In the genome, ORF1a and ORF1ab hold the viral nucleotide content; ORF1a along with ORF1b also encode polyproteins pp1a and pp1ab upon a ribosomal frame-shift between them. These polyproteins are then processed by viral proteinases to produce 16 non-structural proteins which have been found well-conserved in the coronavirus family ^[3].

The probability of a genetic change being passed to the next generation is known as the mutation rate in organisms; whereas, in viruses, one generation refers to the host cell infection cycle which comprises attachment, penetration, uncoating, gene expression, replication, encapsidation, and release ^[4]. Apart from replication, mutations can also occur from genome editing or rapid RNA/DNA damage and when these changes are left uncorrected these are transferred to the next viral generation. Some mutations are beneficial, some are neutral, while others are deleterious but higher mutation rates result in higher genetic diversity. RNA viruses are more prone to genetic variations as compared to DNA viruses, therefore, a small escalation in their mutation rates can cause an RNA virus strain to wipe off locally ^[5]. Cellular organisms have exonucleases that are responsible for correcting the nucleotide misincorporations that occur during the process of replication. Most of the viral RNA replicases lack proofreading activity, therefore, the absence of $3^{\prime}$ prime exonucleases causes a rise in the mutation rate of RNA viruses as compared to the DNA viruses, contributing to the immense number of SARS-CoV-2 variants and its high infectivity ^[6].

Predicting viral mutations can help a lot in understanding the course of the pandemic by identifying potential drug targets and rapid vaccine development. Statistical learning and probabilistic models were used for mutation prediction like indels or substitutions to get insights into sequence evolution ^[7]. Over time, new methods have been designed for mutation prediction tasks in genomic sequences such as statistical relational learning where mutation data is associated with drug resistance information related to the nucleoside and nonnucleoside human immunodeficiency viruses (HIV) reverse transcriptase inhibitors ^[7]. Such methods are dependent on general engineering techniques such as "rational designs" to induce site-specific mutations. Mutation prediction has also been performed on the influenza virus genome; time-series mutation prediction model (Tempel) is one such example that makes use of LSTMs (long short-term memory units) with an attention mechanism. This study was further topped by a classification model that discriminates whether a mutation is imminent in the genomic sequences or at specific residue sites of the influenza virus genome for months or not ^[8]. In our current study, the data preprocessing part has been inspired by the work done in Tempel. In the literature, the mutation prediction task has been performed using a deep neural network, cause and effect relationship, and randomness ^[9]. Apart from using deep neural networks to predict new viral strains, rough set theory has been used to extract point mutation patterns ^[10]. Recently, there have been rapid advancements in the field of NMT which have also escalated the prediction of mutations and their assessment in diverse ways. This includes using large language models (LLMs) to: study viral escape ^[11,12], identify high-risk SARS-CoV-2 variants ^[13], predict mutations in the SARS-CoV-2 genome ^[14], predict antigenic evolution in the SARS-CoV-2 genome and revealing its evolutionary dynamics ^[15,16], predict evolutionary dynamics of proteins ^[17], predict protein structure over evolutionary information ^[18,19], decipher gene regulatory code as one gene can produce various proteins ^[20], and predict the molecular phenotype ^[21].

So far, NMT applications (seq2seq) related to mutation prediction focus on the prediction of the mutations in the influenza virus, Newcastle disease virus, and SARS-CoV-2. The previously proposed models related to machine translation are imprecise in two ways, their training data and their evaluation, i.e., the input and output language have common sequences which creates a bias while making predictions from the decoder, and there is no proper evaluation measure based on which models are evaluated as accuracy is not an appropriate measure to evaluate NMT models. Furthermore, their models do not utilize attention mechanisms which suggests that their models are not information-rich enough to predict diverse mutations ^[22,23,24] like ours. Finally, these models are trained on the protein sequences which means that silent mutations cannot be predicted by these models. Contrary to seq2seq modeling, LLMs have been used not only to study the evolution of viral genomes, but also to study the evolutionary dynamics of eukaryotic genomes and proteomes ^{[17,18,19,20,21]}. However, LLMs used for mutation predictions are more complicated than seq2seq models as they have a wider range of parameters to be tuned and are more computationally expensive. Therefore, in this study, we are using bidirectional gated recurrent units (GRUs) with an attention mechanism to predict mutations in the SARS-CoV-2 genome specifically targeting only seven non-structural proteins (NSPs), i.e., NSP1, NSP3, NSP5, NSP8, NSP9, NSP13, and NSP15. Our proposed model (stacked biGRU with an attention mechanism) is not only less computationally expensive but is also simpler in terms of fine-grained control over architecture and training than LLMs alongside providing good predictions.

We first tried three unidirectional models (RNNs, LSTMs, and GRUs) to predict mutations. Based on slightly better convergence than RNNs and LSTMs, we opted for the GRU model and applied the attention mechanism. Since uni-directional models had convergence issues, we incorporated a bidirectional feature to obtain the proposed model which shows superior performance.

The paper is structured as follows: First, we explain neural machine translation (NMT) and recurrent neural networks (RNNs). Next, we describe data processing by the use of machine learning algorithms for the creation of sequence pairs. Following this, the workings of the proposed models are explained. The significance of the results is elaborated in the discussion section and, lastly, the conclusion marks the end of the paper.

2.   Materials and methods

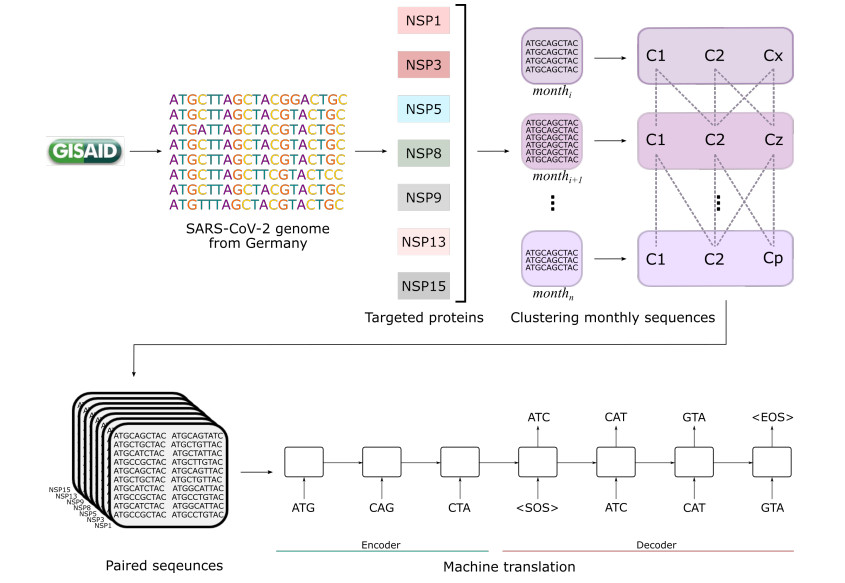
This section describes the protocol adopted for the current study. Figure 1 gives an overview of the workflow. The integrants of this figure are explained in detail.

Figure 1.  Workflow of the current study. Genomic sequence data of seven SARS-CoV-2 proteins is taken from the Global Initiative on Sharing All Influenza Data (GISAID), only belonging to Germany. It is clustered via k-means clustering in terms of months to keep the evolutionary relation intact between the sequences. Two relevant protein sequences are part of one pair which is used to train the recurrent neural networks to perform machine translation task.

DownLoad: Full-Size Img PowerPoint

2.1.   Neural machine translation

Neural machine translation is a famous approach for machine translation problems where an end-to-end trained model learns the meaningful information from the source text and uses it to output its correct translation. Neural networks are used for this purpose which require very little supervision. Unlike the conventional MT models, NMT works by training a single and large neural network that translates the source text into target text correctly/suitably. The NMT model comprises an encoder network and a decoder network. The encoder reads a source string and encodes it into a vector of fixed length known as a context vector. The context vector is taken by the decoder to provide a translation. Encoder and decoder networks are trained together to maximize the probability of a correct translation ^[25]. One way to perform machine translation tasks is through sequence-to-sequence (seq2seq) models.

2.1.1.   Seq2seq modeling

Sequence-to-sequence models are mainly used for language processing tasks, usually implemented with recurrent neural networks (RNNs) or their modified variants like LSTMs or GRUs, etc. Upon giving a sequence of inputs $(s^{\prime}_1, s^{\prime}_2, s^{\prime}_3, ..., s^{\prime}_T),$ sequence-to-sequence models generate a sequence of outputs $(s_1, s_2, s_3, ..., s_T)$ known as source and target sequences, respectively. Seq2seq models can be demonstrated as conditional language models:

where $p(s_t|s_{ < t}, s^{\prime})$ denotes the probability for the output token, given the input sequence $s^{\prime}$ and prior outputs $s_{ < t}$. These models comprise encoder and decoder parts. The encoder is a recurrent neural network and its task is to learn meaningful patterns from the source language and pass it to the decoder. The decoder is a recurrent neural network as well, but it takes a hidden state vector from the encoder and constructs a sequence from the target language, see Figure 2. One drawback is that sequence-to-sequence models suffer from information loss if the length of the input sequences is very long. Thus, to cater to this issue, attention mechanism was proposed ^[25]. Attention allows the model to focus on those parts of the source sequence where precise relevant information is present by using context vectors. The conditional probability changes to

where $W_p$ represents the learnable weight matrix, $[\hat h_t, c_t]$ represents the concatenated vector, $\hat h_t$ is the hidden state of the decoder vector at time point $t$, and $c_t$ denotes the context vector.

Figure 2.  Components of the study: (a) simple LSTM, (b) simple GRU, (c) vanilla RNN, (d) seq2seq translation, and (e) a snapshot of genome sequence data.

DownLoad: Full-Size Img PowerPoint

This was extended by incorporating local and global attention mechanisms by Luong et al. ^[26]. According to Luong's attention, the context vector $c_t$ at each time step $t$ is computed for the output sequence and depends on the attention scores $e_{ti}$ associated with it. It is the weighted sum of hidden states of encoder $h_i$ where attention weights $a_{ti}$ are used as weights:

where $h_{i}$ represents the hidden state of the encoder at time step $i$, and attention weights are computed by applying softmax to the attention scores,

where $m$ is the length of the source sequence and $k$ represents the individual position in the source sequence, and $e_{ti} = \hat h_{t}^{T}h_{i}$ where $\hat h_{t}^{T}$ represents the transpose of the hidden state of the decoder at time step $t$. The context vector is concatenated with the hidden state of the decoder and used as input for the next layer:

2.2.   Recurrent neural networks

Recurrent neural networks (RNNs) are neural networks used to model sequential or time series data and are adapted from standard feed-forward networks. The most important component of an RNN is its hidden state which integrates information over several time points aiding in accurate and precise predictions. For each sequence and time point, it works recursively by taking the input $(x_o, x_1, …, x_t)$, updating the hidden state $(h_o, h_1, …, h_t)$, and predicting an output $(y_o, y_1, …, y_t)$. So for each time point from $0$ to $t$, RNN works by iterating:

where, $w_{hx}$, $w_{hh}$, and $w_{yh}$ is input to hidden, hidden to hidden, and hidden to output weight matrices, respectively. $b_h$ and $b_y$ represent the bias vectors. An RNN unit is shown in Figure 2.

RNNs are trained by computing gradients via backpropagation through time, but sometimes gradients become too large (exploding gradients) or too small (vanishing gradients) ceasing the model to learn. The former can be fixed by simply truncating the gradients; whereas, the latter makes RNNs unsuitable for learning long-term dependencies ^[27].

2.3.   Long short-term memory units

Long short-term memory units (LSTMs) were proposed to resolve the vanishing gradient problem of RNNs, by introducing a cell state (incorporating long-term memory) with three logic gates (forget, input/update, and output gates) alongside a hidden state (which refers to short-term memory) for previous and current time points. For each time point, LSTM iterates by updating three gates. Forget gate $f_{t}$ determines the extent up to which existing memory is forgotten:

Input gate $i_{t}$ regulates the amount of new content to be stored in the cell state $c_{t}$, followed by the generation of a candidate cell state $\tilde{c}_{t}$ which ultimately leads to the updation of the old cell state to a new one, i.e., $c_{t}$:

Output gate $o_{t}$ determines the amount of information required to be output in the form of hidden state $h_{t}$, computed as:

An LSTM unit is shown in Figure 2. Unlike RNNS, LSTMs keep updating their context vector values by incorporating a cell state which makes them suitable for learning long-term dependencies ^[28].

2.4.   Gated recurrent units

Gated recurrent units (GRUs) are simpler versions of LSTMs that capture the dependencies of various time scales adaptively. Unlike LSTMs, GRUs have two gates, i.e., the update and reset gate. The update gate is simply the coalescence of the input and forget gates of LSTM. It also merges the hidden state and cell state of LSTM into one state $h_t$. GRU generates $h_t$ for each time point by updating these two gates, where update gate $z_t$ determines which new information to keep and which past information to get rid of, whereas, reset gate $r_t$ ascertains how much past information to forget ^[28]. See the GRU unit in Figure 2. For a given time point $t$, both gates are computed as:

Activation of candidate state $\tilde{h}_{t}$ is done as:

Generation of the new state ${h}_{t}$ is a linear interpolation of the previous and candidate state, as:

2.5.   Data

2.5.1.   Target proteins

SARS-CoV-2 is composed of structural and non-structural proteins. The former, as the name indicates, participate in making the viral structure while the latter are responsible for viral replication and assembly processes. For mutation prediction, we chose non-structural proteins as their tendency to mutate is few and far between as compared to structural proteins. Out of 16 NSPs, we chose 7 depending on their functionality; namely NSP1, NSP3, NSP5, NSP8, NSP9, NSP13, and NSP15, see Figure 3. NSP1 is mainly responsible for suppressing host innate immune functions and promoting viral protein translation. Therefore, it is known as the host shut-off factor ^[29]. NSP3 also disrupts the host immunity by inhibiting IFN (interferons) production and modifying the endoplasmic reticulum to double-membrane vesicles (DMVs) ^[30]. NSP5 works as the main protease, cleaving ORF1ab to generate more NSPs ^[31]. NSP8 promotes virus replication by making complexes with NSP6 and NSP7. It is also responsible for the identification of virus inhibitors ^[32]. NSP9 is a replicase enzyme blocking mRNA export of the host, and also dampens cytokine and interleukin-$1\alpha/\beta$ production to avoid activation of the host immune system ^[33]. NSP13 blocks interferon activation, downregulates IFIT1 protein expression, and reduces NF-$\kappa\beta$ activation in the host ^[34]. NSP15 works as an RNA endonuclease that evades the host's innate immune response and antagonizes interferon ^[35].

Figure 3.  Protein structures of (a) NSP1 (PDB ID: 7K7P) ^[37], (b) NSP3 (PDB ID: 7NFV) ^[38], (c) NSP5 (PDB ID: 7MHF) ^[39], (d) NSP8 (PDB ID: 7JLT) ^[40], (e) NSP9 (PDB ID: 7BWQ) ^[41], (f) NSP13 (PDB ID: 7RE1) ^[42], (g) NSP15 (PDB ID: 6VWW) ^[43].

DownLoad: Full-Size Img PowerPoint

2.5.2.   Data collection

The SARS-CoV-2 nucleotide sequences used in this study were downloaded from the GISAID repository ^[36]. GISAID (Global Initiative on Sharing All Influenza Data) was established initially to provide influenza virus genomic data worldwide which was further expanded to the provision of SARS-CoV-2 genomic data after the pandemic in late 2019. The selected NSPs' nucleotide sequences were downloaded in the fasta format limited to Germany only.

2.5.3.   Data preprocessing

Data was preprocessed separately for each NSP as their sequence lengths vary. Following the removal of redundant sequences, nucleotide sequences were further subjected to the removal of sequences with inappropriate lengths or those carrying unidentified nucleotides, e.g., 'NN', 'XX', etc. Then sequences were separated based on the months they were reported in, and in this study, we have taken sequences from January 2020 until May 2021 for training and from June 2021 until March 2022 for evaluation purposes. There were a total of 876,554 sequences and we were left with 20,079 training sequences after removing duplicates. Contrary to this, for evaluation, we had 2,164,077 sequences which were reduced to 38,372 after removing duplicates. For further insights into the data, please see Table S1. Since a single nucleotide in the sequence itself does not carry meaningful information and appears just as a character, each nucleotide sequence was transformed into a sequence of codons, i.e., a fusion of three consecutive nucleotides.

2.5.4.   Clustering

For seq2seq translation, we need a pair of two sequences where the first one belongs to the source language, and the other belongs to the target language, i.e., mutated/evolved sequences of SARs-CoV-2. To create the dataset for our seq2seq machine translation task, we applied k-means clustering on all sequences for every month and generated 'N' number of clusters in each month. We computed immediate neighbors of sequences using nearest neighbors, i.e., cluster $C_j, j \in \{ 1, ..., N \}$ from month $m_i$ can have two immediate neighbors (clusters $C_l, l \in \{1, ..., N\})$ from month $m_i+1$. To consider only biologically realistic evolutionary behaviors, we computed Euclidean distance for each sequence $s$ from cluster $C_j$ of month $m_i$ to sequences from the two immediate neighbors (clusters) from month $m_i + 1$, i.e.,

where $\left\Vert \cdot \right\Vert$ represents the Euclidean norm and threshold values 0.5 and 3 are chosen for the selection of sequences in a pair based on this assumption that a virus can have only a few mutations in a month. The distances that are beyond the threshold may depict unrealistic mutations. The process is repeated for all of the sequences of each selected NSP, thus forming a diverse dataset containing various mutations. Please find the script in the supplementary information.

2.6.   Training

All of the models have been trained on Nvidia V100 series GPUs. The training time varies according to the length of the sequences and size of the batches. We have used Adam optimizer for all of our models with a learning rate of 0.0001. We configured the optimizer with default values of decay (0.9, 0.999) and eps (1e-08). For all seven datasets (selected target proteins), the baseline models have been trained for 8000 epochs. The train and test split ratio has been 75 and 25, respectively, for each protein. For smaller sequence lengths, the models show convergence of validation loss but, for longer sequence lengths, models are prone to overfitting and poor learning capabilities, not ensuring any convergence in terms of validation loss even at a higher number of epochs. Figure 4 shows the training of the baseline models for NSP1 ((a)–(c)) and NSP3 ((g)–(i)) being the smaller and larger protein length sequences from our targeted proteins, respectively. Training of the baseline models with the other five datasets is shown in Figures S1–S3. For stacked bidirectional GRUs, models for individual proteins have been trained for 2200 epochs. The shorter the length of the protein, the faster the validation loss of the model converges. Figure 4 (m), (n) shows model loss convergence for NSP1 and NSP3, and Figure S4 shows the remaining five proteins. Negative log-likelihood is used as the loss function for all of the baseline models. Bilingual evaluation understudy (BLEU) scores have been incorporated to evaluate the models.

Figure 4.  Baseline models and BiGRUs (a) vanilla RNN loss convergence with NSP1, (b) simple LSTM loss convergence with NSP1, (c) simple GRU loss convergence with NSP1, (d) BLEU scores for vanilla RNN with NSP1, (e) BLEU scores for simple LSTM with NSP1, (f) BLEU scores for simple GRUs with NSP1, (g) vanilla RNN loss convergence with NSP3, (h) simple LSTM loss convergence with NSP3, (i) simple GRU loss convergence with NSP3, (j) BLEU scores for vanilla RNN with NSP3, (k) BLEU scores for simple LSTM with NSP3, (l) BLEU scores for simple GRUs with NSP3, (m) BiGRUs loss convergence with NSP1, (n) BiGRUs loss convergence with NSP3, (o) BLEU scores for BiGRUs with NSP1, (p) BLEU scores for BiGRUs with NSP3.

DownLoad: Full-Size Img PowerPoint

2.7.   Evaluation

The BLEU score has been used as an evaluation metric that measures the similitude between a reference and predicted sequence in machine translation tasks. It is a standard method for language translation evaluation ranging between 1.0 and 0.0. A score closer to 1.0 means higher similarity while a score closer to 0.0 means higher dissimilarity. It is language-independent, efficient, computationally inexpensive, and shows a high correlation with human evaluation ^[44]. The BLEU score for given and reference text corpus can be calculated by multiplying the brevity penalty (BP) with the geometric average of n-gram precision scores $(p_n)$:

where $w$ represents positive weights for n-grams, and $BP$ can be computed as:

Here, $c$ shows the length of the predicted sequence, whereas $r$ is the length of the reference sequence. We set the BLEU score for 11 different n-grams (1 to 11). 1 to 10 are the usual n-grams, where the number shows the pair length, but the last one is a mixture of all of the first 10-grams.

3.   Results

3.1.   Implementation

3.1.1.   Baseline RNN, GRU, and LSTM

We have proposed three baseline models for seq2seq translation to predict mutations in the SARS-CoV-2 genome. They are, namely, vanilla RNNs, simple LSTMs, and simple GRUs, and all baseline models share the same architecture. They comprise of an encoder and a decoder similar to a usual NMT-based sequence-to-sequence translation model. The encoder is comprised of a single unidirectional layer of RNN and an embedding layer. The embedding layer takes tokens of linearly encoded nucleotide trigrams and converts them into 128-sized 1-dimensional vectors. These vectors are passed through the recurrent layers with a hidden state of size 256. The hidden states from the RNN layer are passed to the decoder of the model. The decoder comprises an embedding and an RNN layer. The RNN layer is coupled with a linear layer having a softmax function as the activation function. The softmax function helps in identifying the most meaningful word (a trigram of nucleotides) at a certain time stamp. In addition, the decoder is fed with the hidden states of the encoder such that the most useful words can be retrieved during the process of translation by computing the attention scores and context vector. The decoder-encoder architecture is trained with the help of teacher forcing to have appropriate convergence.

3.1.2.   Stacked bidirectional GRUs

Due to the simplicity and inability of baseline models to capture complex feature distribution, we created stacked bidirectional GRUs by stacking the identical layers of the model to make a deep model. Such a model is capable enough to learn the complex feature patterns existing in the training data. The model is comprised of an encoder and a decoder, where the encoder consists of one embedding layer and two layers of bidirectional GRUs containing 256 neurons in each layer. Whereas, the decoder contains embedding, attention, GRU, and linear layers. The embedding size is the same as the encoder where a dropout of 0.2 is used. The regularized vectors are passed through linear layers inspired by Luong's attention. Followed by computation of the attention, these values are passed to the GRU layers and ultimately to the linear layer where log softmax has been used as an activation function. This makes the model solve a classification problem where the goal is to find the most probable word in a specific time stamp. According to our experiments, the regularization does not affect the training process a lot, but the length of the hidden size for the GRUs and the embedding size can affect the overfitting of the model by reducing the size of the vectors.

According to our experiments, the models perform quite well with the use of bidirectionality and only 2 stacked layers. All of the models have been implemented using Pytorch and Scikit-learn with Python as the base programming language. We evaluate our models based on the validation and training loss and BLEU scores. The baseline models work in the usual way as the RNN-based encoder-decoder architecture works, i.e., by simply passing the hidden states from the encoder to the decoder. In the case of bidirectional models, the two hidden states, i.e., those based on past and future events, are concatenated with each other from the deep layer of RNNs and then passed to the decoder. This way, the stacked models can learn more about the hidden state vectors. The predictions from the baseline models are not adequate for biological analyses as the models take longer to converge and show poor BLEU scores. Training results for all of the baseline models with each non-structural protein are given in Figures S1–S3.

The computational complexity for stacked bidirectional GRUs is $O(2nd^2)$ and for the attention mechanism is $O(n_{enc}n_{dec}d)$, which makes the total complexity of our model $O((2nd^2)+(n_{enc}n_{dec}d))$. Here, $n$ is the sequence length, $d$ is the size of the hidden states, $n_{enc}$ represents the length of the encoder sequences, and $n_{dec}$ represents the length of the decoder sequences. The $2$ in the notation depicts that the complexity has been doubled because the input sequence is processed in both directions, i.e., forward and backward. Since we have chosen seven non-structural proteins in the current study and trained the models separately, the $n_{enc}$ and $n_{dec}$ will be different for each protein as per the protein length. However, for each protein, the length of these variables will be the same. The complexity of all seven stacked biGRU models is given in Table S2. Computational complexity increases with an increase in the length of the input sequences, however, the computational scalability in terms of resource utilization and model efficiency remains the same. In terms of time, it decreases. The longer the sequences, the greater the time required to execute them.

3.2.   Evaluation of the stacked BiGRUs

For the evaluation of the models, we created a new dataset by collecting nucleotide sequences of a future (concerning the period considered for the training set) time duration, i.e., from June 2021 until March 2022. Thus, obtained data not only consists of new unseen sequences but also consists of mutations that were not present in the period, i.e., January 2020 until May 2021 considered for the training set. Consequently, the evaluation sequence truly represents the evolved/mutated RNA sequences of SARs-CoV-2. The collected data represent raw evaluation sequences which are then subjected to the preprocessing and clustering steps outlined in Sections 2.5.3 and 2.5.4, respectively. Based on this, we obtain a labeled evaluation dataset consisting of a source sequence and its associated mutated sequence for seven non-structural proteins, namely NSP1, NPS3, NSP5, NSP8, NSP9, NSP13, and NPS15. Following this, we feed the (protein-specific) stacked-BiGRU model with the corresponding protein input sequence to obtain a prediction of a most likely mutated nucleotide sequence. The obtained predictions are compared with the ground truth sequence using the BLEU score metrics. The obtained scores are shown in Table 1 and also depicted as bar plots in Figure 5. Based on these scores, we see that the prediction of the stacked BiGRUs is good for all of the proteins. For proteins NSP8 and NSP9, the 9 and 10-gram scores are relatively poor with NSP8 showing below-acceptable performance having values below 0.6 for 9 and 10-gram scores.

Table 1.  Average BLEU scores of the stacked BiGRUs predictions with respect to the ground truth sequences.

Protein	1-gram	2-gram	3-gram	4-gram	5-gram	6-gram	7-gram	8-gram	9-gram	10-gram	11-gram
NSP1	0.997	0.986	0.976	0.963	0.957	0.951	0.945	0.94	0.934	0.928	0.957
NSP3	0.998	0.996	0.991	0.982	0.971	0.96	0.951	0.944	0.937	0.93	0.966
NSP5	0.992	0.982	0.966	0.938	0.917	0.901	0.887	0.874	0.861	0.847	0.915
NSP8	0.976	0.953	0.914	0.861	0.785	0.702	0.648	0.607	0.57	0.542	0.74
NSP9	0.969	0.933	0.904	0.855	0.813	0.781	0.754	0.731	0.71	0.693	0.809
NSP13	0.999	0.998	0.997	0.996	0.995	0.994	0.993	0.992	0.991	0.99	0.994
NSP15	0.999	0.998	0.997	0.996	0.995	0.994	0.992	0.991	0.99	0.989	0.994

---

 | Show Table

DownLoad: CSV

Figure 5.  Average BLEU scores of the stacked BiGRUs on the evaluation set.

DownLoad: Full-Size Img PowerPoint

After performing the above direct evaluation between the predicted and the ground truth sequence, we next want to evaluate the qualitative difference in the translated amino-acid (AA) sequence. To this end, for the above-mentioned seven proteins, we translate the predicted nucleotide sequence to the corresponding AA sequence corresponding to the respective protein. Next, we compare the so-obtained mutated AA sequence $(\hat A^p_{seq})$ with that of the reference AA sequence $(A^p_{seq})$ obtained from the base reference (protein specific indexed by $p$) nucleotide sequence of SARS-CoV-2 and aim to obtain frequency/number of mutations at a given amino acid position of the reference genome. To this end, we perform a string matching of the two sequences, i.e., $A^p_{seq}$ with $\hat A^p_{seq}$, and determine the positions where there are differences between the two. This provides the count/frequency $f$ of mismatch at a particular position $x$ of the reference AA sequence $A^p_{seq}$. Thus, by summing the mutation counts at a given position across all predicted sequence samples, we obtain the mutation frequency/density $f(t, x)$ for some future time $t > t_0$ and position $x$ of an AA chain representing the protein. Accordingly, we have that $f(t_0, x)$ denotes the mutation frequency corresponding to the source/input nucleotide chain, $f(t, x)$ for $t > t_0$ denotes the mutation frequency corresponding to the target/output/ground-truth/measured nucleotide chain, and $\hat f(t, x)$ for $t > t_0$ denotes the mutation frequency of the predicted nucleotide sequence. It is worth noting that the source/input nucleotide sequence (i.e., the sequence fed to the network as input) may have non-zero mutation frequency since the obtained data is that of a mutated virus, thus having differences with respect to the reference nucleotide sequence. Figure 6 depicts stem plots for the mutation frequency of the predicted sequences and the ground truth nucleotide sequences for all seven proteins. Based on this, we see that the obtained predictions are able to detect some of the point mutations in the amino-acid chain. In the case of NSP3, we see that the location of several point mutations, i.e., $x\in\{183,646,890, 1159, 1412, 1682, 1867\}$, were correctly predicted although the counts (i.e., the actual frequency) vary a bit from the ground truth. Similarly, for NSP5, the location of the point mutations matches for $x \in \{157,213,242\}$, for NSP15 at $x \in \{11,132,264\}$, and so on. Predicted frequently occurring point mutations for all targeted proteins are shown in Figures S5–S11.

Figure 6.  Mutation frequency at different amino acid positions of the reference genome. The top subplot indicates the mutation frequency of the input sequence (green stem plots) while the lower subplot denotes the mutation frequency of the target (gray) and predicted sequences (magenta) stem plots, respectively.

DownLoad: Full-Size Img PowerPoint

Correspondingly, the precision and recall scores depicted in Table 2 indicate the high reliability of the model within 2–3 units of positional error. This is confirmed by the precision score, where we see above 80% precision for detecting the point mutations within the 2 units of accuracy and 100% precision for detecting within 3 units of accuracy for all of the target proteins. On the other hand, the recall scores (for detecting point mutations) are pretty low with less than 20% for proteins with an AA sequence length of more than 200. However, NSP8 and NSP9, which have AA sequence lengths less than 200, have recall scores up to 87% and 73% (for point mutations of at most 3 units of error). This indicates that the model is highly selective, especially for proteins with higher sequence lengths $(>300)$ of its corresponding AA (indicated by the Selectivity column of Table 2), and only detects mutations that are positionally precise.

Table 2.  Precision and recall scores for the position of point mutations detected by the stacked BiGRUs. The array values of the true mutations, precision, and recall scores correspond to the matches obtained as per different thresholds, ranging from 0 to 3 units, for error in the position $x$ of the detected point mutation.

Protein	AA sequence length	Mutation count	Predicted mutations	True mutations	Precision	Recall	Selectivity
NSP1	181	85	4	[2, 4, 4, 4]	[0.5, 1, 1, 1]	[0.0223, 0.046, 0.046, 0.046]	0.978
NSP3	1946	360	23	[7, 12, 19, 23]	[0.3, 0.52, 0.83, 1.0]	[0.02, 0.033, 0.052, 0.063]	0.99
NSP5	307	65	11	[3, 8, 11, 11]	[0.27, 0.72, 1.0, 1.0]	[0.04, 0.12, 0.17, 0.17]	0.967
NSP8	199	39	34	[9, 20, 31, 34]	[0.26, 0.52, 0.91, 1.0]	[0.23, 0.51, 0.79, 0.87]	0.844
NSP9	114	19	14	[2, 9, 14, 14]	[0.14, 0.64, 1.0, 1.0]	[0.11, 0.47, 0.73, 0.73]	0.87
NSP13	602	123	2	[0, 1, 2, 2]	[0.0, 0.5, 1.0, 1.0]	[0.0, 0.008, 0.016, 0.016]	0.99
NSP15	347	104	4	[3, 4, 4, 4]	[0.75, 0.5, 1.0, 1.0]	[0.029, 0.0385, 0.0385, 0.0385]	0.99

---

 | Show Table

DownLoad: CSV

Based on these observations, we can conclude that the stacked BiGRUs do a fairly good job at predicting practically relevant predictions of plausible mutations. Furthermore, whenever the model detects a mutation, it seems to be of high precision, with at most 3 units of positional error, thus providing a good indication of the validity of the model and its usefulness.

4.   Discussion

Nucleotide changes in the genome are known as mutations. In this study, we are focusing on point mutations, which are changes in the position of one nucleotide that can either be an insertion, deletion, or transition/transversion. In viruses, mutations play a huge role in the emergence of various viral strains, which either render them weak and in return wipe the entire viral strain or strengthen them. As a result of favorable mutations, viruses can adapt to a wide range of hosts, increase their virulence, better mask, and evade host immune responses. SARS-CoV-2 has created havoc since its emergence and, due to its high mutation rate, it is hard to contain. Therefore, in this current work, we have used recurrent neural networks to predict mutations in its genome. Predicted mutations will help in designing inhibitory molecules to obstruct viral transmission in the future. We have selected non-structural proteins for the mutation prediction task as these proteins tend to change their genomic sequences less as compared to structural ones, thus proffering the designed respective inhibitory molecules to hold their efficacy for a longer time.

In our study, mutation prediction has been defined as a machine translation task. We started with vanilla RNNs, but due to their lack of ability to capture long-term dependencies in data, we tried solving this problem with simple LSTMs and simple GRUs. Both performed better than vanilla RNNs but their losses took longer to converge. Moreover, obtained BLEU scores were also not up to the mark. Since simple GRUs performed slightly better than simple LSTMS, we chose to stack the two bidirectional layers of GRUs and applied the attention mechanism to further exhilarate the predictions.

We trained our models using genomic sequence data of seven targeted proteins–NSP1, NSP3, NSP5, NSP8, NSP9, NSP13, and NSP15–after finding nearest neighbors for sequences and clustering the data. A separate model has been trained for each protein due to their varying sequence lengths. For model training, the sequence data comes from 17 months (i.e., January 2020 to May 2021) and for model evaluation, the sequence data comes from 10 months (i.e., June 2021 to March 2022). The BLEU score has been used as a metric to evaluate the model outcomes. It shows quite good translation results with an average of 0.9 for all of the targeted proteins except NSP8 and NSP9, where 9 and 10-gram scores lie in the range of 0.5 and 0.7. Differences in the metric scores lie in the availability of data for training since the training data for both NSP8 and NSP9 are smaller as compared to the other selected proteins. Contrary to this, other protein models have performed very well, which is depicted in the BLEU scores as well as in precision and recall scores.

In our study, we have made sure that the input and output languages should have some evolutionary relation to eliminate the bias in predictions, unlike other proposed studies where both languages have common sequences. We achieved this by performing k-means clustering and nearest neighbor-joining methods. Moreover, we have used attention mechanisms to enrich the mutation prediction models for this task. We have focused on evaluating the predictions and model performance by using BLEU scores. Implementing all of these features in this study will advance the scope of this work beyond that of previously published work.

We have predicted some new mutations in the seven targeted proteins that did not exist in the training and evaluation data before, see Table 3. Mutation statistics for the whole study are given in Table 4. Further downstream analysis of predicted mutations will help in selecting suitable targeting protein domains to design inhibitory molecules against viruses. This study adds a slightly new direction in fighting the pandemics of the future by preparing beforehand. Our models are generic and will work with any kind of genomic sequence coming from different sources.

Table 3.  Unique predicted mutations that do not exist in training and evaluation data.

Protein	Predicted new mutations
NSP1	W160T, T169G, G179C
NSP3	P511R, R645S, S691T, S696T, T762P, T969P, S1037T, T1045P, T1183P, S1205P, R1340S,
	P1376R, P1557R, S1614T, S1681T, T1778P, S1806T, R1819S
NSP5	I151S, H162V, G173H, T195G, I212S, R221T, L241R, I248S, L249R, I280S
NSP8	Q23D, V25Q, N27V, G28N, V32Q, V33Q, N42V, D51G, Q72D, V82Q, Q87D, N99V, N108V,
	G112N, V114Q, V129Q, N139V, G143N, Q157D, V158Q, N175V, N178V, N191V, Q197D
NSP13	S262C
NSP15	D131E

---

 | Show Table

DownLoad: CSV

Table 4.  Predicted mutation statistics, where t_seq: training sequences, t_mut: mutations in training sequences, e_seq: evaluation sequences, e_mut: mutations in evaluation sequences, p_seq: predicted sequences, p_mut: mutations in predicted sequences, pt_mut: common mutations in predicted and training sequences, pe_mut: common mutations in predicted and evaluation sequences, n_mut: predicted new mutations.

Protein	t_seq	t_mut	e_seq	e_mut	p_seq	p_mut	pt_mut	pe_mut	n_mut
NSP1	864	375	2024	767	288	178	70	175	3
NSP3	13,347	2888	23,999	4195	840	559	295	541	18
NSP5	1002	456	2137	495	227	248	174	118	10
NSP8	577	394	852	384	125	110	40	83	24
NSP13	2674	680	6921	1063	472	218	111	217	1
NSP15	1232	512	2578	858	297	215	94	214	1

---

 | Show Table

DownLoad: CSV

5.   Conclusions

This study focused on the mutation prediction in the SARS-CoV-2 genome using neural machine translation. The sequence data was downloaded from GISAID comprising of sequences from Germany only. The choice of non-structural proteins was made to prolong the efficacy of the designed inhibitory molecules against viral proteins as non-structural proteins rear fewer mutations as compared to structural proteins. To perform machine translation tasks, three models were used as baseline models, i.e., vanilla RNNs, simple LSTMs, and simple GRUs. Since simple GRUs performed much and slightly better than vanilla RNNs and simple LSTMs, respectively, they were chosen to be stacked and implemented with an attention mechanism to further improve the prediction results. The results showed that stacking the layers and attention mechanisms has indeed enhanced the performance of the models. The prediction results highlighted the significance of certain mutations in each of the seven proteins and also produced some new mutations that did not exist in the data before. These findings may contribute to fighting the pandemics of the future by identifying the critical mutations. Although our model can predict mutations in individual proteins, it is unlikely to be any better at doing the same task on the whole genome. In the future, it will be interesting to explore this problem using transformer models on larger protein sequences or whole viral genomes, as transformers are more computationally expensive than stacked biGRUs and can perform such tasks more effectively.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the German Federation of Industrial Research Associations (AiF) within the scope of the AIMPID project (AI-based Mutation Predictions and relevant Protein Inhibitor Development in SARS-CoV-2).

Conflict of interest

The authors declare there is no conflict of interest.