Dynamical analysis of a heterogeneous spatial diffusion Zika model with vector-bias and environmental transmission

1.   Introduction

Zika, caused by the Zika virus, is a mosquito borne disease. It is mainly transmitted to humans through mosquito bites. In March 2015, a large outbreak in Brazil attracted worldwide attention. The World Health Organization stated Zika as a Public Health Emergency of International Concern in February 2016 ^[1]. Zika is associated with Guillain-Barr$\acute{e}$ syndrome and microcephaly ^[2]. It poses a major threat to global health in developing countries ^[3].

Differential equation models are an excellent tool in studying the spread of infectious diseases ^{[4,5,6,7,8,9,10,11]}. Recently, reaction-diffusion models play an important role in exploring the effects of spatial heterogeneity on the spread of Zika ^{[12,13,14,15,16,17,18,19]}. Recently, researches showed that the Zika virus in a water environment could be transmitted to aquatic mosquitoes via breeding ^[20]. This suggested that determination of the route of Zika transmission needs to take environmental factors into account. In our previous article ^[21], the environmental transmission route was introduced into Zika model. We researched dynamical analysis of the system for three incidence functions related to the environmental transmission rate. Then, we extended ^[21] to consider sexual transmissions and spatial heterogeneity ^[22,23]. But, the above models did not consider the vector-bias. In fact, the vector-bias is important for Zika transmission ^[24,25]. However, few Zika models consider the vector-bias, environmental transmission, and spatial heterogeneity simultaneously.

The vector-bias describes how mosquitoes prefer to bite infected people over susceptible ones. To account for the vector-bias in the model, we introduce the parameters $p$ and $l$. $p$ and $l$ represent the probabilities that an adult mosquito arrives at a human at random and bites the human if he/she is infectious and susceptible, respectively. Let $q = \frac{p}{l}$ ($q\geq 1$). Then $q$ is called a vector-bias parameter. In this study, we modify and add the vector-bias to our previous model in ^[23]. We assume that the mosquitoes and humans are living in a bounded domain $\Gamma$ with smooth boundary $\partial\Gamma$. $S_1(t, x)$ and $I_1(t, x)$ indicate densities of susceptible and infectious aquatic mosquitoes at time $t$ and position $x$, respectively. $S_2(t, x)$ and $I_2(t, x)$ represent densities of susceptible and infectious adult mosquitoes at time $t$ and position $x$, respectively. The densities of infectious humans at time $t$ and position $x$ are denoted by $I_3(t, x)$. The densities of the Zika virus in the water environment are denoted by $V(t, x)$ at time $t$ and position $x$. We assume that a susceptible human is unchanging ^[19,24]. The density of susceptible humans is denoted by $H_*(x)$. Inspired by article ^[24], we set the number of newly infectious adult mosquitoes and humans per unit time to $\alpha_{2}(x)\frac{pI_{3}}{pI_{3}+l H_*(x)}S_{2}$ and $\alpha_{3}(x)\frac{lH_*(x)}{pI_{3}+l H_*(x)}I_{2}$, respectively. $\alpha_{2}(x)$ denotes the transmission rate from $I_3$ to $S_2$. $\alpha_{3}(x)$ denotes the transmission rate from $I_2$ to $S_3$. Then, we propose a reaction-diffusion Zika model as follows

for $t > 0.$ $\tau(x)$ represents the birth rate of susceptible aquatic mosquitoes. $K_1(x)$ represents the maximal capacity of aquatic mosquitoes in the water environment. $\alpha_{1}(x)$ denotes the transmission rate from $V$ to $S_1$. $K_2(x)$ denotes the half-saturation constant, which can cause a 50$\%$ chance of catching the Zika virus. $\omega(x)$ denotes the maturity rate of aquatic mosquitoes. $\delta_{1}(x)$ and $\delta_{2}(x)$ denote the death rate of aquatic and adult mosquitoes, respectively. $\gamma(x)$ represents the recovery and death rate of infected humans. The rate of excreting the Zika virus for each infected human is denoted by $\eta(x)$. The clearance rate of $V(x, t)$ is denoted by $\varrho(x)$. $d_{1}(x)$ and $d_{2}(x)$ represent the diffusion coefficients of adult mosquitoes and humans. Here we employ the Neumann boundary condition $\frac{\partial U}{\partial n} = 0,$ ($U = S_2, I_2, I_3$), where $n$ represents the outward unit normal vector on $\partial\Gamma$. Assume that $\tau(x)$, $K_1(x)$, $K_2(x)$, $\alpha_{1}(x)$, $\alpha_{2}(x)$, $\alpha_{3}(x)$, $\omega(x)$, $\delta_{1}(x)$, $\delta_{2}(x)$, $\gamma(x)$, $\eta(x)$, $\varrho(x)$, $d_{1}(x)$, $d_{2}(x)$, and $H_*(x)$ are continuous and positive functions of $x$.

The remainder of this paper is organized as follows: In the next section, we give the well-posedness of system (1.1). In Section 3, the mosquito reproduction number $R_{1}$ and basic reproduction number $R_{0}$ will be established. In Section 4, threshold dynamical behaviors are analyzed. In Section 5, we conduct some numerical simulations. This study ends with a brief conclusion.

2.   The well-posedness

Let $\mathbb{G}: = C(\bar{\Gamma}, \mathbb{R}^{6})$ be a Banach space with the supremum norm $\parallel \cdot\parallel_{\mathbb{G}}$. Let $\mathbb{G^{+}}: = C(\bar{\Gamma}, \; \mathbb{R}_{+}^{6})$. We then have that $(\mathbb{G}, \; \mathbb{G^{+}})$ is a strongly ordered Banach space. Denote

Throughout, we denote $\overline{g} : = \max\limits_{ x\in\bar{\Omega}}g(x)$, $\underline{g} : = \min\limits_{ x\in\bar{\Omega}}g(x).$

Set $\mathbb{F}: = C(\bar{\Gamma}, \mathbb{R})$ and $\mathbb{F}^{+}: = C(\bar{\Gamma}, \mathbb{R}_{+})$. Assume that $\Upsilon_{2}(t)$ and $\Upsilon_{3}(t)$ : $\mathbb{F}\rightarrow \mathbb{F}^{+}$ are the evolution operators associated with

We have that $\Upsilon_{2}(t)$ and $\Upsilon_{3}(t)$ are strongly positive and compact (see Chapter Ⅱ in ^[26] and Theorems 7.3.1 and 7.4.1 in ^[27]). According to Subsection 2.1 in ^[28], one has

for $t\geq0,$ $\psi\in\mathbb{F}.$ Here, $F_{2}(t, x, y)$ and $F_{3}(t, x, y)$ are the Green functions associated with $- \delta_{2}(x)v_{2}+\nabla\cdot(d_1(x)\nabla v_2)$ and $-\gamma(x) v_{3}+\nabla\cdot(d_2(x)\nabla v_3)$ subject to the Neumann boundary condition, respectively.

Let $a_1$ and $a_2$ be the principle eigenvalue of $- \delta_{2}(x)v_{2}+\nabla\cdot(d_1(x)\nabla v_2)$ and $-\gamma(x) v_{3}+\nabla\cdot(d_2(x)\nabla v_3)$ subject to the Neumann boundary condition, respectively. From ^[28], we obtain that there is $\mathcal{M} > 0$ such that $\parallel\Upsilon_{i}(t)\parallel\leq \mathcal{M} e^{a_i t}$ $\forall t\geq 0$, $i = 2, 3.$ According to Theorem 2.27 in ^[29], one has that there exists some $b_2 > 0$ and $b_3 > 0$ such that $F_{2}(t, x, y)\leq b_2 e^{- \underline{\delta_{2}} t}$ and $F_{3}(t, x, y)\leq b_3 e^{- \underline{\gamma } t}$.

Define $\Upsilon_{1}(t)$ and $\Upsilon_{4}(t)$ : $\mathbb{F}\rightarrow \mathbb{F}^{+}$ by

Denote $\Upsilon =$ diag$(\Upsilon_{1}(t), \Upsilon_{1}(t), \Upsilon_{2}(t), \Upsilon_{2}(t), \Upsilon_{3}(t), \Upsilon_{4}(t))$. Define $\mathcal{H} = (\mathcal{H}_1, \mathcal{H}_2, \mathcal{H}_3, \mathcal{H}_4, \mathcal{H}_5, \mathcal{H}_6): \mathbb{G}_{K} \rightarrow \mathbb{G}$ by

for $t\geq 0, x\in\bar{\Gamma}$, and $\theta = (\theta_1, \theta_2, \theta_3, \theta_4, \theta_5, \theta_6)\in \mathbb{G}_{K}$. Then, rewrite system (1.1) as

where $\mathcal{B} =$ diag $(\mathcal{B}_1, \mathcal{B}_1, \mathcal{B}_2, \mathcal{B}_2, \mathcal{B}_3, \mathcal{B}_4)$ and $\mathcal{B}_j(j = 1, 2, 3, 4)$ are given by

System (1.1) is also equivalent to an integral equation as follows:

where $w: = (S_1, I_1, S_2, I_2, I_3, V)$.

Lemma 2.1. For every $\theta \in \mathbb{G}_{K}$, system (1.1) admits a unique nonnegative solution $w(t, \cdot, \theta)\in\mathbb{G}_{K}$ on $[0, \; \infty)$ with $w(0, \cdot, \theta) = \theta$. Moreover, the solution is uniformly bounded and ultimately bounded.

Proof. For any $\theta\in\mathbb{G}_{K}$ and $c > 0$, then one has

and

So, for small enough $c > 0$, one has $\theta+c\mathcal{H}(\theta)\in \mathbb{G}_{K}$, and

By Corollary 4 in ^[30], we can obtain that for any $t$ in its maximal existence interval $[0, t_{\theta})$ with $t_{\theta}\leq\infty$, system (1.1) has a unique mild solution $w(t, \cdot, \theta)$ with $w(0, \cdot, \theta) = \theta$, and $w(0, \cdot, \theta)\in \mathbb{G}_{K}$. Moreover, $w(t, \cdot, \theta)\in\mathbb{G}_{K}$ $\forall$ $t\in[0, t_{\theta})$. $w(t, \cdot, \theta)$ is a classical solution.

Let $M_1(t, x) = S_{1}(t, x)+I_{1}(t, x),$ $M_2(t, x) = S_{2}(t, x)+I_{2}(t, x).$ From (1.1), one has that $(M_1(t, x), M_2(t, x))$ satisfies

for $t > 0.$ Since $w(t, \cdot, \theta)\in\mathbb{G}_{K}$ $\forall$ $t\in[0, t_{\theta})$, we have $M_{1}(t, x) = S_{1}(t, x)+I_{1}(t, x)\leq K_{1}(x)$ for $t\in[0, t_{\theta}),$ $x\in\bar{\Gamma}.$ That is, $S_{1}(t, \cdot)$ and $I_{1}(t, \cdot)$ are bounded on $[0, t_{\theta}).$ From the second equation of (2.3), we have

Consider a comparison system as follows

Let $\iota = \frac{\overline{\omega}\overline{K_1}}{\underline {\delta_{2}}}.$ We then have that $\frac{\partial \iota}{\partial t}-\nabla\cdot(d_1(x)\nabla \iota) -(\overline{\omega} \overline{K_1}-\underline{\delta_{2}}\iota)\geq 0.$ Therefore, $\iota$ is an upper solution of (2.5). By the comparison principle, we have $M_2 (t, x)\leq \iota$ for $t\in[0, \; t_{\theta}),$ $x\in\bar{\Gamma}.$ That is, $S_{2}(t, \cdot)$ and $I_{2}(t, \cdot)$ are bounded on $[0, t_{\theta}).$

From the fifth equation of (1.1), one has

It follows from the comparison principle that $I_{3}(t, x)$ is bounded on $[0, t_{\theta}).$ So, there exists a positive constant $D$ and along with the sixth equation of (1.1), we have $\frac{\partial V }{\partial t} \leq \overline{\eta} D -\underline{\varrho} V$. By the comparison principle, we can obtain that $V(t, x)$ is bounded on $[0, t_{\theta}).$ Therefore, for any initial value $\theta \in \mathbb{G}_{K}$, solutions of system (1.1) exist globally on $[0, +\infty).$

Since $S_{1}(t, x)+I_{1}(t, x)\leq K_1(x)$ for $x\in \bar{\Gamma}, \; t\geq0$, we have that $S_{1}(t, x)$ and $I_{1}(t, x)$ are ultimately bounded. From the third equation of (1.1), we have

According to the comparison principle, $S_{2}(t, x)$ is ultimately bounded. So, there exists $t_0$ such that $S_{2}(t, x)\leq 2\frac{\overline{\omega} \overline{K_1} }{\underline{\delta_2}} = 2\iota$ for $t > t_{0}$, $x\in\bar{\Gamma}.$

From the fourth equation of (1.1), one has

So, $I_{2}(t, x)$ is ultimately bounded. There exists $t_{01}$ such that $I_{2}(t, x)\leq 2\frac{\overline{\omega} \overline{K_{1}}+ 2 \iota\overline{\alpha_{2}} }{\underline{\delta_{2}}}$ for $t > t_{01}$, $x\in\bar{\Gamma}.$

From the fifth equation of (1.1), one has

where $\iota_1 = 2\frac{\overline{\omega} \overline{K_{1}}+ 2 \iota\overline{\alpha_{2}} }{\underline{\delta_{2}}}.$ According to the comparison principle, $I_{3}(t, x)$ is ultimately bounded. So, there exists $t_{02}$ such that $I_{3}(t, x)\leq 2\frac{\overline{\alpha_{3}}\iota_1 }{\underline{\gamma}}$ for $t > t_{02}$, $x\in\bar{\Gamma}.$ Similarly, we can get that $V(t, x)$ is ultimately bounded. Thus, the solution $w(t, x)$ is ultimately bounded.

Next, we give the proof of the uniform boundedness of solutions for system (1.1).

For any $\theta\in\mathbb{G}_{K}$, one has $\theta_1(x)+\theta_2(x)\leq K_1(x),$ $\forall x\in \bar{\Gamma}$, and the solution of system (1.1) $w(t, \cdot, \theta)\in\mathbb{G}_{K}$. Thus, $w_1(t, \cdot, \theta)+w_2(t, \cdot, \theta)\leq K_1(\cdot)$. That is, $S_{1}(t, x)$ and $I_{1}(t, x)$ are uniformly bounded.

From the third equation of (1.1), we have

Then, for any initial value $\theta\in\mathbb{G}_{K}$, we can obtain

For any $c_1 > 0$, choose $\mathcal{N}(c_1) = \mathcal{M} c_1+\frac{b_2\overline{\omega} \overline{K_{1}}\mid\Gamma\mid}{\underline{\delta_{2}}} > 0.$ Then for any initial value $\parallel \theta \parallel_{\mathbb{G}}\leq c_1$ and $\forall t\geq0$, we have $S_{2}(t, x)\leq\mathcal{N}(c_1)$. So, $S_{2}(t, x)$ is uniformly bounded. Similarly, for any $c_2 > 0$, choose $\mathcal{N}(c_2) = \mathcal{M} c_2+\frac{b_2(\overline{\omega} \overline{K_{1}}+\overline{\alpha_2}\mathcal{N}(c_1))\mid\Gamma\mid}{\underline{\delta_{2}}} > 0,$ then, for any initial value $\parallel \theta \parallel_{\mathbb{G}}\leq c_2$ and $\forall t\geq0$, we have $I_{2}(t, x)\leq\mathcal{N}(c_2)$. So, $I_{2}(t, x)$ is uniformly bounded. From the fifth equation of (1.1), for any $c_3 > 0$, choose $\mathcal{N}(c_3) = \mathcal{M} c_3+\frac{b_3\overline{\alpha_3}\mathcal{N}(c_2)\mid\Gamma\mid}{\underline{\gamma}} > 0,$ then, for any initial value $\parallel \theta \parallel_{\mathbb{G}}\leq c_3$ and $\forall t\geq0$, we have $I_{3}(t, x)\leq\mathcal{N}(c_3)$. So, we can obtain that $I_{3}(t, x)$ is uniformly bounded. From the last equation of (1.1), we can obtain $V(t, x)\leq e^{- \underline{\rho} t}\parallel \theta_6\parallel_{\mathbb{F}}+\frac{\overline{\eta}\mathcal{N}(c_3)\mid\Gamma\mid}{\underline{\rho}}(1-e^{- \underline{\rho} t})\leq\parallel \theta_6\parallel_{\mathbb{F}}+\frac{\overline{\eta}\mathcal{N}(c_3)\mid\Gamma\mid}{\underline{\rho}}.$ for any $c_4 > 0$, we choose $\mathcal{N}(c_4) = c_4+\frac{\overline{\eta}\mathcal{N}(c_3)\mid\Gamma\mid}{\underline{\rho}}$ such that $V(t, x)\leq\mathcal{N}(c_4)$ for any initial value $\parallel \theta \parallel_{\mathbb{G}}\leq c_4$ and $\forall t\geq0$. Thus, $V(t, x)$ is uniformly bounded. In short, the solution $w(t, x)$ of system (1.1) is uniformly bounded. This completes the proof of Lemma 2.1. □

3.   Reproduction number

In this section, the mosquito reproduction number $R_{1}$ and basic reproduction number $R_{0}$ will be established though applying the theorem in article ^[31].

3.1.   Mosquito reproduction number $R_{1}$

Linearizing system (2.3) at $(0, 0),$ we can get

Define $P_{1}$ as

In addition, the eigenvalue problem of system (3.1) is given by

According to Lemma 2.2 in ^[32] and Theorem 7.6.1 in ^[27], the following Lemma can be obtained:

Lemma 3.1. Let $\nu_{p1}^{*}: = s(P_{1})$, where $s$ represents the spectral bound. If $\nu_{p1}^{*}\geq 0$, then $\nu_{p1}^{*}$ is a principal eigenvalue of eigenvalue problem (3.3) with a strongly positive eigenfunction.

Define

Assume that $\mathbb{A}_{1}(t):$ $C(\bar{\Gamma}, \mathbb{R}^{2})\rightarrow C(\bar{\Gamma}, \mathbb{R}^{2})$ is the $C_0$-semigroup associated with the following linear system

Let $\phi_m(x)\in C(\bar{\Gamma}, \mathbb{R}^{2})$ be the density of initial fertile mosquitoes, and $\mathbb{L}_1 :C(\bar{\Gamma}, \mathbb{R}^{2})\rightarrow C(\bar{\Gamma}, \mathbb{R}^{2})$ be defined by

Here, $\mathbb{L}_1(\phi_m)(\cdot)$ denotes the distribution of the total new aquatic/adult mosquitoes generated by initial density $\phi_m$. So, the spectral radius of $\mathbb{L}_1$ is $R_{1}$, that is,

When system (1.1) is spatially homogeneous, we can give an explicit representation of $R_{1}$ as follows:

We can then get the following Lemma according to ^[31]:

Lemma 3.2. $R_{1} -1$ has the same sign as $\nu_{p1}^{*}$.

We can then get the following Lemma to hold applying to Lemma 2.5 in ^[32]:

Lemma 3.3. Let $\mathbb{B}: = \{(M_{10}, M_{20})^{T}\in C(\bar{\Gamma}, \mathbb{R}_{+}^{2}):0\leq M_{10}(x)\leq K_1(x)), \forall\; x\in \bar{\Gamma} \}$. Assume that $R_{1} > 1$. Then, we can obtain

with $(M_{10}, M_{20})\in\mathbb{B}\backslash \{(0, 0)\}$. Moreover, $0 < M_1^{*}(x) < K_1(x),$ and $M_2^{*}(x) > 0$ $\forall\; x\in \bar{\Gamma}.$

3.2.   Basic reproduction number $R_{0}$

System (1.1) has two infection-free steady states $E_{0}(x) = (0, 0, 0, 0, 0, 0)$ and $E_{1}(x) = (M_1^{*}(x), 0, M_2^{*}(x), 0, 0, 0)$. When $R_{1} > 1$, $E_{1}(x)$ exists. Linearizing system (1.1) at $E_{1}(x)$ and considering infection compartments, we can then get

for $t > 0$. Denote $P_{2}$ as

In addition, the eigenvalue problem of system (3.6) is given by

for $t > 0$. According to Theorem 7.6.1 in ^[27], the following Lemma can be obtained:

Lemma 3.4. Let $\nu_{p2}^{*}: = s(P_{2})$, where $s$ represents the spectral bound. If $\nu_{p2}^{*}\geq 0$, then $\nu_{p2}^{*}$ is a principal eigenvalue of eigenvalue problem (3.8) with a strongly positive eigenfunction.

Define

Let $\mathbf{u} = (I_{1}, I_{2}, I_{3}, V)^T$, $\nabla\cdot(d(x)\nabla \mathbf{u}) = \left(0, \nabla\cdot(d_1(x)\nabla I_2), \nabla\cdot(d_2(x)\nabla I_3), 0\right)^T$. Assume that $\mathbb{A}_{2}(t):$ $C(\bar{\Gamma}, \mathbb{R}^{4})\rightarrow C(\bar{\Gamma}, \mathbb{R}^{4})$ is the $C_0$-semigroup associated with the linear system

for $t > 0$. Let $\phi_{m2}(x)\in C(\bar{\Gamma}, \mathbb{R}^{4})$ be the density of initial infectious individuals, and $\mathbb{L}_2 :C(\bar{\Gamma}, \mathbb{R}^{4})\rightarrow C(\bar{\Gamma}, \mathbb{R}^{4})$ be defined by

Here, $\mathbb{L}_2(\phi_{m2})(\cdot)$ denotes the distribution of new productive infected individuals generated by initial density $\phi_{m2}$. So, the spectral radius of $\mathbb{L}_2$ is $R_{0}$, that is,

When all parameters of system (1.1) are constants, we can give the actual formula of $R_0$ by

We can then get the following Lemma according to ^[31]:

Lemma 3.5. $R_{0}-1$ has the same sign as $\nu_{p2}^{*}$.

4.   Threshold dynamics

According to Theorem 4.1 in ^[23], we know that $E_{0}(x)$ is globally attractive when $R_1 < 1$. Biologically, the mosquito population will vanish. Under this assumption, it is pointless to study the spread of the Zika disease. Thus, in this study, we just consider the case $R_1 > 1$.

Theorem 4.1. Assume $R_1 > 1$ and $R_{0} < 1$. Then, the disease free state $E_{1}(x) = (M_1^{*}(x), 0, M_2^{*}(x), 0, 0, 0)$ is globally attractive.

Proof. Since $R_{0} < 1$, it follows from Lemma 3.5 that $\nu_{p2}^{*} < 0.$ Then, there exists a sufficiently small $\varsigma > 0$ such that $\nu_{p2\varsigma}^{*} < 0$, where $\nu_{p2\varsigma}^{*}$ is the principal eigenvalue of the following eigenvalue problem

with a strongly positive eigenfunction $(\breve{\chi}_{1}, \breve{\chi}_{2}, \breve{\chi}_{3}, \breve{\chi}_{4})$.

According to Lemma 3.3, when $R_{0}^{M} > 1$, for the above $\varsigma$, there exists $t_1 > 0$ such that $0 < S_{1}(t, x)\leq M_1^{*}(x)+\varsigma, \; 0 < S_{2}(t, x)\leq M_2^{*}(x)+\varsigma,$ $\forall\; x\in\bar{\Gamma}$, $t\geq t_1.$ So, for $t\geq t_1$, we can get

For any initial value $\theta \in \mathbb{G}_{K}$, there exists some $h_{1} > 0$ such that $(I_{1}(t_1, x, \theta), I_{2}(t_1, x, \theta), I_{3}(t_1, x, \theta), V(t_1, x, \theta))\leq h_{1} (\breve{\chi}_{1}, \breve{\chi}_{2}, \breve{\chi}_{3}, \breve{\chi}_{4}),$ $\forall\; x\in\bar{\Gamma}$.

Next, consider a comparison system as follows:

for $t\geq t_1$. Then, system (4.2) admits a solution $h_{1} e^{\nu_{p2\varsigma}^{*}(t-t_{1})}(\breve{\chi}_{1}, \breve{\chi}_{2}, \breve{\chi}_{3}, \breve{\chi}_{4}),$ $\forall\; t\geq t_1$. According to the comparison principle, we can obtain

Hence, $\lim\limits_{t\rightarrow \infty }(I_{1}(t, x), I_{2}(t, x), I_{3}(t, x), V(t, x)) = (0, 0, 0, 0),$ uniformly for $x\in \bar{\Gamma}.$ According to Lemma 3.3, we have $\lim\limits_{t\rightarrow \infty }S_{1}(t, x) = M_1^{*}(x)$ and $\lim\limits_{t\rightarrow \infty }S_{2}(t, x) = M_2^{*}(x),$ uniformly for $x\in \bar{\Gamma}.$ □

Remark 1 Biologically, when $R_{1} > 1$ and $R_{0} < 1$, Theorem 4.1 shows that the Zika disease will eventually disappear.

Let $w(t, x): = (S_1(t, x), I_1(t, x), S_2(t, x), I_2(t, x), I_3(t, x), V(t, x))$ and $\theta(x): = w(0, x).$ Define

Define the solution semiflow of system (1.1) as $\Pi(t):\mathbb{G}_{K} \rightarrow \mathbb{G}_{K}$ and $\Pi(t)\theta = w(t, \cdot, \theta)$ for any $t\geq 0.$ Applying the method described in ^[33,34,35], we can obtain the following Lemma:

Lemma 4.1. Assume that $R_1 > 1,$ and $\theta_2\not\equiv 0,$ and $\theta_4\not\equiv 0.$ If there is a positive constant $\kappa_1$ such that $\liminf\limits_{t\rightarrow +\infty}w_{5}(t, x, \theta)\geq\kappa_1,$ uniformly for all $x\in \bar{\Gamma},$ then there is a positive constant $\kappa_2$ such that

uniformly for all $x\in\bar{\Gamma}$.

Lemma 4.2. Let$P_\partial: = \{\theta\in\partial\mathbb{P} : \Pi(t)\theta\in\partial \mathbb{P}, \forall \; t\geq0 \}.$ Define $\varpi(\theta)$ as the omega limit set of $\left\{ \Pi(t)\theta:t\geq0\right\}$ and $Q = \{E_{0}\}\cup\{E_{1}\}$. Then, $\bigcup_{\theta\in P_{\partial}}\varpi(\theta) = Q.$

Proof. Since $\theta\in P_{\partial}$, we know $\Pi(t)\theta\in\partial \mathbb{P}$ for any $t\geq0$. That is, $w_{2}(t, \cdot, \theta) \equiv 0$, $w_{4}(t, \cdot, \theta) \equiv 0$, $w_{5}(t, \cdot, \theta) \equiv 0$, or $w_{6}(t, \cdot, \theta) \equiv 0$ for any $t\geq0$. In the case where $w_{2}(t, \cdot, \theta) \equiv 0$ for any $t\geq0$, it follows from the second equation of system (1.1) that $w_{1}(t, \cdot, \theta) \equiv 0$ or $w_{6}(t, \cdot, \theta) \equiv 0$ for any $t\geq0$.

Assume $w_{1}(t, \cdot, \theta) \equiv 0$. From the first equation of system (1.1), one has $w_{3}(t, \cdot, \theta) \equiv 0$ and $w_{4}(t, \cdot, \theta) \equiv 0$. $w_{5}(t, \cdot, \theta)$ satisfies

Thus, $\lim\limits_{t\rightarrow \infty }w_{5}(t, x, \theta) = 0$ uniformly for $x\in \bar{\Gamma}$. From the sixth equation of (1.1), one has $\lim\limits_{t\rightarrow \infty }w_{6}(t, x, \theta) = 0$ uniformly for $x\in \bar{\Gamma}$. In other words,

If $w_{1}(t, \cdot, \theta) \equiv 0$ does not hold, then $w_{6}(t, \cdot, \theta) \equiv 0$ holds. From the sixth equation of (1.1), one has $w_{5}(t, \cdot, \theta)\equiv 0$ for any $t\geq0$. So, $w_{4}(t, \cdot, \theta)\equiv 0$ for $t\geq0$. In this case, assume $w_{3}(t, \cdot, \theta) \equiv 0$ for any $t\geq0$, and then $w_{1}(t, \cdot, \theta) \equiv 0$ for any $t\geq0$. This contradicts our assumption. Thus, $w_{3}(t_3, \cdot, \theta)\not\equiv 0$ for some $t_3$. From Lemma 3.3, we can obtain $\lim\limits_{t\rightarrow \infty }(w_{1}(t, x, \theta), \; w_{1}(t, x, \theta)) = (M_1^{*}(x), M_2^{*}(x))$ uniformly for $x\in \bar{\Gamma}$. Thus,

Assume that there exists $t_{4} > 0$ such that $w_{2}(t_4, \cdot, \theta) \not\equiv 0$. From Lemma 3.3, one has $w_{2}(t, \cdot, \theta) > 0$ for any $t > t_{4}.$ So, $w_{4}(t, \cdot, \theta) \equiv 0$, $w_{5}(t, \cdot, \theta) \equiv 0$, $w_{6}(t, \cdot, \theta) \equiv 0$ for $t > t_{4}.$ Assume $w_{4}(t, \cdot, \theta) \equiv 0$ for $t > t_{4}.$ Thus, $w_{5}(t, \cdot, \theta) \equiv 0$ and $w_{6}(t, \cdot, \theta) \equiv 0$ for $t > t_{4}.$ So, $w_{2}(t, \cdot, \theta) \equiv 0$ for $t > t_{4}$. This contradicts our assumption. Similarly, if $w_{5}(t, \cdot, \theta) \equiv 0$ or $w_{6}(t, \cdot, \theta) \equiv 0$ for $t > t_{4},$ then $w_{2}(t, \cdot, \theta) \equiv 0$ for $t > t_{4}$, which contradicts our assumption. Thus, $\bigcup_{\theta\in P_{\partial}}\varpi(\theta) = Q.$ □

Lemma 4.3. Assume that $R_1 > 1$. Then, $E_{0}(x)$ is a uniform weak repeller for $\mathbb{P}$ in the sense that there exists $\mu_1 > 0$ such that

with initial value $\theta\in\mathbb{P}.$

Proof. First, we consider a linear system as follows:

Here, $\hat{v} = (\hat{v}_1, \hat{v}_2)^T$, and

Clearly, $P_1(0) = P_1$. By Lemma 3.1, it follows from $R_{1} > 1$ that $\nu_{p1}^{*} = s(P_1) > 0.$ Since $P_1(\mu_1)$ is a continuous for small enough $\mu_1$, one has $s(P_1(\mu_1)) > 0$ for small enough $\mu_1$. Let $\nu_{p1\mu_1}^{*}: = s(P_1(\mu_1))$. Then, $\nu_{p1\mu_1}^{*} > 0$. Denote $(\hat{\phi}_1, \hat{\phi}_2)$ as the positive eigenfunction corresponding to $\nu_{p1\mu_1}^{*}$. Then, system (4.5) has a solution $(\hat{v}(t, x), \hat{v}(t, x)) = e^{\nu_{p1\mu_1}^{*}t}(\hat{\phi}_1, \hat{\phi}_2)$.

Next, assume (4.7) does not hold. That is,

for some $\hat{\theta}\in \mathbb{P}$. Then, there is a constant $t_{5} > 0$ such that $0 < w_1(t, x, \hat{\theta}),$ $w_2(t, x, \hat{\theta}),$ $w_3(t, x, \hat{\theta}),$ $w_4(t, x, \hat{\theta}),$ $w_5(t, x, \hat{\theta}),$ $w_6(t, x, \hat{\theta}) < \mu_1,$ $x\in \bar{\Gamma}.$ Then, $w_1(t, x, \hat{\theta})$ and $w_3(t, x, \hat{\theta})$ satisfy

Since $w_1(t, x, \hat{\theta}) > 0$ and $w_3(t, x, \hat{\theta}) > 0$ for $t\geq t_{5},$ there exists $\hat{\upsilon}_1 > 0$ such that $(w_1(t_5, x, \hat{\theta}), w_1(t_5, x, \hat{\theta}))\geq \hat{\upsilon}_1(\hat{\phi}_1, \hat{\phi}_2).$ Applying the comparison principle, one has

Due to $\nu_{p1\mu_1}^{*} > 0$, one has $w_1(\cdot, x, \hat{\theta})\rightarrow +\infty$ and $w_3(\cdot, x, \hat{\theta})\rightarrow +\infty$ as $t\rightarrow \infty.$ This contradicts our assumption. It implies that $\{E_{0}(x)\}$ is an isolated invariant set in $\mathbb{P}$, and $W^s(\{E_{0}(x)\})\cap \mathbb{P} = \emptyset$. □

Similar to the proof method of Lemma 4.3, we can draw the following conclusion:

Lemma 4.4. Assume that $R_0 > 1$. Then, $E_{1}(x)$ is a uniform weak repeller for $\mathbb{P}$ in the sense that there exists $\mu_2 > 0$ such that

with initial value $\theta\in\mathbb{P}.$

Next, based on Lemmas 4.2, 4.3, and 4.4, we can obtain the following result:

Theorem 4.2. If $R_1 > 1$ and $R_0 > 1$, then there exists $\varepsilon > 0$ such that, for every initial state $\theta\in\mathbb{P}$, the solution of system (1.1) $w(t, \cdot, \theta)$ satisfies

Proof. By Lemmas 4.3 and 4.4, we can get that $Q$ is an isolated invariant set for $\Pi$ in $\mathbb{P}$, and $W^s(Q)\cap \mathbb{P} = \emptyset$, where $W^s(Q)$ is the stable set of $Q$ for $\Pi$. From Lemma 4.2, we know that any orbit of $\Pi(t)$ in $P_{\partial}$ converges to $Q$ as $t\rightarrow \infty$. So, no subset of $Q$ forms a cycle in $\partial\mathbb{P}$. By the acyclicity theorem on uniform persistence for maps (see Theorem 1.3.1 and Remark 1.3.1 in ^[36]), we conclude that $\Pi$ is uniformly persistent with respect to $(\mathbb{P}, \partial\mathbb{P})$. In addition, the uniform boundedness of the solution of (1.1) implies that $\Pi(t)$ is point dissipative. According to Theorem 3.7 and Remark 3.10 in ^[35], we have that $\Pi(t)$ admits a global attractor $\mathcal{A}$ in $\mathbb{P}$. It follows from $\mathcal{A} = \Pi(t)\mathcal{A}$ that $\theta_2(\cdot) > 0, \theta_4(\cdot) > 0, \theta_5(\cdot) > 0,$ and $\theta_6(\cdot) > 0$ for all $\theta \in \mathcal{A}$. Let $\mathcal{E} = \bigcup_{t\geq0}\Pi(t)\mathcal{A}$. Then, $\mathcal{E}\subset\mathbb{P}$ and $\lim\limits_{t\rightarrow +\infty}d(\Pi(t)\theta, \mathcal{E}) = 0$ for all $\theta \in \mathbb{P}$.

Define a continuous function $\mathbf{Y}$: $\mathbb{G}_{K}\rightarrow [0, +\infty)$ by

Clearly, $\mathbf{Y} (\theta) > 0$ for all $\theta\in \mathcal{E}.$ Since $\mathcal{E}$ is a compact subset of $\mathbb{P}$, we can get $\inf\limits_{\theta\in \mathcal{E}}\mathbf{Y}(\theta) = \min\limits_{\theta\in \mathcal{E}}\mathbf{Y}(\theta) > 0.$ It follows from the attractiveness of $\mathcal{E}$ that there is a positive constant $\bar{\kappa}_1$ such that

From Lemma 4.1, there exists some $\varepsilon > 0$ such that

□

Remark 2 Biologically, when $R_{1} > 1$ and $R_{0} > 1$, Theorem 4.2 shows that the disease will persists.

5.   Numerical simulations

In this section, we give numerical simulations for the dynamical behaviors of the solutions and the effect of some key factors on the transmission of the Zika disease. For this purpose, some parameters are selected with the following values: $\Gamma = (0, \pi)$, $\tau(x) = 1$, $K_1(x) = 500$, $K_2(x) = 16$, $\omega(x) = 0.05$, $\delta_1(x) = 0.15$, $\delta_2(x) = 0.05$, $\eta(x) = 0.1$, $\rho(x) = 0.3$, $H_*(x) = 100$, $\gamma(x) = 0.14$, $d_1(x) = 0.001,$ $d_2(x) = 0.008,$ $p = 0.6$, $l = 0.3$. Under this set of parameters, we calculate the mosquito reproduction number $R_1 = 5 > 1$.

5.1.   Numerical simulation for the dynamical behaviors of the solutions

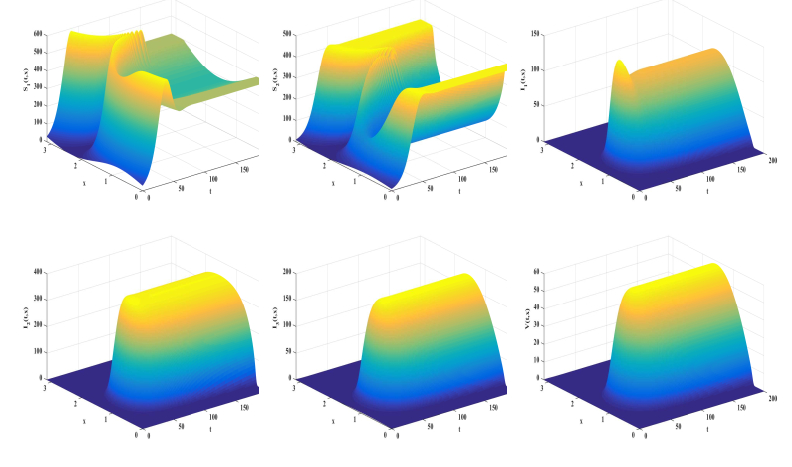
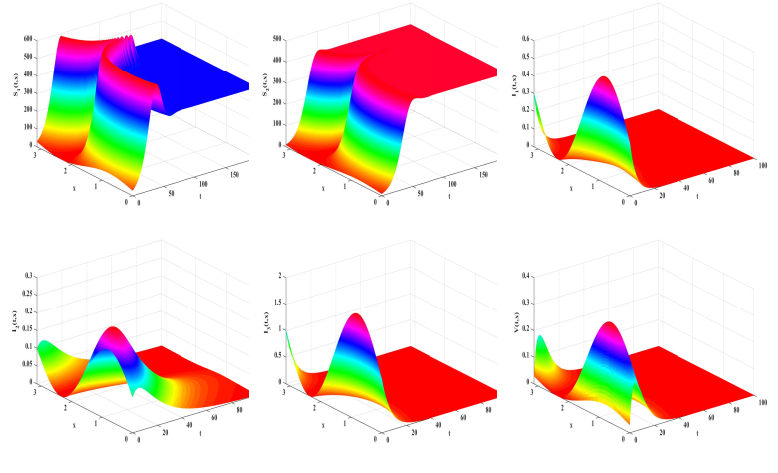
Initial values are selected as $S_{1}(0, x) = 30(1+\sin(2x))$, $I_{1}(0, x) = 0.3(1+\sin(2x))$, $S_{2}(0, x) = 10(1+\sin(2x))$, $I_{2}(0, x) = 0.1(1+\sin(2x))$, $I_{3}(0, x) = 1+\sin(2x)$, $V(0, x) = 0.03(1+\sin(2x))$. To simulate the result of Theorem 4.1, we choose $\alpha_1(x) = 0.001(1-\cos(2x)),$ $\alpha_2(x) = 0.004(1-\cos(2x)),$ $\alpha_3(x) = 0.005(1-\cos(2x)).$ We calculate the basic reproduction number to be $R_0 = 0.0343 < 1$. Figure 1 shows that the Zika disease will be eliminated.

To simulate to result of Theorem 4.2, we set the transmission rate functions as follows:

Then, we calculate $R_0 = 1.0832 > 1$. From Theorem 4.2, we know that system (1.1) is uniformly persistent, which is shown in Figure 2.

5.2.   The effect of some key factors on the transmission of Zika disease

5.2.1.   The effect of the vector-bias $q=\frac{p}{l}$ on $R_0$ and $I_2(t, x)$ and $I_3(t, x)$

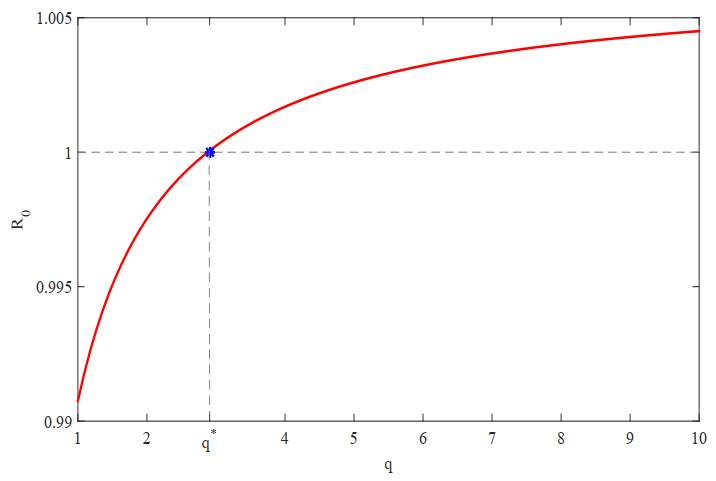
Here, we choose $\alpha_2(x) = 0.14$ and $d_2(x) = 0.011.$ Other parameter values remain unchanged, and other transmission rate functions are selected as in (5.1). Figure 3 shows that the basic reproduction number $R_0$ is an increasing function with $q$. When $q = 1$, i.e., $p = l$, this case indicates no vector-bias, and one has $R_0 = 0.9908 < 1$. The Zika disease will disappear from Theorem 4.1. Then, $R_0$ increases as $q$ increases. When $q > q^*$ $(\mathrm{here} \; q^* = 2.9089)$, we know $R_0 > 1.$ The Zika disease persists from Theorem 4.2. It implies that the vector-bias can cause disease outbreaks. Figure 3 indicates that neglecting the vector-bias will underestimate the risk of disease.

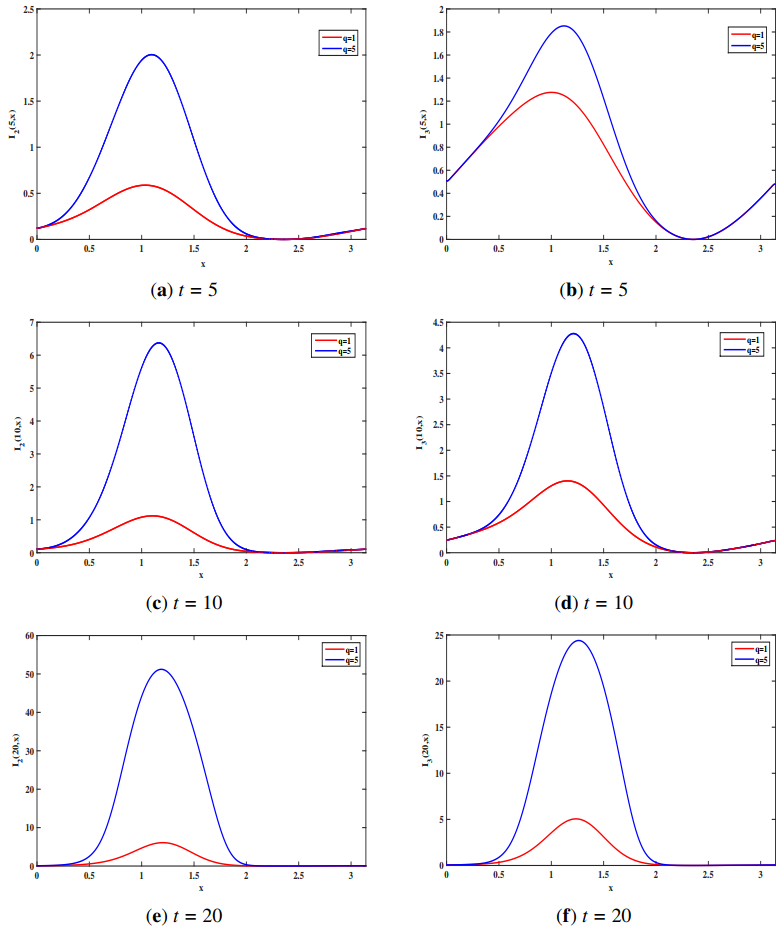
Next, we demonstrate the effect of the vector-bias $q = \frac{p}{l}$ on the infected adult mosquitoes $I_2(t, x)$ and infected humans $I_3(t, x)$. In Figure 4, the red solid curve represents $q = 1$. It indicates no vector-bias. The blue solid curve represents $q = 5$. It indicates that there is a vector-bias. We find that the presence of the vector-bias leads to an increased peak value of $I_2(t, x)$ and $I_3(t, x)$. In addition, as time goes on, the vector-bias has an increasingly strong effect on the peak of the distribution of infected adult mosquitoes and infected humans.

5.2.2.   The effect of the environmental transmission rate $\alpha_1$ on $R_0$ and $I_1(t, x)$ and $V(t, x)$

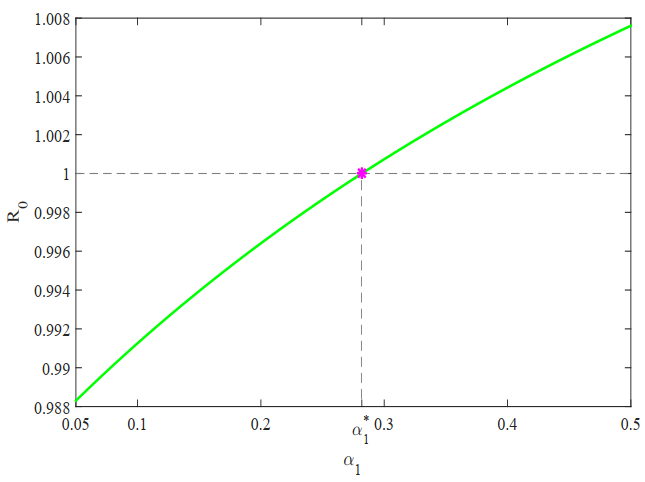
Here, we choose $d_2(x) = 0.01.$ Other parameter values remain unchanged and the transmission rate functions are selected as in (5.1). Figure 5 gives that the basic reproduction number $R_0$ is an increasing function with $\alpha_1$. When $\alpha_1 < \alpha_1^*$, we have $R_0 < 1$. From Theorem 4.1, the Zika disease will disappear. $R_0$ increases as $\alpha_1$ increases. When $\alpha_1 > \alpha_1^*$ $(\mathrm{here} \; \alpha_1^* = 0.2818)$, one has $R_0 > 1.$ The Zika disease persists according to Theorem 4.2. Figure 5 indicates that the environmental transmission is important and indispensable.

Next, we will present the effect of the environmental transmission rate $\alpha_1$ on the distribution of $I_1(t, x)$ and $V(t, x)$. We change the value of $\alpha_1$, and other parameter values remain unchanged. We consider three different values: $\alpha_1 = 0.1, \; 0.2, \; 0.3$. From Figure 6, when the time is fixed, the peak value of infected aquatic mosquitoes increases significantly with the increase of the environmental transmission rate $\alpha_1$. As time goes on, the environmental transmission rate has an increasingly strong effect on the peak of the distribution of infected aquatic mosquitoes and the densities of the Zika virus in the water environment.

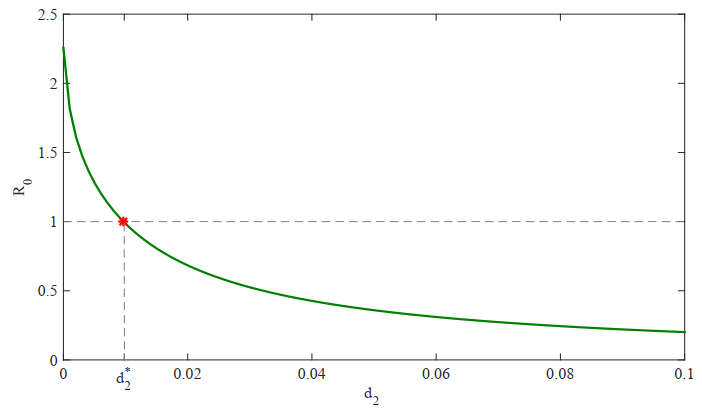
5.2.3.   The effect of the diffusion rate on $R_0$

Here, we just consider the effect of the human diffusion rate $d_2$ on $R_0$. The transmission rate functions are selected as in (5.1). Figure 7 gives that the basic reproduction number $R_0$ is a decreasing function with $d_2$, which is consistent with the results obtained in ^[37,38]. When $d_2 = 0$, this case indicates no diffusion in human population, and one has $R_0 = 2.2571 > 1$. The Zika disease persists according to Theorem 4.2. As $d_2$ increases, $R_0$ decreases. When $d_2 > d_2^*$ $(\mathrm{here} \; d_2^* = 0.0098)$, $R_0 < 1.$ From Theorem 4.1, the Zika disease will disappear. Figure 7 shows that neglecting the human diffusion will overestimate the risk of the Zika disease.

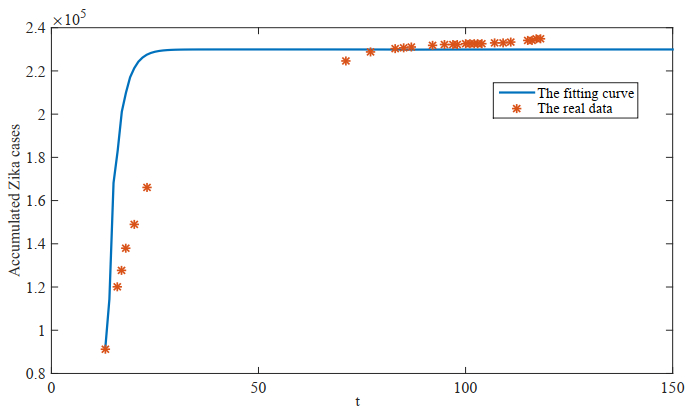
5.3.   A numerical application to Brazil

From the Brazil Ministry of Health ^[39], we collect the weekly reported accumulated Zika cases in Brazil from March 25, 2016 to April 14, 2018. We use model (1.1) to fit the real-world data and take a week as the time unit. Some other parameters can be selected from previous literature ^[21]. $\tau(x) = 1$, $\omega(x) = 0.05\times7$, $\delta_1(x) = 0.15\times7$, $\gamma(x) = 0.1\times7$, $\delta_2(x) = 0.05\times7$, $\alpha_2(x) = 0.025\times7,$ $\alpha_3(x) = 0.028\times7.$ $H_*(x) = 2.05\times 10^{8}$ ^[40]. Other parameters will be estimated by applying the least-squares estimation method. $\alpha_1(x) = 0.0001\times7,$ $\eta(x) = 0.1\times7$, $\rho(x) = 0.3\times7$, $d_1(x) = 0.001,$ $d_2(x) = 0.008,$ $p = 0.4$, $l = 0.3$. $K_1(x) = 1.02\times 10^{9}$, $K_2(x) = 3.28\times 10^{7}$. We can get $R_0 < 1,$ and from Theorem 4.1, the Zika disease will disappear in Brazil. The fitting result for the accumulated cases is given in Figure 8.

6.   Conclusions

This study investigated a reaction-diffusion Zika model based on our previous model in ^[23]. We introduced the vector-bias in the model in article ^[23]. In this study, we considered the combined effects of vector-bias, environmental transmission, and spatial heterogeneity on spread of Zika disease. We defined two threshold indexes: the mosquito reproduction number $R_{1}$ and basic reproduction number $R_{0}$. Dynamical behaviors in terms of $R_{1}$ and $R_{0}$ were analyzed. Finally, we simulated the effects of the vector-bias $q = \frac{p}{l}$, the environmental transmission rate $\alpha_1$, and the human diffusion rate $d_2$ on $R_0$. We found that the ignorance of the vector-bias effect will underestimate the infection risk of the Zika disease and the ignorance of the human diffusion rate effect will overestimate the infection risk.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work is partially supported by the National Natural Science Foundation of China (No.12201007, 12201557, 12101003), the Natural Science Foundation of Anhui province (No. 2108085QA07), Foundation of Zhejiang provincial education department (No. Y202249921), Natural Science Research Project of Anhui Educational Committee (No. 2023AH030021) and Pre-Research National Natural Science Foundation of China of Anhui Polytechnic University (No. Xjky2020134).

Conflict of interest

The authors declare there are no conflicts of interest.