Challenges of existing grid codes and the call for enhanced standards

1.   Introduction

Hopfield neural network (HNN) is in the powerful class of artificial neural networks (ANNs), which has been introduced in the literature by John Hopfield in 1982. Since then, its investigation has become a worldwide focus ^[1,2,3,4,5]. All of those models are real-valued neural networks (NNs). However, complex-valued neural networks (CVNNs) can handle problems that cannot be handled with real-valued parallel networks ^[6,7]. Recently, some authors started the dynamical analysis of CVNNs. For example, in ^[8], Ali et al. studied the finite time stability analysis of delayed fractional-order memristive CVNNs by using the Gronwall inequality, H$\ddot{o}$lder inequality and inequality scaling skills. In ^[9], Zhang and Cao investigated the existence and global exponential stability of periodic solutions of neutral type CVNNs by collecting the Lyapunov functional method with the coincidence degree theory as well as graph theory. In article ^[21], the authors dealt with the problem stability of impulsive CVNNs with time delay.

In the functioning of ANNs, time-delays always exist in the signal transmission between neurons on account to the limited pace of signal exchange and transmission. Thus, it is one of the main reasons poor performance and instability in a system is the presence of delays. Therefore, in recent years, the analysis of the stability of delayed ANNs has been the great attention of researchers, and various results have been discussed in the literature ^{[16,17,18,19,20,21,22]}.

ANNs with neutral-type delays were also very seldom discussed in the existing literature; such models are called neutral-type ANNs. They have been the subject of in-depth studies by many researchers, for instance, Guo and Du ^[17], concerned with the global exponential stability of periodic solution for neutral-type CVNNs.

The theory of passivity is a significant notion of automatic for the analysis and control of models whose certain input/output characteristics are established in terms of energy criteria. The notions of passivity are adapted to several scientific fields and are effective for the regulation of electrical, mechanical, and electromechanical systems present in several fields of engineering, such as robotics, power electronics, aeronautics, etc. Many results are concentrated in the research of the passivity of NN systems. In ^[11], Li and Zheng proved the global exponential passivity for delayed quaternion-valued memristor-based NNs. Ge et al. ^[12] studied the robust passivity analysis for a class of uncertain NNs subject to mixed delays. The problem of passivity analysis for uncertain bidirectional associative memory NNs in the presence of mixed delays are discussed in ^[13]. In ^[35], Khonchaiyaphum et al. studied FTP analysis of neutral-type NNs.

Many researchers have been interested in finite-time control problems of dynamical systems based on the Lyapunov theory of stability to give big attention to the asymptotic model of systems over an infinite time interval. Recently, many interested results have been published. In ^[14], Thuan et al. discussed the robust FTP for a fractional order NNs with uncertainties. In paper ^[19], Wei et al. are focused on a class of coupled quaternion-valued NNs with several delayed couplings to study fixed-time passivity.

The main objective of this manuscript is to deal with the FTP for the following neutral-type CVNNs:

Here, we have

$\circ \;z(\cdot) = [z_{1}(\cdot), \; z_{2}(\cdot), \cdots, \; z_{n}(\cdot)]^{T}\in\mathbb{C}^{n}$ is the complex valued state vector,

$\circ \;\omega(\cdot)\in\mathbb{C}^{n}$ is the disturbance input which belongs to $L^{2}[0, +\infty), p$

$\circ \;u(\cdot)\in\mathbb{C}^{n}$ is the control output,

$\circ \;f(z(\cdot)) = [f(z_{1}(\cdot)), \; f(z_{2}(\cdot)), \cdots, \; f(z_{n}(\cdot))]^{T}\in\mathbb{C}^{n}$ is the complex-valued activation function,

$\circ \;A = diag\{a_{1}, a_{2}, \cdots, a_{n}\} > 0\in\mathbb{R}^{n \times n}$ is a diagonal matrix,

$\circ \;B = (b_{jk})\in\mathbb{C}^{n \times n}, \; C = (c_{jk})\in\mathbb{C}^{n \times n}, \; D = (d_{jk})\in\mathbb{C}^{n \times n}$ are respectively the connection weight matrix and the connection weight matrix with delays,

$\circ \;K_{1}$ is a known real constant matrice with appropriate dimension,

$\circ \;K_{2}$ is a known complex matrice with appropriate dimension.

The initial condition of (1.1) is given as

where $\rho = \max\{ \sup\limits_{t\in\mathbb{R}}(\tau(t), \; \sup\limits_{t\in\mathbb{R}}(h(t))\}$.

The main contributions of our article are :

$\circ$ We use a more adequate hypothesis for the complex-valued activation functions (CVAF) considered in our model. Based on this assumption, a controllable model is formed by divised the real and imaginary parts, and we give a sufficient condition to realize FTP. This result is more general than the existing passivity results on real-valued NNs ^[35,36,37].

$\circ$ A Lyapunov–Krasovskii function that support triple, four, and five integral terms is introduced, and the Wirtinger-type inequality technique and convex combination approach are espoused.

$\circ$ A new set of sufficient conditions in terms of LMIs is derived to guarantee FTB and FTP results. These conditions can be simply found by the Matlab LMI toolbox.

The main contents of the manuscript are outlined as follows: in Section 2, we established new assumptions, definitions, and lemmas for the dynamic systems (1.1), which will be used later. New sufficient conditions on the FTB and FTP are discussed in Section 3. Two examples are presented in Section 4 to verify our results. At last, in Section 5, we end with the conclusion and perspective.

2.   Problem formulation and preliminaries

In this section, we present new necessary assumptions and some definitions and lemmas, which are utilized in the next section.

Assumption 1: The delays $\tau(\cdot)$ and $h(\cdot)$ are differentiable functions satisfies the inequalities below:

Assumption 2: The neuron activation function $f_{k}(\cdot)$ satisfy the below Lipschitz condition:

Furthermore, by means of Assumption 2, it is clear to get

where $L = diag\{l_{1}, \; l_{2}, \cdots, l_{n}\}.$

Assumption 3: The neuron activation functions $f(\cdot)$ can be divided into two parts as follows:

where $z = x+iy, \; i$ shows the imaginary unit, and the real imaginary parts check the below conditions:

1) The partial derivatives $\frac{\partial f}{\partial x}, \; \frac{\partial f}{\partial y}$ exist and are continuous.

2) There exist positive constant numbers $\gamma_{k}^{RR}, \; \gamma_{k}^{RI}, \; \gamma_{k}^{IR}, \; \gamma_{k}^{II}$ such that

Thus, one can obtain that for any $x_{1}, \; x_{2}, \; y_{1}, \; y_{2}\in\mathbb{R},$

for all $k = 1, \; 2, \cdots, \; n.$

Remark 1: As we know, in many literatures ^[29,30,31], after the separation of the activation functions into real-imaginary type, $\frac{\partial f}{\partial x}$ and $\frac{\partial f}{\partial y}$ are still supposed to exist and be continuous and limited. Via these conditions, we can point that they checked the same inequalities given in hypothesis 3 by considering the mean value theorem for multivariable functions. Here, we delete these constraints of the partial derivatives and make the hypothesis into an appropriate one that imaginary and real parts of the activation functions just check the inequalities in hypothesis 3. Consequently, our study can help a broader class of CVAF.

Remark 2: By applying the modulus of a complex number to some simple inequalities, it is worth mentioning that hypothesis 2 is equivalent to hypothesis 3. Therefore, for writing convenience, we will assume that activation functions satisfy hypothesis 2 to study our main results.

Assumption 4: The neuron activation function $f_{k}(\cdot)$ may be divided into two parts according to the complex number $z$ as follows

where $f_{k}^{R}(\cdot), \; f_{k}^{I}(\cdot):\mathbb{R}\rightarrow \mathbb{R},$ then for any $k = 1, \; 2, \cdots, \; n,$ there exist constants $\check{l}^{R}_{k}, \; \hat{l}^{R}_{k}, \; \check{l}^{I}_{k}\; \hat{l}^{I}_{k}$ such that

where $f^{R}_{k}(0) = 0, \; f^{I}_{k}(0) = 0, \; \kappa_{1}, \; \kappa_{2}\in\mathbb{R}, \; \kappa_{1}\neq \kappa_{2}.$

For presentation convenience, we denote

Remark 3: In ^[23,24,25], hypotheses 3 and 4 are given on the activation functions which separate between the real and imaginary parts. Moreover, we can even simply say that hypothesis 3 is quite strict and that it is a special case of hypothesis 2. This fact has already been mentioned in ^[26] and ^[27]. In addition, hypothesis 4 is also a strong constraint. For instance, if the activation functions $f_{k}(z)\; (k = 1, \; 2, \cdots, \; n)$ checked hypothesis 4, we have:

where $z_{1} = x_{1} + iy_{1}, \; z_{2} = x_{2} + iy_{2},$ $l_{k}^{R} = \max \{|\check{l}^{R}_{k}|, \; |\hat{l}^{R}_{k}|\},$ and $l_{k}^{I} = \max \{|\check{l}^{I}_{k}|, \; |\hat{l}^{I}_{k}|\},$ then one can have that

Thus, the activation function $f_{k}(z)\; (k = 1, \; 2, \cdots, \; n)$ satisfies the Lipschitz condition of hypothesis 2. Therefore, hypotheses 3 and 4 imply hypothesis 2, that is, the condition of hypothesis 2 is a special case of hypotheses 3 and 4.

Remark 4: Indeed, when the activation function is given as follows: $f_{k}(z) = f^{R}_{k}(x, \; y)+ if^{I}_{k}(x, \; y)$ includes $f_{k}(z) = f^{R}_{k}(Re (z))+if^{I}_{k}(Im (z))$ as a special case. Therefore, in the following section, we will indicate that $f_{k}(z)$ is of the type of distinct real-imaginary activation functions. Let $z(t) = x(t)+iy(t), \; z(t-\tau(t)) = z^{\tau}(t), \; x(t-\tau(t)) = x^{\tau}(t),$ $y(t-\tau(t)) = y^{\tau}(t), \; x(t-h(t)) = x^{h}(t),$ $y(t-h(t)) = y^{h}(t),$ $B = B^{R}+iB^{I}, \; C = C^{R}+iC^{I}, \; f(z(t)) = f^{R}(x(t), y(t))+if^{I}(x(t), y(t)),$ $f(z^{\tau}(t)) = f^{R}(x^{\tau}(t), y^{\tau}(t))+if^{I}(x^{\tau}(t), y^{\tau}(t)),$ $\omega(t) = \omega^{R}(t)+i\omega^{I}(t),$ and $u(t) = u^{R}(t)+iu^{I}(t),$ then model (1.1) can be divided into imaginary and real parts as the following form

The initial condition of (2.4) is given by:

where $\varphi^{R}(s), \; \varphi^{I}(s)\in \mathcal{C}([-\rho, \; 0], \mathbb{R}^{n}).$

Let $\theta = \left(\begin{array}{c} x \\ y \\ \end{array} \right),$ $\bar{f}(\theta) = \left(\begin{array}{c} f^{R}(x, \; y) \\ f^{I}(x, \; y) \\ \end{array} \right),$ $\bar{f}(\theta^{\tau}) = \left(\begin{array}{c} f^{R}(x^{\tau}, \; y^{\tau}) \\ f^{I}(x^{\tau}, \; y^{\tau})\\ \end{array} \right),$ $\bar{\omega} = \left(\begin{array}{c} \omega^{R} \\ \omega^{I} \\ \end{array} \right),$ $\bar{A} = \left(\begin{array}{cc} A & 0 \\ 0 & A \\ \end{array} \right),$ $\bar{B} = \left(\begin{array}{cc} B^{R} & -B^{I} \\ B^{I} & B^{R} \\ \end{array} \right),$ $\bar{C} = \left(\begin{array}{cc} C^{R} & -C^{I} \\ C^{I} & C^{R} \\ \end{array} \right),$ $\bar{D} = \left(\begin{array}{cc} D^{R} & -D^{I} \\ D^{I} & D^{R} \\ \end{array} \right),$ $\bar{u} = \left(\begin{array}{c} u^{R} \\ u^{I} \\ \end{array} \right), \; \bar{K}_{1} = \left(\begin{array}{cc} K_{1} & 0 \\ 0 & K_{1} \\ \end{array} \right), \; \bar{K}_{2} = \left(\begin{array}{cc} K_{1}^{R} & -K_{1}^{I} \\ K_{1}^{I} & K_{1}^{R} \\ \end{array} \right).$

Model (2.4) can be rewritten as:

with

where $\phi(s) = \left(\begin{array}{c} \varphi^{R}(s) \\ \varphi^{I}(s) \\ \end{array} \right)\in \mathcal{C}([-\rho, 0], \mathbb{R}^{2n}).$

The norm is defined as follows: For every $\phi(\cdot)\in \mathcal{C}([-\rho, 0], \mathbb{R}^{2n}),$ $\|\phi\|_{\hat{h}} = \max\big\{\|\phi\|, \|\phi^{'}\|\big\} = \max\big\{ \sup\limits_{\varsigma\in[-\rho, 0]}|\phi(\theta)|, \; \sup\limits_{\varsigma\in[-\rho, 0]}|\phi^{'}(\varsigma)|\big\}.$

It is clear from (2.3) that:

where, $\bar{L}^{-} = \left(\begin{array}{cc} \check{L}^{R} & 0 \\ 0 & \check{L}^{I} \\ \end{array} \right), \; \; \bar{L}^{+} = \left(\begin{array}{cc} \hat{L}^{R} & 0 \\ 0 & \hat{L}^{I} \\ \end{array} \right).$

Assumption 5: Given a positive value $b^{R}, \; b^{I},$ then $\omega^{R}(t), \; \omega^{I}(t)$ checks

where $\bar{b} = \left(\begin{array}{c} b^{R} \\ b^{I} \\ \end{array} \right).$

Definition 1 (FTB): For a known constant $T_{1} > 0$, system (1.1) is FTB with regard to $(\bar{c}_{1}, \; \bar{c}_{2}, \; T_{1}, \; \bar{L}, \; \bar{b}),$ and $\bar{\omega}(\cdot)$ checked (2.7) if: $\sup\limits_{t_{0}\in[-\bar{\tau}, 0]}\big\{\theta^{T}(t_{0})\bar{L}\theta(t_{0}), \; \dot{\theta}^{T}(t_{0})\bar{L}\dot{\theta}(t_{0})\big\}\leq \bar{c}_{1} \Rightarrow \theta^{T}(t)\bar{L}\theta(t)\leq \bar{c}_{2},$ for $t\in[0, \; T_{1}],$ where $\bar{c}_{1} = \left(\begin{array}{c} c_{11} \\ c_{12} \\ \end{array} \right), \; \bar{c}_{2} = \left(\begin{array}{c} c_{21} \\ c_{22} \\ \end{array} \right), \;$ $0 < c_{11} < c_{21}, \:0 < c_{12} < c_{22},$ $\bar{L} > 0$ is a matrix.

Definition 2(FTP): For a known constant $T_{1} > 0$, system (1.1) is said to be FTP, with regard to $(\bar{c}_{1}, \; \bar{c}_{2}, \; T_{1}, \; \bar{L}, \; \bar{b}),$ if the beelow conditions are checked:

(ⅰ) Model (1.1) is FTB with regard to $(\bar{c}_{1}, \; \bar{c}_{2}, \; T_{1}, \; \bar{L}, \; \bar{b})$.

(ⅱ) For a known constant $\gamma > 0,$ and since the zero initial condition, the below relation is true:

when $\bar{\omega}(\cdot)$ checked (2.7).

Lemma 1 ^[28]: For a symmetric matrix $\vartheta = \vartheta^{T}\geq0$, scalars $e_{1} > e_{2} > 0,$ such that the integrations below are well defined. We have

Lemma 2: For a symmetric matrix $\vartheta = \vartheta^{T}\geq0$, scalars $e_{1} > e_{2} > 0,$ such that the integrations below are well defined. We have

Proof: The proof of Lemma 2 is inspired by the proof of Lemma 2 in ^[28].

For any symmetric matrix $\vartheta = \vartheta^{T}\geq0,$ we have

then after integration of it from $t+u$ to $t,$ from $\lambda$ to $0,$ from $s$ to $0,$ and from $-e_{1}$ to $-e_{2}$ in turn, we can obtain

where

According to Schur complement, ^[16] is equivalent to the below condition: $\Pi_{22} > 0, \; \Pi_{11}-\Pi_{12}\Pi_{22}^{-1}\Pi_{12}^{T}\geq0.$ $\Rightarrow \Pi_{11}\geq\Pi_{12}\Pi_{22}^{-1}\Pi_{12}^{T},$ which is equivalent to inequality (2.9).

This completes the proof.

Lemma 3 ^[38]: For a given symmetric definite matrix $\xi > 0$ and for any differentiable function $\zeta(\cdot): [e_{1}, \; e_{2}]\rightarrow \mathbb{R}^{n}$, the below inequality holds:

where $\chi = \frac{1}{e_{2}-e_{1}} \int_{e_{1}}^{e_{2}}\zeta(s)ds,$ $\Xi_{2}(\xi) = \left(\begin{array}{ccc} \xi & -\xi & 0 \\ \star & \xi & 0 \\ 0 & 0 & 0 \\ \end{array} \right)+\frac{\pi^{2}}{4}\left(\begin{array}{ccc} \xi & \xi & -2\xi \\ \star & \xi & -2\xi \\ \star & \star & 4\xi \\ \end{array} \right).$

Remark 5: In this manuscript, our goal is to know how to determine the sufficient condition to study the FTB and FTP of the proposed model. So, to get the desired objectives, a processable whole model (2.5) is first formed by dividing the initial model into imaginary and real parts and founding an equivalent real-valued model. Second, using the Lyapunov function approach, the design procedure can be easily performed by checked the LMIs, so in the next section the expected conditions will be obtained.

3.   Main results

In this section, we will concentrate on the problem of FTB and FTP.

3.1.   FTB analysis

In this first part, our goal is to study the FTB in the following system:

Theorem 1: Suppose that Assumptions 1–5 hold. Let $\bar{\tau}, \; \mu, \; \bar{h}, \; h_{1},$ and $\delta$ be positive scalars, then system (3.1) is FTB, with respect to $(\bar{c}_{1},$ $\bar{c}_{2},$ $T_{1},$ $\bar{L},$ $\bar{b}),$ if there exists symmetric positive definite matrices $P,$ $Q_{1},$ $Q_{2},$ $R_{01},$ $R_{1},$ $R_{02},$ $R_{2},$ $R_{3},$ $R_{4}$ $R_{5}$ $R_{6},$ $T_{01},$ $T_{2},$ $T_{3}$ and diagonal matrices $M_{1} > 0,$ $M_{2} > 0,$ $M_{3} > 0,$ such that the following LMIs hold:

where

Proof: We consider the Lyapunov functional below:

where

Calculating the time-derivative of $V(\theta(\cdot))$ along any trajectory of model (3.1), we obtain

where

Applying Lemma 3 to the above inequality, we get

where

Similary,

and by applying Lemma 1,

Applying Lemma 1 and 3 to the above inequality, we get

For any $\rho_{1k} > 0, \; \rho_{2k} > 0, \; \rho_{3k} > 0, \; k = 1, \; 2, \cdots, n,$ it follows from (2.3) that

which implies

and

where $M_{1} = diag\{\rho_{11}, \; \rho_{12}, \cdots\rho_{1n}\}, \; M_{2} = diag\{\rho_{21}, \; \rho_{22}, \cdots\rho_{2n}\},$ $M_{3} = diag\{\rho_{31}, \; \rho_{32}, \cdots\rho_{3n}\}.$

Moreover, for any matrices $G_{1}$ and $G_{2}$ with appropriate dimensions, it is true that,

We can say that

where

and $\Omega$ is given in (3.2).

Multiplying by $e^{-\delta t},$ we can obtain

By integrating (3.13] between $0$ to $t,$ such as $t\in [0, \; T_{1}],$ we can write

So,

Letting

we obtain

where

where $\tilde{L} = \max\{|\bar{L}^{+}, \; \bar{L}^{-}|^{2}.$

Furthermore, it follows from (3.14) that

Because of inequalities (3.14) and (3.15), we obtain

From condition (3.3), we arrive at $\theta^{T}(t)L\theta(t) < \bar{c}_{2}.$ From Definition 1, the model (3.1) is FTB with regard to $(\bar{c}_{1}, \; \bar{c}_{2}, \; T_{1}, \; \bar{L}, \; \bar{b}).$

This allowed the proof to be obtained.

Remark 6: In Theorem 1, sufficient conditions are met to verify that the model (3.1) is FTB, then Theorem 2 will present FTP conditions.

3.2.   FTP analysis

In this second part, we study the FTP analysis for the below model

Theorem 2: Suppose that Assumptions 1–5 hold. Let $\bar{\tau}, \; \mu, \; \bar{h}, \; h_{1},$ and $\delta$ be scalars, then system (3.17) is FTP with keeping the parameter $(\bar{c}_{1},$ $\bar{c}_{2},$ $T_{1},$ $\bar{L},$ $\bar{b}),$ if there exists symmetric positive definite matrices $P,$ $Q_{1},$ $Q_{2},$ $R_{01},$ $R_{1},$ $R_{02},$ $R_{2},$ $R_{3},$ $R_{4},$ $R_{5},$ $T_{01},$ $T_{2},$ $T_{3}$ and diagonal matrices $M_{1} > 0,$ $M_{2} > 0,$ $M_{3} > 0,$ and scalar $\beta > 0$ such that the following LMIs (3.18) hold:

where the parameters are kept the same as Theorem 3.1.

Proof: Select the Lyapunov function used in the Theorem 3.1. We get

where $\tilde{\Omega}$ is given in (3.18), then

Multiplying (3.19) by $e^{-\delta t},$ we can get

Integrating the above inequality between $0$ to $T_{1},$ we can write

Consider the zero initial condition for $\theta_{0} = 0$ and we have $V(\theta(0)) = 0,$ then

Since $V(\theta(t))\geq 0,$ we can say from (3.20) that

Finally, we can say that the system (3.17) is FTP. This allowed the proof to be obtained.

Remark 7: It should be emphasized that the LMI approach proposed in this paper is more useful for reducing the conservatism of the delay system, which may lead to obtain less conservative results. This proves the advantage of our proposed method.

Remark 8: We note that the optimal value of $\bar{c}_{2}$ depends on the parameter $\delta,$ then the optimal minimum value of $\bar{c}_{2}$ is determined from the minimum value of $\delta,$ such that the LMIs matrix solution remains feasible.

Remark 9: In the majority of published work, the Lyapunov function theory is the most effective approach to investigating the problem of stability and passivity for divers dynamical models. Moreover, it can be seen that the existing literature ^{[11,12,13,15,19,32,33,34,35]} contains the Lyapunov function with single, double, tripe, and four integral terms. However, in this article, we give the Lyapunov–Krasovskii function with five integral terms such as $\frac{\bar{\tau}^{4}}{24} \int_{-\bar{\tau}}^{0}\int_{\lambda}^{0}\int_{\alpha}^{0}\int_{\gamma}^{0}\int_{t+\beta}^{t}\dot{\theta}^{T}(s)T_{3}\dot{\theta}(s)dsd\beta d\gamma d\alpha d\lambda.$ Different from the published work, this is the first time studying the problem of FTP of neutral-type CVNNs. Via a Lyapunov–Krasovskii function with triple, four and five integral terms, by utilizing Jensons inequality and the Wirtinger-type inequality technique, new sufficient conditions for FTB and FTP are taken in terms of LMIs, which is effective on reducing conservatism.

4.   Numerical examples

In this section, two examples are given to show the feasibility of our results.

Example 1: Consider the following model

where

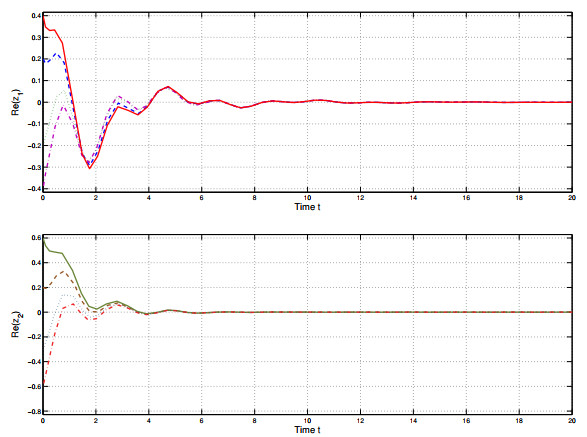
$f_{j}(z) = 0.3(|x_{j}+1|-|x_{j}-1|)+i0.3(|y_{j}+1|-|y_{j}-1|).$ Thus, $L_{1} = L_{2} = 0_{2\times 2}$ and $L_{3} = L_{4} = \left(\begin{array}{cc} 0.3 & 0 \\ 0 & 0.3 \\ \end{array} \right), \Rightarrow$ $\bar{L}_{1} = 0_{4\times 4}$ and $\bar{L}_{2} = 0.3 I_{4}$ $\tau(t) = 0.15(1-\sin(2t)), \; h(t) = 0.15(1-\cos(2t)), \; \omega(t) = 0.9\sin(\pi t)e^{-0.5t}+\sin(\pi t)e^{-0.3t}i$, $\delta = 1, \; \bar{c}_{1} = \left(\begin{array}{c} 0.5 \\ 0.5 \\ \end{array} \right) 0.5, \; \bar{b} = \left(\begin{array}{c} 0.81 \\ 0.60 \\ \end{array} \right), \; T_{1} = 15,$ matrix $\bar{L} = I.$ Using the Matlab LMI toolbox to solve the LMIs (3.2) and (3.3) in Theorem 1, we obtained the feasible solutions for an optimal minimum value of $\bar{c}_{2} = \left(\begin{array}{c} 9.8208 \\ 9.4072 \\ \end{array} \right).$ The trajectories of the solution of system (4.1) in Example 1 are shown in Figures 1 and 2, and the time history of $(Re(z))^{T}L(Re(z))$ and $(Im(z))^{T}L(Im(z))$ are given in Figure 3. Hence, it can be concluded that the system (4.1) is FTB.

Example 2: Consider the following system :

where

$f_{j}(z) = 0.6\tanh(x_{j})+i0.7\tanh(y_{j}).$ Thus, $L_{1} = L_{2} = 0_{2\times 2}$ and $L_{3} = \left(\begin{array}{cc} 0.3 & 0 \\ 0 & 0.3 \\ \end{array} \right), \; L_{4} = \left(\begin{array}{c} 0.35 \\ 0.35 \\ \end{array} \right) \Rightarrow$ $\bar{L}_{1} = 0_{4\times 4}$ and $\bar{L}_{2} = \left(\begin{array}{cccc} 0.3 & 0 & 0 & 0 \\ 0 & 0.3 & 0 & 0 \\ 0 & 0 & 0.35 & 0 \\ 0 & 0 & 0 & 0.35 \\ \end{array} \right),$ $\tau(t) = 0.15(1-\cos(2t)), \; h(t) = 0.15(1-\sin(2t)), \; \omega(t) = 0.2e^{-0.5t}+0.3e^{-0.3t}i,$ $\delta = 1, \; \bar{c}_{1} = \left(\begin{array}{c} 0.1 \\ 0.1 \\ \end{array} \right) 0.5,$ $\bar{b} = \left(\begin{array}{c} 0.019 \\ 0.053 \\ \end{array} \right), \; T_{1} = 12,$ matrix $\bar{L} = I.$ Using the Matlab LMI toolbox to solve the LMIs (3.2) and (3.3) in Theorem 2, we obtained the feasible solutions for an optimal minimum value of $\bar{c}_{2} = \left(\begin{array}{c} 12.4431 \\ 15.0562 \\ \end{array} \right).$ From Table 1, The results presented in this manuscript are significantly better than those of ^{[32,33,34,35]}, which confirms the validity of our work.

The trajectories of the solution of model (4.2) in Example 4 are given in Figure 4 and Figure 5. The time history of $(Re(z))^{T}L(Re(z))$ and $(Im(z))^{T}L(Im(z))$ are given in Figure 6. Hence, it can be concluded that the system (4.2) is FTP.

5.   Conclusions

This paper is focused on the FTP problem of neutral-type complex-valued NNs in the presence of time-varying delays. By using Lyapunov functionals, the Wirtinger inequality, and LMIs, new sufficient conditions are gotten to guarantee the finite-time boundedness and finite-time passivity of our model. Finally, two examples are presented to prove the effectiveness of our main results. In the future work, we will take the challenge to study the finite-time dissipativity of stochastic complex NNs with mixed delays via a non-separation approach and the fixed-time passivity of coupled clifford-valued NNs subject to multiple delayed couplings.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.