Possible magnetic performances of graphene-oxide and it's composites: A brief review

Dedicated to Professor Neil Trudinger on the occasion of his 80th birthday.

1.   Introduction

We consider the fourth-order total variation flow equation in $\mathbb{R}^n$ of the form

We aim to give explicit description of its solutions emanating from piecewise constant radial data. However, it turns out that the definition of a solution is itself non-trivial since $-\Delta$ does not have a bounded inverse on $L^2(\mathbb{R}^n)$. Our first goal is thus to provide a rigorous definition of a solution. Our second goal is to find explicit formula for the solution to (1.1) when the initial datum $u(0, x) = u_0(x)$ is the characteristic function of a ball or an annulus. In other words,

where $\mathbf{1}_K$ is the characteristic function of a set $K\subset\mathbb{R}^n$, i.e.,

Here $B_R$ denotes the open ball of radius $R$ centered at $0\in\mathbb{R}^n$ and $A^{R^1}_{R^0}$ denotes the annulus defined by $A^{R^1}_{R^0} = B_{R_1}\setminus\overline{B_{R_0}}$. Our major concern is whether or not the solution remains a characteristic function throughout the evolution. For example, in the case $u_0 = a_0\mathbf{1}_{B_{R_0}}$, whether or not the solution $u$ of (1.1) is of the form

with a function $a = a(t)$. In other words, we are asking whether the speed $u_t$ on the ball $B_{R(t)}$ and on its complement are constant in the spatial variable. As in the second-order problem ^[3] (see also ^[17]), this leads to the notion of calibrability of a set. In the case of the second-order problem $u_t = \operatorname{div}\left(\nabla u/|\nabla u|\right)$, a ball and its complement are always calibrable and $R(t)\equiv R_0$, i.e., the ball does not expand nor shrink ^[3]. In our problem, $R(t)$ may be non-constant.

We first note that the definition of a solution itself is non-trivial. The fourth-order total variation flow has been mainly studied in the periodic setting ^[12,14] or in a bounded domain with some boundary conditions ^[15]. Formally, it is a gradient flow of the total variation functional

with respect to the inner product

when $\Omega$ is a domain in $\mathbb{R}^n$ or a flat torus $\mathbb{T}^n$. In the periodic setting, i.e., $\Omega = \mathbb{T}^n$ as in ^[12,14], it is interpreted as a gradient flow in $H^{-1}_{av}$ which is the dual space of $H^1_{av}$, the space of average-free $H^1$ functions equipped with the inner product

For the homogeneous Dirichlet boundary condition with bounded $\Omega$, $H^{-1}_{av}$ is replaced by $D^{-1}$, the dual space of $D^1_0 = D^1_0(\Omega)$, which is the completion of $C^\infty_c(\Omega)$ in the norm associated with the inner product $(u, v)_1$; here $C^\infty_c(\Omega)$ denotes the space of all smooth functions compactly supported in $\Omega$. By the Poincaré inequality, both $H^1_{av}$ and $D^1_0(\Omega)$ can be regarded as subspaces of $L^2(\Omega)$. However, if $\Omega$ equals $\mathbb{R}^n$, the situation is more involved. If $n\geq3$, $D^1_0(\mathbb{R}^n)$ is continuously and densely embedded in $L^{2^*}(\mathbb{R}^n)$, where $p^* = np/(n-p)$ so that $2^* = 2n/(n-2)$, by the Sobolev inequality. In fact,

see e.g., ^[11]. On the other hand, if $n\leq2$, $D^1_0$ is isometrically identified with the quotient space $\dot{D}^1(\mathbb{R}^n): = D^1(\mathbb{R}^n)/\mathbb{R}$, when $D^1(\mathbb{R}^n)$ is equipped with inner product $(u, v)_1$ ^[11]. Thus, we need to be careful when $n\leq2$ because an element of $D^1_0(\mathbb{R}^n)$ is determined only up to a constant. In any case, $D^1_0(\mathbb{R}^n)$ is a Hilbert space with the scalar product

Therefore, we can identify $D^1_0(\mathbb{R}^n)$ with its dual space by means of the isometry

On the other hand, let us define a subspace $\widetilde{D}^{-1}(\mathbb{R}^n) \subset D^1_0(\mathbb{R}^n)'$ by

where

Then the closure $D^{-1}(\mathbb{R}^n)$ of $\widetilde{D}^{-1}(\mathbb{R}^n)$ coincides with $D^1_0(\mathbb{R}^n)'$ ^[11]. Note that the restriction to $C_{c, av}^\infty(\mathbb{R}^n)$ in the definition of $\widetilde{D}^{-1}(\mathbb{R}^n)$ in $n = 1, 2$ is necessary for the functionals to be well-posed on $D^1(\mathbb{R}^n)/\mathbb{R}$. In any case, since (by definition) the space of test functions $\mathcal D(\mathbb{R}^n)$ is continuously and densely embedded in $D_0^1(\mathbb{R}^n)$, we also have a continuous embedding $D^{-1}(\mathbb{R}^n) = D^1_0(\mathbb{R}^n)' \subset \mathcal D'(\mathbb{R}^n)$. Throughout the paper, we will often drop $(\mathbb{R}^n)$ in the notation for spaces of functions on $\mathbb{R}^n$, e.g., $D^{-1} = D^{-1}(\mathbb{R}^n)$.

In the first step, we give a rigorous definition of the total variation functional $TV$ on $D^{-1}$. Then we calculate the subdifferential of $TV$ in $D^{-1}$ space. Since it is a homogeneous functional, we are able to apply a duality method ^[3] to characterize the subdifferential, provided that $TV$ is well approximated by nice functions in $D^{-1}$. We know that $C^\infty_{c, av}(\mathbb{R}^n)$ is dense in $D^{-1}$ for $n\leq2$; see e.g., ^[11]. However, it is not immediately clear whether $TV$ is simultaneously approximable. Fortunately, it turns out that for any $w\in D^{-1}$, there is a sequence $w_k\in C^\infty_{c, av}(\mathbb{R}^n)$ which converges to $w$ in $D^{-1}$ and $TV(w_k)\to TV(w)$ as $k\to\infty$. This approximation part is relatively involved since we have to use an efficient cut-off function. Using the approximation, we are able to characterize the subdifferential $\partial_{D^{-1}}TV$ of $TV$ in $D^{-1}$ by adapting the argument in ^[3]. Namely, we have

where $\langle , \ \rangle$ denotes the canonical paring of $D^{-1}$ and $D^1_0$. A vector field $Z$ corresponding to an element of the subdifferential is often called a Cahn-Hoffman vector field. The equation (1.1) should be interpreted as the gradient flow of $TV$ in $D^{-1}$, i.e.,

and its unique solvability for any initial datum $u_0\in D^{-1}$ is guaranteed by the classical theory of maximal monotone operators (^[6,24]). By our characterization of the subdifferential, we are able to give a more explicit definition of a solution which is consistent with that proposed in ^[15]. Namely, for $u_0\in D^{-1}$ with $TV(u_0) < \infty$, a function $u\in C\left([0, T[, D^{-1}\right)$ is a solution to (1.2) with $u(0) = u_0$ if and only if there exists $Z\in L^\infty\left(]0, T[\times\mathbb{R}^n\right)$ satisfying $\operatorname{div}Z \in L^2 \left(0, T; D^1_0(\mathbb{R}^n)\right)$ such that

for a.e. $t\in]0, T[$. This is convenient for calculating explicit solutions.

Unfortunately, in $n\leq2$, for a compactly supported square integrable function $u_0$, we know that $u_0\in D^{-1}$ if and only if $u_0$ is average-free, i.e., $\int_{\mathbb{R}^n}u_0 = 0$ (see Lemma 17). Thus, the characteristic function of any bounded, measurable set of positive measure does not belong to $D^{-1}$. We have to extend a class of initial data $u_0$ such that $u_0 = \psi+w_0$ with $w_0\in D^{-1}$ while $\psi$ is a fixed compactly supported $L^2$ function. We consider a gradient flow $u_t\in-\partial_{D^{-1}}TV(u)$ in the affine space $\psi + D^{-1}$. Since $\partial_{D^{-1}}$ is a directional partial derivative in the direction of $D^{-1}$, it is more convenient to consider solutions to evolutionary variational inequality

for any $g \in \psi +D^{-1}$ ^[2]. In the case $\psi = 0$, it is easy to show that the evolutionary variational inequality is equivalent to (1.2). Indeed, by definition of the subdifferential, (1.2) is equivalent to

for any $g\in D^{-1}$. The left-hand side equals $(\mathrm{d}/\mathrm{d} t)\left(\|u-g\|^2/2\right)$. Thus, the equivalence follows if $\psi = 0$. From now on we assume that $\int_{\mathbb{R}^n}\psi \neq0$.

It is easy to check that there is at most one solution to the evolutionary variational inequality (1.6). The solution $u$ is constructed by solving

and setting $u = w+\psi$. Characterization of the (directional) subdifferential is more involved since $w\mapsto TV(w+\psi)$ is no more positively one-homogeneous. We identify the one dimensional space $\{c\psi|c\in\mathbb{R}\}$ with $\mathbb{R}$ and consider the Hilbert space $E^{-1}$ defined as the orthogonal sum $D^{-1}\oplus\mathbb{R}$. We calculate the subdifferential by the duality method since $TV$ is now positively one-homogeneous on $E^{-1}$. We then project this subdifferential onto $D^{-1}$ to get a characterization of a (directional) subdifferential $\partial_{D^{-1}}TV$. We end up with a characterization of solution to (1.2) similar to (1.3)–(1.5), with (1.5) adjusted in a suitable way. If we also denote $E_0^1 = D^1$ in $n \leq 2$, $E_0^1 = D_0^1$, $E^{-1} = D^{-1}$ in $n \geq3$ and

for $u \in E^{-1}$, $v \in E^1_0$, we end up with the following definition of solution.

Definition 1. Assume that $u_0 \in E^{-1}$. We say that $u\in C([0, \infty[, E^{-1})$ with $u_t\in L^2_{loc}(]0, \infty[, D^{-1})$ is a solution to (1.1) with initial datum $u_0$ if there exists $Z \in L^\infty(]0, \infty[\times \mathbb{R}^n)$ with $\operatorname{div} Z(t, \cdot) \in E_0^1$ for a.e. $t > 0$ such that

for a.e. $t > 0$.

and associated well-posedness result.

Theorem 2. Let $u_0 \in E^{-1}$. There exists a unique solution to (1.1) with initial datum $u_0$.

Our next problem is whether or not the speed of a characteristic function of a set is spatially constant inside and outside of the set. By the general theory (^[6,24]), the speed is determined by the minimal section (canonical restriction) $\partial^0_{D^{-1}}TV$ of $\partial_{D^{-1}}TV$. In other words, $\partial^0_{D^{-1}}TV(u) = v_0$ minimizes $\|v\|_{D^{-1}}$ for $v\in\partial_{D^{-1}}TV(u)$, i.e.,

To motivate the notion of calibrability, we consider a smooth function $u$ such that

where $U$ is a smooth open set. Outside $\overline{U}$, we assume that $\nabla u\neq0$. To fix the idea, we assume that $\partial U$ has negative signature (orientation) in the sense that $u < 0$ outside $\overline{U}$. By our specification of $u$, we see that

Since $\operatorname{div}Z$ is locally integrable, $Z\cdot\nu$ does not jump across $\partial U$, where $\nu$ is the exterior unit normal of $\partial U$. In this case,

Since $\nabla\operatorname{div}Z$ does not have a singular part, $\operatorname{div}Z$ does not jump across $\partial U$. In this case,

However, $v = \Delta\operatorname{div}Z$ may have a non-zero singular part concentrated on $\partial U$ even if $v = v_0$, i.e., $v$ is the minimizer. This phenomenon is observed in ^[12,20,21] in a one-dimensional periodic setting. Different from the second-order problem, this causes expansion or shrinking of the ball when the solution $u$ is of the form $u(t, x) = a(t)\mathbf{1}_{B_{R(t)}}(x)$. If $u > 0$ outside $U$, the minus in (1.11) and (1.12) should be replaced by the plus.

If $\partial^0_{D^{-1}}TV(u)$ is constant on $B_{R(t)}$ and $\left(\overline{B_{R(t)}}\right)^c$, this property is preserved under the evolution, which leads us to definition of calibrability. Note that the value of $\partial^0_{D^{-1}}TV(u)$ on $U$ is determined by $U$ and its signature does not depend on particular value of $u$. We say that $U$ (with negative signature) is calibrable if there exists $Z_0 \in L^\infty(U, \mathbb{R}^n)$ such that $\nabla \operatorname{div} Z_0 \in L^2(U, \mathbb{R}^n)$, $Z_0$ satisfies (1.11), (1.12), $|Z_0|\leq 1$ a.e. in $U$ and $\Delta\operatorname{div} Z_0$ is constant on $U$. We call any such $Z_0$ a calibration for $U$.

Recall that in the case of the second-order problem, we say that $U$ (with negative signature) is calibrable if there exists $\widetilde{Z}_0 \in L^\infty(U, \mathbb{R}^n)$ satisfying (1.11), $|\widetilde{Z}_0|\leq 1$ a.e. in $U$ and $-\operatorname{div}\widetilde{Z}_0$ is a constant function on $U$. This is formally equivalent to $-$calibrability in ^[3,4]. It can be shown that $\widetilde{Z}_0$ is a calibration for $U$ if and only if

and $-\operatorname{div}\widetilde{Z}_0$ is a constant function on $U$, which is the definition of calibrability in ^[17].

Going back to our fourth-order problem, if $Z_0$ is a calibration for $U$, then $w = \operatorname{div}Z_0$ must satisfy

with some constant $\lambda$. If $U$ is bounded, $\lambda$ is determined by (1.11) since

where $\mathcal{H}^{n-1}$ denotes the $n-1$ dimensional Hausdorff and $\mathcal{L}^n$ denotes the Lebesgue measure in $\mathbb{R}^n$. Using this fact, in Section 5 we prove that if $Z_0$ is a calibration for a bounded $U$, then

Moreover, we obtain an "explicit" formula for the constant $\lambda$ in terms of the Saint-Venant problem in $U$.

In the radially symmetric setting, it is not difficult to show that $Z_0$ in (1.16) can be chosen in the form $z\left(|x|\right)\frac{x}{|x|}$. Indeed, if $Z_0$ is belongs to the set of minimizers (1.16), then its rotational average $\overline{Z_0}$ belongs to (1.16) as well, because averaging preserves (1.11), (1.12) and the inequality $|Z|\leq1$. Since the angular part of $\overline{Z_0}$ does not contribute to the divergence, it is possible to delete this part (Lemma 31). We thus conclude that there is an element of (1.16) of form $Z(x) = z(|x|)\frac{x}{|x|}$. Thus, the Eq (1.13) can be written as the third-order ODE of the form

since $\operatorname{div}Z = r^{1-n}(r^{n-1}z)'$. If $U$ is $B_R$ with negative signature, condition (1.11) implies

Since $\operatorname{div}Z = z'+(n-1)z/r$, condition (1.12) implies that

Solving (1.17) under the assumption that $z$ is smooth near zero under conditions (1.18), (1.19), we eventually get a unique solution (1.17)–(1.19) of the form

for all $n\geq1$. It is easy to see that $Z(x) = z(|x|)\frac{x}{|x|}$ satisfies the constraint $|Z|\leq1$ in $B_R$. We conclude that all balls are calibrable. More careful argument is necessary, but we are able to discuss calibrability of an annulus as well as a complement of a ball.

Theorem 3. (i) All balls are calibrable for all $n\geq1$.

(ii) All complement of balls are calibrable except $n = 2$.

(iii) If $n = 2$, all complement of balls are not calibrable.

(iv) All annuli (with definite signature) are calibrable except in $n = 2$.

(v) For $n = 2$, there is $Q_* > 1$ such that an annulus (with definite signature) is calibrable if and only if the ratio of the exterior radius over the interior radius is smaller than or equal to $Q_*$. In other words, $A^{R_1}_{R_0}$ is calibrable if and only if $R_1/R_0\leq Q_*$.

Theorem 3(v) is consistent with (iii) since $R_1 \to\infty$ implies $A^{R_1}_{R_0}$ converges to $\overline{B_{R_0}}^c$, a complement of the closure of the ball $B_{R_0}$. Note that in the case of an annulus, there is a possibility we take a signature which is different on the exterior boundary $\partial B_{R_1}$ and the interior boundary $\partial B_{R_0}$. We also study such indefinite cases.

We now calculate an explicit solution of (1.1) starting from $u_0 = a_0\mathbf{1}_{B_{R_0}}$. We first discuss the case $n\neq2$. Since a ball and its complement is calibrable, the solution is of the form

We take the (radial) calibration $Z_{in}$ in $B_{R(t)}$ and $Z_{out}$ in $\mathbb{R}^n\backslash\overline{B_{R(t)}}$ and set

Here $Z_{out}(x) = z_{out}(|x|)\frac{x}{|x|}$ can be calculated as

while, as we already discussed, $z_{in}$ for $Z_{in}(x) = z_{in}(|x|)\frac{x}{|x|}$ is of the form

This $Z$ satisfies (1.9) and (1.10), and moreover $\operatorname{div}Z\in D^1_0$ for any $t > 0$. Moreover, $\operatorname{div}Z$ is continuous across $\partial B_{R(t)}$. However, $\nabla\operatorname{div}Z$ may jump across $\partial B_{R(t)}$. Actually,

where $\delta_\Gamma(\varphi) = \int_\Gamma\varphi\, d\mathcal{H}^{n-1}$ or $\delta_\Gamma = \mathcal{H}^{n-1}\, \, ∟\, \Gamma$ for a hypersurface $\Gamma$ and $\nu$ is the exterior unit normal of $\partial B_{R(t)}$, i.e., $\nu = x/R(t)$. Here $\lambda = -\frac{n(n+2)}{R^3}$. By a direct calculation, the quantity $\nu\cdot (\nabla\operatorname{div}Z_{in}-\nabla\operatorname{div}Z_{out}) = -\frac{n(n-4)}{R^2}$. Since $u_t = -\Delta\operatorname{div}Z$, by

we conclude that

Since

an explicit form of a solution is given as

As noticed earlier, in the case $n = 2$, the complement of the disk is not calibrable. If $u$ is a radially strictly decreasing function outside $B_R$, we expect $Z_{out}(x) = -x/|x|$ for $|x| > R(t)$. In ^[15], it is proposed that a solution $u$ to (1.1) must satisfy

Since $\operatorname{div}Z_{out} = -(n-1)/|x|^2$ and $\nabla\operatorname{div}Z_{out} = \frac{(n-1)x}{|x|^3}$, this implies

In the case $n = 2$, $\nabla\operatorname{div}Z_{out}\in L^2\left(\left(\overline{B_{R(t)}}\right)^c\right)$ so $Z_{out}$ is a Cahn-Hoffman vector field.

If we start with $u_0 = a_0\mathbf{1}_{B_{R_0}}$ with $a_0 > 0$ for $n = 2$, the expected form of a solution is

where

Analyzing this ODE system, we can deduce qualitative properties of the solution. Summing up our results yields.

Theorem 4. Let $u_0 = a_0\mathbf{1}_{B_{R_0}}$ with $a_0 > 0$.

If $n \geq 3$, then the solution $u$ to (1.1) with initial datum $u_0$ is of the form

and $u(t, x)\equiv0$ for $t\geq t_*$. (The time $t_*$ is called the extinction time.) Moreover, $a(t)$ is decreasing and $a(t)\to0$ as $t\uparrow t_*$.

(i) $R(t)$ is increasing and $R(t)\to\infty$ as $t\uparrow t_*$ for $n = 3$.

(ii) $R(t) = R_0$ for $n = 4$.

(iii) $R(t)$ is decreasing and $R(t)\to0$ as $t\uparrow t_*$ for $n\geq5$.

If $n = 2$, then the solution is not a characteristic function for $t > 0$. It is of the form (1.21) and moves by (1.23). In particular, there is no extinction time, $R(t)$ is increasing and $a(t)$ is decreasing. Moreover, $R(t)\to\infty$ and $a(t)\to0$ as $t\to\infty$. The gap $a(t)-\frac{t}{R(t)^3}$ is always positive.

If $n = 1$, then the solution is of the form $u(t, x) = a(t)\mathbf{1}_{B_R(t)}$ for $t > 0$. Moreover, $R(t)$ is increasing and $a(t)$ is decreasing with $R(t)\to\infty$ and $a(t)\to0$ as $t\to\infty$.

We note that the infinite extinction time observed in $n \leq 2$ is related to the fact that $0$ is not an element of the affine space $u_0+D^{-1}$ where the flow lives if $\int u_0 \neq 0$. In ^[14], finite time extinction for solution to (1.1) is proved in a periodic setting for average zero initial data when the space dimension $n\leq4$ Our result is unrelated to their result because we consider (1.1) in $\mathbb{R}^n$.

The formula (1.21) does not give a solution to (1.1) when $n\geq4$ since $\nabla\operatorname{div}Z_{out}$ does not belong to $L^2\left(\left(\overline{B_{R(t)}}\right)^c\right)$. In the case $n = 3$, this formula is consistent with our definition. If we consider $u_0$ strictly radially decreasing for $|x| > R_0$ and $u_0(x) = u_*$ for $|x|\leq R_0$, then $u_0$ does not belong to the domain of $\partial_{D^{-1}}TV$ for $n\geq4$. In other words, there is no Cahn-Hoffman vector field.

These results contrast with the second-order total variation flow

In the second-order problem, a ball and an annulus are always calibrable with their complements, see e.g., ^[3] or [17, Section 5]. Furthermore, $u_t(t, \cdot)$ is a locally integrable function without singular part for $t > 0$. Thus, for example, the solution starting from $u_0 = a_0\mathbf{1}_{B_{R_0}}$ ($a_0 > 0$) must be $u(t, x) = a(t)\mathbf{1}_{B_{R_0}}$ with $a(t) = -\lambda t+a_0$, where $\lambda$ is the Cheeger ratio, i.e., $\lambda = \mathcal{H}^{n-1}(\partial B_{R_0})/\mathcal{L}^n(B_{R_0})$. In particular, the extinction time $t_*$ equals $t_* = a_0/\lambda$.

We conclude this paper by deriving a system of ODEs prescribing the solution in the case when the initial datum is a piecewise constant, radially symmetric function, which we call a stack. To be precise, we say that $w \in E^{-1}$ is a stack if it is of the form

$0 < R^0 < R^1 < \ldots < R^{N-1}$, $a^k \in \mathbb{R}$. In particular, we obtain

Theorem 5. Let $n \neq2$ and let $u_0$ be a stack. If $u$ is the solution to (1.1), then $u(t, \cdot)$ is a stack for $t > 0$.

In the case $n = 2$, this result is no longer true, as evidenced by Theorem 4. However the solution can still be prescribed by a finite system of ODEs.

A total variation flow type equation

was introduced by ^[31] to describe the height of crystal surface moved by relaxation dynamics below the roughening temperature, where $\beta > 0$. For this equation, characterization of the subdifferential of the corresponding energy was given by Y. Kashima in periodic setting ^[20,21] and under Dirichlet condition on a bounded domain ^[21]. The speed of a facet (a flat part of the graph) is calculated for $n = 1$ in ^[20] and for a ball with the Dirichlet condition under radial symmetry ^[21]. Different from the second-order problem, the speed of a facet is determined not only by the shape of facet. Also it has been already observed in ^[20], that the minimal section may have a delta part although the behavior of the corresponding solution was not studied there. A numerical computation was given in ^[23]. The Eq (1.24) was derived as a continuum limit of models describing motion of steps on crystal surface as discussed in ^[27], where numerical simulation was given; see also ^[22].

In ^[7], a crystalline diffusion flow was proposed and calculated numerically. In a special case, it is of the form $w_t = -\partial^2_x\left(W'(w_x)\right)$, where $W$ is a piecewise linear convex function, when the curve is given as the graph of a function. This equation was analyzed in ^[13] in a class of piecewise linear (in space) solutions.

Fourth-order equations of type (1.1) were proposed for image denoising as an improvement over the second-order total variation flow. For example, the equation

where $f$ is an original image which is given and $\lambda > 0$, corresponds to the Osher-Solé-Vese model ^[28]. The well-posedness of this equation was proved by using the Galerkin method by ^[8].

For (1.1), an extinction time estimate was given in ^[14] for $n = 1, 2, 3, 4$ in the periodic setting. It was extended to the Dirichlet problem in a bounded domain by ^[15]. In the review paper ^[12], it was proved that the solution $u$ of (1.1) in $n = 1$ may become discontinuous instantaneously even if the initial datum is Lipschitz continuous, because the speed may have a delta part.

There are a few numerical studies for (1.1) in the periodic setting. A duality-based numerical scheme which applies the forward-backward splitting has been proposed in ^[16]. A split Bregman method was adjusted to (1.1) and also (1.24) in ^[18]. In these methods, the singularity of the equation at $\nabla u = 0$ is not regularized. However, all above studies deal with either periodic, Dirichlet or Neumann boundary condition for a bounded domain. It has never been rigorously studied in $\mathbb{R}^n$, although in ^[15] there are some preliminary calculations for radial solution in $\mathbb{R}^n$.

This paper is organized as follows. In Section 2, we discuss basic properties of the total variation on $D^{-1}$, notably we show strict density of $C^\infty_{c, av}$. In Section 3, we give a rigorous definition of a solution to (1.1) and obtain a verifiable characterization of solutions. In Section 4, we extend the results of the previous section to include initial data with non-zero average in $n = 1, 2$. In Section 5, we introduce the notion of calibrability. In Section 6, we discuss calibrability of rotationally symmetric sets in $\mathbb{R}^n$. In Section 7, we study solutions emanating from piecewise constant, radially symmetric data.

2.   The total variation functional on $D^{-1}$

In this section, we give a rigorous definition of the total variation $TV$ on $D^{-1}$ and relate it to the usual total variation defined on $L^1_{loc}$. The main tool that we use here as well as in the following section is an approximation lemma, which for a given $w \in D^{-1}$ produces a sequence of nice functions $w_k \in D^{-1}$ that converges to $w$ in $D^{-1}$ and $TV(w_k) \to TV(w)$.

Let us denote

We define $TV \colon D^{-1}(\mathbb{R}^n) \to [0, \infty]$ by

Let us compare this definition with the usual total variation, which we denote here by $\overline{TV}\colon L^1_{loc}(\mathbb{R}^n) \to [0, \infty]$, defined by

First of all, as in the case $\overline{TV}$, we easily check that $TV$ is lower semicontinuous with respect to the weak-* (and, a fortiori, strong) convergence in $D^{-1}(\mathbb{R}^n)$. Indeed, if $v_k \overset{*}{\mathop{\rightharpoonup }} v$ in $D^{-1}(\mathbb{R}^n)$,

In fact, we have

Lemma 6. We have $D(TV) \subset L^1_{loc}$, and so $D(TV) \subset D(\overline{TV})$ with $TV$ and $\overline{TV}$ coinciding on $D(TV)$. In particular, if $n \geq 2$, $D(TV) \subset L^{1^*}(\mathbb{R}^n)$. If $n = 1$,

The proof of this fact is a consequence of the lemma below and we postpone it.

Lemma 7. For any $w \in D^{-1}(\mathbb{R}^n)$ there exists a sequence $w_k \in C^\infty_{c, av}(\mathbb{R}^n)$ such that

and

To prove it, we will use a special choice of cut-off function and associated variant of the Sobolev-Poincaré inequality. For $R > 0$, let us denote by $\vartheta_R$ the element of minimal norm in $D^1_0(\mathbb{R}^n)$ among those $w \in D^1_0(\mathbb{R}^n)$ that satisfy $w(x) = 1$ if $|x|\leq \frac{R}{2}$, $w(x) = 0$ if $|x| \geq R$. It is an easy exercise to show that for $\frac{R}{2} \leq |x| \leq R$

In either case,

Lemma 8. If $p \in [1, n[$ and $q \in [1, p^*]$, then for all $w \in C^1(\mathbb{R}^n)$, $R > 0$ there holds

with $C = C(n, p)$ and

with a different $C = C(n, p)$.

Proof. Let $v \in C^1(\mathbb{R}^n)$. Following the proof of the standard Poincaré inequality by contradiction using Rellich-Kondrachov theorem, we obtain

Applying the Sobolev inequality in $B_1$ to the function $v - \frac{\int \vartheta_1 v}{\int \vartheta_1}$, we upgrade this to

Next, let $v(x) = w(Rx)$ for a given $w \in C^1(\mathbb{R}^n)$. We observe that

and so, by a change of variables $x = y/R$,

Applying the same change of variables to both sides of (2.4) we conclude the proof of (2.2).

The proof of (2.3) is a matter of direct calculation. □

Let us now return to the proof of the approximation lemma.

Proof of Lemma 7. Given $w \in D^{-1}$, let

Equivalently, for $\varphi \in D_0^1(\mathbb{R}^n)$,

Denoting $\widetilde{w} = (-\Delta)^{-1} w$,

We estimate the second term on the r. h. s. using the Poincaré inequality from Lemma 8, taking into account that the support of the integrand is contained in $\overline{A}_R$, where $A_R = B_R \setminus \overline{B}_{R/2}$,

Thus,

and so

Next we estimate $TV(w_{\varepsilon, R})$. Due to lower semicontinuity of $TV$, we can assume without loss of generality that $TV(w) < \infty$. First, we note that $\varrho_\varepsilon * w \in D^{-1}(\mathbb{R}^n) \cap C^\infty(\mathbb{R}^n)$ (^[29,30]) and

Thus, for any $\psi \in L^\infty(\mathbb{R}^n, \mathbb{R}^n)$,

In particular, this implies that $\nabla \varrho_\varepsilon * w \in L^1(\mathbb{R}^n)$ for $\varepsilon > 0$ and $\int |\nabla \varrho_\varepsilon * w| = TV(\varrho_\varepsilon * w) \leq TV(w)$. By Lemma 8,

If $n\geq 3$, together with lower semicontinuity of $TV$, this yields

Taking into account (2.5), by a diagonal procedure we can select sequences $(\varepsilon_k)$, $(R_k)$ such that $w_k : = w_{\varepsilon_k, R_k}$ satisfies both requirements in the assertion. On the other hand, if $n = 1$ or $n = 2$, (2.6) only implies uniform boundedness of $TV(\nabla w_{\varepsilon, R})$.

Let now $n = 2$. Since $w_{\varepsilon, R}$ have compact support, uniform boundedness of $TV(\nabla w_{\varepsilon, R})$ implies uniform bound on $w_{\varepsilon, R}$ in $L^2(\mathbb{R}^n)$ by the Sobolev inequality. As $w_{\varepsilon, R}$ converges to $\varrho_\varepsilon * w$ in $D^{-1}(\mathbb{R}^n)$, we have $\varrho_\varepsilon * w \in L^2(\mathbb{R}^n)$. This allows us to improve (2.6):

The r. h. s. of (2.7) converges to $TV(w)$ as $R\to \infty$ and we conclude as before.

Next, consider $n = 1$. In this case, finiteness of $TV(w)$ implies that $\varrho_\varepsilon * w \in L^\infty(\mathbb{R}^n)$ and there exist $g_\varepsilon^\pm \in \mathbb{R}$ such that

Now, let $\eta^\pm_R$ be the element of minimal norm in $D_0^1(\mathbb{R})$ under constraints

(Clearly, $\eta^\pm_R$ is a continuous, piecewise affine function.) We have

On the other hand, since $\eta^\pm_R$ are compactly supported and $\varrho_\varepsilon * w$ coincides as distribution with a locally integrable function, we can calculate

so $g^\pm_\varepsilon = 0$. Therefore, we can estimate

Since we have shown that $\varrho_\varepsilon * w(x) \to 0$ as $x \to \pm \infty$, the averages on the r. h. s. converge to $0$ and we conclude as before.

□

As a first application of the approximation lemma, we demonstrate Lemma 6 announced before.

Proof of Lemma 6. Let $w \in D(TV)$ and let $(w_k) \subset C_{c, av}^\infty(\mathbb{R}^n)$ be the sequence provided by Lemma 7. Let first $n > 1$. Since $\nabla w_k$ is uniformly bounded in $L^1(\mathbb{R}^n, \mathbb{R}^n)$, by the Sobolev embedding $w_k$ is uniformly bounded in $L^{1^*}(\mathbb{R}^n)$. Therefore, $w \in L^{1^*}(\mathbb{R}^n)$.

In case $n = 1$, since $\nabla w_k$ are compactly supported and uniformly bounded in $L^1(\mathbb{R})$, $w_k$ is uniformly bounded in $L^\infty(\mathbb{R})$. From these two bounds it follows that $w \in L^\infty(\mathbb{R})$ and that $\nabla w$ is a finite signed measure on $\mathbb{R}$. In particular, $w$ has essential limits at $\pm \infty$. Reasoning as in the final part of the proof of Lemma 7, we show that these limits vanish. □

3.   Existence and characterization of the flow on $D^{-1}$

For a gradient flow of a convex functional, there is a general theory initiated by Y. K$\overline{\rm o}$mura ^[24] and developed by H. Brézis ^[6] and others. It is summarized as follows.

Proposition 9 (^[6]). Let $H$ be a real Hilbert space. Let $\mathcal{E}$ be a lower semicontinuous, convex functional on $H$ with values in $]\!-\!\infty, \infty]$. Assume that $D(\mathcal{E})$ is dense in $H$. Then, for any $u_0\in H$, there exists a unique solution $u\in C\left([0, \infty[\, , H\right)$ which is absolutely continuous in $(\delta, T)$ (for any $\delta < T < \infty$) satisfying

Moreover,

If $\mathcal{E}(u_0) < \infty$, then $s = 0$ is allowed. In particular, $u_t\in L^2(0, \infty; H)$.

As in ^[2], this solution satisfies the evolutionary variational inequality

for any $f\in H$. Indeed, by definition, $u_t\in-\partial\mathcal{E}(u)$ is equivalent to saying

for any $f\in H$. The evolutionary variational inequality is not only an equivalent formulation of the gradient flow $u_t\in-\partial\mathcal{E}(u)$, but also apply to a gradient flow of a metric space by replacing $\|u-f\|_H$ by distance between $u$ and $f$; see ^[2] for the theory.

To be able to actually find solutions to (3.1), we need to characterize the subdifferential of the total variation in the space $D^{-1} = D^{-1}(\mathbb{R}^n)$. The basic idea of the proof is a duality argument, which has been carried out in the case of $L^2$ subdifferentials. In the case of $L^2$ setting, the idea goes back to the unpublished note of F. Alter and a detailed proof is given in ^[3]. Let $\mathcal{E}$ be a functional on a real Hilbert space $H$ equipped with an inner product $(\cdot, \cdot)_H$. The main idea is to characterize the subdifferential $\partial\mathcal{E}$ by the polar $\mathcal{E}^0$ of $\mathcal{E}:H\to[-\infty, \infty]$ which is defined by

where $D(\mathcal{E}) = \left\{u\in H \bigm| |\mathcal{E}(u)| < \infty\right\}$. We first recall a lemma [3, Lemma 1.7].

Lemma 10. Let $\mathcal{E}$ be convex. Assume that $\mathcal{E}$ is positively one-homogeneous, i.e.,

for all $\lambda > 0$, $u\in H$. Then, $v\in\partial\mathcal{E}(u)$ if and only if $\mathcal{E}^0(v)\leq 1$ and $(u, v)_H = \mathcal{E}(u)$.

Remark 11. By general theory of convex functionals, we know that

if $\mathcal{E}$ is a non-negative, lower semicontinuous, convex, positively one-homogeneous functional [3, Proposition 1.6].

This property is essential for the proof of

Theorem 12. Let $\Psi\colon D^{-1} \to [0, \infty]$ by defined by

Then $(TV)^0 = \Psi$.

Remark 13. (i) By definition, $\Psi$ is a convex, lower semi-continuous, positively one-homogeneous function, so $(\Psi^0)^0 = \Psi$.

(ii) if $\Psi(v) < \infty$, the infimum is attained. Theorem 12 together with Lemma 10 implies the following characterization of the subdifferential of $TV$.

Theorem 14. An element $v\in D^{-1}$ belongs to $\partial TV(u)$ if and only if there is $Z\in L^\infty(\mathbf{R}^n)$ with $\operatorname{div}Z\in D^1_0$ such that

(i) $|Z| \leq 1$

(ii) $v = \Delta \operatorname{div}Z$

(iii) $-\langle u, \operatorname{div}Z \rangle = TV(u)$.

Proof. By Lemma 10 and Theorem 12,

The property $\Psi(v)\leq1$ together with Remark 13(ii) implies (i), (ii) and $\operatorname{div}Z\in D^1_0$.

It is not difficult to check the converse. □

Proof of Theorem 12. The inequality $TV^0\leq\Psi$:

We take $v\in D^{-1}$ with $\Psi(v) < \infty$. By Remark 13(ii), there is $Z\in L^\infty(\mathbb{R}^n)$ with $v = \Delta\operatorname{div}Z$ with $\operatorname{div}Z\in D^1_0$ such that $\Psi(v) = \|Z\|_\infty$. By Lemma 7, there is $u_k\in C^\infty_{c, av}$ such that $TV(u_k)\to TV(u)$, $u_k\to u$ in $D^{-1}$. We observe that

Sending $k\to\infty$, we conclude that

By definition of $\Psi$, this implies $TV^0\leq\Psi$.

The inequality $\Psi\leq TV^0$:

By definition,

Since

we observe that

This implies that $TV^0\geq(\Psi^0)^0 = \Psi$. □

Now that the subdifferential of $TV$ in $D^{-1}$ is calculated, we are able to justify an explicit definition of a solution proposed in ^[15].

Theorem 15. Assume that $u\in C\left([0, \infty[\, , D^{-1}\right)$. Then $u$ is a solution of $u_t\in-\partial_{D^{-1}}TV(u)$ with $u_0 = u(0)$ in the sense of Proposition 9 if and only if there exists $Z\in L^\infty\bigl(]0, \infty[\times\mathbb{R}^n\bigr)$ satisfying

such that for a.e. $t\in]0, \infty[$ there holds

and

(If $TV(u_0) < \infty$, $\delta = 0$ is allowed.)

The Theorem essentially follows from Theorem 14. We only need to justify that a Cahn-Hoffman vector field $Z$ defined separately for every time instance by Theorem 14 can be chosen to be jointly measurable, i.e., $Z\in L^\infty\bigl(]0, \infty[\times\mathbb{R}^n\bigr)$. As in the second-order case [3, section 2.4], this can be done by recalling that Bochner functions can be well approximated by piecewise constant functions. Since our situation is slightly different, let us include the argument for completeness. We begin with a lemma which is a version of [3, Lemma A.8] suited to our needs.

Lemma 16. Let $v \in L^1_{loc}(]0, \infty[, X)$, where $X$ is a Banach space and let $N \subset]0, \infty[$ have Lebesgue measure $0$. Then for each $\varepsilon > 0$ there exists a countable family $\mathcal{G}$ of disjoint closed intervals $I_k = \overline{B(t_k, r_k)}$, $k \in \mathbb{N}$, such that $t_k$ is a Lebesgue point for $v$, $t_k \not \in N$,

and

Proof. Referring e.g., to [6, p. 140], $\mathcal{L}^1$-a.e. point $t\in]0, \infty[$ is a Lebesgue point for $v$, i.e.,

Let $A$ be the set of Lebesgue points of $v$ contained in $]0, \infty[\setminus N$ and let us take

Using Besicovitch covering theorem [9, Corollary 1 on p. 35] with $U = ]0, \infty[$ and (for example) $\mathrm{d}\mu(t) = e^{-t}\, \mathrm{d}t$, we obtain a candidate for the family $\mathcal{G}$. We check that indeed

□

Proof of Theorem 15. Applying Lemma 16 to $u_t$, for each $\varepsilon > 0$ we obtain a partition of $]0, \infty[$ (up to a set of Lebesgue measure $0$) into disjoint closed intervals $I_k = \overline{B(t_k, r_k)}$, $k \in \mathbb{N}$ such that

and

By (3.2) and Theorem 14, for $k \in \mathbb{Z}$ there exist $Z_k \in L^\infty(\mathbb{R}^n)$ such that

Further denoting

we have

We immediately deduce that there exists $Z \in L^\infty([0, \infty[\times \mathbb{R}^n)$ with $|Z|\leq 1$ a.e. and a subsequence $Z^{\varepsilon_j}$ such that $Z^{\varepsilon_j}$ converges to $Z$ weakly-* in $Z \in L^\infty([0, \infty[\times \mathbb{R}^n)$. Moreover, for any $\varphi \in C^\infty_c([0, \infty[\times \mathbb{R}^n)$,

at least along a subsequence. Since on the other hand

we infer that $u_t = - \Delta \operatorname{div} Z$ and in particular $\operatorname{div} Z^{\varepsilon_j} \to \operatorname{div} Z$ in $L^1_{loc}(]0, \infty[, D^1_0)$. Finally, we observe that $u^\varepsilon \to u$ in $L^\infty_{loc}(]0, \infty[, D^{-1})$. Moreover, since $t \to TV(u(t))$ is non-increasing, we have $TV(u^\varepsilon) \to TV(u)$ in $L^1_{loc}(]0, \infty[)$. Therefore, for any $\varphi \in C_c(]0, \infty[)$,

□

4.   Extension to $E^{-1}$

Unfortunately, in the case $n\leq2$, the characteristic function $\mathbf{1}_A$ of a set $A$ of positive measure is not in $D^{-1}$ since $\int \mathbf{1}_A \neq0$. We shall define a new space containing $\mathbf{1}_A$ as follows. We take a function $\psi\in L^2(\mathbb{R}^n)$ with compact support such that $\int_{\mathbb{R}^n}\psi = 1$. We introduce a vector space

This space is independent of the choice of $\psi$. Indeed, let $\psi_i \in L^2(\mathbb{R}^n)$ be compactly supported and $\int \psi_i = 1$ ($i = 1, 2$). An element $w+c\psi_1\in E^{-1}_{\psi_1}$ can be rewritten as

The next lemma implies $q = c(\psi_1-\psi_2)\in D^{-1}(\mathbb{R}^n)$ since $\int q = 0$. We then conclude that $w+c\psi_1\in E^{-1}_{\psi_2}$.

Lemma 17. Assume that $n\leq2$. A compactly supported function $q\in L^2(\mathbb{R}^n)$ belongs to $D^{-1}(\mathbb{R}^n)$ if and only if $\int_{\mathbb{R}^n}q = 0$.

Proof. If $q\in D^{-1} \cap L^1$, then

where $[1]$ stands for the element of $D_0^1$ whose representatives are $1$ as well as $0$.

Now suppose that a compactly supported function $q\in L^2(\mathbb{R}^n)$ satisfies $\int_{\mathbb{R}^n}q = 0$. Given a $[\varphi] \in D_0^1$, by the Poincaré inequality, we have for any $R > 0$, independently of the representative $\varphi \in D^1$,

In particular, $\varphi \in L^2_{loc}$. Taking into account this and the assumption $\int q = 0$, we see that the linear functional

on $D_0^1$ is well defined. Moreover, if $R > 0$ is large enough that $\mathrm{supp}\, q \subset B_R$,

Thus, the functional defined by (4.1) is bounded, i.e., $q \in D^{-1}$.

□

Since $E^{-1}_\psi$ is independent of the choice of $\psi$, we suppress $\psi$ and denote this space by $E^{-1}$. In case $n \geq 3$, we will use notation $E^{-1} = D^{-1}$. We also denote $E^1_0 = D^1$ if $n \leq 2$, $E^1_0 = D^1_0$ if $n\geq 3$. For $u \in E^{-1}$, $v \in E^1_0$, we denote

where $u = w + c \psi$, $w \in D^{-1}$, $\psi \in L^2_c$, $\int \psi = 1$. As before, we check that the value of $\langle u, v \rangle_E$ does not depend on the choice of this decomposition.

We recall that if $n \geq 3$, $E_0^1 = D_0^1$ and $E^{-1} = D^{-1}$ come with a Hilbert space structure. We also define inner products on $E_0^1$, $E^{-1}$ in case $n \leq 2$ by

for $u_i = w_i+c_i\psi$, $w_i\in D^{-1}$, $c_i\in\mathbb{R}$ ($i = 1, 2$). This gives an orthogonal decomposition

We note that although the values of those products may depend on the choice of $\psi$, the topologies they induce on $E^1_0$, $E^{-1}$ do not. Formula (4.2) associates to any $u \in E^{-1}$ a continuous linear functional on $E^1_0$. The resulting mapping is an isometric isomorphism between $E^{-1}$ and the continuous dual to $E^1_0$.

We extend $TV$ onto $E^{-1}$ by defining

As usual, we check that $TV$ is a convex, weakly-* (and strongly) lower semicontinuous functional. In particular, for a fixed $g\in E^{-1}$, the functional $w\mapsto TV(w+g)$ is convex and lower semicontinuous on $D^{-1}$. We next give a definition of a solution of $u_t\in-\partial TV(u)$ in the space $E^{-1}$. It turns out the idea of evolutionary variational inequality is very convenient since it is a flow in an affine space $g+D^{-1}$ for some $g\in E^{-1}$.

Definition 18. Assume that $u_0 \in E^{-1}$. We say that $u:[0, \infty[\, \to E^{-1}$ is a solution to

in the sense of EVI (evolutionary variational inequality) with initial datum $u_0$ if

(i) $u-g$ is absolutely continuous on $[\delta, T]$ (for any $0 < \delta < T < \infty$) with values in $D^{-1}$ and continuous up to zero with $u(0) = u_0$ and

(ii) $u-g$ satisfies the evolutionary variational inequality, i.e.,

holds for a.e. $t > 0$, provided that $g\in E^{-1}$ is such that $u_0-g\in D^{-1}$.

Theorem 19. For any $u_0\in E^{-1}$, there exists a unique solution $u$ of (4.3) in the sense of EVI. Moreover, if $u^i$ is the solution to (4.3) in the sense of EVI with $u^i(0) = u^i_0 \in E^{-1}$ for $i = 1, 2$, then

provided that $u^1_0 - u^2_0 \in D^{-1}$.

Proof. Uniqueness follows from contractivity (4.4), which is established by a standard reasoning ^[2]. We give a short proof for the reader's convenience and for completeness. Let $u^i$ ($i = 1, 2$) be a solution to (4.3) in the sense of EVI with initial datum $u^i_0$ such that $u^1_0 - u^2_0\in D^{-1}$. Since $u^i$ are solutions, we also have $u^i(t)-u^i_0\in D^{-1}$ for $t\geq0$ and so $u^1_0 - u^2(t)\in D^{-1}$, $u^2_0 - u^1(t)\in D^{-1}$. Thus, EVI yields

for a.e. $t > 0$. We conclude that $\left\| u^1(t)-u^2(t) \right\|^2$ is non-increasing, in particular (4.4) holds.

The existence is a bit more involved. For $u_0 = w_0+g_0\in E^{-1}$ with $w_0\in D^{-1}$, we consider the gradient flow of the form

Applying Proposition 9, there is a unique solution $w$ to (4.5) for $w_0\in D^{-1}$. This solution satisfies the evolutionary variational inequality

for any $f\in D^{-1}$. Setting $u = w+g_0$, $g = f+g_0$, we end up with

Since $g$ can be taken arbitrary such that $u_0-g\in D^{-1}$, this shows that $u$ is the solution of (4.3) in the sense of EVI; condition (i) follows easily from Proposition 9. □

It is non-trivial to characterize the subdifferential $\partial_{D^{-1}}TV$. For this purpose, we introduce a mapping $I$ which plays a role analogous to $-\Delta$ in $n \geq 3$.

Lemma 20. Let $n \leq 2$. The mapping $I\colon E^1_0 \to E^{-1}$ defined by

is an isometric isomorphism.

Proof. It is clear that $I(f)\in E^{-1}$ and $I$ is linear. For given $u = w+c\psi\in E^{-1}$ with $w\in D^{-1}$, $c\in\mathbb{R}$, there is $\overline{f}\in D^1_0$ such that $(-\Delta)\overline{f} = w$. Since a representative $f$ of $\overline{f}$ is determined up to an additive constant, there is a unique representative $f$ such that

Thus, the mapping $I$ is surjective. If $I(f) = 0$, then $(-\Delta) [f] = 0$ so $[f] = 0$. Thus $f$ is a constant. Since $\int f\, \psi = 0$, this constant must be zero, so $f = 0$. Thus, $I$ is injective. Recalling our definitions of inner products on $E^1_0$, $E^{-1}$, it is easy to check that $I$ is an isometry. □

We have a characterization of the polar of $TV$ in $E^{-1}$ as in Theorem 12.

Theorem 21. Let $n \leq 2$. Let $\Psi$ be given by

for $v\in E^{-1}$. Then $(TV)^0 = \Psi$.

Admitting this fact, we are able to give a characterization of the subdifferential.

Theorem 22. Let $n \leq2$. An element $v \in E^{-1}$ belongs to $\partial_{E^{-1}}TV(u)$ if and only if there is $Z\in L^\infty(\mathbb{R}^n)$ with $\operatorname{div}Z\in E_0^1$ such that

(i) $|Z| \leq 1$

(ii) $v = I(-\operatorname{div}Z)$

(iii) $-\langle u, \operatorname{div}Z \rangle_E = TV(u).$

Proof of Theorem 22. The proof parallels that of Theorem 14. By Lemma 10 and Theorem 21

The properties (i), (ii) together with $\operatorname{div}Z\in E^1_0$ are equivalent to $\Psi(v)\leq1$. Since

the Euler equation $(u, v)_{E^{-1}} = TV(u)$ is equivalent to (iii). □

Proof of Theorem 21. The proof parallels that of Theorem 12. We first prove that

for $v = I(-\operatorname{div}Z)$. This implies $TV^0\leq\Psi$. The estimate $(u, v)_{E^{-1}}\leq \|Z\|_\infty$ formally follows from the identity (4.6). Indeed, by (4.6), we see

If $u$ is in $C^\infty_c({\mathbb{R}^n})$, then, by this formula, we obtain

By approximation, as in the proof of Theorem 12, we conclude the desired estimate.

The other inequality $\Psi\leq TV^0$ follows from $TV\leq\Psi^0$. The proof of $TV\leq\Psi^0$ is parallel to that of Theorem 12 by replacing $\Delta\operatorname{div}Z$ by $I(-\operatorname{div}Z)$ and the $D^{-1}$ inner product by the $E^{-1}$ inner product, respectively, if one notes the identity (4.6). Since $I$ is an isometry, $\Psi$ is lower semicontinuous, and we conclude that $\Psi = TV^0$ by Remark 11.

□

We have to be careful, since the $E^{-1}$ gradient flow

does not correspond to the total variation flow $u_t = (-\Delta)\operatorname{div}\left(\nabla u/|\nabla u|\right)$. By Theorem 22(iii), $Z = \nabla u/|\nabla u|$ if $\nabla u\neq0$. Thus the $E^{-1}$ gradient flow is formally of the form

To recover the original total variation flow, we consider "partial" subdifferential in the direction of $D^{-1}$. Let $P$ be the orthogonal projection from $E^{-1}$ to $D^{-1}$. Then, by definition,

The equation

is now formally of the form

since $c\psi$ is time-independent. Here is a precise statement.

Theorem 23. Let $n \leq 2$. Consider the functional $\mathcal{F}:w\mapsto TV(w+c\psi)$ on $D^{-1}$ for a fixed $c\in\mathbb{R}$ and $\psi$. Then, $\partial_{D^{-1}}\mathcal{F}(w) = P\partial_{E^{-1}}TV(u)$ for $u = w+c\psi$. In particular, an element $v\in D^{-1}$ belongs to $\partial_{D^{-1}}\mathcal{F}(w)$ if and only if there is $Z\in L^\infty(\mathbb{R}^n)$ with $\operatorname{div}Z\in E^1_0$ such that

(i) $|Z| \leq 1$,

(ii) $v = \Delta\operatorname{div}Z$,

(iii) $- \langle u, \operatorname{div}Z \rangle_E = TV(u)$.

(In case $n\leq 2$, by $\Delta\operatorname{div}Z$ we understand $\Delta[\operatorname{div}Z]$.) This characterization is important to calculate the solution of $u_t = (-\Delta)\operatorname{div}\left(\nabla u/|\nabla u|\right)$ for $n\leq2$ explicitly. In fact, we can recover the characterization of a solution in the sense of EVI analogous to the one in Theorem 15, amounting to Theorem 2.

Proof of Theorem 2. This is almost immediate. However, like in the case of Theorem 15, we need to justify that the vector field $Z$ can be chosen to be jointly measurable with respect to $(t, x)$. We proceed as in the proof of Theorem 15. The difference is, now we need to pass to the limit with

but convergence of $v^\varepsilon$ in $L^1_{loc}(]0, \infty[, D^{-1})$ gives only $[\operatorname{div} Z^\varepsilon] \to [\operatorname{div} Z] \in L^1_{loc}(]0, \infty[, D^1_0)$. To deal with this problem, let us choose $\psi \in C^1_c(\mathbb{R}^n)$ and let $c \in \mathbb{R}$ be such that $u(t) - c \psi \in D^{-1}$ for $t > 0$. Then we also have $u^\varepsilon(t) - c \psi \in D^{-1}$ for $t > 0$, $\varepsilon > 0$ and

Testing with $\varphi \in C_c(]0, \infty[)$ and using weak-* convergence of $Z^\varepsilon$ in $L^\infty(]0, \infty[\times \mathbb{R}^n)$ we get

at which point we conclude as in the proof of Theorem 15. □

5.   The notion of calibrability

We are interested in sets where the speed of solution $u_t$ is spatially constant. The speed is given as minus the minimal section of the subdifferential, i.e.,

Since $\partial_{D^{-1}} TV(u)$ is closed and convex, $\partial^0_{D^{-1}} TV(u)$ is uniquely determined if $\partial_{D^{-1}} TV(u)\neq\emptyset$. Since we have characterized the subdifferential, we end up with

Although the minimizer $v$ is unique, the corresponding $Z$ may not be unique. Let $U$ be a smooth open set in $\mathbb{R}^n$. We consider a smooth function $u$ such that

and $\partial_{D^{-1}} TV(u)\neq\emptyset$. Such a closed set is often called a facet. Assume further that $\nabla u\neq0$ outside $\overline{U}$. Let $Z$ be a vector field satisfying $v = \Delta\operatorname{div}Z$ for $v\in\partial TV(u)$. It is easy to see that outside the facet $\overline{U}$,

by $- \langle u, \operatorname{div}Z \rangle_E = TV(u)$. Since $\|v\|_{D^{-1}} = \|\operatorname{div}Z\|_{D^1_0}$, we see that

Since $\operatorname{div}Z$ is locally integrable, the normal trace is well-defined from inside as an element of $L^\infty(\partial U)$ ^[3] and it must agree with that from outside, i.e.,

where $\nu(x)$ is the exterior unit normal of $\partial U$ and

Since $\operatorname{div}Z$ is in $E^1_0$, its trace from inside and outside must agree, i.e.,

Note that $\kappa(x)$ is the sum of all principal curvatures, equal to $n-1$ times the (inward) mean curvature, of $\partial U$ at $x$.

Let $Z_0$ be a minimizer corresponding to $v = \partial^0_{D^{-1}} TV(u)$. Since the value $Z_0$ outside $\overline{U}$ is always the same, we consider its restriction on $U$ and still denote by $Z_0$. Then, $Z_0$ is a minimizer of

Although $\operatorname{div}Z_0 \in D^1_0(\mathbb{R}^n)$ so that $\nabla\operatorname{div}Z_0 \in L^2(\mathbb{R}^n, \mathbb{R}^n)$, the quantity $\nabla\operatorname{div}Z_0$ may jump across $\partial U$. Thus $\Delta\operatorname{div}Z_0$ may contain singular part which is a driving force to move the facet boundary "horizontally" during its evolution under the fourth-order total variation equation as observed in the previous section and earlier in ^[12]. In the second-order problem, the speed does not contain any singular part so the jump discontinuity does not move.

We are interested in a situation where $\Delta\operatorname{div}Z_0$ is constant over $U$. In the spirit of ^[25], we call any continuous function $\chi \colon \partial U \to \{-1, 1\}$ a signature for $U$.

Definition 24. Let $U$ be a smooth open set in $\mathbb{R}^n$ with signature $\chi$. We say that $U$ is ($D^{-1}$-)calibrable (with signature $\chi$) if there exists $Z_0$ satisfying the constraint

with boundary conditions

with the property that

We call any such $Z_0$ a ($D^{-1}$-)calibration for $U$ (with signature $\chi$).

From the definition of calibration, we easily deduce

Proposition 25. Let $U$ be a smooth bounded domain in $\mathbb{R}^n$. Assume that $Z_0$ is a calibration for $U$ with signature $\chi$. Then, $w_0 = \operatorname{div}Z_0$ is a solution to the Saint-Venant problem

with the constraint

where $\lambda$ is some constant.

Appealing to this relation between calibrability and the Saint-Venant problem, we can prove the following

Theorem 26. Let $U$ be a smooth bounded domain in $\mathbb{R}^n$. Suppose that $Z^*$ is a calibration for $U$ with signature $\chi$. Then $Z^*$ is a minimizer of (5.2).

Proof. We first note that $w_* = \operatorname{div}Z_*$ must satisfy (5.8). We consider the minimization problem for

under the Dirichlet condition (5.7) and the constraint (5.8). Since the problem is strictly convex, there is a unique minimizer $\overline{w}$ in $D^1_0(U)$. By Lagrange's multiplier method, $\overline{w}$ must satisfy (5.6) because of the constraint (5.8). (Actually, a weak solution $\overline{w}$ of (5.6) is a smooth solution of (5.6), (5.7) by the standard regularity theory of linear elliptic partial differential equations [19, Chapter 6].) As we see in Lemma 27 below, the constant $\lambda$ is uniquely determined by (5.6) and (5.8). For $\overline{w}$, there always exists $Z\in C^\infty(\overline{U})$ such that

Indeed, let $p$ be a solution of the Neumann problem

Such a solution $p$ always exists since $\overline{w}$ satisfies the compatibility condition (5.8) and it is smooth up to $\overline{U}$; see e.g., ^[11,19]. If we set $Z = \nabla p$, then $Z$ satisfies the desired property (5.9). Thus, the minimum $e(\overline{w})$ of the Dirichlet energy under the constraint (5.8) agrees with

Since $w_* = \overline{w}$ and $|Z_*|\leq1$, this shows that $Z_*$ is a minimizer of (5.2). □

Lemma 27. Let $U$ be a smooth bounded domain in $\mathbb{R}^n$. Let $w$ solve

for $\lambda\in\mathbb{R}$, $f\in C(\partial U)$. This solution can be written as

where $w_{\mathrm{sv}}$ solves the Saint-Venant problem

and $h_f$ is the harmonic extension of $f$ to $U$. In particular, if $\int_U w = c$ is given then $\lambda$ is uniquely determined by

since $w_{\mathrm{sv}} > 0$ in $U$.

Proof. The decomposition $w = \lambda w_{\mathrm{sv}}+h_f$ is rather clear. The property $w_{\mathrm{sv}} > 0$ in $U$ follows from the maximum principle ^[19]. □

From Lemma 27 we also deduce the following formula for vertical speed of calibrable facets in terms of the solution to the Saint-Venant problem.

Proposition 28. Let $U$ be a smooth bounded domain in $\mathbb{R}^n$ and $\lambda \in \mathbb{R}$. If $Z$ is a calibration for $U$ with signature $\chi$ satisfying

then

where $w_{\mathrm{sv}}$ is the solution to the Saint-Venant problem (5.10).

Proof. We recall (5.12) and calculate

□

We now compare the definition of calibrability for the second-order problem.

Definition 29. Let $U$ be a smooth open set in $\mathbb{R}^n$ with signature $\chi$. We say that $\overline{U}$ is ($L^2$-)calibrable if there is $Z_0$ satisfying the constraint $|Z_0|\leq1$ in $U$ and the boundary condition $\nu\cdot Z_0 = \chi$ with the property that $\operatorname{div}Z_0$ is a constant over $U$.

This definition is slightly weaker than the calibrability used in ^[26], where $a(t)\mathbf{1}_U$ is a solution of the total variation flow in $\mathbb{R}^n$ with some function $a(t)$ of $t$; see also ^[3]. This requires that $\partial^0_{L^2}TV(u)$ is constant not only on $U$ but also $U^c$. Our definition follows from that of ^[5].

6.   Calibrability of rotationally symmetric sets

Definition 30. We say that a Lebesgue measurable subset $U$ (defined up to a set of measure zero) of $\mathbb{R}^n$ is a generalized annulus if $U$ is non-empty, open, connected and rotationally symmetric, i.e., invariant under the linear action of $SO(n)$ on $\mathbb{R}^n$.

It is easy to see that any generalized annulus is a ball, an annulus, the complement of a ball or the whole space $\mathbb{R}^n$. In other words, any generalized annulus is of form

In this section we will settle the question which generalized annuli are calibrable.

Lemma 31. Let $U$ be a generalized annulus. Suppose that $U$ is calibrable with signature $\chi$. Then there exists a calibration $\overline{Z}$ for $(U, \chi)$ of form $\overline{Z}(x) = z(|x|)\frac{x}{|x|}$.

Proof. Let $Z$ be any calibration for $(U, \chi)$. Let $\mu_n$ be the Haar measure on $S\!O(n)$. We define $\overline{Z}$ as the average

It is an exercise in vector calculus to check that $\overline{Z}$ satisfies boundary conditions (5.4) and that $\Delta \operatorname{div} \overline{Z}$ is a constant (equal to $\Delta \operatorname{div} Z$) on $U$. By convexity, $|\overline{Z}|\leq 1$. Thus $\overline{Z}$ is a calibration for $(U, \chi)$. By definition, it is invariant under rotations, i.e.,

for $L \in S\!O(n)$, $x \in \mathbb{R}^n$. In the case $n = 1$ this already shows that $\overline{Z}$ is in the desired form. In higher dimensions, we consider the orthogonal decomposition

Both $\overline{Z}\vphantom{Z}^\perp$ and $\overline{Z}\vphantom{Z}^T$ are invariant under rotations. In particular, for any given $R > 0$, the restriction of $\overline{Z}\vphantom{Z}^T$ to $\mathbb{S}^{n-1}_R$ is an invariant tangent vector field on $\mathbb{S}^{n-1}_R$. Note that any such vector field is smooth. If $n = 3$, it follows by the hedgehog uncombability theorem [10, Proposition 7.15] that $\overline{Z}\vphantom{Z}^T \equiv 0$. If $n > 3$, any vector field invariant on $\mathbb{S}^{n-1}$ is in particular invariant on a sphere $\mathbb{S}^2$ containing any given point in $\mathbb{S}^{n-1}$, so the same conclusion follows. Thus, we have

By rotational invariance, we have $\overline{z}(x) = z(|x|)$, which concludes the proof.

We are left with the case $n = 2$ in which there exists a one-dimensional space of invariant tangent fields on $\mathbb{S}^{n-1} = \mathbb{S}^1$ spanned by $e^T(x) : = (x_2, - x_1)$. Thus, we have

We calculate

Thus, we can disregard $\overline{Z}\vphantom{Z}^T$ and choose $\overline{Z}\vphantom{Z}^\perp$ as our calibration, since it satisfies conditions (5.3)–(5.5) (recall that $\overline{Z}\vphantom{Z}^T$ and $\overline{Z}\vphantom{Z}^\perp$ are orthogonal). As before, we see that

□

Let $U$ be a generalized annulus. By Lemma 31, if $U$ is calibrable, then there exists a calibration $Z$ for $U$ of form $Z = z(|x|)\frac{x}{|x|}$. It follows from (5.10) that $z$ needs to satisfy the ODE

The general solution to this ODE is

where $c_0 = - \frac{\lambda}{2n(n+2)}$ if $n\neq 2$ and

where $c_0 = - \frac{\lambda}{16}$ if $n = 2$. We will now try to find a calibration for $U$ by solving a suitable boundary value problem for (6.1).

6.1.   Balls

Let $U = B_R(0)$. To focus attention, we choose $\chi = -1$ on $\partial U$. In this case, boundary conditions (5.4) lead to

If $n\geq 2$, in order to satisfy the requirements $|Z|\leq 1$ and $\nabla \operatorname{div} Z$, we need to restrict to $c_1 = c_3 = 0$ in (6.2). We make the same choice also in case $n = 1$, as it leads to the right result. Then, applying (6.4) in (6.2) or (6.3), we obtain a system of two affine equations for two unknowns $\lambda, c_2$. We solve it obtaining

We check that $z$ satisfies $|z|\leq 1$ on $[0, R]$, so $Z$ is a calibration for $B_R$. Thus, all balls are calibrable in any dimension.

6.2.   Complements of balls

Let $U = \mathbb{R}^n \setminus B_R$. For consistency with the previous case, we choose $\chi = 1$ on $\partial U$. In this case, boundary conditions (5.4) also lead to

Let us first assume that $n \geq 3$. In order to satisfy the requirement $|Z|\leq 1$, we need to restrict to $\lambda = c_2 = 0$ in (6.2). Again, applying (6.4) in (6.2) leads to a system of two affine equations for two unknowns $c_1, c_3$. We solve it obtaining

Again, we easily check that $z$ satisfies $|z|\leq 1$ on $[0, R]$, so $Z$ is a calibration for $B_R$.

In the omitted cases $n = 1, 2$, requirement $|Z|\leq 1$ implies $\lambda = c_1 = c_2 = 0$ in (6.2). If $n = 1$, there exists $z$ of such form satisfying (6.7): $z(r) \equiv -1$, consistently with (6.8). On the other hand, if $n = 2$, applying (6.7) to (6.2) with $\lambda = c_1 = c_2 = 0$ leads to a contradiction.

Summing up, all complements of balls are calibrable if $n\neq 2$. On the other hand, if $n = 2$ all complements of balls turn out not to be calibrable.

6.3.   Annuli

Let now $U = A_{R_0}^{R_1} = B_{R_1}\setminus B_{R_0}$, $0 < R_0 < R_1$. In this case $\partial U$ has two connected components, so there exist two distinct choices of signature: constant and non-constant. Let us first consider the former. To focus attention, we choose $\chi \equiv -1$. Then, boundary conditions (5.4) take form

Applying (6.9) to (6.2) or (6.3) leads to a system of four affine equations with four unknowns. In the case $n \neq 2$, the solution is

This can be rewritten in a form emphasizing homogeneity:

where we denoted $Q = R_1/R_0$. We can further simplify it to

We need to check whether condition $|Z|\leq 1$ is satisfied. We calculate

Using the form (6.12), we can check that $c_0 > 0$, $c_1 > 0$ for all $Q > 1$. Therefore, $w$ has at most one zero on the half-line $r > 0$. Consequently, $z''$ has at most one zero, so $z$ has at most one inflection point. Taking into account (6.9), $z$ cannot have a local extremum on $]R_0, R_1[$. Thus, $|z|\leq 1$ on $]R_0, R_1[$ and $Z$ is a valid calibration.

In the case $n = 2$, the solution is

which can be rewritten (again, denoting $Q = R_1/R_0$) as

As before, we calculate the second derivative of $z$:

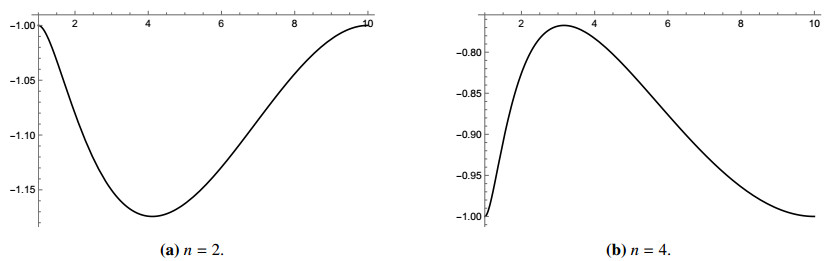
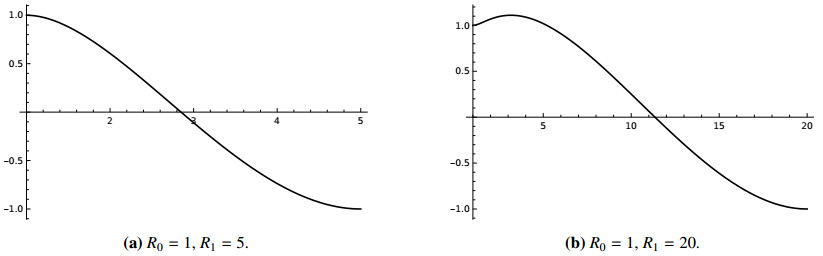
The polynomial $w$ has at most $2$ positive roots, and so does $z''$. By (6.9), at least one of them belongs to $]R_0, R_1[$. Furthermore, since $c_0 > 0$ for $Q > 1$, $z''(r)$ is positive for large values of $r$. Taking into account these observations, we deduce that $|z|\leq 1$ on $[R_0, R_1]$ if and only if $z''(R_0) \leq 0$ (compare Figure 1). This inequality is equivalent to

We compute

We observe that $m$ has exactly one zero $Q_*$ on $]1, +\infty[$, and $m(Q) \leq 0$ if and only if $Q \leq Q_*$. Therefore, $Z$ is a valid calibration for $A_{R_0}^{R_1}$ with signature $-1$ if and only if $R_1/R_0 \leq Q_*$. By (6.15) it is evident that $Q_* > 3$. Numerical computation using Wolfram Mathematica shows that $Q_* \approx 9.7$. Thus, $A_{R_0}^{R_1}$ with constant signature is calibrable if and only if $R_1/R_0 \leq Q_*$. This concludes the proof of Theorem 3.

Now, let us consider non-constant signature. We assume that $\chi = 1$ on $\partial B_{R_0}$ and $\chi = -1$ on $\partial B_{R_1}$. This choice leads to

If $n\neq 2$, the solution to the resulting affine system is

which we rewrite as

We note that in case $n = 1$ the solution reduces to

while in case $n = 3$ it reduces to

In both of these cases $z$ is constant and we have $\lambda = c_0 = 0$. On the other hand, if $n \geq 4$, we can check that $c_0 > 0$ for $Q > 1$. Recalling (6.13), we observe that $z''$ has at most two zeros on the positive half-line and $z''(r) > 0$ for large values of $r$. On the other hand, by (6.16), if $z$ has $N$ local extrema on $]R_0, R_1[$, it needs to have at least $N+1$ inflection points. We deduce from these conditions that $z$ has exactly one local maximum and no local minima, and therefore $z \geq -1$ on $]R_0, R_1[$ (compare Figure 2). It remains to check whether $z\leq 1$ on $]R_0, R_1[$. Let now

Then, by (6.1), (6.16), $f$ is a solution to the second-order elliptic problem

where

Since $c_0 \geq 0$, we have $\lambda < 0$ for $Q > 1$. By the classical weak maximum principle [19, Theorem 3.1.],

Now, if $z$ has a local maximum at $r_0$, then $z'(r_0) = 0$, so $f(r_0) = \frac{z(r_0)}{r_0}$. Consequently,

so $z < 0$ on $[R_0, R_1]$. Thus, if $n\neq 2$, all annuli with non-constant signature are calibrable.

We move to the case $n = 2$. Now, the solution to the affine system for coefficients of $z$ is

or equivalently

We can check that in this case $c_0 < 0$ for $Q > 1$. By the same argument as in the previous case, we show that $z < -1$ in $]R_0, R_1[$ (compare Figure 2), so it does not define a valid calibration. Thus, in the case $n = 2$ all annuli with non-constant signature are not calibrable.

7.   Explicit solutions

7.1.   Balls

In this section, our goal is to provide explicit description of solutions to (1.1) emanating from the characteristic function of a ball

In the case of second-order total variation flow, the solutions with initial datum (7.1) are known to be of form

with finite extinction time, i.e., there exists $t_* > 0$ such that $a(t) = 0$ for $t \geq t_*$. In the fourth order case, based on the treatment of case $n = 1$ in ^[12], we would expect the solutions to have the form

at least until an extinction time beyond which $u(t, \cdot) \equiv 0$. This intuition turns out to be correct in every dimension except $n = 2$.

Let first $n \geq 3$. As we have checked in Section 6, in this case both balls and complements of balls are calibrable. Thus, as long as the solution is of form (7.2) in time instance $t \geq 0$, we expect a valid Cahn-Hoffman vector field $Z$ to be given by

where $Z_{in}$ is the calibration w constructed for a ball $B_R$ and $Z_{out}$ is the calibration we constructed for the complement of that ball, recall:

We further calculate:

It is straightforward to check that $\operatorname{div} Z \in D^1(\mathbb{R}^n) \cap L^{2^*}(\mathbb{R}^n) = D_0^1(\mathbb{R}^n)$. Next, we deduce

Then, using the identity $\frac{\mathrm{d}}{\mathrm{d} t} \int_{\mathbb{R}^n} u = \int_{\mathbb{R}^n} u_t$, we obtain (recall notation (7.2))

Summing up, evolution of initial datum (7.1) is given by (7.2) with $a$, $R$ satisfying

This system can be explicitly solved by noticing that

and therefore

along trajectories. The solution is

We note that the solution satisfies

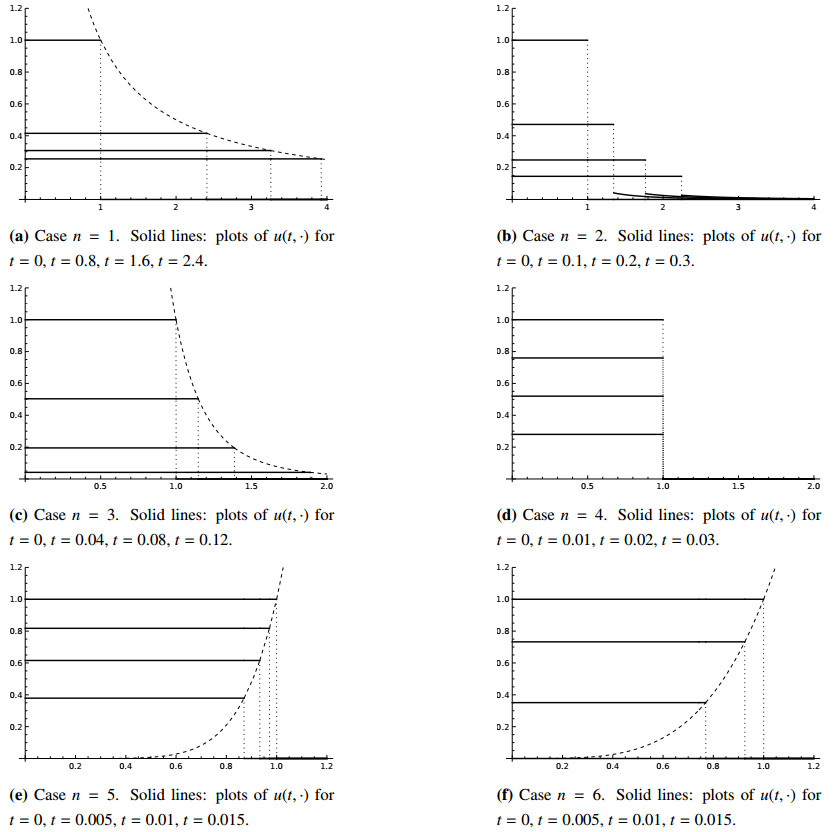
along trajectories. (This "first integral" could also have been used to solve the system (7.7).) Let us point out a few observations concerning the solutions (compare Figure 3):

● the extinction time is equal to $t_* = \frac{a_0 R_0^3}{n(4n-10)}$,

● if $n = 3$, $R(t)$ is increasing and $R(t) \to + \infty$ as $t \to t_*^-$,

● if $n = 4$, $R(t) = R_0$ is constant,

● in higher dimensions, $R(t)$ is decreasing and $R(t) \to 0$ as $t \to t_*^-$.

In the case $n = 2$ we were able to exhibit a calibration for the ball $B_R$, but not for its complement. Another possible ansatz on the Cahn-Hoffman vector field of form (7.3) is one where $Z_{in}$ is the calibration we constructed for $B_R$ and $Z_{out}$ is the choice considered in ^[15]:

We calculate

hence

If $n \geq 4$, this would lead to $u(t)$ being radially strictly increasing for positive $t$ and large values of $|x|$, which would be at odds with our choice of $Z_{out}$. In fact, if $n \geq 4$, $\operatorname{div} Z \not \in D_0^1(\mathbb{R}^n)$ for any $Z$ of this form. However, in smaller dimensions this ansatz remains a viable option. If $n = 3$, it leads to the same solution as before. On the other hand, if $n = 2$, we obtain a solution which is not of form (7.2). Instead, we are led to assume

We have:

and, recalling (7.12),

Thus, we arrive at ODE system

This system is not autonomous, but it can be integrated by noticing that along trajectories

and so

This implies, first of all, that

for all $t > 0$ and the form of solution (7.12) is preserved as long as the solution does not vanish. Furthermore, we can rewrite the system (7.13) in decoupled form

These equations can be explicitly integrated:

We observe that the solutions exist globally and

In particular $u$ stays in the form (7.12) for all $t > 0$.

Finally we consider $n = 1$. In this case, both ansätze considered before lead to the same solution:

which coincides with (7.5). Repeating the calculations following (7.5), we obtain a solution of form (7.2) satisfying (7.8), i.e.,

Note that now, as opposed to the case $n \geq 3$, the coefficient multiplying $t$ is positive. Like in $n = 2$, the extinction time is infinite and we have

This concludes the proof of Theorem 4.

7.2.   Stacks

Using the calibrations we constructed for generalized annuli, we will now derive a system of ODEs locally prescribing the solution emanating from any piecewise constant, radially symmetric datum (a stack).

Definition 32. Let $w \in D(TV)$. We say that $w$ is a stack if there exists a number $N \in \mathbb{N}$ and sequences $0 < R^0 < R^1 < \ldots < R^{N-1}$, $a^0, a^1, \ldots, a^N$ with $a^k \in \mathbb{R}$ such that

Suppose first that $n\neq 2$, in which case all connected components of level sets of any stack $w$ are calibrable. Let $u_0$ be a stack

where $a^{k-1}\neq a^k$ for $k = 1, \ldots, N$, $a^N_0 = 0$. We expect that if $u$ is the solution emanating from $u_0$, then $u(t, \cdot)$ is a stack of form

with $a^N(t) = 0$ for all $t > 0$, and that $a^{k-1}\neq a^k$, $k = 1, \ldots, N$ for small $t$. We construct a Cahn-Hoffman vector field $Z(t, \cdot)$ for $u(t, \cdot)$ by pasting together calibrations $Z^k$ for $B_{R^0(t)}$, $A_{R^k(t)}^{R^{k+1}(t)}$, $\mathbb{R}^n \setminus B_{R^{N-1}(t)}$ with suitable choice of signatures. We have

We denote

The values of $d^k$ are functions of $R^0, \ldots, R^{N-1}$. Assuming that $R^k$ are regular enough and $\varepsilon$, $|t-s|$ are small enough, we have

whence

Further, for $k = 0, \ldots, N$, we denote by $\lambda^k$ the value of $-\Delta \operatorname{div} Z^k(t, \cdot)$ which is constant since $Z^k$ is a calibration. Then, we can write down the system of ODEs for $a^k$ and $R^k$:

Let $c_0^k$ denote $c_0$ given by (6.17) if $\mathrm{sgn}\, (a^{k+1} - a^k) = \mathrm{sgn}\, (a^k - a^{k-1})$ or by (6.10) if $\mathrm{sgn}\, (a^{k+1} - a^k) \neq \mathrm{sgn}\, (a^k - a^{k-1})$, with $R^{k+1}$ and $R^k$ in place of $R_1$ and $R_0$. Then, we have

We observe that in a neighborhood of any initial datum $R^0_0, \ldots, R^{N-1}_0$, $a^0_0, \ldots, a^N_0$, $R^k_0 < R^{k+1}_0$, $a^k_0 \neq a^{k+1}_0$, the r. h. s. of (7.20) is regular in $R^0, \ldots, R^{N-1}$, $a^0, \ldots, a^N$, so locally the system has a unique solution. Unique solvability fails when a time instance $t > 0$ is reached such that $a^k(t) = a^{k+1}(t)$, $R^k(t) = R^{k+1}(t)$ or $R_0 = 0$. In such case $u(t, \cdot)$ is again a stack with a smaller $N$, and we can restart our procedure. This concludes the proof of Theorem 5.

Next we deal with the remaining case of dimension $n = 2$. In this case, our attempt to obtain a radial calibration failed for complements of balls and for some annuli. Again, let $u_0$ be a stack of form (7.17). For $k = 1, \ldots, N$, let $\sigma^k = \mathrm{sgn}\, (a^k_0 - a^{k-1}_0)$. We assume the following ansatz on the solution $u$ and the associated field $Z$ for small $t > 0$:

We complete the definition of a Cahn-Hoffman field $Z$ consistent with (7.22), (7.23) by pasting the calibrations $Z^k$ with suitable choice of signatures into the gaps left in (7.23). This leads to

Moreover, $u_t(t, \cdot) \in M(\mathbb{R}^2)$ and

for $k = 0, \ldots, N-1$, where $(\nabla \operatorname{div} Z)^\pm$ are the one sided limits as $|x| \to (R^k)^\pm$. The values of $d^k$ are functions of $R^0, \ldots, R^{N-1}$. Reasoning as in the case $n \neq 2$, the evolution of $R^k$ is governed by equations

The values $u(t, x)\big|_{|x| = (R^k)^+}$ are either prescribed by ODEs

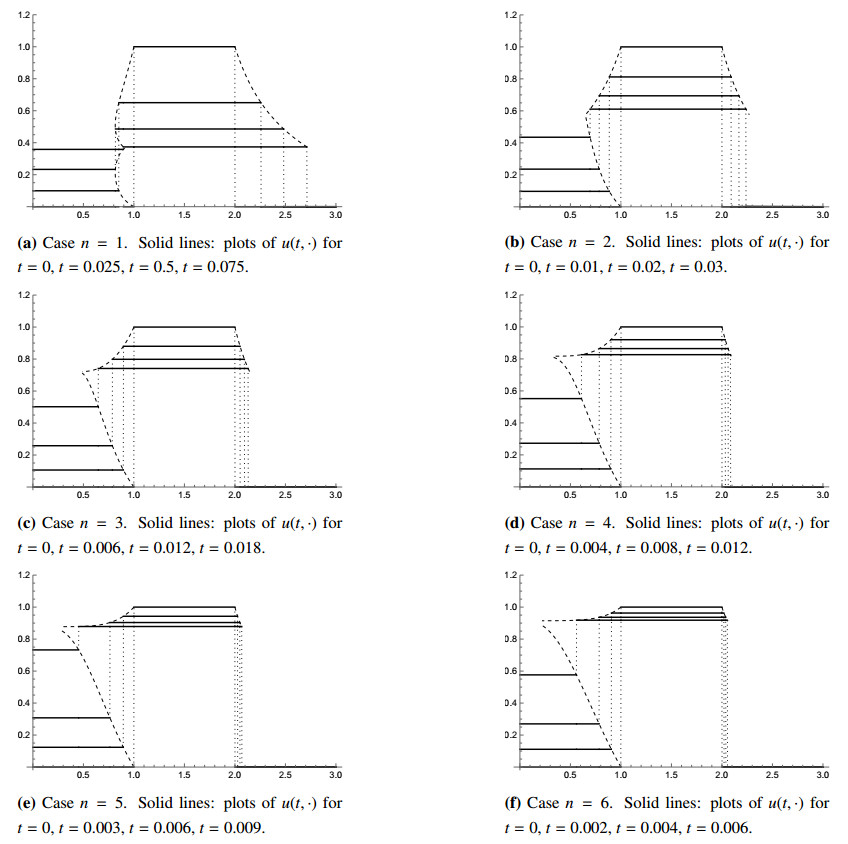
with $\lambda^k$ functions of $R^0, \ldots, R^{N-1}$ in calibrable regions where $u(t, x) = a^k(t)$, or explicitly determined by $u_t(t, x) = \sigma^k /|x|^3$ in bending regions. It is important to note that in the case $\sigma^k \neq \sigma^{k+1}$, $R^{k-1} \leq R^k/Q_*$ the functions $d^k, \lambda^k$ do not depend on $R^{k-1}$. Thus, one can first solve a part of the system (7.24), (7.25) for the outer annuli, then calculate $u$ in the bending region (without knowing a priori its inner boundary) and move on to solving innermore parts of (7.24), (7.25). This way, finding the solution is indeed again reduced to solving a system of ODEs. We include Figure 4 illustrating the evolution of stacks on the example of the characteristic function of an annulus.

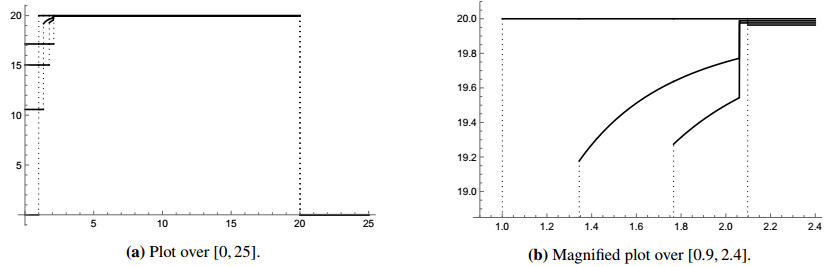
In the case of thick annuli in $n = 2$, the qualitative behavior resulting from this procedure is rather intricate and may be surprising. To showcase this, we include Figures 5 and 6 depicting the evolution emanating from the characteristic function of a thick annulus.

Let us explain the evolution in a few words. The inner part of the initial facet corresponding to the annulus instantaneously bends downwards. Meanwhile, the outer boundary of the facet expands outwards, at relatively low speed (practically invisible in the picture). Since the ratio of outer to inner radius of the facet is constant, this means that the whole facet slowly moves outwards. The combined effect of this and the bending results in the very steep (but continuous!) part of the graph between the facet and the bending part. At the same time, the facet corresponding to the inside ball also expands outwards, gradually consuming the bending part. In the final pictured time instance, the whole bending part has disappeared and the solution is a stack again.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the anonymous reviewers for their helpful comments.

The first author of the work was partly supported by the Japan Society for the Promotion of Science (JSPS) through the grants Kakenhi: No. 19H00639, No. 18H05323, No. 17H01091, and by Arithmer Inc. and Daikin Industries, Ltd. through collaborative grants.

The second author of the work was partly supported by JSPS through the grant Kakenhi No. 18H05323.

This work was created during the last author's JSPS Postdoctoral Research Fellowship at the University of Tokyo. The last author was partly supported by the Kakenhi Grant-in-Aid No. 21F20811.

Conflict of interest

The authors declare no conflict of interest.