A qualitative analysis of a model on alpha-synuclein transport and aggregation in neurons

1.   Introduction

Parkinson's disease (PD) is a neurological disease. The name is associated with James Parkinson, who was the first to describe the disease conditions in 1817. The standard conditions of PD are generally motor disorder; however, there are non-motor forms, which similarly have a major effect on the patient's life ^[1]. The cause of the disease is due to dopamine deficiency in the brain area known as the substantia nigra. This deficiency is responsible for the motor symptoms that appear on patients. Also, Lewy bodies in the brain are considered to be another cause for PD because it was present in the anatomy of patients' bodies. It was found that Lewy bodies included a collection of alpha-synuclein ($ \alpha $-syn) ^[2,3,4].

Mathematical models, both theoretical and empirical, have contributed greatly in understanding the biological mechanism behind neurodegenerative diseases ^[5]. Most developed models are quantitative; nevertheless, they were beneficial in exploring alternative treatments for the disease ^[6]. Recently, in ^[7], they classified PD models into two largely types: mechanistic models and phenotypic models. The primary purpose of the phenotypic models is to distinguish the variations between healthy and diseased patients quantitatively regarding aspects of PD symptoms. In contrast, mechanistic models are related to the pathology aspect of PD. They further classify the mechanistic models into $ \alpha $-syn aggregation models, pathogenesis models, and pathology propagation models.

Some of these models were expressed as compartmental models. For example, in ^[8] they modeled the electrophysiology of the substantia nigra pars compacta using a single-compartment model. Whereas, the model in ^[9] explored the onset conditions of PD by proposing a compartmental model with four state variables representing the concentration of both monomeric and polymeric $ \alpha $-syn in the soma and the synapse. The models' simulations concluded that the failure of $ \alpha $-syn degradation leads to the abnormal accumulation of misfolded $ \alpha $-syn observed in PD. They considered $ \alpha $-syn as an infectious agent that propagates in a prion-like manner. Moreover, the transportation of $ \alpha $-syn in axons from the soma to the synapse is modeled in ^[10]. They proposed two models to investigate the effect of two kinds of transport of $ \alpha $-syn in the axons: active and diffusion. Also, they simulated $ \alpha $-syn transport in healthy and diseased axons, where the latter led to $ \alpha $-syn accumulation in Lewy bodies. On the other hand, in ^[11], the model analyzed the relation between $ \alpha $-syn aggregation and proteasome activity. Proteasomes are responsible for the degradation of unwanted proteins, which allows for a cell to maintain homeostasis. The compartment model consisted of three main concentrations: fibrils, proteasome-fibril complex and the free proteasome. They predicted that if the ratio between proteasome and $ \alpha $-syn protofilament is reduced below a certain threshold level, then the accumulation of $ \alpha $-syn aggregation increases.

Most of the above models were investigated numerically. In this paper, we examine the model in ^[9] by employing the stability theory of nonlinear ordinary differential equations ^[12,13,14]. Also, we address theoretically the limitations in the model, that is, we assume different half-lives of monomeric and polymeric $ \alpha $-syn in the soma and in the synapse. To our knowledge, this is the first analytical investigation executed on $ \alpha $-syn propagation models. The significance of this analysis lies in obtaining the equilibrium point in closed form. As a result, it enables the determination of the critical parameters involved in decreasing or increasing the level of the equilibrium value depending on the desired target. This study is expected to give more insight into Parkinson's disease for pharmacological interventions.

The comprehensive qualitative study is structured as follows. In Section 2, we briefly describe the model in ^[9] with its notations. Basic qualitative analysis of the model is given in Section 3, such as obtaining the positively invariant region for the model and finding the equilibrium point. In Section 4, we scrutinize the local and global stability of the equilibrium point. To assert the qualitative results, we perform numerical simulations in Section 5. Also, in this section, the sensitivity analysis is executed to inspect the role of parameters in the equilibrium value. The conclusion of this study is given in Section 6.

2.   The $ \alpha $-syn transport and aggregation model

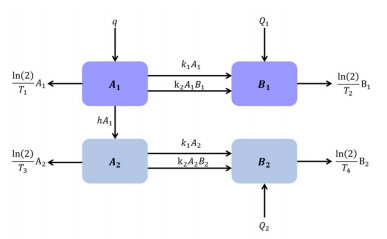
In our study, we investigate theoretically the mathematical model presented by Kuznetsov in ^[9]. The model describes the dynamics of $ \alpha $-syn transport and aggregation in neurons. The presence of $ \alpha $-syn protein in the neuron is divided into four disjoint classes. $ A_{1}(t) $ represents $ \alpha $-syn concentration in soma as a monomer at time $ t $; $ B_{1}(t) $ represents $ \alpha $-syn concentration in soma as misfolded at time $ t $; $ A_{2}(t) $ represents $ \alpha $-syn concentration in synapse as a monomer at time $ t $; $ B_{2}(t) $ represents $ \alpha $-syn concentration in synapse as misfolded at time $ t $.

We briefly describe the dynamics according to Kuznetsov as follows. In the soma, monomeric $ \alpha $-syn concentration increases due to its synthesis at a rate of $ q $. During the process of polymerization, the concentration of monomeric $ \alpha $-syn decays in order to produce misfolded $ \alpha $-syn. Also, monomeric $ \alpha $-syn concentration decreases, in the soma, as a result of being transferred to the synapse. Similar dynamics take place in the synapse (see Figure 1). In our theoretical examination of the model, we assume that both monomeric and polymeric (misfolded) $ \alpha $-syn in the soma decay with the rate of $ \frac{ln(2)}{T_{1}} $ and $ \frac{ln(2)}{T_{2}} $, respectively. Also, monomeric and polymeric (misfolded) $ \alpha $-syn in the synapse decay with the rate of $ \frac{ln(2)}{T_{3}} $ and $ \frac{ln(2)}{T_{4}} $, respectively. To facilitate the analytical investigations, we only consider the case of constant entry rate of misfolded $ \alpha $-syn from outside the neuron toward the soma and synapse. Based on the conservation of monomeric and polymeric $ \alpha $-syn in the soma and synapse, the model is expressed by the following system of nonlinear ordinary differential equations:

The variables and parameters used in (2.1) are summarized in Table 1 as in ^[9]. It can be seen that the first two equations in (2.1) form an independent subsystem that can be analyzed separately. However, we will analyze the model as one whole system.

3.   Basic analysis

One of the essential concepts to examine when studying compartmental models is the equilibrium points. In this section, we derive the conditions for the existence of the equilibrium points of system (2.1). Also, we prove the positivity and boundedness of the feasible region of the system.

3.1.   Positivity and boundedness

Theorem 3.1. If the initial values of system (2.1) are $ A_{1}(0)\geq0 $, $ B_{1}(0)\geq0 $, $ A_{2}(0)\geq0 $, and $ B_{2}(0)\geq0 $, then the solutions of the system: $ (A_{1}(t), B_{1}(t), A_{2}(t), B_{2}(t)) $ are non-negative for all $ t > 0 $.

Proof. Let $ A_{1}(0)\geq0 $, according to the first equation in system (2.1), we have,

It can be written as:

Thus,

Integration gives,

Since $ A_{1}(0) $ is non-negative, and the exponential function is always positive, then $ A_1(t) $ is non-negative for all $ t > 0 $. Next, from the second equation in (2.1), we have

Since $ Q_1 $ and $ A_1 $ are non-negative, then

Similarly, using the method of integrating factor, we obtain

By applying the same approach to the rest of the equations in system (2.1), we obtain

Since $ A_{1}(0), B_{1}(0), A_{2}(0) $ and $ B_{2}(0) $ are non-negative and the exponential function is always positive, then the solution $ (A_{1}(t), B_{1}(t), A_{2}(t), B_{2}(t)) $ is non-negative for all $ t > 0 $. □

Theorem 3.2. All solutions $ (A_{1}(t), B_{1}(t), A_{2}(t), B_{2}(t)) $ of model (2.1) are bounded for all $ t > 0 $.

Proof. Adding the first and second equations in (2.1), we have,

Let $ \delta = min\{\frac{ln(2)}{T_{1}}+\frac{h}{v_{1}}, \frac{ln(2)}{T_{2}}\} $, then $ A_{1}^{'}+B_{1}^{'}\leq q+Q_{1}-\delta (A_{1}+B_{1}), $ which can be written as:

Integration gives,

Therefore, $ \lim sup_{t\rightarrow \infty}(A_{1}+B_{1})\leq \frac{q+Q_{1}}{\delta} $.

Following the same approach for the last two equations in (2.1), we obtain

where $ \mu = min\{\frac{ln(2)}{T_{3}}, \frac{ln(2)}{T_{4}}\} $. Then, $ \lim sup_{t\rightarrow \infty}(A_{2}+B_{2})\leq\frac{Q_{2} v_2+A_{1}h}{\mu v_2}\leq \frac{Q_{2} v_2d+(q+Q1)h}{\mu v_2d} $.

Note that in the first part of this theorem, we have proved that the sum of $ A_1+B_1 $ is less than or equal to the constant $ (q+Q1)/d $. Since $ A_1 $ and $ B_1 $ are positive (from Theorem 3.1), then $ A_1+B_1\leq\text{constant} $ yields that $ A_1\leq\text{constant} $. Therefore, $ A_1 $ is less than or equal to the constant $ (q+Q1)/d $. Thus, the sum of $ A_2+B_2 $ is less than a constant since $ A_1 $ is less than a constant. Hence, all solutions of model (2.1) are bounded for all $ t > 0 $. □

Theorem 3.3. The feasible region of model (2.1):

$ \Omega = \{(A_{1}, B_{1}, A_{2}, B_{2})\in\mathrm{R}^{4}_{+}:0\leq A_{1}+B_{1}\leq \frac{q+Q_{1}}{\delta}, $ $ 0\leq A_{2}+B_{2}\leq \frac{Q_{2} v_2+A_{1}h}{\mu v_2} \} $ is positively invariant, where $ \delta = min\{\frac{ln(2)}{T_{1}}+\frac{h}{v_{1}}, \frac{ln(2)}{T_{2}}\} $, and $ \mu = min\{\frac{ln(2)}{T_{3}}, \frac{ln(2)}{T_{4}}\} $.

Proof. In Theorem 3.1, we proved that if the initial values are non-negative, then also the state variables are non-negative for all $ t > 0 $. We now prove that if the state variables initially begin in $ \Omega $, then it stays there. Let $ (A_{1}(0), B_{1}(0), A_{2}(0), B_{2}(0)) \in \Omega $, then

Since at the boundary $ A_{1}+B_{1} = \frac{1}{\delta}(q+Q_{1}) $ and $ A_{2}+B_{2} = \frac{1}{\mu}(Q_{2}+A_{1}\dfrac{h}{v_{2}}) $. Thus, the solution stays within the region according to Nagumo-Bony-Brezis Theorem ^[15,16,17]. Hence, the region $ \Omega $ is positively invariant. □

3.2.   Equilibrium point

To find the equilibrium point of the model, we set all the rates in (2.1) to zero, that is,

By adding (3.1) and (3.2), we obtain,

Thus,

Substituting $ A_{1} $ into (3.2), we get the following:

which is a second degree equation of the form $ \beta_1B_{1}^2+\beta_2B_{1}+\beta_3 = 0, $ where

Since $ \beta_1 > 0 $ and $ \beta_3 < 0 $, then, $ \beta_2 < \sqrt{\beta_2^{2}-4\beta_1\beta_3}. $ Thus, the feasible solution for $ B_1 $ is:

From (3.1), we have

Since $ B_1 $ is positive, then $ A_{1} $ is also positive. Now, solving equation (3.3) for $ A_2 $, we get

Substituting for $ A_2 $ into (3.4), we obtain the following equation

where

Here, $ \mu_1 > 0 $ and $ \mu_3 < 0 $. Thus, $ \mu_2 < \sqrt{\mu_2^{2}-4\mu_1\mu_3}. $ Hence, the feasible solution for $ B_2 $ is

$ B_2 $ is positive, thus $ A_2 $ is positive.

Theorem 3.4. Model (2.1) has a unique equilibrium point, $ E^* = (A^*_1, B^*_1, A_2^*, B_2^*) $, where

Here $ \beta_1, \beta_2, \beta_3, \mu_1, \mu_2 $ and $ \mu_3 $ are given in (3.5) and (3.6).

4.   Stability analysis

In this section, we investigate the stability of the equilibrium point of model (2.1) both locally and globally. We state the following theorems.

Theorem 4.1. The equilibrium point $ E^* $, if it exists, is locally asymptotically stable if $ max\{\frac{k_2A^*_{1}T_2}{ln(2)}, \frac{k_2A^*_{2}T_4}{ln(2)}\} < 1. $

Proof. First, we compute the Jacobin matrix of system (2.1) evaluated at $ E^* $:

Then, the characteristic equation, $ |\mathrm{J}- \lambda \mathrm{I}| = 0 $, yield

Note that from (3.1), $ -k_{1}-k_{2}B^*_1-\frac{ln(2)}{T_{1}}-\frac{h}{v_{1}} = -\frac{q}{A^*_1}, $ and from (3.3), $ -k_{1}-k_{2}B_{2}^*-\frac{ln(2)}{T_{3}} = -\frac{hA^*_1}{v_2A^*_2}. $ Rewrite (4.1) in the form:

where,

Thus, the roots of (4.2) and (4.3) are respectively

Now, $ \alpha_1 $ is negative since, by using (3.2), we have

If $ \alpha_2 > 0 $, $ \lambda_{1, 2} $ have negative real parts. Hence, the sufficient condition for $ \lambda_{1, 2} $ to be negative is when

Also, from (3.4), we obtain

If $ \alpha_4 > 0 $, $ \lambda_{3, 4} $ have negative real parts. Hence, the sufficient condition for $ \lambda_{3, 4} $ to be negative is when

We conclude that $ E^* $, if it exists, is locally asymptotically stable if $ max\{\frac{k_2A^*_{1}T_2}{ln(2)}, \frac{k_2A^*_{2}T_4}{ln(2)}\} < 1. $ □

To investigate the global stability of the equilibrium point $ E^* $, we use the algebraic approach given in ^[18].

Theorem 4.2. The equilibrium point $ E^* = (A_1^*, B_1^*, A_2^*, B_2^*) $, if it exists, is globally asymptotically stable if $ v_2\geq v_1. $

Proof. First, we define a Lyapunov function,

where $ a_{i} > 0 $ (i = 1, 2, 3). Clearly, $ \mathrm{L} $ is a positive definite function in $ \Omega $. Next, we find the derivative of $ \mathrm{L} $ with respect to t.

where

Let

Thus, we get

Collecting the terms, we have

The coefficients of the Lyapunov function may be any constant as long as these coefficients satisfy that the Lyapunov function is positive definite in the feasible region. By letting the coefficients of the Lyapunove function, $ a_{1} = a_{2} = a_{3} = 1 $, we get

Construct the function set $ \Gamma = \{y_{0}, y_{1}, y_{2}, y_{3}, \frac{1}{y_{0}}, \frac{1}{y_{1}}, \frac{1}{y_{3}}, \frac{y_{0}}{y_{1}}, \frac{y_{0}}{y_{2}}, \frac{y_{2}}{y_{3}}\}. $ There are six groups associated with $ \Gamma $ such that the product of the functions within a group is unity. The six groups are, respectively,

Define the function $ \mathrm{H} $ using the above groups as:

where $ b_{k}\geq0 $ (k = 1, 2, ..., 6). Next, we obtain the parameters $ b_{k} $ such that

By equating the coefficients of similar terms on both sides, we get the following equations:

We must show that all the previous equations are satisfied and $ b_{i} (i = 1, 2, ..., 6) $ are nonnegative. Clearly, $ b_{i} (i = 2, ..., 6) $ are nonnegtive. We have only to prove that $ b_1 $ is nonnegative. Now,

Thus, $ b_1 > 0 $ if $ v_2\geq v_1. $

Equation (4.10) is satisfied since

Here, we have used (3.2). Similarly, by using (3.4), equation (4.11) is satisfied and by using (3.3), equation (4.12) is satisfied. As for equation (4.13), we have

By using (3.1) and (3.3), we obtain

Thus, equation (4.13) is satisfied. Lastly, we verify equation (4.14) as follows:

Note that we have used (3.1), (3.2), (3.3) and (3.4) in the above calculations. Finally, we show that $ d\mathrm{L}/dt $ is negative definite. Let $ \Omega^* \subset \Omega $ such that:

Thus, the largest invariant set of system (2.1) on $ \Omega^* \subset \Omega $ is the equilibrium point $ E^* $. Therefore, by the LaSalle's Invariance Principle ^[14], $ E^* $, if it exists, is globally asymptotically stable if $ v_2\geq v_1. $ □

5.   Numerical analysis

In this section, we illustrate numerical simulations of model (2.1) using Matlab to substantiate the qualitative results. Moreover, a sensitivity analysis is executed to investigate the effect of the models' parameters on the equilibrium point $ E^* $.

5.1.   Numerical experiments

Three numerical experiments are conducted by solving model (2.1) numerically. The values of the parameters are taken from ^[9], which are presented in Table 2, except for the parameters $ T_2 $ and $ T_4 $. It is possible to check that the parameters, indeed, satisfy the conditions given in Theorems 4.1 and 4.2.

Figure 2 illustrates the numerical simulations of model (2.1) under the following three different initial conditions:

$ a. $ $ A_{1}(0) = 0.006 $, $ B_{1}(0) = 0 $, $ A_{2}(0) = 0 $ and $ B_{2}(0) = 0 $,

$ b. $ $ A_{1}(0) = 0.001 $, $ B_{1}(0) = 0.09 $, $ A_{2}(0) = 0.001 $ and $ B_{2}(0) = 0.09 $,

$ c. $ $ A_{1}(0) = 0.06 $, $ B_{1}(0) = 0.09 $, $ A_{2}(0) = 0.05 $ and $ B_{2}(0) = 0.1 $.

The figure shows that in all three experiments, the solution curves tend to the equilibrium,

By evaluating the equilibrium point in Theorem 3.4, using the parameters' values in Table 2, we get the same values in (5.1). This demonstrates the agreement with the analytical results.

5.2.   Sensitivity analysis

We compute the normalized sensitivity index (elasticity) of $ E^* = (A_1^*, B_1^*, A_2^*, B_2^*) $ with respect to the models' parameters given in Table 2 by using the formula in ^[14]:

where $ p $ denotes any parameter. In particular, we examine the sensitivity of the misfolded $ \alpha $-syn equilibrium in the soma and the synapse, i.e., $ B_1^* $ and $ B_2^* $, respectively.

Table 3 displays the elasticity of $ B_1^* $ and $ B_2^* $, that is, the percentage value of increase (or decrease) in $ B_1^* $ and $ B_2^* $ after a $ 1% $ increase in the parameter. For instance, a $ 1% $ increase in $ h $ corresponds to a reduction in $ B^*_1 $ by $ 0.4050% $, and a $ 0.5962% $ increase in $ B^*_2 $. Moreover, we can see from the table that the most significant decline in $ B^*_1 $ is from increasing the parameter $ h $. However, increasing $ h $ leads to an increase of $ B^*_2 $. This effect is understandable since increasing $ h $ means increasing the transport rate of monomeric $ \alpha $-syn from the soma to the synapse. Consequently, monomeric $ \alpha $-syn concentration in the soma becomes less, which, in turn, leads to a reduction in the concentration of $ \alpha $-syn polymer in the soma. At the same time, in the synapse, $ \alpha $-syn monomer is increasing, due to transportation from the soma, which leads to $ \alpha $-syn aggregation. On the other hand, the most significant decline in $ B^*_2 $ comes from increasing the parameter $ v_2 $, while, $ v_2 $ has no effect on $ B^*_1 $. The drop in $ B^*_2 $ is a possible result from the inverse proportionality between volume and concentration, since $ v_2 $ is the volume of the neuron synapse and part of the axon is included in $ v_2 $. As for the remaining parameters, they all participate in increasing $ B^*_1 $ with different percentages. However, $ B^*_2 $ increases with all parameters except for $ Q_1 $ and $ T_2 $ (see Table 3).

Furthermore, The variations in $ B^*_1 $ and $ B^*_2 $ with respect to the parameters are illustrated in Figure 3 and Figure 4, respectively. The curves were generated by plotting $ B^*_1 $ and $ B^*_2 $ as a function of one parameter. At the same time, the values of the remaining parameters are fixed as in Table 2. It can be seen that the alterations of $ B^*_1 $ and $ B^*_2 $ in the figures, corresponding to each parameter, are consistent with their sensitivity index calculated in Table 3.

The simulations suggest that the values of $ B^*_1 $ and $ B^*_2 $ descent when:

● reducing the rate of $ \alpha $-syn synthesis, $ q $,

● minimizing the decay rate of monomeric $ \alpha $-syn, $ k_1 $, during polymerization,

● constricting the production rate of polymeric $ \alpha $-syn, $ k_2 $, during polymerization,

● shortening the half life of the monomeric $ \alpha $-syn in the soma and synapse, $ T_1 $ and $ T_3 $, respectively.

The implications of the sensitivity analysis assist in constructing therapeutic strategies. Specific treatments may be attempted through targeting critical parameters that contribute to lowering the polymeric $ \alpha $-syn equilibrium level. Such as limiting the burden of $ \alpha $-syn, reducing the rates of nucleation and autocatalytic growth of $ \alpha $-syn and increasing the efficiency of $ \alpha $-syn degradation machinery.

6.   Conclusions

In this paper, we analyzed qualitatively the compartmental model proposed in ^[9] describing the $ \alpha $-synuclein aggregation and transportation within the neuron. By assuming different half-lives of monomeric and polymeric $ \alpha $-syn in the soma and in the synapse, we expanded the model in ^[9] theoretically. The analysis produced a unique equilibrium point, $ E^* $, that exists without any conditions within the feasible region $ \Omega $. Moreover, we examined the local stability of $ E^* $ using the linearization method and its global stability using a Lyapunov function with the algebraic approach. Under the criteria, $ max\{\frac{k_2A^*_{1}T_2}{ln(2)}, \frac{k_2A^*_{2}T_4}{ln(2)}\} < 1, $ the equilibrium point was locally asymptotically stable. Moreover, if $ v_2\geq v_1 $, then $ E^* $ was globally asymptotically stable. In addition, numerical simulations were executed to support the analytical results. It has been shown numerically that for different initial conditions, the model converges to the equilibrium point, $ E^* $, stated in Theorem 3.4. The models' parameters used in the simulations were taken from ^[9], and they satisfied the above stability conditions.

The equilibrium point was analyzed further to determine its sensitivity to the models' parameters. In particular, we investigated the sensitivity of the equilibrium values of the misfolded $ \alpha $-syn, $ B^*_1 $ and $ B^*_2 $. The analysis was carried out using the sensitivity index formula as well as illustrating the dependency of $ B^*_1 $ and $ B^*_2 $ on the parameters numerically. Both procedures were consistent and agreed with the numerical simulations obtained in ^[9]. Also, the suggested treatments concluded from the analysis are in line with the therapeutic approaches in the literature.

Conflict of interest

The authors declare that there is no conflicts of interest.