A new mathematical model for tuberculosis epidemic under the consciousness effect

1.   Introduction

Humanity has fought epidemics for centuries, and millions of people have lost their lives. From time to time, these outbreaks manifest themselves in the form of plague, smallpox, HIV/AIDS, SARS, avian flu, and influenza. One of these epidemics is tuberculosis (TB) which is popularly known. Tuberculosis is a long-term bacterial and infectious disease caused by the microbe "mycobacterium tuberculosis (MTB)". The way of transmission is often caused by sputum that a tuberculosis patient spits into the environment, or by Bacillus-laden droplets that are scattered when coughing. Although tuberculosis is an infection that can occur in more than one organ, it is mainly observed in the lungs and mediastinal lymph nodes of the lungs. Bacillus is emitted from an active tuberculosis patient by coughing, sneezing, or other means through droplets into the air in saliva, and the infection is spread by removing particles suspended in the air. It is one of the oldest known diseases, that can be maintained, although still continues to be one of the world's most common and deadly infectious diseases, and more than three million people per year are died due to TB ^[1]. People who experience tuberculosis can continue their healthy lives for months without any symptoms. During this period, the person's immune system tries to prevent the development of the disease by fighting against the MTB bacterium. But in cases where the immune system cannot show sufficient resistance, tuberculosis microbes become active and tuberculosis disease occurs ^[2].

24th of March is commemorated every year as "World Tuberculosis Day", dedicated to the day of March 24, 1882, when MTB Bacillus was discovered by Robert Koch in order to end the global TB epidemic and paved the way for the diagnosis and treatment of the disease. About a quarter of the world's population has been infected with tuberculosis Bacillus. The increase in HIV/AIDS infection in the world also increases the global threat of TB. 30.000 people are being infected with tuberculosis and 4.500 of them die due to tuberculosis every day. In the world, 54 million lives have been saved and tuberculosis has been reduced by 42% by global efforts since 2000. The World Health Organization (WHO) has implemented its global tuberculosis eradication strategy and the WHO European Region Tuberculosis Action Plan 2016-2020, identifying the steps to be taken after 2015. In this context, it is aimed to reduce TB incidence by 90% all over the world by 2030 ^[3].

The first mathematical model given by Waaler et al. ^[4] was established by taking into account relationships with other social sciences, and the potentials of this model are shown in three examples that show how the model can help predict the tendency of tuberculosis, either in a given state, which develops spontaneously suddenly or under the influence of certain control programs. In particular, these examples emphasize that the model can be profitable in evaluating specific control programs, reflecting the effects of tuberculosis on its natural tendency. Schulzer et al. (1994) ^[5] presented a mathematical model to study the accelerating effect of HIV infection on TB disease, while Castillo-Chavez and Feng (1997) ^[6] revealed differences between two TB individuals with and without drug-resistant TB. In another study, it was stated that the effect of exogen on the qualitative dynamics of TB was too great ^[7]. Monte-Carlo simulations were conducted to determine the likelihood that 10,000 clinical patients receiving different doses of moxifloxacin could reach or exceed the point of exposure to the drug required to suppress their resistance to moxifloxacin in TB ^[8]. In addition, it was concluded that advanced TB diagnostic techniques have a significant impact on t-related disease and death rates in HIV endemic areas, and it was emphasized that as TB rates continue to increase, advanced diagnostic techniques should be considered as TB control strategies ^[9].

Analysis of the mathematical model created in research on multidrug-resistant (CID) and common drug-resistant (YID) strains in South Africa, the region with the highest TB rate worldwide, has yielded important results for the next 10 years. It showed that the spread of TB culture and drug sensitivity among adults in South Africa could save more than 47.000 lives and prevent more than 7.000 cases of CID-TB in the period from 2008 to 2017. This corresponds to a 17% decrease in total TB deaths and a 47% decrease in CID-TB deaths ^[10]. Bowong and Tewa (2009) ^[11] proved that the TB system they studied was asymptotically globally stable and has a single stable equilibrium, and showed that depending on the basic reproductive rate, this stable structure occurs either in a regional disease state or in disease-free situations. Aparicio and Castillo-Chavez (2009) analyzed a TB model they established on three separate classes: a homogeneous mixture with the probability of standard virus hit, a non-homogeneous mixture containing "household-household" contacts, and a mixture grouped by age, and discussed the factors affecting TB. From these factors, they examined in detail the effects of population growth, stochasticism, clustering of contacts, and age structure on disease dynamics. In a study where a new deterministic mathematical model was created, Liu and Zhang (2011) ^[12] described the effects of vaccination and treatment on the spread of tuberculosis. Tewa et al. (2012) ^[13] took into account that it is possible for TB-sensitive individuals to switch from one part to another, and proved the existence-uniqueness of related endemic balances in quadratic forms using the Lyapunov function. Trauer et al. ^[14] The model presented by (2014) simulated program-based responses to tuberculosis in extreme endemic countries in the Asia-Pacific region and stated that the model could not be adjusted according to the predicted rate of a hit without allowing reinfection during the delay. In another study, by adding vaccine parameters to the mathematical model, it was aimed to infect the least people among susceptible individuals and to minimize the number of infected individuals ^[15].

January 2005 December 2012 in a mathematical model created with a focus on tuberculosis data in China ^[16] fit the relevant data and thus determined the optimal parameter values of the model using the chi-square test; with these parameters, they calculated the effective number of disease reproduction each year. Dodd et al. (2016) ^[17], in their study of children in the 22 countries where TB cases are most common, they set a benchmark for the rates of tuberculosis cases at the country level and developed recommendations to prevent TB cases at these rates. In another study ^[18], a model describing the impact of a public health education campaign for tuberculosis and comparing it with data from Senegal was developed. Taking into account the results found, they suggested that some data could be added to the model, such as chronological age and/or spatial structure, which takes into account sensitivity by age, to observe the difference between the approaches of individuals in rural and urban areas to TB. Vinh et al. (2018) ^[19] the passage of the virus in the world is one of the cities most likely HIV/AIDS and TB happens very fast synchronization between the dynamics of a city, Ho Chi Minh City (HCMC-Vietnam). In their study, a mathematical model to integrate many data sources HCMC the dynamics of TB was explored. This study was the first detailed study on TB at HCMC and provides information on TB dynamics at HCMC from 1996 to 2005. In ^[20], the authors considered two different treatment strategies: one of them is to point out the impact of treating latent TB infection (LTBI) in the elderly in addition to current TB control strategies. The other one is the treatment of infected individuals with anti-TB drugs. A lot of modeling studies have also been conducted in relation to significant area of science and infectious illnesses including COVID-19 ^{[21,22,23,24,25,26,27,28,29,30,31,32]}, cancer cells-cancer stem cells ^[33], optimal control and bifurcation ^[34], alcoholism ^[35], cholera ^[36,37], Parkinson's disease ^[38], disturbance effect in intracellular calcium dynamic on fibroblast cells ^[39], HIV ^[40,41], babesiosis ^[42], predator-prey ^[43,44], viral system with the non-cytolytic immune assumption ^[45], Nipah virus ^[46], an epidemic model with general interference function and high-order perturbation ^[47], potential scenarios for wastewater treatment ^[48], Gompertz growth model ^[49], a general epidemic model with logistic growth ^[50], synchronization ^[51], a sewage treatment model ^[52].

2.   Model formulation

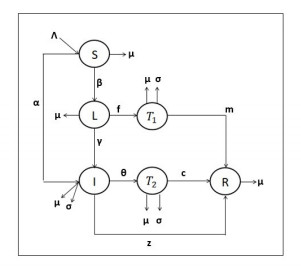
In the present TB model, population compartments consist of six populations: Susceptible ($S$), Latent ($L$), Treatment for latently infected individuals ($T_{1}$), Infected ($I$), Treatment for the actively infected individuals ($T_{2}$) and Recovered ($R$) which mean that Susceptible: Individuals susceptible to disease, Latent: those who are latently infected by tuberculosis, that is, individuals who do not experience the disease actively, Treatment 1: Preventive treatment applied optionally to patients with latent tuberculosis, that is, conscious individuals who accept this treatment, Infected: Individuals who are actively living the disease with reduced body resistance, Treatment 2: Curative treatment applied to infected individuals, Recovered: Individuals who have survived tuberculosis disease. In Tuberculosis (TB) model that we have constructed, the $\Lambda$ parameter includes all people, and a certain part of them are thought to be susceptible to the disease. In other words, the state of being susceptible to this disease is not considered for all people. Because some people completely isolate themselves from society. For this reason, these individuals do not get the disease. There is also a protective treatment (consciousness) compartment that covers conscious individuals, considering that it will play a significant role in ending the disease. Transitions between compartments depend on the proportions which fall into the range $[0.1]$. In this model, from the susceptible compartment at the rate of $\beta$ to the hidden TB compartment, and also from the susceptible compartment at the rate of $\alpha$, individuals switch to the infected compartment. Although the hidden TB compartment has high body resistance and contains the virus in its body, it has not yet actively experienced the disease and cannot transmit it to other individuals in the society where it is located. For this reason, protective treatment is applied to the individuals in this compartment to ensure that the recovered individuals are transferred to the compartment in which they are stated. Individuals who accepted this treatment have been also considered as conscious individuals. Protective treatment has been applied to individuals in the ratio of $f$ individuals in the hidden TB compartment, and individuals in the ratio of $m$ have given positive responses to the treatment and moved to the recovered compartment.

Infected individuals live actively and can infect other people. At the same time, the disease becomes active due to the decrease in body resistance of individuals at the rate of $\gamma$ from the hidden TB compartment and passes to the compartment where the infected individuals are located. Individuals at the rate of $z$ in the infected compartment can join those who recover without any treatment method. Meanwhile, by applying the main treatment method to the infected individuals at the ratio of $\theta$, individuals at the rate of $c$ in this compartment join the individuals who have overcome the disease and recovered. Normal death occurs in the rate of $\mu$ in all of these compartments, but death from disease occurs in the fraction of $\sigma$ in the individuals $I$, $T_1$ and $T_2$ compartments as shown in Figure 1.

The model is therefore given by the following set of ordinary differential equations:

subject to the initial conditions (IC),

where $(S(t), L(t), T_1(t), I(t), T_2(t), R(t))\in {\mathbb{R}}^6_+$. The functions $S(t)$, $L(t)$, $T_1(t)$, $I(t)$, $T_2(t)$, $R(t)$ and their derivatives are considered to be continuous at $t\geq0$ in this situation.

3.   Analysis of the model

The positivity and boundedness of the solution for the recommended model (2.1) are given in this section. The existence conditions and stability findings for the equilibria are then given.

3.1.   Positivity of solutions and determining the biologically invariant region

We begin with the following theorem to this subsection:

Theorem 1. The proposed model (2.1)'s solution set $\left\{S\left(t\right), L\left(t\right), T_1\left(t\right), I\left(t\right), T_2\left(t\right), R\left(t\right) \right\}$ combined with the IC (2.2), is non-negative for all $t > 0$.

Proof 1. According to the study's suggestion ^[55], we evaluate the first equation while accounting for the nonlinear system of equations (2.1):

which means that

By integrating Equation (3.2) and using the exponential growth condition, we get

this gives

Theorem 2. In area $\mathcal{A}\subset {\mathbb{R}}^6_+$, given by following, the solutions of system (2.1) with IC (2.2) are specified:

Proof 2. By taking the total population, we have

Then we have the following for the whole population

Equation (3.7)'s solution is presented as

where $N_0 = N(0)$ is the definition of the beginning population. With the aid of the Birkhoff-Rota theorem, we can state that if $N_0 < \frac{\Lambda}{\mu}$, then as $t\rightarrow \infty$, asymptotically $N(t)\rightarrow \frac{\Lambda}{\mu}$ in Eq (3.5), and the overall population size becomes $N(t)\rightarrow \frac{\Lambda}{\mu}$, then $0 \le N \le \frac{\Lambda}{\mu}$. As a result, region $\mathcal{A}$ is where all of the model's viable solutions converge ^[57].

3.2.   Existence-Uniqueness of solution of model (2.1)

Firstly, we start by the following Volterra-type integral equations:

Let us define the following kernels as

The following theorem then emerges:

Theorem 3. If the following inequality is confirmed, then $\varphi_{1}, \varphi_{2}, \varphi_{3}, \varphi_{4}, \varphi_{5}$ and $\varphi_{6}$ are in accordance with the Lipschitz assumptions and contractions:

where, $\left\| S \right\| \leq m_{1}$, $\left\| L \right\| \leq m_{2}$, $\left\| T_1 \right\| \leq m_{3}$, $\left\| I \right\| \leq m_{4}$, $\left\| T_2 \right\| \leq m_{5}$, $\left\| R \right\| \leq m_{6}$, $q_{1} = \beta m_{2}+ \alpha m_{4} +\mu, \ q_{2} = \beta m_{1}+ \gamma m_{4} +f +\mu$, $q_{3} = m+\mu+\sigma$, $q_{4} = \gamma m_{2}+\alpha m_{1}+\theta+z+\mu+\sigma$, $q_{5} = c+\mu+\sigma$ and $q_{6} = \mu.$

Proof 3. Let $S_1$ and $S_2$ be two functions for the kernel $\varphi_{1}$; $L_1$ and $L_2$ be two functions for the kernel $\varphi_{2}$; $T_{1_{1}}$ and $T_{1_{2}}$ be two functions for the kernel $\varphi_{3}$; $I_1$ and $I_2$ be two functions for the kernel $\varphi_{4}$; $T_{2_{1}}$ and $T_{2_{2}}$ be two functions for the kernel $\varphi_{5}$; and $R_1$ and $R_2$ be two functions for the kernel $\varphi_{6}.$ Then we have

and

As a result, kernels $\varphi_{1}$, $\varphi_{2}$, $\varphi_{3}$, $\varphi_{4}$, $\varphi_{5}$ and $\varphi_{6}$ satisfy the Lipschitz requirements, and if $0\leq q_{1}, q_{2}, q_{3}, q_{4}, q_{5}, q_{6} < 1,$ then $q_{1}, q_{2}, q_{3}, q_{4}, q_{5}$ and $q_{6}$ is likewise a contraction of kernels $\varphi_{1}$, $\varphi_{2}$, $\varphi_{3}$, $\varphi_{4}$, $\varphi_{5}$ and $\varphi_{6},$ respectively. It establishes the theorem.

In light of kernels $\varphi_{1}$, $\varphi_{2}$, $\varphi_{3}$, $\varphi_{4}$, $\varphi_{5}$ and $\varphi_{6}$, the system described in Eq (3.9) can be rewritten as follows:

We can proceed with the following recursive formula

where $S_{0} \left(t\right) = S\left(0\right)$, $L_{0} \left(t\right) = L\left(0\right)$, $T_{1_0} \left(t\right) = T_1\left(0\right)$, $I_{0} \left(t\right) = I\left(0\right)$, $T_{2_0} \left(t\right) = T_2\left(0\right)$ and $R_{0} \left(t\right) = R\left(0\right).$ Then we can write

where $S_{n}\left(t\right) = \sum_{j = 1}^{n}{\Psi_{n}\left(t\right)}$, $L_{n}\left(t\right) = \sum_{j = 1}^{n}{\Delta_{n}\left(t\right)}$, $T_{1_{n}}\left(t\right) = \sum_{j = 1}^{n}{\Phi_{n}\left(t\right)}$, $I_{n}\left(t\right) = \sum_{j = 1}^{n}{\Pi_{n}\left(t\right)}$, $T_{2_{n}}\left(t\right) = \sum_{j = 1}^{n}{\Theta_{n}\left(t\right)}$ and $R_{n}\left(t\right) = \sum_{j = 1}^{n}{\Xi_{n}\left(t\right)}.$ By taking the norm of both sides of Eq (3.15), we have

Since the kernels satisfy the Lipschitz condition (see Theorem 3), we get

Then, using the final inequality, we arrive at:

We derive the following theorem from these findings.

Theorem 4. The suggested TB model has a solution under the presumption that we get $t_{max}$ holding:

Proof 4. Taking into account the functions $S\left(t\right)$, $L\left(t\right)$, $T_1\left(t\right)$, $I\left(t\right)$, $T_2\left(t\right)$ and $R\left(t\right)$ are bounded and their kernels $\varphi_{1}$, $\varphi_{2}$, $\varphi_{3}$, $\varphi_{4}$, $\varphi_{5}$ and $\varphi_{6}$ hold the Lipschitz condition, we can give the following by taking Eq (3.18) into account,

The functions in Eq (3.20) are now demonstrated to be the solutions of the specified TB model. We believe

Then we now present that the terms stated in Eq (3.21) maintain that $\left\|\omega_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\vartheta_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\varkappa_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\varepsilon_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\varsigma_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$ and $\left\|\varrho_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0.$ Because of having

and

recursively carrying out this procedure, we obtain

and

Considering these last two inequalities at $t_{max}$ point, we have

and

The final step is taken, after applying the limit on both sides of the final inequalities as $n \rightarrow \bf{\infty},$ and by taking into account the theorem's 3.3 conclusions, we get $\left\|\omega_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\vartheta_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\varkappa_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\varepsilon_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$, $\left\|\varsigma_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0$ and $\left\|\varrho_{\bf{\infty}}\left(t\right) \right\|\rightarrow 0.$

Theorem 5. The TB model constructed in the paper has a unique solution.

Proof 5. Suppose that there is a different systemic solution, such as $S_{1}\left(t\right)$, $L_{1}\left(t\right)$, $T_{1_{1}}\left(t\right)$, $I_{1}\left(t\right)$, $T_{2_{1}}\left(t\right)$ and $R_{1}\left(t\right)$. After that we get

When both sides of Eq (3.23) are subjected to the norm, we get

As a result of the kernels $\varphi_{1}$, $\varphi_{2}$, $\varphi_{3}$, $\varphi_{4}$, $\varphi_{5}$ and $\varphi_{6}$ satisfying the Lipschitz criterion, we can write

which gives

Hence, we have $\left\| S \left(t\right)-S_{1} \left(t\right)\right\| = 0$, $\left\| L \left(t\right)-L_{1} \left(t\right)\right\| = 0$, $\left\| T_1 \left(t\right)-T_{1_{1}} \left(t\right)\right\| = 0$, $\left\| I \left(t\right)-I_{1} \left(t\right)\right\| = 0$, $\left\| T_2 \left(t\right)-T_{2_{1}} \left(t\right)\right\| = 0$ and $\left\| R \left(t\right)-R_{1} \left(t\right)\right\| = 0$ which demonstrate $S \left(t\right) = S_{1} \left(t\right)$, $L \left(t\right) = L_{1} \left(t\right)$, $T_1 \left(t\right) = T_{1_{1}} \left(t\right)$, $I \left(t\right) = I_{1} \left(t\right)$, $T_2 \left(t\right) = T_{2_{1}} \left(t\right)$ and $R \left(t\right) = R_{1} \left(t\right).$ As a result, the model is shown to have a unique solution, proving the theorem.

4.   Equilibria, stability and reproduction number

To determine the system (3.7) equilibrium points, we set:

Six steady states are produced by solving system Eq (4.1) collectively. According to their biological importance, we provide these equilibria and describe their local behavior. The disease-free equilibrium (DFE), which is denoted as the first equilibrium point, stated as $\Omega_1 = (\frac{\Lambda }{\mu}, 0, 0, 0, 0, 0)$, this indicates that there is no cell population. Co-equilibrium point, which is the second equilibrium point, is given as

The third equilibrium is another co-equilibrium point presented by

Finally, the endemic equilibrium is given as

where $M = \dfrac{1}{\mu (\beta +\gamma)-\alpha (f+ \mu) +\beta \sigma +\beta (\theta +z)}.$

In the next subsection, we proceed with the evaluation of the reproduction number so that one can have some idea about the dynamics of the disease by using this value. Moreover, we show the local stability results of equilibria that have been obtained for the system in the form of theorems and proofs.

4.1.   Basic reproduction number

The population group that the model we are considering here assumes is heterogeneous, with non-homogeneous individuals that have been grouped. First, we provide the solution set as:

then we use the next generation matrix approach described in ^[58] to evaluate the system (2.1)'s fundamental reproduction number. Following that, we define the solution set provided by Eq (4.2) as the difference between two matrices:

where

The matrix generation approach is used to define $F = \bigg[\frac{\partial F_i(\Omega_1)}{\partial t_j} \bigg]$ and $V = \bigg[\frac{\partial V_i(\Omega_1)}{\partial t_j} \bigg]$, $1 \le i, j \le 2$ for the F and V matrices of uninfected division at the equilibrium point $\Omega_1.$ As more explicitly, they can be written in the following forms:

where the matrix V is non-singular and the matrix F is non-negative. With the use of the matrix $FV^{-1}$'s spectral radius at the equilibrium point $\Omega_1$, the disease's fundamental reproduction number is computed, which is indicated by two cases namely $\mathcal{R}_{0_1}$ and $\mathcal{R}_{0_2}$:

in which

Theorem 6. In the epidemic model, the disease-free equilibrium point $\Omega_1$ is locally asymptotically stable (LAS) if $\mathcal{R}_{0} < 1$, else unstable.

Proof 6. Now, we take into consideration the following Jakobian matrix to highlight the stability criteria at the DFE point indicated as $\Omega_1$.

The characteristic equation (CE) of matrix $\mathcal{J}(\Omega_1)$ can thus be found as:

where

are the solutions of the CE. It is obvious that $\lambda_{1, 2, 4, 6}$ are negative. Furthermore, we can obtain that $\lambda_3$ is negative if $\mathcal{R}_{0_1} < 1$ and $\lambda_5$ is negative as well if $\mathcal{R}_{0_2} < 1,$ which means that if $\mathcal{R}_{0} = \max \left[\mathcal{R}_{0_1}, \mathcal{R}_{0_2}\right] < 1$ the DFE is LAS. The proof is finished with this.

Theorem 7. The second equilibrium point $\Omega_2$ of the epidemic model is locally asymptotically stable if $\mathcal{R}_{0_1} > 1$, otherwise there is at least one unbounded solution.

Proof 7. In order for the stability of $\Omega_2(\lambda)$, we have the following characteristic equation:

where

The remaining two roots, namely $\lambda_5$ and $\lambda_6$, satisfy the following equation:

in which $A = \mathcal{R}_{0_1} \mu$, $B = \dfrac{\Lambda\beta}{\mathcal{R}_{0_1}}(\mathcal{R}_{0_1}-1)$. According to the Routh-Hurwitz stability criteria second order ^[59,60], the coefficients of the quadratic characteristic equation given in Eq (4.4) must satisfy the following conditions if the roots of the equation have negative real part:

which means that the following inequalities hold:

5.   Numerical results

The significance of numerical results for the TB model we developed by taking the consciousness parameter into account is covered in this section. In the present paper, for the simulation, we have taken the parameter values as given in Table 1. In Table 1, we have considered the values as a parameter of "year". We have utilized the parameter value as the year in all of our simulations and graphs.

Figure 2 depicts the population dynamics in the model's behaviors and densities. In Figure 3, the impact of the parameter $\alpha$is depicted, which stands for the rate of transmission of susceptible individuals to infected compartment, on the people who have infected and latent. Considering Figure 3, it is possible to draw the conclusion that when the parameter rises from $0.0006$ to $0.00014,$ when the populations in I increases, the population of L decreases.

We have demonstrated the efficiency of the parameter $\beta$ in 4, which represents the rate of susceptible individuals to enter the hidden TB compartment, on the latent and infected classes. By considering Figure 4, it can be concluded that as the parameter increases from $0.0008$ to $0.0023$, when the populations in $L$ increase, the population of $I$ decreases. In Figure 5, we have rededicated the consciousness effect for the number of infected individuals with TB. According to Figure 5, we have concluded that as the parameter $f$ increases from $0.6$ to $0.85$, the number of infected individuals with TB decreases. This result is very important in terms of determining a parameter that helps to reduce the number of TB cases.

In Figure 6, in relation to the parameter $z$, we have shown the population density of the $R$ class. The figure makes it evident that as the parameter's values rise from $0.4$ to $0.9$, the density of the $R$ class rises along with it.

6.   Concluding remarks

In this study, we have constructed an $SLT_{1}IT_{2}R$ model that contains an effective consciousness strategy for the TB epidemic disease. With the help of the aforementioned model, we have highlighted the usefulness and various facets of consciousness. We have established the biologically possible zone, the solutions' positivity, and their boundlessness. The existence and uniqueness (E & U) of the solutions are demonstrated using the Lipschitz criteria.

The effectiveness of the factors on the population dynamics has been supplied based on the results that are shown in the figures. The dynamics of the population's behaviors and densities in the model are shown in Figure 2. Figures 3 and 4 show, respectively, how the parameters $alpha$ and $beta$ have an impact on latent and infected people. In Figure 5, we have described the dynamics of the consciousness population by taking $f$ values into account. According to Figure 5, we have concluded that as the parameter $f$ increases from $0.6$ to $0.85$, the number of infected individuals with TB virus decreases. This result is very important in terms of determining a parameter that helps to reduce the number of TB cases. We display the population density of the recovered people in relation to parameter $z$ in Figure 6, which is the proportion of infected individuals recovering without treatment.

The impacts of the treatment and being educated thoughts can be highlighted in future studies by employing appropriate control strategies. Additionally, the fractional order can be taken into consideration when applying the integer-order model.

Acknowledgments

The authors would like to thank the reviewers and editors of this paper for their careful attention to detail and constructive feedback that improved the presentation of the paper greatly.

The authors were supported by TUBITAK (The Scientific and Technological Research Council of Türkiye). Fatma Özköse was supported by Research Fund of the Erciyes University. Project Number: FDS-2021-11059.

Conflicts of interest

Dr. Mehmet Yavuz is a Guest Editor of special issue "Theoretical and Numerical Study of Nonlinear Models (Dynamical Systems)" for Mathematical Modelling and Control. Dr. Mehmet Yavuz was not involved in the editorial review and the decision to publish this article.

The authors declare that they have no conflicts of interest to report regarding the present study.