UV radiation sensitivity of bacteriophage PhiX174 - A potential surrogate for SARS-CoV-2 in terms of radiation inactivation

1.   Introduction

Due to the wide variety of applications in fields including associative memories, signal processing, parallel computation, pattern recognition, neural networks have drawn a lot of interest in recent years. In many real-world systems, artificial neural networks, neural networks, biological systems have inevitable applications. ^{[1,2,3,4,5,6,7]}. Due to the obvious transmission frequency of interconnected neurons and the finite switching speeds of the amplifiers, time delays are ineluctably given. Their presence might affect a system's stability by causing oscillation and instability features ^{[8,9,10,11,12,13,14,15,16,17,18]}. Delayed dynamical networks and many time-delay system kinds have been studied, and numerous important outcomes have been presented ^{[19,20,21,22,23,24,25]}.

Kosko was the first person to propose that BAM-NNs could be important to the NNs theory ^[26]. Furthermore, BAM neural frameworks involving delays attracted significant thought and underwent in-depth research. While there is no connection between neurons in the same layer, neurons in another layer are entirely interconnected to those in the first layer. It performs a two-way affiliated hunt to store bipolar vector combines by cycles of forward and backward propagation information streams between the two layers, and it sums up the single-layer auto-cooperative Hebbian connection to a two-layer design coordinated hetero acquainted circuits. As a result, it has numerous applications in the fields of artificial intelligence and pattern identification ^{[27,28,29,30,31,32,33,34,35]}. Appropriately, the BAM neural system has been generally concentrated on both in principle and applications. This makes focusing on the stability of the BAM neural framework, which has largely been studied, fascinating and fundamental ^{[36,37,38,39,40,41,42,43,44]}.

The synchronization control of chaotic networks plays vital role in applications such as image encryption, secure communication, DC-DC motor and etc. ^{[45,46,47,48]}. Satellites play a significant part in the advancement of space technology, civic, military, and scientific endeavors. In particular, feedback control, adaptive control, sampled-data control, and other strategies have been employed to synchronize and regulate the satellite systems ^[49,50]. Recently, the issue of memristive BAM networks synchronization with stochastic feedback gain variations in ^[50].

It is inferred that in real-world scenarios, a nearby float framework as noted in practical model controller does not avoid the proceed out of coefficient uncertainty, leading to the murkiness in controller execution caused by the required word length in any updated structures or additional parameter turning in the final controller use. Along the same ideas, it is crucial to design a non-fragile controller such that it is insensitive to uncertainty. Non-fragile control has developed into a fascinating topic in both theory and practical application. There has been extensive research into the use of non-fragile controllers in recent years ^[51,52]. However, the problem of non-fragile control of a BAM delayed neural network and controller gain fluctuation has not been thoroughly examined.

This study examines the non-fragile synchronization for a BAM delayed neural network and a randomly occurring controller gain fluctuation, which is motivated by the studies. New stability requirements for BAM neural networks with arbitrarily occurring controller gain fluctuation are derived in terms of LMI by building an appropriate Lyapunov-Krasovskii functional (LKF) and using conventional integral inequality techniques. Solving the suggested LMI condition yields the gain matrices for the proposed controller design. Finally, a numerical example is used to illustrate the proposed strategy.

Notations: In this work, $\mathbb{R}^p$ represents Euclidean space of p dimension. $\mathbb{R}^{p\times q}$ denotes the set of all $p\times q$ real matrices. The identity matrix is denoted by I. Here $R > 0(<0)$ represents $R$ is a symmetric positive (negative) definite matrices. The elements below the main diagonal of a symmetric matrixl is given by '*'.

2.   Problem statement and preliminaries

In this study, we will investigate the synchronization of BAM delayed neural network with randomly occurring. The BAM NNs with time-varying delay components can be modeled as follows

where $\gamma_i(\aleph) \ and \ \delta_j(\aleph)$ are the state variables of the neuron at time $\aleph$ respectively. The non linear functions $\tilde{f}_j(\cdot), \ \tilde{g}_i(\cdot)$ are neuron activation functions. The positive constants $a_i, b_j$ denote the time scales of the respective layers of the neurons. $w_{ij}^{(1)}, \ w_{ij}^{(2)}, \ v_{ji}^{(1)}, \ v_{ji}^{(2)}$ are connection weights of the network. $I_i\ and \ J_j$ denotes the external inputs. $\sigma(\aleph), \kappa(\aleph)$ are time varying delays satisfying

and, $\sigma, \ \kappa, \ \mu_1,$ and $\mu_2$ are constants.

Consequently, the corresponding compact matrix form can be used to describe the master system (2.1) as,

where, $\mathscr{B} = diag[b_1, b_2, ..., b_n] > 0, \ \ \mathscr{A} = diag[a_1, a_2, ..., a_n] > 0, \ \mathscr{W}_k = (w_{ij}^{(k)})_{(n\times n)}, \ \mathscr{V}_k = (v_{ij}^{(k)})_{(n\times n)}, k = 1, 2.$

Assumption (1). $\tilde{g}_{j}(\cdot), \tilde{f}_{i}(\cdot)$ are neuron activation functions, which is bounded, then there exist constants $\mathbf{H}^{-}_{i}, \ \mathbf{H}^{+}_{i}, \ \mathbf{L}^{-}_{j}, \ \mathbf{L}^{+}_{j}$ such that

where, $j = 1, .., n, i = 1, ... m,$ and $\varrho, \phi \in \mathbb{R}$ with $\phi \neq\varrho$. We define the subsequent matrices for ease of notation:

Master system and slave system state variables are represented by $\theta(\aleph), \lambda(\aleph)$ and $\hat{\theta}(\aleph)$ and $\hat{\lambda}(\aleph)$, respectively. We take into account the master system's slave system in the follows.

We choose the following non-fragile controller:

Here the controller gain matrices are given by $\mathscr{K}_1, \mathscr{K}_2$. The matrix $\Delta \mathscr{K}_i(\aleph) (i = 1, 2)$ satisfy

and

where $\mathscr{H}_i, \mathscr{E}_i$ are known constant matrices. To desribe randomly accuring control gain fluctuation we introduced the stachastic variables $\phi(\aleph), \varrho(\aleph) \in \mathbb{R}$. It is a sequence of white noise generated by Bernoulli distribution with values of zero or one

where $0 \leq \varrho, \phi \leq 1$ is constant.

Set the synchronization error signals $\varpi(\aleph) = \hat{\lambda}(\aleph)-\lambda(\aleph)$ and $\zeta(\aleph) = \hat{\theta}(\aleph)-\theta(\aleph)$. Error dynamics between systems (2.3) and (2.5) can therefore be written as follows:

where $g(\zeta(\aleph)) = \tilde{g}(\hat{\theta}(\aleph))-\tilde{g}(\theta(\aleph))$, and $f(\varpi(\aleph)) = \tilde{f}(\hat{\lambda}(\aleph))-\tilde{f}(\lambda(\aleph))$.

The following crucial conditions are used to obtain our main findings:

Lemma 2.1. ^[53] (Schur complement) Let $\mathscr{Z}$, $\mathscr{V}, \mathscr{O}$ be given matrices such that $\mathscr{Z} > 0$, then

Lemma 2.2. ^[54] Given matrices $\mathscr{Z} = \mathscr{Z}^T, \mathscr{R}, \mathscr{O}$ and $\mathscr{Q} = \mathscr{Q}^T > 0$ with appropriate dimensions

for all $\mathbf{L}(\aleph)$ satisfying $\mathbf{L}^T(\aleph)\mathbf{L}(\aleph)\leq I$ if and only if there exists a scalar $\varepsilon > 0$ such that

Lemma 2.3. ^[55] For a given matrix $Z \in S_n^+$ and a function $\varsigma : [c, d] \rightarrow \mathbb{R}^n$ whose derivative $\dot{\varsigma} \in P C ([c, d], \mathbb{R}^n)$, the following inequalities hold: $\int_{c}^{d} \dot{\varsigma}^T(r)Z\dot{\varsigma}(r)dr \geq \frac{1}{d-c} \ \hat{\varphi} \overline{Z} \hat{\varphi},$ where $\overline{Z} = diag \{ Z, 3Z, 5Z \}, \ \hat{\varphi} = [\varphi_1^T\ \varphi_2^T\ \varphi_3^T]^T$, $\varphi_1 = \varsigma(d)-\varsigma(c), \ \varphi_2 = \varsigma(d)+\varsigma(c)-\frac{2}{d-c}\int_c^d \varsigma(r)dr$, $\varphi_3 = \varsigma(d)-\varsigma(c)+\frac{6}{d-c}\int_c^d \varsigma(r)dr -\frac{12}{(d-c)^2}\int_c^d \int_c^d \varsigma(u)duds.$

3.   Stability results

The necessary requirements for guaranteeing the stability of system (2.10) are established in this part.

Theorem 3.1. From Assumption (A), $\phi, \varrho,$ and $\epsilon_i$ are positive scalars, if there exist symmetric matrices $\mathscr{P}_i > 0, \ \mathscr{Q}_i > 0, \ \mathscr{R}_i > 0, \ \mathscr{Z}_i > 0, \ any \ matrices \ \mathscr{J}_i$ and $\mathscr{G}_i, \ diagonal \ matrices \ \mathscr{S}_i > 0 \ (i = 1, 2)$ satisfying

where

When this happens, the system (2.10) is asymptotically stable and $\mathscr{K}_i = \mathscr{J}_i^{-1}\mathscr{G}_i.$ are control gain matrices.

Proof. Take into account the LKF candidate below:

where

The infinitesimal operator $\mathcal{L} \ of V(\zeta_\aleph, \varpi_\aleph, \aleph)$ is:

Using the stochastic derivative of $V(\zeta_\aleph, \varpi_\aleph, \aleph)$, we can determine:

By applying Lemma 2.3 in (2.17), we can obtain

where

From the assumption (A), there exists a diagonal matrices $\mathscr{S}_1 > 0, \ \mathscr{S}_2 > 0 \ and \ \mathbf{H}_i, \ \mathbf{L}_i (i = 1, 2)$, the following inequalities hold:

The following equations satisfy for any matrices $\mathscr{J}_1, \mathscr{J}_2$ and scalar $\epsilon_1, \epsilon_2$:

substituting $({3.4})$–$({3.6}),$ and $({3.7})$–$(3.23)$ in (3.3), we get

where $\xi(\aleph) = \bigg[\zeta^T(\aleph) \ \zeta^T(\aleph-\kappa) \ g^T(\zeta(\aleph)) \ g^T(\zeta(\aleph-\kappa(\aleph))) \ \int_{\aleph-\kappa}^{\aleph}\zeta^T(s)ds \ \int_{\aleph-\kappa}^{\aleph}\int_{s}^{\aleph}\zeta^T(s)duds \ \dot{\zeta}^T(\aleph) \ \varpi^T(\aleph) \\ \varpi^T(\aleph-\sigma) \ f^T(\varpi(\aleph)) \ f^T(\varpi(\aleph-\kappa(\aleph))) \ \int_{\aleph-\sigma}^{\aleph}\varpi^T(s)ds \ \int_{\aleph-\sigma}^{\aleph}\int_{s}^{\aleph}\varpi^T(s)duds \ \dot{\varpi}^T(\aleph) \bigg]^T.$

It gives that $\Xi \ < 0$. This demonstrates that the system (2.10) is asymptotically stable using the Lyapunov stability theory. The proof is now complete.

Theorem 3.2. Under Assumption (A), $\phi, \varrho$ and $\epsilon_i$ are positive scalars, then there exist symmetric matrices $\mathscr{P}_i > 0, \ \mathscr{Q}_i > 0, \ \mathscr{R}_i > 0, \ \mathscr{Z}_i > 0,$ diagonal matrices $\mathscr{S}_i > 0$, for any matrices $\mathscr{J}_i$, $\mathscr{G}_i,$ and scalars $\rho_i > 0 \ (i = 1, 2)$ such that

where

The controller gain matrices are also provided by in equation (2.6) are given by $\mathscr{K}_i = \mathscr{J}_i^{-1}\mathscr{G}_i.$

Proof. By using Schur complement,

From Lemma 2, we get

It is clear that the disparities in (3.15) still exist. The evidence is now complete.

4.   Numerical example

Two examples are provided in this part to show the applicability of our findings.

Example 4.1. The following BAM neural network with time varying delays:

with the following parameters:

Additionally, we take $\kappa = 3.2, \ \sigma = 3.2, \ \mu_1 = 0.9, \ \mu_2 = 0.9, \ \phi = 0.9, \ \varrho = 0.9, \ \epsilon_1 = 0.5,$ and $\epsilon_2 = 0.5$. By solving the LMIs in Theorem 3.2, we get

As well as the following non-fragile controller gains matrices:

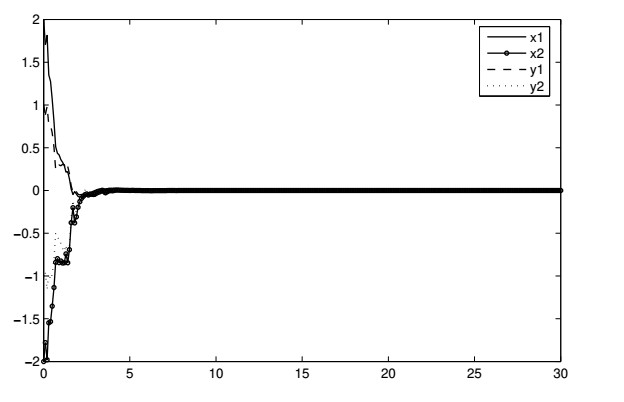
In this scenario is proved the given system is asymptotically stable. In Figure 1, state response are depicted.

5.   Conclusions

The issue of BAM delayed neural networks with non-fragile control and controller gain fluctuation has been examined in this article. To ensure the stability of the aforementioned systems, delay-dependent conditions are established. In terms of linear matrix inequalities (LMIs), necessary conditions are obtained by building an L-K functional and utilizing the traditional integral inequality technique. This technique ensures asymptotically stability of addressed to the concerned neural networks. Lastly, a numerical example is provided to demonstrate the viability of the findings in this study. Stochastic differential equations and complex networks both respond well to this approach in future research.