A strategy for hepatitis diagnosis by using spherical $q$-linear Diophantine fuzzy Dombi aggregation information and the VIKOR method

1.   Introduction

The problem of recovering low-rank and sparse matrices or tensors from small sets of linear measurements occurs in many areas, such as the foreground in video surveillance ^[1], hyperspectral compressive sensing ^[2] and image denoising ^[3]. Mathematically, the optimization model of a matrix recovery is described as follows:

where $\|A\|_{*} = \Sigma _{k = 1}^{r}\sigma_{k}(A)$, $\sigma_{k}(A)$ denotes the $k$th largest singular value of $A\in {\mathbb{R}}^{n_{1}\times n_{2}}$ of rank $r$. $\|E\|_{1}$ denotes the sum of the absolute values of the matrix entries and $\lambda$ is a positive weighting parameter. $Q\subseteq {\mathbb{R}}^{n_{1}\times n_{2}}$ is a linear subspace, and $P_{Q}$ denotes the projection onto $Q$. Since the matrix recovery problem is closely connected to the robust principal component analysis (RPCA) problem, then it can be formulated in the same way as RPCA. Further, many theoretical results and algorithmic methods for recovering a low-rank and sparse matrix or tensor have been obtained; for example, see ^{[1,2,4,5,6,7,8,9,10,11,12]}, and the references therein.

Wright et al. ^[6], Li^[13], Chen and Xu ^[14] studied the robust matrix completion problem that we call matrix compressive recovery namely, $P_{Q} = P_{\Omega}$, where $\Omega$ is a random subset of indices for the known entries. Further, (1.1) is formulated as follows:

In ^[1], Candès et al. have proved that both $A$ and $E$ can be recovered by solving (1.2) with high probability. Meanwhile, an algorithm and some applications in the area of video surveillance were discussed in detail. Li ^[13] also gave some new theorems and models for solving (1.2). Then Chen and Xu ^[14] discussed (1.2) via the augmented Lagrange multiplier (ALM) method and studied its application in image restoration. Meng et al. proposed the following problem in ^[3]:

They also used the ALM algorithm for solving (1.3), but they did not discuss the convergence. Li et al. ^[15] proved that the ALM algorithm was convergent for the optimization (1.3). Further, they stated that (1.3) was equivalent to (1.2). Chen et al. ^[16] provided a new unified performance guarantee that an exact recovery can be obtained when minimizing the nuclear norm plus $l_1$ norm.

Then the robust formulation has been improved to deal with Gaussian noise ^[17], leading to the following convex optimization problem (convex robust matrix completion):

He et al. ^[18,19] developed a robust version of the Grassmannian rank-one update subspace estimation (GROUSE) ^[20] algorithm named the Grassmannian robust adaptive subspace tracking algorithm (GRASTA), which aims at solving the problem of robust subspace tracking. Their algorithm can be cast to solve problems formulated as

where $Gr(m, r)$ is the Grassman manifold. The advantage of their algorithm is that it is designed to tackle the problem of online subspace estimation from incomplete data; hence it can also be cast to solve online low-rank matrix completion where we observe one column of the matrix $M$ at a time.

In 2018, Chiang et al. ^[21] proposed a general model

which exploits side information to better learn low-rank matrices from missing and corrupted observations, and show that the proposed model can be further applied to several popular scenarios such as matrix completion and RPCA.

On the other hand, for a given low-rank $r$ and sparse level $|S|_0$, some non-convex models and algorithms were proposed.

In 2014, a non-convex algorithm based on alternating projections, namely AltProj, was presented in ^[22] which solves the following problem:

where $r^{\ast}$ is the rank of the underlying low rank matrix, $\Omega$ denotes the support set of the underlying sparse matrix and $|\Omega|$ is the cardinality of $\Omega$. AltProj iteratively updates $L$ by projecting the matrix $D-S$ onto the space of rank-$r$ matrices (denoted by $\mathcal L_{r}$, ) which can be done via the singular value decomposition, followed by truncating out small singular values, and then updating $S$ by projecting the matrix $D-L$ onto the space of sparse matrices (denoted by $\mathcal S$, ) which can be done by the hard thresholding operator. In 2016, Gu et al. ^[23] factorized $L$ into the product of two matrices, that is $L = UV$, and performd alternating minimization over both matrices. Yi et al. ^[24] applied a similar factorization and an alternating descent algorithm. Then, a method based on manifold optimization which reduces the dependence on the condition number of the underlying low-rank matrix theoretically was proposed by Zhang and Yang ^[25]. In 2019, an accelerated AltProj was proposed by Cai et al. ^[26] and empirical performance evaluations showed the advantage of the accelerated AltProj over other state-of-the-art algorithms for RPCA.

In 2015, Wang et al. ^[27] proposed a proximal alternating robust subspace minimization method for solving the practical matrix completion problem under the prevalent case where the rank of $A$ and the cardinality of $\Omega$ are upper bounded by some known paremeters $r$ and $k$ via the following non-convex, non-smooth optimization model:

where $\mathbb{R}_\Omega^{m\times n}$ denotes the set of $m\times n$ matrices whose supports are subsets of $\Omega$ and $K_S$ is a finite constant introduced to facilitate the convergence proof.

In this paper, we develop an alternating directional method and its variant equipped with the non-monotone search procedure for solving low-rank and sparse structure matrix completion problems from incomplete data. By introducing a parameter $\alpha$, we consider the following problem:

where $\alpha$ represents the sparsity ratio of the sparse part. Based on the factorization $L = UV$ with $U\in \mathbb{R}^{m\times r}$ and $V\in \mathbb{R}^{r\times n}$, (1.9) can be represented as

where $f(U, V, S) = \frac{1}{2}\|P_\Omega(D-UV-S)\|_{F}^{2}.$

The rest of this paper is organized as follows. In Section 2, we give the proposed algorithms in details. Convergence analysis is discussed under mild condition in Section 3. In Section 4, we compare Algorithm 1 with Algorithm 2 through numerical experiments to illustrate the efficiency of the non-monotone technique, also compare the proposed algorithms with the previous algorithm to show the effectiveness of the new algorithms. Finally, we conclude the paper in Section 5.

2.   Proposed algorithms

In this section, we develop two alternating directional methods for solving (1.10), where one of $U, V$ and $S$ is solved in the Gauss-Seidel manner while the other two variables are fixed until convergence. In both algorithms, we apply a single step of the steepest gradient descent method with exact step-size to solve the least square subproblems with respect to variable $U$ or $V$. If $f(U, V, S)$ is denoted by $f_{V, S}(U)$ when $V$ and $S$ are held constant while $f_{U, S}(V)$ when $U$ and $S$ are held constant. The steepest descents about $U$ and $V$ are

and

respectively. The associated exact step-sizes are denoted by $t_{U}$ and $t_{V}$, and can be computed explicitly by

Based on the above discussion, the concrete algorithms can be formally described as Algorithm 1 and Algorithm 2, where Algorithm 1 updates $S$ by minimizing $f(U, V, S)$ with the sparsity level constraint while Algorithm 2 updates it by a non-monotone search approach.

Algorithm 1. Input: $P_\Omega(D)$, $U_{0}\in \mathbb{R}^{m\times r}$, $V_{0}\in \mathbb{R}^{r\times n},$ sparsity parameter $\alpha$, $S_{0}\in \mathbb{R}^{m\times n}$ with $|S_{0}|\leq\alpha |\Omega|$;

Repeat

$1)$ $\nabla f_{V_k, S_k}(U_k) = -\big(P_{\Omega}(D)-P_{\Omega}(U_k V_k +S_k)\big)V^T_k$

$2)$ $t_{U_k} = \frac{||\nabla f_{V_k, S_k}(U_k)||^2_F}{||P_\Omega\big(\nabla f_{V_k, S_k}(U_k)V_k\big)||^2_F}$

$3)$ $U_{k+1} = U_{k}-t_{U_k}\nabla f_{V_k, S_k}(U_k)$

$4)$ $\nabla f_{U_{k+1}, S_k}(V_k) = -U^{T}_{k+1}\big(P_{\Omega}(D)-P_{\Omega}(U_{k+1} V_k +S_k)\big)$

$5)$ $t_{V_k} = \frac{||\nabla f_{U_{k+1}, S_k}(V_k)||^2_F}{||P_\Omega\big(U_{k+1}\nabla f_{U_{k+1}, S_k}(V_k)\big)||^2_F}$

$6)$ $V_{k+1} = V_{k}-t_{V_k}\nabla f_{U_{k+1}, S_k}(V_k)$

$7)$ $S_{k+1} = \hbox{arg}\min\limits_{ |S|\leq\alpha |\Omega|} ||P_{\Omega}(D-U_{k+1} V_{k+1} -S)||^2_F$.

Until termination criteria is reached.

Algorithm 2. Input: $P_\Omega(D)$, $U_{0}\in \mathbb{R}^{m\times r}$, $V_{0}\in \mathbb{R}^{r\times n},$ integer $l\geq 0$, sparsity parameter $\alpha$, $S_{0}\in \mathbb{R}^{m\times n}$ with $|S_{0}|\leq\alpha |\Omega|$;

Repeat

$1)$ $\nabla f_{V_k, S_k}(U_k) = -\big(P_{\Omega}(D)-P_{\Omega}(U_k V_k +S_k)\big)V^T_k$

$2)$ $t_{U_k} = \frac{||\nabla f_{V_k, S_k}(U_k)||^2_F}{||P_\Omega\big(\nabla f_{V_k, S_k}(U_k)V_k\big)||^2_F}$

$3)$ $U_{k+1} = U_{k}-t_{U_k}\nabla f_{V_k, S_k}(U_k)$

$4)$ $\nabla f_{U_{k+1}, S_k}(V_k) = -U^{T}_{k+1}\big(P_{\Omega}(D)-P_{\Omega}(U_{k+1} V_k +S_k)\big)$

$5)$ $t_{V_k} = \frac{||\nabla f_{U_{k+1}, S_k}(V_k)||^2_F}{||P_\Omega\big(U_{k+1}\nabla f_{U_{k+1}, S_k}(V_k)\big)||^2_F}$

$6)$ $V_{k+1} = V_{k}-t_{V_k}\nabla f_{U_{k+1}, S_k}(V_k)$

$7)$ Set $\bar{S}_{k} = \hbox{arg}\min\limits_{ |S|\leq \alpha |\Omega|} ||P_{\Omega}(D-U_{k+1} V_{k+1} -S)||^2_F$ and update

where $\tau_{k}$ satisfies the following non-monotone condition:

Until termination criteria is reached.

Remark 1. In the above algorithms, $|S|$ is the number of non-zero entries of $S$ and the termination criteria is $\frac{||P_{\Omega}(D-U_{k+1} V_{k+1} -S_{k+1})||^2_F}{||P_\Omega(D)||_F^2} < \epsilon.$

Remark 2. By preserving the entries of $P_{\Omega}(D-U_{k+1} V_{k+1})$ with top $\alpha |\Omega|$ large magnitudes and setting the rest to zero, we obtain the sparse matrix $S_{k+1}$ in Algorithm 1 and $\bar{S}_{k}$ in Algorithm 2.

Remark 3. Algorithm 2 is different from Algorithm 1 in that it employs the non-monotone search procedure for updating $S$. The non-monotone line search technique relaxes the single-step descent into a multi-step descent, which greatly improves the computational efficiency. The next section also gives the convergence analysis of the proposed algorithms. In Section 4, many work verified numerically that the non-monotone technique outperforms the traditional monotone strategies. Hence, we here utilize the non-monotone search technique to improve the performance of the proposed algorithms.

3.   Convergence analysis

In this section, we discuss the global convergence monotone Algorithm 1 and non-monotone Algorithm 2. Theoretically, that is an equivalent verification of the robust PCA can reasonably express the mutual encouragement between the low-rank and structured sparsity.

Before that, we first list some notations and preliminaries for the coming main result. For the ease of exposition, let $\{U_{k}, V_{k}, S_{k}\}$ be the sequence generated by Algorithm 1 or Algorithm 2, and

Two propositions are provided first before analysing the convergence, they are the conditions of Lemma 3.6 in ^[26]:

● $|H|\geq\frac{8}{3}\beta\mu_0\gamma(m+n)\log n$;

● the matrix $L$ is $\mu_0$-relevant.

Lemma 1. The sequence $\{U_k, V_k, S_k\}$ generated by Algorithm 2 satisfies:

Proof. By simple deduction

Similarly, we have

Theorem 1. Suppose that there exist $(U_i^TU_i)^{-1}$ and $(V_i^TV_i)^{-1}$ and they are bounded. Then, the sequence $\{U_k, V_k, S_k\}$ generated by Algorithm 2 satisfies:

and

Proof. According to $S_{k+1}$ given by Algorithm 2, we obtain

together with Lemma 1, which implies that

Since

and

then

where $\sigma_{ir}$ is the $i$th largest singular value of the matrix $V_i$.

Similarly, we have

where $\tilde{\sigma}_{ir}$ is the $i$th largest singular value of the matrix $U_i$.

Consequently, $\sum\limits_{i = 1}^\infty(\sigma_{ir}^2\|\nabla_{V_{i}, S_i}(U_i)\|_F^2+\tilde{\sigma}_{ir}^2 \|\nabla_{U_{i+1}, S_i}(V_i)\|_F^2+|\Omega|\tau_i^2)$ is convergent. Thus,

and

The theorem is true from the assumptions.

In addition, from the Lemma 3.6 of ^[28], there exists a scalar $c\ (0 < c < 1)$, such that

Hence,

where $0 < c_1 < 1, \sigma_{k_1}$ is the top singular value of $V_k$. Therefore,

Similarly,

The proof is completed.

Theorem 2. Assume that the sequence $\{U_k, V_k\}$ is bounded and there exist $(U_k^TU_k)^{-1}$ and $(V_k^TV_k)^{-1}$. Then

and

Proof. The $\{L_k\}$ is bounded from the sequence $\{U_k, V_k\}$ is bounded. Then there exists a sub-sequence $\{L_{k_i}\}$ is closed to $L_*^\alpha$. It is noted that

Then

Thus,

That is to say,

Let $D-L_* = S_*$. Then

which shows that

The proof is completed.

4.   Numerical experiments

In this section, we apply the proposed algorithms to solve two problems: some matrix recovery tasks with incomplete samples and some background modeling in video processing. We compare our algorithms and the AM algorithm in ^[23] in the senses of the iteration step (denoted as IT) and the total CPU time (denoted as CPU) in second. Moreover, R.error and Error represent the relative deviation of the deserved matrices (or images) from the given matrices (or images), which are computed by the following formulas:

and

In our implementations, all the codes were written by Matlab R2019b and run on a PC with Intel Xeon E5 processor 2.5GHz and 20GB memory.

4.1.   Numerical experiments for recovering a random matrix

In the experiments, the dimension $n$ of a square matrix $X\in \mathbb{R}^{n\times n}$ is denoted as Size$(X)$ in the list. For each concerned $X$, the sampling density is denoted as Den$(X)$ may be 60%, 70%, 75% and 80%, the rank of the low-rank component is denoted by Rank$(L)$ may be 50, 60, 90 and 100, and the sparsity ratio of sparse part is denoted by Spa$(S)$ may be 5% and 10%. In total, we obtain some instances for each dimension. In each instance, the test matrix is randomly generated. The numerical results are provided in Tables 1–3. Here, the iteration is terminated once the current iterations obey R.error $< 10^{-4}$ or the criterion is not satisfied after 10000 iteration steps. The symbol "-" indicates that the iteration is failing.

For Algorithm 2, we set $l = 2$ and the initial thresholding value in each iteration to be the $p+1$-th largest number of the absolute values of all elements of $S_{k}$, where $p$ is the required number of the non-zero entries of $S$, i.e., $p = \alpha |\Omega|$. By the way, Alg 1 and Alg 2 represent the abbreviations of Algorithm 1 and Algorithm 2, respectively.

The results recorded in Tables 1–3 show that the proposed algorithms are feasible and efficient for solving some matrix recovery tasks with incomplete samples. It is worth mentioning that our proposed algorithms are more effective than AM algorithm (see ^[23]) for large-size problems since both of the algorithms can obtain a solution within reasonable time for the problems with size $10000\times 10000$.

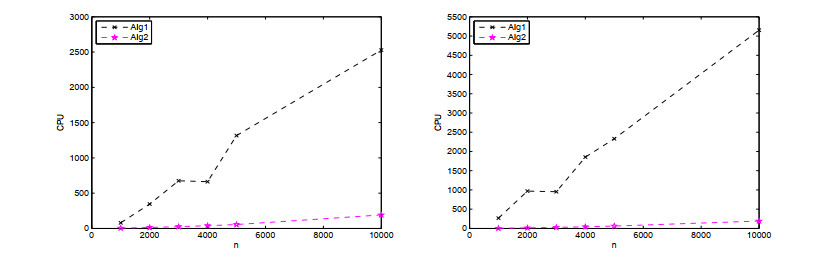
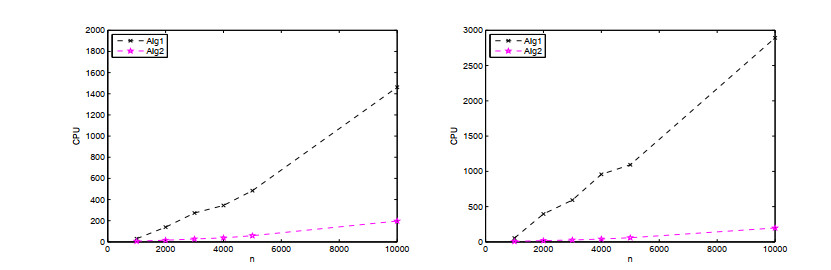
Moreover, the results recorded in Figures 1–2 illustrate the superiority of non-monotone decrease in the iteration procedure of Algorithm 2. We observe Algorithm 2 outperforms Algorithm 1 since the CPU times of Algorithm 2 are much shorter than those of Algorithm 1 and the relative error of Algorithm 2 is smaller than those of Algorithm 1. The acceleration ratio of Algorithm 2 with $60\%$ samples is 13.3 (the left in Figure 1) and 26.8 (the right in Figure 1) respectively, that with $80\%$ samples is 8.0 (the left in Figure 1) and 18.1 (the right in Figure 2) respectively.

4.2.   Numerical experiments for recovering the real data

In order to verify the performance of the new algorithms in solving practical problems, we compare Algorithm 2 and the AM algorithm for solving the background modeling in video processing. The problem of the background modeling is to separate the foreground and the background in the video. We use the AM algorithm and our Algorithm 2 to separate the foreground and the background for four real videos from ^[29]. All videos meet the requirement of the low-rank sparse structure since the background of all frames are relevant and the moving objects are sparse and independent. In our tests, each data matrix consists of the first 200 frames of each video. For example, the first video consists of the first 200 frames with a resolution of $144\times 176$, the size of the matrix should be $25344\times200$ by converting each frame into a vector. Here, the iteration is terminated once the current iterations obey Error $< 10^{-7}$ or the criterion is not satisfied after 3000 iteration steps.

The results recorded in Figures 3–6 are the separation of one frame of each video sequence under $D = A+E$ model. $D$ is the original image, $A$ denotes its background (the low-rank part) and $E$ its foreground (the sparse part).

Table 4 lists the Error and the running time CPU(S) of the experiments. From Table 4, we can see that the running time of the AM is about 2.8–5.4 times that of Algorithm 2, and the accuracy of Algorithm 2 is also always higher than that of AM algorithm in Figures 3–6 and Table 4, so the advantage of Algorithm 2 in the recovery of high-dimensional array is obvious.

5.   Conclusions

In this paper, we focus on the problem of recovering a matrix that is the sum of a low-rank matrix and a sparse matrix from a subset of its entries. This model can characterize many problems arising from the areas of signal and image processing, statistical inference, and machine learning. We propose an alternating directional method for solving the low-rank matrix sparse structure model. The key idea of the method is that each block variables are solved in the Gauss-Seidel manner while the others are fixed until convergence. We further develop a version of our algorithm by introducing non-monotone search technique to improve the performance of the new algorithm. Both versions are theoretically proved to be globally convergent under some requirements. Based on computational records, we observe that both algorithms are computationally inexpensive to find satisfactory results and the non-monotone strategy performs much better than the monotone one from these instances.

Acknowledgments

The authors are very much indebted to the anonymous referees for their helpful comments and suggestions which greatly improved the original manuscript of this paper. The authors are so thankful for the support from the special fund for science and technology innovation teams of Shanxi province (202204051002018) and the scientific research project of Returned Overseas Chinese in Shanxi Province, China (2022-169).

Conflict of interest

The authors declare that they have no conflict of interests.