Positive weak solutions for heterogeneous elliptic logistic BVPs with glued Dirichlet-Neumann mixed boundary conditions

1.   Introduction and previous results

This work is devoted to analyze the existence of positive weak solutions of the following heterogeneous elliptic logistic boundary value problem with mixed and glued Dirichlet-Neumann boundary conditions given by

where the following assumptions are assumed:

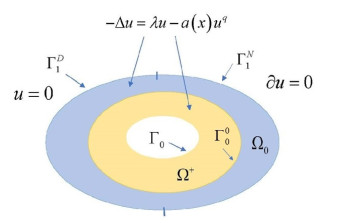
$\rm i)$ The domain $\Omega$ is a bounded domain of $\mathbb{R}^N$, $N\geq 2$ of class ${\mathcal C}^2$, with boundary $\partial \Omega = \Gamma_0 \cup \Gamma_1$, where $\Gamma_0$ and $\Gamma_1$ are two disjoint components of $\partial \Omega$ and $\Gamma_1 = \Gamma_1^{\mathcal{D}} \cup \Gamma_1^{\mathcal{N}}$, being $\Gamma_1^{\mathcal D}$ and $\Gamma_1^{\mathcal N}$ two connected pieces, open and closed respectively as $N-1$ dimensional manifolds, such that $\partial \Gamma_1^{\mathcal D} = \partial \Gamma_1^{\mathcal N} \subset \Gamma_1^{\mathcal N}$;

$\rm ii)$ $-\Delta$ stands for the minus Laplacian operator in $\mathbb{R}^N$ and $\lambda \in \mathbb{R}$;

$\rm iii)$ The potential $a \in {\mathcal C}(\bar{\Omega})$, with $a > 0$, measures the spatial heterogeneities in $\Omega$ and satisfies that

Set $\Omega^+: = \Omega \setminus \bar{\Omega}_0$.

$\rm iv)$ $\partial u = \nabla u \circ \bar{n}$, where $\bar{n}$ is the outward normal vector field to $\partial \Omega$.

Figure 1 shows a possible configuration of the domain $\Omega$, its boundary $\partial \Omega = \Gamma_0 \cup \Gamma_1^{\mathcal D} \cup \Gamma_1^{\mathcal N}$ and the boundary conditions in each piece of the boundary.

The positive solutions of (1.1) are the positive steady-states of the associated evolutionary problem given by

which describes the dynamics of the positive solutions of many reaction-diffusion problems appearing in the applied sciences and engineering. In population dynamics, (1.2) describes the dynamics of a population inhabiting a heterogeneous environment $\Omega$, growing accordingly with a generalized logistic law. From this point of view, $v(x, t)$ stands for the population density, $-\Delta v(x, t)$ is the diffusion term, $\lambda$ is the growth rate of the population and $a(x)$ measures the saturation effect responses to the population stress in $\Omega^+$. As for the boundary conditions, the homogeneous Dirichlet boundary condition on $\Gamma_0 \cup \Gamma_1^{\mathcal D}$ means that $\Gamma_0 \cup \Gamma_1^{\mathcal D}$ are hostile regions, and the homogeneous Neumann boundary condition on $\Gamma_{1}^{\mathcal N}$ guarantees no migration or null flux of population through $\Gamma_1^{\mathcal N}$. The different boundary conditions considered in (1.1) and (1.2) may be due to a heterogeneous distribution of the natural resources through the boundary or close to the boundary. The analysis of the positive solutions of (1.1) is crucial to have a complete understanding of the long time behavior of the positive solutions of (1.2). Also, the analysis of the existence of positive weak solutions of (1.1) is pivotal in the study of the asymptotic behavior as $\gamma \uparrow \infty$ of the strong positive solutions of heterogeneous logistic elliptic boundary value problems with nonlinear mixed boundary conditions like the following

where $b \in {\mathcal C}(\Gamma_1)$ with $b > 0$ on $\Gamma_1$ and

which stand for again the positve steady-states of the associated parabolic problem with nonlinear flux on $\Gamma_1$. In this kind of problems, when $\lambda$ belongs to a suitable interval, the limiting profile of the strong positive solutions when $\gamma \uparrow \infty$, is a positive weak solution of (1.1), as it will be proved elsewhere. The proof of this fact is out the scope of this work.

Although we have assumed throughout this paper that $\Gamma_1$ splits in two connected pieces $\Gamma_1^{\mathcal D}$ and $\Gamma_1^{\mathcal N}$, the results of this work may be generalized in a natural way to cover the case when $\Gamma_1$ splits in $2k$ connected pieces $\left\{ \Gamma_{1i}^{\mathcal D}, \, \Gamma_{1, i}^{\mathcal N}\right\}_{i = 1}^k$, where now

with $\Gamma_1^{\mathcal D}$ and $\Gamma_1^{\mathcal N}$ unconnected and where each piece $\Gamma_{1i}^{\mathcal D}$, $i = 1, \ldots, k$ is between two consecutive pieces of the family $\left\{ \Gamma_{1j}^{\mathcal N}\right\}_{j = 1}^k$ and viceversa.

On the other hand, owing to ^[5], the results into this work also may be generalized to cover the case when, instead of imposing a Neumann boundary condition on $\Gamma_1^{\mathcal N}$, it is imposed a boundary condition of Robin type like $\partial u+b(x)u = 0$, where $b \in {\mathcal C}(\Gamma_1^{\mathcal N})$ with arbitrary sign satisfies adequate technical conditions. The novelty of the results in this work is considering glued Dirichlet and Neumann boundary conditions on a same component of the boundary. These results are pioners in the field, because up the knowledge of the author, this is the first time where this kind of logistic problems have been analyzed.

Before stating our main findings, we introduce some notations and previous results. Let us denote

and let $H^1_*(\Omega)$ be the clousure in $H^1(\Omega)$ of the set of functions ${\mathcal C}_{\Gamma_0 \cup \Gamma_1^{\mathcal D}}^{\infty}(\Omega)$, that is

By construction if $u \in H_*^1(\Omega)$, then $u = 0$ on $\Gamma_0 \cup \Gamma_1^{\mathcal D}$. In the same way, taking into account that $\partial \Omega_0 = \Gamma_0^0 \cup \Gamma_1 = \Gamma_0^0 \cup \Gamma_1^{\mathcal D} \cup \Gamma_1^{\mathcal N}$, we denote

and

Also we denote

that is, any function belonging to $\tilde{H}_*^1(\Omega_0)$ is the extension by $0$ to $\bar{\Omega}$ of a previous function belonging to $H_*^1(\Omega_0)$. By definition, if $u \in \tilde{H}_*^1(\Omega_0)$ then $u = 0$ in $\Gamma_1^{\mathcal D} \cup \Gamma_0^0 \cup \Omega^+ \cup \Gamma_0$. Also, by construction it is clear that

By a positive weak solution of (1.1) we mean any function $\varphi \in H^1_*(\Omega)$ satisfying

and such that for each $\xi \in {\mathcal C}_{\Gamma_0 \cup \Gamma_1^{\mathcal D}}^{\infty}(\Omega)$, or $\xi \in H_*^1(\Omega)$, the following holds

In particular, taking $\xi = \varphi \in H^1_*(\Omega)$ we have that

Thus, since any positive weak solution of (1.1) can not be constant, it follows from (1.6) that if (1.1) possesses a positive weak solution $\varphi$ for the value $\lambda$ of the parameter, then

and therefore, $\lambda > 0$ is a necessary condition for the existence of positive weak solutions of (1.1).

Hereafter we denote $\mathfrak{B}^{\mathcal N}$, $\mathfrak{B}^*(\Gamma_1^{\mathcal N})$ and $\mathfrak{B}_0^*(\Gamma_1^{\mathcal N})$ the boundary operators defined by

and

and by $\mathfrak{D}$ the Dirichlet boundary operator on $\partial \Omega$. Clearly, $\mathfrak{B}^{\mathcal N} = \mathfrak{B}^*(\Gamma_1)$. Also we denote

In the sequel we will say that a function $u \in W_p^2(\Omega)$, $p > N$ is strongly positive in $\Omega$, and we will denote it by $u \gg 0$, if $u(x) > 0$ for each $x\in \Omega \cup \Gamma_1$ and $\partial u(x) < 0$ for each $x\in \Gamma_0$ such that $u(x) = 0$.

Let us consider the eigenvalue problem

By a principal eigenvalue of (1.8) we mean any eigenvalue of it which possesses a one-signed eigenfunction and in particular a positive eigenfunction. Owing to the results in [1,Theorem 12.1] it is known that (1.8) possesses a unique principal eigenvalue, denoted in the sequel by $\sigma_1^{\Omega}[-\Delta, \mathfrak{B}^{\mathcal N}]$, which is the least eigenvalue of (1.8) and it is simple. Moreover, the positive eigenfunction $\varphi_1^{\mathcal N}$ associated to it, unique up multiplicative constant, satisfies

and in addition

A function $\varphi \in W_p^2(\Omega)$ for $p > N$ is said to be a positive strict supersolution of the problem $(-\Delta, \Omega, \mathfrak{B}^{\mathcal N})$, if $\varphi > 0$ in $\Omega$ and the following hold

with some of the inequalities strict. Since any positive constant $\mu > 0$ is a positive strict supersolution of the problem $(-\Delta, \Omega, \mathfrak{B}^{\mathcal N})$, it follows from the characterization of the strong maximum principle given in [2,Theorem 2.4] that

Now, for any $K \in L_{\infty}(\Omega)$, let us denote ${\mathcal L}_K: = -\Delta +K$ and let us consider the eigenvalue problem with mixed boundary conditions and glued Dirichlet-Neumann boundary conditions on $\Gamma_1$ given by

A function $\varphi$ is said to be a weak solution of (1.12) if $\varphi \in H^1_*(\Omega)$ and for each $\xi \in H_*^1(\Omega)$ the following holds

The value $\mu$ is an eigenvalue of (1.12), if there exists a weak solution $\varphi \neq 0$ of (1.12) associated to $\mu$. In that case, it is said that $\varphi$ is a weak eigenfunction of (1.12) associated to the eigenvalue $\mu$. By a principal eigenvalue of (1.12) we mean any eigenvalue of it which possesses a one-signed eigenfunction and in particular a positive eigenfunction.

Owing to the results in [5,Theorem 1.1] it is known that (1.12) possesses a unique principal eigenvalue, denoted in the sequel by $\sigma_1^{\Omega}[{\mathcal L}_K, \mathfrak{B}^*(\Gamma_1^{\mathcal N})]$, which is simple and the smallest eigenvalue of all others eigenvalues of (1.12). Moreover, the positive eigenfunction $\varphi^*$ associated to it, unique up multiplicative constant, satisfies that $\varphi^* \in H^1_*(\Omega)$ and

Furthermore, $\sigma_1^{\Omega}[{\mathcal L}_K, \mathfrak{B}^*(\Gamma_1^{\mathcal N})]$ comes characterized by

Also, owing to [5,Corollary 3.5] the following hold

In the same way, substituting in (1.12) $\Omega$ by $\Omega_0$ and $\mathfrak{B}^*(\Gamma_1^N)$ by $\mathfrak{B}_0^*(\Gamma_1^N)$, owing to [5,Theorem 1.1] we obtain the following variationl characterization for $\sigma_1^{\Omega_0}[{\mathcal L}_K, \mathfrak{B}_0^*(\Gamma_1^{\mathcal N})]$

In the particular case when $K = 0$, that is, when ${\mathcal L}_0: = -\Delta$, set

and

Owing to (1.11) and (1.14)–(1.16) the following hold

and

where $\varphi^*$ and $\varphi_0^*$ stand for the positive principal eigenfunctions associated to $\sigma_1^{\Omega}[\mathfrak{B}^*(\Gamma_1^{\mathcal N})]$ and $\sigma_1^{\Omega_0}[\mathfrak{B}_0^*(\Gamma_1^{\mathcal N})]$, respectively, unique up multiplicative constant. Taking into account (1.4) and the variational characterizations (1.17) and (1.18), it is clear that

The statements and proofs of the main findings of this work appear in Proposition 1 and Theorem 1. The main technical tools used to carry out the mathematical analysis of this work are variational and monotonicity techniques.

The distribution of the rest of this paper is the following. In Section 2 is given a necessary condition for the existence of positive weak solutions of (1.1), sharper than (1.7), and some results about the pointing profile of such solutions. In Section 3 is given a sufficient condition for the exsitence of positive weak solutions of (1.1) depending on the $\lambda$-parameter, the spatial dimension $N \geq 2$ and the exponent $q > 1$ of the reaction term.

2.   Necessary condition for the existence of positive weak solutions of (1.1)

In this section is given a necessary condition for the existence of positive weak solutions of (1.1) sharper than (1.7), and some partial results about the pointing profile and regularity of the weak positive solutions of (1.1). The main result of this section establishes the following

Proposition 1. Let $u$ be a positive weak solution of (1.1) for the value $\lambda$ of the parameter. Then,

and

Moreover:

a) If $u \in L_{\infty}(\Omega^+)$, then

and

b) If

then $u \in H^2(\Omega')$ for any subdomain $\Omega' \subset \subset \Omega$.

c) If

then $u \in C(K)$ in any compact subset $K \subset \Omega$.

Proof. Let us denote

Owing to (1.19) and (1.20) we know that

To prove (2.1), let $u \in H^1_*(\Omega)$ be a positive weak solution of (1.1) for the value $\lambda$ of the parameter. Then

Now, since $u(x) \geq 0$ a.e. in $\Omega$ and $a(x) > 0$ for all $x\in \Omega^+$, we have that

and hence, since $u \in H^1_*(\Omega) \setminus \left\{ 0 \right\}$, it follows from (2.7), (2.8) and (1.17) that

and therefore,

We now prove that (1.1) does not possess a positive weak solution for $\lambda = \sigma_1^*$. To prove it we will argue by contradiction. Let us assume that $v \in H^1_*(\Omega)$ is a positive weak solution of (1.1) for $\lambda = \sigma_1^*$ and let $\varphi^*$ be the positive principal eigenfunction associated to $\sigma_1^*$, normalized so that $\int_{\Omega}(\varphi^*)^2 = 1$. Owing to (1.13) and (1.17) we know that

and

Since $v \in H^1_*(\Omega)$ is a positive weak solution of (1.1) for $\lambda = \sigma_1^* > 0$, we have that

and for any $\xi \in H^1_*(\Omega)$ the following holds

Also, it follows from (1.6) that

Moreover, necessarily

because on the contrary, if

then for all $\xi \in H^1_*(\Omega)$ we have that

and (2.12) becomes

Then, $v \in H_*^1(\Omega)$ is a weak positive eigenfunction associated to $\sigma_1^*$ and therefore, owing to the simplicity of $\sigma_1^*$ guaranted by [5,Theorem 1.1], there exists $\alpha > 0$ such that

Now, it follows from (2.11) and (2.17) that $v(x) > 0$ a.e. in $\Omega^+$ which contradicts (2.15). This completes the proof of (2.14). Then, since $(2.14)$ holds, we have that

and hence, (2.13) and (2.18) imply that

which contradicts the variational characterization of $\sigma_1^*$ given by (1.17), and completes the proof of the fact that (1.1) does not possess a positive weak solution for $\lambda = \sigma_1^*$. This fact, together with (2.10) and (1.19), complete the proof of (2.1).

We now prove (2.2). To prove it we will argue by contradiction. Indeed, let $v \in H_*^1(\Omega)$ be a positive weak solution of (1.1) for the value $\lambda$ of the parameter and let assume that $v = 0$ in $\Omega^+$. Then, (2.1) holds,

and since

(2.19) becomes

Now, since $v > 0$ in $\Omega$, it follows from (2.20) that $(\lambda, v)$ is a principal eigenpair of the problem

and owing to the uniqueness of the principal eigenvalue of (2.21) guaranteed by [5,Theorem 1.1], we have that $\lambda = \sigma_1^*$, which contradicts (2.1) and completes the proof of (2.2).

We now prove (2.3) and (2.4). If $u \in H^1_*(\Omega)\cap L_{\infty}(\Omega^+)$ is a positive weak solution of (1.1) for the value $\lambda$ of the parameter, then $u$ is a positive weak solution of the eigenvalue problem

where the potential

Now, since (2.22) fits into the abstract framework of (1.12), it follows from the uniqueness of the principal eigenvalue of (2.22) and the structure of its positive eigenfunction, unique up multiplicative constant (cf.[5,Theorem 1.1]) that

and

This completes the proof of (2.4). Now, taking into account the variational characterization of the principal eigenvalue $\sigma_1^{\Omega}[-\Delta+a(x)u^{q-1}, \mathfrak{B}^*(\Gamma_1^{\mathcal N})]$ given by

(2.23), the definition of $\tilde{H}_*^1(\Omega_0)$, (1.4) and (1.18), the following hold

which completes the proof of (2.3).

We now prove b). Let $u \in H^1_*(\Omega)$ be a positive weak solution of (1.1). Owing to the Rellich-Kondrachov theorem we have that under condition (2.5) the following holds

Then, since $u \in H^1_*(\Omega)$, it follows from (2.24) that $u^q \in L_2(\Omega)$ and since $a \in {\mathcal C}(\bar{\Omega})$, we have that the function

Now, since $u \in H^1(\Omega)$ satisfies

in the weak sense, owing to (2.25) it follows from [6,Theorem 8.8] that $u \in H^2(\Omega')$ for any subdomain $\Omega' \subset \subset \Omega$, which completes the proof of b).

We now prove c). Let $u$ be a positive weak solution of (1.1) and let $K$ be a compact subset of $\Omega$. Let pick up $\Omega'$ a subdomain of $\Omega$ satisfying

Owing to (2.6) it follows from b) that

Now, since for $N = 3$ under the general assumptions we have that

the result follows from (2.26)–(2.28). This completes the proof of c).

This completes the proof.

Remark 1. It should be pointed out that owing to (1.19), (2.1) provides us with a necessary condition for the existence of positive weak solution of (1.1) sharper than (1.7). In fact, as it will be shown in the following section, the lower bound about the $\lambda$-parameter for the existence of positive weak solution of (1.1) given by (2.1) is optimal.

3.   Sufficient condition for the existence of positive weak solutions of (1.1)

In this section is given a sufficient condition for the existence of positive weak solutions of (1.1) depending on the $\lambda$ parameter, on the exponent $q > 1$ of the reaction term and on the spatial dimension $N \geq 2$. To prove it are used some of the arguments given in [7,Theorem 2]. The main result of this section establishes the following

Theorem 1. Assume that

and either:

i) $N = 2$ (and $q > 1$), or

ii) $N \geq 3$ and $1 < q < \frac{N+2}{N-2}$.

Then, (1.1) posseses a positive weak solution. Moreover, if $v$ stands for such a positive weak solution of (1.1), then $v > 0$ in $\Omega^+$.

Proof. At the beginning we remark that (1.19) and (3.1) imply that

To prove the existence of a weak positive solution of (1.1) for each $\lambda$ satisfying (3.1), we will consider the functional

and we will show that it reaches its minimum in a positive function of $H_*^1(\Omega)$. Before proving the existence of such a global minimum $\varphi_m \in H_*^1(\Omega)$ of $\Phi$ in $H^1_*(\Omega)$, we will prove that if it exists, then it is nontrivial, that is, $\varphi_m \neq 0$, and it may be considered positive. Indeed, since (3.1) holds, taking into account the variational characterization of the principal eigenvalue $\sigma_1^{\Omega}[\mathfrak{B}^*(\Gamma_1^{\mathcal N})]$ we have that

Hence, there exists $\tilde{\varphi} \in H_*^1(\Omega) \setminus \{ 0\}$ such that

and therefore,

We can assume that $\tilde{\varphi} > 0$ because on the contrary we can replace $\tilde{\varphi}$ by $\vert \tilde{\varphi}\vert$.

Since $\tilde{\varphi} \in H^1_*(\Omega)$, it follows from the Rellich-Kondrachov Theorem that under condition $i)$, that is, $N = 2$ and $q > 1$, or under condition $ii)$, that is $N \geq 3$ and $q \in \left(1, \frac{N+2}{N-2}\right)$, we have that $\tilde{\varphi} \in L_{q+1}(\Omega)$ and hence

Now, for each $\varepsilon > 0$, let us consider the positive function

We have that

and hence, owing to (3.3) and (3.4), we infer that $\Phi (\tilde{\varphi}_{\varepsilon}) < 0$ for $\varepsilon > 0$ small enough. Then, a possible minimum $\varphi_m \in H^1_*(\Omega)$ of $\Phi$ must be nontrivial. Moreover, we can assume that $\varphi_m > 0$ because on the contrary, since $\Phi (\varphi_m) = \Phi(\vert \varphi_m \vert)$, we can replace $\varphi_m \neq 0$ by $\vert \varphi_m \vert > 0$.

Now, in order to prove the existence of the global minimum of $\Phi$ in $H_*^1(\Omega)$, we will prove that $\Phi$ is coercive and weakly lower semicontinuous.

To prove that $\Phi$ is coercive we will argue by contradiction, assuming the existence of a sequence $u_n \in H^1_*(\Omega)$, $n\geq 1$ satisfying

and

for some $C > 0$. Then, it follows from (3.5) and (3.6) that

because on the contrary, if there exists a subsequence on $u_n$, again labeled by $n$ such that

for some positive constant $D > 0$, then, since $\lambda > 0$ (cf. (3.2)), it follows from (3.6) and (3.8) that

and hence

which implies, together with (3.8), that $u_n$ is bounded in $H^1_*(\Omega)$, which contradicts (3.5). This proves that under conditions (3.5) and (3.6), (3.7) holds.

Now, set

By construction,

Taking into account the definition of $v_n$, it follows from (3.6) and (3.9) that

and hence,

Now, (3.7), (3.9) and (3.11) imply that $v_n$ is a bounded sequence in $H_*^1(\Omega)$ and therefore, along some subsequence of $v_n$, again labeled by $v_n$. we have that $v_n$ converges strongly in $L_2(\Omega)$, that is

and $v_n$ converges weakly in $H^1(\Omega)$,

It follows from (3.9) and (3.12) that

Also, owing to (3.10) the following holds

Hence,

and therefore, owing to (3.7) it follows from (3.15) that

Now, owing to the Fatou Lemma, it follows from (3.12) and (3.16) that

and since $a(x) > 0$ for all $x \in \Omega^+$ we have that

Thus, owing to (3.17) and (3.7), letting $n\rightarrow \infty$ in (3.11) we obtain that

On the other hand, it follows from (3.14) and (3.17) that

Also, since by construction $v_n = 0$ on $\Gamma_0 \cup \Gamma_1^{\mathcal D}$, $n\geq 1$, taking into account (3.12) we have that

in the sense of traces. We now show that

Since $\Gamma_0^0 = \partial \Omega_0 \cap \Omega = \partial \Omega^+ \cap \Omega$, let us consider the trace operator on $\Gamma_0^0$, $\tilde{\gamma} \in {\mathcal L}(H^1(\Omega^+), L_2(\Gamma_0^0))$. Owing to the continuity of $\tilde{\gamma}$, it follows from (3.17) the existence of $\tilde{K} > 0$ such that

and therefore $v = 0$ on $\Gamma_0^0$, which proves (3.21). Then, (3.18)–(3.21) imply that $v \in H_*^1(\Omega_0)$ and since $\Vert v \Vert_{L_2(\Omega_0)} = 1$, it follows from (3.18) and the variational characterization for $\sigma_1^{\Omega_0}[\mathfrak{B}_0^*(\Gamma_1^{\mathcal N})]$ that

which contradicts (3.1) and proves that $\Phi$ is coercive.

We now prove that $\Phi$ is weakly lower semicontinuous in $H^1_*(\Omega)$. To prove it, let $u_n$ be a sequence such that $u_n \rightharpoonup u$. Then, $u_n$ is bounded in $H^1(\Omega)$ and

By compactness we have that $u_n \rightarrow u$ in $L_2(\Omega)$ and hence,

and

Then, it follows from (3.22) and (3.23) that

Now, let us consider the sequence $f_n = a \vert u_n \vert ^{q+1} \geq 0$ and $f = a \vert u \vert^{q+1}$. Owing to (3.24) $f_n(x) \rightarrow f(x)$ a.e. in $\Omega$ and hence, the Fatou's Lemma implies that

that is,

Now, (3.23), (3.25) and (3.26) imply that

and therefore $\Phi$ is weakly lower semicontinuous.

Then, since $\Phi$ is coercive and weakly lower semicontinuos, it follows from ^[8], ^[4] that $\Phi$ reaches a global minimun $\varphi_m$ in $H_*^1(\Omega)$ and, as it was remarked at the beginning of the proof, it may be considered positive, that is, $\varphi_m > 0$. Now, differentiating $\Phi$ at $\varphi_m$ in any direction $\xi \in H^1_*(\Omega)$ we obtain that

and since $\Phi$ reaches its global minimum at $\varphi_m$, it follows from (3.27) that

which proves, under condition $i)$ or $ii)$, the existence of a weak positive solution $\varphi_m$ of (1.1) for any $\lambda$ satisfying (3.1). The fact that $v = \varphi_m > 0$ in $\Omega^+$ follows from Proposition 1.

This completes the proof.

Acknowledgments

Supported by the Ministry of Science, Innovation and Universities under grant PGC2018-097104-B-I00 and by the Ministry of Science and Innovation under grant PID2021-123343NB-I00

Conflict of interest

The author declares no conflict of interest.