Cylinder shell (CS) structures are widely applied in marine industry applications with the characteristics of high loading ability and high energy absorption performance. In this study, the triply periodic minimal surfaces (TPMS) lattices were filled into double cylinder shell structures to construct the cylinder shell (TPMS-CS) structures. The mechanical and energy absorption performances of these structures were investigated by simulation analysis. First, the finite element (FE) model of TPMS-CS structures was verified by experiments. Then, the crashworthiness characteristics of three different kinds of TPMS-CS, namely, primitive, diamond, and gyroid, under axial loading were studied using FE simulation. The results indicate that the diamond-based TPMS-CS structures exhibit a higher energy absorption efficiency compared to their counterparts. Next, parametric studies were carried out to investigate the influence of the design parameters (the relative density of the TPMS, and the inner and outer shell thickness) on the crashworthiness of TPMS-CS structures. Finally, to obtain the optimum design for the TPMS-CS, an optimization framework was proposed by combining the three surrogate models (KGR, PRS, RBF) and multi-objective particle swarm optimization. The optimum design of the D-TPMS-CS structures was obtained based on the proposed optimization framework. The TPMS-CS structures proposed in this study can also be applied in other engineering applications as energy absorbers.
Citation: Laiyu Liang, Huaiming Zhu, Dong Wei, Yaozhong Wu, Weijia Li. Energy absorption and multi-objective optimization of TPMS filled cylinder shell structures[J]. Electronic Research Archive, 2023, 31(5): 2834-2854. doi: 10.3934/era.2023143
| [1] | Xiaoyan Song, Lianfeng Lai, Shungen Xiao, Yaohong Tang, Mengmeng Song, Jie Zhang, Yong Zhang . Bionic design and multi-objective optimization of thin-walled structures inspired by conchs. Electronic Research Archive, 2023, 31(2): 575-598. doi: 10.3934/era.2023028 |
| [2] | Dongtao Wang, Ping Xu, Chengxing Yang, Shuguang Yao, Zhen Liu . Crashworthiness performance of gradient energy-absorbing structure for subway vehicles under quasi-static loading. Electronic Research Archive, 2023, 31(6): 3568-3593. doi: 10.3934/era.2023181 |
| [3] | Chao Ma, Hong Fu, Pengcheng Lu, Hongpeng Lu . Multi-objective crashworthiness design optimization of a rollover protective structure by an improved constraint-handling technique. Electronic Research Archive, 2023, 31(7): 4278-4302. doi: 10.3934/era.2023218 |
| [4] | Zhiqing Li, Wenbin Zhang, Yuanfei Li . Structural stability for Forchheimer fluid in a semi-infinite pipe. Electronic Research Archive, 2023, 31(3): 1466-1484. doi: 10.3934/era.2023074 |
| [5] | Wenjie Wang, Suzhen Wen, Shen Gao, Pengyi Lin . A multi-objective dynamic vehicle routing optimization for fresh product distribution: A case study of Shenzhen. Electronic Research Archive, 2024, 32(4): 2897-2920. doi: 10.3934/era.2024132 |
| [6] | Ming Wei, Congxin Yang, Bo Sun, Binbin Jing . A multi-objective optimization model for green demand responsive airport shuttle scheduling with a stop location problem. Electronic Research Archive, 2023, 31(10): 6363-6383. doi: 10.3934/era.2023322 |
| [7] | Mingtao Cui, Wennan Cui, Wang Li, Xiaobo Wang . A polygonal topology optimization method based on the alternating active-phase algorithm. Electronic Research Archive, 2024, 32(2): 1191-1226. doi: 10.3934/era.2024057 |
| [8] | Ziqiang Wang, Chunyu Cen, Junying Cao . Topological optimization algorithm for mechanical-electrical coupling of periodic composite materials. Electronic Research Archive, 2023, 31(5): 2689-2707. doi: 10.3934/era.2023136 |
| [9] | Furong Xie, Yunkai Gao, Ting Pan, De Gao, Lei Wang, Yanan Xu, Chi Wu . Novel lightweight connecting bracket design with multiple performance constraints based on optimization and verification process. Electronic Research Archive, 2023, 31(4): 2019-2047. doi: 10.3934/era.2023104 |
| [10] | Donghyeon Kim, Jinsung Kim . GPU-accelerated non-dominated sorting genetic algorithm III for maximizing protein production. Electronic Research Archive, 2024, 32(4): 2514-2540. doi: 10.3934/era.2024116 |
Cylinder shell (CS) structures are widely applied in marine industry applications with the characteristics of high loading ability and high energy absorption performance. In this study, the triply periodic minimal surfaces (TPMS) lattices were filled into double cylinder shell structures to construct the cylinder shell (TPMS-CS) structures. The mechanical and energy absorption performances of these structures were investigated by simulation analysis. First, the finite element (FE) model of TPMS-CS structures was verified by experiments. Then, the crashworthiness characteristics of three different kinds of TPMS-CS, namely, primitive, diamond, and gyroid, under axial loading were studied using FE simulation. The results indicate that the diamond-based TPMS-CS structures exhibit a higher energy absorption efficiency compared to their counterparts. Next, parametric studies were carried out to investigate the influence of the design parameters (the relative density of the TPMS, and the inner and outer shell thickness) on the crashworthiness of TPMS-CS structures. Finally, to obtain the optimum design for the TPMS-CS, an optimization framework was proposed by combining the three surrogate models (KGR, PRS, RBF) and multi-objective particle swarm optimization. The optimum design of the D-TPMS-CS structures was obtained based on the proposed optimization framework. The TPMS-CS structures proposed in this study can also be applied in other engineering applications as energy absorbers.
Cylindrical shell structures, which have high specific stiffness and strength [1], high bucking resistance [2,3], and outstanding energy absorption performance [4,5], have been widely used as underwater vehicle hulls and ship propellers. Over the past decades, numerous research has been conducted to achieve more efficient structural configurations, such as composite sandwich cylindrical shells [6], lattice cylindrical shells (LCS) [7,8], and functionally graded designs [9,10]. Lattice structures, such as honeycomb [11,12,13], foam [14], and strut-based lattice [15,16], are widely used in the design of LCS. It has been shown that the LCS is more efficient in load-carrying and energy absorption than the cylindrical shell.
For example, Zhang et al. [17] built the FE and analytical models to study the crushing responses of the lattice cylindrical shells. The optimization design was also conducted to seek the minimum weight design of the LCS structures. It was found that the Kagome and triangular LCS possess higher load-carrying efficiency compared with the hexagonal counterpart. Chen et al. [18] investigated the deformation and failure mechanism of the graded LCS with triangular and hexagonal configurations under axial impact loading. Numerical and theoretical models were constructed based on the FE method and one-dimension shock theory. The results show that the crashworthiness performances of these LCSs are significantly affected by relative density and the density gradient along the crushing direction can enhance energy absorption for LCS structures. A hierarchical honeycomb cylindrical structure was proposed and investigated by experimental tests [19]. It was found that the proposed structure exhibits excellent deformation recovery and energy absorption capabilities.
Recently, researchers have found that the TPMS lattices possess superior mechanical and crashworthiness behaviors compared to the struct-based lattices [20,21]. For example, Zhang et al. [22] investigated the mechanical and energy absorption properties of the TPMS sheet structure to the body-centered cubic lattice by experimental and numerical methods. It was found that the TPMS sheet structures are significantly superior to body-centered lattices in mechanical and energy absorption properties. Qiu et al. [23] proposed a three-dimensional functionally graded TPMS structure and studied their mechanical properties using experimental and numerical techniques. It was found that a higher volume fraction and the proper adoption of gradient could improve the energy absorption capability of the proposed structures. Yin et al. [24] studied the energy absorption behaviors of the TPMS sheet structures under axial loading by experimental and numerical methods. It was found the crashworthiness performance was affected by the level constant and the shell thickness. Moreover, multi-objective optimization was conducted to achieve an optimal design for the TPMS sheet structures.
Nowadays, researchers have constructed LCS structures with TPMS lattices. For example, Wang et al. [8] constructed a Gyroid lattice-based cylindrical shell structure by a mapping method and studied their energy absorption and deformation modes using experimental tests and numerical simulations. The results show that the Gyroid lattice cylindrical shell exhibit superior mechanical and energy absorption properties compared to its counterparts. The parametric study showed that the energy absorption properties were significantly affected by the relative density, and geometric gradients. Following the proposed mapping method, Zhu et al. [7] proposed a modified mapping method to design the Diamond lattice cylindrical shell structure and investigated their energy absorption performances by experimental and numerical methods. The experimental and simulation results show that deformation modes and crashworthiness performances were significantly affected by relative density, cell size, radial variation coefficient, and mapping angle.
The LCS structures should be used with surrounded shells to facilitate engineering applications. To the author's best knowledge, the crashworthiness and optimization design of the TPMS filled cylinder shell structures has not been reported to date.
In this study, the energy absorption performances of TPMS-CS structures under axial compression were investigated. Firstly, the TPMS-CS structures were designed based on the LCS and double cylindrical shells. Then, the FE model was built to simulate the crushing responses and verified by the results of the test. Parametric studies were carried out to study the influence of the relative density of the TPMS, outer shell thickness, and inner shell thickness on the energy absorption of TPMS-CS structures. Finally, the optimal design of TPMS-CS structures was achieved by a surrogate-based optimization method.
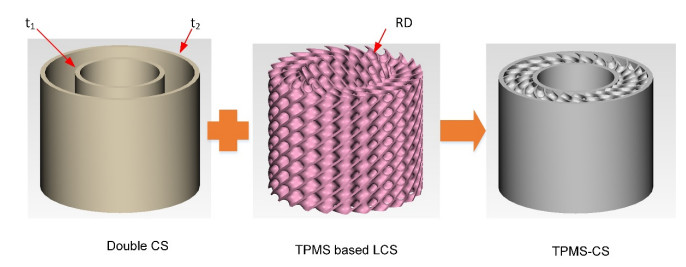
The proposed TPMS filled cylindrical shell (TPMS-CS) structure consists of a TPMS based lattice shell structure (LCS) and a double cylinder shell structure, as shown in Figure 1. The TPMS based LCSs are derived according to the mapping method proposed in ref [7,8]. Three TPMSs are used to construct the TPMS-LCSs, i.e., Primitive (P), Diamond (D), and Gyroid (G) surfaces, which can be described using the level-set function φ [20,25]:
| φP(x,y,z)=cos(ωx)+cos(ωy)+cos(ωz)φD(x,y,z)=sin(ωx)sin(ωy)sin(ωz)+cos(ωx)cos(ωy)cos(ωz)+sin(ωx)cos(ωy)cos(ωz)+cos(ωx)cos(ωy)sin(ωz)φG(x,y,z)=cos(ωx)sin(ωy)+cos(ωy)sin(ωz)+cos(ωz)sin(ωx) | (1) |
where x,y,z are spatial coordinates, ω=2π/l, and l is the length of a unit cell. The sheet-based TPMS is derived from the equation φ2≤c2, the relative density (RD) is controlled by the constant c [25].
In this study, the geometric parameters of TPMS-CS structures are set as follows: height H=24mm, outer diameter Dout=30mm, inner diameter Din=18mm, l=6mm. Three design parameters are considered in this study, namely, inner shell thickness (t1), outer shell thickness (t2), and TPMS filled relative density (RD), as shown in Figure 1.
The FE model is built to simulate the axial crushing process of the TPMS-CS structures by commercial finite element software LS-DYNA. The established FE model of TPMS-CS is shown in Figure 2. The TPMS-CS is compressed with a rigid wall with a compressive velocity of 1 m/s and the TPMS-CS is placed on a fixed rigid wall. The rigid walls are defined as rigid bodies with the MAT-20 rigid material model. The TPMS-CS is modeled by the Belytschko–Tsay shell elements with reduced integration. The MAT-24 is used to simulate the TPMS-CS, which is made of 316L stainless steel. The base material parameters are used from the ref [7] and listed in Table 1.
| Parameters | Value |
| Density (g/cm3) | 7.98 |
| Young's modulus (GPa) | 190 |
| Yield stress (MPa) | 633 |
| Ultimate stress (MPa) | 1074 |
| Poisson's ratio | 0.3 |
To simulate the contact between the TPMS-CS and the rigid walls, the "automatic node to surface" contact algorithm is employed in this study [26]. To account self-contact of the TPMS-CS itself during compression, the "automatic single surface" contact algorithm is adopted. For static and dynamic friction, a friction coefficient is set to 0.3 for all contact conditions [27,28]. Mesh size convergence tests are conducted to obtain the optimal mesh size, and a mesh size of 0.4 mm × 0.4 mm is adopted in this study.
To evaluate the energy absorption properties of the TPMS-CSs, the crashworthiness indicators include Energy Absorption (EA), Specific Energy Absorption (SEA), Peak Crushing Force (PCF), and Crush Force Efficiency (CFE) are used in this study.
EA is defined as the total energy absorption of the whole energy absorber, and can be expressed as follows,
| EA=∫d0F(x)dx | (2) |
where d is the effective crushing distance, which is defined as the crushing distance at which energy efficiency has the maximum value [29]. F(x) is the instantaneous crushing force at the crushing distance x.
SEA is used to evaluate the energy absorption efficiency of the energy absorber with different materials and weights, which is defined as the energy absorption per unit mass, and can be calculated as follows,
| SEA=EAm | (3) |
where m is the mass of the structure.
The PCF is the maximum value of the crushing force during the whole crushing process. The crushing force efficiency (CFE) is the uniformity of crushing force in the crushing process, which can be calculated as follow,
| CFE=MCFPCF×100% | (4) |
where MCF is the average crushing force within the effective deformation distance and can be derived as follows,
| MCF=EAd | (5) |
The experimental results were adopted from the reference [7] and compared with the results of the FE model which building by the above-introduced method to verify the accuracy of the FE model. In the literature, the Diamond LCS (D-LCS) was compressed with a velocity of 5 mm/min, and the deformation modes of the D-LCS and force-displacement curves of tests were recorded. The comparisons of the deformation modes and the force-displacement curves between the reference and simulation results are shown in Figure 3. It is seen that similar deformation patterns are founded both in reference and simulation results, and the force-displacement curves are in good agreement.
Furthermore, the crashworthiness indicators of the experimental tests and simulations are listed in Table 2. The results of EA and PCF show that the error between simulation and reference results is no more than 2%, which proves the accuracy of the FE model used in this study.
| Indicators | Test (average) | Reference results | This paper | Error (%) |
| EA (J) | 633.38 | 669.97 | 672.15 | 0.33 |
| PCF (kN) | 65.86 | 66.07 | 65.92 | -1.34 |
Three different kinds of TPMS-CS structures (P, D, G) were investigated using FE analysis to explore their energy absorption performances. All the structures have the same structural parameters: t1=2mm, t2=2mm, and RD=20%.
Figure 4 gives the deformation modes of the three kinds of TPMS-CS structures after compression. It is shown that all the TPMS-CS structures deformed in a layer-by-layer mode, which is similar to the cylindrical shells [30].
Figure 5 shows the force-displacement curves of the three TPMS-CS structures. All the TPMS-CS structures exhibit similar crushing force responses. Specifically, the plateau stress of D-TPMS-CS is higher than two other structures.
Table 3 further gives the crashworthiness indicators of the three kinds of TPMS-CS structures. The results show that the D-TPMS-CS possesses the highest EA and SEA as expected. Specifically, the SEA of D-TPMS-CS is improved by 2.7% and 3.5% compared with that of G-TPMS-CS and P-TPMS-CS, respectively. However, the PCF of D-TMPS-CS is also higher than the other two structures. For crushing force efficiency, D-TPMS-CS exhibits the highest CFE among all the TPMS-CS structures. The results indicate that the D-TPMS-CS structure exhibits better energy absorption capacity and efficiency.
| TPMS-CS | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 4126.79 | 386.62 | 54.98 | 0.59 |
| D | 4272.38 | 412 | 56.92 | 0.65 |
| G | 4158.38 | 368.61 | 55.40 | 0.63 |
To study the effect of design parameters on the crashworthiness of the TPMS-CS structures, three design parameters, i.e., inner shell thickness (t1), outer shell thickness (t2), and the relative density of filled TPMS (RD) were considered in this section.
To investigate the effect of the inner shell thickness t1on the crashworthiness of TPMS-CS, the FE analysis was carried out by changing the t1 from 1 mm to 3 mm. All the TPMS-CS structures have identical parameters for outer shell thickness t2=2mm and RD=20%.
Figure 6 plots the force-displacement curves of three TPMS-CS structures with different t1. The results show that all the curves exhibit three distinct regions: elastic deformation region, plateau stress region, and densification region. The plateau stress of all the TPMS-CS structures is improved with the increase of t1. Interestingly, the crushing force increases rapidly at the densification region when the t1 possess a higher value.
Table 4 and Figure 7 give the calculated results of structural crashworthiness indicators. It is shown that the EA and SEA of all three TPMS-CS structures increase with the increase of t1, and the P-TPMS-CS with t1=3mm has the highest EA (5623.44 J) and SEA (60.16 kJ/kg). The results indicate that the P-TPMS-CS and D-TPMS-CS exhibit better energy absorption ability.
| TPMS | t1 (mm) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 1 | 2624.98 | 316.75 | 46.34 | 0.46 |
| 1.5 | 3367.45 | 316.55 | 51.13 | 0.59 | |
| 2 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 2.5 | 4872.01 | 391.79 | 57.81 | 0.69 | |
| 3 | 5623.44 | 585.47 | 60.16 | 0.53 | |
| D | 1 | 2861.39 | 268 | 50.51 | 0.59 |
| 1.5 | 3539.74 | 374.37 | 53.75 | 0.6 | |
| 2 | 4272.38 | 412 | 56.92 | 0.65 | |
| 2.5 | 4849.31 | 443.49 | 57.55 | 0.7 | |
| 3 | 5556.85 | 657.25 | 59.45 | 0.54 | |
| G | 1 | 2795.62 | 283.27 | 49.34 | 0.55 |
| 1.5 | 3495.27 | 373.79 | 53.07 | 0.52 | |
| 2 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 2.5 | 4676.69 | 417.58 | 55.50 | 0.62 | |
| 3 | 5441.84 | 688.81 | 58.22 | 0.44 |
The PCF of all the TPMS-CS structures also increases with the increase of t1 and increases rapidly while the t1 is bigger than 2.5 mm. The G-TPMS-CS has the highest PCF (688.81 kN) at t1=3mm.
For the crushing force efficiency, the CFE of P, D-TPMS-CS structures first increase with the increase of t1 and then decreases with the increase of t1 at t1=2.5mm. There is no obvious trend in the CFE of G-TPMS-CS structures. The D-TPMS-CS have the highest CFE (0.7) at t1=2.5mm.
To investigate the effect of the outer shell thickness t2on the crashworthiness of TPMS-CS, the FE analysis was carried out by changing the t2 from 1 mm to 3 mm. All the TPMS-CS structures have identical parameters for inner shell thickness t1=2mm and RD=20%.
Figure 8 plots the force-displacement curves of three TPMS-CS structures with different t2. All the force-displacement curves have similar trends. It can be seen that all the crushing force responses are increased with the increase of t2.
Table 5 and Figure 9 give the calculated results of structural crashworthiness indicators. It is shown that the EA and SEA of all three TPMS-CS structures increased with the increase of t1, and the D-TPMS-CS with t2=3mm has the highest EA (5192.63 J) and SEA (60.72 kJ/kg). The results indicate that the D-TPMS-CS exhibits better energy absorption ability.
| TPMS | t2 (mm) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 1 | 3010.19 | 247.62 | 46.60 | 0.68 |
| 1.5 | 3473.58 | 272.14 | 49.74 | 0.66 | |
| 2 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 2.5 | 4562.29 | 401.88 | 56.82 | 0.63 | |
| 3 | 5180.25 | 418.58 | 60.57 | 0.64 | |
| D | 1 | 3402.73 | 269.93 | 52.67 | 0.7 |
| 1.5 | 3740.50 | 362.63 | 53.57 | 0.67 | |
| 2 | 4272.38 | 412 | 56.92 | 0.62 | |
| 2.5 | 4780.99 | 420.25 | 59.55 | 0.64 | |
| 3 | 5192.63 | 410.63 | 60.72 | 0.66 | |
| G | 1 | 3228.56 | 250.35 | 49.98 | 0.72 |
| 1.5 | 3669.70 | 332.73 | 52.55 | 0.61 | |
| 2 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 2.5 | 4681.38 | 428.02 | 58.30 | 0.61 | |
| 3 | 5128.39 | 400.52 | 59.96 | 0.63 |
The PCF of all the TPMS-CS structures also increases with the increase of t2, and the PCF increases slowly at high outer shell thickness. The P-TPMS-CS have the highest PCF (418.58 kN) at t2=3mm.
For the crushing force efficiency, the CFE of all the TPMS-CS structures first decreases with the increase of t2 and then increases past t2=2mm. The G-TPMS-CS have the highest CFE (0.72) at t2=1mm.
To investigate the influence of the TPMS filled relative density RD on the crashworthiness of TPMS-CS, the FE analysis was carried out by changing the RD from 10% to 30%. All the TPMS-CS structures have identical parameters for outer shell thickness t2=2mm and inner shell thickness t1=2mm.
Figure 10 plots the force-displacement curves of three TPMS-CS structures with different RD. All the force-displacement curves have similar trends. It can be seen that all the crushing force responses are increased with the increase of RD.
Table 6 and Figure 11 give the calculated results of structural crashworthiness indicators. It is shown that the EA of all three TPMS-CS structures increased with the increase of RD, and the D-TPMS-CS with RD=30% have the highest EA (4707.5 J). The EA of all the TPMS-CS structures is almost constant with the increase of RD.
| TPMS | RD (%) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 10 | 3692.58 | 287.98 | 55.61 | 0.66 |
| 15 | 3916.53 | 338.1 | 55.37 | 0.64 | |
| 20 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 25 | 4400.68 | 415.63 | 55.42 | 0.59 | |
| 30 | 4653.71 | 454.06 | 55.59 | 0.57 | |
| D | 10 | 3765.75 | 325.32 | 56.71 | 0.64 |
| 15 | 4048.45 | 357.1 | 57.23 | 0.63 | |
| 20 | 4272.38 | 372.24 | 56.92 | 0.64 | |
| 25 | 4538.83 | 386.46 | 57.16 | 0.65 | |
| 30 | 4707.5 | 423.33 | 56.22 | 0.62 | |
| G | 10 | 3753.15 | 309.67 | 56.52 | 0.67 |
| 15 | 4004.82 | 347.01 | 56.62 | 0.64 | |
| 20 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 25 | 4311.71 | 378.74 | 54.31 | 0.63 | |
| 30 | 4560.05 | 444 | 54.47 | 0.57 |
The PCF of all the TPMS-CS structures also increases with the increase of RD. The P-TPMS-CS have the highest PCF (454.06 kN) at RD=30%.
For the crushing force efficiency, the CFE of P, G-TPMS-CS structures decreases with the increase of RD. There is no obvious trend in the CFE of D-TPMS-CS structures. The results indicate that the RD of TPMS-CS structures should be properly adopted.
In crashworthiness applications, the TPMS-CS structures should absorb as much energy as possible, while the PCF should be limited within a threshold value to guarantee the security of occupants [31,32,33]. In this regard, the optimization objectives of the TPMS-CS are to maximum SEA and minimum PCF. From the previous section, the simulation results indicate that the diamond TPMS-CS structures exhibit superior crashworthiness performances. Thus, we conduct the optimization design for the diamond TPMS-CS structures in this section.
From the discussion in the previous section, the crashworthiness indicators of the TPMS-CSs are affected by the inner shell thickness (t1), outer shell thickness (t2), and the relative density of TPMS (RD). Therefore, the mathematical optimization formulation for this optimization problem can be defined as follows,
| {Min.{−SEA(t1,t2,RD),PCF(t1,t2,RD)}s.t.1mm≤t1,t2≤2mm0.1≤RD≤0.3 | (6) |
To generate the surrogate models, the first step is to sample the reasonable design sampling points. Design of Experiment (DOE) is the typical way to address how to explore the entire design space properly. Among the available DOE techniques, the Latin Hypercube sampling (LHS) is adopted because it can efficiently produce the uniformly-distributed sampling points in the design space [34,35].
Crashworthiness optimization typically needs a larger amount of simulations. As an effective alternative, surrogate models are usually employed in literature to calculate the values of the objective function. In this study, three kinds of surrogate models, namely, Kriging (KRG) [36], polynomial response surface (PRS) [37], and radial basis function (RBF) [38] are used to approximate the objective function responses. The core functions of these surrogate models are listed in Table 7.
| Surrogate model | Approximate function ˆy(x) | Correlation function |
| KRG | ˆβ+rT(x)R−1(y−fˆβ) | R(xi,xj)=exp(−m∑k=1θk|xik−xjk|2) 0.05≤θk≤100 |
| PRS | b0+n∑i=1bixi+n∑i=1n∑j=1bijxixj+n∑i=1n∑j=1n∑k=1bijkxixjxk | None |
| RBF | ns∑i=1λiφ(r(xi,x)) | φ(r(xi,x))=√‖x−xi‖2+c2 c=1.0 |
To evaluate the accuracy of these three different surrogate models, additional assessment sample points should be generated. Three kinds of metrics, namely, square value (R2), relative average absolute error (RAAE), and relative maximum absolute error (RMAE) are used in this study [40,41]. The mathematic expression of these metrics is given as,
| R2=1−q∑i=1(yi−ˆyi)2q∑i=1(yi−−y)2 | (7) |
| RAAE=q∑i=1|yi−ˆyi|q∑i=1|yi−−y| | (8) |
| RMAE=max{|yi−ˆyi|,⋯,|yi−ˆyq|}q∑i=1|yi−−y|/q | (9) |
where yi is the exact function value at the assessment point i, ˆy is the corresponding surrogate value, −y is the mean value of yi, and q is the number of assessment points.
In general, the R2 and RAAE indicates the overall performance of the surrogate model, while the RMAE indicates the local accuracy of the surrogate model. Overall, the larger the R2, or the smaller the RMSE and RMAE, the better the accuracy of the surrogate model.
To solve the proposed optimization problem, a multi-objective optimization method using the surrogate models and the multi-objective particle swarm optimization (MOPSO) algorithm [42,43] was developed. Firstly, the design points were generated using the Latin hypercube sampling (LHS) method. Secondly, the objective responses for the TPMS-CS structures were derived using the FE model at the design points. Three different kinds of surrogate models were constructed, and the error metrics were compared to choose the most accurate one for the following optimization design. Finally, the MOPSO algorithm was used to obtain the Pareto optimal solutions.
In this study, 40 training points were selected from the design space by the LHS method to construct the surrogate models. To evaluate the accuracy of the surrogate models, additional 10 assessment sampling points were generated from the design space and the error metrics of three surrogate models are listed in Table 8. It is shown that the KRG surrogate model exhibits the best accuracy performance. Thus, the KRG model was used to evaluate the objective value of the D-TPMS-CS structures in the following optimization design.
| Surrogate model | Response | R2 | RAAE | RMAE |
| KGR | SEA | 0.9750 | 0.1251 | 0.2954 |
| PCF | 0.9351 | 0.1691 | 0.4205 | |
| PRS | SEA | 0.9708 | 0.1454 | 0.3295 |
| PCF | 0.8667 | 0.3211 | 0.4905 | |
| RBF | SEA | 0.9334 | 0.2160 | 0.4070 |
| PCF | 0.7429 | 0.2911 | 0.5734 |
The Pareto frontier of the D-TPMS-CS structure for the optimization problem was plotted in Figure 12. To guarantee the safety of the occupants, the PCF value was limited to 300 kN in this study, and the optimum design (t1=1mm, t2=2.87mm, and RD=17.6%) was selected from the Pareto frontier. Furthermore, the FE analysis was carried out on the optimum points to obtain the FE values which were compared with the optimization results, as listed in Table 9. It can be found that the error between the surrogate model predicted value and FE simulation value in the PCF and SEA is less than 7%, which indicates the proposed optimization framework has high accuracy and acceptability.
| Indicator | FE value | Predict value | Error (%) |
| SEA (kJ/kg) | 57.17 | 60.19 | 5.28 |
| PCF (kN) | 319.56 | 298.08 | -6.72 |
In this paper, a series of novel TPMS lattices filled cylindrical shell (TPMS-CS) structures are proposed and their energy absorption properties are studied using FE analysis. The comparison of crashworthiness among different TPMS-CS structures, the parametric studies, and the multi-objective optimization design is conducted in this study. Some conclusions can be concluded as follows:
● By analyzing the energy absorption performances of three different TPMS-CS structures under axial loading, the SEA of D-TPMS-CS increased by 2.7% and 3.5% than the other two TPMS-CS structures. It can be concluded that the D-TPMS-CS structure exhibits the highest energy absorption ability and efficiency than the other two structures.
● The parametric studies show that the inner shell thickness, outer shell thickness, and relative density of filled TPMS have significant influence on the crashworthiness performances of TPMS-CS structures.
● The multi-objective optimization design method, which combines three surrogate models (KRG, PRS, RBF) and a multi-objective particle swarm optimization algorithm, was carried out to seek the optimum configuration of D-TPMS-CS structure (t1=1mm, t2=2.87mm, and RD=17.6%). The relative errors of the proposed method are less than 7%.
This work was supported by the Science and Technology Research Project of Education Department of Hubei Province (Grant No. B2022006), the WUST national defence preresearch foundation (Grant No. GF202010). Numerical calculation is supported by High-Performance Computing Center of Wuhan University of Science and Technology.
The authors declare there is no conflict of interest.
| [1] |
T. N. Doan, N. T. Thanh, P. Van Chuong, N. C. Tho, N. T. Ta, H. N. Nguyen, Analysis of stress concentration phenomenon of cylinder laminated shells using higher-order shear deformation Quasi-3D theory, Compos. Struct., 232 (2020), 111526. https://doi.org/10.1016/j.compstruct.2019.111526 doi: 10.1016/j.compstruct.2019.111526

|
| [2] |
P. Jiao, Z. Chen, H. Ma, P. Ge, Y. Gu, H. Miao, Buckling behaviors of thin-walled cylindrical shells under localized axial compression loads, Part 1: Experimental study, Thin-Walled Struct., 166 (2021), 108118. https://doi.org/10.1016/J.Tws.2021.108118 doi: 10.1016/J.Tws.2021.108118

|
| [3] |
H. Wagner, C. Hühne, M. Janssen, Buckling of cylindrical shells under axial compression with loading imperfections: An experimental and numerical campaign on low knockdown factors, Thin-Walled Struct., 151 (2020), 106764. https://doi.org/10.1016/J.Tws.2020.106764 doi: 10.1016/J.Tws.2020.106764

|
| [4] |
S. M. Hosseini, M. Shariati, Experimental analysis of energy absorption capability of thin-walled composite cylindrical shells by quasi-static axial crushing test, Thin-Walled Struct., 125 (2018), 259–268. https://doi.org/10.1016/j.tws.2018.01.026 doi: 10.1016/j.tws.2018.01.026

|
| [5] |
D. Karagiozova, N. Jones, Dynamic effects on buckling and energy absorption of cylindrical shells under axial impact, Thin-Walled Struct., 39 (2001), 583–610. https://doi.org/10.1016/S0263-8231(01)00015-5 doi: 10.1016/S0263-8231(01)00015-5

|
| [6] |
P. B. Su, B. Han, M. Yang, Z. H. Wei, Z. Y. Zhao, Q. C. Zhang, et al., Axial compressive collapse of ultralight corrugated sandwich cylindrical shells, Mater. Des., 160 (2018), 325–337. https://doi.org/10.1016/j.matdes.2018.09.034 doi: 10.1016/j.matdes.2018.09.034

|
| [7] |
H. Zhu, P. Wang, D. Wei, J. Si, Y. Wu, Energy absorption of diamond lattice cylindrical shells under axial compression loading, Thin-Walled Struct., 181 (2022), 110131. https://doi.org/10.1016/j.tws.2022.110131 doi: 10.1016/j.tws.2022.110131

|
| [8] |
Y. Wang, X. Ren, Z. Chen, Y. Jiang, X. Cao, S. Fang, et al., Numerical and experimental studies on compressive behavior of Gyroid lattice cylindrical shells, Mater. Des., 186 (2020), 108340. https://doi.org/10.1016/j.matdes.2019.108340 doi: 10.1016/j.matdes.2019.108340

|
| [9] |
H. Huang, Q. Han, Nonlinear elastic buckling and postbuckling of axially compressed functionally graded cylindrical shells, Int. J. Mech. Sci., 51 (2009), 500–507. https://doi.org/10.1016/j.ijmecsci.2009.05.002 doi: 10.1016/j.ijmecsci.2009.05.002

|
| [10] |
Y. Wu, L. Sun, P. Yang, J. Fang, W. Li, Energy absorption of additively manufactured functionally bi-graded thickness honeycombs subjected to axial loads, Thin-Walled Struct., 164 (2021), 107810. https://doi.org/10.1016/j.tws.2021.107810 doi: 10.1016/j.tws.2021.107810

|
| [11] |
J. Fang, G. Sun, N. Qiu, T. Pang, S. Li, Q. Li, On hierarchical honeycombs under out-of-plane crushing, Int. J. Solids Struct., 135 (2018), 1–13. https://doi.org/10.1016/j.ijsolstr.2017.08.013 doi: 10.1016/j.ijsolstr.2017.08.013

|
| [12] |
X. Niu, F. Xu, Z. Zou, T. Fang, S. Zhang, Q. Xie, In-plane dynamic crashing behavior and energy absorption of novel bionic honeycomb structures, Compos. Struct., 299 (2022), 116064. https://doi.org/10.1016/j.compstruct.2022.116064 doi: 10.1016/j.compstruct.2022.116064

|
| [13] |
X. Niu, F. Xu, Z. Zou, Bionic inspired honeycomb structures and multi-objective optimization for variable graded layers, J. Sandwich Struct. Mater., 25 (2023), 215–231. https://doi.org/10.1177/10996362221127969 doi: 10.1177/10996362221127969

|
| [14] |
M. F. Ashby, The properties of foams and lattices, Phil. Trans. R. Soc. A, 364 (2006), 15–30. https://doi.org/10.1098/rsta.2005.1678 doi: 10.1098/rsta.2005.1678

|
| [15] |
H. S. Abdulhadi, A. Mian, Effect of strut length and orientation on elastic mechanical response of modified body-centered cubic lattice structures, Proc. Inst. Mech. Eng., Part L: J. Mater.: Des. Appl., 233 (2019), 2219–2233. https://doi.org/10.1177/1464420719841084 doi: 10.1177/1464420719841084

|
| [16] |
Y. Wang, B. Ramirez, K. Carpenter, C. Naify, D. C. Hofmann, C. Daraio, Architected lattices with adaptive energy absorption, Extreme Mech. Lett., 33 (2019), 100557. https://doi.org/10.1016/J.Eml.2019.100557 doi: 10.1016/J.Eml.2019.100557

|
| [17] |
Y. Zhang, Z. Xue, L. Chen, D. Fang, Deformation and failure mechanisms of lattice cylindrical shells under axial loading, Int. J. Mech. Sci., 51 (2009), 213–221. https://doi.org/10.1016/j.ijmecsci.2009.01.006 doi: 10.1016/j.ijmecsci.2009.01.006

|
| [18] |
L. Chen, J. Zhang, B. Du, H. Zhou, H. Liu, Y. Guo, et al., Dynamic crushing behavior and energy absorption of graded lattice cylindrical structure under axial impact load, Thin-Walled Struct., 127 (2018), 333–343. https://doi.org/10.1016/j.tws.2017.10.048 doi: 10.1016/j.tws.2017.10.048

|
| [19] |
B. Du, L. Chen, W. Wu, H. Liu, Y. Zhao, S. Peng, et al., A novel hierarchical thermoplastic composite honeycomb cylindrical structure: Fabrication and axial compressive properties, Compos. Sci. Technol., 164 (2018), 136–145. https://doi.org/10.1016/j.compscitech.2018.05.021 doi: 10.1016/j.compscitech.2018.05.021

|
| [20] |
Y. Wu, J. Fang, C. Wu, C. Li, G. Sun, Q. Li, Additively manufactured materials and structures: A state-of-the-art review on their mechanical characteristics and energy absorption, Int. J. Mech. Sci., 246 (2023), 108102. https://doi.org/10.1016/j.ijmecsci.2023.108102 doi: 10.1016/j.ijmecsci.2023.108102

|
| [21] |
N. Qiu, J. Zhang, F. Yuan, Z. Jin, Y. Zhang, J. Fang, Mechanical performance of triply periodic minimal surface structures with a novel hybrid gradient fabricated by selective laser melting, Eng. Struct., 263 (2022), 114377. https://doi.org/10.1016/j.engstruct.2022.114377 doi: 10.1016/j.engstruct.2022.114377

|
| [22] |
L. Zhang, S. Feih, S. Daynes, S. Chang, M. Y. Wang, J. Wei, et al., Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading, Addit. Manuf., 23 (2018), 505–515. https://doi.org/10.1016/j.addma.2018.08.007 doi: 10.1016/j.addma.2018.08.007

|
| [23] |
N. Qiu, J. Zhang, C. Li, Y. Shen, J. Fang, Mechanical properties of three-dimensional functionally graded TPMS structures, Int. J. Mech. Sci., 246 (2023), 108118. https://doi.org/10.1016/j.ijmecsci.2023.108118 doi: 10.1016/j.ijmecsci.2023.108118

|
| [24] |
H. Yin, Z. Liu, J. Dai, G. Wen, C. Zhang, Crushing behavior and optimization of sheet-based 3D periodic cellular structures, Composites, Part B, 182 (2020), 107565. https://doi.org/10.1016/j.compositesb.2019.107565 doi: 10.1016/j.compositesb.2019.107565

|
| [25] |
O. Al-Ketan, R. K. Abu Al-Rub, Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices, Adv. Eng. Mater., 21 (2019), 1900524. https://doi.org/10.1002/Adem.201900524 doi: 10.1002/Adem.201900524

|
| [26] |
H. Sun, C. Ge, Q. Gao, N. Qiu, L. Wang, Crashworthiness of sandwich cylinder filled with double-arrowed auxetic structures under axial impact loading, Int. J. Crashworthiness, 27 (2022), 1383–1392. https://doi.org/10.1080/13588265.2021.1947071 doi: 10.1080/13588265.2021.1947071

|
| [27] |
Y. Wu, J. Fang, Y. He, W. Li, Crashworthiness of hierarchical circular-joint quadrangular honeycombs, Thin-Walled Struct., 133 (2018), 180–191. https://doi.org/10.1016/j.tws.2018.09.044 doi: 10.1016/j.tws.2018.09.044

|
| [28] |
Y. Wu, J. Fang, Z. Cheng, Y. He, W. Li, Crashworthiness of tailored-property multi-cell tubular structures under axial crushing and lateral bending, Thin-Walled Struct., 149 (2020), 106640. https://doi.org/10.1016/j.tws.2020.106640 doi: 10.1016/j.tws.2020.106640

|
| [29] |
Y. Zhang, M. Lu, C. H. Wang, G. Sun, G. Li, Out-of-plane crashworthiness of bio-inspired self-similar regular hierarchical honeycombs, Compos. Struct., 144 (2016), 1–13. https://doi.org/10.1016/j.compstruct.2016.02.014 doi: 10.1016/j.compstruct.2016.02.014

|
| [30] |
G. Sun, S. Li, Q. Liu, G. Li, Q. Li, Experimental study on crashworthiness of empty/aluminum foam/honeycomb-filled CFRP tubes, Compos. Struct., 152 (2016), 969–993. https://doi.org/10.1016/j.compstruct.2016.06.019 doi: 10.1016/j.compstruct.2016.06.019

|
| [31] |
J. Fang, G. Sun, N. Qiu, N. H. Kim, Q. Li, On design optimization for structural crashworthiness and its state of the art, Struct. Multidiscip. Optim., 55 (2017), 1091–1119. https://doi.org/10.1007/s00158-016-1579-y doi: 10.1007/s00158-016-1579-y

|
| [32] |
J. Fang, Y. Gao, G. Sun, G. Zheng, Q. Li, Dynamic crashing behavior of new extrudable multi-cell tubes with a functionally graded thickness, Int. J. Mech. Sci., 103 (2015), 63–73. https://doi.org/10.1016/j.ijmecsci.2015.08.029 doi: 10.1016/j.ijmecsci.2015.08.029

|
| [33] |
G. Sun, T. Pang, J. Fang, G. Li, Q. Li, Parameterization of criss-cross configurations for multiobjective crashworthiness optimization, Int. J. Mech. Sci., 124 (2017), 145–157. https://doi.org/10.1016/j.ijmecsci.2017.02.027 doi: 10.1016/j.ijmecsci.2017.02.027

|
| [34] |
J. S. Park, Optimal Latin-hypercube designs for computer experiments, J. Stat. Plann. Inference, 39 (1994), 95–111. https://doi.org/10.1016/0378-3758(94)90115-5 doi: 10.1016/0378-3758(94)90115-5

|
| [35] |
N. Qiu, Y. Gao, J. Fang, Z. Feng, G. Sun, Q. Li, Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases, Finite Elem. Anal. Des., 104 (2015), 89–101. https://doi.org/10.1016/j.finel.2015.06.004 doi: 10.1016/j.finel.2015.06.004

|
| [36] |
Y. Wu, W. Li, J. Fang, Q. Lan, Multi-objective robust design optimization of fatigue life for a welded box girder, Eng. Optim., 50 (2018), 1252–1269. https://doi.org/10.1080/0305215X.2017.1395023 doi: 10.1080/0305215X.2017.1395023

|
| [37] |
X. Song, G. Sun, G. Li, W. Gao, Q. Li, Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models, Struct. Multidiscip. Optim., 47 (2013), 221–231. https://doi.org/10.1007/s00158-012-0820-6 doi: 10.1007/s00158-012-0820-6

|
| [38] |
H. M. Gutmann, A radial basis function method for global optimization, J. Global Optim, 19 (2001), 201–227. https://doi.org/10.1023/A:1011255519438 doi: 10.1023/A:1011255519438

|
| [39] |
A. I. J. Forrester, A. J. Keane, Recent advances in surrogate-based optimization, Prog. Aerosp. Sci., 45 (2009), 50–79. https://doi.org/10.1016/j.paerosci.2008.11.001 doi: 10.1016/j.paerosci.2008.11.001

|
| [40] |
J. Fu, Q. Liu, K. Liufu, Y. Deng, J. Fang, Q. Li, Design of bionic-bamboo thin-walled structures for energy absorption, Thin-Walled Struct., 135 (2019), 400–413. https://doi.org/10.1016/j.tws.2018.10.003 doi: 10.1016/j.tws.2018.10.003

|
| [41] |
N. Qiu, Z. Jin, J. Liu, L. Fu, Z. Chen, N. H. Kim, Hybrid multi-objective robust design optimization of a truck cab considering fatigue life, Thin-Walled Struct., 162 (2021), 107545. https://doi.org/10.1016/j.tws.2021.107545 doi: 10.1016/j.tws.2021.107545

|
| [42] |
C. A. C. Coello, G. T. Pulido, M. S. Lechuga, Handling multiple objectives with particle swarm optimization, IEEE Trans. Evol. Comput., 8 (2004), 256–279. https://doi.org/10.1109/TEVC.2004.826067 doi: 10.1109/TEVC.2004.826067

|
| [43] |
J. Fang, Y. Gao, G. Sun, N. Qiu, Q. Li, On design of multi-cell tubes under axial and oblique impact loads, Thin-Walled Struct., 95 (2015), 115–126. https://doi.org/10.1016/j.tws.2015.07.002 doi: 10.1016/j.tws.2015.07.002

|
| 1. | Xinyu He, Ce Yang, Mingqiu Zheng, Hanzhi Zhang, Yadong Du, A fast evaluation method for surface area, volume fraction, and hydraulic diameter of TPMS with different geometric characteristics, 2024, 0954-4062, 10.1177/09544062241277342 | |
| 2. | T Dabasa, H G Lemu, Y Regassa, Literature review on thin-walled and cellular structure designs for energy absorption, 2023, 1294, 1757-8981, 012046, 10.1088/1757-899X/1294/1/012046 | |
| 3. | Sheng Li, Laiyu Liang, Ping Yang, Shaoan Li, Yaozhong Wu, Bending Performance of Diamond Lattice Cylindrical Shells, 2025, 18, 1996-1944, 272, 10.3390/ma18020272 | |
| 4. | Zihao Li, Shiqiang Li, Jiajing Liu, Zhifang Liu, Jianyin Lei, Zhihua Wang, Response mechanisms and energy absorption properties of hybrid sheet TPMS lattices under static and dynamic loading, 2025, 210, 02638231, 112980, 10.1016/j.tws.2025.112980 | |
| 5. | Dong Wei, Shaoan Li, Laiyu Liang, Longfei Sun, Yaozhong Wu, Low-Velocity Impact Response of Sandwich Structure with Triply Periodic Minimal Surface Cores, 2025, 17, 2073-4360, 712, 10.3390/polym17060712 | |
| 6. | Mingzhu Dang, Honghao Xiang, Jingjing Li, Chunsheng Ye, Chao Cai, Qingsong Wei, Mechanical Response and Superelastic Properties of Cu-11.85Al-3.2Mn-0.1Ti TPMS Structures Printed by Laser Powder Bed Fusion, 2025, 38, 2192-8258, 10.1186/s10033-024-01170-x |
| Parameters | Value |
| Density (g/cm3) | 7.98 |
| Young's modulus (GPa) | 190 |
| Yield stress (MPa) | 633 |
| Ultimate stress (MPa) | 1074 |
| Poisson's ratio | 0.3 |
| Indicators | Test (average) | Reference results | This paper | Error (%) |
| EA (J) | 633.38 | 669.97 | 672.15 | 0.33 |
| PCF (kN) | 65.86 | 66.07 | 65.92 | -1.34 |
| TPMS-CS | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 4126.79 | 386.62 | 54.98 | 0.59 |
| D | 4272.38 | 412 | 56.92 | 0.65 |
| G | 4158.38 | 368.61 | 55.40 | 0.63 |
| TPMS | t1 (mm) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 1 | 2624.98 | 316.75 | 46.34 | 0.46 |
| 1.5 | 3367.45 | 316.55 | 51.13 | 0.59 | |
| 2 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 2.5 | 4872.01 | 391.79 | 57.81 | 0.69 | |
| 3 | 5623.44 | 585.47 | 60.16 | 0.53 | |
| D | 1 | 2861.39 | 268 | 50.51 | 0.59 |
| 1.5 | 3539.74 | 374.37 | 53.75 | 0.6 | |
| 2 | 4272.38 | 412 | 56.92 | 0.65 | |
| 2.5 | 4849.31 | 443.49 | 57.55 | 0.7 | |
| 3 | 5556.85 | 657.25 | 59.45 | 0.54 | |
| G | 1 | 2795.62 | 283.27 | 49.34 | 0.55 |
| 1.5 | 3495.27 | 373.79 | 53.07 | 0.52 | |
| 2 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 2.5 | 4676.69 | 417.58 | 55.50 | 0.62 | |
| 3 | 5441.84 | 688.81 | 58.22 | 0.44 |
| TPMS | t2 (mm) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 1 | 3010.19 | 247.62 | 46.60 | 0.68 |
| 1.5 | 3473.58 | 272.14 | 49.74 | 0.66 | |
| 2 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 2.5 | 4562.29 | 401.88 | 56.82 | 0.63 | |
| 3 | 5180.25 | 418.58 | 60.57 | 0.64 | |
| D | 1 | 3402.73 | 269.93 | 52.67 | 0.7 |
| 1.5 | 3740.50 | 362.63 | 53.57 | 0.67 | |
| 2 | 4272.38 | 412 | 56.92 | 0.62 | |
| 2.5 | 4780.99 | 420.25 | 59.55 | 0.64 | |
| 3 | 5192.63 | 410.63 | 60.72 | 0.66 | |
| G | 1 | 3228.56 | 250.35 | 49.98 | 0.72 |
| 1.5 | 3669.70 | 332.73 | 52.55 | 0.61 | |
| 2 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 2.5 | 4681.38 | 428.02 | 58.30 | 0.61 | |
| 3 | 5128.39 | 400.52 | 59.96 | 0.63 |
| TPMS | RD (%) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 10 | 3692.58 | 287.98 | 55.61 | 0.66 |
| 15 | 3916.53 | 338.1 | 55.37 | 0.64 | |
| 20 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 25 | 4400.68 | 415.63 | 55.42 | 0.59 | |
| 30 | 4653.71 | 454.06 | 55.59 | 0.57 | |
| D | 10 | 3765.75 | 325.32 | 56.71 | 0.64 |
| 15 | 4048.45 | 357.1 | 57.23 | 0.63 | |
| 20 | 4272.38 | 372.24 | 56.92 | 0.64 | |
| 25 | 4538.83 | 386.46 | 57.16 | 0.65 | |
| 30 | 4707.5 | 423.33 | 56.22 | 0.62 | |
| G | 10 | 3753.15 | 309.67 | 56.52 | 0.67 |
| 15 | 4004.82 | 347.01 | 56.62 | 0.64 | |
| 20 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 25 | 4311.71 | 378.74 | 54.31 | 0.63 | |
| 30 | 4560.05 | 444 | 54.47 | 0.57 |
| Surrogate model | Approximate function ˆy(x) | Correlation function |
| KRG | ˆβ+rT(x)R−1(y−fˆβ) | R(xi,xj)=exp(−m∑k=1θk|xik−xjk|2) 0.05≤θk≤100 |
| PRS | b0+n∑i=1bixi+n∑i=1n∑j=1bijxixj+n∑i=1n∑j=1n∑k=1bijkxixjxk | None |
| RBF | ns∑i=1λiφ(r(xi,x)) | φ(r(xi,x))=√‖x−xi‖2+c2 c=1.0 |
| Surrogate model | Response | R2 | RAAE | RMAE |
| KGR | SEA | 0.9750 | 0.1251 | 0.2954 |
| PCF | 0.9351 | 0.1691 | 0.4205 | |
| PRS | SEA | 0.9708 | 0.1454 | 0.3295 |
| PCF | 0.8667 | 0.3211 | 0.4905 | |
| RBF | SEA | 0.9334 | 0.2160 | 0.4070 |
| PCF | 0.7429 | 0.2911 | 0.5734 |
| Indicator | FE value | Predict value | Error (%) |
| SEA (kJ/kg) | 57.17 | 60.19 | 5.28 |
| PCF (kN) | 319.56 | 298.08 | -6.72 |
| Parameters | Value |
| Density (g/cm3) | 7.98 |
| Young's modulus (GPa) | 190 |
| Yield stress (MPa) | 633 |
| Ultimate stress (MPa) | 1074 |
| Poisson's ratio | 0.3 |
| Indicators | Test (average) | Reference results | This paper | Error (%) |
| EA (J) | 633.38 | 669.97 | 672.15 | 0.33 |
| PCF (kN) | 65.86 | 66.07 | 65.92 | -1.34 |
| TPMS-CS | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 4126.79 | 386.62 | 54.98 | 0.59 |
| D | 4272.38 | 412 | 56.92 | 0.65 |
| G | 4158.38 | 368.61 | 55.40 | 0.63 |
| TPMS | t1 (mm) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 1 | 2624.98 | 316.75 | 46.34 | 0.46 |
| 1.5 | 3367.45 | 316.55 | 51.13 | 0.59 | |
| 2 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 2.5 | 4872.01 | 391.79 | 57.81 | 0.69 | |
| 3 | 5623.44 | 585.47 | 60.16 | 0.53 | |
| D | 1 | 2861.39 | 268 | 50.51 | 0.59 |
| 1.5 | 3539.74 | 374.37 | 53.75 | 0.6 | |
| 2 | 4272.38 | 412 | 56.92 | 0.65 | |
| 2.5 | 4849.31 | 443.49 | 57.55 | 0.7 | |
| 3 | 5556.85 | 657.25 | 59.45 | 0.54 | |
| G | 1 | 2795.62 | 283.27 | 49.34 | 0.55 |
| 1.5 | 3495.27 | 373.79 | 53.07 | 0.52 | |
| 2 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 2.5 | 4676.69 | 417.58 | 55.50 | 0.62 | |
| 3 | 5441.84 | 688.81 | 58.22 | 0.44 |
| TPMS | t2 (mm) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 1 | 3010.19 | 247.62 | 46.60 | 0.68 |
| 1.5 | 3473.58 | 272.14 | 49.74 | 0.66 | |
| 2 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 2.5 | 4562.29 | 401.88 | 56.82 | 0.63 | |
| 3 | 5180.25 | 418.58 | 60.57 | 0.64 | |
| D | 1 | 3402.73 | 269.93 | 52.67 | 0.7 |
| 1.5 | 3740.50 | 362.63 | 53.57 | 0.67 | |
| 2 | 4272.38 | 412 | 56.92 | 0.62 | |
| 2.5 | 4780.99 | 420.25 | 59.55 | 0.64 | |
| 3 | 5192.63 | 410.63 | 60.72 | 0.66 | |
| G | 1 | 3228.56 | 250.35 | 49.98 | 0.72 |
| 1.5 | 3669.70 | 332.73 | 52.55 | 0.61 | |
| 2 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 2.5 | 4681.38 | 428.02 | 58.30 | 0.61 | |
| 3 | 5128.39 | 400.52 | 59.96 | 0.63 |
| TPMS | RD (%) | EA (J) | PCF (kN) | SEA (kJ/kg) | CFE |
| P | 10 | 3692.58 | 287.98 | 55.61 | 0.66 |
| 15 | 3916.53 | 338.1 | 55.37 | 0.64 | |
| 20 | 4126.79 | 386.62 | 54.98 | 0.59 | |
| 25 | 4400.68 | 415.63 | 55.42 | 0.59 | |
| 30 | 4653.71 | 454.06 | 55.59 | 0.57 | |
| D | 10 | 3765.75 | 325.32 | 56.71 | 0.64 |
| 15 | 4048.45 | 357.1 | 57.23 | 0.63 | |
| 20 | 4272.38 | 372.24 | 56.92 | 0.64 | |
| 25 | 4538.83 | 386.46 | 57.16 | 0.65 | |
| 30 | 4707.5 | 423.33 | 56.22 | 0.62 | |
| G | 10 | 3753.15 | 309.67 | 56.52 | 0.67 |
| 15 | 4004.82 | 347.01 | 56.62 | 0.64 | |
| 20 | 4158.38 | 368.61 | 55.40 | 0.63 | |
| 25 | 4311.71 | 378.74 | 54.31 | 0.63 | |
| 30 | 4560.05 | 444 | 54.47 | 0.57 |
| Surrogate model | Approximate function ˆy(x) | Correlation function |
| KRG | ˆβ+rT(x)R−1(y−fˆβ) | R(xi,xj)=exp(−m∑k=1θk|xik−xjk|2) 0.05≤θk≤100 |
| PRS | b0+n∑i=1bixi+n∑i=1n∑j=1bijxixj+n∑i=1n∑j=1n∑k=1bijkxixjxk | None |
| RBF | ns∑i=1λiφ(r(xi,x)) | φ(r(xi,x))=√‖x−xi‖2+c2 c=1.0 |
| Surrogate model | Response | R2 | RAAE | RMAE |
| KGR | SEA | 0.9750 | 0.1251 | 0.2954 |
| PCF | 0.9351 | 0.1691 | 0.4205 | |
| PRS | SEA | 0.9708 | 0.1454 | 0.3295 |
| PCF | 0.8667 | 0.3211 | 0.4905 | |
| RBF | SEA | 0.9334 | 0.2160 | 0.4070 |
| PCF | 0.7429 | 0.2911 | 0.5734 |
| Indicator | FE value | Predict value | Error (%) |
| SEA (kJ/kg) | 57.17 | 60.19 | 5.28 |
| PCF (kN) | 319.56 | 298.08 | -6.72 |