A fuzzy neural network-based automatic fault diagnosis method for permanent magnet synchronous generators

Xueyan Wang; Xueyan Wang

doi:10.3934/mbe.2023392

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 5: 8933-8953. doi: 10.3934/mbe.2023392

Previous Article Next Article

Research article

A fuzzy neural network-based automatic fault diagnosis method for permanent magnet synchronous generators

Xueyan Wang ^,

College of Intelligent Manufacturing, Zibo Vocational Institute, Shandong, 255300, China

Academic Editor:Yang Kuang

Received: 29 December 2022 Revised: 10 February 2023 Accepted: 15 February 2023 Published: 09 March 2023

In recent years, automatic fault diagnosis for various machines has been a hot topic in the industry. This paper focuses on permanent magnet synchronous generators and combines fuzzy decision theory with deep learning for this purpose. Thus, a fuzzy neural network-based automatic fault diagnosis method for permanent magnet synchronous generators is proposed in this paper. The particle swarm algorithm optimizes the smoothing factor of the network for the effect of probabilistic neural network classification, as affected by the complexity of the structure and parameters. And on this basis, the fuzzy C means algorithm is used to obtain the clustering centers of the fault data, and the network model is reconstructed by selecting the samples closest to the clustering centers as the neurons in the probabilistic neural network. The mathematical analysis and derivation of the T-S (Tkagi-Sugneo) fuzzy neural network-based diagnosis strategy are carried out; the T-S fuzzy neural network-based generator fault diagnosis system is designed. The model is implemented on the MATLAB/Simulink platform for simulation and verification, the experiments show that the T-S fuzzy diagnosis strategy is significantly improved, and the design purpose is achieved. The fuzzy neural network has a parallel structure and can perform parallel data processing. This parallel mechanism can solve the problem of large-scale real-time computation in control systems, and the redundancy in parallel computation can make the control system highly fault-tolerant and robust. The fault diagnosis model based on an improved probabilistic neural network is applied to the fault data to verify the effectiveness and accuracy of the model.

Keywords:

Citation: Xueyan Wang. A fuzzy neural network-based automatic fault diagnosis method for permanent magnet synchronous generators[J]. Mathematical Biosciences and Engineering, 2023, 20(5): 8933-8953. doi: 10.3934/mbe.2023392

Related Papers:

[1]	Shaimaa A. M. Abdelmohsen, D. Sh. Mohamed, Haifa A. Alyousef, M. R. Gorji, Amr M. S. Mahdy . Mathematical modeling for solving fractional model cancer bosom malignant growth. AIMS Biophysics, 2023, 10(3): 263-280. doi: 10.3934/biophy.2023018
[2]	Mati ur Rahman, Mehmet Yavuz, Muhammad Arfan, Adnan Sami . Theoretical and numerical investigation of a modified ABC fractional operator for the spread of polio under the effect of vaccination. AIMS Biophysics, 2024, 11(1): 97-120. doi: 10.3934/biophy.2024007
[3]	Yasir Nadeem Anjam, Mehmet Yavuz, Mati ur Rahman, Amna Batool . Analysis of a fractional pollution model in a system of three interconnecting lakes. AIMS Biophysics, 2023, 10(2): 220-240. doi: 10.3934/biophy.2023014
[4]	Marco Menale, Bruno Carbonaro . The mathematical analysis towards the dependence on the initial data for a discrete thermostatted kinetic framework for biological systems composed of interacting entities. AIMS Biophysics, 2020, 7(3): 204-218. doi: 10.3934/biophy.2020016
[5]	Mehmet Yavuz, Kübra Akyüz, Naime Büşra Bayraktar, Feyza Nur Özdemir . Hepatitis-B disease modelling of fractional order and parameter calibration using real data from the USA. AIMS Biophysics, 2024, 11(3): 378-402. doi: 10.3934/biophy.2024021
[6]	Larisa A. Krasnobaeva, Ludmila V. Yakushevich . On the dimensionless model of the transcription bubble dynamics. AIMS Biophysics, 2023, 10(2): 205-219. doi: 10.3934/biophy.2023013
[7]	Carlo Bianca . Differential equations frameworks and models for the physics of biological systems. AIMS Biophysics, 2024, 11(2): 234-238. doi: 10.3934/biophy.2024013
[8]	Mohammed Alabedalhadi, Mohammed Shqair, Ibrahim Saleh . Analysis and analytical simulation for a biophysical fractional diffusive cancer model with virotherapy using the Caputo operator. AIMS Biophysics, 2023, 10(4): 503-522. doi: 10.3934/biophy.2023028
[9]	Bertrand R. Caré, Pierre-Emmanuel Emeriau, Ruggero Cortini, Jean-Marc Victor . Chromatin epigenomic domain folding: size matters. AIMS Biophysics, 2015, 2(4): 517-530. doi: 10.3934/biophy.2015.4.517
[10]	David Gosselin, Maxime Huet, Myriam Cubizolles, David Rabaud, Naceur Belgacem, Didier Chaussy, Jean Berthier . Viscoelastic capillary flow: the case of whole blood. AIMS Biophysics, 2016, 3(3): 340-357. doi: 10.3934/biophy.2016.3.340

Abstract

1. Introduction

Numerous mathematical models have been established to predict and study the biological system. In the past four decades, there have been far-reaching research on improving cell mass production in chemical reactors [1]. The chemostat model is used to understand the mechanism of cell mass growth in a chemostat. A chemostat is an apparatus for continuous culture that contains bacterial populations. It can be used to investigate the cell mass production under controlled conditions. This reactor provides a dynamic system for population studies and is suitable to be used in a laboratory. A substrate is continuously added into the reactor containing the cell mass, which grows by consuming the substrate that enters through the inflow chamber. Meanwhile, the mixture of cell mass and substrate is continuously harvested from the reactor through the outflow chamber. The dynamics in the chemostat can be investigated by using the chemostat model [2].

Ordinary differential equations (ODEs) are commonly used for modelling biological systems. However, most biological systems behaviour has memory effects, and ODEs usually neglect such effects. The fractional-order differential equations (FDEs) are taken into account when describing the behaviour of the systems' equations. A FDEs is a generalisation of the ODEs to random nonlinear order [3]. This equation is more effective because of its good memory, among other advantages [4]–[8]. The errors occuring from the disregarded parameters when modelling of phenomena in real-life also can be reduced. FDEs are also used to efficiently replicate the real nature of various systems in the field of engineering and sciences [9]. In the past few decades, FDEs have been used in biological systems for various studies [5], [6], [10]–[17].

Since great strides in the study of FDEs have been developed, the dynamics in the chemostat can be investigated using the mathematical model of the chemostat in the form of FDEs. Moreover, there have been few studies on the expansion of the chemostat model with fractional-order theory. Thus, we deepen and complete the analysis on the integer-order chemostat model with fractional-order theory and discuss the stability of the equilibrium points of the fractional-order chemostat model. Next, the bifurcation analysis for the fractional-order chemostat model is conducted to identify the bifurcation point that can change the stability of the system. The analysis identifies the values of the fractional-order and the system parameters to ensure the operation of the chemostat is well-controlled.

2. Materials and methods

2.1. Definition of Caputo derivative

Recently, there are many approaches to define fractional operators such as by Caputo, Riemann-Liouville, Hadamard, and Grunwald-Letnikov [3]. However, Caputo is often used due to its convenience in various applications [18]. Caputo is also useful to encounter an obstacle where the initial condition is done in the differential of integer-order [19]. In this paper, we applied Caputo derivative to define the system of fractional-order. The Caputo derivative for the left-hand side is defined as

$D_{t}^{α} f (t) = \frac{1}{Γ (n - α)} \int_{0}^{t} \frac{f^{(n)} τ}{{(t - τ)}^{α - n + 1}} d τ,$ (2.1)

where Г denotes the function of gamma, n is an integer, where $n - 1 < α < n$ [18].

2.2. Adams-type predictor corrector method

The Adams-type predictor-corrector method is one of the technique that have been proposed for fractional-order differential equations [19]–[21]. The Adams-type predictor-corrector method is a analysis of numerical algorithm that involves two basics steps: predictor and corrector. The predictor formula can be described as

$\begin{array}{l} y_{h}^{P} (t_{n + 1}) = \sum_{k = 0}^{α - 1} \frac{t_{n + 1}^{k}}{k!} y_{0}^{(k)} + \frac{1}{Γ (α)} \sum_{j = 0}^{n} b_{j, n + 1} f (t_{j}, y_{h} (t_{j})), \end{array}$ (2.2)

meanwhile the corrector formula can be determined by

$y_{h} (t_{n + 1}) = \sum_{k = 0}^{α - 1} \frac{t_{n + 1}^{k}}{k!} + \frac{h^{α}}{Γ (α + 2)} f (t_{n + 1}, y_{h}^{P} (t_{n + 1})) + \frac{h^{α}}{Γ (α + 2)} \sum_{j = 0}^{n} f (t_{j}, y_{h} (t_{j})) .$ (2.3)

The predictor-corrector method is also called as the PECE (Predict, Evaluate, Correct, Evaluate) method [22]. The procedure of the predictor-corrector method can be explained as follows

(i) Calculate the predictor step, $y_{h}^{P} (t_{n + 1})$ in Eq. (2.2).

(ii) Evaluate $f (t_{n + 1}, y_{h}^{P} (t_{n + 1}))$ .

(iii) Calculate the corrector step, $y_{h} (t_{n + 1})$ in Eq. (2.3).

(iv) Evaluate $f (t_{n + 1}, y_{h} (t_{n + 1}))$ .

The procedure repeatedly predicts and corrects the value until the corrected value becomes a converged number [21]. This method is able to maintain the stability of the properties and has good accuracy. Moreover, this method also has lower computational cost than other methods [23]. The algorithm of the Adams-type predictor-corrector method proposed by [22] is shown in Appendix.

2.3. Stability analysis of fractional-order system

The conditions of stability for integer-order differential equations and fractional-order differential equations are different. Both systems could have the same steady-state points but different stability conditions [24], [25]. The stability condition for fractional-order differential equations can be stated by Theorem 1 and the Routh-Hurwitz stability condition as described by Proposition 1.

Theorem 1 [5], [6], [26]. The commensurate system of fractional-order where $x \in ℝ$ and $0 < α < 1$ is locally asymptotically stable if the eigenvalues of the Jacobian matrix evaluated at the steady-state point is satisfied by

$| a r g (λ) | > \frac{α π}{2} .$ (2.4)

Proposition 1 [5], [6], [26]. Suppose the characteristic polynomial is $P (λ) = λ^{2} + b λ + c$ of the Jacobian matrix which evaluated at the steady-state. The eigenvalues of the Jacobian matrix will satisfy Eq. (2.4) in Theorem 1 if

$b > 0, c > 0,$ (2.5)

$b < 0, 4 c > b^{2}, | t a n^{- 1} (\frac{\sqrt{4 c - b^{2}}}{b}) | > \frac{α π}{2} .$ (2.6)

The stability theorem on the fractional-order systems and fractional Routh-Hurwitz stability conditions are introduced to analyze the stability of the model. The fractional Routh-Hurwitz stability conditions is specifically introduced for the eigenvalues of the Jacobian matrix that obtained in quadratic form. The proof of this proposition is shown in Appendix.

2.4. Hopf bifurcation analysis of fractional-order system

Bifurcation can be defined as any sudden change that occurs while a parameter value is varied in the differential equation system and it has a significant influence on the solution [27]. An unstable steady-state may becomes stable and vice versa. A slight changes in the parameter value may change the system's stability. Despite the steady-state point and the eigenvalues of the system of fractional-order are similar as the system of integer-order, the discriminant method used for the stability of the steady-state point is different. Accordingly, the Hopf bifurcation condition in the fractional-order system is slightly different as compared with the integer-order system.

2.4.1. Hopf bifurcation analysis of fractional order α

Fractional order α can be selected as the bifurcation parameter in a fractional-order system, but this is not allowed in an integer-order system. The existence of Hopf bifurcation can be stated as in Theorem 2.

Theorem 2 [28]. Assume α* as the critical value of the fractional-order. When bifurcation parameter α passes over critical value α*, which is $α^{*} \in (0,1)$ , Hopf bifurcation occurs at the steady-state point if the following conditions are satisfied

(i) 1. The characteristic equation of chemostat system has a pair of complex conjugate roots, $λ_{1,2} = p \pm i q$ , while the other eigenvalues are negative real roots.

(ii) Critical value $m (α^{*}) = \frac{α^{*} π}{2} - m i n | a r g (λ) | = 0$ .

(iii) $\frac{d m (α)}{d α} |_{α = α^{*}} \neq 0$ (condition of transversality).

Proof. Condition (i) is not easy to obtain due to the selected parameter's value. However, this condition can be managed under some confined conditions. In fact, the washout steady-state solution of the chemostat model has two negative real roots. The remaining two roots depend on the characteristic of the polynomial from the no-washout steady-state solution.

Condition (ii) can be satisfied with the existence of critical value α* and when $a r g (λ)$ is equivalent to $a r c t a n (\frac{q}{p})$ . Thus, the solution of critical value $m (α^{*})$ can be written as

$α^{*} = \frac{α^{*} π}{2} - a r c t a n (\frac{q}{p}) = 0, α^{*} \in (0,1) .$ (2.7)

The integer system required p = 0 for the bifurcation's operating condition. For the fractional-order system, the operating condition of the system will change into $m (α^{*}) = \frac{α^{*} π}{2} - m i n | a r g (x) | = 0$ . For condition (iii), the condition of $m (α)$ changes when bifurcation parameter $α$ passes over critical value α*. For example, the steady-state point is asymptotically stable for $0 < α < α^{*}$ and unstable when $α < α^{*} < 1$ . Thus, Hopf bifurcation exists at $α = α^{*}$ .

2.4.2. Hopf bifurcation analysis of parameters value

In studying the dynamic process of chemostat, the parameters such as $Q, S_{0}, µ, k, γ$ and β are usually used as the bifurcation parameter since these parameters have significant effects on the dynamic process of the system of fractional-order and integer-order. Fractional-order α is considered fixed and the initial substrate concentration S₀ is studied as the control parameter. The existence of the Hopf bifurcation can be stated as in Theorem 3.

Theorem 3 [28]. Assume $S_{0}^{*}$ as the critical value of the fractional-order. When bifurcation parameter S₀ passes over critical value $S_{0}^{*}$ , Hopf bifurcation occurs at the steady-state point if the following conditions are satisfied

(i) The characteristic equation of chemostat system has a pair of complex conjugate roots, $λ_{1,2} = p (S_{0}) \pm i q (S_{0})$ , while the other eigenvalues are negative real roots.

(ii) Critical value $m (S_{0}^{*}) = \frac{α π}{2} - m i n | a r g (λ (S_{0}^{*})) | = 0$ .

(iii) $\frac{d m (S_{0}^{*})}{d (S_{0}^{*})} |_{S_{0} = S_{0}^{*}} \neq 0$ (condition of transversality).

Proof. This theorem can be proved in the same way as Theorem 2. Therefore, condition (i) can be guaranteed. Condition (ii) can be satisfied with the existence of critical value $S_{0}^{*}$ and when $a r g [λ (S_{0}^{*})]$ is equivalent to $a r c t a n [\frac{q (S_{0}^{*})}{p (S_{0}^{*})}]$ . Thus, the solution of critical value $m (S_{0}^{*})$ can be written as

$S_{0}^{*} = \frac{α π}{2} - a r c t a n (\frac{q (S_{0}^{*})}{p (S_{0}^{*})}) = 0.$ (2.8)

For condition (iii), the condition of $m (S_{0}^{*})$ changes when bifurcation parameter S₀ passes over critical value $S_{0}^{*}$ . For example, the steady-state point is asymptotically stable when $0 < S_{0} < S_{0}^{*}$ and unstable when $S_{0} < S_{0}^{*} < 1$ . Thus, Hopf bifurcation exists at $S_{0} = S_{0}^{*}$ [28].

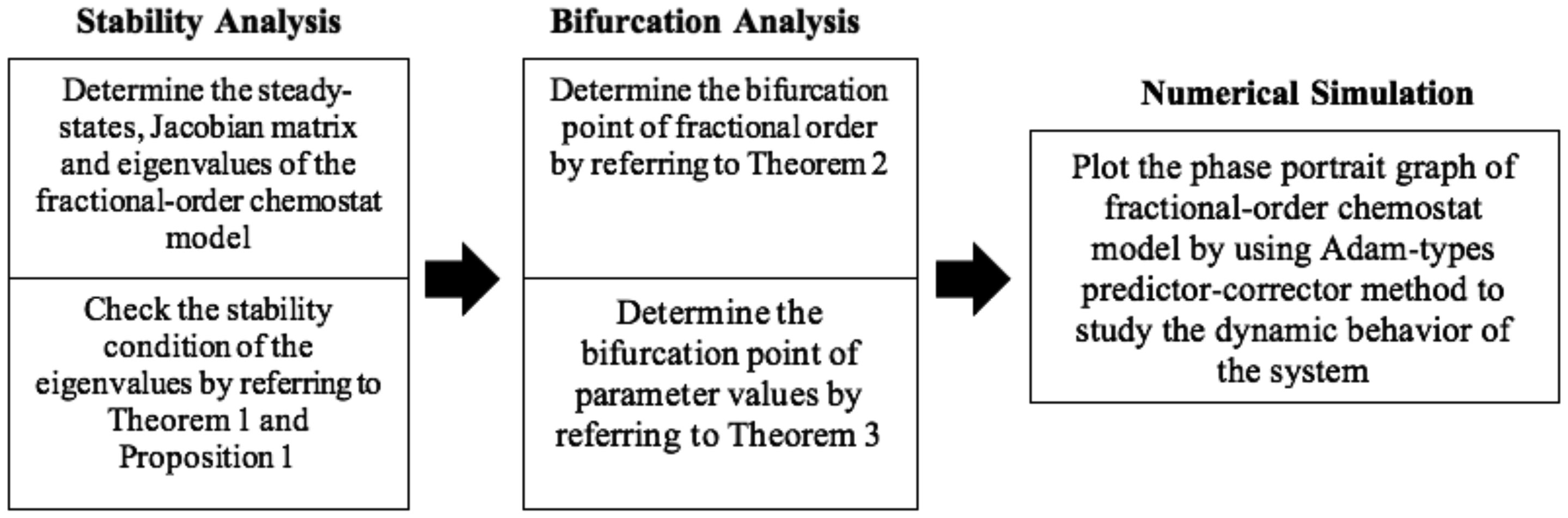
Firstly, determine the steady-states, Jacobian matrix and eigenvalues of the fractional-order chemostat model. The stability properties of the fractional-order chemostat model were estimated by using the stability and bifurcation analyses with FDEs by referring to Theorem 1 and Proposition 1. Then, determine the bifurcation point of fractional-order by referring to Theorem 2 and determine the bifurcation point of parameter values by referring to Theorem 3. Next, plot the phase portrait of fractional-order chemostat model by using Adam-types predictor-corrector method to study the dynamic behaviour of the system. Figure 1 depicts the flowchart of this research. This flowchart can be applied to all problems with suitable parameter values.

Figure 1. Mathematical analysis of fractional-order chemostat model.

DownLoad: Full-Size Img PowerPoint

3. Results and Discussion

3.1. Fractional-order chemostat model

An integer-order chemostat model that considered a variable yield coefficient and the Monod growth model from [1] is studied in this section. The chemostat system can be written as

$\begin{array}{l} \frac{d S}{d t} & = Q (S_{0} - S) - \frac{µ S X}{(k + S) (γ + β S)}, \\ \frac{d X}{d t} & = Q (- X) + \frac{µ S X}{k + S}, \end{array}$ (3.1)

with the initial value of $X_{0} = 0$ , where the sterile feed case was assumed. The integer-order chemostat system of Eq. (3.1) is extended to the fractional-order differential equation

$\begin{array}{l} \frac{d^{α} S}{d t^{α}} & = Q (S_{0} - S) - \frac{µ S X}{(k + S) (γ + β S)}, \\ \frac{d^{α} X}{d t^{α}} & = Q (- X) + \frac{µ S X}{k + S} . \end{array}$ (3.2)

Let Eq. (3.2) equal to zero in order to find the steady-state solutions

$Q (S_{0} - S) - \frac{µ S X}{(k + S) (γ + β S)} = 0,$ (3.3)

$Q (- X) + \frac{µ S X}{k + S} = 0.$ (3.4)

By solving Eq. (3.4), the following solutions are obtained

$S^{*} = \frac{k Q}{µ - Q},$ (3.5)

$X^{*} = 0.$ (3.6)

From Eq. (3.3), if $X^{*} = 0$ , then $S^{*} = S_{0}$ . If $S^{*} = \frac{k Q}{µ - Q}$ , then

$X^{*} = \frac{(k Q + Q S_{0} - S_{0} µ) (- Q γ + k Q β + γ µ)}{{(µ - Q)}^{2}} .$ (3.7)

Hence, the solutions of steady-state for the chemostat model are

(i) Washout:

$(S_{0}^{*}, X_{0}^{*}) = (S_{0},0) .$ (3.8)

(ii) No Washout:

$(S_{1}^{*}, X_{1}^{*}) = (ρ, (S_{0} - ρ) (γ + β ρ)),$ (3.9)

where

$\begin{array}{l} ρ = \frac{k Q}{µ - Q} . \end{array}$

The steady-state solutions are physically meaningful if their components are positive. Therefore, $S_{0} > 0$ for the washout steady-state solution exists by biological meaning. The no-washout steady-state solution will only exist when $0 < ρ < S_{0}$ . The Jacobian matrix of no washout steady-state as in Eq. (3.10) can be used to investigate the stability properties of the fractional-order chemostat model.

$J = [\begin{matrix} - Q + \frac{X (- k γ + S^{2} β) µ}{{(k + S)}^{2} {(γ + S β)}^{2}} & \frac{S µ}{(k + S) (γ + S β)} \\ \frac{k X µ}{{(k + S)}^{2}} & - Q + \frac{S µ}{k + S} \end{matrix}] .$ (3.10)

3.2. Stability of washout and no-washout steady-state solution

The solution of steady-state in Equation (3.8) represents the washout situation, where the cell mass is wholly removed from the reactor and where the substrate concentration is at the same stock as in the beginning. This state must always be unstable in order to ensure that the cell mass is able to grow in the chemostat. This is because the cell mass will be continuously removed from the chemostat if the washout steady-state is stable. The Jacobian matrix for the washout steady-state solution can be written as

$J = [\begin{matrix} - Q & - \frac{S_{0} µ}{(k + S_{0}) (γ + S_{0} β)} \\ 0 & - Q + \frac{S_{0} µ}{k + S_{0}} \end{matrix}] .$ (3.11)

The eigenvalues of this matrix are

$λ_{1} = - Q,$ (3.12)

$λ_{2} = \frac{- k Q - Q S_{0} + S_{0} µ}{k + S_{0}} .$ (3.13)

The eigenvalues in Eq. (3.12) and Eq. (3.13) are real. The washout steady-state solution is stable if Q>0 and $ρ > S_{0}$ where $ρ = \frac{k Q}{µ - Q}$ . The steady-state solution in Eq. (3.9) represents the no-washout situation. No-washout situation is where the cell mass is not removed and stay growth in the chemostat.This state is important. The steady-state solution is substituted into the Jacobian matrix in Eq. (3.10) and can be written as

$J = [\begin{matrix} - Q + \frac{µ (S_{0} - ρ) (β ρ^{2} - k γ)}{{(k + ρ)}^{2} (β ρ - γ)} & - \frac{µ ρ}{(k + ρ) (β ρ + γ)} \\ \frac{k µ (S_{0} - ρ) (β ρ - γ)}{{(k + ρ)}^{2}} & - Q + \frac{µ ρ}{k + ρ} \end{matrix}] .$ (3.14)

The eigenvalues of the Jacobian matrix in terms of the characteristic polynomial are

$P (λ) = λ^{2} + b λ + c,$ (3.15)

where

$b = 2 Q + \frac{µ (S_{0} - 2 ρ)}{(k + ρ)} + \frac{µ ρ (ρ - S_{0})}{{(k + ρ)}^{2}} + \frac{β µ ρ (ρ - S_{0})}{(k + ρ) (γ + β ρ)},$ (3.16)

and

$\begin{array}{l} c = & Q^{2} + \frac{Q µ (S_{0} - 2 ρ)}{(k + ρ)} + \frac{(µ ρ - S_{0} µ) (µ ρ - Q ρ)}{{(k + ρ)}^{2}} + \frac{µ^{2} ρ^{2} (S_{0} - ρ)}{{(k + ρ)}^{3}} \\ - \frac{Q β µ ρ (S_{0} - ρ)}{(k + ρ) (γ + β ρ)} + \frac{(S_{0} µ - µ ρ) (µ ρ γ + 2 µ β ρ^{2})}{{(k + ρ)}^{2} (γ + β ρ)} \\ + \frac{(µ ρ - S_{0} µ) (µ ρ^{2} γ + µ β ρ^{3})}{{(k + ρ)}^{3} (γ + β ρ)} . \end{array}$ (3.17)

The eigenvalues of the no-washout steady-state solution were evaluated with Routh-Hurwitz condition in Proposition 1. Based on the eigenvalues in Eq. (3.15) and by referring to the study by [5], the eigenvalues' condition can be simplified as the following two cases

(i) If b>0 or equivalent to $\frac{γ}{β} > P_{1}$ , the no-washout steady-state solution of the system in Eq. (3.2) is asymptotically stable. P₁ can be written as

$P_{1} = - \frac{µ ρ (ρ - S_{0})}{2 Q (k + ρ)} - \frac{ρ (ρ - S_{0})}{(S_{0} - ρ)} - \frac{(k + ρ)}{µ ρ (ρ - S_{0})} - ρ,$ (3.18)

(ii) If b<0 or equivalent to $\frac{γ}{β} < P_{1}$ and $t a n^{- 1} (\frac{\sqrt{4 c - b^{2}}}{b}) > \frac{α π}{2}$ , the no-washout steady-state solution of the system in Eq. (3.2) is asymptotically stable. The condition of $t a n^{- 1} (\frac{\sqrt{4 c - b^{2}}}{b}) > \frac{α π}{2}$ is also equivalent to $4 c o s^{2} (\frac{α π}{2}) c > b^{2}$ , which can be simplified as $\frac{γ}{β} > P_{2}$ . Then, this case can be concluded and written as $P_{2} < \frac{γ}{β} < P_{1}$ where

$P_{2} = \frac{µ ρ (ρ - S_{0})}{2 c o s (\frac{α π}{2}) \sqrt{c} (k + ρ)} - \frac{µ ρ (ρ - S_{0})}{2 Q (k + ρ)} - \frac{ρ (ρ - S_{0})}{(S_{0} - ρ)} - k - 2 ρ .$ (3.19)

Then, if $P_{2} < \frac{γ}{β} < P_{1}$ , the no-washout steady-state solution of the system in Eq. (3.2) is asymptotically stable.

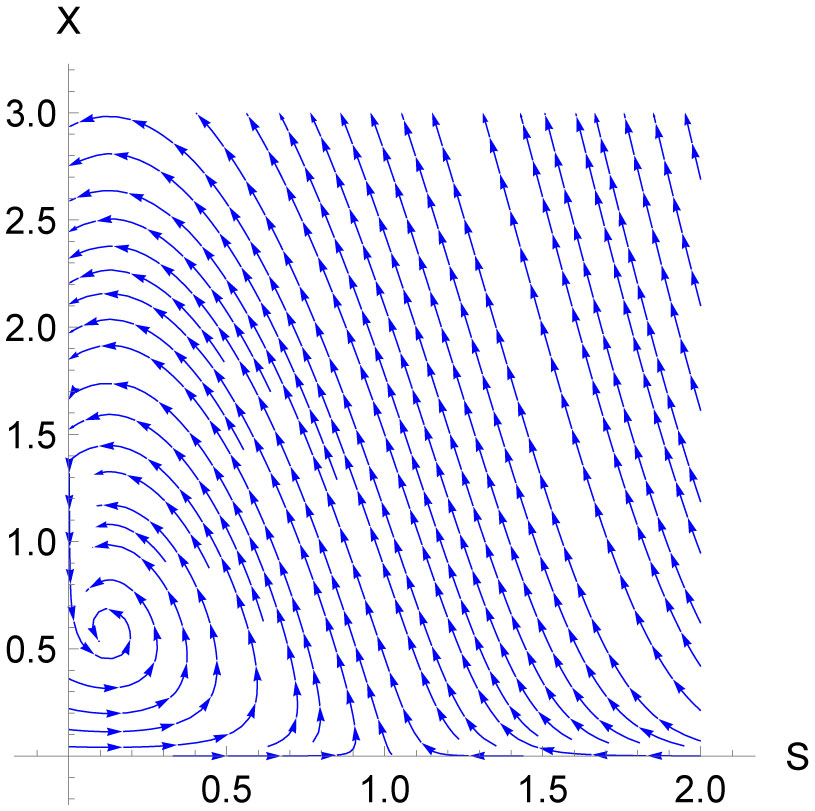
The parameter values of the fractional-order chemostat model are provided in Table 1. The initial substrate concentration, S₀ and ρ were assumed as non-negative values to ensure that the steady-state solutions were physically meaningful. The stability diagram of the steady-state solutions is plotted in Figure 2.

Table 1. Parameter values.

Parameters	Description	Values	Units
k	Saturation constant	1.75	gl⁻¹
Q	Dilution rate	0.02	l²gr⁻¹
µ	Maximum growth rate	0.3	h⁻¹
γ	Constant in yield coefficient	0.01	–
β	Constant in yield coefficient	5.25	lg⁻¹
S₀	Input concentration of substrate	1	gl⁻¹

| Show Table

DownLoad: CSV

Figure 2. Stability diagram of the steady-state solutions when $α = 1$ .

DownLoad: Full-Size Img PowerPoint

The washout steady-state solution is stable if Q > 0 and $ρ > S_{0}$ . From Figure 2, it shows that the unstable solution of washout steady-state, as the eigenvalues did not fulfil the condition of $ρ > S_{0}$ . By choosing the appropriate parameter values, the unstable washout steady-state solution could ensure that the washout condition does not occur in the chemostat. Meanwhile, the solution of no-washout steady-state is stable.

3.3. Hopf bifurcation analysis of the order of fractional-order system

The steady-state solutions of the fractional-order chemostat model for the parameter values given in Table 1 are

(i) Washout:

$(S_{0}^{*}, X_{0}^{*}) = (1,0),$ (3.20)

(ii) No Washout:

$(S_{1}^{*}, X_{1}^{*}) = (\frac{1}{8}, \frac{3731}{6400}) .$ (3.21)

The eigenvalues obtained from the washout steady-state solution are

$λ_{1} = - \frac{1}{50},$ (3.22)

$λ_{2} = - \frac{49}{550},$ (3.23)

and the eigenvalues from the no-washout steady-state solution are

$λ_{1} = \frac{- 2552 + \sqrt{411098126 i}}{399750},$ (3.24)

$λ_{2} = \frac{- 2552 - \sqrt{411098126 i}}{399750},$ (3.25)

Based on Eq. (3.22) to Eq. (3.25), these satisfied the first condition of Hopf bifurcation in Theorem 2. There exists a pair of complex conjugate roots and the other eigenvalues are negative real roots. The transversality condition as the third condition is also satisfied. The eigenvalues of the washout steady-state solution based on the chemostat system is not imaginary, and so there is no existence of Hopf bifurcation in the washout steady-state solution. According to Theorem 2, the critical value of the fractional-order as stated in the second condition can be obtained as

$m (α^{*}) = \frac{α^{*} π}{2} - m i n | a r g (λ) | = 0,$ (3.26)

$α^{*} = \frac{2}{π} m i n | a r g (λ) |,$ (3.27)

where

$a r g (λ) = a r c t a n (\frac{q}{p}),$ (3.28)

$α^{*} = \frac{2}{π} a r c t a n (\frac{q}{p}) = \frac{2}{π} a r c t a n (\frac{\frac{\sqrt{411098126}}{399750}}{\frac{2552}{399750}}) = 0.9202904711 \approx 0.9.$ (3.29)

Value of p and q are obtained from Eq. (3.24) and Eq. (3.25) by assuming parameter value in Table 1. Hence, when $α^{*} = 0.9$ , the chemostat system in Eq. (3.2) shows Hopf bifurcation, at which the system stability would be altered.

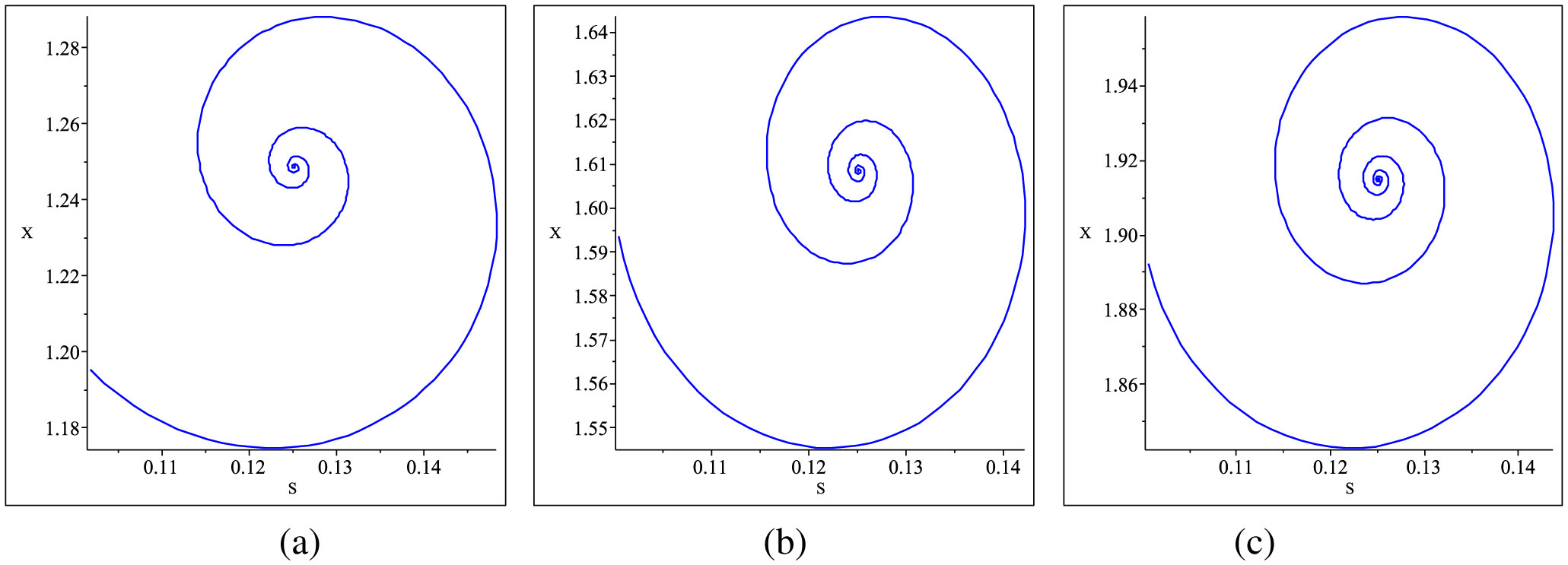
Figure 3 is plotted to determine the dynamic behaviour at the Hopf bifurcation point. The phase portrait diagrams of cell mass concentration against substrate concentration are plotted for values of order of the fractional is $α = 0.9$ .

Figure 3. Phase portrait plot of fractional-order chemostat system with $α = 0.9$ .

DownLoad: Full-Size Img PowerPoint

The running state of the fractional-order chemostat system when fractional order α at the Hopf bifurcation point is shown. The fractional-order chemostat system changed its stability once Hopf bifurcation occurred. Therefore, we conjecture that the system of fractional-order chemostat may be lost or gain its stability when the fractional order α is less than the Hopf bifurcation point, or $α < 0.9$ or otherwise. This shows that increasing or decreasing the value of α may destabilise the stable state of the chemostat system. Therefore, these results show that the running state of the fractional-order chemostat system is affected by the value of α.

3.4. Hopf bifurcation analysis of initial concentration of substrate

The initial concentration of the substrate, S₀, was chosen as the control parameter, while fractional order α was fixed. The solutions of steady-state of the fractional-order chemostat model with S₀ as the control parameter are

(i) Washout:

$(S_{0}^{*}, X_{0}^{*}) = (S_{0},0),$ (3.30)

(ii) No Washout:

$(S_{1}^{*}, X_{1}^{*}) = (\frac{1}{8}, \frac{533 (- 1 + 8 S_{0})}{6400}) .$ (3.31)

The eigenvalues obtained from the washout steady-state solution are

$λ_{1} = - \frac{1}{50},$ (3.32)

$λ_{2} = - \frac{7 (1 - 8 S_{0})}{50 (- 7 - 4 S_{0}},$ (3.33)

and the eigenvalues from the no-washout steady-state solution are

$λ_{1} = - 4204 + 1652 S_{0} + \frac{\sqrt{2} \sqrt{1364552 S_{0}^{2} - 245579768 S_{0} + 38666153}}{399750} i,$ (3.34)

$λ_{2} = - 4204 + 1652 S_{0} - \frac{\sqrt{2} \sqrt{1364552 S_{0}^{2} - 245579768 S_{0} + 38666153}}{399750} i .$ (3.35)

These satisfied the first condition of Hopf bifurcation in Theorem 3. There exist a pair of complex conjugate roots in terms of S₀, and the other eigenvalues were negative real roots in terms of S₀. The transversality condition as the third condition is also satisfied. According to Theorem 3, the critical value of the fractional order as stated in the second condition can be obtained as follows

$m (S_{0}^{*}) = \frac{α^{*} π}{2} - m i n | a r g (λ) | = 0.$ (3.36)

By referring to the study by [18], Eq. (3.37) can also be calculated as

$\frac{q^{'} (S_{0}^{*}) p (S_{0}^{*}) - q (S_{0}^{*}) p^{'} (S_{0}^{*})}{q^{2} (S_{0}^{*}) + p^{2} (S_{0}^{*})} \neq 0.$ (3.37)

From the calculations, the critical value of the initial concentration of the substrate is $S_{0} = 2.54$ . When $S_{0} = 2.54$ , the chemostat system shows Hopf bifurcation, at which the stability of the system would be altered.

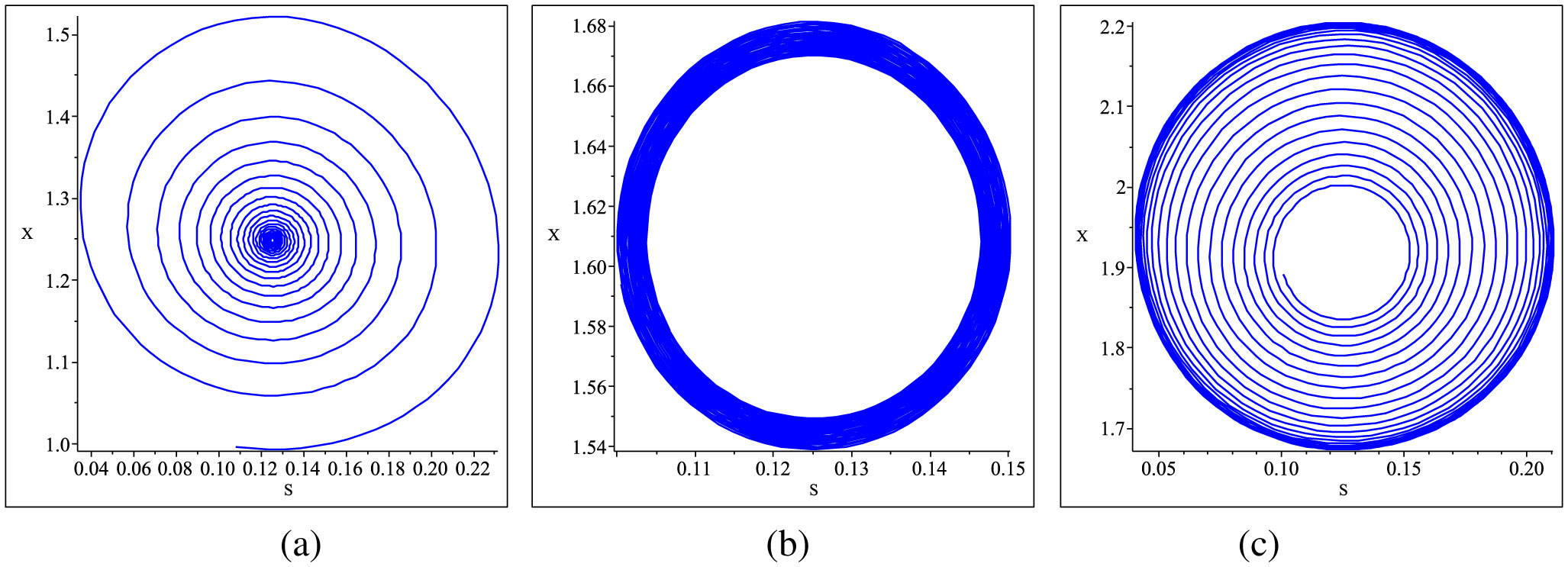
Figure 4 presents the phase portrait diagrams of concentration of cell mass against concentration of substrate when $α = 1$ for different values of the initial concentration of the substrate, which are $S_{0} = 2$ , $S_{0} = 2.54$ and $S_{0} = 3.5$ .

Figure 4. Phase portrait plot of chemostat system with $α = 1$ (a) $S_{0} = 2$ (b) $S_{0} = 2.54$ and (c) $S_{0} = 3.5$ .

DownLoad: Full-Size Img PowerPoint

The change in the running state when the value of the initial substrate concentration passes through the Hopf bifurcation point is shown. The stability of the fractional-order chemostat system changed once Hopf bifurcation occurred. In Figure 3(a), the fractional-order chemostat system is in a stable state when the initial substrate concentration value is less than the Hopf bifurcation point, or $S_{0} < 2.54$ . Meanwhile, when the value of the initial substrate concentration passes through the Hopf bifurcation point, or $S_{0} \geq 2.54$ , the fractional-order chemostat system lost its stability. This shows that increasing the value of the initial substrate concentration may destabilise the stable state of the chemostat system. These results show that the running state of the fractional-order chemostat system is affected by the value of the initial substrate concentration. In real-life application, the value of the initial substrate should remain at $S_{0} \geq 2.54$ to ensure that the chemostat system is at the unstable state. This is because the unstable state is suitable for the production of cell mass [1]. Unstable state means the system always move away after small disturbance, so the system must be at the unstable state because there will be a change in amount of cell mass production.

Figure 5 depicts the phase portrait diagrams of cell mass concentration against substrate concentration when $α = 0.9$ for different values of the initial concentration of the substrate, which are $S_{0} = 2$ , $S_{0} = 2.54$ and $S_{0} = 3.5$ .

Figure 5. Phase portrait plot of chemostat system with $α = 0.9$ (a) $S_{0} = 2$ (b) $S_{0} = 2.54$ and (c) $S_{0} = 3.5$ .

DownLoad: Full-Size Img PowerPoint

The Hopf bifurcation points of system of fractional-order chemostat and system of integer-order chemostat are different. Figure 4 shows the fractional-order chemostat system at a stable state for all values of the initial substrate concentration when $α = 0.9$ . The chemostat system destabilised the stable state when the initial substrate concentration value is $S_{0} \geq 2.54$ , as shown in Figure 3(b) and Figure 3(c). This shows that the dynamic behaviour of the fractional-order chemostat system is different compared with the integer-order chemostat system. In actual application, the value of the initial substrate should remain at $S_{0} \geq 2.54$ to ensure that the chemostat system can be well controlled in order to be suitable for cell mass production.

4. Conclusions

The stability analysis of the fractional-order chemostat model was conducted based on the stability theory of FDEs. The integer-order chemostat model was extended to the FDEs. There are two steady-state solutions obtained, which are washout and no-washout steady-state solutions. The Hopf bifurcation of the order of α occured at the solutions of steady-state when the Hopf bifurcation conditions is fulfilled. The results show that the increasing or decreasing the value of α may stabilise the unstable state of the chemostat system. Therefore, the running state of the fractional-order chemostat system is affected by the value of α. The Hopf bifurcation of the initial concentration of the substrate, S₀, also occurred when the Hopf bifurcation condition is fulfilled. As the evidence from the phase portrait plots, increase the value of the initial substrate concentration may destabilise the stable state of the chemostat system. The value of the initial substrate should remain at $S_{0} \geq 2.54$ to ensure that the chemostat system is at the unstable state since the unstable state is suitable for the production of cell mass. These dynamical analyses are important to provide suitable values of the fractional-order and the parameters in order to ensure the controllability and stability of the chemostat to suit the actual chemostat environment.

References

[1]	K. Zhou, J. Tang, Harnessing fuzzy neural network for gear fault diagnosis with limited data labels, Int. J. Adv. Manuf. Technol., 115 (2021), 1005–1019. https://doi.org/10.1007/s00170-021-07253-6 doi: 10.1007/s00170-021-07253-6
[2]	R. Li, J. Chen, X. Wu, Fault diagnosis of rotating machinery using knowledge-based fuzzy neural network, Appl. Math. Mech., 27 (2006), 99–108. https://doi.org/10.1007/s10483-006-0113-1 doi: 10.1007/s10483-006-0113-1
[3]	M. Alexandru, Analysis of induction motor fault diagnosis with fuzzy neural network, Appl. Artif. Intell., 17 (2003), 105–133. https://doi.org/10.1080/713827102 doi: 10.1080/713827102
[4]	J. Luo, J. Huang, H. Li, A case study of conditional deep convolutional generative adversarial networks in machine fault diagnosis, J. Intell. Manuf., 32 (2021), 407–425. https://doi.org/10.1007/s10845-020-01579-w doi: 10.1007/s10845-020-01579-w
[5]	K. Zhou, E. Diehl, J. Tang, Deep convolutional generative adversarial network with semi-supervised learning enabled physics elucidation for extended gear fault diagnosis under data limitations, Mech. Syst. Signal Process., 185 (2023), 109772. https://doi.org/10.1016/j.ymssp.2022.109772 doi: 10.1016/j.ymssp.2022.109772
[6]	Y. He, H. Tang, Y. Ren, A. Kumar, A semi-supervised fault diagnosis method for axial piston pump bearings based on DCGAN, Meas. Sci. Technol., 32 (2021), 125104. https://doi.org/10.1088/1361-6501/ac1fbe doi: 10.1088/1361-6501/ac1fbe
[7]	Z. Guo, K. Yu, A. K. Bashir, D. Zhang, Y. D. Al-Otaibi, M. Guizani, Deep information fusion-driven POI scheduling for mobile social networks, IEEE Network, 36 (2022), 210–216. https://doi.org/10.1109/MNET.102.2100394 doi: 10.1109/MNET.102.2100394
[8]	L. Yang, Y. Li, S. X. Yang, Y. Lu, T. Guo, K. Yu, Generative adversarial learning for intelligent trust management in 6G wireless networks, IEEE Network, 36 (2022), 134–140. https://doi.org/10.1109/MNET.003.2100672 doi: 10.1109/MNET.003.2100672
[9]	Z. Guo, K. Yu, N. Kumar, W. Wei, S. Mumtaz, M. Guizani, Deep distributed learning-based POI recommendation under mobile edge networks, IEEE Internet Things J., 10 (2023), 303–317. https://doi.org/10.1109/JIOT.2022.3202628 doi: 10.1109/JIOT.2022.3202628
[10]	Z. Zhou, Y. Su, J. Li, K. Yu, Q. M. J. Wu, Z. Fu, et al., Secret-to-image reversible transformation for generative steganography, IEEE Trans. Dependable Secure Comput., 2022 (2022), 1–17. https://doi.org/10.1109/TDSC.2022.3217661 doi: 10.1109/TDSC.2022.3217661
[11]	L. Zhao, Z. Bi, A. Hawbani, K. Yu, Y. Zhang, M. Guizani, ELITE: An intelligent digital twin-based hierarchical routing scheme for softwarized vehicular networks, IEEE Trans. Mobile Comput., 2022 (2022). https://doi.org/10.1109/TMC.2022.3179254
[12]	A. Rohan, S. H. Kim, RLC fault detection based on image processing and artificial neural network, Int. J. Fuzzy Logic Intell. Syst., 19 (2019), 78–87. https://doi.org/10.5391/IJFIS.2019.19.2.78 doi: 10.5391/IJFIS.2019.19.2.78
[13]	I. Jlassi, A. J. M. Cardoso, A single method for multiple IGBT, current, and speed sensor faults diagnosis in regenerative PMSM drives, IEEE J. Emerging Sel. Top. Power Electron., 8 (2019), 2583–2599. https://doi.org/10.1109/JESTPE.2019.2918062 doi: 10.1109/JESTPE.2019.2918062
[14]	D. T. Hoang, H. J. Kang, A motor current signal-based bearing fault diagnosis using deep learning and information fusion, IEEE Trans. Instrum. Meas., 69 (2019), 3325–3333. https://doi.org/10.1109/TIM.2019.2933119 doi: 10.1109/TIM.2019.2933119
[15]	E. A. Bhuiyan, M. M. A. Akhand, S. K. Das, M. F. Ali, Z. Tasneem, Md. R. Islam, et al., A survey on fault diagnosis and fault tolerant methodologies for permanent magnet synchronous machines, Int. J. Autom. Comput., 17 (2020), 763–787. https://doi.org/10.1007/s11633-020-1250-3 doi: 10.1007/s11633-020-1250-3
[16]	Z. Ullah, S. T. Lee, J. Hur, A torque angle-based fault detection and identification technique for IPMSM, IEEE Trans. Ind. Appl., 56 (2019), 170–182. https://doi.org/10.1109/TIA.2019.2947401 doi: 10.1109/TIA.2019.2947401
[17]	Y. Zou, Y. Zhang, H. Mao, Fault diagnosis on the bearing of traction motor in high-speed trains based on deep learning, Alexandria Eng. J., 60 (2021), 1209–1219. https://doi.org/10.1016/j.aej.2020.10.044 doi: 10.1016/j.aej.2020.10.044
[18]	G. Rigatos, N. Zervos, M. Abbaszadeh, P. Siano, D. Serpanose, V. Siadimas, Neural networks and statistical decision making for fault diagnosis of PM linear synchronous machines, Int. J. Syst. Sci., 51 (2020), 2150–2166. https://doi.org/10.1080/00207721.2020.1792579 doi: 10.1080/00207721.2020.1792579
[19]	S. Zhang, H. Zhao, J. Xu, W. Deng, A novel fault diagnosis method based on improved adaptive variational mode decomposition, energy entropy, and probabilistic neural network, Trans. Can. Soc. Mech. Eng., 44 (2019), 121–132. https://doi.org/10.1139/tcsme-2018-0195 doi: 10.1139/tcsme-2018-0195
[20]	P. Zhang, Z. Cui, Y. Wang, S. Ding, Application of BPNN optimized by chaotic adaptive gravity search and particle swarm optimization algorithms for fault diagnosis of electrical machine drive system, Electr. Eng., 104 (2022), 819–831. https://doi.org/10.1007/s00202-021-01335-0 doi: 10.1007/s00202-021-01335-0
[21]	F. Raj, V. K. Kannan, Particle swarm optimized deep convolutional neural sugeno-takagi fuzzy PID controller in permanent magnet synchronous motor, Int. J. Fuzzy Syst., 24 (2022), 180–201. https://doi.org/10.1007/s40815-021-01126-6 doi: 10.1007/s40815-021-01126-6
[22]	M. A. Saeed, M. El-Saadawi, Practical implementation and testing of RNN based synchronous generator internal-fault protection, Recent Pat. Electr. Electron. Eng., 12 (2019), 181–189. https://doi.org/10.2174/2352096511666180605095153 doi: 10.2174/2352096511666180605095153
[23]	S. Lu, R. Yan, Y. Liu, Q. Wang, Tacholess speed estimation in order tracking: A review with application to rotating machine fault diagnosis, IEEE Trans. Instrum. Meas., 68 (2019), 2315–2332. https://doi.org/10.1109/TIM.2019.2902806 doi: 10.1109/TIM.2019.2902806
[24]	M. Xue, H. Yan, M. Wang, H. Shen, K. Shi, LSTM-based intelligent fault detection for fuzzy Markov jump systems and its application to tunnel diode circuits, IEEE Trans. Circuits Syst. II Express Briefs, 69 (2021), 1099–1103. https://doi.org/10.1109/TCSII.2021.3092627 doi: 10.1109/TCSII.2021.3092627
[25]	F. F. M. El-Sousy, M. M. Amin, O. A. Mohammed, Robust optimal control of high–speed permanent–magnet synchronous motor drives via self-constructing fuzzy wavelet neural network, IEEE Trans. Ind. Appl., 57 (2020), 999–1013. https://doi.org/10.1109/TIA.2020.3035131 doi: 10.1109/TIA.2020.3035131
[26]	S. Lu, G. Qian, Q. He, F. Liu, Y. Liu, Q. Wang, In situ motor fault diagnosis using enhanced convolutional neural network in an embedded system, IEEE Sensors J., 20 (2019), 8287–8296. https://doi.org/10.1109/JSEN.2019.2911299 doi: 10.1109/JSEN.2019.2911299
[27]	A. Abid, M. T. Khan, J. Iqbal, A review on fault detection and diagnosis techniques: basics and beyond, Artif. Intell. Rev., 54 (2021), 3639–3664. https://doi.org/10.1007/s10462-020-09934-2 doi: 10.1007/s10462-020-09934-2
[28]	S. Li, H. Won, X. Fu, M. Fairbank, D. C. Wunsch, E. Alonso, Neural-network vector controller for permanent–magnet synchronous motor drives: Simulated and hardware-validated results, IEEE Trans. Cybern., 50 (2019), 3218–3230. https://doi.org/10.1109/TCYB.2019.2897653 doi: 10.1109/TCYB.2019.2897653
[29]	F. Wan, X. Miao, B. Ravelo, Q. Yuan, J. Cheng, Q. Ji, et al., Design of multi–scale negative group delay circuit for sensors signal time–delay cancellation, IEEE Sensors J., 19 (2019), 8951–8962. https://doi.org/10.1109/JSEN.2019.2921834 doi: 10.1109/JSEN.2019.2921834
[30]	X. Shen, G. Shi, H. Ren, W. Zhang, Biomimetic vision for zoom object detection based on improved vertical grid number YOLO algorithm, Front. Bioeng. Biotechnol., 10 (2022), 905583. https://doi.org/10.3389/fbioe.2022.905583 doi: 10.3389/fbioe.2022.905583
[31]	L. Chen, W. Li, Y. Yang, W. Miao, Evaluation and optimization of vehicle pedal comfort based on biomechanics, Proc. Inst. Mech. Eng. Part D, 234 (2020), 1402–1412. https://doi.org/10.1177/0954407019878355 doi: 10.1177/0954407019878355
[32]	Z. Guo, K. Yu, A. Jolfaei, F. Ding, N. Zhang, Fuz-Spam: Label smoothing-based fuzzy detection of spammers in internet of things, IEEE Trans. Fuzzy Syst., 30 (2022), 4543–4554. https://doi.org/10.1109/TFUZZ.2021.3130311 doi: 10.1109/TFUZZ.2021.3130311
[33]	L. Zhao, Z. Yin, K. Yu, X. Tang, L. Xu, Z. Guo, et al., A fuzzy logic based intelligent multi-attribute routing scheme for two-layered SDVNs, IEEE Trans. Network Serv. Manage., 2022 (2022). https://doi.org/10.1109/TNSM.2022.3202741
[34]	Z. Guo, Y. Shen, S. Wan, W. Shang, K. Yu, Hybrid intelligence-driven medical image recognition for remote patient diagnosis in internet of medical things, IEEE J. Biomed. Health Inf., 26 (2022), 5817–5828. https://doi.org/10.1109/JBHI.2021.3139541 doi: 10.1109/JBHI.2021.3139541
[35]	C. Chen, Z. Liao, Y. Ju, C. He, K. Yu, S. Wan, Hierarchical domain-based multi-controller deployment strategy in SDN-enabled space-air-ground integrated network, IEEE Trans. Aerospace Electron. Syst., 58 (2022), 4864–4879. https://doi.org/10.1109/TAES.2022.3199191 doi: 10.1109/TAES.2022.3199191
[36]	Z. Zhou, Y. Li, J. Li, K. Yu, G. Kou, M. Wang, et al., Gan-siamese network for cross-domain vehicle re-identification in intelligent transport systems, IEEE Trans. Network Sci. Eng., 2022 (2022). https://doi.org/10.1109/TNSE.2022.3199919

This article has been cited by:

Xiaomeng Ma, Zhanbing Bai, Sujing Sun, Stability and bifurcation control for a fractional-order chemostat model with time delays and incommensurate orders, 2022, 20, 1551-0018, 437, 10.3934/mbe.2023020

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)