Bioleaching of critical metals using microalgae

1.   Introduction

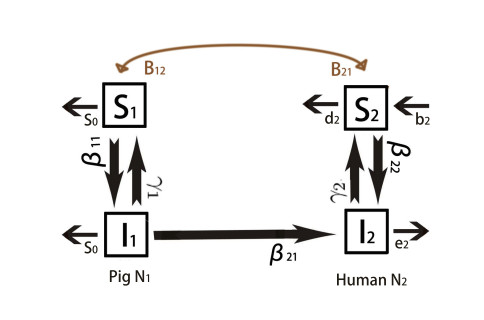
Domestic pigs originated from the Eurasian wild boar (Sus scrofa), which first appeared about 9000 years ago ^[1]. They are essential for the transmission of swine influenza. Human beings raise domestic pigs, and then slaughter them for pork ^[2]. Domestic pigs grow in the food and environment provided by human beings, while human beings get the necessary nutrients by eating them. Consequently, in the breeding process, the swine flu virus is transmitted to human beings through domestic pig-human contact ^[2,3]. According to this process, a new breed-slaughter model with swine influenza transmission can be proposed as a model (1.1).

Domestic pig population $N_1(x, t)$ and human population $N_2(x, t)$ are assumed to be divided into 2 epidemiological compartments: susceptibles ($S_i(x, t)$) and infectives ($I_i(x, t)$) at time $t$ and location $x$, $i = 1, 2$. Susceptibles can become infected by means of intra-species or inter-species transmission and then recover as new susceptibles. The notation $B_{12}$ represents the human breeding parameter for the population growth of domestic pigs, while $B_{21}$ represents the nutrients from eating domestic pigs to increase the birth rate of human beings. The notation $s_0$ represents the slaughter rate of domestic pigs. It's noteworthy that domestic pigs cannot survive independently without human beings, but human beings can still survive well without the supply of pork ^[2]. Restrictions on the development of human population mainly come from intra-species competition.

For humans, the notation $r_2 = b_2-d_2$ is the intrinsic growth rate of humans, where $b_2$ and $d_2$ represents the natural natality rate and mortality rate, respectively. $K_2$ is the environmental carrying capacity of human population without domestic pig supply. $e_2$ is the additional mortality rate of humans caused by swine flu. For domestic pigs, $\omega_0$ represents the intraspecific competition. During the spread of swine flu, the parameters $\beta_{ij}$ represent the per capita incidence rate from species $j$ to species $i$, where $i, j = 1, 2$. $\gamma_i$ denote the recovery rate for domestic animals and humans, $i = 1, 2$. $D_1$ and $D_2$ are the diffusion coefficients for domestic animals and humans. It is noteworthy that all parameters mentioned above is positive.

The main purpose of this paper is to propose a new breed-slaughter model with swine influenza transmission, and study the dynamic behavior of it. And then, we focus on the invasion process of infected domestic animals into the habitat of humans. Under certain conditions as in Theorem 2, we construct a propagating terrace linking human habitat to animal-human coexistent habitat, then to swine flu natural foci, which is divided by spreading speeds. Firstly, we calculate the equilibrium points of the model without spatial heterogeneity as a model (1.2) and analyze the existence of them by the persistence theory. Secondly, we discuss their stability by the basic reproduction number. Thirdly, we use these equilibrium points to construct a propagating terrace linking them by spreading speeds.

In model (1.2), domestic pig population $N_1(t)$ and human population $N_2(t)$ are assumed to be divided into 2 epidemiological compartments: susceptibles ($S_i(t)$) and infectives ($I_i(t)$) at time $t$, $i = 1, 2$. Other parameters are the same with model (1.1).

2.   Breed-slaughter system

At first, we focus on the breed-slaughter system without swine flu transmission and spatial heterogeneity.

If $I_1(0) = I_2(0) = 0$, $N_1(0) > 0$ and $N_2(0) > 0$, model (1.2) turns to a new breed-slaughter system without swine influenza transmission as model (2.1).

Similar to the competition system in ^[4], breed-slaughter system also has abundant dynamic results. For the positive equilibrium point

of model (2.1), we have three cases:

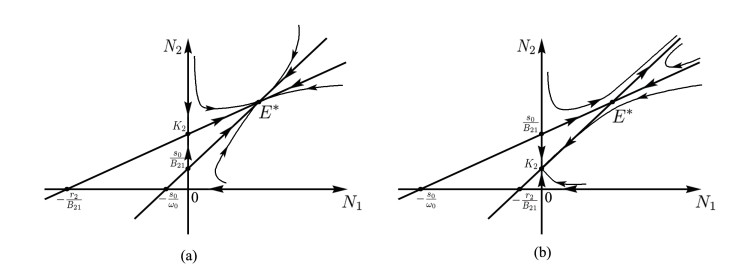
(a). If $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \}$, the positive equilibrium point $E^*$ of model (2.1) is stable (Figure 2(a)).

(b). If $B_{12} B_{21} > \frac{\omega_0 r_2}{K_2}$ and $s_0 > \max \{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \}$, the positive equilibrium point $E^*$ of model (2.1) is unstable (Figure 2(b)).

(c). Other than the condition as (a) or (b), the positive equilibrium point $E^*$ of model (2.1) does not exist.

3.   Breed-slaughter system with swine flu transmission

In order to reflect the effect of interspecific interaction on swine influenza transmission during breeding process as model (1.2), we suppose that $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$ to guarantee the existence and the stability of the boundary equilibrium point

with $I_1(0) = I_2(0) = 0$ in model (1.2).

After calculation, we summarize that there are at most 6 equilibrium points in ${\mathbb{R}}_+^4$ of the system (1.2): $E_0 = (0, 0, 0, 0)$, $E_1 = (0, 0, K_2, 0)$, $E_2 = (0, 0, \overline{S_2}, \overline{I_2})$, $E_3 = (N^*_1, 0, N^*_2, 0)$, $E_4 = (N'_1, 0, S'_2, I'_2)$, $E_5 = (S^*_1, I^*_1, S^*_2, I^*_2)$, where $\overline{S_2} = \frac{e_2+\gamma_2+d_2}{\beta_{22}}$, $\overline{I_2} = \frac{\beta_{22} K_2-(e_2+\gamma_2+d_2)}{\beta_{22}}$, $N^*_1 = N'_1 = \frac{{r_2 }(s_0 - B_{12} K_2)}{B_{12} B_{21} K_2 - \omega_0 r_2}$, $N^*_2 = \frac{K_2 (s_0 B_{21} - \omega_0 r_2)}{B_{12} B_{21} K_2 - \omega_0 r_2}$, $S'_2 = \frac{e_2+\gamma_2+d_2}{\beta_{22}}$, $I'_2 = \frac{\beta_{22} K_2(1+\frac{s_0B_{21}-B_{12}B_{21}K_2}{B_{12}B_{21}K_2-\omega_0r_2})-(e_2+\gamma_2+d_2)}{\beta_{22}}$. The exact expression of $E_5$ is unknown. However, under certain conditions as in Theorem 2, we can obtain its existence by persistence theory ^[5,6,7].

If there is no domestic pigs participation, namely $N_1(0) = S_1(0) = I_1(0) = 0$, The persistence and the stability of boundary equilibrium $E_2 = (0, 0, \overline{S}_2, \overline{I}_2)$ has been proved in ^[8]. Similarly, we define $R_0 = \frac{\beta _{22} K_1}{b_2 + e_2 + \gamma _2 }$. And then, we can get the following lemma.

Lemma 1. If $N_1(0) = S_1(0) = I_1(0) = 0$ and $I_2(0) > 0$, $\{ 0 \} \times \{ 0 \} \times {\mathbb{R}}_+^2$ is a invariant set of system (1.2). The trivial equilibrium point $E_0$ in model (1.2) is unstable, and we have following two cases:

(a) If $R_0 \leq 1$, the disease-free equilibrium point $E_1$ of model (1.2) is stable;

(b) If $R_0 > 1$, model (1.2) has a unique equilibrium point $E_2$ in the interior of $\{ 0 \} \times \{ 0 \} \times {\mathbb{R}}_+^2$, which is stable, and $E_1$ is unstable.

Furthermore, we consider the transmission process of human influenza with domestic pigs participating, but not infected from them. Namely $I_1(0) = 0$, $I_2(0) > 0$ and $N_i(0) > 0$, $i = 1, 2$. The persistence and the stability of boundary equilibrium $E_4 = (N'_1, 0, S'_2, I'_2)$ is similar to Lemma 1. Taking $E_3$ as the original point by coordinate translation, we can get the following lemma by the persistence theory ^[5,9,10], when $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$.

According to the definition of basic reproduction number in a single population as ^[5,11,12], we define $R_1 = \frac{\beta _{1} N^*_1}{s_0 + \gamma _1 }$ as the basic reproduction number of swine flu transmission in demotic pig population and $R_2 = \frac{\beta _{22} N^*_2}{e_2+\gamma_2+d_2}$ as the basic reproduction number of swine flu transmission in human population.

Lemma 2. If $N_1(0) = S_1(0) > 0$, $I_1(0) = 0$ and $I_2(0) > 0$, ${\mathbb{R}}_+ \times \{ 0 \} \times {\mathbb{R}}_+^2$ is a invariant set of system (1.2). The trivial equilibrium point $E_0$ and the boundary equilibrium point $E_1$, $E_2$ in model (1.2) are unstable when $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$, and we have following two cases:

(a) If $R_2 \leq 1$, the disease-free equilibrium point $E_3$ of model (1.2) is stable;

(b) If $R_2 > 1$, model (1.2) has a unique equilibrium point $E_4$ in the interior of ${\mathbb{R}}_+ \times \{ 0 \} \times {\mathbb{R}}_+^2$, which is stable, and $E_3$ is unstable.

Next we focus on the discussion about the existence and the stability of the positive equilibrium point $E_5 = (S^*_1, I^*_1, S^*_2, I^*_2)$. At first, we define $R_s = \max \{R_1, R_2 \}$. Then, we get the theorem as the following.

Theorem 1. If $N_i(0) > 0$ and $I_i(0) > 0$, $i = 1, 2$, ${\mathbb{R}}_+^4$ is a invariant set of system (1.2). The trivial equilibrium point $E_0$ and the boundary equilibrium point $E_1$, $E_2$ in model (1.2) are unstable when $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$, and we have following three cases:

(a) If $R_s \leq 1$, the disease-free equilibrium point $E_3$ of model (1.2) is stable;

(b) If $R_s > 1$, $R_1 < R_2$ and $R_1 \leq 1$, model (1.2) has a unique equilibrium point $E_4$ except for $E_0$, $E_1$, $E_2$ and $E_3$, which is stable, and $E_3$ is unstable;

(c) If $R_s > 1$ and $R_1 \geq R_2$ (or $R_2 > R_1 > 1$) model (1.2) has a unique equilibrium point $E_5$ in the interior of ${\mathbb{R}}_+^4$, which is stable, and $E_3$ and $E_4$ are unstable.

Proof. If $R_s \leq 1$, $E_4$ and $E_5$ do not exist. Similar to the results of Lemma 2 (a), the disease-free equilibrium point $E_3$ of model (1.2) is stable.

Then we consider the results of system (1.2) when $R_s > 1$ and $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$. At first, we define

$D_2$ and ${\widetilde{D}}_2$ are forward invariant.

Let $\Omega^\ast$ consists of equilibria $E_0$, $E_1$, $E_2$, $E_3$ and $E_4$. These equilibria cannot be chained to each other in $D_1$. By analyzing the flow in neighborhood of each equilibrium, it is easy to see that $\Omega^\ast$ is isolated in $D$ and $D_1$ is a uniform strong repeller for ${\widetilde{D}}_2$.

If $x(t) = (S_1(t), I_1(t), S_2(t), I_2(t))$ stays close to $E_2$, we have two cases: if $I_1(0) = I_2(0) = 0$, then $I_1(t) = I_2(t) = 0$; if $I_1(0) > 0$ or $I_2(0) > 0$, then $I_2(t) > 0$. Therefore, $E_2$ is isolated in D. Similarly, we can prove that $E_0$, $E_1$ and $E_3$ are isolated in $D$.

For $E_4$ and $E_5$, we have two cases: (A). $R_1 < R_2$ and $R_1 \leq 1$; (B). $R_1 \geq R_2$ or $R_2 > R_1 > 1$.

(A). $R_1 < R_2$ and $R_1 \leq 1$

If $R_1 < R_2$ and $R_1 \leq 1$, $E_5$ do not exist. Similar to the results of Lemma 2 (b), the boundary equilibrium point $E_4$ of model (1.2) is stable.

(B). $R_1 \geq R_2$ or $R_2 > R_1 > 1$

If $x(t) = (S_1(t), I_1(t), S_2(t), I_2(t))$ stays close to $E_4$, we have two cases: if $I_1(0) = 0$, then $I_1(t) = 0$; if $I_1(0) > 0$, then $I_1(t) > 0$. Since $(S_1(t), I_1(t), S_2(t), I_2(t))$ satisfying system (1.2) has no invariant subset other than $E_4$ in its neighborhood. $E_4$ is isolated in $D$ and a uniform weak repeller for ${\widetilde{D}}_2$. Therefore, we can prove that $E_0$, $E_1$, $E_2$, $E_3$ and $E_4$ are isolated in $D$.

Using Proposition 4.3 in ^[5], we can prove that $D_1$ is a uniform weak repeller for ${\widetilde{D}}_2$; and using Theorem 4.5 in ^[5], we can prove that $D_1$ is a uniform strong repeller for ${\widetilde{D}}_2$.

Then we get that there exists an $\epsilon > 0$ such that

with $N_i(0) > 0$ and $I_i(0) > 0$, $i = 1, 2$.

Therefore, if $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$, $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$ and $R_1 \geq R_2$ ($R_2 > R_1 > 1$), there exists at least one internal equilibrium of system (1.2) ^[9,10,13].

Next, we use Theorem 2 in ^[11] to discuss the basic reproduction number of system (1.2).

The Jacobian matrix of $(I_1, I_2)$ is

Let $J = F-V$, $F$ be the rate of appearance of new infections in compartment $I$, $V$ be the rate of transfer of individuals out of compartment $I$. Then, we get

We call $FV^{-1}$ be the next generation matrix for the model (1.2) and set $R_s = \rho (FV^{-1} \big|_{E_3})$, where $\rho(A$) denotes the spectral radius of a matrix $A$.

Then we get

Finally, using Theorem 2 in ^[11], we can prove Theorem 1.

4.   Propagating terrace of swine flu

The basic reproduction number is an important threshold value in the research of the epidemic mathematical model, which determines the disease to break out or not. However, it is not sufficient to discuss the breed-slaughter model with interspecific interaction. The main purpose of this paper is to investigate invasion process of infected domestic animal into human habitat. And we construct a propagating terrace linking human habitat $E_1$ to animal-human coexistent habitat $E_3$, then to swine flu natural foci $E_4$ (or $E_5$), which is divided by certain spreading speeds. The propagating terrace can describe the spatio-temporal continuous change of the transmission of swine flu.

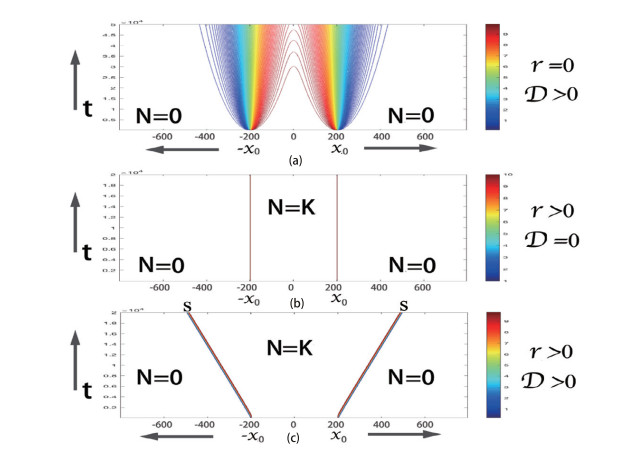
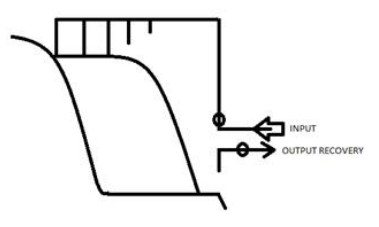
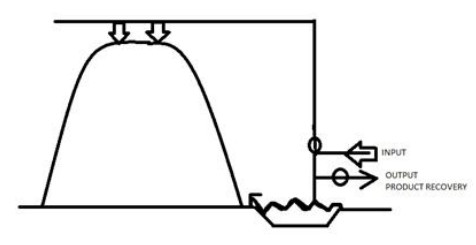
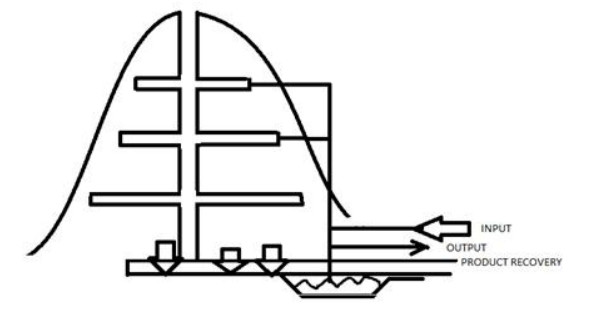
Based on the heterogeneity of the population structure and the temporal and spatial continuity of the mammal movement, the population's spatial factor is considered in the spread of swine flu. If the swine flu host populations are distributed differently in space, the diffusion term may change their local population structure, thus change the swine flu epidemic. In order to describe the population invasion process, we set the initial value is zero in the area $x \in (-\infty, - x_0) \cup (x_0, \infty)$. The area of $(- x_0, x_0)$ is the original habitat of $N$, and $N$ will invade to the area of $x \in (-\infty, - x_0) \cup (x_0, \infty)$ at the spreading speed $s$ ^[14].

The definition of spreading speed of a single population is the positive value $s$ satisfied with the conditions as follows,

and

in the model [4.1]

The biological description of spreading speed $s$ has been shown in the third figure of Figure 3. The value of $s$ approximates the inverse of the slope of the color lines. It is easy to see that the co-effect of diffusion and reproduction leads to the population territory expansion, in which the local diffusion rate $D$ guarantees the population spatial invasion to new areas and the reproduction rate $r$ guarantees its development on occupied areas. The spreading speed of a single population in the model [4.1] is expressed by $s: = 2\sqrt{D r}$ by ^[14]. However, it is not enough to study the swine flu with more than one host species ^{[15,16,17,18,19,20]}. We redefine the spreading speeds at the human-animal interface, as shown below.

Due to the participation of two populations, some notations need to be redefined. The notations $s$ and $x_0$ are replaced by $s_i$, $x_i$, with $i = 1, 2$, corresponding to the two swine flu host populations.

Then we construct a propagating terrace linking human habitat $E_1$ to animal-human coexistent habitat $E_3$, then to swine flu natural foci $E_4$ (or $E_5$), which is divided by certain spreading speeds. The propagating terrace can describe the spatio-temporal continuous change of the transmission of swine flu, which can be show in Theorem 2.

Theorem 2. For system (1.1), if $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$, $B_{21} N^*_1 < r_2$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$, the initial conditions satisfy that $0 < S_1(x, 0) < N^*_1$, $x\in[-x_1, x_1]$; $S_1(x, 0) = 0$, $x\in(-\infty, x_1)\cup(x_1, \infty)$, for some $x_1 > 0$; $0 < I_1(x, 0) < N^*_1$, $x\in[-x_2, x_2]$; $I_1(x, 0) = 0$, $x\in(-\infty, x_2)\cup(x_2, \infty)$, for some $x_2 > 0$; $S_2(x, 0) = K_2$, $I_2(x, 0) = 0$, $x\in {\mathbb{R}}$.

We set

Suppose that $s_1 > s_2$, $x_1 > x_2$, then there are three cases about the invasion process as following:

(a) $R_s \leq 1$,

The system (1.1) forms a propagating terrace, linking $E_1$ to $E_3$.

(b) If $R_s > 1$, $R_1 < R_2$ and $R_1 \leq 1$,

The system (1.1) forms a propagating terrace, linking $E_1$ to $E_3$, then to $E_4$.

(c) If $R_s > 1$ and $R_1 \geq R_2$ (or $R_2 > R_1 > 1$),

The system (1.1) forms a propagating terrace, linking $E_1$ to $E_3$, then to $E_5$.

Proof. The epidemic of swine flu originates in the interaction between humans and domestic animals in the breeding process, so the breaking out of swine flu would lag behind this process. Therefore, we first confirm the propagating terrace linking $E_1$ and $E_3$.

The breed-slaughter system without swine flu transmission can be transferred to model (4.2).

Let $(N_1, N_2)$ be a solution to system (4.2) with the initial condition $0 < N_1(x, 0) < N^*_1$, $x\in[-x_1, x_1]$; $N_1(x, 0) = 0$, $x\in(-\infty, x_1)\cup(x_1, \infty)$, for some $x_1 > 0$; $N_2(x, 0) = K_2$, $x\in {\mathbb{R}}$.

If $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$, we claim that $(N_1(x, t), N_2(x, t)) \in \Sigma$, $\forall x \in {\mathbb{R}}, t \in [0, \infty)$, where

By the strong maximum principle, $N_1\geq0$ for $t > 0$. Then we get

By a comparison, $N_2\geq X$, where $X$ is the solution to

Then we get the result

Set $u: = N_1$ and $v: = N_2-K_2$. Then $\frac{\partial N_2(x, t)}{\partial t}$ can be rewritten as

Due to $u = N_1 \in [0, N^*_1]$ and $v = N_2-K_2 \geq 0$ then

By the strong maximum principle, if follows that $v \leq Y$ in ${\mathbb{R}} \times [0, \infty)$, where $Y$ is the solution to

Then we have

Given $\epsilon > 0$, we choose $\delta > 0$ small enough such that $2 \sqrt{D_1 (B_{12} K_2-s_0+B_{12} \delta)} < s_1 + \epsilon$.

For this $\delta$, we claim that there is $\tau \gg 1$ such that $Y(x, t) < \delta+ M u(x, t)$, $\forall x \in {\mathbb{R}}$, $t\geq \tau$, for some positive constant $M$. Then it follows that $N_1$ satisfies

Therefore, according to the comparison principle and the definition of spreading speed ^{[14,15,16,19,21]}, for any $c \in (2 \sqrt{D_1 (B_{12} K_2-s_0+B_{12} \delta)}, s_1 + \epsilon)$, it follows that ${\lim_{t \to+ \infty } \sup_{\left| x \right| > ct} {N_1 (x, t)}} = 0$, and then ${\lim_{t \to+ \infty } \sup_{\left| x \right| > ct} {N_2 (x, t)}} = K_2$.

Because of the arbitrariness of $\epsilon$, we get

Thus, if the swine flu does not break out, namely $R_s \leq 1$, for system (1.1),

Then we set $U: = N^*_1-N_1$ and $V: = N^*_2-N_2$. Similar to the proof before, we can get

If $R_s \leq 1$, for system (1.1),

Next we consider the propagating terrace linking $E_3$ to ($E_4$ or $E_5$). Let $(S_1, I_1, S_2, I_2)$ be a solution to system (1.1) with the initial condition $S_1(x, 0) = N^*_1$, $S_2(x, 0) = N^*_2$, $I_2(x, 0) = 0$, $x\in {\mathbb{R}}$. $I_1(x, 0) > 0$, $x\in[-x_2, x_2]$; $I_1(x, 0) = 0$, $x\in(-\infty, x_2)\cup(x_2, \infty)$, for some $x_2 > 0$.

If $B_{12} B_{21} < \frac{\omega_0 r_2}{K_2}$ and $s_0 < \min \left\{ \frac{\omega_0 r_2}{B_{21}}, B_{12} K_2 \right\}$, we claim that $(S_1(x, t)+I_1(x, t), S_2(x, t)+I_2(x, t)) \in \Sigma$, $\forall x \in {\mathbb{R}}, t \in [0, \infty)$.

For the spreading speed when $R_s > 1$, comparison principle and strong maximum principle are no longer applicable due to the complexity of system (1.1). However, we can calculate the minimum wave speed from largest eigenvalue of its linearized system at $E_3$ as ^[22] to link $E_3$ and $E_4$ (or $E_5$).

For the following eigenvalue problem

where

J is the jacobian matrix,

For $\lambda \geq 0$, the eigenvalues of the matrix

are $D_1 \lambda^2 + \beta_{11} N^*_1-(s_1+\gamma_1)$, $D_2 \lambda^2 +\beta_{22}N^*_2-(e_2+\gamma_2+d_2)$ and other two impossible results, which cannot define positive wave speed.

Thus, the minimum wave speed can be defined as follows, which can be divided the propagating terrace, linking $E_3$ to $E_4$ (or $E_5$).

If $R_s > 1$, there are two cases: (A). $R_1 < R_2$ and $R_1 \leq 1$; (B). $R_1 \geq R_2$ or $R_2 > R_1 > 1$.

(A). If $R_1 < R_2$ and $R_1 \leq 1$, then $E_5$ does not exist. $s_2 = 2 \sqrt{D_2 (\beta_{22} N^*_2 - e_2-\gamma_2-d_2)}$, then we get

Combining the results before, linking $E_1$ to $E_3$, then

The system (1.1) forms a propagating terrace, linking $E_1$ to $E_3$, then to $E_4$.

(B). If $R_1 \geq R_2$ or $R_2 > R_1 > 1$, set $s_2 = \max \left\{ 2 \sqrt{D_1 (\beta_{11} N^*_1 - s_0-\gamma_1)}, 2 \sqrt{D_2 (\beta_{22} N^*_2 - e_2-\gamma_2-d_2)} \right\}$. then we get

The system (1.1) forms a propagating terrace, linking $E_1$ to $E_3$, then to $E_5$.

5.   Simulations

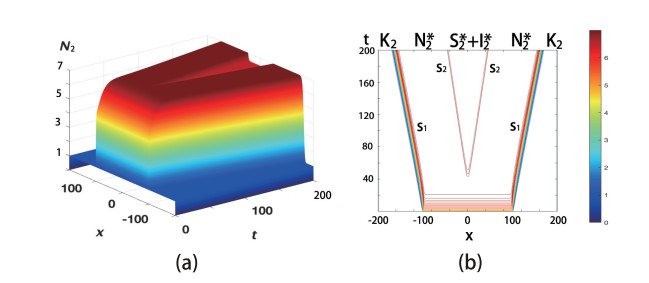
If $s_1 > s_2$, $x_1 > x_2$ and $R_s > 1$, $R_1 > R_2 > 1$, then in Figure 4, the blue area represents the original habitat area of humans at the population size of $E_1$. After domesticating pigs, the red part will be shared with the two species at $E_3$. While after swine flu transmitting between domestic pigs and humans, the internal red part will be shared again with two populations at $E_5$ with swine flu transmission. It is a biological description of propagating terrace of humans with swine flu transmission, which is the local spacial variation of the population.

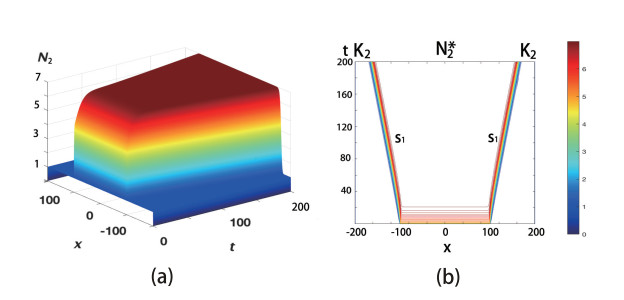
If $s_1 > s_2, x_1 > x_2$ and $R_s \leq 1$, then in Figure 5, the blue area represents the original habitat area of humans at the population size of $E_1$. After domesticating pigs, the red part will be shared with the two species at $E_3$. Because $R_s \leq 1$, there is no swine flu transmission during the breed and slaughter process. Then the propagating terrace links unstable equilibrium $E_1$ and stable equilibrium $E_2$.

6.   Discussions

We establish a new swine flu mathematical model to reflect the dynamic process of swine flu transmission with interspecific action between domestic pigs and humans, in which the roles of different species will no longer be at the same level. Domestic pigs cannot survive independently without human beings, but human beings can still survive well without the supply of pork. By our new swine flu model, we find that the human-animal interface has promoted the cross-species transmission of swine flu and resulted in the prevalence of flu in humans. In addition, the threshold values of population development and disease transmission are also discussed in order to provide a scientific basis for future health decision makers in swine flu prevention and control. We propose the zoonotic basic reproduction number $R_s$, which is more applicable to the study of swine flu transmission. Then, it is analyzed that the spreading speed of different species forming propagating terraces is influenced by the intrinsic growth rate $r$ and diffusion rate $D$.

In this paper, the equilibrium points of the model are calculated and we analyze the existence of the equilibrium points by the persistence theory. Then we discuss their stability by the basic reproduction number. In addition, after redefining the spreading speed, we divide the propagating terrace with two populations, which is an unprecedented task. We concern with the invasion process of infected domestic animals into the habitat of humans. Under certain conditions as in Theorem 2, we construct a propagating terrace linking human habitat to animal-human coexistent habitat, then to swine flu natural foci, which is divided by spreading speeds.

Acknowledgments

This work is supported by the National Natural Science Foundation of China, 11771044.

Conflict of interest

The authors declared that they have no conflicts of interest to this work.