Effective surveillance during smart cities' sustainable development allows their cleanliness to be maintained by reusing waste to produce renewable energy. This study quantifies the biodegradable waste generated in specific regions of several cities and presents ways to convert it into renewable energy. This energy can then be used to partially support regional energy demands. This study explores ways of reducing carbon emissions for biodegradable waste collection processes in regional centers, ultimately sending the biodegradable waste to the energy conversion center. The smart production system allows for the flexible production and autonomation of rates of conversion; green technology depends on each regional center's research management, which is a decision variable for reducing carbon emissions. The major contribution of this study is to consider an energy supply chain management with flexibility of energy conversion under the reduction of carbon emissions, which leads to a sustainable ESCM with the global maximum profit. This study uses mathematical modeling to decrease biodegradable waste with conversion of energy through a classical optimization technique. The solution to this mathematical model yielded significant results, providing insight into waste reduction, reduced carbon emissions and the conversion of biodegradable waste to energy. The model is examined using numerical experiments, and its conclusion supports the model with the fundamental assumptions. Results of sensitivity analysis provide insight into the reduction and re-utilization of wastes, carbon emission reduction, and the benefits of using renewable energy.
Citation: Mitali Sarkar, Yong Won Seo. Biodegradable waste to renewable energy conversion under a sustainable energy supply chain management[J]. Mathematical Biosciences and Engineering, 2023, 20(4): 6993-7019. doi: 10.3934/mbe.2023302
| [1] | Heba S. Mohammed, Zubair Ahmad, Alanazi Talal Abdulrahman, Saima K. Khosa, E. H. Hafez, M. M. Abd El-Raouf, Marwa M. Mohie El-Din . Statistical modelling for Bladder cancer disease using the NLT-W distribution. AIMS Mathematics, 2021, 6(9): 9262-9276. doi: 10.3934/math.2021538 |
| [2] | M. Nagy, H. M. Barakat, M. A. Alawady, I. A. Husseiny, A. F. Alrasheedi, T. S. Taher, A. H. Mansi, M. O. Mohamed . Inference and other aspects for $ q- $Weibull distribution via generalized order statistics with applications to medical datasets. AIMS Mathematics, 2024, 9(4): 8311-8338. doi: 10.3934/math.2024404 |
| [3] | Najwan Alsadat, Mahmoud Abu-Moussa, Ali Sharawy . On the study of the recurrence relations and characterizations based on progressive first-failure censoring. AIMS Mathematics, 2024, 9(1): 481-494. doi: 10.3934/math.2024026 |
| [4] | Ekramy A. Hussein, Hassan M. Aljohani, Ahmed Z. Afify . The extended Weibull–Fréchet distribution: properties, inference, and applications in medicine and engineering. AIMS Mathematics, 2022, 7(1): 225-246. doi: 10.3934/math.2022014 |
| [5] | Nora Nader, Dina A. Ramadan, Hanan Haj Ahmad, M. A. El-Damcese, B. S. El-Desouky . Optimizing analgesic pain relief time analysis through Bayesian and non-Bayesian approaches to new right truncated Fréchet-inverted Weibull distribution. AIMS Mathematics, 2023, 8(12): 31217-31245. doi: 10.3934/math.20231598 |
| [6] | Ayed. R. A. Alanzi, M. Qaisar Rafique, M. H. Tahir, Farrukh Jamal, M. Adnan Hussain, Waqas Sami . A novel Muth generalized family of distributions: Properties and applications to quality control. AIMS Mathematics, 2023, 8(3): 6559-6580. doi: 10.3934/math.2023331 |
| [7] | Aisha Fayomi, Ehab M. Almetwally, Maha E. Qura . A novel bivariate Lomax-G family of distributions: Properties, inference, and applications to environmental, medical, and computer science data. AIMS Mathematics, 2023, 8(8): 17539-17584. doi: 10.3934/math.2023896 |
| [8] | Monthira Duangsaphon, Sukit Sokampang, Kannat Na Bangchang . Bayesian estimation for median discrete Weibull regression model. AIMS Mathematics, 2024, 9(1): 270-288. doi: 10.3934/math.2024016 |
| [9] | Mohammed Albassam, Muhammad Ahsan-ul-Haq, Muhammad Aslam . Weibull distribution under indeterminacy with applications. AIMS Mathematics, 2023, 8(5): 10745-10757. doi: 10.3934/math.2023545 |
| [10] | Refah Alotaibi, Mazen Nassar, Zareen A. Khan, Ahmed Elshahhat . Analysis of Weibull progressively first-failure censored data with beta-binomial removals. AIMS Mathematics, 2024, 9(9): 24109-24142. doi: 10.3934/math.20241172 |
Effective surveillance during smart cities' sustainable development allows their cleanliness to be maintained by reusing waste to produce renewable energy. This study quantifies the biodegradable waste generated in specific regions of several cities and presents ways to convert it into renewable energy. This energy can then be used to partially support regional energy demands. This study explores ways of reducing carbon emissions for biodegradable waste collection processes in regional centers, ultimately sending the biodegradable waste to the energy conversion center. The smart production system allows for the flexible production and autonomation of rates of conversion; green technology depends on each regional center's research management, which is a decision variable for reducing carbon emissions. The major contribution of this study is to consider an energy supply chain management with flexibility of energy conversion under the reduction of carbon emissions, which leads to a sustainable ESCM with the global maximum profit. This study uses mathematical modeling to decrease biodegradable waste with conversion of energy through a classical optimization technique. The solution to this mathematical model yielded significant results, providing insight into waste reduction, reduced carbon emissions and the conversion of biodegradable waste to energy. The model is examined using numerical experiments, and its conclusion supports the model with the fundamental assumptions. Results of sensitivity analysis provide insight into the reduction and re-utilization of wastes, carbon emission reduction, and the benefits of using renewable energy.
The Weibull distribution is one of the most important lifetime model. It has many applications in statistics, bioscience, chemistry, engineering, economics and finance. The Exponential and Rayleigh, among other, distributions are specials. It is suitable for modeling data with hazard functions of different forms. It is proper in the cases where an item consists of multiple components and each component has an identical failure time distribution and the item fails when the weakest part fails [15]. A random variable X is said to have Weibull distribution if its cdf and pdf are respectively defined by
| G(x)=1−exp(−δxφ), | (1.1) |
| g(x)=δφxφ−1exp(−δxφ), | (1.2) |
where δ>0 andφ>0 are respectively the scale and shape parameters for x > 0. Because of the widespread study and applications of the Weibull distribution, there is a need for new generalizations. Several generalizations distributions of Eq (1.1) have been studied in the literature. Kumaraswamy generalized power Weibull distribution has been discussed by Selim and Badar [23]. A new three-parameter lifetime model, the Truncated Weibull Lomax (TWL) distribution has been proposed by Al-marzoki and Al-said [3]. The exponentiated power generalized Weibull distribution has been investigated by Pena-ramirez et al. [17]. A recurrence relations for the single and product moments of order statistics for power generalized Weibull (PGW) distribution have been established by Kumar and Dey [14]. Using these recurrence relations, they obtained the means, variances and covariances of all order statistics for different sample sizes in an efficient manner. Some useful generalizations of the standard Weibull distribution have been introduced by Ramos et al. [18] to describe the lifetime of two important components of sugarcane harvesting machines. The mathematical background of the considered model was discussed and different discrimination procedures were used to obtain the best fit for each component. The inverse Weibull generated (IW-G) family with two extra positive parameters was generated from inverse Weibull random variable [10]. Four special models for the new family, some mathematical properties, the estimation of the model parameters and an applications to real data were offered. A new two-parameter model, the inverse weighted Lindley (IWL) distribution with upside-down bathtub hazard rate was introduced by Ramos et al. [19]. A detailed account of useful mathematical properties of the new distribution, a numerical simulation and an application using a real data set were offered. The alpha power inverse Weibull (APIW) distribution was proposed by Basheer [6]. He explored various useful properties along with the estimation of the APIW parameters and an application of the new model to a real data representing the waiting time before customer service in the bank was provided. Moreover, Ramos et al. [20] introduced an extended Poisson family of life distribution via a new approach to generate flexible parametric families of distributions. They discussed several mathematical properties and inferential procedures of the proposed model. The applicability of considered model to real situation was illustrated by an important data set. Further, the exponentiated power generalized Weibull power series (EPGWPS) family of distributions, has been obtained by compounding the exponentiated power generalized Weibull and power series distributions by Aldahlan et al. [2]. Bayesian inferences for the inverse generalized gamma (IGG) distribution parameters under non-informative priors, namely, the Jeffreys prior and the reference prior was discussed by Ramos et al. [21], and the potentiality of the IGG model was analysed by employing real environmental data. The GIKum and its distribution function [12], is given by
| F(x)=[1−(1+xγ)−α]β, | (1.3) |
where x>0 and α>0,β>0,γ>0 are shape parameters. Let s(t) be the pdf of a random variable T ∈[a,b], where −∞≤a<b<∞ and consider ξ[G(x)] be a function of the cdf of a random variable X, the T−X family of distributions [4], is defined as
| F(x)=∫ξ[G(x)]as(t)dt, | (1.4) |
assuming the following conditions are satisfied.
(1)ξ[G(x)]∈[a,b].
(2)ξ[G(x)] is differentiable and monotonically non decreasing function.
(3)ξ[G(x)]→a, as x→−∞ and ξ[G(x)]→b, as x→∞.
Our motivation here is to introduce a new more flexible model so called the extended generalized inverted Kumaraswamy Weibull (EGIKw-Weibull) distribution. It is rarly to get closed forms of statistical quntities of distributions, here we derive closed formes for most statistical quantities for the new model, including moments, moment generating function, reliability function, Rényi Entropy etc. The new model shows higher flexibility as compared to other commonly used standard distributions. Its hazard function shows different shapes that makes it a preferable choice for modeling the monotonic and non-monotonic hazard behaviors which are more likely to be encountered in practical situations like, human mortality, reliability analysis and biomedical applications. The remaining of this paper is organized as follows: the formation of the EGIKw-Weibull distribution and its reliability measures are provided in section 2; the density and distribution functions of EGIKw-Weibull distribution and some mathematical properties of the proposed model are derived in section 3; parameters are estimated using the maximum likelihood method (MLE) method in section 4; Monte Carlo simulation is employed in section 5, to investigate the model; two real applications are given in section 6 to demonstrate the properties; finally, the concluding remarks are given in section 7.
Using G(x,ϑ) and g(x,ϑ) from Eq (1.1) and Eq (1.2), in Eq (1.4), the cdf of the EGIKw-Weibull distribution is given by
| FEGIKw−W(x)=αβγ∫[1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ0tγ−1(1+tγ)−α−1[1−(1+tγ)−α]β−1dt=[1−{1+([1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ)γ}−α]β, | (2.1) |
where x≥0, α>0, β>0, γ>0 and λ>0 are shape parameters. For φ=1 we obtain the EGIKw-Exponential distribution. The corresponding pdf is given by
| fEGIKw−W(x)=αβγλδφxφ−1exp(−δxφ)[1−exp(−δxφ)]λγ−1×[1−[1−exp(−δxφ)]λ]−γ−1×{1+([1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ)γ}−α−1×[1−{1+([1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ)γ}−α]β−1. | (2.2) |
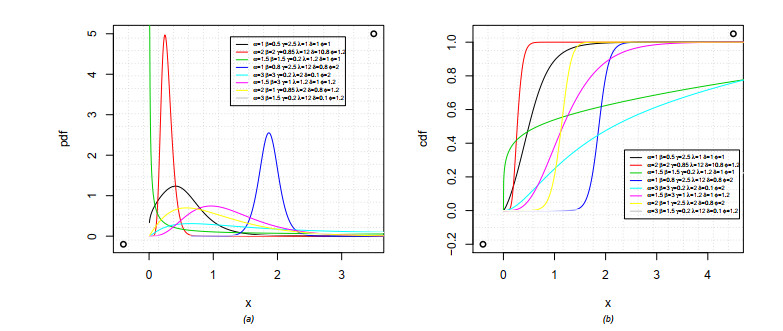
This extension gives a highly flexible life distribution which admits different degrees of kurtosis and asymmetry. Figure 1(a) shows the unimodality and positivity skewed. The graphical representation of the cdf of the EGIKw-Weibull distribution is given in Figure 1(b). The plot at other parametric values produces similar shapes. In insurance problems and biomedical applications, it is often general to use the survival function to depict the distribution of survival time. Let the random variable X denotes the survival time and FX(x) be the cdf or the failure probability by time x, then the survival function is given by
| Sx(x)=P(X>x)=1−Fx(x). |
The survival function is the probability of survival beyond time x. The survival function of X ∼ EGIKw-Weibull is given by
| Sx(x)=1−[1−{1+([1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ)γ}−α]β. | (2.3) |
For brevity purpose, a graphical representation of the survival function of the EGIKw-Weibull distribution at selected parameter values is shown in Figure 2(a). The hazard rate function commonly used in lifetime modeling because it gives the amount of risk to fail. The hazard rate for EGIKw-Weibull is given as
| h(x,ϕ)=αβγλδφxφ−1exp(−δxφ)[1−exp(−δxφ)]λγ−1×[1−[1−exp(−δxφ)]λ]−γ−1×{1+([1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ)γ}−α−1×[1−{1+([1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ)γ}−α]β−1×{1−[1−{1+([1−exp(−δxφ)]λ1−[1−exp(−δxφ)]λ)γ}−α]β}−1, | (2.4) |
where x>0 and ϕ=α,β,γ,λ,δ,φ. The EGIKw-Weibull model shows versatility and high flexibility. Its hazard rate function follows an upside down bathtub shape over time, when α<β<γ<λ and δ>φ. In this situation, hazard rate decreases as proportion parameters increase. The hazard rate offers a J-shaped trend over time, when α>β>γ>λ and δ>φ. In this scenario, the hazard rate increases as proportion parameters increase. Further, the hazard rate exhibits an exponential decreasing trend with increase in time, when α⩾β⩾γ⩾λ and δ≶φ. Similarly, the hazard rate function of the considered model offers various shapes, such as monotonically increasing, bathtub shape, constant and increasing-decreasing almost linearly, monotonically decreasing, constant and exponential increasing, and upside down bathtub shapes, for different parametric values. These attractive features render the EGIKw-Weibull distribution suitable for modeling the monotonic and non-monotonic hazard behaviors which are more likely to be encountered in practical situations like, human mortality, reliability analysis and biomedical applications thus enhancing its adaptability to fit diverse lifetime data, Figure 2(b). The quantile function is given by
| Q(u)=xu=F−1(u)=[−1δlog{1−(1+((1−u1β)−1α−1)−1γ)−1λ}]1φ, | (2.5) |
the random numbers from EGIKw-Weibull distribution can be simulated using the expression Eq (2.5), where U ∼ Uniform (0,1). In particular, the median of the EGIKw-Weibull distribution can be derived by substituting u=0.5 in Eq (2.5), we have
| Median=[−1δlog{1−(1+((1−0.51β)−1α−1)−1γ)−1λ}]1φ. |
Note that the EGIKw-Weibull distribution of models outlined above reduces to GIKw-Weibull distribution for γ=1 and for γ=1,λ=1 we obtain the exponentinated generalized Weibull distribution. Hence the parameter γ of the EGIKw-Weibull distribution offers more flexibility to the extremes for the pdf curves. That's why the new distribution becomes more appropriate for analyzing data sets that exhibit heavy-tail.
Here properties of EGIKw-Weibull distribution are discussed.
By using the binomial expansions in Eq (2.1), we obtain the linear combination for EGIKw-Weibull cdf (for γ>0 integer) as
| F(x)=∞∑i,j,k=0wi,j,k[1−exp(−δxφ)]λ(γj+k), | (3.1) |
where w_{i, j, k} = \left(-1\right) ^{i+j}\binom{\beta }{i}\binom{\alpha i+j-1 }{j}\binom{\gamma j+k-1}{k} . Otherwise, for \gamma > 0 real non-integer, we have
| \begin{equation} F(x) = \sum\limits_{r = 0}^{\infty }z_{r}\left[ 1-\exp (-\delta x^{\varphi })\right] ^{r}, \end{equation} | (3.2) |
where the coefficient z_{r} = \sum_{i, j, k = 0}^{\infty }\sum_{l = r}^{\infty }\left(-1\right) ^{l+r}\left(_{\quad l}^{\lambda \left(\gamma j+k\right) }\right) \left(_{r}^{l}\right) w_{i, j, k} is sum of constants. Moreover the EGIKw-Weibull cdf can be expressed in terms of Weibull Exponential-G cdf, s as
| \begin{equation} F(x) = \sum\limits_{r = 0}^{\infty }z_{r}V_{r}\left( x\right) , \end{equation} | (3.3) |
where V_{r}\left(x\right) = \left[1-\exp (-\delta x^{\varphi })\right] ^{r} is the Weibull Exponential-G cdf with power parameter r. The corresponding expansions for the EGIKw-Weibull density fucntion are respectively obtained by differentiation of Eq (3.1) for \gamma > 0 integer and of Eq (3.2) and Eq (3.3) for \gamma > 0 real non-integer, as
| \begin{eqnarray} f(x) & = &\delta \varphi x^{\varphi -1}\exp (-\delta x^{\varphi })\sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }}{w}_{i, j, k}\left[ 1-\exp (-\delta x^{\varphi }) \right] ^{\lambda \left( \gamma j+k\right) -1}, \end{eqnarray} | (3.4) |
| \begin{eqnarray} f(x) & = &\delta \varphi x^{\varphi -1}\exp (-\delta x^{\varphi })\sum\limits_{r = 0}^{\infty }\breve{z}_{r}\left[ 1-\exp (-\delta x^{\varphi }) \right] ^{r}, \end{eqnarray} | (3.5) |
| \begin{eqnarray} f(x) & = &\sum\limits_{r = 0}^{\infty }\overset{^{\prime \prime }}{z}_{r}v_{r+1}\left( x\right) , \end{eqnarray} | (3.6) |
where \overset{^{\prime \prime }}{w}_{i, j, k} = \lambda \left(\gamma j+k\right) w_{i, j, k}, \; \breve{z} _{r} = (r+1)z_{r+1}, \; \overset{^{\prime \prime }}{z}_{r} = z_{r+1} for \; r = 0, 1, 2, ... , and v_{r+1}\left(x\right) = (r+1)\delta \varphi x^{\varphi -1}\exp (-\delta x^{\varphi })\left[1-\exp (-\delta x^{\varphi })\right] ^{r} is the Weibull Exponential-G density with parameter (r+1) .
For p and q non-negative integers, the ordinary moments are defined by
| \begin{eqnarray} \tau _{p, q} = E[X^{p}G(X)^{q}] & = &\int x^{p}G\left( x\right) ^{q}g\left( x\right) dx \\ & = &\delta \varphi \int_{0}^{\infty }x^{p+\varphi -1}\exp (-\delta x^{\varphi })\left[ 1-\exp (-\delta x^{\varphi })\right] ^{q}dx \\ & = &\frac{1}{\delta ^{\frac{p}{\varphi }}}\sum\limits_{l = 0}^{q}\binom{q}{l}(-)^{l} \frac{\Gamma \left( \frac{p}{\varphi }+1\right) }{(l+1)^{\frac{p}{\varphi } +1}}. \end{eqnarray} | (3.7) |
The p^{th} ordinary moment for an integer for \gamma > 0 can be expressed as
| \begin{equation} \mu _{p}^{^{\prime }} = E(X^{p}) = \sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }}{w}_{i, j, k}\;\tau _{p, \lambda \left( \gamma j+k\right) -1}, \end{equation} | (3.8) |
where \overset{^{\prime \prime }}{w}_{i, j, k} , is defined in Eq (3.4) and \tau _{p, \lambda \left(\gamma j+k\right) -1} , is the (p, \lambda \left(\gamma j+k\right) -1)^{th} PWM of Weibull distribution given in Eq (3.7). For a non-integer \gamma > 0 , we can write
| \begin{equation} \mu _{p}^{^{\prime }} = E(X^{p}) = \sum\limits_{r = 0}^{\infty }\breve{z}_{r}\;\tau _{p, r}, \end{equation} | (3.9) |
where \breve{z}_{r} , is defined in Eq (3.5) and \tau _{p, r} , is the (p, r)^{th} PWM of Weibull distribution. Moreover, we can also provide the moments of the EGIKw-Weibull distribution in terms of Weibull Exponential-G moments. Let X_{r+1} has Weibull Exponential-G distribution with cdf, V_{r+1}(x) = \left[1-\exp (-\delta x^{\varphi }) \right] ^{r} and pdf, v_{r+1}(x) = (r+1)\delta x^{\varphi -1}\exp (-\delta x^{\varphi })\left[1-\exp (-\delta x^{\varphi })\right] ^{r} with power parameter (r+1) , the p^{th} ordinary moment of Weibull Exponential-G distribution (for \gamma > 0 non-integer) is given as
| \begin{equation} E(X_{r+1}^{p}) = \int_{0}^{\infty }x^{p}v_{r+1}(x)dx. \nonumber \end{equation} |
Hence the p^{th} moment of the EGIKw-Weibull distribution can be expressed in terms of infinite weighted sum of Weibull Exponential-G moments as
| \begin{equation} \mu _{p}^{^{\prime }} = \sum\limits_{r = 0}^{\infty }\overset{^{\prime \prime }}{z} _{r}\int_{0}^{\infty }x^{p}v_{r+1}(x)dx, \end{equation} | (3.10) |
where \overset{^{\prime \prime }}{z}_{r} , is defined in Eq (3.6).
The moment generating function (MGF) for an integer \gamma > 0 , can be derived using Eq (3.4) as
| \begin{eqnarray} M(t) & = &\delta \sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }}{w} _{i, j, k}\int_{0}^{\infty }x^{\varphi -1}\exp (tx)\exp (-\delta x^{\varphi }) \left[ 1-\exp (-\delta x^{\varphi }) \right] ^{\lambda \left( \gamma j+k\right) -1}dx, \\ & = &\sum\limits_{i, j, k, l, u = 0}^{\infty }\overset{^{\prime \prime }}{w} _{i, j, k, l, u}\int_{0}^{\infty }x^{\varphi (u+1)-1}\exp (tx)dx, \\ & = &\sum\limits_{i, j, k, l, u = 0}^{\infty }\overset{^{\prime \prime }}{w}_{i, j, k, l, u} \frac{\Gamma \left( \varphi (u+1)\right) }{\left( -t\right) ^{\varphi (u+1)}} , \end{eqnarray} | (3.11) |
where \overset{^{\prime \prime }}{w}_{i, j, k, l, u} = w_{i, j, k}\binom{\lambda \left(\gamma j+k\right) -1}{l} \frac{\delta ^{u+1}(l+1)^{u}}{u!}\left(-1\right) ^{l+u} . For a non-integer \gamma > 0 an alternative representation for M(t) can be derived from Eq (3.5) as
| \begin{eqnarray} M(t) & = &\sum\limits_{r = 0}^{\infty }\breve{z}_{r}\int \exp (tx)g\left( x\right) G\left( x\right) ^{r}dx, \\ & = &\delta \sum\limits_{r = 0}^{\infty }\breve{z}_{r}\int_{0}^{\infty }x^{\varphi -1}\exp (tx)\exp (-\delta x^{\varphi })\left[ 1-\exp (-\delta x^{\varphi }) \right] ^{r}dx, \\ & = &\sum\limits_{r, u = 0}^{\infty }\sum\limits_{l = 0}^{r}\breve{z}_{r}\binom{r}{l}\frac{\delta ^{u+1}(l+1)^{u}}{u!}\left( -1\right) ^{l+u}\frac{\Gamma \left( \varphi (u+1)\right) }{\left( -t\right) ^{\varphi (u+1)}}. \end{eqnarray} | (3.12) |
Another representation for M(t) in terms of Weibull Exponential-G MGF, for a non-integer \gamma > 0 is obtained from Eq (3.6) as
| \begin{eqnarray} M(t) & = &\sum\limits_{r = 0}^{\infty }\overset{^{\prime \prime }}{z} _{r}\int_{0}^{\infty }\exp (tx)\;v_{r+1}\left( t\right) dx, \\ & = &\sum\limits_{r = 0}^{\infty }\overset{^{\prime \prime }}{z}_{r}M_{r+1}\left( t\right) , \end{eqnarray} | (3.13) |
where M_{r+1}\left(t\right) is the mgf of X\sim Weibull Exponential-G random variable with power parameter (r+1) .
Let X be a EGIKw-Weibull random variable with mean \mu = E(X) and median M . The mean deviation about the mean \delta _{\mu }(X) and about the median \delta _{M}(X) are respectively defined by
| \begin{eqnarray} \delta _{\mu }(X) & = &E(|X-\mu _{1}^{^{\prime }}|) = 2\mu _{1}^{^{\prime }}F(\mu _{1}^{^{\prime }})-2T(\mu _{1}^{^{\prime }}), \end{eqnarray} | (3.14) |
| \begin{eqnarray} \delta _{M}(X) & = &E(|X-M|) = \mu _{1}^{^{\prime }}-2T(M), \end{eqnarray} | (3.15) |
where T(z) = \delta \varphi \int_{0}^{z}x^{\varphi }\exp (-\delta x^{\varphi })dx. = \delta ^{-1/\varphi }\curlyvee \left(1/\varphi +1, \delta z^{\varphi }\right) is first GIKw-Weibull incomplete moment with \curlyvee (., .) the incomplete gamma function, \mu _{1}^{\prime } = E(X) is the first ordinary moment, M = Median (X) denotes the median determined from the Eq (2.5) for u = 1/2 , and F(\mu _{1}^{^{\prime }}) comes from Eq (2.1). Using the quantile function, two additional forms for T(x) are obtained. Firstly, when \gamma > 0 an integer,
| T(z) = \sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }}{w}_{i, j, k}\int_{0}^{ \left[ 1-\exp (-\delta z^{\varphi })\right] }u^{\lambda \left( \gamma j+k\right) -1}Q(u)du, |
where Q(u) is the EGIKw-Weibull quantile functin given in Eq (2.5) and the second representation for \gamma > 0 is derived as
| T(z) = \sum\limits_{r = 0}^{\infty }\breve{z}_{r}\int_{0}^{\left[ 1-\exp (-\delta z^{\varphi })\right] }u^{r}Q(u)du. |
Alternatively using EGIKw-Weibull density Eq (3.6), in terms of Exponential-G distribution we obtain,
| T(z) = \sum\limits_{r = 0}^{\infty }\overset{^{\prime \prime }}{z}_{r}\int_{0}^{z}x \;v_{r+1}\left( x\right) dx, |
where \overset{^{\prime \prime }}{w}_{i, j, k}, \breve{z}_{r}, \overset{ ^{\prime \prime }}{z}_{r} are given in Eqs (3.4–3.6).
The Rényi [22], is one of the most popular measures of entropy and for EGIKw-Weibull distribution, it is defined as
| \begin{eqnarray} I_{\zeta }(x) & = &\frac{1}{1-\zeta }\log \bigg(\left( \alpha \beta \gamma \lambda \varphi \delta \right) ^{\zeta } \\ &&\sum\limits_{i, j, k = 0}^{\infty }\tilde{w}_{i, j, k}\int_{0}^{\infty }\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda \left( \gamma j+k\right) +\zeta (\gamma \lambda -1)}x^{\zeta \left( \varphi -1\right) }\exp (-\zeta \delta x^{\varphi })dx\bigg), \\ & = &\frac{1}{1-\zeta }\log \bigg(\left( \alpha \beta \gamma \lambda \varphi \delta \right) ^{\zeta }\sum\limits_{i, j, k = 0}^{\infty }\tilde{w}_{i, j, k, t} \int_{0}^{\infty }x^{\zeta \left( \varphi -1\right) }\exp (-\delta x^{\varphi }\left( \zeta +t\right) )dx\bigg), \\ & = &\frac{1}{1-\zeta }\log \bigg(\left( \alpha \beta \gamma \lambda \varphi \delta \right) ^{\zeta }\sum\limits_{i, j, k = 0}^{\infty }\tilde{w}_{i, j, k, t}\frac{ \Gamma \left( \zeta -\frac{\zeta -1}{\varphi }\right) }{\varphi \left[ \delta \left( \zeta +t\right) \right] ^{\left( \zeta -\frac{\zeta -1}{ \varphi }\right) }}\bigg), \end{eqnarray} | (3.16) |
where \tilde{w}_{i, j, k, t} = (-1)^{i+j+t}\binom{\zeta (\beta -1)}{i}\binom{ \alpha i+\zeta (\alpha +1)+j-1}{j}\binom{\gamma j+\zeta (\gamma +1)+k-1}{k} \binom{\lambda \left(\gamma j+k\right) +\zeta (\gamma \lambda -1)}{t} .
Let X_{1} be a random variable having EGIKw-Weibull distribution with pdf, f_{1}(x) given in Eq (2.2) with parameters \alpha _{1}, \beta _{1}, \gamma _{1}, \lambda _{1}, \delta, \varphi and X_{2} be a random variable having the cdf F_{2}(x) given in Eq (2.1) with parameters \alpha _{2}, \beta _{2}, \gamma _{2}, \lambda _{2}, \delta, \varphi . Assuming X_{1} and X_{2} to be independent, the reliability function {R} is defined by
| \begin{eqnarray} R & = &P(Y < X) = \int f_{1}(x)F_{2}(x)dx \\ & = &\alpha _{1}\beta _{1}\gamma _{1}\lambda _{1}\varphi \delta \int_{0}^{\infty }x^{\varphi -1}\exp (-\delta x^{\varphi })\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\gamma _{1}\lambda _{1}-1} \\ &&\times \left[ 1-\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda _{1}} \right] ^{-\gamma _{1}-1} \\ &&\times \left[ 1+\left( \dfrac{\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda _{1}}}{1-\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda _{1}}}\right) ^{\gamma _{1}}\right] ^{-\alpha _{1}-1} \\ &&\times \left[ 1-\left[ 1+\left( \frac{\left[ 1-\exp (-\delta x^{\varphi }) \right] ^{\lambda _{1}}}{1-\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda _{1}}}\right) ^{\gamma _{1}}\right] ^{-\alpha _{1}}\right] ^{\beta _{1}-1} \\ &&\times \left[ 1-\left[ 1+\left( \frac{\left[ 1-\exp (-\delta x^{\varphi }) \right] ^{\lambda _{2}}}{1-\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda _{2}}}\right) ^{\gamma _{2}}\right] ^{-\alpha _{2}}\right] ^{\beta _{2}}dx. \end{eqnarray} | (3.17) |
Alternatively, with the change of variable x = Q_{1}(u) , where Q_{1} (u) denotes the EGIKw-Weibull quantile function Eq (2.5) corresponding to f_{1}(x) , we have
| \begin{eqnarray} R & = &\int_{0}^{1}F_{2}(Q_{1}(u))du \\ & = &\int_{0}^{1}\left\{ 1-\left[ 1+\left\{ \left[ 1+\left\{ \left( 1-u^{\frac{ 1}{\beta _{1}}}\right) ^{-\frac{1}{\alpha _{1}}}-1\right\} ^{-\frac{1}{ \gamma _{1}}}\right] ^{\frac{\lambda _{2}}{\lambda _{1}}}-1\right\} ^{-\gamma _{2}}\right] ^{-\alpha _{2}}\right\} ^{\beta _{2}}du. \end{eqnarray} | (3.18) |
In particular, from this expression we see that R does not depend on the baseline distribution characterized by the cdf \left[1-\exp (-\delta x^{\varphi })\right] . Various forms of R for \gamma _{1}, \gamma _{2} > 0 integer, by using linear expression can be obtained as
| \begin{eqnarray} f_{1}(x) & = &\varphi \delta x^{\varphi -1}\exp (-\delta x^{\varphi })\sum\limits_{t, u, v = 0}^{\infty }\overset{^{\prime \prime }}{w}_{t, u, v}\left[ 1-\exp (-\delta x^{\varphi }) \right] ^{\lambda _{1}\left( \gamma _{1}u+v\right) -1}, \\ F_{2}(x) & = &\sum\limits_{i, j, k = 0}^{\infty }\bar{w}_{i, j, k}\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda _{2}\left( \gamma _{2}j+k\right) }, \end{eqnarray} |
where \overset{ ^{\prime \prime }}{w}_{t, u, v}=\lambda_{1}\left(\gamma_{1} u+v\right)(-1)^{t+u}\left(\begin{array}{c} \beta_{1} \\ t \end{array}\right)\left(\begin{array}{c} \alpha_{1} t+u-1 \\ u \end{array}\right)\left(\begin{array}{c} \gamma_{1} u+v-1 \\ v \end{array}\right) and \bar{w}_{i, j, k}=(-1)^{i+j} \left(\begin{array}{c}\beta_{2} \\ i\end{array}\right)\left(\begin{array}{c}\alpha_{2} i+j-1 \\ j\end{array}\right)\left(\begin{array}{c}\gamma_{2} j+k-1 \\ k\end{array}\right) . Thus, we have
| \begin{eqnarray} R & = &\varphi \ \delta \sum\limits_{i, j, k, t, u, v = 0}^{\infty }\bar{w}_{i, j, k}\overset{ ^{\prime \prime }}{w}_{t, u, v} \\ &&\int_{0}^{\infty }x^{\varphi -1}\exp (-\delta x^{\varphi })\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda _{1}\left( \gamma _{1}u+v\right) +\lambda _{2}\left( \gamma _{2}j+k\right) -1}dx \\ & = &\sum\limits_{i, j, k, t, u, v = 0}^{\infty }\frac{\bar{w}_{i, j, k}\overset{^{\prime \prime }}{w}_{t, u, v}}{\lambda _{1}\left( \gamma _{1}u+v\right) +\lambda _{2}\left( \gamma _{2}j+k\right) }. \end{eqnarray} | (3.19) |
Similar expressions can be obtained for the case \gamma _{1}, \gamma _{2} > 0 non-integers.
Various expressions for EGIKw-Weibull Lorenz L(p) and Bonferroni B(p) curves for \gamma > 0 integer, are given as
| \begin{eqnarray} L(p) & = &\frac{E_{X\leq x}}{E(X)} = \frac{1}{E(X)}\int_{0}^{x}tf(t)dt \\ & = &\frac{\delta \varphi }{\mu }\sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }}{w}_{i, j, k}\int_{0}^{x}t^{\varphi }\exp (-\delta t^{\varphi })\left[ 1-\exp (-\delta t^{\varphi })\right] ^{\lambda \left( \gamma j+k\right) -1}dt \\ & = &\frac{\delta \varphi }{\mu }\sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }}{w}_{i, j, k}\binom{ \lambda \left( \gamma j+k\right) -1}{l}\left( -1\right) ^{l}\int_{0}^{x}t^{\varphi }\exp (-\delta t^{\varphi }\left( l+1\right) )dt \\ & = &\frac{\delta }{\mu }\sum\limits_{i, j, k, l = 0}^{\infty }\overset{^{\prime \prime }}{ w}_{i, j, k}\binom{\lambda \left( \gamma j+k\right) -1}{l}\left( -1\right) ^{l} \dfrac{\curlyvee \left( 1/\varphi +1, \delta \left( l+1\right) x^{\varphi }\right) }{\left[ \delta \left( l+1\right) \right] ^{1/\varphi +1}}. \end{eqnarray} | (3.20) |
Equivalently based upon EGIKw-Weibull quantile function Eq (2.5) we have
| L(p) = \frac{1}{\mu }\sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }}{w} _{i, j, k}\int_{0}^{\left[ 1-\exp (-\delta t^{\varphi })\right] }u^{\lambda \left( \gamma j+k\right) -1}Q(u)du. |
Alternatively using the expression given in Eq (3.6) in terms of Exponential-G density v_{r}\left(t\right) we have
| L(p) = \frac{1}{\mu }\sum\limits_{i, j, k = 0}^{\infty }\frac{\overset{^{\prime \prime }}{ w}_{i, j, k}}{\lambda \left( \gamma j+k\right) }\int_{0}^{x}tv_{\lambda \left( \gamma j+k\right) }\left( t\right) dt. |
The corresponding expressions for the Bonferroni Curve are given by
| \begin{eqnarray} B(p) & = &\frac{E_{X\leq x}}{F(X)E(X)} = \frac{L(X)}{F(X)} = \frac{1}{F(X)E(X)} \int_{0}^{x}tf(t)dt \end{eqnarray} | (3.21) |
| \begin{eqnarray} & = &\frac{\delta }{\mu F(x)}\sum\limits_{i, j, k, l = 0}^{\infty }\overset{^{\prime \prime }}{w}_{i, j, k}\binom{\lambda \left( \gamma j+k\right) -1}{l}\left( -1\right) ^{l}\frac{\curlyvee \left( 1/\varphi +1, \delta \left( l+1\right) x^{\varphi }\right) }{\left[ \delta \left( l+1\right) \right] ^{1/\varphi +1} }. \\ &&\text{and} \\ B(p) & = &\frac{1}{\mu F(X)}\sum\limits_{i, j, k = 0}^{\infty }\overset{^{\prime \prime }} {w}_{i, j, k}\int_{0}^{G(x)}u^{\lambda \left( \gamma j+k\right) -1}Q(u)du \\ & = &\frac{1}{\mu F(X)}\sum\limits_{i, j, k = 0}^{\infty }\frac{\overset{^{\prime \prime } }{w}_{i, j, k}}{\lambda \left( \gamma j+k\right) }\int_{0}^{x}tv_{\lambda \left( \gamma j+k\right) }\left( t\right) dt, \end{eqnarray} | (3.22) |
where \curlyvee (., .) is the upper incomplete gamma function. Similar expressions can be obtained for the case of \gamma > 0 non-integer using Eq (3.5).
The residual life plays an important role in life testing situations and reliability theory. The n^{th} moment of the residual life is defined as
| \begin{eqnarray} m_{n}(t) & = &E\left[ \left( X-t\right) ^{n}/X > t\right] = \frac{1}{R(t)} \int_{t}^{\infty }\left( x-t\right) ^{n}f\left( x\right) dx \\ & = &\frac{1}{R(t)}\sum\limits_{a = 0}^{n}\left( _{a}^{n}\right) (-t)^{n-a}\int_{t}^{\infty }x^{a}f\left( x\right) dx. \end{eqnarray} | (3.23) |
For \gamma > 0 integer, using pdf Eq (3.4) we have
| \begin{eqnarray} m_{n}(t) & = &\frac{\delta \varphi }{S(t)}\sum\limits_{i, j, k = 0}^{\infty }\sum\limits_{a = 0}^{n}\overset{^{\prime \prime }}{w}_{i, j, k}\left( _{a}^{n}\right) (-t)^{n-a} \\ &&\times \int_{t}^{\infty }x^{a+\varphi -1}\exp (-\delta x^{\varphi })\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda \left( \gamma j+k\right) -1}dx \\ & = &\frac{\delta \varphi }{S(t)}\sum\limits_{i, j, k, l = 0}^{\infty }\sum\limits_{a = 0}^{n} \overset{^{\prime \prime }}{w}_{i, j, k, l}\left( _{a}^{n}\right) (-t)^{n-a}\int_{t}^{\infty }x^{a+\varphi -1}\exp (-\delta x^{\varphi }\left( l+1\right) )dx \\ & = &\frac{\delta }{S(t)}\sum\limits_{i, j, k, l = 0}^{\infty }\sum\limits_{a = 0}^{n}\overset{ ^{\prime \prime }}{w}_{i, j, k, l}\left( _{a}^{n}\right) (-t)^{n-a}\dfrac{ \Gamma \left( a/\varphi +1, \delta \left( l+1\right) t^{\varphi }\right) }{ \left[ \delta \left( l+1\right) \right] ^{a/\varphi +1}}, \end{eqnarray} | (3.24) |
where \overset{^{\prime \prime }}{w}_{i, j, k, l} = \overset{^{\prime \prime }}{w }_{i, j, k}\binom{\lambda \left(\gamma j+k\right) -1}{l} (-1)^{l} and \Gamma (., .) is lower incomplete gamma function, similarly using the EGIKw-Weibull quantile function for \gamma > 0 non-integer, we have
| \begin{equation} m_{n}(t) = \dfrac{1}{S(t)}\sum\limits_{r = 0}^{\infty }\sum\limits_{a = 0}^{n}\breve{z} _{r}\left( _{a}^{n}\right) (-t)^{n-a}\int_{\left[ 1-\exp (-\delta t^{\varphi })\right] }^{1}u^{r}Q(u)^{a}du. \end{equation} | (3.25) |
An alternative representation can be derived from Weibull Exponential-G distribution, as
| \begin{equation} m_{n}(t) = \dfrac{1}{S(t)}\sum\limits_{r = 0}^{\infty }\sum\limits_{a = 0}^{n}\overset{^{\prime \prime }}{z}_{r}\left( _{a}^{n}\right) (-t)^{n-a}\int_{t}^{\infty }x^{a}v_{r+1}\left( x\right) dx, \end{equation} | (3.26) |
where S(x) = 1-F(x) is the EGIKw-Weibull survival function and v_{r+1} is the Weibull Exponential-G density function as given in Eq (3.6).
Let X_{1}, X_{2}, ..., X_{n} be a random sample of size n from the EGIKw-Weibull distribution and X_{(1)}, X_{(2)}, ..., X_{(n)} are the corresponding order statistics, then the pdf of i^{th} order statistic can be obtained as
| \begin{eqnarray} f_{i:n}(x) & = &\frac{f(x)}{B(i, n-i+1)}F(x)^{i-1}\left[ 1-F(x)\right] ^{n-i} \\ & = &\frac{f(x)}{B(i, n-i+1)}\sum\limits_{h = 0}^{n-i}(-1)^{h}\left( _{\ h}^{n-i}\right) F(x)^{h+i-1}, \end{eqnarray} | (3.27) |
where B(., .) is the beta function and F(x) is the EGIKw-Weibull cdf. Replacing Eq (3.2) in above expression, we have
| \begin{eqnarray} F(x)^{h+i-1} & = &\left[ \sum\limits_{t = 0}^{\infty }z_{t}\left[ 1-\exp (-\delta t^{\varphi })\right] ^{t}\right] ^{h+i-1} \\ & = &\sum\limits_{t = 0}^{\infty }c_{t, h+i-1}\left[ 1-\exp (-\delta t^{\varphi })\right] ^{t}, \end{eqnarray} | (3.28) |
where c_{0, h+i-1} = \left(z_{0}\right) ^{h+i-1}, \ c_{t, h+i-1} = \left(tz_{0}\right) ^{-1}\sum_{m = 1}^{t}\left[m(h+i)-t\right] z_{m}c_{t-m, h+i-1}. Using Eq (3.28) in Eq (3.27), with f(x) given in Eq (3.4) for \gamma > 0 integer, and with f(x) Eq (3.5) for \gamma > 0 non-integer, we respectively obtain
| \begin{eqnarray} f_{i:n}(x) & = &\frac{\delta \varphi t^{\varphi -1}\exp (-\delta t^{\varphi }) }{B(i, n-i+1)}\sum\limits_{l, j, k, t = 0}^{\infty }\sum\limits_{h = 0}^{n-i}\frac{ \overset{ ^{\prime \prime }}{w}_{l, j, k}c_{t, h+i-1}\left( -1\right) ^{h}\left( _{\ h}^{n-i}\right) }{\left[ 1-\exp (-\delta t^{\varphi })\right] ^{-\left( \lambda \left( \gamma j+k\right) +t-1\right) }}, \\ &&\text{and} \\ f_{i:n}(x) & = &\frac{\delta \varphi t^{\varphi -1}\exp (-\delta t^{\varphi }) }{B(i, n-i+1)}\sum\limits_{r, t = 0}^{\infty }\sum\limits_{h = 0}^{n-i}\breve{z} _{r}c_{t, h+i-1}\left( -1\right) ^{h}\left( _{\ h}^{n-i}\right) \left[ 1-\exp (-\delta t^{\varphi })\right] ^{r+t}. \end{eqnarray} | (3.29) |
The corresponding expressions for moments, the mgf and other properties of the EGIKw-Weibull order statistics can be obtained likewise.
In this section, we employ the method of MLE to estimate the unknown parameters of EGIKw-Weibull distribution. We consider independent random variables X_{1}, X_{2}..., X_{n}, from an EGIKw-Weibull distribution with parameter vector \Theta = (\alpha, \beta, \gamma, \lambda, \varphi, \delta)^{\prime }. The log-likelihood l(\Theta) = \log L(\Theta) for the model parameters obtained from Eq (2.2) is
| \begin{eqnarray} l(\Theta ) & = &n\log (\alpha \beta \gamma \lambda \delta \varphi )+\left( \varphi -1\right) \sum\limits_{i = 1}^{n}\log x-\delta \sum\limits_{i = 1}^{n}x^{\varphi }-\left( \lambda +1\right) \\ &&\times \sum\limits_{i = 1}^{n}\log \left[ 1-\exp (-\delta x^{\varphi })\right] -\left( \gamma +1\right) \\ &&\times \sum\limits_{i = 1}^{n}\log \left[ \left[ 1-\exp (-\delta x^{\varphi }) \right] ^{-\lambda }-1\right] -\left( \alpha +1\right) \\ &&\times \sum\limits_{i = 1}^{n}\log \left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }\right] +\left( \beta -1\right) \\ &&\times \sum\limits_{i = 1}^{n}\log \left[ 1-\left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }\right] ^{-\alpha } \right] . \end{eqnarray} | (4.1) |
The components of score vector U = (U_{\alpha }, U_{\beta }, U_{\gamma }, U_{\lambda }, U_{\varphi })^{^{\prime }} are given by
| \begin{eqnarray} U_{\alpha } & = &\frac{n}{\alpha }-\sum\limits_{i = 1}^{n}\log \left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }\right] +\left( \beta -1\right) \\ &&\times \sum\limits_{i = 1}^{n}\frac{\log \left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }\right] }{\left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }\right] ^{\alpha }-1}, \\ U_{\beta } & = &\frac{n}{\beta }+\sum\limits_{i = 1}^{n}\log \left[ 1-\left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma } \right] ^{-\alpha }\right] , \\ U_{\gamma } & = &\frac{n}{\gamma }-\sum\limits_{i = 1}^{n}\log \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) \\ &&+\left( \alpha +1\right) \sum\limits_{i = 1}^{n}\frac{\log \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) }{1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }}-\left( \beta -1\right) \alpha \\ &&\times \sum\limits_{i = 1}^{n}\frac{\log \left( \left[ 1-\exp (-\delta x^{\varphi }) \right] ^{-\lambda }-1\right) \left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }\right] ^{-1}}{\left[ \left( 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }\right) ^{\alpha }-1\right] }, \end{eqnarray} |
| \begin{eqnarray} U_{\lambda } & = &\frac{n}{\lambda }-\sum\limits_{i = 1}^{n}\log \left[ 1-\exp (-\delta x^{\varphi })\right] -\left( \gamma +1\right) \sum\limits_{i = 1}^{n}\frac{\log \left[ 1-\exp (-\delta x^{\varphi })\right] }{\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }-1\right) } \\ &&-\left( \alpha +1\right) \gamma \sum\limits_{i = 1}^{n}\frac{\log \left[ 1-\exp (-\delta x^{\varphi })\right] }{\left( 1-\left[ 1-\exp (-\delta x^{\varphi }) \right] ^{\lambda }\right) \left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }\right] } \\ &&+\sum\limits_{i = 1}^{n}\frac{\log \left[ 1-\exp (-\delta x^{\varphi })\right] }{ \left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }\right] ^{\alpha }-1} \\ &&\times \frac{\alpha \gamma \left( \beta -1\right) }{\left( 1-\left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }\right) \left[ 1+\left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }\right] }, \\ U_{\delta } & = &\frac{n}{\delta }-\sum\limits_{i = 1}^{n}x^{\varphi }-\left( \lambda +1\right) \sum\limits_{i = 1}^{n}\frac{x^{\varphi }}{\exp (\delta x^{\varphi })-1} -\lambda \left( \gamma +1\right) \\ &&\times \sum\limits_{i = 1}^{n}\frac{x^{\varphi }}{\left[ \left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }-1\right] \left[ \exp (\delta x^{\varphi })-1 \right] }+\gamma \lambda \left( \alpha +1\right) \\ &&\times \sum\limits_{i = 1}^{n}\frac{x^{\varphi }\left[ \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }+1\right] ^{-1} }{\left[ \left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }-1 \right] \left[ \exp (\delta x^{\varphi })-1\right] }-\alpha \gamma \lambda \left( \beta -1\right) \\ &&\times \sum\limits_{i = 1}^{n}\frac{x^{\varphi }\left[ \exp (\delta x^{\varphi })-1 \right] ^{-1}\left[ \left( \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }+1\right) ^{\alpha }-1\right] ^{-1}}{\left[ \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }+1\right] \left[ \left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }-1\right] }, \end{eqnarray} |
| \begin{eqnarray} U_{\varphi } & = &\frac{n}{\varphi }+\sum\limits_{i = 1}^{n}\log x-\delta \sum\limits_{i = 1}^{n}x^{\varphi }\log x-\delta \left( \lambda +1\right) \sum\limits_{i = 1}^{n}\frac{x^{\varphi }\log x}{\exp (\delta x^{\varphi })-1}-\delta \lambda \left( \gamma +1\right) \\ &&\times \sum\limits_{i = 1}^{n}\frac{x^{\varphi }\log x}{\left[ \left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }-1\right] \left[ \exp (\delta x^{\varphi })-1\right] }+\delta \gamma \lambda \left( \alpha +1\right) \\ &&\times \sum\limits_{i = 1}^{n}\frac{x^{\varphi }\log x\left[ \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }+1\right] ^{-1} }{\left[ \left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }-1 \right] \left[ \exp (\delta x^{\varphi })-1\right] }-\alpha \delta \gamma \lambda \left( \beta -1\right) \\ &&\times \sum\limits_{i = 1}^{n}\frac{x^{\varphi }\log x\left[ \left( \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{-\gamma }+1\right) ^{\alpha }-1\right] ^{-1}}{\left[ \left( \left[ 1-\exp (-\delta x^{\varphi })\right] ^{-\lambda }-1\right) ^{\gamma }+1\right] \left[ \left[ 1-\exp (-\delta x^{\varphi })\right] ^{\lambda }-1\right] \left[ \exp (\delta x^{\varphi })-1\right] }. \end{eqnarray} |
Setting these equations to zero and solving them simultaneously yields the MLEs of the GKw-E parameters. Since there are no close form for these MLEs, a numerical solution to these equations can be determined by using a standard statistical software.
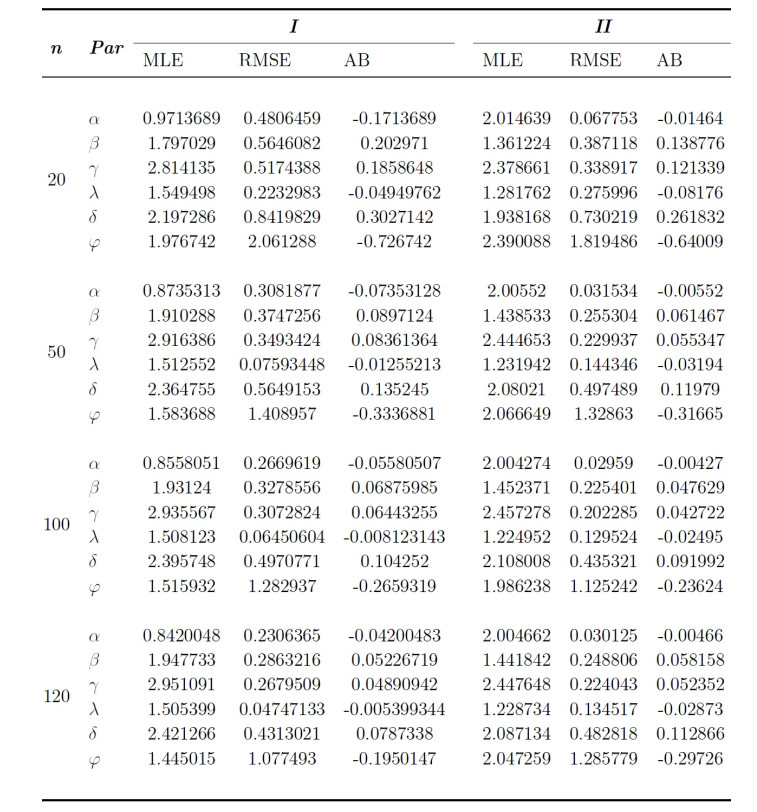
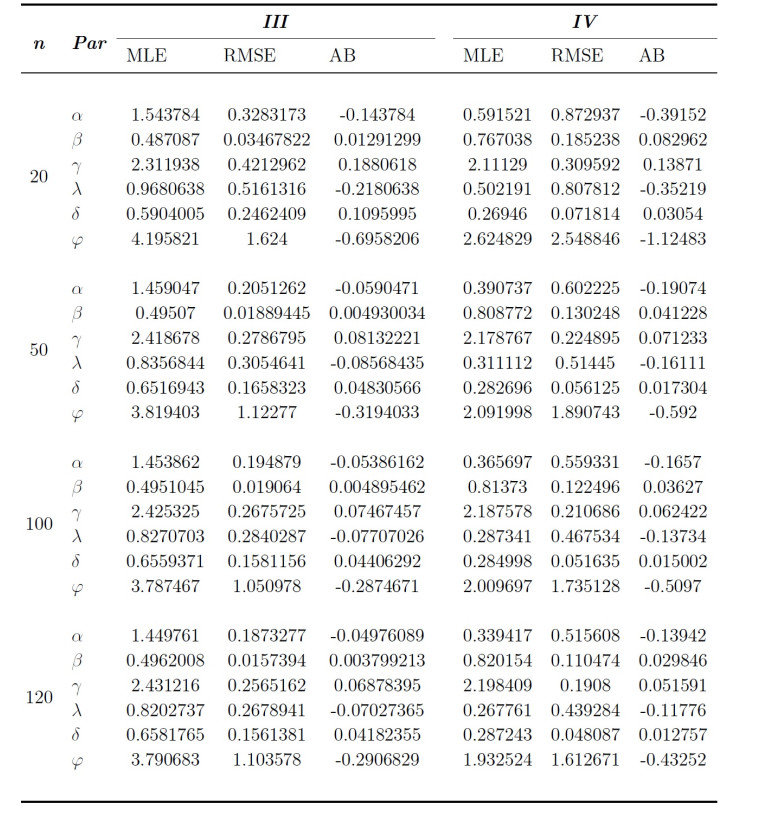
In this section, an extensive numerical investigation is carried out to examine the performance of MLEs for EGIKw-Weibull model. The performance of estimators is evaluated through their average bias (AB) and root mean square errors (RMSE) for different sample sizes. The quantile function is given in Eq (2.5) is used to generate random samples from the EGIKw-Weibull distribution. The simulations experiment is repeated for N = 2, 000 times, for each set of parameters with sample sizes n = 20, 50, 100 and 120 and assumed parametric values I:(\alpha = 0.8, \beta = 2.0, \gamma = 1.5, \lambda = 3.0, \delta = 2.5, \varphi = 1.25), \ II:(\alpha = 2.0, \beta = 1.5, \gamma = 1.2, \lambda = 2.5, \delta = 2.2, \varphi = 1.75), \ III:(\alpha = 1.4, \beta = 0.5, \gamma = 0.75, \lambda = 2.5, \delta = 0.7, \varphi = 3.5)\ \text{and}\ IV:(\alpha = 0.2, \beta = 0.85, \gamma = 0.15, \lambda = 2.25, \delta = 0.3, \varphi = 1.5) . The AB and RMSE values of the parameters \alpha, \beta, \gamma, \lambda, \delta \ \text{and}\ \varphi for different sample sizes are presented in Table 1 and Table 2. From the results of these Tables, it is clear that the AB and RMSE for the estimators of the parameters are showing decreasing pattern as the sample size increases. The results indicate that the method of MLE performs quite well in estimating the model parameters of the proposed distribution.
|
|
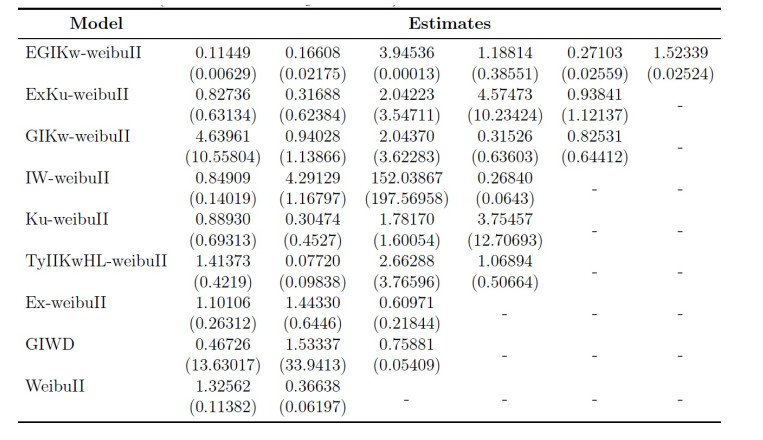
This section provides two real applications to show how the proposed distribution can be applied in practice. The importance and potentiality of the EGIKw-Weibull distribution are examined and compared with the other fitted models namely the exponentiated Kumaraswamy-Weibull (ExKu-weibuII) distribution [9], generalized Inverted Kumaraswamy Weibull (GIKw-Weibull) distribution [11], the inverse Weibull Weibull (IW-weibuII) distribution [10], the Kumaraswamy-Weibull (Ku-weibuII) distribution [7], Type II Half Logistic Weibull (TyIIKwHL-weibuII) distribution [11], exponentiated Weibull (Ex-weibuII) distribution [16], generalized inverse Weibull distribution[8] (GIWD) and the well known Weibull distribution. To do so, we consider two real applications: first, the life of fatigue fracture of Kevlar data [1], and secondly, the gauge lengths data [13].
The first data set has 76 observations and represents the life of fatigue fracture of Kevlar 373/epoxy subjected to constant pressure at 90 percent stress level until all had failed. Among other applications, the data set has been used to assess the superiority of the Transmuted Gompertz distribution over the Gompertz distribution [1].
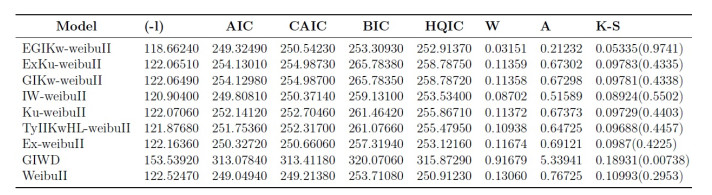
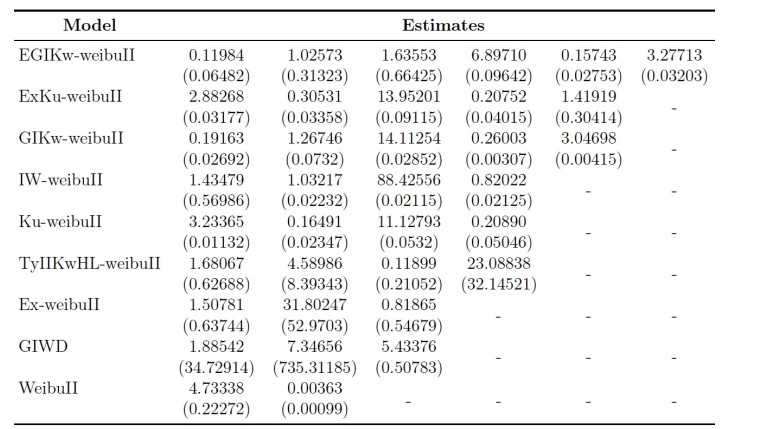
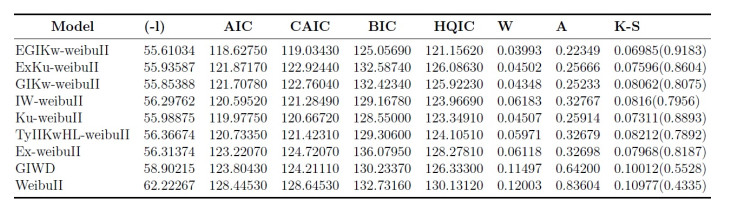
The second data set consists of 63 observations and represents the gauge lengths of 10 mm as reported in [13]. For each model, we estimate the parameters by using the method of MLE and adopt the maximum value of log(likelihood) evaluated at MLEs (-l) , minimum value of the Cram'er-vonMises ( W^{*} ) statistics, Anderson-Darling ( A^{*} ) and Kolmogorov-Smirnov (K-S) test statistics for model comparison purposes. In general, the smaller the values of these statistics, the better the fit to the data. The TTT transformation curves of these data sets are depicted in Figure 3(a) and Figure 3(b) respectively, which suggest an increasing frf for both data sets and therefore, indicate that the proposed model is suitable for fitting these data [5]. Furthermore, the key descriptive statistics of the data set 1 are listed in Table 3. Table 4 gives the MLEs of parameters with there corresponding standard errors in parenthesis. To compare goodness-of-fit of considered models, the computed goodness-of-fit measures are provided in Table 5. The estimated pdf , cdf , PP -plots and QQ -plots of the various models are respectively plotted in Figures 4–7, for the first data set. The key descriptive statistics, estimates of the parameters as well as the values of the goodness of fit statistics for data set 2 are listed in Tables 6–8. The estimated pdf , cdf , PP -plots and QQ -plots of the different models are plotted in Figures 8–11 for the second data set. We note that the EGIKw-Weibull distribution provides the best fit for both data sets. Hence, the proposed six parameter Weibull distribution is superior to other well known models in term of empirical model fitting to real data.

|
|
|

|
|
|
There has been a growing interest among statisticians and applied researchers in constructing flexible lifetime models to improve the modeling of survival data. As a result, significant progress has been made towards the generalization of the traditional Weibull model. In this article, a new six parameter Weibull extension named the EGIKw-Weibull distribution is proposed. The EGIKw-Weibull model is motivated by the fact that the generalization provides more flexibility to analyze positive real-life data. Graphs of the pdf, cdf, hrf and cumulative hrf of the distribution are presented. From Figure 1(a), it can be seen that the shape of the distribution is extremely left skewed, and Figure 2(b) shows that the hazard rate function of the EGIKw-Weibull distribution exhibits various shapes. That support using it in modeling the monotonic and non-monotonic hazard behaviors which are more likely to be encountered in practical situations like, human mortality, reliability analysis and biomedical applications. Various properties of the new model have been derived and explicit expressions for order statistics have been provided that makes analysis of data available. Parameter estimation is done by the method of MLE. Finally, a Monte Carlo Simulation study has been provided to assess the performance of the proposed model. The practical importance of the proposed distribution is demonstrated using two real applications, it is found that the EGIKw-Weibull model is well fitted as compared to its competing models, Tables 4, 5, 7 and 8.
The authors would like to thank the editor and the anonymous referees for their suggestions that improve the first edition of the paper.
The authors declare that they have no conflicts of interest.
| [1] |
A. S. Mahapatra, A. Dasgupta, A. K. Shaw, B. Sarkar, An inventory model with uncertain demand under preservation strategy for deteriorating items, RAIRO Oper. Res., 56 (2022), 4251–4280. https://doi.org/10.1051/ro/2022145 doi: 10.1051/ro/2022145

|
| [2] |
D. Yadav, R. Singh, A. Kumar, B. Sarkar, Reduction of pollution through sustainable and flexible production by controlling by-products, J. Environ. Inf., 40 (2022), 106–124. https://doi.org/10.3808/jei.202200476 doi: 10.3808/jei.202200476

|
| [3] |
B. Sarkar, J. Joo, Y. Kim, H. Park, M. Sarkar, Controlling defective items in a complex multi-phase manufacturing system, RAIRO Oper. Res., 56 (2022), 871–889. https://doi.org/10.1051/ro/2022019 doi: 10.1051/ro/2022019

|
| [4] |
A. S. Mahapatra, M. S. Mahapatra, B. Sarkar, S. K. Majumder, Benefit of preservation technology with promotion and time-dependent deterioration under fuzzy learning, Expert Syst. Appl., 201 (2022) 117169. https://doi.org/10.1016/j.eswa.2022.117169 doi: 10.1016/j.eswa.2022.117169

|
| [5] |
B. Sarkar, B. Ganguly, S. Pareek, L. E. Cárdenas-Barrón, A three-echelon green supply chain management for biodegradable products with three transportation modes, Comput. Ind. Eng., 174 (2022), 108727. https://doi.org/10.1016/j.cie.2022.108727 doi: 10.1016/j.cie.2022.108727

|
| [6] |
M. Sarkar, Y. W. Seo, Renewable energy supply chain management with flexibility and automation in a production system, J. Cleaner Prod., 324 (2021), 129149. https://doi.org/10.1016/j.jclepro.2021.129149 doi: 10.1016/j.jclepro.2021.129149

|
| [7] |
H. M. Wee, W. H. Yang, C. W. Chou, M. V. Padilan, Renewable energy supply chains, performance, application barriers, and strategies for further development, Renewable Sustainable Energy Rev., 16 (2012), 5451–5465. https://doi.org/10.1016/j.rser.2012.06.006 doi: 10.1016/j.rser.2012.06.006

|
| [8] |
I. D. Wangsa, T. M. Yang, H. M. Wee, The effect of price-dependent demand on the sustainable electrical energy supply chain, Energies, 11 (2018), 1645. https://doi.org/10.3390/en11071645 doi: 10.3390/en11071645

|
| [9] |
Y. Fernando, P. S. Bee, C. J. C. Jabbour, A. M. T. Thomé, Understanding the effects of energy management practices on renewable energy supply chains: Implications for energy policy in emerging economies, Energy Policy, 118 (2018), 418–428. https://doi.org/10.1016/j.enpol.2018.03.043 doi: 10.1016/j.enpol.2018.03.043

|
| [10] |
T. Mukherjee, I. Sangal, B. Sarkar, T. M. Alkadash, Mathematical estimation for maximum flow of goods within a cross-dock to reduce inventory, Math. Biosci. Eng., 19 (2022), 13710–13731. https://doi.org/10.3934/mbe.2022639 doi: 10.3934/mbe.2022639

|
| [11] |
B. Sarkar, D. Takeyeva, R. Guchhait, M. Sarkar, Optimized radio-frequency identification system for different warehouse shapes, Knowl. Based Syst., 258 (2022), 109811. https://doi.org/10.1016/j.knosys.2022.109811 doi: 10.1016/j.knosys.2022.109811

|
| [12] |
A. T. Hoang, P. S. Varbanov, S. Nižetić, R. Sirohi, A. Pandey, R. Luque, et al., Perspective review on Municipal Solid Waste-to-energy route: Characteristics, management strategy, and role in circular economy, J. Cleaner Prod., 359 (2022), 131897. https://doi.org/10.1016/j.jclepro.2022.131897 doi: 10.1016/j.jclepro.2022.131897

|
| [13] |
P. Alam, M. Sharholy, A. H. Khan, K. Ahmad, T. Alomayri, N. Radwan, A. Aziz, Energy generation and revenue potential from municipal solid waste using system dynamic approach, Chemosphere, 299 (2022), 134351. https://doi.org/10.1016/j.chemosphere.2022.134351 doi: 10.1016/j.chemosphere.2022.134351

|
| [14] |
S. Varjani, H. Shahbeig, K. Popat, Z. Patel, S. Vyas, A. V. Shah, D. Barceló, H. H. Ngo, C. Sonne, S. S. Lam, M. Aghbashlo, M. Tabatabaei, Sustainable management of municipal solid waste through waste-to-energy technologies, Bioresour. Technol., 355 (2022), 127247. https://doi.org/10.1016/j.biortech.2022.127247 doi: 10.1016/j.biortech.2022.127247

|
| [15] |
M. S. Habib, M. Omair, M. B. Ramzan, T. N. Chaudhary, M. Farooq, B. Sarkar, A robust possibilistic flexible programming approach toward a resilient and cost-efficient biodiesel supply chain network, J. Cleaner Prod., 366 (2022), 132752. https://doi.org/10.1016/j.jclepro.2022.132752 doi: 10.1016/j.jclepro.2022.132752

|
| [16] |
L. C. Malav, K. K. Yadav, N. Gupta, S. Kumar, G. K. Sharma, S. Krishnan, et al., A review on municipal solid waste as a renewable source for waste-to-energy project in India: Current practices, challenges, and future opportunities, J. Cleaner Prod., 277 (2020), 123227. https://doi.org/10.1016/j.jclepro.2020.123227 doi: 10.1016/j.jclepro.2020.123227

|
| [17] |
M. Mohammadi, I. Harjunkoski, Performance analysis of waste-to-energy technologies for sustainable energy generation in integrated supply chains, Comput. Chem. Eng., 140 (2020), 106905. https://doi.org/10.1016/j.compchemeng.2020.106905 doi: 10.1016/j.compchemeng.2020.106905

|
| [18] |
R. Zhao, L. Sun, X. Zou, M. Fujii, L. Dong, Y. Dou, et al., Towards a Zero Waste city-an analysis from the perspective of energy recovery and landfill reduction in Beijing, Energy, 223 (2021), 120055. https://doi.org/10.1016/j.energy.2021.120055 doi: 10.1016/j.energy.2021.120055

|
| [19] |
M. Sarkar, B. D. Chung, Flexible work-in-process production system in supply chain management under quality improvement, Int. J. Prod. Res., 58 (2020), 3821–3838. https://doi.org/10.1080/00207543.2019.1634851 doi: 10.1080/00207543.2019.1634851

|
| [20] |
A. S. H. Kugele, W. Ahmed, B. Sarkar, Geometric programming solution of second degree difficulty for carbon ejection controlled reliable smart production system, RAIRO Oper. Res., 56 (2022), 1013–1029. https://doi.org/10.1051/ro/2022028 doi: 10.1051/ro/2022028

|
| [21] |
B. Sarkar, B. K. Dey, M. Sarkar, S. J. Kim, A smart production system with an autonomation technology and dual channel retailing, Comput. Ind. Eng., 173 (2022), 108607. https://doi.org/10.1016/j.cie.2022.108607 doi: 10.1016/j.cie.2022.108607

|
| [22] |
A. K. Mondal, S. Pareek, K. Chaudhuri, A. Bera, R. K. Bachar, B. Sarkar, Technology license sharing strategy for remanufacturing industries under a closed-loop supply chain management bonding, RAIRO Oper. Res., 56 (2022), 3017–3045. https://doi.org/10.1051/ro/2022058 doi: 10.1051/ro/2022058

|
| [23] |
S. K. Hota, S. K. Ghosh, B. Sarkar, Involvement of smart technologies in an advanced supply chain management to solve unreliability under distribution robust approach, AIMS Environ. Sci., 9 (2022), 461–492. https://doi:10.3934/environsci.2022028 doi: 10.3934/environsci.2022028

|
| [24] | M. Sarkar, B. Sarkar, A. Dolgui, An automated smart production with system reliability under a leader-follower strategy of supply chain management, in IFIP International Conference on Advances in Production Management Systems, 663 (2022), 459–467. |
| [25] |
L. Čuček, P. S. Varbanov, J. J. Klemeš, Z. Kravanj, Total footprints-based multi-criteria optimisation of regional biomass energy supply chains, Energy, 44 (2012), 135–145. https://doi.org/10.1016/j.energy.2012.01.040 doi: 10.1016/j.energy.2012.01.040

|
| [26] |
Q. Bai, Y. Gong, M. Jin, X. Xu, Effects of carbon emission reduction on supply chain coordination with vendor-managed deteriorating product inventory, Int. J. Prod. Econ., 208 (2019), 83–99. https://doi.org/10.1016/j.ijpe.2018.11.008 doi: 10.1016/j.ijpe.2018.11.008

|
| [27] |
J. Yang, Z. Zhang, M. Hong, M. Yang, J. Chen, An oligarchy game model for the mobile waste heat recovery energy supply chain, Energy, 210 (2020), 118548. https://doi.org/10.1016/j.energy.2020.118548 doi: 10.1016/j.energy.2020.118548

|
| [28] |
S. Kumar, K. Sigroha, Meenu, K. Kumar, B. Sarkar, Manufacturing/remanufacturing based supply chain management under advertisements and carbon emissions process, RAIRO Oper. Res., 56 (2022), 831–851. https://doi.org/10.1051/ro/2021189 doi: 10.1051/ro/2021189

|
| [29] |
B. Sarkar, S. Kar, K. Basu, R. Guchhait, A sustainable managerial decision-making problem for a substitutable product in a dual-channel under carbon tax policy, Comput. Ind. Eng., 172 (2022), 108635. https://doi.org/10.1016/j.cie.2022.108635 doi: 10.1016/j.cie.2022.108635

|
| [30] |
B. Oryani, A. Moridian, B. Sarkar, S. Rezania, H. Kamyab, M. K. Khan, Assessing the financial resource curse hypothesis in Iran: The novel dynamic ARDL approach, Resour. Policy, 78 (2022), 102899. https://doi.org/10.1016/j.resourpol.2022.102899 doi: 10.1016/j.resourpol.2022.102899

|
| [31] |
B. Sarkar, B. Ganguly, S. Pareek, L. E. Cárdenas-Barrón, A three-echelon green supply chain management for biodegradable products with three transportation modes, Comput. Ind. Eng., 174 (2022), 108727. https://doi.org/10.1016/j.cie.2022.108727 doi: 10.1016/j.cie.2022.108727

|
| [32] |
R. K. Bachar, S. Bhuniya, S. K. Ghosh, A. AlArjani, E. Attia, M. S. Uddin, et al., Product outsourcing policy for a sustainable flexible manufacturing system with reworking and green investment, Math. Biosci. Eng., 20 (2023), 1376–1401. https://doi.org/10.3934/mbe.2023062 doi: 10.3934/mbe.2023062

|
| [33] |
G. Gallego, I. Moon, The distribution free newsboy problem: Review and extensions, J. Oper. Res. Soc., 44 (1993), 825–834. http://dx.doi.org/10.1057/jors.1993.141 doi: 10.1057/jors.1993.141

|
| 1. | Qasim Ramzan, Muhammad Amin, Muhammad Faisal, Bayesian inference for modified Weibull distribution under simple step‐stress model based on type‐I censoring, 2022, 38, 0748-8017, 757, 10.1002/qre.3011 | |
| 2. | Hong Wang, Badamasi Abba, Jianxin Pan, Classical and Bayesian estimations of improved Weibull–Weibull distribution for complete and censored failure times data, 2022, 38, 1524-1904, 997, 10.1002/asmb.2698 | |
| 3. | Ahmed Elhassanein, A New Type I Half-Logistic Inverse Weibull Distribution with an Application to the Relief Times Data of Patients Receiving an Analgesic, 2022, 12, 2156-7018, 184, 10.1166/jmihi.2022.3937 | |
| 4. | Rashad A. R. Bantan, Shakaiba Shafiq, M. H. Tahir, Ahmed Elhassanein, Farrukh Jamal, Waleed Almutiry, Mohammed Elgarhy, Muhammad Gulzar, Statistical Analysis of COVID-19 Data: Using A New Univariate and Bivariate Statistical Model, 2022, 2022, 2314-8888, 1, 10.1155/2022/2851352 | |
| 5. | Shuanghong Qu, Yushan Guo, Yajing Xu, Hua Li, Zaoli Yang, A General Numerical Algorithm for CDO Pricing Based on Single Factor Copula Framework and Nonhomogeneous Assumptions, 2022, 2022, 1563-5147, 1, 10.1155/2022/3802445 | |
| 6. | Qasim Ramzan, Sadia Qamar, Muhammad Amin, Huda M. Alshanbari, Amna Nazeer, Ahmed Elhassanein, Ahmed Mostafa Khalil, On the Extended Generalized Inverted Kumaraswamy Distribution, 2022, 2022, 1687-5273, 1, 10.1155/2022/1612959 | |
| 7. | Saurabh L. Raikar, Dr. Rajesh S. Prabhu Gaonkar, Jaya algorithm in estimation of P[X > Y] for two parameter Weibull distribution, 2021, 7, 2473-6988, 2820, 10.3934/math.2022156 | |
| 8. | Ahmed Elhassanein, S.S. Askar, On Statistical Properties of a New Bivariate Modified Lindley Distribution with an Application to Financial Data, 2022, 2022, 1099-0526, 1, 10.1155/2022/2328831 | |
| 9. | Mahmoud Ragab, Ahmed Elhassanein, David Carf, A New Bivariate Extended Generalized Inverted Kumaraswamy Weibull Distribution, 2022, 2022, 1687-9139, 1, 10.1155/2022/1243018 | |
| 10. | Showkat Ahmad Lone, Qasim Ramzan, Laila A. AL-Essa, The exponentiated Ailamujia distribution: Properties and application, 2024, 108, 11100168, 1, 10.1016/j.aej.2024.09.036 | |
| 11. | Neeraj Poonia, Deepak Prajapati, Sarita Azad, The bivariate exponentiated additive Weibull distribution and its multivariate extension with applications, 2024, 188, 03608352, 109886, 10.1016/j.cie.2024.109886 |

|

|

|

|

|

|

|

|