1.
Introduction
The linear Diophantine problem of Frobenius is to find the largest integer which is not expressed by a nonnegative linear combination of given positive relatively prime integers a1,a2,…,al. Such a largest integer is called the Frobenius number [3], denoted by g(A)=g(a1,a2,…,al), where A={a1,a2,…,al}. In the literature on the Frobenius problem, the Sylvester number or genus n(A)=n(a1,a2,…,al), which is the total number of integers that cannot be represented as a nonnegative linear combination of a1,a2,…,al [4].
There are many aspects to studying the Frobenius problem. For example, there are algorithmic aspects to find the values or the bounds, complexity of computations, denumerants, numerical semigroup, applications to algebraic geometry and so on (see e.g., [5,6]). Nevertheless, one of the motivations for our p-generalizations originates in the number of representations d(n;a1,a2,…,al) to a1x1+a2x2+⋯+alxl=n for a given positive integer n. This number is equal to the coefficient of xn in 1/(1−xa1)(1−xa2)⋯(1−xal) for positive integers a1,a2,…,al with gcd(a1,a2,…,al)=1 [4]. Sylvester [7] and Cayley [8] showed that d(n;a1,a2,…,al) can be expressed as the sum of a polynomial in n of degree k−1 and a periodic function of period a1a2⋯al. In [9], the explicit formula for the polynomial part is derived by using Bernoulli numbers. For two variables, a formula for d(n;a1,a2) is obtained in [10]. For three variables in the pairwise coprime case d(n;a1,a2,a3). For three variables, in [11], the periodic function part is expressed in terms of trigonometric functions, and its results have been improved in [12] by using floor functions so that three variables case can be easily worked with-in the formula.
In this paper, we are interested in one of the most general and most natural types of Frobenius numbers, which focuses on the number of representations. For a nonnegative integer p, the largest integer such that the number of expressions that can be represented by a1,a2,…,al is at most p is denoted by gp(A)=gp(a1,a2,…,al) and may be called the p-Frobenius number. That is, all integers larger than gp(A) have at least the number of representations of p+1 or more. This generalized Frobenius number gp(A) is called the p-Frobenius number [1,2], which is also called the k-Frobenius number [13] or the s-Frobenius number [14]. When p=0, g(A)=g0(A) is the original Frobenius number. One can consider the largest integer g∗p(a1,a2,…,al) that has exactly p distinct representations (see e.g., [13,14]). However, in this case, the ordering g∗0≤g∗1≤⋯ may not hold. For example, g∗17(2,5,7)=43>g∗18(2,5,7)=42. In addition, for some j, g∗j may not exist. For example, g∗22(2,5,7) does not exist because there is no positive integer whose number of representations is exactly 22. Therefore, in this paper we do not study g∗p(A) but gp(A).
Similarly to the p-Frobenius number, the p-Sylvester number or the p-genus np(A)=np(a1,a2,…,al) is defined by the cardinality of the set of integers which can be represented by a1,a2,…,al at most p ways. When p=0, n(A)=n0(A) is the original Sylvester number.
In this paper, we are interested in one of the most crucial topics, that is, to find explicit formulas of indicators, in particular, of p-Frobenius numbers and p-Sylvester numbers. In the classical case, that is, for p=0, explicit formulas of g(a1,a2) and n(a1,a2) are shown when l=2 [3,4]. However, for l≥3, g(A) cannot be given by any set of closed formulas which can be reduced to a finite set of certain polynomials [15]. For l=3, there are several useful algorithms to obtain the Frobenius number (see e.g., [16,17,18]). For the concretely given three positive integers, if the conditions are met, the Frobenius number can be completely determined by the method of case-dividing by A. Tripathi [19]. Although it is possible to find the Frobenius number by using the results in [19], it is another question whether the Frobenius number can be given by a closed explicit expression for some special triplets, and special considerations are required. Only for some special cases, explicit closed formulas have been found, including arithmetic, geometric, Mersenne, repunits and triangular (see [20,21,22] and references therein).
For p>0, if l=2, explicit formulas of gp(a1,a2) and np(a1,a2) are still given without any difficulty (see e.g., [23]). However, if l≥3, no explicit formula had been given even in a special case. However, quite recently, we have succeeded in giving explicit formulas for the case where the sequence is of triangular numbers [1] or of repunits [2] for the case where l=3.
In this paper, we give an explicit formula for the p-Frobenius number for the Fibonacci number triple (Fi,Fi+2,Fi+k) (i,k≥3). Here, the n-th Fibonacci number Fn is defined by Fn=Fn−1+Fn−2 (n≥2) with F1=1 and F0=0. Our main result (Theorem 6.1 below) is a kind of generalizations of [24,Theorem 1] when p=0. However, when p>0, the exact situation is not completely similar to the case where p=0, and the case by case discussion is necessary. As analogues, we also show explicit formulas of gp(Li,Li+2,Li+k) for Lucas numbers Ln with i,k≥3. Here, Lucas numbers Ln satisfy the recurrence relation Ln=Ln−1+Ln−2 (n≥2) with L0=2 and L1=1. By using our constructed framework, we can also find explicit formulas of the p-Sylvester numbers np(Fi,Fi+2,Fi+k) and np(Li,Li+2,Li+k). Our result (Theorem 13) can extend the result in [24,Corollary 2]. The main idea is to find the explicit structure of the elements of an Apéry set [25]. In addition, we use a complete residue system, studied initially by Selmer [26]. By using Apéry sets, we construct the first least set of the complete residue system, then the second least set of the complete residue system, and the third, and so on. As a basic framework, we use a similar structure in [2]. We can safely say that one of our theorems (Theorem 6.1 below) is a kind of generalization of [24,Theorem 1]. Nevertheless, for each nonnegative integer p, the exact situation is not completely similar, but the case by case discussion is necessary.
2.
Preliminaries
Without loss of generality, we assume that a1=min{a1,a2,…,al}. For each 0≤i≤a1−1, we introduce the positive integer m(p)i congruent to i modulo a1 such that the number of representations of m(p)i is bigger than or equal to p+1, and that of mi−a1 is less than or equal to p. Note that m(0)0 is defined to be 0. The set
is called the p-Apéry set of A={a1,a2,…,al} for a nonnegative integer p, which is congruent to the set
When p=0, the 0-Apéry set is the original Apéry set [25].
It is hard to find any explicit formula of gp(a1,a2,…,al) when l≥3. Nevertheless, the following convenient formulas are known (see [28]). After finding the structure of m(p)j, we can obtain p-Frobenius or p-Sylvester numbers for triple (Fi,Fi+2,Fi+k).
Lemma 1. Let k, p and μ be integers with k≥2, p≥0 and μ≥1. Assume that gcd(a1,a2,…,al)=1. We have
Remark. When p=0, (2.1) is the formula by Brauer and Shockley [27]:
where mj=m(0)j (1≤j≤a1−1) with m0=0. When p=0, (2.2) is the formula by Selmer [26]:
Note that m0=m(0)0=0. A more general form by using Bernoulli numbers is given in [28], as well as the concept of weighted sums [29,30].
It is necessary to find the exact situation of 0-Apéry set Ap(Fi,0), the least complete residue system, which was initially studied in [26]. Concerning Fibonacci numbers, we use the framework in [24].
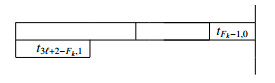
Throughout this paper, for a fixed integer i, we write
for short. Then, we shall construct the set of the least complete residue system Ap(Fi;0). That is, mj≢mh(modFi) (0≤j<h≤Fi−1), and if for a positive integer M, M≡j and M≠mj (0≤j≤Fi−1), then M>mj. Then, for the case p=1 we shall construct the second set of the least complete residue system Ap(Fi;1). That is, m(1)j≢m(1)h(modFi) (0≤j<h≤Fi−1), m(1)j≡mj(modFi) (0≤j≤Fi−1), and there does not exist an integer M such that m(1)j>M>mj and M≡j(modFi). Similarly, for p=2, we shall construct the third set of the least complete residue system Ap(Fi;2). That is, m(2)j≢m(2)h(modFi) (0≤j<h≤Fi−1), m(2)j≡m(1)j(modFi) (0≤j≤Fi−1), and there does not exist an integer M such that m(2)j>M>m(1)j and M≡j(modFi).
By using a similar frame as in [24], we first show an analogous result about Lucas triple (Li,Li+2,Li+k) when p=0. As a preparation we shall show the result when p=0, with a sketch of the proof. The results about Fibonacci numbers can be applied to get those about Lucas numbers. When p=0, by setting integers r and ℓ as Li−1=rFk+ℓ with r≥0 and 0≤ℓ≤Fk−1 and by using the identity Ln=LmFn−m+1+Lm−1Fn−m, we can get an analogous identity of the Fibonacci one in [24,Theorem 1].
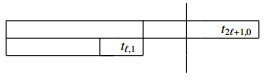
Theorem 1. For integers i,k≥3 and r=⌊(Li−1)/Fk⌋, we have
Proof. Consider the linear representation
Then, by gcd(Li,Li+2)=1, we can prove that the above table represents the least complete residue system {0,1,…,Li−1}(modLi).
That is, we can prove that none of two elements among this set is not congruent modulo Fi, and if there exists an element congruent to any of the elements among this set, then such an element is bigger and not in this set.
When r=0, the largest element among all the tx,y's in this table is tℓ,0. When r≥1, the largest element is either tFk−1,r−1 or tℓ,r. Since tFk−1,r−1<tℓ,r is equivalent to Fk−2Li<(Li−rFk)Li+2, the result is followed by the identity (2.3). The first case is given by tℓ,r−Li, and the second is given by tFk−1,r−1−Li.
3.
Main results when p=1
Now, let us begin to consider the case p≥1. We shall obtain the Frobenius number using Lemma 1 (2.1). For this it is necessary to know the structure of the elements of the p-Apéry set, and the structure of the elements of the p-Apéry set depends on the structure of the elements of the (p−1)-Apéry set. Therefore, in the case of p=1, the structure of the elements of the 1-Apéry set is analyzed from the structure of the elements of the 0-Apéry set, which is the original Apéry set, thereby obtaining the 1-Frobenius number. When p=1, we have the following.
Theorem 2. For i≥3, we have
When r=⌊(Fi−1)/Fk⌋≥1, that is, k≤i−1, we have
Remark. When r≥1 and k=i−1,i−2,i−3,i−4,i−5, we have more explicit formulas.
Proof. Put the linear representation
For given Fi and Fk, integers r and ℓ are determined uniquely as Fi−1=rFk+ℓ with 0≤ℓ≤Fk−1.
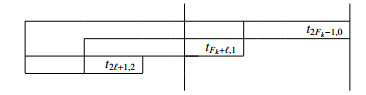
The second set Ap(Fi;1) can be yielded from the first set Ap(Fi;0) as follows. Assume that r≥1. Only the first line {t0,0,t1,0,…,tFk−1,0} moves to fill the last gap in the (r+1)-st line, and the rest continue to the next (r+2)-nd line. Everything else from the second line shifts up by 1 and moves to the next right block (When r=1, the new right block consists of only one line tFk,0,⋯,tFk+ℓ,0, but this does not affect the final result).
The first group is summarized as
for 0≤x≤Fk−1 and 1≤y≤r−1 or 0≤x≤ℓ and y=r. This congruence is valid because
The second group is valid because for 0≤x≤Fk−ℓ−2,
The third group is valid because for 0≤x≤ℓ,
Assume that r=0. The first set Ap(Fi;0) consists of only the first line. If 2ℓ+1≥Fk, then the second set Ap(Fi;1) can be yielded by moving to fill the last gap in the line, the rest continuing to the next line.
They are valid because for 0≤j≤Fk−ℓ−2,
and for 0≤j≤2ℓ+1−Fk,
If 2ℓ+1≤Fk−1, then the second set Ap(Fi;1) can be yielded by moving to fill the last gap in the line only.
They are valid because for 0≤j≤ℓ,
Next, we shall decide the maximal element in the second set Ap(Fi;1) (and also in the first set Ap(Fi;0)).
Case 1 (1) Assume that r=0 and 2ℓ+1≤Fk−1. The second condition is equivalent to 2Fi≤Fk, which is equivalent to i≤k−2. The largest element in the second set Ap(Fi;1), which is congruent to {0,1,…,Fi−1}(modFi), is given by t2ℓ+1,0=(2Fi−1)Fi+2.
Case 1 (2) Assume that r=0 and 2ℓ+1≥Fk. The second condition is equivalent to 2Fi−1≥Fk, which is equivalent to i≥k−1≥3. In this case there are two possibilities for the largest element in the second set Ap(Fi;1): tFk−1,0=(Fk−1)Fi+2 or t2ℓ+1−Fk,1=(2Fi−1)Fi+2−Fk−2Fi. However, because of i≥k−1≥3, always tFk−1,0<t2ℓ+1−Fk,1.
Case 2 Assume that r≥1. This condition is equivalent to Fi−1≥Fk, which is equivalent to i≥k+1.
In this case there are four possibilities for the largest element in the second set Ap(Fi;1):
However, it is clear that t2Fk−1,r−2<tFk−1,r. Because i≥k+1, tFk+ℓ,r−1<tFk−1,r. Thus, the only necessity is to compare tFk−1,r and tℓ,r+1, and tFk−1,r>tℓ,r+1 is equivalent to (Fi−rFk)Fi+2>Fk−2Fi.
Finally, rewriting the forms in terms of Fi+2 and Fi+k and applying Lemma 1 (2.1), we get the result. Namely, the formula (3.1) comes from Case 1 (1). The formulas (3.2) and (3.3) come from Case 1 (2) when k=i+1 and k=i, respectively. The general formula (3.4) comes from Case 2.
4.
The case p=2
When p=2, we have the following.
Theorem 3. For i≥3, we have
When r=⌊(Fi−1)/Fk⌋≥2, that is, k≤i−2, we have
Remark. When k=i−2 and k=i−3, we can write this more explicitly as
respectively. The formulas (4.7) and (4.8) hold when r=2 and r=4, respectively.
Proof. When p=2, the third least complete residue system Ap(Fi;2) is determined from the second least complete residue system Ap(Fi;1). When r≥2, some elements go to the third block.
Case 1 (1) Let r=0 and Fk≥3ℓ+3=3Fi. Since for ℓ+1≤j≤2ℓ+1,
the third set Ap(Fi;2) is given by
As the maximal element is t3ℓ+2,0, by (2.1), we have
Case 1 (2) Let r=0 and 2Fi=2ℓ+2≤Fk≤3ℓ+2=3Fi−1. Since tj,0≡tℓ+j+1,0(modFi) (ℓ+1≤j≤Fk−ℓ−2), and for 0≤j≤3ℓ+2−Fk,
the third set Ap(Fi;2) is
The first elements t2ℓ+1,0,…,tFk−1,0 are in the last of the first line, and the last elements t0,1,,…,t3ℓ+2−Fk,1 are in the first part of the second line. Hence, the maximal element is tFk−1,0=(Fk−1)Fi+2 or t3ℓ+2−Fk,1=(3Fi−1)Fi+2−Fk−2Fi. Therefore, when (3Fi−Fk)Fi+2≥Fk−2Fi, g2(Fi,Fi+2,Fi+k)=(3Fi−1)Fi+2−(Fk−2+1)Fi. When (3Fi−Fk)Fi+2<Fk−2Fi, g2(Fi,Fi+2,Fi+k)=(Fk−1)Fi+2−Fi.
Case 1 (3) Let r=0 and Fk≤2ℓ+1=2Fi−1. Since for ℓ+1≤j≤Fk−1
and for 0≤j≤2ℓ+1−Fk
the third set Ap(Fi;2) is
The first elements t2ℓ+2−Fk,1,…,tℓ,1 are in the second line of the first block, and the last elements are tFk,0,…,t2ℓ+1,0 in the first line of the second block. So, the maximal element is tℓ,1=(Fi+Fk−1)Fi+2−Fk−2Fi or t2ℓ+1,0=(2Fi−1)Fi+2. Since Fk≤2Fi−1, only when k=i+1, we have g2(Fi,Fi+2,Fi+k)=(Fi+Fk−1)Fi+2−(Fk−2+1)Fi. When k≤i, we have g2(Fi,Fi+2,Fi+k)=(2Fi−1)Fi+2−Fi.
Case 2 (1) Let r=1 and 2ℓ+2≤Fk, that is, 23Fi≤Fk≤Fi−1. This case happens only when i=4 and k=3. Since for ℓ+1≤j≤Fk−1
for 0≤j≤ℓ
and for 0≤j≤ℓ
the third set Ap(Fi;2) is
The first elements tFk+ℓ+1,0,…,t2Fk−1,0 are in the first line of the second block, the second elements tFk,1,…,tFk+ℓ,1 are in the second line of the second block, and the last elements tℓ+1,2,…,t2ℓ+1,2 in the third line of the first block. So, the maximal element is one of t2Fk−1,0=(2Fk−1)Fi+2, tFk+ℓ,1=(Fi+Fk−1)Fi+2−Fk−2Fi or t2ℓ+1,2=(2Fi−1)Fi+2−2Fk−2Fi. As i=4 and k=3, t2ℓ+1,2=34 is the largest. Hence, g2(Fi,Fi+2,Fi+k)=(2Fi−1)Fi+2−(2Fk−2+1)Fi, that is, g2(F4,F6,F7)=34−F4=31.
Case 2 (2) Let r=1 and 2ℓ+1≥Fk, that is, (Fi−1)/2<Fk≤(2Fi−1)/3. This relation holds only when k=i−1≥4. Since tj,1≡tFk+j,0(modFi) (ℓ+1≤j≤Fk−1), tj,2≡tFk+j,1(modFi) (0≤j≤ℓ), tFk+j,0≡tℓ+1+j,2(modFi) (0≤j≤Fk−ℓ−2), and for 0≤j≤2ℓ+1−Fk
the third set Ap(Fi;2) is
So, the maximal element is one of t2Fk−1,0=(2Fk−1)Fi+2, tFk+ℓ,1=(Fi+Fk−1)Fi+2−Fk−2Fi, tFk−1,2=(3Fk−1)Fi+2−2Fk−2Fi or t2ℓ+1−Fk,3=(2Fi−1)Fi+2−3Fk−2Fi. As k=i−1≥4, t2ℓ+1−Fk,3=(2Fi−1)Fi+2−3Fi−3Fi is the largest. Hence, g2(Fi,Fi+2,F2i−1)=(2Fi−1)Fi+2−(3Fi−3+1)Fi.
Case 3 Let r≥2. The part
in the second block among the second set Ap(Fi;1) corresponds to the part
in the third block among the third least set Ap(Fi;2)* because
*When r=2, only the last shorter line remains, and t3Fk−1,r−3 in table 9 does not appear. However, this does not affect the result.
for 0≤j≤Fk−1 and 1≤h≤r−2 or 0≤j≤ℓ and h=r−1. The part tℓ+1,r,…,tFk−1,r in the first block among the second set Ap(Fi;1) corresponds to the part tFk+ℓ+1,r−1,…,t2Fk−1,r−1 in the second block among the third set Ap(Fi;2) because for ell+1≤j≤Fk−1
The part t0,r+1,…,tℓ,r+1 in the first block among the second set Ap(Fi;1) corresponds to the part tFk,r,…,tFk+ℓ,r in the second block among the third set Ap(Fi;2) because for 0≤j≤ℓ
The first line tFk,0,…,t2Fk−ℓ−2,t2Fk−ℓ−1,…,t2Fk−1,0 in the second block among the second set Ap(Fi;1) corresponds to two parts tℓ+1,r+1,…,tFk−1,r+1 and t0,r+2,…,tℓ,r+2 in the first block among the third set Ap(Fi;2) because for 0≤j≤Fk−ℓ−2
and for 0≤j≤ℓ,
Hence, the third set Ap(Fi;2) is given by
There are six candidates for the maximal element:
However, it is easy to see that the first four values are less than the last two. Hence, if (Fi−rFk)Fi+2≥Fk−2Fi, then g2(Fi,Fi+2,Fi+k)=tℓ,r+2−Fi=(Fi+2Fk−1)Fi+2−((r+2)Fk−2+1)Fi. If (Fi−rFk)Fi+2<Fk−2Fi, then g2(Fi,Fi+2,Fi+k)=tFk−1,r+1−Fi=((r+2)Fk−1)Fi+2−((r+1)+1)Fk−2Fi.
Finally, we rewrite the form as the linear combination of Fi+2 and Fi+k and apply Lemma 1 (2.1). The formula (4.1) comes from Case 1 (1). The formula (4.2) comes from Case 1 (2). The formulas (4.3) and (4.4) come from Case 1 (3). The formula (4.5) comes from Case 2 (1) (2). The general formula (4.6) comes from Case 3.
5.
The case p=3
When p=3, we have the following.
Theorem 4. For i≥3, we have
When r=⌊(Fi−1)/Fk⌋≥3, that is, k≤i−3, we have
Proof. When p=3, the fourth least complete residue system Ap(Fi;3) is determined from the third least complete residue system Ap(Fi;2). When r≥3, some elements go to the fourth block. The proof of the cases r=0,1,2 is similar to that of Theorem 3 and needs more case-by-case discussions, and it is omitted.
In the table,  denotes the area of the n-th least set of the complete residue system Ap(Fi;n−1). Here, each m(n−1)j, satisfying m(n−1)j≡j(modFi) (0≤j≤Fi−1), can be expressed in at least n ways, but m(n−1)j−Fi can be expressed in at most n−1 ways. As illustrated in the proof of Theorem 4.1, two areas (lines) of ④ in the first block correspond to the first line of ③ in the third block, two areas (lines) of ④ in the second block correspond to two areas (lines) of ③ in the first block, two areas (lines) of ④ in the third block correspond to two areas (lines) of ③ in the second block, and the area of ④ in the fourth block correspond to the area of ③ in the third block except the first line. Eventually, the maximal element of the fourth set of the complete residue system is from the first block, that is, tFk−1,r+2=((r+3)Fk−1)Fi+2−(r+2)Fk−2Fi or tℓ,r+3=(Fi+3Fk−1)Fi+2−(r+3)Fk−2Fi. Hence, if (Fi−rFk)Fi+2≥Fk−2Fi, then g3(Fi,Fi+2,Fi+k)=tℓ,r+3−Fi=(Fi+3Fk−1)Fi+2−((r+3)Fk−2+1)Fi. If (Fi−rFk)Fi+2<Fk−2Fi, then g3(Fi,Fi+2,Fi+k)=tFk−1,r+2−Fi=((r+3)Fk−1)Fi+2−((r+2)Fk−2+1)Fi. Notice that r≥3 implies that k≤i−3.
denotes the area of the n-th least set of the complete residue system Ap(Fi;n−1). Here, each m(n−1)j, satisfying m(n−1)j≡j(modFi) (0≤j≤Fi−1), can be expressed in at least n ways, but m(n−1)j−Fi can be expressed in at most n−1 ways. As illustrated in the proof of Theorem 4.1, two areas (lines) of ④ in the first block correspond to the first line of ③ in the third block, two areas (lines) of ④ in the second block correspond to two areas (lines) of ③ in the first block, two areas (lines) of ④ in the third block correspond to two areas (lines) of ③ in the second block, and the area of ④ in the fourth block correspond to the area of ③ in the third block except the first line. Eventually, the maximal element of the fourth set of the complete residue system is from the first block, that is, tFk−1,r+2=((r+3)Fk−1)Fi+2−(r+2)Fk−2Fi or tℓ,r+3=(Fi+3Fk−1)Fi+2−(r+3)Fk−2Fi. Hence, if (Fi−rFk)Fi+2≥Fk−2Fi, then g3(Fi,Fi+2,Fi+k)=tℓ,r+3−Fi=(Fi+3Fk−1)Fi+2−((r+3)Fk−2+1)Fi. If (Fi−rFk)Fi+2<Fk−2Fi, then g3(Fi,Fi+2,Fi+k)=tFk−1,r+2−Fi=((r+3)Fk−1)Fi+2−((r+2)Fk−2+1)Fi. Notice that r≥3 implies that k≤i−3.
6.
General p case
Repeating the same process, when r is big enough that r≥p, that is, k is comparatively smaller than i, as a generalization of (3.4), (4.6) and (5.3), we can have an explicit formula.
Theorem 5. Let i≥3 and p be a nonnegative integer. When r=⌊(Fi−1)/Fk⌋≥p with (r,p)≠(0,0), we have
Remark. When p=0, Theorem 5 reduces to [24,Theorem 1] except r=0.
On the other hand, k is comparatively larger than i. As a generalization of (3.1), (4.1) and (5.1), we can also have the following formula.
Proposition 1. For i,k≥3, we have
when (p,h)=(3,4), (4,4), (5,5), (6,5), (7,5), (8,5), (9,6), (10,6), (11,6), (12,6), (13,6), (14,6), (15,7), (16,7), (17,7), (18,7), (19,7), (20,7), (21,7), (22,7), (23,7), (24,8), ….
The proof depends on the fact
Nevertheless, such h's are not necessarily sharp because even if (p+1)FiFi+2−Fi−Fi+2>F2i+h, it is possible to have gp(Fi,Fi+2,Fi+k)=gp(Fi,Fi+2) (k≥i+h).
7.
Lucas numbers
The formulas about Fibonacci numbers can be applied to obtain those about Lucas numbers. The discussion is similar, though the value ⌊(Li−1)/Fk⌋ is different from ⌊(Fi−1)/Fk⌋. So, we list the results only.
When p=1, we have the following.
Theorem 6. For i≥3, we have
When r=⌊(Li−1)/Fk⌋≥1, that is, k≤i+1, we have
When p=2, we have the following.
Theorem 7. For i≥3, we have
When r=⌊(Li−1)/Fk⌋≥2, that is, k≤i except i=k=3, we have
When p=3, we have the following.
Theorem 8. For i≥3, we have
When r=⌊(Li−1)/Fk⌋≥3, that is, k≤i−1, we have
For general p, when r is not less than p, we have an explicit formula.
Theorem 9. Let i≥3 and p be a nonnegative integer. When r=⌊(Li−1)/Fk⌋≥p with (r,p)≠(0,0), we have
8.
The number of representations
By using the table of complete residue systems, we can also find explicit formulas of the p-Sylvester number, which is the total number of nonnegative integers that can only be expressed in at most p ways. When p=0, such a number is often called the Sylvester number.
8.1. Main results when p=1
When p=1, we have the following.
Theorem 10. For i≥3, we have
When r=⌊(Fi−1)/Fk⌋≥1, that is, k≤i−1, we have
Proof. When r=0 and 2ℓ+1≤Fk−1, by Fi−1=ℓ,
Hence, by Lemma 1 (2.2), we have
which is (8.1).
When r=0 and 2ℓ+1≥Fk, by Fi−1=ℓ,
Since Fi+k=Fi+2Fk−FiFk−2,
Hence, by Lemma 1 (2.2), we have
which is (8.2).
When r≥1, by Fi−1=rFk+ℓ, we have
Hence, by Lemma 1 (2.2), we have
which is (8.3).
8.2. The case p=2
When p=2, we have the following.
Theorem 11. For i≥3, we have
When r=⌊(Fi−1)/Fk⌋≥2, that is, k≤i−2, we have
Proof. When r=0 and Fk≥3ℓ+3, by Fi−1=ℓ, we have
Hence, by Lemma 1 (2.2), we have
which is (8.4).
When r=0 and 2ℓ+2≤Fk≤3ℓ+2, by Fi+k=Fi+2Fk−FiFk−2, we have
Hence, we have
This case occurs only when k=i+2. Hence, we get (8.5).
When r=0 and Fk≤2ℓ+1, we have
Hence, we have
This case occurs only when k=i+1. Hence, by rewriting we get (8.6).
When r=1 and 2ℓ+2≤Fk, by Fi−1=Fk+ℓ, we have
Hence, we have
This case occurs only when k=i. Hence, we get (8.7).
When r=1 and 2ℓ+1≥Fk, we have
Hence, we have
This case occurs only when k=i−1. Hence, after rewriting, we get (8.8).
When r≥2, by Fi−1=rFk+ℓ, we have
Hence, by Lemma 1 (2.2), we have
which is (8.9).
8.3. The case p=3
When p=3, we have the following. The process is similar, and the proof is omitted.
Theorem 12. For i≥3, we have
When r=⌊(Fi−1)/Fk⌋≥3, that is, k≤i−3, we have
8.4. General p case
We can continue to obtain explicit formulas of np(Fi,Fi+2,Fi+k) for p=4,5,…. However, the situation becomes more complicated. We need more case-by-case discussions.
For general p, when r≥p, we can have an explicit formula.
Theorem 13. Let i≥3 and p be a nonnegative integer. When r=⌊(Fi−1)/Fk⌋≥p, we have
Remark. When p=0, Theorem 13 reduces to [24,Corollary 2].
Sketch of the proof of Theorem 13. We have
Hence, by Lemma 1 (2.2), we have
which is (8.11).
9.
Example
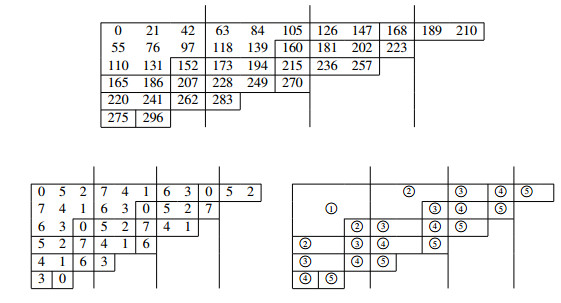
Consider the Fibonacci triple (F6,F8,F10). Since F6−1=2F4+1, we see that r=2 and ℓ=1. Then, we can construct the first least set, the second least and 3rd, 4th and 5th least sets of the complete residue systems as follows.
Therefore, by Lemma 1 (2.1) with (2.3), we obtain that
By Lemma 1 (2.2) with (2.4), we obtain that
On the other hand, from (3.4), by (F6−2F4)F8>F2F6, we get
From (4.6) and (5.2), we get
respectively. From (8.3), (8.9) and (8.10), we get
respectively.
10.
Open problems
In [31], a more general triple g(Fa,Fb,Fc) is studied for distinct Fibonacci numbers with a,b,c≥3. In [32], the Frobenius number g(a,a+b,2a+3b,…,F2k−1a+F2kb) is given for relatively prime integers a and b. Will we be able to say anything in terms of these p-Frobenius numbers?
Acknowledgments
The authors thank the anonymous referees for careful reading of this manuscript.
Conflict of interest
The authors declare there is no conflict of interest.











 DownLoad:
DownLoad:

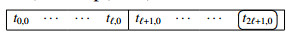
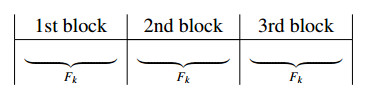



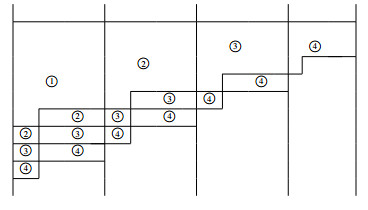
 denotes the area of the
denotes the area of the