A bionic topology optimization method with an additional displacement constraint

1.   Introduction

Optimization design makes up for the shortcomings of traditional design methods, such as long cycle, low efficiency, and high cost, and promotes a huge change in the concept of structural design. For structural optimization, Optimization design techniques mainly include size optimization, shape optimization and topology optimization, among which topology optimization technology is considered to be most important ^[1]. Topology optimization can automatically generate structural layouts with maximized performance for a given design domain and boundary conditions ^[2], and can provide abundant space and flexibility in the design ^[3]. Meanwhile, the optimized topologies have better structural performance than the structures designed manually based on engineers' intuition and experience^[4]. Hence, topology optimization technology is extremely attractive and has been widely used in various engineering fields, such as architecture ^[5], automotive ^[6], and aerospace ^[7]. Over the past few decades, topology optimization technique has been widely explored, and a large number of topology optimization methods can be found in the engineering literature, of which density-based method, evolutionary procedures, and level set method are the most representative ^[8].

Early topology optimization studies focused more on solving compliance minimization problems with a predefined volume constraint. However, in engineering practice, the compliance value obtained only under volume constraint lacks engineering significance ^[9], and the optimal value of the predefined volume fraction cannot be predicted. Therefore, this optimization problem is not suitable for real engineering applications. To compensate for this, adding a displacement constraint seems to be good way. Displacement, as an important measure of stiffness, is usually constrained in real structural design. For example, in optimal design of an aircraft wing, to maintain the aerodynamic performance, the exterior surface should undergo minimal shape change when subjected to aerodynamic forces ^[10], which requires that the surface displacement should be kept within a certain limit.

In considering displacement constraints, Huang and Xie ^[11] extended the BESO method to the stiffness optimization with a material volume constraint and a local displacement constraint. Zuo et al. ^[12] and Zuo and Xie ^[13] extended the BESO method to multiple constraints of displacement and frequency in addition to the amount of material usage, and later they also proposed a global control method for displacements of continuum structures based on the BESO approach. Sivapuram and Picelli ^[14] proposed a topology optimization method of binary structures based on the BESO method, which can deal with the topology optimization problem with displacement constraint. Rong et al. ^[15] developed an improved density-based optimization method for the displacement constrained topology volume minimization under multiple load cases. Ye et al. ^[16] proposed a topology optimization of multimaterial continuum structure with displacement constraint based on ICM method. Xia et al. ^[17] presented a uncertainty-oriented topology optimization of interval parametric structures with local stress and displacement reliability constraints. Wang et al. ^[18] built an uncertainty-oriented cross-scale topology optimization model with global stress reliability constraint, local displacement constraint, and micro-manufacturing control based on evidence theory.

Although researchers have proposed some topology optimization methods with displacement constraints, relatively speaking, the research results in this direction are still relatively limited. Meanwhile, the existing methods also have certain shortcomings, such as difficulty in obtaining sensitivity information, and difficulty in selecting an appropriate volume fraction under displacement constraints. To overcome the shortcomings of traditional methods and open up a new idea, this paper extends an improved bionic topology optimization method to solve the topology optimization problem with an additional displacement constraint. In this method, a cost-weighted sum of stiffness and mass (a measure more relevant to engineering) is used as the objective function, and the volume constraint is no longer used. The updates of density design variables are not based on sensitivity information, but on an improved bone remodeling algorithm, which makes the method simpler and easier to implement.

The remainder of this paper is organized as follows. In Section 2, an earlier defined topology optimization problem is extended to one with an additional displacement constraint. The details and implementation of the proposed method are presented in Section 3. Section 4 shows 2D and 3D examples with discussions. The conclusions are drawn in Section 5.

2.   Optimization problem

Structural topology optimization problems are usually formulated in terms of maximizing stiffness subjected to volume constraints. Whereas in our previous paper ^[19], we believed that the topology optimization problem should be a multi-objective optimization problem, which is defined as a cost weighted sum of stiffness and mass, i.e.,

where $\varphi$ is a cost function, $\omega$ is the weighting factor that measures the cost of mass and strain energy in the optimization problem, $\boldsymbol {\rho}$ is the vector of density design variables, $\rho_{\text{real}}$ is the density of solid material, $\rho_{\text{min}}$ is the minimum value of density to prevent numerical singularities, $\widetilde{U}_0$ and $M_0$ are the total strain energy and the total mass of the initial solid structure, respectively. Here,

where ${\mathit{\boldsymbol{D}}}$ is the displacement vector, ${\mathit{\boldsymbol{K}}}$ is the global stiffness matrix, $U_{a, i}$ is the average strain energy density of the $i$ element under multiple loading cases, $v_i$ and $\rho_i$ are the volume and density of the $i$ element, respectively, and $n$ is the number of discrete elements.

The derivative of objective function with respect to the density of the $i$ element is:

where ${\mathit{\boldsymbol{d}}}_i$ is nodal displacement vector of the $i$ element, $\bar{{\mathit{\boldsymbol{k}}}}_i$ is its stiffness matrix, which can be expressed as:

where $\bar{{\mathit{\boldsymbol{k}}}}_{0i}$ is the elemental stiffness matrix corresponding to real density, $\gamma$ is a penalization factor in order to ensure black-and-white solutions.

So, the derivative of $\bar{{\mathit{\boldsymbol{k}}}}_i$ with respect to $\rho_i$ is:

Now, Eq (2.3) can be written as

From the above formula, the optimality condition of the optimization problem defined by Eq (2.1) can be known as:

The left and right sides of the above formula are respectively defined as:

where $S_i$ and $k$ are called the mechanical stimulus of $i$ element and the threshold, respectively, so that the optimization problem can be solved later using the bone remodeling algorithm. Meanwhile, Eq (2.6) shows that different optimal solutions of the optimization problem can be obtained by adjusting the $k$ value.

Based on the above information, the topology optimization problem with an additional displacement constraint is stated as:

where $d_{tn}$ and $d_{tn}^*$ are the displacement of target node $tn$ and its constraint. The target node can be any node in the design domain.

3.   Optimization method

3.1.   Setting of $k$ value

In the optimization problem section, the regulating effect of the threshold $k$ on the optimization solution has been mentioned. Hence, for the optimization problem with additional displacement constraint, in order to obtain the optimal solution satisfying the displacement constraint, establishing the relationship between the threshold and the displacement of the displacement of the target node is necessary. According to Eqs (2.7) and (2.8), the threshold $k$ can also be expressed as:

Equation (3.1) shows that the threshold $k$ is not only related to the nodal displacement of the element, but also to this elemental density. Therefore, the threshold $k$ that satisfies the displacement constraint cannot be solved directly according to the constraint displacement. Meanwhile, Eq (3.1) also shows that increasing the threshold $k$ can increase the nodal displacement of the element when the elemental density becomes the real density.

Based on the above facts, to find a suitable $k$ value, the threshold $k$ is assumed to be able to evolve according to the relationship between the target node displacement and the constraint displacement referring to the evolution idea of the BESO method. The evolution equation for the threshold $k$ is defined as:

where $N$ is the number of iterations. $\delta$ is the evolutionary ratio, which is defined as

where $d_{tn}^{N-1}$ is the target node displacement after the algorithm converges when the threshold $k$ is $k_{N-1}$. In the first iteration, stiffness and mass are assumed to be equally important, i.e., $\omega = 0.5$, the initial value of the threshold $k$ is calculated by Eq (2.8) as:

3.2.   Update of material properties based on an improved bone remodeling algorithm

Density is used to characterize the material distribution. $\rho_i = \rho_{\text{real}}$ corresponds to a solid element, $\rho_i = \rho_{\text{min}}$ to a void element, and the intermediate density will be penalized. At each time step, the change in density can be calculated as:

where $g(t)$ is a progressive function, which is constructed as:

where $t$ is the time step at current $k$ value, $p$ is the time step to achieve full control of $k$ value, and $\alpha$ is constant.

$f_j(i)$ is a spatial influence function, which is redefined as

where $d_j(i)$ is the distance between centers of the element $j$ and element $i$. $d$ is the distance at which the influence of the element $j$ decays to $36.8\%$. $\beta$ is the spatial influence radius, which is beneficial to save computational cost, especially for large-scale computing.

After each time step, the elemental density will be updated according to the following rule:

The Poission' ratio is assumed to be a constant independent of design variables. The Young's modulus $E_i$ can be expressed by the elemental density $\rho_i$ and the penalization factor $\gamma$ as:

where $E_{\text{min}}$ is a very small value that prevents the stiffness matrix from becoming singular, $E_{\text{real}}$ is the Young's modulus of the real material.

3.3.   Convergence Criteria

For the topology optimization problem with additional displacement constraint, convergence should be confirmed on both the objective function and target node displacement.

The convergence criterion of the objective function at the current $k$ value is defined as:

where $\theta$ is a specified small value, $\varphi(t)$ is the cost function at the current time step, and $X$ is set to 5, which means that the value of the cost function remains almost constant over 10 consecutive time steps. Noted that the convergence criterion should not be judged during the action phase of the progressive function.

The convergence criterion of the target node displacement is expressed as:

where $\varepsilon$ is an allowable displacement error.

3.4.   Algorithm implementation

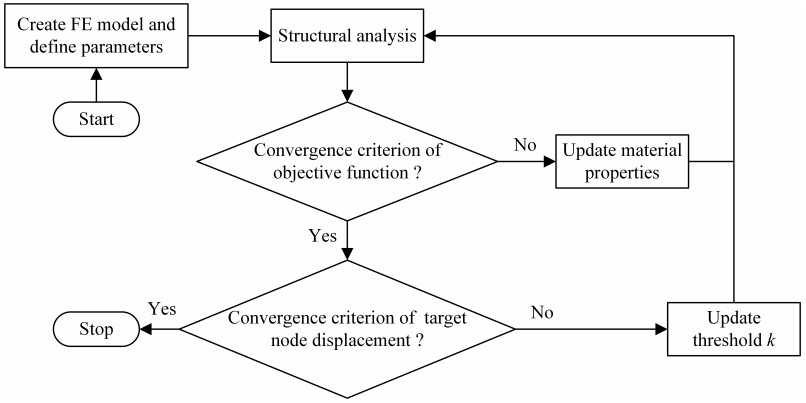
An implementation flowchart of the proposed method is illustrated in Figure 1. The evolutionary iteration procedure is briefly summarized as:

Step 1: Discretize the whole design domain using finite element mesh and impose boundary and loading conditions to create the FE model.

Step 2: Define the relevant parameters required by the algorithm, including material properties and density, progressive function, spatial influence function, penalization factor, convergent criteria, maximum iteration number, constraint displacement, etc.

Step 3: Calculate the initial value of the threshold $k$ by Eq (3.4).

Step 4: Carry out finite element analysis and output the data for calculating the change in density and the objective function.

Step 5: Update the elemental densities according to Eq (3.8) to calculate Young's modulus by Eq (3.9), and assign new material properties to elements.

Step 6: Repeat steps 4–5 until the convergence criterion of the objective function at the current $k$ value is met.

Step 7: Output the target node displacement to judge whether the displacement convergence criterion or maximum iteration number are satisfied. If no, update the threshold $k$ and then go back to step 4.

Step 8: Output results.

4.   Numerical examples

In all examples, unless otherwise stated, the common parameter settings in all examples are shown in Table 1.

4.1.   Example 1

The first example is a topology optimization problem of a 2D beam structure under concentrated loading, as shown in Figure 2. The size of the design domain is $100\ \rm mm \times 50\ \rm mm \times 1\ \rm mm$. Only its two bottom corners are used as support points, in which the left bottom corner is fixed, and the vertical displacement of the right bottom corner is limited. A vertical force of $1\ \rm KN$ is applied downward at the middle of its upper edge. The design domain is divided into $100 \times 50$ four-node plane stress elements.

To prove that the proposed method can be used to solve the displacement constraint problem of other nodes besides the loading node, the horizontal displacement of the right support node is constrained. Before the optimization starts, the horizontal displacement of this node is $3.7 \times 10^{-2}\ \rm mm$. Here, the constraint displacement values are set to be $4.1 \times 10^{-2}$, $4.3 \times 10^{-2}$, and $4.5 \times 10^{-2}\ \rm mm$, respectively. The optimal topologies obtained are shown in Figure 3. From the figure, the optimal topologies obtained under different displacement constraints are different, but all topological contours are relatively clear, which indicates that the proposed method can find the optimal black-and-white solutions with no checkerboards according to the displacement constraints.

Figure 4 shows the evolutionary histories of the displacement, total cost, total mass, total strain energy, and threshold. As shown in the figure, the displacements can all converge to their own constraint values under different displacement constraints. Since the same initial threshold is used, the results of the first iteration are the same under different displacement constraints. As the constraint displacement value increases, the effective material in the structure decreases and the total strain energy accordingly increases, but the total cost (objective function) decreases. Different displacement constraints have different threshold evolution curves, but all curves are in form of fast first then slow. This evolutionary form helps the proposed method to quickly find the optimal solution that satisfies the displacement constraint, and also shows that the defined threshold formula is reasonable and effective. The greater the difference between the initial target node displacement and its constraint, the more pronounced this form will be. The evolving relationship between the threshold and the displacement also proves the aforementioned conclusion that increasing the threshold can increase the target node displacement. From the evolution curve of each index, the entire iterative process is relatively stable, which indicates that the proposed method can run smoothly.

4.2.   Example 2

In second example, a topology optimization problem of a 2D beam structure under a uniform loading is considered as shown in Figure 5. The example has the same design domain size and number of discrete elements as Example 1. The two bottom corners of the design domain are fixed, and a uniformly distributed load $P = 10\ \rm N/mm$ is applied on its top surface. The area within $2\ \rm mm$ from the top surface is defined as the non-design area, that is, the elements in this area are assigned the real density. A displacement constraint is applied to the vertical displacement of the middle position on the top surface, and the constraint displacement value is set to be $-2.7 \times 10^{-2} \rm\; mm$. The displacement before optimization here is $-1.88 \times 10^{-2} \rm\; mm$.

Figure 6 shows the optimal topologies obtained at different iterations. From the figure, the evolution process of the topology can be seen, and it can be known that a topology similar to the optimal one is obtained after 5 iterations, which indicates that the proposed method has a good optimization rate. The optimal topology clearly shows that it is consistent with real arch bridges observed in nature, which confirms the correctness and effectiveness of the proposed method.

The evolutionary histories of the displacement, total cost, total mass, total strain energy, and threshold are shown in Figure 7. The evolution law of each indicator similar to that in Example 1 can be observed from the figure, which illustrates the robustness of the proposed method. In the final stage, the target node displacement can converge to its constraint value.

4.3.   Example 3

The proposed method can be directly used to solve the topology optimization problems of 3D structures with additional displacement constraints. Figure 8 shows a topology optimization problem of a 3D cantilever beam structure. The design domain with the dimensions $60\ \rm mm \times 20\ \rm mm \times 4\ \rm mm$ is discretized into $60 \times 20 \times 4$ eight-node hexahedral stress elements. Its one end is fully fixed, and a vertical downward and uniformly distributed load $P = 100\ \rm N/mm$ is applied to the lower edge of its other end. The maximum displacement of the structure is constrained, and its constraint value is set to be $-14.2 \; \times \; 10^{-2}$ mm. The maximum displacement of the structure with full material is $-7.38\; \times\; 10^{-2}\; \rm\; mm$.

The optimal topologies obtained at different iterations are shown in Figure 9. The evolution process of the topology can be seen in the figure. Different numbers of iterations correspond to different topologies, but as the number of iterations increases, the effective material in the structure decreases. All topological contours at different iterations are relatively clear, and there is no checkerboard phenomenon, which indicates that the proposed method has good optimization ability.

Figure 10 shows the evolutionary histories of the displacement, total cost, total mass, total strain energy, and threshold. It can be observed that the evolution law of each indicator is similar to that in 2D examples, which proves that the proposed method can be directly extended to solve the topology optimization problems of 3D structures with additional displacement constraints. The evolution process of each index is relatively stable, indicating that the proposed method still runs smoothly when solving 3D problems. The maximum displacement of the structure can quickly converge to its constraint value, which indicates that the proposed method still has a good optimization rate when dealing with 3D problems.

5.   Conclusions

Based on real engineering application requirements, this paper has extended an improved bionic topology optimization method to solve the topology optimization problem with an additional displacement constraint, which provides a new approach to solving such problems. To find the optimal solution that satisfies the displacement constraint, the explicit relationship between the threshold and target node displacement is constructed. 2D and 3D examples show that the proposed method is indeed able to obtain a convergent design satisfying the predefined displacement limit, demonstrating the effectiveness and feasibility of the proposed method in dealing with topology optimization problems with an additional displacement constraint. The resulting topologies have clear contours and no checkerboard phenomenon. The evolution curves of indicators in examples reveal that the proposed method has good optimization performance, and also proves that the constructed explicit relationship between the threshold and target node displacement is reasonable and high efficient. In future work, the optimization capabilities of the proposed method will be further explored and extended to address some more cutting-edge problems, such as solving topology optimization problems of complex 3D geometries with multi-materials and displacement constraints.

Acknowledgments

This work is supported by the National Natural Science Foundation of China [grant number 51475373, 51375390, and 61603302] and the Research and Development Projects in Shaanxi Province [grant number 2020F-152, and 2022ZDLGY03-06].

Conflict of interest

We declare there is no conflicts of interest.