Modelling Botswana's HIV/AIDS response and treatment policy changes: Insights from a cascade of mathematical models

1.   Introduction

With the progression of technology, minimally invasive surgical (MISR) robots have incrementally supplanted traditional surgical approaches, demonstrating superior performance in terms of operative clarity, user-friendliness, and operational adaptability ^[1]. Moreover, the implementation of MIS robots is commonly associated with enhanced patient outcomes, reduced pain levels, minimized blood loss and scarring, as well as shortened recovery time ^[2]. However, due to the lack of direct access to the surgical site, surgeons tend to exert excessive force, resulting in tissue damage ^[3]. The absence of haptic feedback is widely recognized as a significant challenge in current robot-assisted laparoscopic surgery ^[4,5]. The accuracy of force feedback is crucial for determining tissue properties and executing delicate surgical procedures. The accuracy of force feedback is crucial for the identification of tissue properties and the execution of precise surgical procedures.

Force feedback plays a pivotal role in surgical procedures, facilitating surgeons to perceive the mechanical characteristics of tissues, assess their anatomical structure, and execute precise force-control actions for ensuring safe tissue manipulation ^[6,7]. To demonstrate the feasibility and efficacy of force feedback in laparoscopic surgery, Wagner and Semere incorporated a commercially available force/torque sensor at the distal end of the surgical instrument to precisely measure tool-tissue forces. The measured forces were then fed back to the master robot through a teleoperation system, enabling the effective execution of blunt dissection tasks. Remarkably, this implementation of force feedback resulted in a significant 50% reduction in applied force and an impressive 66% decrease in tissue damage error ^[8,9].

To date, extensive research has been conducted on the force feedback of minimally invasive surgical robots. The existing methods for estimating forces in surgical robots can be broadly categorized into direct force sensing and sensorless force estimation ^[10,11]. In the direct force sensing method, the force exerted by the surgical tool on the tissue is quantified through an integrated sensor positioned either on or in close proximity to the tool ^[12,13]. Using piezoresistive sensors, Abiri et al. ^[14] developed a device that can be affixed to the tip of a surgical instrument for measuring interaction forces. Furthermore, Reiley et al. ^[15] incorporated strain gauges onto the shafts of surgical tools for measuring interaction forces. However, challenges such as biocompatibility, sterilization, and miniaturization impose limitations on the feasibility of this approach ^[16,17]. The exposure to high temperatures, pressures, and humidity during sterilization procedures may potentially inflict damage upon electronic components ^[18]. Zarrin et al. ^[19] and Carotenuto et al. ^[20] proposed a laparoscopic sensing instrument based on Fiber Bragg grating (FBG) that demonstrates resistance to high-temperature sterilization. However, the durability of the fiber is inadequate and it exhibits mechanical limitations during complex movements.

In contrast, sensorless force estimation methods enable the prediction of forces using existing resources, obviating the need for additional electronics. Haghighipanah et al. ^[21] and Wang et al. ^[22], employed a cable tension disturbance observer on the surgical robot's end effector to quantify external forces. Tholey et al. ^[23] and Zhao et al. ^[24] utilized the driving motor's current as an estimation of the force exerted between the gripper and tissue at the distal end of the surgical robot. However, the utilization of these motion-based methods poses challenges in acquiring precise modeling information for surgical tools or robotic operators, thereby hindering the establishment of an accurate method for predicting interaction forces. In addition, there are vision-based force estimation methods. When force is applied, the deformation of the soft tissues is captured by the camera. This information is then used to predict the actual force exerted on the object ^[25,26,27]. Noohi et al. ^[28] propose a virtual template-based approach for estimating tool-soft tissue interactions using monocular camera images. In ^[25], relying exclusively on endoscopic images acquired by the stereo camera, Haouchine employed a dynamic biomechanical model based on organ shape to accurately estimate the contact force at the tool tip. To enhance force estimation accuracy, Mozaffari et al. ^[29] introduced a neural fuzzy inference system for identifying tool-tissue forces and maximum local stress in laparoscopic surgery. Despite extensive research on replacing force sensors with image sensors, occlusion, optical noise, and camera motion can still introduce interference in the image, thereby impacting the accuracy of force estimation. These studies demonstrate that both approaches relying on dynamic motion information and strategies based on advanced visual analysis exhibit a certain level of stability, robustness, and efficacy in estimating applied forces. Although these methods have inherent limitations in terms of predictive accuracy, they possess significant potential for wide-ranging applications in the field of force estimation.

Building upon the aforementioned research, this study aims to further investigate and advance the new trajectory of force estimation technology. We propose a novel approach for clamping force prediction based on mechanical clamp blade motion parameters. In this methodology, a backpropagation (BP) neural network is employed to construct a soft tissue force prediction model by considering the interplay between soft tissue pressure, instrument displacement, motion speed, and indenter contact area. The BP neural network exhibits exceptional capabilities in nonlinear analysis, generalization, and fault tolerance, rendering it suitable for effectively capturing the intricate mapping relationship between the clamping force of soft tissue and the motion parameters of the clamp blade. However, the convergence speed of BP neural networks is often slow and they are prone to getting trapped in local optima. Therefore, this study proposes the integration of the sparrow search algorithm (SSA) to enhance the predictive performance of the model for clamping force in dynamic and non-linear surgical environments by optimizing the weights and thresholds of BP neural networks. The proposed algorithm surpasses existing algorithms, such as the genetic algorithm (GA), in terms of search accuracy, convergence speed, and stability ^[30,31]. This is crucial for facilitating rapid and precise decision-making in surgical applications. The model's prediction performance was validated through an in vitro compression experiment on pig kidney tissue. This model not only enables real-time clamping force prediction, but also facilitates more accurate estimation of the force between the instrument and tissue during future surgical procedures, thereby enhancing surgical safety and efficacy.

The remaining sections of the paper are organized as follows: Section 2 provides a detailed description of the design and implementation of soft tissue compression experiments. Section 3 elaborates on the algorithms employed for predicting soft tissue gripping force, along with their theoretical foundations. In Section 4, we present experimental results and conduct an in-depth analysis of the performance of our proposed prediction model. Finally, Section 5 summarizes the research findings and discusses potential avenues for future investigation.

2.   Grip force prediction algorithm

Soft tissues exhibit intricate nonlinear and stage-dependent characteristics, posing challenges for traditional modeling approaches to accurately capture their behavior. Therefore, in this study, we propose a mechanical model based on the SSA-optimized BP neural network to precisely simulate the dynamic mechanical response of soft tissues under continuous compression. The proposed approach integrates the SSA's capability in global optimization with the efficiency of the BP neural network for function approximation and simulation of complex system behavior, enabling a comprehensive understanding of soft tissue's mechanical response under compression.

2.1.   BP neural network

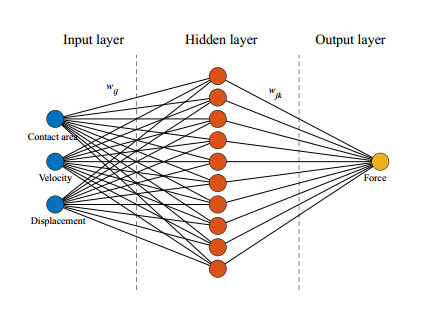
In our study, we employ BP neural networks to forecast the mechanical properties of soft tissues. BP networks are renowned for their inherent capability to automatically discern intricate relationships between input and output data, a crucial aspect in comprehending the nonlinear mechanical response exhibited by soft tissues. Through the network's self-learning and adaptive capabilities, we can encode the mechanical behavior of soft tissue into its weights, thereby achieving more accurate simulation and prediction of its response.

The BP neural network is comprised of multiple layers, typically including an input layer, one or more hidden layers, and an output layer. In this study, the structure of the soft tissue force prediction model based on the BP neural network is illustrated in Figure 1, enabling the network to effectively capture data patterns ranging from simple to intricate.

The operation process of the BP neural network is primarily divided into two stages: forward propagation and backpropagation. During the forward propagation phase, the input signal undergoes a sequential pass through each layer of the network. At each node, the input signal is multiplied by its corresponding weight, added to the bias term, and then transformed into an output signal using an activation function. The input $s_{j}^{(l)}$ of each neuron j in each layer l is obtained through a linear combination of the activation values $o_{j}^{(l-1)}$, weights $w_{{y}}^{(l)}$, and biases $b_{j}^{(l)}$ from the previous layer, which can be calculated as follows:

The activation value $o_{j}^{(l)}$ of neuron j corresponds to the output obtained by applying the input signal through the activation function:

where $f(\cdot)$ is the activation function, and the sigmoid function $f(x) = \frac{1}{1+e^{-x}}$ is usually chosen.

In the backpropagation phase, the network's weight and threshold are updated through error minimization between the network output and target output. Specifically, the network error is defined as the sum of squared differences between the desired output and actual output:

where $y_{k}$ is the target output value, $o_{k}^{(L)}$ is the actual output value of the network, L represents the output layer, and k traverses all output neurons. Therefore, the error gradient is calculated as follows:

The error gradient for neuron k in the output layer L is as follows:

The error gradient for neuron j in hidden layer l (l < L) is as follows:

The weight and threshold adjustments of the neural network are updated using the gradient descent method:

where, $\eta$ is the learning rate, a positive number less than 1.

The formula for determining the number of neurons in the hidden layer is:

where m is the number of nodes in the hidden layer, n is the number of nodes in the input layer, o is the number of nodes in the output layer, and a is a constant between 1 and 10.

The BP neural network demonstrates exceptional performance in automatically extracting association rules between input and output data, while effectively retaining the acquired knowledge within its network weights, thereby exhibiting remarkable self-learning and adaptive characteristics. However, when confronted with complex nonlinear data such as soft tissue mechanics, BP networks encounter specific challenges. These include relatively slow convergence rates and high sensitivity to initial weight settings, which may result in the network getting trapped in local minima during the learning process and failing to accurately approximate intricate real-world models. This limitation becomes particularly evident when processing soft tissue data characterized by complex mechanical behavior, necessitating optimization of relevant parameters to overcome these challenges.

2.2.   Sparrow search algorithm

The SSA, proposed by Xue and Shen in 2020 ^[32], is based on the behavioral patterns observed in sparrow populations, encompassing the distinct roles of producers, followers, and scouts. By simulating the foraging and predator avoidance strategies of these characters, SSA demonstrated superior capabilities in global search. We integrate this algorithm with a BP neural network to optimize the initialization and adjustment process of the BP network by leveraging SSA's global search abilities. This integration not only enhances the convergence speed of the model, but also improves its adaptability in tackling complex and nonlinear problems, particularly in simulating the mechanical behavior of soft tissues.

A population of n sparrows can be represented as:

where d represents the dimensionality of the problem variable to be optimized and n denotes the number of sparrows. In the subsequent optimization problem, d signifies the number of BP parameters that need to be optimized, that is, the total number of weights and biases in the BP neural network. Consequently, all sparrows' fitness values can be expressed as:

where f is the fitness value. According to the above SSA principle, the optimization objective function can be established as:

where N is the total number of training sets. y_k and $o_{k}^{(L)}$ are the true and predicted values of the kth data, respectively. The fitness function indicates that we ultimately want to get a network with a small training set error. The producer position is updated during the process of population iteration as follows:

where t represents the current iteration value, j represents the dimension between 1 and d, $X_{i, j}^{t}$ represents the value of the jth dimension when the ith sparrow iterates t times, and ${item}_{\text {max }}$ is the number with the most iterations. $R_{2} \in[0, 1]$ and $S T \in[0.5, 1.0]$ represent the alarm value and safety threshold, respectively. The variable Q is a random number that conforms to a normal distribution, while L represents an 1*d matrix consisting of all elements equal to 1. If $R_{2} < S T$, then the sparrow population is safe. Otherwise, some sparrows perceive danger, and all sparrows must quickly move to a safe area.

The follower's position is continuously updated, ensuring constant monitoring of the producer. In the event that the follower detects a superior food source, it engages in competitive interactions to acquire it. If successful, the follower obtains access to the food resource; otherwise, it continues its vigilant surveillance.

where $X_{p}^{t}$ represents the best position occupied by the producer, and $X_{ {worst }}^{t}$ indicates the current worst position. A represents an 1*d matrix where the elements are randomly assigned values of either 1 or -1, and $A^{*} = A^{T}\left(A A^{T}\right)-1$. When $i>n / 2$, the ith follower exhibits a suboptimal fitness value attributed to its state of hunger.

The sparrow position is updated in the event of danger as follows:

Scouts constitute 10–20 percent of the population, with $X_{{test }}^{t}$ representing the current optimal proportion. The variable $\beta$ follows a standard normal distribution with a mean of 0 and a variance of 1. $K \in[-1, 1]$ is a random number. $f_{i}$ represents the current fitness value of the sparrow. $f_{g}$ and $f_{w}$ are the current best and worst fitness values. The constant $\varepsilon$ represents the minimum value required to prevent zero partitioning error. The value of $f_{i}>f_{g}$ indicates that the sparrow is positioned at the periphery of the population, rendering it susceptible to predation by hazardous factors. The condition $f_{{i}} = f_{g}$ indicates that the sparrow positioned in the center of the population possesses awareness of potential threats and necessitates repositioning closer to other sparrows. K represents both the direction of movement for the sparrow and serves as a control coefficient for determining step size ^[33].

2.3.   Establishing the SSA-BP model

The present study introduces a novel prediction model that combines the SSA algorithm with the BP neural network, aiming to enhance the precision of soft tissue gripping force prediction in micro-invasive surgery. During the training process, we initially determine the specific structural parameters of the input layer, hidden layer, and output layer. Subsequently, SSA is employed to explore optimal weights and biases. The initialization of sparrow population parameters includes specifying the number of sparrows in the population, proportion of discoverers, warning value threshold, and maximum iteration count. In order to precisely guide the optimization process, the fitness function of SSA is defined as the error function of the neural network for evaluating and adjusting the search strategy. Subsequently, based on optimal weight and optimal deviation, prediction of clamping force in soft tissue is performed. The flow chart illustrating the entire optimization process is presented in Figure 2. The key steps of the SSA-BP prediction model are outlined as follows:

1) Construct the initial BP neural network and initialize the weights and biases of the network.

2) Configure the parameters of the SSA algorithm, including sparrow population size, alarm value, safety threshold, and iteration number. Evaluate and rank the fitness of each individual sparrow, identify the location of current optimal and worst solutions, and update the sparrow's fitness in subsequent iterations.

3) Employ SSA to optimize the BP prediction model and iterate through the optimization process until reaching either a predetermined error range or maximum number of iterations.

4) Upon completion of iteration, apply the optimized weights and deviations obtained by SSA to the BP network.

5) Utilize the optimized BP network model for predicting and analyzing collected soft tissue pressure data.

2.4.   Evaluation index

The evaluation indices employed in this study encompass root mean square error (RMSE), mean square error (MSE), mean absolute error (MAE), sum of squares of error (SSE), and coefficient of determination (R²). The evaluation of model prediction error and prediction effect primarily relies on RMSE, MSE, MAE, SSE, and R². A smaller value for RMSE, MSE, MAE, and SSE indicates a better prediction effect, while a larger value for R² suggests an improved prediction effect. The following equations represent the calculation formulas for RMSE, MSE, MAE, SSE, and R². In these equations, $o_{k}^{(L)}$ denotes the predicted output value, $y_{k}$ represents the actual value, $\overline{{y}}$ signifies the mean value of $y_{k}$, and N corresponds to the number of samples.

3.   Experimental design

In this study, a series of in vitro experiments were conducted to simulate surgical procedures and construct a model that accurately reflects the mechanical response of biological soft tissues. The experimental design was rigorous and the data obtained were highly accurate, ensuring the reliability of the developed model.

3.1.   Experimental equipment

The primary equipment utilized in the experiment is the SHIMADZU (EZ-LX) universal mechanical testing machine, manufactured by Shimadzu Corporation (Japan). This device features a high-precision force sensor, and its mechanical arm is equipped with a specially designed clamp blade to facilitate swift replacement of experimental instruments without compromising the data reading accuracy of the sensor during experimentation. The experimental setup, as depicted in Figure 3, was utilized as the test platform. Its operation involved controlling the clamp blades with varying contact areas to achieve a uniform compression at low speed until reaching the predetermined compression depth. Subsequently, compression was halted and the force sensor reading was recorded.

3.2.   Experimental material

Considering the influence of the contact area between the clamp leaf and soft tissue during surgical procedures, three types of indenters were designed to simulate various operation scenarios, each with different contact areas. The indenter utilized in the experiment, as depicted in Figure 4, exhibits respective contact areas of 45.76, 29.29, and 16.47 mm². Detailed dimensions of the indenter are provided in Table 1. This variation allows for an assessment of the impact that contact area has on pressure.

3.3.   Experimental sample

The pig kidney was selected as the experimental sample to simulate laparoscopic surgery due to its high availability and similar tissue characteristics to human abdominal organs. Specifically, pig kidneys offer an ideal model for simulating urinary system surgery. Following removal from pigs, the samples were cut into standardized chunks (30 ± 1 mm × 15 ± 1 mm, thickness 8 ± 1 mm) and stored in portable coolers to maintain freshness and biomechanical stability. The experiment commenced within 5 hours after removal to ensure preservation of the tissue's biomechanical properties.

3.4.   Experimental parameters

The experimental parameters encompass compression depth and loading speed to replicate the clamping procedure in real surgical scenarios.

1) Compression depth: To prevent direct contact between the forceps leaf and the support platform beneath the tissue sample during experimentation, which could potentially overload the sensor, a strict upper limit of compression depth was imposed equal to the thickness of the sample. Considering that the treated pig kidney tissue sample had an approximate thickness of 8mm, a maximum compression depth of 3mm was set during experimentation to ensure test process safety and data reliability.

2) Loading speed: The study revealed that the average clamping velocity of the laparoscopic clamp on soft tissue during the operation ranged from 1.2 to 2.4 mm/s ^[34,35,36]. To accurately simulate surgical conditions, forceps blades were subjected to four different loading speeds in this experiment: 0.5, 1, 1.5, and 2 mm/s, aiming to investigate the impact of varying speeds on compression efficacy.

3.5.   Experimental process

In order to ensure the stability of the biological properties of the soft tissues throughout the experiment, we opted for a controlled temperature range of 24 ± 2 ℃ and a humidity range of 45–55%. Prior to the commencement of the experiment, the sample was extracted from the cooler and allowed to cool down at room temperature. Subsequently, the clamp blade indenter was affixed to the sensor of the mechanical testing machine ensuring proper alignment with the sample on the test platform. Compression experiments were performed at four different loading speeds, each compression reaching its predetermined maximum depth, while real-time monitoring and recording of force variations were facilitated by dedicated software integrated into the testing apparatus. Figure 5 illustrates an experimental scenario depicting pig kidney tissue compression using forceps leaves.

4.   Results and algorithm evaluation

4.1.   Analysis of compression experiment results

Based on the obtained experimental data on compression, a preliminary analysis was conducted on the mechanical properties of pig kidney tissue. The temporal pressure curve is depicted in Figure 6.

As illustrated in Figure 6, the stress of pig kidney tissue under static load can be categorized into two distinct stages. In the initial stage, namely from O to 𝐺₀, the pressure exhibits a non-linear increase over time until it reaches its peak value 𝐺₀. This initial phase of rapid growth reflects the immediate elastic response of the organization and is referred to as the stress response phase. In the transition stage from 𝐺₀ to 𝐺₁, the pressure gradually decreases over time and eventually reaches a stable state. At 𝐺₀𝐺₁, the curve demonstrates a decreasing pressure trend with respect to time, indicating that the tissue undergoes relaxation under continuous stress. This stage signifies the gradual adaptation of the material to applied stress and is characteristic of stress relaxation. Although the relaxation process can theoretically extend for several hours until complete tissue relaxation is achieved, this study specifically focuses on the initial phase of relaxation, i.e., the stress variations over a brief time period. During the experiment, the duration of the relaxation stage was less than 60 seconds, yet it yielded a significant effect on tissue relaxation.

This study focuses on the modeling and optimization of stress segments exhibiting hyperelastic behavior during compression in the stress response phase. The influence of experimental parameters, such as press speed and indenter's accessible area, on the applied pressure during interaction with soft tissue is thoroughly investigated and analyzed. By constructing a mechanical model based on collected experimental data, we accurately describe and predict the behavior of soft tissue under compressive forces.

4.1.1.   Influence analysis of the contact area of indenter

During the compression experiment, precise control of indenter movement speed was achieved using computer software. The compression speeds were set at 0.5, 1, 1.5, and 2 mm/s to simulate the compression of diverse biological tissues with different contact areas. Each indenter continuously compressed pig kidney tissue at its corresponding speed until reaching a preset compression depth, after which the compression was halted to record data. This allowed for obtaining the relationship between pressure exerted by three distinct forceps indenters on pig kidney tissue and compression depth under various loading speeds, as depicted in Figure 7.

As shown in Figure 7, the relationship between the pressure exerted by the clamp indenter with different contact area and the compression depth under constant speed is analyzed. The findings demonstrate a consistent increase in pressure with an expanding contact area of the indenter, indicating a discernible pattern. Specifically, larger contact areas result in higher peak pressures applied to pig kidney tissue. This phenomenon can be attributed to increased deformation volume of pig kidney tissue during compression due to larger contact areas, leading to greater strain. Considering the viscoelastic properties inherent in pig kidney tissue, this translates into a substantial increase in pressure when interacting with an indenter featuring a larger contact area at equivalent compression depths.

4.1.2.   Influence analysis of pressing speed

To accurately assess the influence of pressing speed on compression force, we maintained a constant contact area for the indenter while varying the compression speed, as depicted in Figure 8.

The pressure-compression depth relation curve in Figure 8 reveals that, under identical conditions, an increase in compression speed results in a strengthened interaction between the indenter and pig kidney tissue, consequently elevating the peak force value. This phenomenon signifies that higher compression speeds amplify the impact force exerted by the indenter on the structure, leading to more pronounced structural deformation within a shorter duration and subsequently generating augmented pressure.

Through comparative analysis of the data presented in Figures 7 and 8, it was observed that porcine kidney tissue exhibited similar rates of force change when pressure was applied by indenters with different contact areas at a fixed compression speed. However, altering the compression speed while maintaining a constant contact area resulted in significant differences in the rate of force change. This finding suggests that during the force-response phase of the compression experiment, the impact of compression speed on the force experienced by pig kidney tissue is more critical than that of contact area size.

4.2.   Analysis of model prediction results

In this study, to assess the prediction efficiency of the SSA-BP neural network model, we employed two classical neural network prediction models for comparison: the standard BP neural network and the GA-BP (Genetic Algorithm optimized BP) neural network. All models were evaluated on an identical dataset to ensure impartiality.

As a model capable of mapping multi-dimensional functions, the BP neural network possesses inherent advantages in addressing complex relationship analysis. In our experimental setup, the input layer comprises three neurons corresponding to the compression depth, compression speed, and contact area of the indenter. The number of neurons in the hidden layer was determined using an empirical formula, resulting in a final network structure of 3-10-10-1. The learning rate is set at 0.0001 with an expected prediction accuracy of 10e-8 and a maximum iteration limit of 5000. Moreover, we specify the tansig function as the transfer function between the input layer and hidden layer while employing the purelin function as the transfer function between hidden layer and output layer. During the training process, we utilize the traindx algorithm as our chosen training method.

The GA-BP neural network models employ genetic algorithms to optimize the initial weights and thresholds of the network. Key parameters encompass a population size of 45 individuals, a maximum number of genetic iterations set at 55, a generation gap value of 0.85, a crossover probability of 0.6, and a mutation probability amounting to 0.022.

The SSA-BP neural network model employs the SSA for optimizing the network parameters. The parameter configuration of the model includes a population size of 20, a maximum iteration count of 30, a discoverer's share in the population set at 15%, and a maximum safety threshold limited to 0.7.

The present study compares and analyzes the root mean square error (RMSE) iteration of the three distinct models during the training process, with the corresponding results presented in Figures 9–11. The error curve of the SSA-BP model (Figure 11) reveals that it achieves the lowest RMSE on both the validation and test sets at the 36th iteration, indicating superior convergence performance compared to GA-BP and standard BP models. The error curve of the GA-BP model, in contrast, exhibits a tendency to plateau after 15 iterations, implying a potential convergence towards a local optimum solution. This outcome underscores the efficacy of SSA optimization strategies in expediting the training process of BP neural networks and showcasing notable advantages in achieving rapid convergence towards lower error levels.

In order to evaluate the training efficacy of the aforementioned prediction model, we compare the predicted data from the experimental sample with the actual experimental data. Figure 12 illustrates the test results obtained using SSA-BP, GA-BP, and BP neural network models. It is evident that optimizing the BP neural network with SSA has significantly enhanced its predictive performance, resulting in a higher correlation between optimized predictions and actual data compared to those generated by the GA-BP model. The comparison of absolute error (AE) among SSA-BP, GA-BP, and BP neural networks is illustrated in Figure 13. It can be observed that the initial network error is below 0.15 N, while the GA-optimized BP network achieves an error rate below 0.1 N and the SSA-optimized BP network attains an even lower error rate below 0.05 N. These results demonstrate that the SSA-BP neural network model exhibits excellent predictive performance and successfully meets the desired target.

To ensure the reliability of simulation results, three prediction models were compared and analyzed based on their performance indexes, which included RMSE, MSE, MAE and SSE. Generally speaking, lower values of these indicators indicate better predictive performance and higher model accuracy. The GA-BP and SSA-BP neural network models exhibit significant improvement in all error indicators when compared to the standard BP model, as depicted in Figure 14. Notably, the SSA-BP model demonstrates the most substantial reduction in errors. The coefficient of determination (R2) serves as a crucial metric for assessing the efficacy of model fitting to a given dataset. Notably, the SSA-BP neural network exhibits the highest R2 value, indicating superior data fitting capability. Consequently, the SSA-BP model demonstrates enhanced predictive capability compared to other comparative models.

5.   Conclusions

The present study aims to investigate the force feedback in minimally invasive surgery, with a specific focus on the intricate interaction between surgical instruments and delicate biological soft tissues. In order to address the issue of inadequate clamping force feedback mechanisms in existing minimally invasive surgical robot systems, this study proposes a clamping force detection scheme based on clamp blade parameters. Through a series of compression tests conducted on isolated pig kidney tissue using a universal test machine, the relationship between pressure and compression depth, compression speed, and contact area of the indenter is thoroughly analyzed, leading to the establishment of a mechanical model. This model utilizes an SSA-optimized BP neural network for accurate estimation and prediction of clamping force during surgery. A comparative analysis with traditional BP models and GA-BP models reveals that the SSA-BP model outperforms both in terms of prediction accuracy and convergence speed. Notably, when considering key performance indicators such as the RMSE, MSE, MAE, and SSE, the SSA-BP model demonstrates superior predictive ability and higher degree of fit.

In summary, the main conclusions of this study are as follows:

1) The key factors influencing the clamping force of surgical instruments were determined through rigorous experimentation, providing a solid empirical foundation for the development of mechanical models.

2) The proposed SSA-BP neural network model exhibits remarkable advantages in accurately predicting force feedback, thereby enhancing its predictive accuracy.

3) Simulation results validate the potential of the SSA-BP model in significantly improving the precision of clamping force prediction within minimally invasive surgical robot systems.

Future work will primarily focus on enhancing the model's generalization capabilities and validating it across a broader range of biological soft tissues. Furthermore, there will be an exploration of integrating this predictive model into existing minimally invasive surgical robot systems to enhance their force-feedback mechanisms and improve overall surgical safety and efficiency.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This paper is supported by National Natural Science Foundation of China under grant No. 52305066.

Conflict of interest

The authors declare there is no conflict of interest.