1. Introduction

Lyme disease accounts for over 90$\%$ of all reported vector-borne disease in the United States. Its current invasive spread in the eastern U.S. constitutes a major public health concern [1,6]. In the eastern United States, Lyme disease is caused by the bacterium Borrelia burgdorferi, with the blacklegged tick Ixodes scapularis serving as the principal vector. B. burgdorferi-infected I. scapularis are found at highest densities in endemic foci in the Northeast and upper Midwestern United States. However, increasing incidence of human cases is related, in part, to the ongoing geographical spread of ticks into new areas such as Michigan, Indiana, Ohio and Virginia (Hahn et. al. [9]).

Ticks are capable of moving only very short distances independently, so their fast and large scale spatial spread cannot be attributed solely to their own mobility. Rather, large-scale changes in tick distribution arise as a consequence of the movement of ticks by the vertebrate hosts to which they attach while feeding (see, e.g., [4,5,10,15]). Among such hosts are, in the order of the distances they can move, white-footed mice Peromyscus leucopus, white-tailed deer Odocoileus virginianus, and some migratory birds. Mice can be infected by this bacterium and therefore can transmit the pathogen, and can also transport the tick nymphs. In [4], a reaction diffusion system is proposed to model the advance of the natural infection cycle mediated by the white-footed mouse. Although white-tailed deer diffusion is also mentioned in the model, since the deer cannot be infected and accordingly do not transmit the bacterium the focus of [4] is on the transmission dynamics, the role of deer diffusion in the spatial spread of the pathogen is not discussed in detail in [4]. In relation to birds, in addition to the works [3,18], there have been some works that quantitatively model the role of bird migration in the tick's range expansion, see, e.g., [23].

This paper focuses on the role of white-tailed deer in spreading the ticks. Over the past 50 years, white-tailed deer populations have undergone explosive population growth due to reversion of agricultural lands to forest and restrictions on hunting. This expanding deer population is believed to have facilitated blacklegged tick expansion throughout the Northeast and Midwest [2]. To understand this, we first point out an important difference between birds and deer in transporting I. scapularis and B. burgdorferi. On the one hand, birds carrying the infected immature stages of the tick are capable of traveling longer distances than deer. On the other hand, if immature ticks dropping from birds are to establish a new population they must survive one or two moults and then find a mate, which will be unlikely if they are dropped far from existing populations. In contrast, during fall deer will be carrying numerous already-mated female ticks, each of which becomes engorged with blood while on the deer and then falls to the ground ready to lay approximately 2000 eggs that can form the basis of a new tick population at that location. This observation seems to suggest that deer play a more important role in the tick's range expansion in regions inhabited by white-tailed deer.

In this study we use a spatial model to quantitatively investigate the role of white-tailed deer dispersal in the spatial spread of I. scapularis (and hence B. burgdorferi). Our model combines age structure with the dispersal of deer leading to a system with two time delays and spatial nonlocality resulting from the dispersal of the deer when the adult ticks are attached to them enjoying blood meals. We will begin, in the next section, with a detailed derivation of the model.

---

2. Model formulation

To assess the rate at which deer can transport blacklegged ticks into new areas, we develop a differential equation model with spatial effects that describes the stage-structured tick population and its transport by deer. Blacklegged ticks typically undergo a 2-year life cycle in which the larvae quest for a host (typically a small mammal or bird), and if successful feed for several days, drop back to the ground, and later moult into a nymph. The nymph then quests, feeds and moults -again typically on a small mammal. The final adult life stage (which is male or female) then quests and feeds (typically on a deer), falls to the ground when fully engorged and then produces approximately $2000$ eggs that hatch into the next generation of larvae.

The mouse population (which feeds the immature ticks) and the deer population (which feeds the adult ticks) are assumed to be homogeneous and constant over time in both the tick-infested and tick-free regions. Mouse home ranges are much smaller than those of deer, so the only significant movement of ticks is by deer transporting adult females while they feed. Because of this, and for simplicity, we assume that larvae and nymphs do not disperse. Since the average time a tick spends attached to a deer is around one week, the relevant deer movements are assumed to be those undertaken in the course of each deer's normal home range activity, rather than long-distance directional movements associated with natal dispersal or seasonal migration.

Consider a spatial domain $\Omega\subset\mathbb{R}^n$, which at this point could be either finite or infinite. Let $L(x, t)$ and $N(x, t)$ be the population densities of larvae and nymphs at time $t$, location $x\in\Omega$. Denote by $A_q(x, t)$ and $A_f(x, t)$ the populations of questing adults and female fed adults respectively. Taking into account the above assumptions and scenarios, we propose the following mathematical model for $t \ge 0$, $x\in\Omega$:

$\left\{ \begin{split} & \frac{\partial L(x, t)}{\partial t} = b r_4{\rm e}^{-d_4\tau_1}A_f(x, t-\tau_1)-d_1L(x, t)-r_1 L(x, t), \\ & \frac{\partial N(x, t)}{\partial t} = r_1g(L(x, t))-d_2N(x, t)-r_2N(x, t), \\ &\frac{\partial A_q(x, t)}{\partial t} = r_2N(x, t)-d_3A_q(x, t)-r_3A_q(x, t), \\ &\frac{\partial A_f(x, t)}{\partial t} = \frac{r_3}{2}\int_{\Omega}{k(x, y){\rm e}^{-d_3\tau_2}A_q(y, t-\tau_2)\, dy} -r_4A_f(x, t) -d_4A_f(x, t), \end{split} \right.$

(1)

where the parameters are defined in Table 1. The table also gives the values of the parameters for the stage-structured components of the model which were all, except for $\tau_1$, used in the non-spatial model for Ixodes scapularis life cycles in [7] which were adopted from the earlier work [17]. In [17], $\tau_1$ was taken as the time delay for pre-oviposition and was determined by $1300 \times c^{ -1.42}$ where $c$ is the temperature in celsius, and hence, when $c$ varies between $15^o$ and $30^o$, $\tau_1$ will be between 27.80 and 10.40 days. For simulation convenience, we take $\tau_1 = 20$ days in this paper. In [7], $\tau_1$ was given the range of 20-200 days.

The structure of system (1) can be visualized with the help of the diagram in Fig. 1.

A very important aspect of model (1) is the term with the integral, which models the transport of adult ticks by deer. Note that $A_q$ and $A_f$ are respectively the numbers of questing adults and female adults that are already fed and are no longer attached to deer. There is no variable in system (1) representing the actual number of adult ticks that are attached to the deer. Such a variable is unnecessary in system (1), since it is already a closed system determining the variables $L$, $N$, $A_q$ and $A_f$. However, a variable representing the ticks attached to deer is useful for explaining the derivation of the integral term in (1), which is the rate at which female adults drop off the deer after feeding. Next, we present a detailed derivation of that integral term. We let $u_{\rm deer}(x, t, a)$, where $x\in\Omega\subset\mathbb{R}^n$ is a vector if $n\geq 2$, be the population density of ticks that are attached to deer. Here $a$ is an age variable representing age since attaching to a deer (not age since the tick's birth). We assume that $u_{\rm deer}(x, t, a)$ satisfies the standard McKendrick-von Foerster equation for an age-structured population:

$\begin{split} &\left(\frac{\partial}{\partial t}+\frac{\partial}{\partial a}\right) u_{\rm deer}(x, t, a) = -d_3 u_{\rm deer}(x, t, a)+D\nabla^2 u_{\rm deer}(x, t, a), \\ & \, \, \, \mbox{for} \, \, \, x\in\Omega, \;\;a\in(0, \tau_2), \;\;t>0, \end{split}$

(2)

where $D>0$ is the diffusion coefficient of the deer, since the ticks under discussion are attached to deer. The population of ticks attached to deer at $(x, t)$ is $A_{\rm deer}(x, t)$, given by

$A_{\rm deer}(x, t) = \int_0^{\tau_2}u_{\rm deer}(x, t, a)\, da.$

(3)

Differentiating (3) and using (2) gives

$\frac{\partial A_{\rm deer}(x, t)}{\partial t} = u_{\rm deer}(x, t, 0)-u_{\rm deer}(x, t, \tau_2)-d_3 A_{\rm deer}(x, t) +D\nabla^2 A_{\rm deer}(x, t).$

(4)

The rate at which ticks drop off the deer after feeding is $u_{\rm deer}(x, t, \tau_2)$, and we shall show that this term equals the integral term in the fourth equation of (1). To aid in the calculation of $u_{\rm deer}(x, t, \tau_2)$, define

$u_{\rm deer}^{\xi}(x, a) = u_{\rm deer}(x, a+\xi, a)e^{d_3 a}.$

(5)

Differentiating with respect to $a$, and using (2),

$\frac{\partial u_{\rm deer}^{\xi}(x, a)}{\partial a} = D\nabla^2 u_{\rm deer}^{\xi}(x, a), \;\;\;\;x\in\Omega.$

This is the heat equation, and its solution can be expressed in the form

$u_{\rm deer}^{\xi}(x, a) = \int_{\Omega}K(x, y, a)u_{\rm deer}^{\xi}(y, 0)\, dy$

(6)

where the Green's function $K(x, y, a)$, a non-negative function, satisfies

$\frac{\partial K(x, y, a)}{\partial a} = D\nabla_x^2 K(x, y, a), \;\;\;\;K(x, y, 0) = \delta(x-y)$

(7)

and the boundary conditions to which the deer are subjected at $\partial\Omega$. Here, $\delta$ is the Dirac delta function and $\nabla_x^2$ is the Laplacian operator computed with respect to the first argument $x\in\Omega$ of $K(x, y, a)$, with $y$ treated as constant (recall $x$ and $y$ are vectors unless $\Omega$ is a one-dimensional domain). Using (5) and (6), and setting $a = \tau_2$, $\xi = t-\tau_2$,

$u_{\rm deer}(x, t, \tau_2) = e^{-d_3\tau_2}\int_{\Omega}K(x, y, \tau_2)u_{\rm deer}(y, t-\tau_2, 0)\, dy.$

But $u_{\rm deer}(x, t, 0)$ is the rate at which questing adults attach to deer. The term representing this is the last term in the third equation of (1), and therefore

$u_{\rm deer}(x, t, 0) = r_3A_q(x, t).$

Therefore

$u_{\rm deer}(x, t, \tau_2) = e^{-d_3\tau_2}\int_{\Omega}K(x, y, \tau_2)r_3A_q(y, t-\tau_2)\, dy.$

After the insertion of a factor $\frac{1}{2}$, since only the females will lay eggs, we complete the derivation of the integral term in the fourth equation of (1) with

$k(x, y) = K(x, y, \tau_2).$

The kernel $k(x, y)$ accounts for the probability that a questing adult that attaches to a deer at location $y$ will be engorged after $\tau_2$ time units and drop to the ground at location $x$. For some particular domains $\Omega$ and boundary conditions it is possible to solve (7) to find $K(x, y, a)$, and hence $k(x, y)$ in (1), explicitly. For example, if $\Omega = [0, l]$, with homogeneous Neumann (zero flux) boundary conditions, then $K_x(0, y, a) = K_x(l, y, a) = 0$ and

$k(x, y) = K(x, y, \tau_2) = \frac{1}{l}\left[1+ \sum \limits_{n = 1}^{\infty } \Big\{\cos \frac{n \pi}{l}(x-y)+\cos \frac{n \pi}{l}(x+y) \Big\} e ^{-D(n \pi/l)^2\tau_2 }\right].$

If $\Omega = [0, l]$, with homogeneous Dirichlet boundary conditions, then

$k(x, y) = \frac{1}{l}\sum\limits_{n = 1}^\infty \Big\{\cos\frac{n\pi}{l}(x-y)- \cos\frac{n\pi}{l}(x+y)\Big\} e^{-D(n\pi/l)^2\tau_2 }.$

We are interested mainly in the case when $\Omega = (-\infty, \infty)$, which may provide a reasonable approximation for a long and narrow domain. For this case,

$k(x, y) = \Gamma (x-y),\, \, \, \, \mbox{where} \, \, \, \, \Gamma (z) : = \frac{1}{\sqrt{4 D \tau_2 \pi }}e^{-\frac{z^2}{4 D\tau_2}}$

(8)

which was derived in [12,19].

We point out that, just recently, starting from a version of the McKendrick-von Foerster equation without spatial effects but with temporal periodicity, Liu et al [14] also derived a periodic model with age structure for a tick population. A threshold dynamics result is obtained for the model in [14].

To prevent the tick population from increasing to unrealistic levels, density dependence is incorporated into model (1) through a simple nonlinear relationship between questing larvae and questing nymphs. The biological basis for this relationship is that there should be an upper limit to the number of larvae that the mouse population is able to feed -an equivalent relationship was assumed in [21]. This leads us to propose the following expression for the function $g(L)$ in (1):

$g(L) = \left\{ \begin{array}{ll} \displaystyle{\frac{N_{cap}}{L_{cap}}}\, L \, \, \, \, \mbox{for} \, \, \, L \in [0, L_{cap}], \\\\ N_{cap} \, \, \, \, \mbox{for} \, \, \, L \in [L_{cap}, \infty). \end{array} \right.$

(9)

The function $g(L)$ in (9) is not differentiable at $L = L_{cap}$. For mathematical convenience, we adopt the following alternative:

$g(L) = \frac{N_{cap}k_2L}{k_1+k_2L} = \frac{N_{cap}L}{k_1/k_2+L} = \frac{N_{cap}L}{h+L},$

(10)

which is smooth and yet captures the main features of the function given by (9). In the remainder of this paper, we always use (10) for $g(L)$, with the parameter $h$ adjusting $g'(0) = N_{cap}/h$.

For the majority of this paper we have in mind model (1) for $x \in (-\infty, \infty)$, with the nonlinear function given by (10) and the kernel $k(x, y)$ by (8). In Section 3 we justify the well-posedness of the model by verifying the positivity and boundedness of all solution variables, identify the tick's basic reproduction number $\mathcal{R}_0$, addressing the stability of the extinction steady state and discussing the existence and stability of a positive constant steady state when $\mathcal{R}_0>1$. In Section 4 we focus on traveling wave front solutions that connect the extinction equilibrium with the positive equilibrium. The minimum wave speed of such traveling wave fronts is closely related to the spatial spread rate of the tick population and therefore is of great significance. By analyzing the characteristic equation of the linearization of the model at the extinction equilibrium, we find a critical value $c^*$ which is proved to be a lower bound of the minimal wave speed in the sense that there is no traveling wave front with speed $c<c^*$. Dependence of $c^*$ on the dispersion rate $D$ and productive rate $b$ is also numerically explored. In Section 5, guided by the results from Section 4, we numerically explore the existence of traveling wave fronts and investigate the spread rate. We present some simulation results which suggest that $c^*$ is not only the minimum wave speed but also the spread rate for the tick population. Therefore, the dependence of $c^*$ on the dispersion rate $D$, which is numerically explored in Section 4, may help evaluate the role of the white tailed deer in the geographical spread of the ticks. We conclude the paper with Section 6, in which we summarize the main results and discuss some possible future research projects related to this work. Since the model contains a spatial non-local term and two time delays, finding numerical solutions to the traveling wave equations is challenging. For the readers' convenience, we include an appendix summarizing the details of the numerical methods used.

---

3. Analysis of the model

---

3.1. Well-posedness

Associated to (1) are the following biologically and mathematically meaningful initial conditions:

$\left\{ \begin{split} &L(x, 0), \, \, N(x, 0)\, \, \mbox{are continuous for} \, \, x \in \Omega \, \, \mbox{with}\, \, L(x, 0) \ge 0, \, \, \, N(x, 0) \ge 0; \\ &A_q(x, s)\, \, \mbox{is continuous for} \, \, (x, s) \in \Omega \times [-\tau_2, 0] \, \, \mbox{with} \, \, A_q(x, s) \ge 0; \\ & A_f(x, s)\, \, \mbox{is continuous for} \, \, (x, s) \in \Omega \times [-\tau_1, 0] \, \, \mbox{with}\, \, A_f(x, s) \ge 0. \end{split} \right.$

(11)

Using the method of steps, one can easily see that the initial value problem (1)-(11) has a unique solution for $t \in [0, t_{\infty})$ for some $t_{\infty} >0$. Furthermore, using the method of variation of parameters in (1), one obtains

$\left\{ \begin{split} & L(x, t) = L(x, 0)e^{-(d_1+r_1)t}+br_4e^{-d_4\tau_1}\int_{0}^{t}A_f(x, s-\tau_1)e^{(d_1+r_1)(s-t)}\, ds, \\ & N(x, t) = N(x, 0)e^{-(d_2+r_2)t}+r_1N_{cap}\int_{0}^{t}\frac{L(x, s)}{h+L(x, s)}e^{(d_2+r_2)(s-t)}\, ds, \\ &A_q(x, t) = A_q(x, 0)e^{-(d_3+r_3)t}+r_2\int_{0}^{t}N(x, s)e^{(d_3+r_3)(s-t)}\, ds, \\ &A_f(x, t) = A_f(x, 0)e^{-(d_4+r_4)t} \\ & \qquad\qquad\qquad +\frac{r_3}{2}e^{-d_3\tau_2}\int_{0}^{t}\int_{\Omega}k(x, y) A_q(y, s-\tau_2)e^{(d_4+r_4)(s-t)}\, dy\, ds. \end{split} \right.$

(12)

Let $\tau = \min\{\tau_1, \tau_2\}$. By the initial condition (11), we have $L(0, x)\ge 0$, $N(0, x)\ge 0$, $A_q(\theta, x)\ge 0$ for $\theta \in [-\tau_2, 0]$, and $A_f(\theta, x)\ge 0$ for $\theta\in[-\tau_1, 0]$. Thus all the second terms on the right hand sides of the above equations are nonnegative for $t \in(0, \tau]$. If $L(0, x)>0$, then from the first equation we have $L(t, x)>0$ for $t\in[0, \tau]$, and a recursive argument yields that $L(t, x)>0$ actually for all $t>0$. This will also consecutively lead to $N(t, x)>0$, $A_q(t, x)>0$ and $A_f(t, x)>0$ for $t>0$. Moreover, we can see that the positivity of any one of the four components at $t = 0$ is sufficient to ignite the positivity of all components of the corresponding solution for $t>0$.

Next, we prove an important property of the kernel $k(x, y)$ in (1).

Proposition 1. If $\Omega = (-\infty, \infty)$, or if $\Omega\subset\mathbb{R}^n$ is finite and homogeneous Neumann boundary conditions are applied, then

$\int_{\Omega}k(x, y)\, dx = 1, \;\;\;\;for \;\;all \;\;y\in\Omega.$

If $\Omega$ is finite with homogeneous Dirichlet boundary conditions, then

$\int_{\Omega}k(x, y)\, dx<1, \;\;\;\;for \;\;all \;\;y\in\Omega.$

Proof. When $\Omega = (- \infty, \infty)$, the conclusion is a result of (8) and the property of normal distribution. Now assume $\Omega \subset \mathbb{R}^n$ is bounded and consider the quantity $\int_{\Omega}K(x, y, a)\, dx$. Recall that $K$ satisfies (7). In the case of homogeneous Neumann boundary conditions, $\nabla_xK(x, y, a)\cdot \mathbf{n} = 0$ on $\partial\Omega$ and therefore

$\frac{\partial}{\partial a}\int_{\Omega}K(x, y, a)\, dx = D\int_{\Omega}\nabla^2_xK(x, y, a)\, dx = D\int_{\partial\Omega}\nabla_x K(x, y, a)\cdot \mathbf{n}\, dS = 0$

where $\mathbf{n}$ is the outward pointing unit normal to $\partial\Omega$ and $dS$ is a surface element. Hence, if $y\in\Omega$,

$\int_{\Omega}k(x, y)\, dx = \int_{\Omega}K(x, y, \tau_2)\, dx = \int_{\Omega}K(x, y, 0)\, dx = \int_{\Omega}\delta(x-y)\, dx = 1.$

In the case of homogeneous Dirichlet boundary conditions we have $K(x, y, a) = 0$ for $x\in\partial\Omega$, yet we know $K(x, y, a)>0$ inside $\Omega$, for all $a>0$. Therefore $\nabla_xK(x, y, a)\cdot \mathbf{n}\leq 0$ on $\partial\Omega$ in this case and so $\int_{\Omega}K(x, y, a)\, dx$ decreases with $a$. Therefore, this time we have $<$ replacing $=$ in the middle element of the above, with the consequence that $\int_{\Omega}k(x, y)\, dx<1$. The proof is complete.

Next, we show that the solution is bounded for $x \in \Omega$ and $t \in [0, t_{\infty})$. Firstly, applying the boundedness of $g(L)$ to the second equation of (1), we obtain

$\frac{\partial N(x, t)}{\partial t} \le r_1 N_{cap}-(d_2+r_2)N(x, t).$

This implies that

$\limsup\limits_{t \to \infty} N(x, t) \le \frac{r_1 N_{cap}}{d_2+r_2}, \, \, \, \, \mbox{for all} \, \, \, \, x \in \Omega,$

proving boundedness of $N(x, t)$. Applying the same argument to the other three equations of (1), in the order of $N \to A_q \to A_f \to L$, we conclude that $L(x, t), \, \, A_q(x, t)$ and $A_f(x, t)$ are all bounded for $x \in \Omega$ and $t \in [0, t_{\infty})$.

---

3.2. Extinction steady state and its stability

Irrespective of the domain $\Omega$ or boundary conditions, system (1) always has the extinction steady state (trivial steady state) $E_0 = (0, 0, 0, 0)$. Linearizing (1) at $E_0$ leads to

$\left\{ \begin{split} \frac{\partial u_1(x, t)}{\partial t}& = br_4e^{-d_4\tau_1}u_4(x, t-\tau_1)-(d_1+r_1)u_1(x, t), \\ \frac{\partial u_2(x, t)}{\partial t}& = \frac{r_1N_{cap}}{h}u_1(x, t)-(d_2+r_2)u_2(x, t), \\ \frac{\partial u_3(x, t)}{\partial t}& = r_2u_2(x, t)-(d_3+r_3)u_3(x, t), \\ \frac{\partial u_4(x, t)}{\partial t}& = \frac{r_3}{2}\int_{\Omega}k(x, y)e^{-d_3\tau_2}u_3(y, t-\tau_2)\, dy-(d_4+r_4)u_4(x, t). \end{split} \right.$

(13)

Consider the case $\Omega = (-\infty, \infty)$, or a bounded $\Omega \subset \mathbb{R}^n$ with homogeneous Neumann boundary conditions. Tracking the average time and recruitment during each stage in (13), one obtains the basic reproduction number $R_0$ of the model:

$\begin{array}{l} R_0& = & \frac{b r_4 e^{-d_4 \tau_1}}{d_1+r_1} \, \cdot\frac{(r_1/h) N_{cap}}{d_2+r_2} \, \cdot \frac{r_2}{d_3+r_3} \, \cdot \frac{(r_3/2)e^{-d_3 \tau_2}}{d_4+r_4} \\ & = & \frac{N_{cap}b}{2h}e^{-(d_3\tau_2+d_4\tau_1)} \prod\limits_{i = 1}^4\frac{r_i}{d_i+r_i}.\end{array}$

(14)

From the biological interpretation of $R_0$, we anticipate that $E_0$ will be locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$. We prove this by analyzing the linear stability of the extinction steady state of (13).

Substituting the ansatz $u_i(x, t) = e^{\lambda t} \psi_i(x)$ into (13), we obtain the following eigenvalue problem:

$\left\{ \begin{split} &\lambda \psi_1(x) = br_4e^{-d_4\tau_1}e^{-\lambda\tau_1}\psi_4(x)-(d_1+r_1)\psi_1(x), \\ &\lambda \psi_2(x) = \frac{r_1N_{cap}}{h}\psi_1(x)-(d_2+r_2)\psi_2(x), \\ &\lambda \psi_3(x) = r_2\psi_2(x)-(d_3+r_3)\psi_3(x), \\ &\lambda \psi_4(x) = \frac{r_3}{2}e^{-d_3\tau_2}e^{-\lambda\tau_2}\int_{\Omega}k(x, y)\psi_3(y)\, dy-(d_4+r_4)\psi_4(x). \end{split} \right.$

(15)

We shall show that the dominant eigenvalue $\lambda^*$ of the linearised system is a real number. The sign of $\lambda^*$ determines the stability of the extinction equilibrium $E_0$: when $\lambda^*<0$, $E_0$ is asymptotically stable; and when $\lambda^*>0$, $E_0$ is unstable. If the domain $\Omega = (-\infty, \infty)$, or if $\Omega$ is finite with homogeneous Neumann boundary conditions, then the sign of $\lambda^*$ depends solely on the value of $R_0$. The stability result for these cases can be formulated as follows.

Proposition 2. If $\Omega = (-\infty, \infty)$, or if $\Omega\subset\mathbb{R}^n$ is finite and homogeneous Neumann boundary conditions are applied, then the extinction steady state $E_0 = (0, 0, 0, 0)$ of system (1) is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$, where $R_0$ is given by (14).

Proof. Let $\lambda\in\mathbb{C}$ be any eigenvalue, with $\psi_i$, $i = 1, \ldots, 4$ as introduced above. The first equation of (15) gives

$\psi_4(x) = \frac{\lambda+d_1+r_1}{br_4e^{-d_4\tau_1}e^{-\lambda\tau_1}}\psi_1(x).$

(16)

Similarly, from the second and third equations of (15),

$\psi_1(x) = \frac{(\lambda+d_2+r_2)h}{r_1N_{cap}}\psi_2(x),$

(17)

and

$\psi_2(x) = \frac{\lambda+d_3+r_3}{r_2}\psi_3(x).$

(18)

The fourth equation of (15) then yields

$\begin{split} e^{-\lambda\tau_1}e^{-\lambda\tau_2} &\int_{\Omega}k(x, y)\psi_3(y)\, dy \\ & = \frac{2h(\lambda+d_4+r_4)(\lambda+d_1+r_1)(\lambda+d_2+r_2)(\lambda+d_3+r_3)}{bN_{cap}e^{-d_4\tau_1}e^{-d_3\tau_2}r_1r_2r_3r_4}\psi_3(x), \\ & = \frac{2h\prod_{i = 1}^{4}(\lambda+d_i+r_i)}{bN_{cap}e^{-(d_3\tau_2+d_4\tau_1)} \prod_{i = 1}^4 r_i} \psi_3(x) \end{split}$

so that

$e^{-\lambda\tau_1}e^{-\lambda\tau_2} \int_{\Omega}k(x, y)\psi_3(y)\, dy = \frac{\prod_{i = 1}^{4}(\lambda+d_i+r_i)}{R_0\prod_{i = 1}^{4}(d_i+r_i)}\psi_3(x).$

(19)

Integrating with respect to $x$ over $\Omega$, changing the order of the double integral that arises, and using the first statement of Proposition 1, we obtain the characteristic equation for $\lambda$ to be

$f_1(\lambda) = f_2(\lambda)$

(20)

where

$f_1(x) = R_0e^{-(\tau_1+\tau_2)x}\prod\limits_{i = 1}^4 (d_i+r_i),$

(21)

$f_2(x) = \prod\limits_{i = 1}^4 (x+d_i+r_i).$

(22)

Noting that $f_1(x)$ is deceasing with $f_1(-\infty) = \infty$ and $f_1(\infty) = 0$, and $f_2(x)$ is a $W$ shaped function and is increasing after its largest root $- x_m = - \min \{d_i+r_i; i = 1, 2, 3, 4\}$, we know that (20) has a unique real root $\lambda^*$ on $(-x_m, \infty)$ and it is the dominant real root since $f_1(x) <f_2(x)$ for $x >\lambda^*$. We claim that $\lambda^*$ is indeed the dominant root (the root of greatest real part) of the characteristic equation (20). To this end, we let $\lambda$ be any root in $\mathbb{C}$ and show that ${\rm Re}\, \lambda\leq \lambda^*$. Indeed, taking the absolute value of (20) gives

$\begin{array}{l} R_0e^{-(\tau_1+\tau_2)({\rm Re}\, \lambda)}\prod\limits_{i = 1}^4 (d_i+r_i) & = &\prod\limits_{i = 1}^4 |\lambda+d_i+r_i| \\ & \geq&\prod\limits_{i = 1}^4 |{\rm Re}\, \lambda+d_i+r_i|, \end{array}$

that is, $f_1({\rm Re}\, \lambda)\geq f_2({\rm Re}\, \lambda)$, implying that ${\rm Re}\, \lambda\leq \lambda^*$. This claim means that the dominant root in $\mathbb{C}$ of the characteristic equation is precisely the dominant real root $\lambda^*$.

Finally, by the aforementioned properties of $f_1(x)$ and $f_2(x)$, it is obvious that $\lambda^*<0$ when $f_1(0)<f_2(0)$ (i.e. $R_0<1$) and $\lambda^*>0$ when $f_1(0)>f_2(0)$ (i.e. $R_0>1$). Thus, all eigenvalues of (13) have negative real parts when $R_0<1$, and there exists a real positive eigenvalue when $R_0>1$. Now, by Theorems 2.16 and 2.17 in Thieme [20], we conclude the stability (under $R_0<1$) and instability (under $R_0>1$), completing the proof.

Remark. The above argument fails in the case of homogeneous Dirichlet boundary conditions applied to a finite domain $\Omega$, since in that case $\int_{\Omega} k(x, y)\, dx$ is not equal to 1. However, we may still assert that if $R_0<1$ the extinction steady state is locally asymptotically stable. The reason is that for the Dirichlet problem the second statement of Proposition 1 is applicable. Taking the absolute value of (19),

$\begin{array}{l} \frac{\prod_{i = 1}^{4}|\lambda+d_i+r_i|}{R_0\prod_{i = 1}^{4}(d_i+r_i)}|\psi_3(x)| & = &e^{-({\rm Re}\, \lambda)(\tau_1+\tau_2)}\left|\int_{\Omega}k(x, y)\psi_3(y)\, dy \right| \\ & \leq&e^{-({\rm Re}\, \lambda)(\tau_1+\tau_2)}\int_{\Omega}k(x, y)|\psi_3(y)|\, dy.\end{array}$

Integrating over $x\in\Omega$ and changing the order of integration, but this time using the second statement of Proposition 1, we obtain

$\frac{\prod_{i = 1}^{4}|{\rm Re}\, \lambda+d_i+r_i|}{R_0\prod_{i = 1}^{4}(d_i+r_i)} \leq \frac{\prod_{i = 1}^{4}|\lambda+d_i+r_i|}{R_0\prod_{i = 1}^{4}(d_i+r_i)} \leq e^{-({\rm Re}\, \lambda)(\tau_1+\tau_2)}$

which implies that $f_2({\rm Re}\, \lambda)\leq f_1({\rm Re}\, \lambda)$ and therefore that ${\rm Re}\, \lambda$ belongs to an interval of values for which the graph of the quartic curve $y = f_2(x)$ lies below that of the exponential $y = f_1(x)$. However, in the situation when $R_0<1$, such intervals include only negative real numbers and it follows that ${\rm Re}\, \lambda<0$. The difference with the Dirichlet problem is that $R_0>1$ does not necessarily imply that the dominant eigenvalue $\lambda^*>0$, although an argument can be made that we do have $\lambda^*>0$ when $R_0>1$ if the domain $\Omega$ is sufficiently large. The reason is that as the domain increases in size without bound, $\int_{\Omega} k(x, y)\, dx$ approaches 1. This can be shown using a scaling argument to be found in the proof of Proposition 5.1 of Gourley and Ruan [8]. In fact, if $\Omega$ is bounded and homogeneous Dirichlet boundary conditions are applied on $\partial \Omega$, $R_0$ as defined in (14) is no longer the basic reproduction number, though it is still an important parameter relevant to the stability of the extinction steady state. For the Dirichlet problem the basic reproduction number is the right hand side of (14) multiplied by $\hat{K}$, where $\hat{K}$ is the spectral radius of the linear operator $F: X_0 \to X_0$ defined by

$(F\phi)(x) = \int_{\Omega} k(x, y) \phi (y)\, dy,\;\;\;\; x \in \Omega$

(23)

where $X_0 = \left\{ \phi \in C(\Omega, \mathbb{R}); \phi |_{\partial \Omega} = 0\right\}$.

---

3.3. Persistence steady state and its stability

In the case $\Omega = ( -\infty, \infty)$, or $\Omega \subset \mathbb{R}^n$ with homogeneous Neumann boundary conditions on $\partial\Omega$, we have seen from Subsection 3.2 that, when $\mathcal{R}_0>1$ (equivalently, $\lambda^*>0$), the extinction steady state $E_0$ becomes unstable. In this case, straightforward calculations show that there exists a positive steady state $E^+ = (L^+, N^+, A^+_q, A^+_f)$ given by

$L^+ = h(R_0-1), \;\;N^+ = \frac{d_3+r_3}{r_2}A^+_q, \;\;A^+_q = \frac{d_4+r_4}{\frac{r_3}{2}e^{-d_3\tau_2}}A^+_f,\;\; A^+_f = \frac{d_1+r_1}{br_4e^{-d_4\tau_1}}L^+.$

When this persistence (positive) steady state exists, it is locally asymptotically stable. The arguments are similar to those just described for studying the linear stability of the extinction steady state. Linearizing system (1) at $E^+ = (L^+, N^+, A^+_q, A^+_f)$, we obtain

$\left\{ \begin{split} &\frac{\partial v_1(x, t)}{\partial t} = br_4e^{-d_4\tau_1}v_4(x, t-\tau_1)-(d_1+r_1)u_1(x, t), \\ &\frac{\partial v_2(x, t)}{\partial t} = \frac{r_1N_{cap}}{hR^2_0}v_1(x, t)-(d_2+r_2)v_2(x, t), \\ &\frac{\partial v_3(x, t)}{\partial t} = r_2v_2(x, t)-(d_3+r_3)v_3(x, t), \\ &\frac{\partial v_4(x, t)}{\partial t} = \frac{r_3}{2}\int_{\Omega}k(x, y)e^{-d_3\tau_2}v_3(y, t-\tau_2)\, dy-(d_4+r_4)v_4(x, t). \end{split} \right.$

(24)

This linear system is the same as (13) except that $h$ is replaced by $\hat{h} = h R_0^2$. Thus, a composed parameter $\hat{R}_0$ obtained by replacing $h$ with $hR_0^2$, that is $\hat{R}_0 = \frac{1}{R_0^2} R_0 = \frac{1}{R_0}$, determines the stability of $E^+$: if $R_0>1$ (i.e., $\hat{R}_0<1$) then $E^+$ is not only biologically meaningful but also locally asymptotically stable.

---

4. Traveling wave solutions and the spreading speed

In this section, we consider $\Omega = ( -\infty, \infty)$ and explore the existence of traveling wave solutions of (1), which are solutions of the form

$L(x, t) = \varphi_1(x+ct), \, \, N(x, t) = \varphi_2(x+ct), \, \, A_q(x, t) = \varphi_3(x+ct), \, \, A_f(x, t) = \varphi_4(x+ct).$

Here, $\varphi = (\varphi_1, \varphi_2, \varphi_3, \varphi_4) \in C^2({\mathbb R}, {\mathbb R}^4)$ is called the profile of the traveling wave, $s: = x+ct$ is the moving variable, and $c>0$ is the wave speed. Substituting this form of solution into system (1), we find that $\varphi = (\varphi_1, \varphi_2, \varphi_3, \varphi_4)$ satisfies

$\left\{ \begin{split} &c\varphi'_1(s) = br_4e^{-d_4\tau_1}\varphi_4(s-c\tau_1)-(d_1+r_1)\varphi_1(s), \\ &c\varphi'_2(s) = r_1g(\varphi_1(s))-(d_2+r_2)\varphi_2(s), \\ &c\varphi'_3(s) = r_2\varphi_2(s)-(d_3+r_3)\varphi_3(s), \\ &c\varphi'_4(s) = \frac{r_3}{2}\int_{-\infty}^{+\infty} \Gamma(z)e^{-d_3\tau_2}\varphi_3(s-z-c\tau_2)\, dz-(d_4+r_4)\varphi_4(s), \end{split} \right.$

(25)

where $\Gamma(y)$ is the Gaussian kernel given in Section 2. When $\mathcal{R}_0>1$, $E_0 = (0, 0, 0, 0)$ and $E^+ = (\varphi^+_1, \varphi^+_2, \varphi^+_3, \varphi^+_4)$ are equilibria of (25), where $\varphi^+_1 = L^+, \, \, \varphi^+_2 = N^+, \, \, \varphi^+_3 = A_q^+$ and $\varphi^+_4 = A^+_f$.

We are interested in traveling wave fronts that connect $E_0$ and $E^+$, and therefore we apply the following asymptotic boundary conditions to (25):

$\lim\limits_{s\to-\infty}\varphi_i = 0, \;\; \lim\limits_{s\to+\infty} \varphi_i(s) = \varphi^+_i, \;\;i = 1, 2, 3, 4.$

(26)

Linearizing system (25) at the trivial equilibrium $E_0$ yields the following linear system:

$\left\{ \begin{split} &c\varphi'_1(s) = br_4e^{-d_4\tau_1}\varphi_4(s-c\tau_1)-(d_1+r_1)\varphi_1(s), \\&c\varphi'_2(s) = \frac{r_1N_{cap}}{h}\varphi_1(s)-(d_2+r_2)\varphi_2(s), \\ &c\varphi'_3(s) = r_2\varphi_2(s)-(d_3+r_3)\varphi_3(s), \\ &c\varphi'_4(s) = \frac{r_3}{2}\int_{-\infty}^{+\infty} \Gamma(z)e^{-d_3\tau_2}\varphi_3(s-z-c\tau_2)\, dz-(d_4+r_4)\varphi_4(s). \end{split} \right.$

(27)

The characteristic equation associated with (27) is

$P(\lambda, c) = 0$

(28)

where

$P(\lambda, c) = \left|\begin{array}{cccc} c\lambda+d_1+r_1&0&0 &-br_4e^{-d_4\tau_1}e^{-c\tau_1\lambda}\\ -\frac{r_1N_{cap}}{h}&c\lambda+d_2+r_2&0&0\\ 0 &-r_2&c\lambda+d_3+r_3&0\\ 0 &0 &-\frac{r_3}{2}e^{-d_3\tau_2}e^{-c\tau_2\lambda}\bar k(\lambda)& c\lambda+d_4+r_4 \end{array}\right|,$

where

$\bar k(\lambda) = \int_{-\infty}^{+\infty} \Gamma(y)e^{-\lambda y}\, dy = \frac{1}{\sqrt{4D\tau_2\pi}}\int_{-\infty}^{+\infty}e^{-\frac{y^2}{4D\tau_2}}e^{-\lambda y}\, dy = e^{D\tau_2\lambda^2}.$

Evaluating the determinant on the left hand side of (28), we obtain

$\prod\limits_{i = 1}^{4}[c\lambda+(d_i+r_i)] -\frac{r_1r_2r_3r_4bN_{cap}}{2h}e^{-(d_4\tau_1+d_3\tau_2)} e^{D\tau_2\lambda^2-c(\tau_1+\tau_2)\lambda} = 0;$

that is

$\prod\limits_{i = 1}^{4}[c\lambda+(d_i+r_i)] -R_0\left[\prod\limits_{i = 1}^{4}(d_i+r_i)\right]e^{D\tau_2\lambda^2-c(\tau_1+\tau_2) \lambda} = 0.$

(29)

Generically, the behaviour of solutions of (25)-(26) at $-\infty$ is qualitatively reflected by the behaviour of solutions of (27) at $-\infty$. Note that, generically, only positive real roots of the characteristic equation (29) can lead to positive solutions of (1) that tend to $0$ as $s \to -\infty$, because a negative real root of (29) corresponds to an unbounded solution and complex roots correspond to a solution that oscillates about $0$ and therefore assumes negative values. Therefore, in order for (25)-(26) to have a positive solution (corresponding to a traveling wave front connecting $E_0$ and $E^+$), it is necessary that (29) should have at least one real positive root.

Set

$\begin{split} &H_1(\lambda, c) = \prod\limits_{i = 1}^{4}[c\lambda+(d_i+r_i)], \\ &H_2(\lambda, c) = R_0\left[\prod\limits_{i = 1}^{4}(d_i+r_i)\right]e^{D\tau_2\lambda^2-c(\tau_1+\tau_2)\lambda}. \end{split}$

Then (29) can be rewritten as $H_1(\lambda, c) = H_2(\lambda, c)$. From elementary calculus, one knows that $H_1(\lambda, c)$ is of $W$ shape but is increasing for $\lambda>0$, and $H_2(\lambda, c)$ is of $U$ shape with the minimum attained at a positive value of $\lambda$. It can be shown that there exists a $c^*>0$ such that, when $c<c^*$, $H_2(\lambda, c)> H_1(\lambda, c)$ and (29) has no real positive roots; when $c = c^*$, (29) has one real positive root $\lambda^*$; and when $c>c^*$, (29) has two real positive roots $\lambda_2 > \lambda_1 >0$. Indeed $c^*$ is given by

$c^* = \min\limits_{c>0}\left\{c: H_1(\lambda, c) = H_2(\lambda, c) \rm{\: has\: positive\: real\: roots\: with\: respect\: to\: \lambda}\right\}$

and is determined by the tangential conditions:

$H_1(\lambda, c) = H_2(\lambda, c), \;\; {\rm and }\;\; \frac{\partial H_1}{\partial \lambda}(\lambda, c) = \frac{\partial H_2}{\partial \lambda}(\lambda, c), \;\; \lambda>0.$

(30)

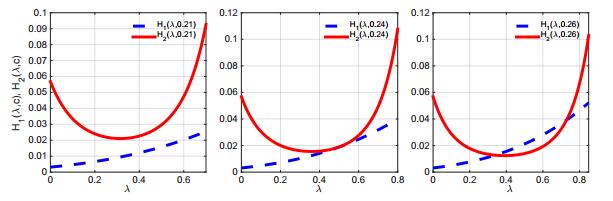
There is no explicit formula for $c^*$, but $c^*$ can be numerically computed for given values of the model parameters. To demonstrate this, we choose the baseline parameter values as: $b = 3000$, $r_1 = 0.13$, $r_2 = 0.13$, $r_3 = 0.03$, $r_4 = 0.03$, $d_1 = 0.3$, $d_2 = 0.3$, $d_3 = 0.1$, $d_4 = 0.1$, $\tau_1 = 20$, $\tau_2 = 10$ as given in Table 1, and $N_{cap} = 5000$, $h = 100$ and $D = 1$. Then, straightforward calculation by (14) gives $R_0 = 18.18$, and (30) gives $c^* = 0.24$. For these parameter values, $H_1(\lambda, c)$ and $H_2(\lambda_2, c)$ are illustrated in Fig. 2.

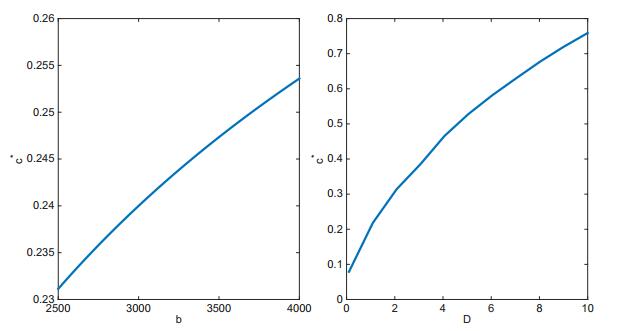
Based on (30), we may also numerically explore the dependence of $c^*$ on some model parameters. As examples, we present some results on its dependence on the production rate $b$ of ticks and the diffusion rate $D$ of white tailed deer in Fig. 3. Note that, if equation (29) is rewritten in terms of $\tilde{\lambda}$, where $c\lambda = \tilde{\lambda}$, it becomes evident that what matters is the value of $D/c^2$ and therefore that $c^*$ scales with $\sqrt{D}$. The numerically computed relationship between $c^*$ and $D$, shown in the second panel of Fig. 3, is very consistent with this observation. It highlights the need for the experimental determination of the value of $D$, the diffusion coefficient of the deer, because once we know $D$, and the proportionality constant in the relationship between $c^*$ and $\sqrt{D}$, we also know the spread rate $c^*$ that our model predicts. Diffusion coefficients can in practice be estimated using recapture data or radio tracking.

From the above we have seen that, for $c<c^*$, (29) has no real positive root and hence (1) cannot have a traveling wave front with speed $c$ connecting $E_0$ and $E^+$. It is expected that $c^*$ is indeed the minimum wave speed in the sense that, for every $c>c^*$, system (1) has such a connecting traveling wave front with speed $c$. The proof of the existence of a traveling wave front with speed $c>c^*$ involves the construction of suitable upper and lower solutions to the wave profile equation (25). The argument is very lengthy and the details are subtle, and we leave it for a more mathematical paper (in preparation). In that paper, we will also prove that $c^*$ is not only the minimal wave speed but also the asymptotic rate of spread for (1) when $R_0>1$.

---

5. Numerical simulation

Although we defer to another paper the proof that $c^*$ is both the minimal wave speed and the speed of spread for (1) when $R_0>1$, we will in this section provide some numerical simulation results that support these claims. We start by numerically demonstrating the existence of traveling wave front solutions of system (1). For this purpose, we choose the baseline parameters as in Fig. 2. For these parameter values, $c^*$ is numerically computed as $c^* = 0.24$. We use a numerical method described in [12] which is summarized in the appendix. For convenience, we choose the same baseline parameters as in Fig. 2, giving $R_0 = 18.18,$ and the positive steady state

$(L^+, N^+, A_q^+, A_f^+) = (1.72\times 10^3, 1.43 \times 10^3, 1.43 \times 10^3, 60.63).$

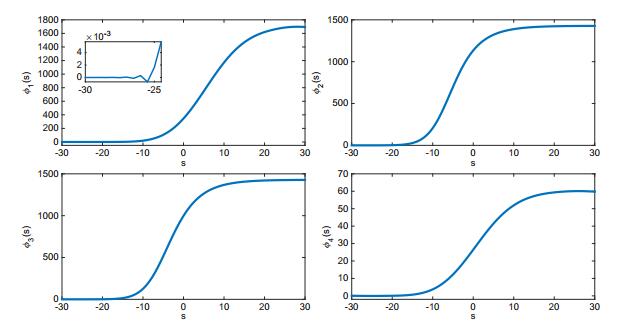
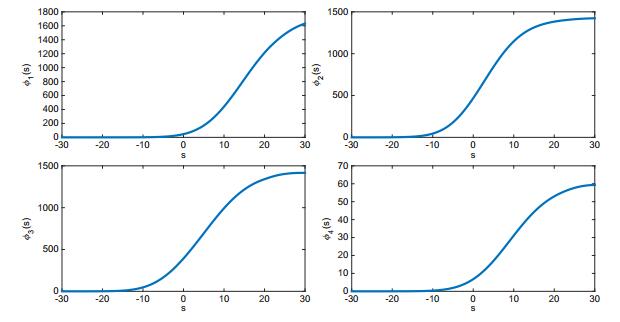
Fig. 4 shows that there is no traveling wave solution for $c = 0.1<c^*$, since $\phi_1, \phi_2, \phi_3$ may take negative values. Fig. 5 shows the existence and profile of a traveling wave front with $c = 0.4> c^*$.

Next, we numerically simulate solutions of the original initial value problem (1) to observe the time evolution of solutions toward a traveling wave front. To estimate the spreading rate, we use the same approach as was mentioned in [16]. The idea is to assume some threshold population density $\hat u$, below which we cannot numerically detect the presence of the population. By tracking the propagation of such a threshold density we can then estimate the spreading rate. In other words, if we denote by $\hat x$ the location where the population density reaches the threshold $\hat u$, then the asymptotic rate of spread is given by

$c = \lim\limits_{t\to \infty}\frac{d\hat x(t)}{dt}.$

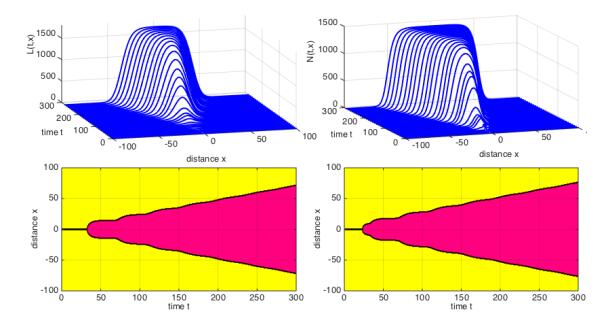
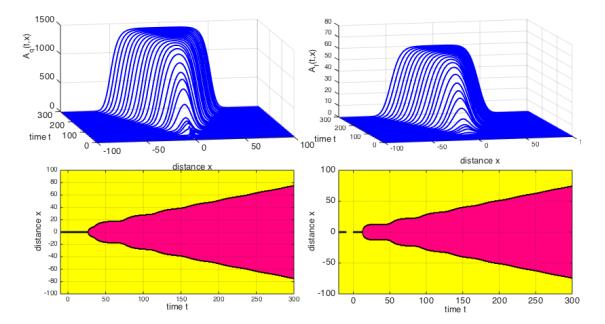
With the model parameter values given above, Fig. 6(a)-(b) and Fig. 7(a)-(b) show the evolution of the $(L, N)$ components and the $(A_q, A_f)$ components of the solution of (1). The shaded regions in Fig. 6(c)-(d) and Fig. 7(c)-(d) mark the regions in space where the population size is larger than $0.1$. The upper-lower boundaries of these areas are straight lines that have slope approximately equal to $\pm c^* = \pm 0.24$, coinciding with the minimal wave speed for the traveling wave fronts of (1) that connect $E^0$ and $E^+$ when $R_0>1$.

---

6. Conclusion and discussion

In this paper, based on the fact that blacklegged ticks are only capable of moving very short distances by themselves and the general belief that dispersal of ticks over appreciable distances is via transport on the white tailed deer on which the adult ticks feed, we developed a spatial differential equation model for a stage-structured tick population. In addition to well-posedness, we identified a basic reproduction ratio $R_0$ for the tick population and discussed the stability of the extinction steady state $E_0$ and the persistence steady state $E^+$ in terms of $R_0$.

We also discussed traveling wave front solutions to the model that connect $E_0$ and $E^+$. Such solutions describe tick invasion as a wave of transition from the extinction steady state to a persistence steady state of ticks. We obtained a lower bound $c^*$ for the speed of such propagating traveling wave fronts, in the sense that the model cannot have traveling fronts with speed $c<c^*$. We also performed some numerical simulations for the wave profile equation and the results suggest that $c^*$ is the minimal wave speed, meaning that for every $c>c^*$ there is a traveling wave front of speed $c$ connecting the extinction and persistence steady states $E_0$ and $E^+$.

We also numerically simulated the solutions of the original initial value problem (1). The results not only demonstrate the evolution of solutions toward a traveling wave front, but also suggest that $c^*$ is the asymptotic rate of spread of the tick population. Note that $c^*$ is determined by two algebraic equations that can be solved numerically, though not analytically. The dependence of $c^*$ on important model parameters can also be explored numerically. For example, since we are concerned with how the dispersion of white tailed deer affects the spatial spreading speed, we numerically explored the dependence of $c^*$ on the diffusion rate $D$, as shown in Fig. 3(b), by which one can immediately estimate $c^*$ as long as the diffusion rate $D$ is known. This clearly demonstrates the role played by deer dispersal. We point out that $c^*$ in this paper only accounts for the spread speed caused by the white-tailed deer diffusion; however, as is shown in Caraco et al [4], some smaller mammals, such as the white-footed mouse Peromyscus leucopus, can also play a role in the range expansion of the tick Ixodes scapularis. Therefore, even if the deer diffusion rate is available so that $c^*$ can actually be obtained, it may not give the actual range expansion speed of the tick. In order to obtain a better or more accurate estimate/prediction of geographical spread speed of the tick Ixodes scapularis, it would be natural to derive a model that combines the roles of mice and deer. Toward that goal, our model establishes a framework, and we leave it for a future research project.

Theoretically confirming that $c^*$ is not only the minimal wave speed but also the spreading rate of the model system is more challenging. In a forthcoming and more mathematical paper [11], by reformatting our model into the framework of [22] and applying some recent results for such a set-up, we achieve this goal.

In this paper, we have concentrated mainly on the case when the spatial domain is $\Omega = ( -\infty, \infty)$. In the real world, a two dimensional domain is clearly more realistic and there are a variety of realistic possibilities including both bounded and unbounded two-dimensional domains, and various boundary conditions. Both the domain itself and the boundary conditions affect the kernel $k(x, y)$ (see, e.g., [13] and the examples given in Section 2 of this paper) and result in a variety of systems giving rise to various mathematical and ecological issues of interest.

---

7. Appendix A: Numerical method

To solve the wave equations (25) with asymptotic boundary condition (26) numerically, we truncate ${\mathbb R} = (-\infty, \infty)$ to $[-M, M]$, where $M$ is a very large number, and take the uniform partition: $s_1 = -M$, $s_{2n+1} = M$, $s_j = s_1+(j-1)\triangle$, where $\triangle = 2M/2n = M/n$, $j = 1, 2, \ldots, 2n+1$. Then, for $s_j$ ($j = 2, \ldots, 2n$),

$\left\{ \begin{array}{l} c\varphi'_1(s_j) = br_4e^{-d_4\tau_1}\varphi_4(s_j-c\tau_1)-(d_1+r_1)\varphi_1(s_j), \\ c\varphi'_2(s_j) = r_1g(\varphi_1(s_j))-(d_2+r_2)\varphi_2(s_j), \\ c\varphi'_3(s_j) = r_2\varphi_2(s_j)-(d_3+r_3)\varphi_3(s_j), \\ c\varphi'_4(s_j) = \frac{r_3}{2}e^{-d_3\tau_2}\int_{-\infty}^{+\infty}k(s_j-y-c\tau_2)\varphi_3(y)\, dy-(d_4+r_4)\varphi_4(s_j). \end{array} \right.$

(31)

The asymptotic boundary conditions $\lim_{s\to-\infty}\varphi_i(s) = 0$ and $\lim_{s\to+\infty}\varphi_i(s) = \varphi^*_i$ are then translated to

$\varphi_i(-M) = 0, \:\: \varphi_i(M) = \varphi^*_i;\\ \varphi_i(s) = 0, \: s<-M; \:\: \varphi_i(s) = \varphi^*_i, \:\: s>M, \:\:i = 1, \ldots, 4.$

It then follows that

$\begin{array}{l} f_1(\varphi_3, s_j)&: = &\int_{-\infty}^{+\infty}k(y)\varphi_3(s_j-y-c\tau_2)\, dy \\ & = &\int_{-\infty}^{+\infty}k(s_j-y-c\tau_2)\varphi_3(y)\, dy \\ & = &\left(\int_{-\infty}^{-M}+\int_{-M}^{M}+\int_{M}^{+\infty}\right)k(s_j-y-c\tau_2)\varphi_3(y)\, dy \\ & = &\int_{-M}^{M}k(s_j-y-c\tau_2)\varphi_3(y)\, dy+\varphi_3(M)\int_{M}^{+\infty}k(s_j-y-c\tau_2)\, dy.\end{array}$

Applying the composite trapezium rule for integrals, we obtain

$\begin{split} &\int_{-M}^{M}k(s_j-y-c\tau_2)\varphi_3(y)\, dy = \frac{\triangle}{2} [\, \, k(s_j-s_1-c\tau_2)\varphi_3(s_1) \\ & +2\sum\limits_{l = 2}^{2n}k(s_j-s_l-c\tau_2)\varphi_3(s_l)+k(s_j-s_{2n+1}-c\tau_2)\varphi_3(s_{2n+1})\, \, ], \end{split}$

(32)

and

$\begin{array}{l} \int_{M}^{+\infty}k(s_j-y-c\tau_2)\, dy & = &\int_{-\infty}^{s_j-M-c\tau_2}k(y)\, dy \\ & = &\frac{1}{2}\left(1-\int_{s_j-M-c\tau_2}^{-s_j+M+c\tau_2}k(y)\, dy\right) \end{array}$

$\begin{array}{l} & = &\frac{1}{2}\left\{1-\frac{\triangle}{2}\left[k(s_j-M-c\tau_2)+k(-s_j+M+c\tau_2)\right.\right.\\ &&\left.\left.+2\sum\limits_{l = 2}^{2[2n+m_2-(j-1)]}k(s_j-M-c\tau_2+(l-1)\triangle)\right]\right\}.\end{array}$

Then

$f_1(\varphi_3, s_j) = \triangle\sum\limits_{l = 2}^{2n}k(s_j-s_l-c\tau_2)\varphi_3(s_l)+f_2(s_j)$

where

$\begin{array}{l} f_2(s_j)& = &\frac{\triangle}{2}[k(s_j-s_1-c\tau_2)\varphi_3(s_1)+k(s_j-s_{2n+1}-c\tau_2)\varphi_3(s_{2n+1})]\\ && +\varphi_3(M)\int_{M}^{+\infty}k(s_j-y-c\tau_2)\, dy \\ & = &\frac{\triangle}{2}k(s_j-M-c\tau_2)\varphi_3^* +\varphi_3^*\int_{M}^{+\infty}k(s_j-y-c\tau_2)\, dy \\ & = &\frac{\triangle}{2}k(s_j-M-c\tau_2)\varphi_3^* \\ &&+\frac{\varphi_3^*}{2}\left\{1-\frac{\triangle}{2}\left[k(s_j-M-c\tau_2)+k(-s_j+M+c\tau_2)\right]\right.\\ &&\left. -\triangle\sum\limits_{l = 2}^{2[2n+m_2-(j-1)]}k(s_j-M-c\tau_2+(l-1)\triangle)\right\}\\ & = &\frac{\varphi_3^*}{2}\left\{1-\triangle\sum\limits_{l = 2}^{2[2n+m_2-(j-1)]}k(s_j-M-c\tau_2+(l-1)\triangle)\right\}.\end{array}$

Let $m_1 = \frac{c\tau_1}{\triangle}$ and $m_2 = \frac{c\tau_2}{\triangle}$. Then $s_j-c\tau_1 = s_{j-m_1}$. Using conventional numerical differentiation, we see that

$\left\{ \begin{split} &c\, \frac{\varphi_1(s_{j+1})-\varphi_1(s_{j-1})}{2\triangle} = br_4e^{-d_4\tau_1}\varphi_4(s_{j-m_1})-(d_1+r_1)\varphi_1(s_{j}), \\ &c\, \frac{\varphi_2(s_{j+1})-\varphi_2(s_{j-1})}{2\triangle} = r_1g(\varphi_1(s_j))-(d_2+r_2)\varphi_2(s_j), \\ &c\, \frac{\varphi_3(s_{j+1})-\varphi_3(s_{j-1})}{2\triangle} = r_2\varphi_2(s_j)-(d_3+r_3)\varphi_3(s_j), \\ &c\, \frac{\varphi_4(s_{j+1})-\varphi_4(s_{j-1})}{2\triangle} = \frac{r_3}{2}e^{-d_3\tau_2}f_1(\varphi_3, s_j)-(d_4+r_4) \varphi_4(s_j), \end{split} \right.$

(33)

for $j = 2, \ldots, 2n$, or

$\left\{ \begin{split} &c\varphi_1(s_{j+1})-c\varphi_1(s_{j-1})-2\triangle br_4e^{-d_4\tau_1}\varphi_4(s_{j-m_1})+2\triangle(d_1+r_1)\varphi_1(s_j) = 0, \\ &c\varphi_2(s_{j+1})-c\varphi_2(s_{j-1})-2\triangle r_1g(\varphi_1(s_j))+2\triangle(d_2+r_2)\varphi_2(s_j) = 0, \\ &c\varphi_3(s_{j+1})-c\varphi_3(s_{j-1})-2\triangle r_2\varphi_2(s_j)+2\triangle(d_3+r_3)\varphi_3(s_j) = 0, \\ &c\varphi_4(s_{j+1})-c\varphi_4(s_{j-1})-\triangle r_3e^{-d_3\tau_2}f_1(\varphi_3, s_j)+2\triangle(d_4+r_4)\varphi_4(s_j) = 0 \\ \end{split} \right.$

(34)

for $j = 2, \ldots, 2n$. The second equation in (34) is equivalent to the following equation:

$c\varphi_2(s_{j+1})-c\varphi_2(s_{j-1})-\frac{2}{h}\triangle r_1N_{cap}\varphi_1(s_j)+2\triangle(d_2+r_2)\varphi_2(s_j)\\ +\frac{c}{h}\varphi_1(s_j)\varphi_2(s_{j+1})-\frac{c}{h}\varphi_1(s_j)\varphi_2(s_{j-1})+\frac{2}{h}\triangle(d_2+r_2)\varphi_1(s_j)\varphi_2(s_j) = 0.$

Thus, system (34) can be expressed as

$\left[\begin{array}{cccc} M_{11} &0 &0 &M_{14}\\ M_{21} &M_{22}&0 &0\\ 0 &M_{32}&M_{33}&0\\ 0&0&M_{43}&M_{44} \end{array}\right]\left[ \begin{array}{c} \varphi_1(s_2)\\ \vdots\\ \varphi_1(s_{2n})\\ \varphi_2(s_2)\\ \vdots\\ \varphi_2(s_{2n})\\ \varphi_3(s_2)\\ \vdots\\ \varphi_3(s_{2n})\\ \varphi_4(s_2)\\ \vdots\\ \varphi_4(s_{2n})\\ \end{array}\right]+\left[ \begin{array}{c} C_1\\ C_2\\ C_3\\ C_4\\ \end{array}\right] = 0,$

(35)

where

$\begin{split} & M_{ii} = \left[\begin{array}{ccccc} 2\triangle (d_i+r_i)& c&&&0 \\ -c &2\triangle (d_i+r_i)&c& & \\ && \ddots& &\\ & &-c&2\triangle (d_i+r_i)&c\\ 0&&&-c&2\triangle (d_i+r_i) \end{array}\right], \\ & i = 1, \ldots, 4, \end{split}$

$M_{14} = \left[\begin{array}{cccccc} 0&&&&& \\ \vdots&&&&& \\ 0&&&&& \\ -2\triangle b r_4 e^{-d_4\tau_1}&&&&&\\ & \ddots&&&& \\ & &-2\triangle b r_4 e^{-d_4\tau_1}& 0& \dots&0 \\ \end{array}\right],$

$M_{21} = \left[\begin{array}{ccc} -\frac{2}{h}\triangle r_1N_{cap}&&0 \\ &\ddots& \\ 0& &-\frac{2}{h}\triangle r_1N_{cap} \\ \end{array}\right],$

$M_{32} = \left[\begin{array}{ccc} -2\triangle r_2&&0 \\ &\ddots & \\ 0& &-2\triangle r_2 \\ \end{array}\right],$

$M_{43} = -r_3\triangle^2e^{-d_3\tau_2} \hat{M}_{43}$ with

$\hat{M}_{43} = \left[\begin{array}{cccc} k(s_2-s_2-c\tau_2)& k(s_2-s_3-c\tau_2)& \dots& k(s_2-s_{2n}-c\tau_2) \\ k(s_3-s_2-c\tau_2)& k(s_3-s_3-c\tau_2)& \dots& k(s_3-s_{2n}-c\tau_2) \\ \vdots&&& \\ k(s_{2n}-s_2-c\tau_2)& k(s_{2n}-s_3-c\tau_2)& \dots& k(s_{2n}-s_{2n}-c\tau_2) \\\end{array}\right],$

$C_1 = \left[ \begin{array}{c} 0\\ \vdots\\ 0\\ c\varphi^*_1 \end{array}\right], C_3 = \left[ \begin{array}{c} 0\\ \vdots\\ 0\\ c\varphi^*_3 \end{array}\right], C_4 = \left[ \begin{array}{c} -\triangle r_3 e^{-d_3\tau_2}f_2(s_2)\\ -\triangle r_3 e^{-d_3\tau_2}f_2(s_3)\\ \vdots\\ c\varphi^*_4-\triangle r_3 e^{-d_3\tau_2}f_2(s_{2n})\\ \end{array}\right],$

$C_2 = \left[ \begin{array}{c} \frac{1}{h}\varphi_1(s_2)[c\varphi_2(s_3)+2\triangle (d_2+r_2)\varphi_2(s_2)]\\ \frac{1}{h}\varphi_1(s_3)[c\varphi_2(s_4)-c\varphi_2(s_2)+2\triangle (d_2+r_2)\varphi_2(s_3)]\\ \vdots\\ \frac{1}{h}\varphi_1(s_{2n-1})[c\varphi_2(s_{2n})-c\varphi_2(s_{2n-2})+2\triangle (d_2+r_2)\varphi_2(s_{2n-1})]\\ c\varphi^*_2+\frac{1}{h}\varphi_1(s_{2n})[c\varphi_2^*-c\varphi_2(s_{2n-1})+2\triangle (d_2+r_2)\varphi_2(s_{2n})]\\ \end{array}\right].$

The algebraic system (35) can then be solved numerically using Matlab.

---

Acknowledgments.

This work was initiated at the Current Topics Workshop: Spatial-Temporal Dynamics in Disease Ecology and Epidemiology, held at the Mathematical Biosciences Institute (MBI) at Ohio State University during October 10-14,2011. The workshop was organized by R. Liu, J. Tsao, J. Wu and X. Zou, and was funded by the NSF through the MBI. We thank Dr. G. Hickling for bringing this problem to a group discussion which stimulated this research project. We also thank those participants at the workshop who offered helpful suggestions and advice on the model, and particularly Drs. Hickling and Tsao for their valuable input during the discussions at the MBI and for providing some valuable references.

---