Self-organizing map based differential evolution with dynamic selection strategy for multimodal optimization problems

1.   Introduction

Multimodal optimization problems (MMOPs), which require to find all optimal solutions simultaneously, have been investigated in recent years ^[1]. In the real world, many engineering problems have more than one solution, such as structural damage detection ^[2], varied-line-spacing holographic grating design problem ^[3], protein structure prediction ^[4], and job shop scheduling problem ^[5]. Therefore, traditional algorithms which deal with single-solution optimization problems no longer meet the practical needs, and the new effective multi-solution optimization algorithms need to be designed to solve an increasing number of complex multi-solution problems. However, how to balance the diversity and convergence of population is still a challenge when dealing with MMOPs.

Evolutionary algorithms (EAs) have been an effective method for dealing with single-solution optimization problems for a long time, such as genetic algorithm (GA) ^[6], differential evolution (DE) ^[7,8,9], and particle swarm optimization (PSO) ^{[10,11,12,13]}. When EAs are used to solve single-solution optimization problems, all individuals within the population evolve towards the only one global optimum. While in MMOPs, there are multiple global optima to be found, and traditional EA methods cannot solve MMOPs effectively. Therefore, many scholars have adopted the improved EAs to solve MMOPs recently, such as the crowding clustering GA ^[14] that employs standard crowding strategy to eliminate genetic drift, the distance-based PSO ^[15] that eliminate the need to specify any niching parameter and the dual-strategy DE ^[16] that balance exploration and exploitation in generating offspring.

Although many efforts have been put into solving MMOPs, there are still some limitations when dealing with MMOPs. Firstly, how to divide the population to form effective niches is a challenge. Secondly, niches created by some techniques cannot cover all the possible regions of global optima, making it impossible to find out all optima. Thirdly, how to balance exploration and exploitation remains a challenge.

Therefore, this paper utilizes a self-organizing map (SOM) based niching method to deal with MMOPs. SOM has been a classic and useful tool in machine learning area for a long time ^[17,18], which can map high dimensional input data onto 2-dimensional plane while preserving the topology relations among input data. The potential of SOM in solving MMOPs is yet to be fully explored.

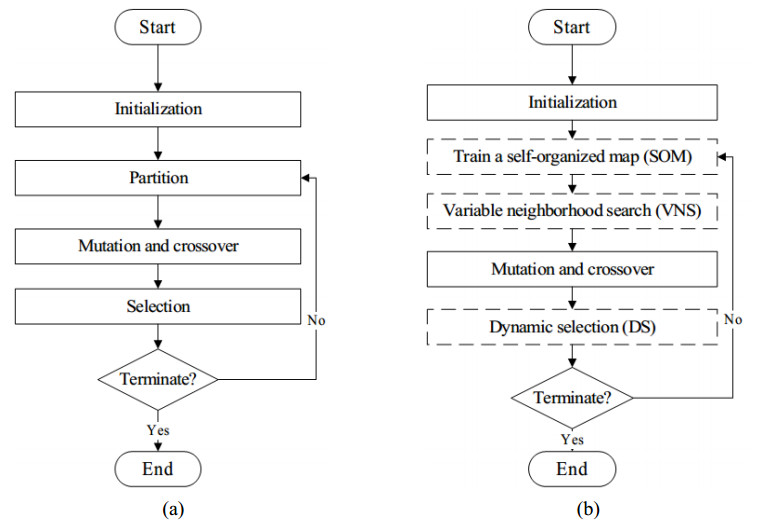
Consequently, we propose a SOM based DE with dynamic selection (DS) strategy (SOMDE-DS) to solve MMOPs more effectively. The framework of proposed SOMDE-DS and the differences between a standard DE and SOMDE-DS in solving MMOPs are shown in Figure 1. The advantages of our SOMDE-DS are listed as follows.

1) A SOM based niching method is proposed to divide the population reasonably by using similarity information among individuals. Specifically, the individuals with high similarities map to the same neuron and form a cohesive niche.

2) A variable neighborhood search (VNS) strategy is introduced to expand the search space. For some niches that are too small to find global optima, the VNS is carried out to expand the sizes and further to locate more global optima. In this way, small-sized niches are enriched and thus can find more optima that locate outside of the original niches.

3) A DS strategy based on the different evolution phases is proposed to balance the exploration and exploitation ability of population. Combining local selection and global selection strategy, DS strategy can explore more optima in the early evolution stage while maintain and refine found optima in the later evolution stage.

The rest of this paper is organized as follows. In Section 2, the process of DE and SOM is introduced as background knowledge for SOMDE-DS. Then SOMDE-DS is detailed in Section 3. Following are thorough experiments in Section 4 to verify the ability of SOMDE-DS to solve MMOPs effectively. Finally, the conclusions are given in Section 5.

2.   Materials and methods

2.1.   DE and SOM

2.1.1.   DE

DE, which is Proposed by R. Storn and K. V. Price in 1995 ^[19], is a powerful tool for global optimization over continuous spaces. In recent years, DE has been an attractive optimization tool for lots of researchers and the reasons are obvious ^[7]. Comparing with other EAs, DE has the advantages of simplicity, better performance and fewer control parameters ^[20]. These are also the reasons why we choose DE to make improvements on solving MMOPs.

1) Simplicity. A traditional DE consists of four steps, which are initialization, mutation, crossover and selection. Comparing with other EAs (e.g., genetic programming), DE is more straightforward and easier to implement, which makes it easier for researchers in other fields to make good use of it.

2) Better performance. At the first international contest on evolutionary optimization held in Nagoya, Japan in 1996, DE ranks third among all optimization algorithms and first in all EAs ^[21]. In the following CEC competitions, DE still ranks high among all EAs. From CEC 2014 to CEC 2016, DE variants take the first place in a continuous three years ^[22,23,24]. In CEC 2017 and CEC 2018, the best DE variants still hold the third and the second place ^[25,26].

3) Fewer control parameters. In classic DE, there are only three parameters, that is, probability of crossover, scaling factor and population size. The way these parameters work and contribute to the result has been deeply studied in recent research ^[27]. It is easy for us to fine-tune these parameters to get better performance.

A classical DE algorithm can be divided into four steps: initialization, mutation, crossover, and selection. The framework of the original DE is shown in Algorithm 1.

1) Initialization. Randomly initialize individual x_{i, G}, where i = 1, …, NP. NP represents the size of population and G means the number of current generations.

2) Mutation. Mutated individual v_i is generated by

where F is scaling factor and three different individuals chosen to mutate are represented by x_{r1, G}, x_{r2, G} and x_{r3, G}.

3) Crossover. Trial vector u_{ij, G+1} is generated according to the following formula

where pc is probability of crossover.

4) Selection. To select a better individual, u_{ij, G+1} is compared with x_{i, G}. If f(u_{ij, G+1}) is better than f(x_{i, G}), u_{ij, G+1} is inherited to next generation; otherwise x_{i, G} is retained.

2.1.2.   SOM

SOM, introduced by T. Kohonen in 1982, is a data-analysis method that visualizes similarity relations in a set of data items ^[17,18]. As a nonlinear projection tool, SOM can map data vectors with high dimensionality onto a 2-dimensional plane, preserving the topological relationship of the original vectors. In a trained SOM model, vectors with high similarity will be mapped to the same neuron ^[28]. In this paper, we take the advantages of SOM and use it as a clustering technique. Comparing with other unsupervised data-analysis methods like K-means clustering ^[29], the trained models of SOM are capable of capturing topologic relations that are the same as the source data and therefore clusters formed by SOM are more cohesive. The working mechanism of SOM is detailed in Algorithm 2 and the layout of SOM is illustrated in Figure 2. There are two layers in a standard SOM model, that are the competition layer and the input layer. Input vectors from input layer will be mapped to the neurons in the competition layer, according to the similarity between input vectors and the neurons, which can be measured in the form of some kind of distance (i.e., Euclidean distance). Therefore, input vectors with high similarities will be mapped to the same neuron and cohesive clusters are formed.

2.1.3.   SOM in solving continuous optimization problems

Works have been done with SOM to solve continuous optimization problems. On the basis of PSO with elite learning strategy, Jing et al. combined it with SOM to tackle multimodal multi-objective problems. In reference ^[30], Qu et al. firstly employed speciation to solve multimodal multi-objective problems, where a self-organized mechanism is proposed to improve the performance of the speciation. Hu et al. ^[31] adopted SOM to build a good neighborhood relation for the improved pigeon-inspired optimization in order to better solve multimodal multi-objective optimization problems. Zhang et al. ^[32] used SOM to establish the neighborhood relationship among current solutions to control the generation of a new solution. A. Kashtiban and S. Khanmohammadi ^[33] use SOM based method to detect the number of niches, within which a simple GA is independently converging to the actual optima. In conclusion, SOM plays an important role in forming the neighborhood relationship. In this paper, SOM is used as the same way.

2.2.   Related works on MMOP

In opposed to single-solution optimization problems ^[34], which have only one global optimum, MMOPs have multiple optimal solutions. In recent years, EAs have attracted a lot of attention in the field of solving MMOPs. However, in the beginning, EAs are designed for solving optimization problem with only one global optimum. Hence various modifications have been made to traditional EAs to enable them to handle MMOPs effectively. In general, there are three main methods that enable EAs to better solve MMOPs, including the niching-based methods, the novel evolution operator-based methods and the multiobjectivization-based methods.

1) Niching-based methods

The idea of niching technique is to discover and maintain multiple subpopulations at the same time to ensure population diversity. When population diversity is ensured, finding and maintaining multiple solutions at the same time is possible.

Lots of work have been done in incorporating EAs with niching techniques to better solve MMOPs. Yang et al. ^[35] took the difference among niches into consideration and develop an adaptive multimodal continuous ant colony optimization algorithm. A. Hackl et al. ^[36] used only clusters of fireflies which gather around promising local solutions to find better solutions. Two of the most well-known DE variants that incorporated niching technique are crowding DE (CDE) ^[37] and species-based DE (SDE) ^[38]. Combining the idea of neighborhood, Qu et al. ^[39] proposed neighborhood based CDE (NCDE) and neighborhood based SDE (NSDE). Li et al. ^[40] combined PSO and ring topology to propose r2PSO and r3PSO, which achieved the target of niching without niching parameters. Wei et al. ^[41] proposed a penalty-based DE, in which the neighboring solutions of elite solutions are penalized. Lin et al. ^[42] divide the population into multiple species by nearest-better clustering. Based on the affinity propagation clustering, Wang et al. ^[43] develop an automatic niching DE with contour prediction. Xu et al. ^[44] use detect-multimodal method to estimate the radius and use the estimated radius to divide the population into species. Liang et al. ^[45] combined a clustering-based special crowding distance method and a distance-based elite selection mechanism to enable DE to better solve multimodal multiobjective optimization problems. On the basis of affinity propagation clustering, Hu et al. ^[46] added a novel mutation and adaptive local search strategy to propose a niching backtracking search algorithm for solving multimodal multiobjective optimization problems.

In conclusion, the core of niching-based method is niching technique. Lots of works have been done in integrating EAs with a novel niching technique, and then novel local search strategies are added to improve the performance in solving MMOPs.

2) Novel evolution operator-based methods

The novel evolution operator-based methods usually modify evolution operators to make EAs better solve MMOPs. Qu et al. ^[15] proposed a local search operator to enhance the search ability and convergence of PSO. Epitropakis et al. ^[47] develop two new mutation strategies that incorporated spatial information of possible solution without introducing any extra parameter. Besides, a novel reinitialization mechanism was also proposed by Epitropakis et al. ^[48] to investigate unexplored regions of search space while maintain the best found solutions. Wang ^[49] employed adaptive parameter control and example-based learning to enhance the performance of PSO in solving MMOPs. Liu et al. ^[50] use the dynamic regulation to improve local search ability effectively.

To sum up, novel evolution operator-based methods focus on the modification on the evolutionary operations. Most of existing works are done in initialization, mutation and crossover to enhance the search ability of EAs in order to locate more optima at the same time.

3) Multiobjectivization-based methods

The idea of the multiobjectivization-based methods is to transform the MMOPs into the multiobjective optimization problems (MOPs). Then multi-objective optimization evolutionary algorithms (MOEAs) can be used to solve the transformed problem and multiple global optima of the original MMOPs can be obtained. Cheng et al. ^[51] transformed MMOPs into MOPs to approximate the fitness landscape of the original problem, and then a peak detection method was used to obtain precise locations of global optima. Wang et al. ^[52] transformed MMOPs into MOPs with two conflicting objectives. Therefore, an MOEA is used to find the Pareto set of the MOP, and multiple optimal solutions of the MMOP can be located at the same time. Yu et al. ^[53] transformed MMOPs into MOPs with triple objectives, two of which conflict with each other and the extra objective can be used to improve the diversity of the population greatly. In reference ^[54], V. Steinhoff et al. proposed a single-objective multi-objective gradient sliding algorithm (SOMOGSA) to solve single-objective optimization problems using multi-objective approach. In reference ^[55], P. Aspar et al. examined the inner mechanisms of SOMOGSA to prove that single-objective optimization problems can be solved effectively by using multiobjectivization and the potential of multiobjectivization is huge. In reference ^[56], C. Grimme et al. studied the challenges and researched the potentials of solving continuous multimodal multi-objective optimization.

Comparing with niching-based methods and novel evolution operator-based method, multiobjectivation-based methods are relatively new. The main focus of these methods is constructing extra objectives to make good use of the advantages of multiobjective optimization. Some works have been done in the mechanism of multiobjectivization, but the inner mechanism and the potential of multiobjectivizaiton are still to be fully discovered.

2.3.   SOMDE-DS

In this section, the main framework of SOMDE-DS is firstly given. Secondly, the SOM-based niching strategy is introduced. Then, the VNS strategy and DS strategy are detailed, respectively.

2.3.1.   Main framework

The framework of SOMDE-DS is given in Algorithm 3. Firstly, randomly initialize the population with size NP and set the number of current generations fe to 0. Secondly, we use the whole population of current generation to train a SOM and use it to divide the population into several niches. Then the VNS strategy is applied to enrich the small-sized niches and niches with overlap are obtained. Following is mutation and crossover operation. Finally, the DS strategy is used to update current population.

2.3.2.   SOM for niching

Due to the fact that SOM can capture the original topologic information of the source data, SOM is used for niching in SOMDE-DS. The working mechanism of SOM is detailed in Algorithm 2. In the first step, we randomly initialize the SOM with small weight vectors to minimize the influence of initial weight vectors. Then we train a SOM with all individuals in current population. Every time an individual is put into the SOM, the corresponding winning weight vector and its neighboring weight vectors are calculated. Then all neighboring weight vectors, as well as the winning weight vector itself are updated. Figure 3 shows that after training, the model of SOM matched the distribution of the current population, and therefore a better clustering result can be obtained.

2.3.3.   VNS

In the original DE, mutation operation is carried out within the whole population. Offspring generated in this manner may differ greatly from its parent. In solving single-solution optimization problems, this mutation strategy can fully explore the search space. However, this global mutation strategy cannot achieve satisfactory results when dealing with MMOPs since there are multiple optimal regions in the whole search space. By using this kind of mutation strategy, it is easily to cause the whole population to converge to only one optimal solution, which contradicts the goal of MMOPs. Thus, niching technique is integrated with DE to make it better solve MMOPs.

By using the trained SOM, the whole population can be divided into several niches. However, there is a situation where the number of individuals of a specific niche is too small to find global optima. To improve this situation, we designed a VNS strategy to locate more optimal regions. Figure 4 shows that with VNS strategy, small niches are enlarged and thus are enabled to locate more optimal regions. The process for enlarging niches is described as follows. Firstly, all individuals which map to the same neuron form a niche. Secondly, if the number of individuals within the niche is below a certain number M, individuals from nearest neighboring niche are merged into the niche one by one until the size of the niche reaches M. M represents the minimal number of individuals within a single niche. When the number is too small, it may cause the loss of diversity of population, while when the number is too big, it may cost more computational resources without improving the results obviously. This process of VNS is detailed in Algorithm 4

2.3.4.   DS

In the original DE, the produced offspring only competes with its parent. In this way, a better individual may be reserved but the opportunity to simultaneously eliminate a worse individual is lost. To improve this situation, a crowding based selection strategy is introduced in CDE ^[37], where every produced offspring competes with its nearest individual in the population. The crowding operation can be carried out within a single niche or the whole population. The former is called local selection while the latter is global selection.

Local selection strategy with niching technique benefits for exploring new optima. In comparison, global selection strategy is good at maintain and refine found optima. To make good use of these two strategies, we combine local selection and global selection to get a DS strategy, adapting to the different stages of evolution. The idea of this strategy is to use local selection to explore new optima in the early evolution stage and to use global selection to maintain and refine found optima in the later stages. In practice, we set two thresholds, one is of maximum number of function evaluations fe_t and the other is of probability p_l. When the threshold of maximum number of function evaluations fe_t is exceeded, only global selection strategy is used to maintain and refine found optima.

When the number of current function evaluations is below the threshold, a random number p_i between [0, 1] is generated to balance diversity and convergence. If p_i is below the threshold of probability p_l, local selection strategy is used to improve the convergence of population, otherwise, global selection strategy is used to maintain and refine best individuals.

Both fe_t and p_l work together to balance diversity and convergence of the population. The best setting of these two parameters for each function differs from each other. When fe_t and p_l are too big, the algorithm cannot get a stable result. When they are too small, the algorithm may not converge well. With our preliminary tests, SOMDE-DS performs well when fe_t is 0.9 and p_l is 0.6. The DS strategy is detailed in Algorithm 5.

3.   Results

This section is the experimental part, which mainly focuses on three contents. Firstly, SOMDE-DS and classic MMOP optimization algorithms are compared to verify its feasibility of solving MMOPs effectively. Secondly, we compared the situation of different mutation strategies and selection strategies in SOMDE-DS. Finally, the influence of different parameters on SOM is studied.

3.1.   Benchmark functions and compared algorithms

CEC'2013 ^[57], a widely used benchmark function set for IEEE CEC'2013 special session and competition on niching methods for multimodal function optimization. This function set consists of 20 multimodal test functions, dimensions of which range from 1 to 20. With widely used simple functions and complex composite functions included, CEC'2013 is regarded as a suitable benchmark for evaluation in solving MMOPs.

To examine the ability of SOMDE-DS to solve MMOPs, we choose six well-known EAs with niching techniques to compete with SOMDE-DS, that are NCDE, NSDE, CDE, SDE, r2PSO and r3PSO. Among these six compared algorithms. CDE and SDE are DEs with two most well-known niching techniques. NCDE and NSDE is the development of classic CDE and SDE with the concept of neighborhood mutation. r2PSO and r3PSO are two well-known PSO algorithms with no extra niching parameters using ring topology. The performance of NCDE, NSDE, r2PSO and r3PSO in solving MMOPs are outstanding. Thus, competition with other six well-known multimodal algorithms should prove the superiority of SOM in niching and the ability of SOMDE-DS to better solve MMOPs.

3.2.   Performance metrics

To measure the performance of SOMDE-DS and other multimodal optimization algorithms, two commonly used criteria peak ratio and success rate ^[58] are calculated by the results of 40 independent runs on each function.

3.1.1.   Peak ratio

Peak ratio (PR) is the ratio of average peaks detected out of all peaks in the given function by an algorithm. It can be calculated as Eq (3):

where N is the number of runs for each test function, peaks_found_i is the number of global optima found in the i^th run and no_peak is the number of global optima of the current test function.

3.1.2.   Success rate

Success rate (SR) is the rate of successfully detecting all desired optima out of 11 runs for each function. It can be calculated as Eq (4):

where count_i denotes whether all global optima are found in this run or not. When all global optima are found, count_i is 1 otherwise 0.

PR measures the ability to find the global optima of an algorithm while SR represents the ability to find all global optima in a single run. To further illustrate the differences among tested algorithms, convergence is also telegraphed in several selected functions.

3.1.3.   Parameter settings

The parameter settings of SOMDE-DS are as follows, probability of crossover pc as 0.5, scaling factor as 0.9, minimum size of niche M as 10, the threshold of number of function evaluations fe_t as $0.9 \times MaxFEs$, the threshold of probability p_l as 0.6. The influences of these parameters are discussed in the experiment part.

The parameter settings for other tested EAs are as follows. In CDE, scaling factor is 0.5, probability of crossover is 0.9 and crowding factor is 100. In SDE, the species radius is set to 0.5 for each benchmark function. The neighborhood size of NCDE and NSDE is set to 20. In r2PSO and r3PSO, φ is 4.1 and χ is 0.7298. The settings for CEC'2013 benchmark can be referred in ^[57]. All tested algorithms run 40 times independently for each function on the benchmark CEC'2013.

3.2.   The compared results between SOMDE-DS and other tested multimodal optimization algorithms

Table 1 shows the results of SOMDE-DS and other widely used multimodal algorithms in solving MMOPs, where the best PR value of each function are emphasized in boldface. Besides, Mann-Whitney U test is carried out between SOMDE-DS and every other EA with a confidence interval of 95%. There are three different results in the test represented by three different symbols, that is "≈", "+" and "−" respectively. "≈" means that the performance of SOMDE-DS on this function is similar to corresponding algorithm. "+" means that SOMDE-DS performs significantly better than corresponding algorithm, while "−" means that SOMDE-DS performs significantly to corresponding algorithm. From Table 1, it is clear that SOMDE-DS achieves the best results on most functions except for F7, F9 and F19. Among all multimodal algorithms, SOMDE-DS gets first place for 17 times in total, which is the best among all tested algorithms. Besides that, the results of the Mann-Whitney U test also show that SOMDE-DS performs better than every other algorithm in the manner of statistics.

It can be clearly seen from Figure 5 that the SOMDE-DS performs better than other methods in comparison in selected four functions (i.e., F2, F9, F11 and F18). Specifically, SOMDE-DS converges faster and finds more optima in any situation.

In addition, to better illustrate the convergence of SOMDE-DS, the fitness landscape and distribution of all individuals under three different situations are listed. Specifically, four different functions (i.e., F3, F7, F10 and F11) are shown in Figures 6–9 respectively and each of them includes the results of initialization, the results after several generations of evolution and the final results. F3 is a simple 2D function with only 1 global optimum and 4 local optima. In addition to locating the only 1 global optimum, SOMDE-DS also locates the 4 local optima, which proves its superiority in niching. Both F7 and F10 are widely used benchmark functions with multiple global optima. The number of global optima of F7 is 18, and that of F10 is 12. From Figures 7 and 8, it can be observed that in the early stage of evolutions, niches are formed around every global optimum. At the end of evolutions, every global optimum of both two functions is located. F11 is a complex composite function with 6 global optima. It can be seen from Figure 9 that, SOMDE-DS is still able to most optima of F11.

4.   Discussion

4.1.   Parameter analysis

There are three key parameters in SOMDE-DS, that is M for the minimal size of niches, fe_t for the threshold of max function evaluations and p_l for the bound between global selection and local selection. In order to find out the influence of these three parameters, we conduct three comparison experiments.

4.1.1.   The study of M

From Table 2, when M is set to 10, SOMDE-DS gets the best performance. It can be seen that, the change of minimal size of niche M does not change the results significantly, and therefore, it is safe to say that, SOMDE-DS is not sensitive to the parameter M.

4.1.2.   The study of p_l and fe_t

p_l is an important parameter in DS strategy and the compared results among different values of p_l is shown in Table 3. When the value of p_l is too high, DS strategy prefers global selection and when the value is too low, local selection is preferred. The unbalance between global selection and local selection lead to worse results. The experiment results show that 0.6 may be a proper value for p_l.

fe_t is another important parameter in DS strategy and the compared results among different values of fe_t are shown in Table 4. When the value of fe_t is too low, local selection is inhibited, and thus the convergence of population is also suppressed. The results of other three values of fe_t are similar and this can be credited to the fast convergence of SOMDE-DS.

In conclusion, p_l should be a proper medium value between [0, 1] and fe_t should be a medium or higher value. The value of both p_l and fe_t are involved in the exploration and exploitation of the proposed algorithm, and different values do make a difference to the results.

4.2.   Component analysis

To investigate the influence of DE operators, we studied 3 mutation strategies and 2 selection strategies in addition to the original one. There is only one difference between each variant and our original method, either mutation or selection.

4.2.1.   Mutation

It can be seen from Table 5, that the local best individual guided mutation variant and global best individual guided mutation variant do not perform well. When the global best mutation strategy is used, the direction of mutation is dominated by the global best individual in the whole population, eliminating the role of clustering. Consequently, this variant degrades to a global best individual guided DE and it is no wonder that this variant does not perform well. The defect of the local best individual guided mutation variant is similar to that of the global one. Guided by the best individual in the niche, every other individual int the same niche is likely to converge to the same optima, leading to poor performance.

Although the performance of the current mutation variant is not as good as the original one, it does perform way better than the two best individual guided mutation variants. Comparing the results of the original method with that of the current mutation variant, it is easy to notice that the current mutation variant does extremely bad in F8. Every offspring produced using the current mutation strategy is similar to its parent, meaning that the ability to explore new space is pretty weak. Therefore, this variant performs extremely badly in a 3D function with a wide search space like F8. From the results, the original one is better. On balance, the original is more universal.

4.2.2.   Selection strategy

From Table 6, notice that the original method does not perform as well as the global selection variant in F7 and F9 but performs way better than the latter in F8. It is a tradeoff of combining local selection and global selection. Comparing the local selection variant and the global one, the former performs better than the latter in F8 while worse in F7 and F9. Although the local selection variant is good at locating multiple global optima, it's hard for it to maintain these global optima. There are up to 81 peaks in F8, meaning that there is more than one peak within a niche. Therefore, frequent selections in a small niche will lead to convergence to one peak, losing the diversity of the niche.

In conclusion, the local selection variant is good at locating multiple optima while global selection one is doing well in maintain found optima. Using DS strategy that combines local selection and global selection strategies, SOMDE-DS can explore new global optima as well as maintaining already found optima.

Through the analysis above, it can be considered that the original strategy, that is random mutation combined with DS strategy, provides the best performance.

4.3.   SOM analysis

In this part, we dive into the core of our algorithm, SOM. We investigate two core components of SOM to see their influence on results of our proposed SOMDE-DS, one is neighborhood function and the other is the size of SOM.

4.3.1.   Neighborhood function

Neighborhood function determines the rate of change of the neighborhood around the winner neuron ^[18]. A proper neighborhood function should be selected according to the dataset. We test four commonly used neighborhood functions to see how they work with our algorithm. The four functions are Gaussian, Mexican Hat, Triangle, and Bubble. The results are shown in Table 7.

From Table 7, it can be observed that the results of the four variants are similar, meaning that neighborhood functions do not have a visible impact on the final results. As mentioned above, the selection of the neighborhood function is dominated by the dataset. However, all of the input data used in our SOM is randomly generated and evolves on their own, meaning that there is probably no particular pattern among these data. If there is, it should be credited to the target function, which guides the evolution of data. Hence in most cases, there is no significant difference between every two variants. Besides that, there is a situation where a variant performs better than the others in some functions, for example, the Gaussian variant performs the best in F8. The reason is that the Gaussian neighborhood function is the most suitable for F8.

To draw a conclusion, there is no common pattern in the input data, hence the performance of the four variants is similar. Different neighborhood functions do not make great difference to the performance of SOMDE-DS.

4.3.2.   Size of SOM

Another component that might influence the results of SOMDE-DS is the size of SOM. We set the size of SOM as$\sqrt {5 \times \sqrt {NP} }$according to the widely accepted principle. In addition to the original size, we choose 3 different sizes for comparison, one is 3 by 3, one is$\sqrt {2 \times \sqrt {NP} }$by$\sqrt {2 \times \sqrt {NP} }$and the final one is$\sqrt {NP}$by$\sqrt {NP}$in ascending order. Most of the test functions in the benchmark CEC' 2013 have 6 or 8 global optima, and therefore 3 by 3 may be a suitable size to see whether a SOM with a size similar to the number of global optima would provide a better result. Likewise, we suggest that$\sqrt {NP}$by$\sqrt {NP}$is a suitable size to test whether a SOM with a size similar to the size of the population would provide a better result. And finally, we choose one more size between these two sizes, that is$\sqrt {2 \times \sqrt {NP} }$by$\sqrt {2 \times \sqrt {NP} }$for comparison.

As it can be observed from Table 8, there is no significant difference among all these variants in most functions. That is to say, regardless of the size, SOM is capable of capturing the similarities among the whole population in most cases.

Therefore, in most cases, neither neighborhood function nor the size of SOM does not have a significant effect on the performance. The former is caused by the randomness of the input data while the latter should be credited to the outstanding ability of SOM to capture the similarities in different sizes.

4.4.   Dielectric composite design problem

The objective of this problem is to design a dielectric composite with desired effective permittivity in the direction of the field applied ^[59]. Usually, the desire composite consists of two different materials, and therefore the effective permittivity can be calculated as Eq (5):

where${\varepsilon _1}$and${\varepsilon _2}$are the permittivity of the first and the second material, respectively.${\varepsilon _{com}}$ is the permittivity of the composite and g is the concentration of the first material. Assume that the desired permittivity of the composite is 1.5, the permittivity of the first material ranges from 10 to 30 and the concentration of the first material varies between 0.1 and 0.9 ^[59]. Then the problem can be written as a multimodal optimization problem with parameters ${\varepsilon _1}$ and g as in Eq (6):

SOMDE-DS is used to solve this problem and the evolution is shown in Figure 10.

At first, individuals are randomly generated. Then during the evolution, all individuals evolve towards their corresponding optima. It took a few iterations for almost all individuals to converge to global optima. It can be concluded that SOMDE-DS not only perform well in benchmark but also can solve practical engineering problems.

5.   Conclusions

In this paper, a novel SOM based MMOP algorithm SOMDE-DS is proposed. SOM is trained with the current population and then used to divide the population into several clusters. Then, these clusters are further aggregated to form more reasonable and overlapping niches by proposed VNS. After the formation of these niches, the offspring are generated by the mutation and crossover operations. Finally, the proposed DS strategy can effectively select promising individuals into next generation.

In conclusion, the SOM and VNS strategy ensure the similarity between individuals within the same niches and increase the possibility to locate more global optima. DS strategy effectively balance the ability of locating new optima and maintaining the found optima. Compared with several wildly used multimodal algorithms, SOMDE-DS can achieve satisfying results. Besides, the experimental results in solving a real-world application (i.e., dielectric composite design problem) also illustrate the effectiveness of our algorithm.

Although the proposed SOMDE-DS algorithm performs well in solving MMOPs, there are still some limitations in this study. For example, the sensitivity study is done separately without considering the interaction effect between the different algorithm parameters. Therefore, further researches should fully figure out the interactive mechanisms of the different algorithm parameters.

Acknowledgments

This work is suppored by Guangdong Basic and Applied Basic Research Foundation (2021A151511073) and suppored by the Fundametal Research Funds for the Central Universities, JLU: 93K172021K17.

Conflict of interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work, there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled.